Next Article in Journal
Effect of Mixing Light-Burned MgO with Different Activity on the Expansion of Cement Paste
Next Article in Special Issue
Fermi Surface Structure and Isotropic Stability of Fulde-Ferrell-Larkin-Ovchinnikov Phase in Layered Organic Superconductor β″-(BEDT-TTF)2SF5CH2CF2SO3
Previous Article in Journal
New Trends in Lithium Niobate: From Bulk to Nanocrystals
Previous Article in Special Issue
Real Space Quantum Cluster Formulation for the Typical Medium Theory of Anderson Localization
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 11
Issue 11
10.3390/cryst11111358
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The FFLO State in the Dimer Mott Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br

by
Shusaku Imajo
* and
Koichi Kindo
Institute for Solid State Physics, The University of Tokyo, Kashiwa 277-8581, Japan
*
Author to whom correspondence should be addressed.
Crystals 2021, 11(11), 1358; https://doi.org/10.3390/cryst11111358
Submission received: 25 October 2021 / Revised: 2 November 2021 / Accepted: 5 November 2021 / Published: 8 November 2021
(This article belongs to the Special Issue New Spin on Metal-Insulator Transitions)
Browse Figures
Versions Notes

Abstract

:
The superconducting phase diagram for a quasi-two-dimensional organic superconductor, κ-(BEDT-TTF)2Cu[N(CN)2]Br, was studied using pulsed magnetic field penetration depth measurements under rotating magnetic fields. At low temperatures, Hc2 was abruptly suppressed even by small tilts of the applied fields owing to the orbital pair-breaking effect. In magnetic fields parallel to the conducting plane, the temperature dependence of the upper critical field Hc2 exhibited an upturn and exceeded the Pauli limit field HP in the lower temperature region. Further analyses with the second derivative of the penetration depth showed an anomaly at 31–32 T, which roughly corresponded to HP. The origin of the anomaly should not be related to the orbital effect, but the paramagnetic effect, which is almost isotropic in organic salts, because it barely depends on the field angle. Based on these results, the observed anomaly is most likely due to the transition between the Bardeen-Cooper-Schrieffer (BCS) and the Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) states. Additionally, we discuss the phase diagram and physical parameters of the transition by comparing them with other FFLO candidates.

1. Introduction

Superconductivity is one of the most intriguing topics in material science, both in terms of basic research and applications. Superconductivity appears when electron pairs are formed and condense in metals. The BCS theory explains the conventional superconductivity that appears in a variety of simple metals and alloys. However, the details of unconventional superconductivity are yet to be elucidated. Unconventional superconductivity is commonly realized nearby metal–insulator transitions, where electron correlations are enhanced. Even in unconventional superconductivity, the electrons are paired by attraction, as suggested by the BCS theory; thus, the details of the pairing mechanism are one of the main topics for unconventional superconductivity studies. The FFLO state, which is one of the unconventional pairings, was proposed by Fulde and Ferrell [1] as well as Larkin and Ovchinnikov [2] in 1964. In the FFLO state, the electrons in a pair have unbalanced momenta, and their total center-of-mass momentum q is finite. The finite q, which modifies the superconducting order parameter with the additional term, exp(iqr) for the FF state [1] and cos(qr) for the LO state [2], induces the spatial modulation of the superconductivity. The superconducting region and the normal-state region appear alternately in real space because the normal state appears at the node positions where the additional term becomes zero. The FFLO state is regarded as an inhomogeneous state, which breaks the rotational symmetry [1,2,3,4,5]. At zero field, the uniform BCS-type pairing with q = 0 is more stable than the inhomogeneous FFLO state; however, when applying magnetic fields, the Zeeman effect causes the Fermi surface to split depending on the spin directions. Above the field where the Zeeman splitting is comparable with the condensation energy of the superconductivity, known as the Pauli limit HP [6], the BCS superconductivity is destroyed. This is known as the paramagnetic pair-breaking effect. However, the FFLO state can be favorable even above HP by pairing on the split Fermi surfaces owing to the finite q. Thus, the FFLO state can appear only at high fields above the HP. In higher magnetic fields, the FFLO state is also suppressed, and many theories [7,8,9] predict that the stability in magnetic fields is affected by various parameters. For example, in the case of isotropic three-dimensional superconductivity, the FFLO phase is very small in the H-T phase diagram [1,2]. Moreover, the difference between the FF state and LO state becomes larger in fields sufficiently higher than HP. It is expected that the superconducting symmetry and the strength of orbital pair-breaking effects also play an important role in the stability of the FFLO state. The investigation of Hc2 curve above HP is be important to discuss the details of the FFLO state.
To realize an FFLO state, two conditions need to be met: first, the electronic system should be in a clean limit, and second, the orbital pair-breaking effect should be sufficiently suppressed. The FFLO state hosts the spatial modulation in real space owing to the additional vector q, and impurities smear this modulated pattern with scattering. Therefore, a clean electronic system, in which the mean-free path l is sufficiently larger than the coherence length ξ‖, is typically required [4,10]. Some theories suggest that the FFLO state can survive even in some disordered systems [11,12]. For the orbital effect, the Maki parameter αM, 21/2Horb/HP, where Horb is the orbital limit, must exceed 1.8 [13,14], because the superconductivity gets destroyed at lower fields before the FFLO state appears if the orbital effect is strong. Basically, for the most superconductivity, the orbital effect is so strong that superconductivity does not survive up to HP. The orbital effect is suppressed when the vortices do not penetrate the superconductor, or the coherence length is sufficiently small, because it originates from the kinetic energy of the supercurrent around the vortices by the Lorentz force. Therefore, the FFLO state may be possible when a magnetic field is precisely applied parallel to the conduction plane of the low-dimensional superconductor, to prevent the magnetic flux from penetrating the superconducting plane, or in the case of heavy electron systems. [4,15,16].
The charge-transfer complex κ-(BEDT-TTF)2Cu[N(CN)2]Br (hereafter, abbreviated as κ-Br) is known as a high-Tc (~12 K) organic superconductor. This salt consists of the organic donor BEDT-TTF layer and the counter anion layer Cu[N(CN)2]Br, as shown in Figure 1. κ-Br has intensively been investigated because of its unconventional superconductivity and proximity to the Mott metal–insulator transition [17,18]. The superconductivity is presumably classified in the d-wave symmetry originating from antiferromagnetic spin fluctuations [17,18,19,20], which grow near the antiferromagnetic Mott insulator phase. The superconductivity has a large superconducting energy gap, leading to a large upper critical field Hc2. Due to the experimental difficulty in performing high-field measurements up to Hc2, the superconducting phase diagram in magnetic fields has not been clarified completely until our recent report [21]. The field-temperature superconducting phase diagram exhibited an upturn of Hc2 in a low-temperature and high-field region, which may exceed HP. Moreover, this can be scaled with that of κ-(BEDT-TTF)2Cu(NCS)2 (κ-NCS), which is one of the prime FFLO candidates [22,23,24,25]. Basically, the large effective mass and the electronically quasi-two-dimensionality, suppressing the orbital effect and enhancing the nesting of Fermi surfaces, are advantageous for stabilizing the FFLO state. Although this implies that κ-Br also hosts the FFLO state above HP, there have been no reports on the FFLO phase for κ-Br. Since the electronic structures in the other organic FFLO candidates found so far, such as λ-(BETS)2GaCl4 (λ-GaCl4), β″-(BEDT-TTF)2SF5CH2CF2SO3 (β″-SF5), and β”-(BEDT-TTF)4[(H3O)Ga(C2O4)3]PhNO2 (β″-GaPhNO2), are different in various aspects, it is necessary to consider several factors for discussing the parameters of the FFLO state. The comparison κ-Br with κ-NCS, which has a very similar electronic state, must be useful to discuss common points underlying the FFLO state. To detect the BCS-FFLO transition, a probe that can yield information even in the superconducting state is needed. As is found in a number of previous studies [23,26,27], the penetration depth is a very sensitive and high-resolution probe of the superconducting state even in short-time pulsed magnetic fields. Therefore, we performed penetration depth measurements to identify κ-Br as the FFLO candidate by detecting the phase boundary between the uniform superconductivity and the FFLO state. Additionally, compared with other FFLO candidates, universal features unique to the FFLO state are discussed.

2. Radiofrequency (rf) Penetration Depth Measurements

The single crystal measured in the present study was synthesized electrochemically. The out-of-plane electrical resistance of the sample we measured in this study has been reported in [21]. For the rf penetration depth measurements with a tunnel diode oscillator (TDO), the sample, whose dimension was approximately 0.5 mm × 0.5 mm × 0.1 mm, was placed in one of two circles of a 0.7 mm-diameter 8-shaped coil, which could cancel out the voltage induced by the field change of pulsed magnetic fields. The direction of the magnetic field was changed by rotating the sample stage. The TDO circuit was operated at F~82 MHz with LC oscillators, similar to the reported design [26,28]. In this setup, the skin depth of the normal state significantly exceeded the sample thickness, and therefore, the change in the frequency ΔF originated only from the penetration depth of the superconductivity. These measurements were performed in a 4He cryostat placed in a 60 T pulse magnet, installed at the International MegaGauss Science Laboratory, Institute for Solid State Physics, The University of Tokyo.

3. Results

3.1. Characterization of the Measured Sample

To evaluate whether the present sample was enough clean to host the FFLO state or not, we first estimated the mean-free path l from the quantum oscillations in resistivity, as shown in Figure 2a. The low-field behavior was related to the suppression of the superconductivity. The origin of the peak structure at approximately 10 T has been discussed in previous studies [29,30]. Above 40 T, the Shubnikov–de Haas oscillation was observed. The oscillation frequency was approximately 3900 T, which is consistent with the reported value [31]. Using the Lifshitz–Kosevich formula, the mean-free path l was obtained as ~130 nm, which was several times larger than the typical values 30–70 nm [31] and 20 times larger than the in-plane coherence length ξ||=6–7 nm [21,32]. This implies that the present sample was sufficiently clean to form a spatially modulated pattern of the FFLO state.
In Figure 2b, we present the field dependence of ΔF in the perpendicular fields. At 13 K, which is higher than the critical temperature Tc, the field dependence originated from the magnetoresistance of the Cu wires composing the coil. Below Tc, a large response of ΔF was observed at low fields owing to the emergence of superconductivity. The data above 15 T indicated that the magnetoresistance of Cu did not have a large temperature dependence in this temperature region. The difference in ΔF between 0 T and 20 T was directly related to the shift of the penetration depth of the superconductivity Δλ, as shown in the following equation:
[ΔF(0 T)−ΔF(20 T)]/F = xΔλ/r,
where r and x represent the effective sample radius and filling factor of the sample in the coil, respectively. The absolute value of the penetration depth λ(T) is given by the sum of the change and zero-temperature value, λ(T) = Δλ + λ(0). Because the superfluid density ρ(T) is determined by the relation ρ(T) = [λ(0)/λ(T)]2, the Rutgers equation [33],
16π2ΔCp(Tc)λ(0)=φ0TcdHc2′(Tc)ρ′(Tc),
leads to λ(0) = 0.6 ± 0.2 μm with the reported parameters, heat capacity jump ΔCp(Tc) = 0.6–0.7 J/Kmol [18,19,20,21] and the slope of Hc2 at Tc, μ0Hc2′(Tc)~−15 T/K [21,34]. Despite the large error, the value showed a good agreement with the reported values λ(0) = 0.5–0.7 μm [35,36,37]. The inset shows λ(T) with a fit to the d-wave case (blue dashed curve) [38]. Although a large error made the precise determination of the pairing symmetry difficult, the d-wave model was acceptable for the present data. This result indicated that ΔF reflects the change in penetration depth in the superconducting state.

3.2. Magnetic-Field Dependence of ΔF and d2(ΔF)/dH2 in Nearly Parallel Fields

In Figure 3a, we present the ΔF data at 1.4 K in fields almost parallel to the conducting plane (θ~0°), because the FFLO state occurs at lower temperatures when the orbital effect is sufficiently suppressed. At θ = 0°, the onset of the change in ΔF from the normal state was approximately 37 T, which was almost consistent with the reported value of Hc2 [21]. By tilting the angle from θ = 0°, Hc2 was suppressed. Figure 3b shows the second-field derivative of ΔF. The black lines represent the field-independent baseline of the normal state, and the black dotted curves are the eye guides. This plot further indicates that Hc2 was approximately 37 T at θ = 0°. Notably, these curves had some anomalies (green box and blue triangle) below Hc2, which were not clear in the ΔF data in Figure 3a. This behavior was similar to the results reported in earlier rf penetration depth studies for other organic FFLO candidates [23,26,27]. The anomaly at 31–32 T indicated by the blue triangles appeared to have a bare angle dependence, while the anomaly indicated by the green boxes showed the angle dependence. The angle dependence of the transition should not be significant in organics with weak spin-orbit coupling because the phase transition to the FFLO state is determined by the Zeeman effect; therefore, the anomaly indicated by the blue triangles at 31–32 T is considered to be the BCS-FFLO transition, namely HFFLO = 31–32 T. In fact, the angle-independent behavior was observed in other FFLO candidates [23,25,26,39,40].

3.3. Temperature Dependence of ΔF and d2(IF)/dH2 in Perfectly Parallel Fields (θ = 0°)

To discuss the stability of the FFLO state against temperature, in Figure 4, we present the field-dependent ΔF (a) and its second derivative (b) at θ = 0°. The symbols shown here are the same as those used in Figure 3b. The BCS–FFLO transition (blue triangle) was observed below 4.0 K and showed a slight temperature dependence, as shown by the blue dashed curve. The additional anomaly in the FFLO state (green box) was immediately smeared out with increasing temperature above 1.4 K. Considering the angle-dependent behavior and the observation at low temperatures, the anomaly indicated by the green box may be related to the vortex transitions in the FFLO state [40,41].

4. Discussion

In Figure 5a, we organized the obtained Hc2 and HFFLO in parallel fields as an H-T phase diagram. The Hc2 data reported in the previous study [21] were also plotted. The Hc2 obtained in this study (red circle) was consistent with the reported data (gray box). The blue triangles denote the fields in which a kink is observed in Figure 4b. From the initial slope of the Hc2 curve (solid line) near Tc, the orbital limit field Horb and the perpendicular coherence length ξ⊥ were estimated to be approximately 130 T, larger than Hc2, and 0.3 nm, five times smaller than the interlayer spacing 1.5 nm [31], respectively. These values indicate that the superconductivity was two-dimensional, and the orbital pair-breaking effect was quenched in parallel fields. To discuss the destruction of superconductivity, only the paramagnetic pair-breaking effect was considered. In a simple assumption based on the BCS theory, this effect gave the Pauli limit μ0HP = 1.76kBTc/(21/2μB)~1.84(Tc[K])[T] from the balance between the superconducting energy gap Δ0 = 1.76 kBTc and the Zeeman energy gμBH. However, this assumption often does not work for organic superconductors, because the superconductivity in organics is usually strong-coupling and has unconventional pairing symmetry [19,20,21]. In Agosta’s papers [16,23], to discuss the relation between HP and HFFLO more precisely, the following formula:
μ0HP = αkBTc/{21/2(g*/g)μB},
which includes the electron correlation and the coupling strength based on McKenzie’s paper [42], was employed. Notably, g* is the effective g-factor, including all many-body effects, and α is the coupling constant of the superconducting gap amplitude. The renormalized ratio g*/g is experimentally determined using quantum oscillation measurements. In addition, g*/g can be estimated by the ratio of the electronic heat capacity coefficient γ and the Pauli paramagnetism χP, because g*/g can be equal to Wilson’s ratio Rw [42]. For κ-Br, this relation led to μ0HP = 31–32 T, which corresponded to the present HFFLO. This coincidence indicates that the anomaly observed in this study was caused by the transition to the FFLO state. Moreover, the Maki parameter αM~5.7 was sufficiently larger than required. From the angle dependence of Hc2 shown in Figure 3, the FFLO state should exist only in the limited region near the parallel direction θ~0° because of the disappearance by the slight misalignment. This fragility to the orbital effect is also a characteristic of the FFLO state [14,43].
For comparison with other organic FFLO candidates, the H-T phase diagram in a parallel field was reduced by HP and Tc, as shown in Figure 5b. The Hc2 and HFFLO data for other salts are also shown [23,25,26,27,39,44,45]. The parameters, Tc, g*/g, and α, which were used for the estimation of HFFLO, are listed in Table 1. We used a typical value by referring to several references, because there is often some sample dependence in these parameters, and Tc depends on the measurement method and definition. Despite the large differences in their electronic states, such as the Fermi surface and dimensionality, these superconductors shared similar H/HP-T/Tc phase diagrams. In the κ-type dimer-Mott electronic phase diagram, κ-Br and κ-NCS were located near the Mott metal–insulator boundary [17,18], indicating strong electron correlations originating from the large onsite Coulomb repulsion with the growth of the antiferromagnetic fluctuations. This characteristic resulted in a relatively large g*/g and α of κ-Br and κ-NCS. Althoughλ-GaCl4 and β″-SF5 have significantly different Fermi surfaces [46,47], their parameters were almost identical and gave a similar HFFLO. For β″-GaPhNO2, the electronic state was expected to be near the charge-ordered phase on its electronic phase diagram and had a strong charge instability, which induced strong-coupling superconductivity α~2.5 [48]. Regardless of the variety in these electronic systems, the calculated HP coincided with HFFLO, as listed in Table 1. This fact demonstrated that the paramagnetic effect, which was the factor underlying HP, mainly governed the transition between the BCS and FFLO states, as predicted by a number of theories. Indeed, the dashed curve shown in the right axis in Figure 5b, which is the temperature dependence of the BCS-type superconducting gap, roughly describes the BCS region (light orange). Importantly, the paramagnetic pair-breaking was determined by the competition between the superconducting gap and the Zeeman effect. However, the Hc2 curves above HP indicated that there were small differences in the stability of the FFLO state at high fields. The theoretical curve for simple d-wave superconductivity (red dotted curve) [9] was qualitatively similar to the obtained phase diagram. Nevertheless, the data in Figure 5b were not accurate enough to discuss small differences with the simple model, and therefore, it would be necessary to discuss with an appropriate theoretical model for the electronic system of each material rather than the simple model. The parameters related to the stability of the FFLO state are likely the dimensionality and the shape of the Fermi surface as well as the gap symmetry. For example, (TMTSF)2ClO4, which was expected to exhibit the FFLO state [49], had a quasi-one-dimensional system, and the difference was expected to be significant. Although its superconducting phase showed strange differences in electrical resistivity and specific heat measurements [50,51], it might be interesting to discuss it through HP. As for the research method to discuss the FFLO state in more detail, for example, the in-plane angular dependence from Refs. [51,52] may be useful. Further research should be completed along with theoretical predictions.

5. Conclusions

We performed high-field rf-penetration depth measurements to determine whether the FFLO state manifested as a high-field superconducting state distinct from the BCS state in the organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. From the quantum oscillation and the phase diagram, it was confirmed that the electronic system was sufficiently clean and two-dimensional to stably host the FFLO state. As has been discussed for the FFLO state in other candidates, the transition field between the BCS and FFLO states had no angle dependence, whereas the FFLO state was very sensitive to the field angle and was immediately smeared out by the slight misalignment. Compared to other organic FFLO candidates, their H/HP-T/Tc superconducting phase diagrams suggest that HP certainly corresponds to HFFLO, regardless of the electronic states underlying the superconductivity. This verifies that the BCS-FFLO transition is determined by the competition between the Zeeman energy and the superconducting condensation energy. The FFLO state appears at very high fields above 31–32 T, because κ-Br can also be discussed in this framework, and its HP is enhanced by the large superconducting gap originating from the strong electron correlations growing in proximity to the Mott metal-insulator boundary.

Author Contributions

Conceptualization, S.I.; methodology, S.I. and K.K.; investigation, S.I. writing, S.I.; funding acquisition, S.I. and K.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was partially supported by the Japan Society for the Promotion of Science KAKENHI Grant No. 20K14406.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are available from the corresponding author upon reasonable request.

Acknowledgments

We thank Y. Kohama (ISSP, the University of Tokyo) for advice on the rf-TDO measurement.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fulde, P.; Ferrell, R.A. Superconductivity in a strong spin exchange field. Phys. Rev. 1964, 135, A550. [Google Scholar] [CrossRef]
  2. Larkin, A.I.; Ovchinnikov, Y.N. Inhomogeneous state of superconductors. Sov. Phys. JETP 1965, 20, 762. [Google Scholar]
  3. Casalbuoni, R.; Nardulli, G. Inhomogeneous superconductivity in condensed matter and QCD. Rev. Mod. Phys. 2004, 76, 263. [Google Scholar] [CrossRef] [Green Version]
  4. Matsuda, Y.; Shimahara, H. Fulde-Ferrell-Larkin-Ovchinnikov state in heavy fermion superconductors. J. Phys. Soc. Jpn. 2007, 76, 051005. [Google Scholar] [CrossRef] [Green Version]
  5. Imajo, S.; Nomura, T.; Kohama, Y.; Kindo, K. Nematic response of the Fulde-Ferrell-Larkin-Ovchinnikov state. arXiv 2021, arXiv:2110.12774. [Google Scholar]
  6. Clogston, A.M. Upper limit for the critical field in hard superconductors. Phys. Rev. Lett. 1962, 9, 266–267. [Google Scholar] [CrossRef]
  7. Shimahara, H.; Rainer, D. Crossover from Vortex States to the Fulde-Ferrell-Larkin-Ovchinnikov State in Two-Dimensional s- and d-Wave Superconductors. J. Phys. Soc. Jpn. 1997, 66, 3591. [Google Scholar] [CrossRef]
  8. Shimahara, H. Transition from the vortex state to the Fulde–Ferrell–Larkin–Ovchinnikov state in quasi-two-dimensional superconductors. Phys. Rev. B 2009, 80, 214512. [Google Scholar] [CrossRef] [Green Version]
  9. Croitoru, M.D.; Buzdin, A.I. In Search of Unambiguous Evidence of the Fulde–Ferrell–Larkin–Ovchinnikov State in Quasi-Low Dimensional Superconductors. Condens. Matter 2017, 2, 30. [Google Scholar] [CrossRef] [Green Version]
  10. Aslamazov, L.G. Influence of impurities on the existence of an imhomogeneous state in a ferromagnetic superconductor. Sov. Phys. JETP 1969, 28, 773. [Google Scholar]
  11. Cui, Q.; Yang, K. Fulde-Ferrell-Larkin-Ovchinnikov state in disordered s-wave superconductors. Phys. Rev. B 2008, 78, 054501. [Google Scholar] [CrossRef] [Green Version]
  12. Vorontsov, A.B.; Vekhter, I.; Graf, M.J. Pauli-limited upper critical field in dirty d-wave superconductors. Phys. Rev. B 2008, 78, 180505. [Google Scholar] [CrossRef] [Green Version]
  13. Maki, K.; Tsuneto, T. Pauli Paramagnetism and Superconducting State. Prog. Theor. Phys. 1964, 31, 945. [Google Scholar] [CrossRef]
  14. Gruenberg, L.W.; Gunther, L. Fulde-Ferrell effect in type-II superconductors. Phys. Rev. Lett. 1966, 16, 996. [Google Scholar] [CrossRef]
  15. Wosnitza, J. Spatially Nonuniform Superconductivity in Quasi-Two-Dimensional Organic Charge-Transfer Salts. Crystals 2018, 8, 183. [Google Scholar] [CrossRef] [Green Version]
  16. Agosta, C.C. Inhomogeneous Superconductivity in Organic and Related Superconductors. Crystals 2018, 8, 285. [Google Scholar] [CrossRef] [Green Version]
  17. Kanoda, K. Metal-Insulator Transition in κ-(ET)2X and (DCNQI)2M: Two Contrasting Manifestation of Electron Correlation. J. Phys. Soc. Jpn. 2006, 75, 051007. [Google Scholar] [CrossRef]
  18. Nakazawa, Y.; Imajo, S.; Matsumura, Y.; Yamashita, S.; Akutsu, H. Thermodynamic Picture of Dimer-Mott Organic Superconductors Revealed by Heat Capacity Measurements with External and Chemical Pressure Control. Crystals 2018, 8, 143. [Google Scholar] [CrossRef] [Green Version]
  19. Taylor, O.J.; Carrington, A.; Schlueter, J.A. Specific-Heat Measurements of the Gap Structure of the Organic Superconductors κ-(ET)2Cu[N(CN)2]Br and κ-(ET)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 057001. [Google Scholar] [CrossRef] [Green Version]
  20. Imajo, S.; Kindo, K.; Nakazawa, Y. Symmetry change of d-wave superconductivity in κ-type organic superconductors. Phys. Rev. B 2021, 103, L060508. [Google Scholar] [CrossRef]
  21. Imajo, S.; Nakazawa, Y.; Kindo, K. Superconducting Phase Diagram of the Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br above 30 T. J. Phys. Soc. Jpn. 2018, 87, 123704. [Google Scholar] [CrossRef]
  22. Lortz, R.; Wang, Y.; Demuer, A.; Bottger, P.H.M.; Bergk, B.; Zwicknagl, G.; Nakazawa, Y.; Wosnitza, J. Calorimetric Evidence for a Fulde-Ferrell-Larkin-Ovchinnikov Superconducting State in the Layered Organic Superconductor κ-(BEDT−TTF)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 187002. [Google Scholar] [CrossRef] [Green Version]
  23. Agosta, C.C.; Jin, J.; Coniglio, W.A.; Smith, B.E.; Cho, K.; Stroe, I.; Martin, C.; Tozer, S.W.; Murphy, T.P.; Palm, E.C.; et al. Experimental and semiempirical method to determine the Pauli-limiting field in quasi-two-dimensional superconductors as applied to κ-(BEDT-TTF)2Cu(NCS)2: Strong evidence of a FFLO state. Phys. Rev. B 2012, 85, 214514. [Google Scholar] [CrossRef] [Green Version]
  24. Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Miyagawa, K.; Kanoda, K.; Mitrović, V.F. Evidence of Andreev bound states as a hallmark of the FFLO phase in κ-(BEDT-TTF)2Cu(NCS)2. Nat. Phys. 2014, 10, 928. [Google Scholar] [CrossRef]
  25. Agosta, C.C.; Fortune, N.A.; Hannahs, S.T.; Gu, S.; Liang, L.; Park, J.; Schlueter, J.A. Calorimetric Measurements of Magnetic-Field-Induced Inhomogeneous Superconductivity Above the Paramagnetic Limit. Phys. Rev. Lett. 2017, 118, 267001. [Google Scholar] [CrossRef] [Green Version]
  26. Coniglio, W.A.; Winter, L.E.; Cho, K.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting phase diagram and FFLO signature in λ-(BETS)2GaCl4 from rf penetration depth measurements. Phys. Rev. B 2011, 83, 224507. [Google Scholar] [CrossRef] [Green Version]
  27. Cho, K.; Smith, B.E.; Coniglio, W.A.; Winter, L.E.; Agosta, C.C.; Schlueter, J.A. Upper critical field in the organic superconductor β”-(ET)2SF5CH2CF2SO3: Possibility of Fulde-Ferrell-Larkin-Ovchinnikov state. Phys. Rev. B 2009, 79, 220507. [Google Scholar] [CrossRef] [Green Version]
  28. Imajo, S.; Sugiura, S.; Akutsu, H.; Kohama, Y.; Isono, T.; Terashima, T.; Kindo, K.; Uji, S.; Nakazawa, Y. Extraordinary π-electron superconductivity emerging from a quantum spin liquid. Phys. Rev. Res. 2021, 3, 033026. [Google Scholar] [CrossRef]
  29. Zuo, F.; Schlueter, J.A.; Kelly, M.E.; Williams, J.M. Mixed-state magnetoresistance in organic superconductors κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 1996, 54, 11973. [Google Scholar] [CrossRef]
  30. Zuo, F.; Schlueter, J.A.; Williams, J.M. Interlayer magnetoresistance in the organic superconductor κ-(BEDT−TTF)2Cu[N(CN)2]Br near the superconducting. Phys. Rev. B 1999, 60, 574. [Google Scholar] [CrossRef]
  31. Mielke, C.H.; Harrison, N.; Rickel, D.G.; Lacerda, A.H.; Vestal, R.M.; Montgomery, L.K. Fermi-surface topology of κ-(BEDT−TTF)2Cu[N(CN)2]Br at ambient pressure. Phys. Rev. B 1997, 56, R4309. [Google Scholar] [CrossRef]
  32. Ito, H.; Watanabe, M.; Nogami, Y.; Ishiguro, T.; Komatsu, T.; Saito, G.; Hosoito, N. Magnetic Determination of Ginzburg-Landau Coherence Length for Organic Superconductor κ-(BEDT-TTF)2X (X=Cu(NCS)2,Cu[N(CN)2]Br): Effect of Isotope Substitution. J. Phys. Soc. Jpn. 1991, 60, 3230. [Google Scholar] [CrossRef]
  33. Kim, H.; Kogan, V.G.; Cho, K.; Tanatar, M.A.; Prozorov, R. Rutgers relation for the analysis of superfluid density in superconductors. Phys. Rev. B 2013, 87, 214518. [Google Scholar] [CrossRef] [Green Version]
  34. Kovalev, A.E.; Ishiguro, T.; Kondo, T.; Saito, G. Specific heat of organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br under a magnetic field parallel to the conducting plane. Phys. Rev. B 2000, 62, 103. [Google Scholar] [CrossRef]
  35. Yoneyama, N.; Higashihara, A.; Sasaki, T.; Nojima, T.; Kobayashi, N. Impurity Effect on the In-plane Penetration Depth of the Organic Superconductors κ-(BEDT-TTF)2X (X = Cu(NCS)2 and Cu[N(CN)2]Br). J. Phys. Soc. Jpn. 2004, 73, 1290. [Google Scholar] [CrossRef] [Green Version]
  36. Lang, M.; Toyota, N.; Sasaki, T.; Sato, H. Magnetic penetration depth of κ-(BEDT-TTF)2Cu[N(CN)2]Br, determined from the reversible magnetization. Phys. Rev. B 1992, 46, 5822. [Google Scholar] [CrossRef]
  37. Wakamatsu, K.; Miyagawa, K.; Kanoda, K. Superfluid density versus transition temperature in a layered organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br under pressure. Phys. Rev. Res. 2020, 2, 043008. [Google Scholar] [CrossRef]
  38. Prozorov, R.; Giannetta, R.W. Magnetic penetration depth in unconventional superconductors. Supercond. Sci. Technol. 2006, 19, R41. [Google Scholar] [CrossRef] [Green Version]
  39. Imajo, S.; Kobayashi, T.; Kawamoto, A.; Kindo, K.; Nakazawa, Y. Thermodynamic evidence for the formation of a Fulde-Ferrell-Larkin-Ovchinnikov phase in the organic superconductor λ-(BETS)2GaCl4. Phys. Rev. B 2021, 103, L220501. [Google Scholar] [CrossRef]
  40. Sugiura, S.; Isono, T.; Terashima, T.; Yasuzuka, S.; Schlueter, J.A.; Uji, S. Fulde–Ferrell–Larkin–Ovchinnikov and vortex phases in a layered organic superconductor. NPJ Quantum Mater. 2018, 4, 7. [Google Scholar] [CrossRef]
  41. Sugiura, S.; Terashima, T.; Uji, S.; Yasuzuka, S.; Schlueter, J.A. Josephson vortex dynamics and Fulde-Ferrell-Larkin-Ovchinnikov superconductivity in the layered organic superconductor β”-(BEDT-TTF)2SF5CH2CF2SO3. Phys. Rev. B 2019, 100, 014515. [Google Scholar] [CrossRef]
  42. McKenzie, R.H. Wilson’s ratio and the spin splitting of magnetic oscillations in quasi-two-dimensional metals. arXiv 1999, arXiv:9905044. [Google Scholar]
  43. Uji, S.; Terashima, T.; Nishimura, M.; Takahide, Y.; Konoike, T.; Enomoto, K.; Cui, H.; Kobayashi, H.; Kobayashi, A.; Tanaka, H.; et al. Vortex Dynamics and the Fulde- Ferrell-Larkin-Ovchinnikov State in a Magnetic-Field-Induced Organic Superconductor. Phys. Rev. Lett. 2006, 97, 157001. [Google Scholar] [CrossRef] [PubMed]
  44. Beyer, R.; Bergk, B.; Yasin, S.; Schlueter, J.A.; Wosnitza, J. Angle-Dependent Evolution of the Fulde-Ferrell-Larkin-Ovchinnikov State in an Organic Superconductor. Phys. Rev. Lett. 2012, 109, 027003. [Google Scholar] [CrossRef] [Green Version]
  45. Uji, S.; Iida, Y.; Sugiura, S.; Isono, T.; Sugii, K.; Kikugawa, N.; Terashima, T.; Yasuzuka, S.; Akutsu, H.; Nakazawa, Y.; et al. Fulde-Ferrell-Larkin-Ovchinnikov superconductivity in the layered organic superconductor β”-(BEDT-TTF)4[(H3O)Ga(C2O4)3]C6H5NO2. Phys. Rev. B 2018, 97, 144505. [Google Scholar] [CrossRef] [Green Version]
  46. Mielke, C.; Singleton, J.; Nam, M.-S.; Harrison, N.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting properties and Fermi-surface topology of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 (BETS≡bis(ethylene-dithio)tetraselenafulvalene). J. Phys. Condens. Matter 2001, 13, 8325. [Google Scholar] [CrossRef]
  47. Yasuzuka, S.; Uji, S.; Terashima, T.; Sugii, K.; Isono, T.; Iida, Y.; Schlueter, J.A. In-Plane Anisotropy of Upper Critical Field and Flux-Flow Resistivity in Layered Organic Superconductor β”-(ET)2SF5CH2CF2SO3. J. Phys. Soc. Jpn. 2015, 84, 094709. [Google Scholar] [CrossRef]
  48. Imajo, S.; Akutsu, H.; Kurihara, R.; Yajima, T.; Kohama, Y.; Tokunaga, M.; Kindo, K.; Nakazawa, Y. Anisotropic Fully Gapped Superconductivity Possibly Mediated by Charge Fluctuations in a Nondimeric Organic Complex. Phys. Rev. Lett. 2020, 125, 177002. [Google Scholar] [CrossRef]
  49. Aizawa, H.; Kuroki, K.; Tanaka, Y. Pairing Competition in a Quasi-One-Dimensional Model of Organic Superconductors (TMTSF)2X in Magnetic Field. J. Phys. Soc. Jpn. 2009, 78, 124711. [Google Scholar] [CrossRef] [Green Version]
  50. Yonezawa, S.; Maeno, Y.; Bechgaard, K.; Jérome, D. Nodal superconducting order parameter and thermodynamic phase diagram of (TMTSF)2ClO4. Phys. Rev. B 2012, 85, 140502. [Google Scholar] [CrossRef] [Green Version]
  51. Yonezawa, S.; Kusaba, S.; Maeno, Y.; Auban-Senzier, P.; Pasquier, C.; Bechgaard, K.; Jérome, D. Anomalous In-Plane Anisotropy of the Onset of Superconductivity in (TMTSF)2ClO4. Phys. Rev. Lett. 2008, 100, 117002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  52. Croitoru, M.D.; Buzdin, A.I. Resonance in-plane magnetic field effect as a means to reveal the Fulde-Ferrell-Larkin-Ovchinnikov state in layered superconductors. Phys. Rev. B 2012, 86, 064507. [Google Scholar] [CrossRef] [Green Version]
  53. Weiss, H.; Kartsovnik, M.V.; Biberacher, W.; Balthes, E.; Jansen, A.G.M.; Kushch, N.D. Angle-dependent magnetoquantum oscillations in κ−(BEDT−TTF)2Cu[N(CN)2]Br. Phys. Rev. B 1999, 60, R16259. [Google Scholar] [CrossRef]
  54. Imajo, S.; Dong, C.; Matsuo, A.; Kindo, K.; Kohama, Y. High-resolution calorimetry in pulsed magnetic fields. Rev. Sci. Instrum. 2021, 92, 043901. [Google Scholar] [CrossRef] [PubMed]
  55. Wosnitza, J.; Crabtree, G.W.; Wang, H.H.; Geiser, U.; Williams, J.M.; Carlson, K.D. de Haas–van Alphen studies of the organic superconductors α-(ET)2(NH4)Hg(SCN)4 and κ-(ET)2Cu(NCS)2 [with ET = bis(ethelenedithio)-tetrathiafulvalene]. Phys. Rev. B 1992, 45, 3018. [Google Scholar] [CrossRef]
  56. Tanatar, M.A.; Ishiguro, T.; Tanaka, H.; Kobayashi, H. Magnetic field–temperature phase diagram of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 studied via thermal conductivity. Phys. Rev. B 2002, 66, 134503. [Google Scholar] [CrossRef] [Green Version]
  57. Imajo, S.; Kanda, N.; Yamashita, S.; Akutsu, H.; Nakazawa, Y.; Kumagai, H.; Kobayashi, T.; Kawamoto, A. Thermodynamic Evidence of d-Wave Superconductivity of the Organic Superconductor λ-(BETS)2GaCl4. J. Phys. Soc. Jpn. 2016, 85, 043705. [Google Scholar] [CrossRef]
  58. Imajo, S.; Yamashita, S.; Akutsu, H.; Kumagai, H.; Kobayashi, T.; Kawamoto, A.; Nakazawa, Y. Gap Symmetry of the Organic Superconductor λ-(BETS)2GaCl4 Determined by Magnetic-Field-Angle-Resolved Heat Capacity. J. Phys. Soc. Jpn. 2019, 88, 023702. [Google Scholar] [CrossRef]
  59. Koutroulakis, G.; Kühne, H.; Schlueter, J.A.; Wosnitza, J.; Brown, S.E. Microscopic Study of the Fulde-Ferrell-Larkin- Ovchinnikov State in an All-Organic Superconductor. Phys. Rev. Lett. 2016, 116, 067003. [Google Scholar] [CrossRef]
  60. Beckmann, D.; Wanka, S.; Wosnitza, J.; Schlueter, J.A.; Williams, J.M.; Nixon, P.G.; Winter, R.W.; Gard, G.L.; Ren, J.; Whangbo, M.-H. Characterization of the Fermi surface of the organic superconductor β”-(ET)2SF5CH2CF2SO3 by measurements of Shubnikov-de Haas and angle-dependent magnetoresistance oscillations and by electronic band-structure calculations. Eur. Phys. J. B 1998, 1, 295. [Google Scholar] [CrossRef]
  61. Wanka, S.; Hagel, J.; Beckmann, D.; Wosnitza, J.; Schlueter, J.A.; Williams, J.M.; Nixon, P.G.; Winter, R.W.; Gard, G.L. Specific heat and critical fields of the organic superconductor β”−(BEDT−TTF)2SF5CH2CF2SO3. Phys. Rev. B 1998, 57, 3084. [Google Scholar] [CrossRef] [Green Version]
  62. Bangura, A.F.; Coldea, A.I.; Singleton, J.; Ardavan, A.; Akutsu-Sato, A.; Akutsu, H.; Turner, S.S.; Day, P.; Yamamoto, T.; Yakushi, K. Robust superconducting state in the low-quasiparticle-density organic metals β”−(BEDT−TTF)4[(H3O)M(C2O4)3]∙Y: Superconductivity due to proximity to a charge-ordered state. Phys. Rev. B 2005, 72, 014543. [Google Scholar] [CrossRef] [Green Version]
Crystals 11 01358 g001 550
Figure 1. Crystal structure of κ-(BEDT-TTF)2Cu[N(CN)2]Br. As divided by the red dashed lines, this material has the two-dimensional layered structure. θ represents the angle from a-axis to b-axis, used for the magnetic-field direction applied in this study.
Figure 1. Crystal structure of κ-(BEDT-TTF)2Cu[N(CN)2]Br. As divided by the red dashed lines, this material has the two-dimensional layered structure. θ represents the angle from a-axis to b-axis, used for the magnetic-field direction applied in this study.
Crystals 11 01358 g001
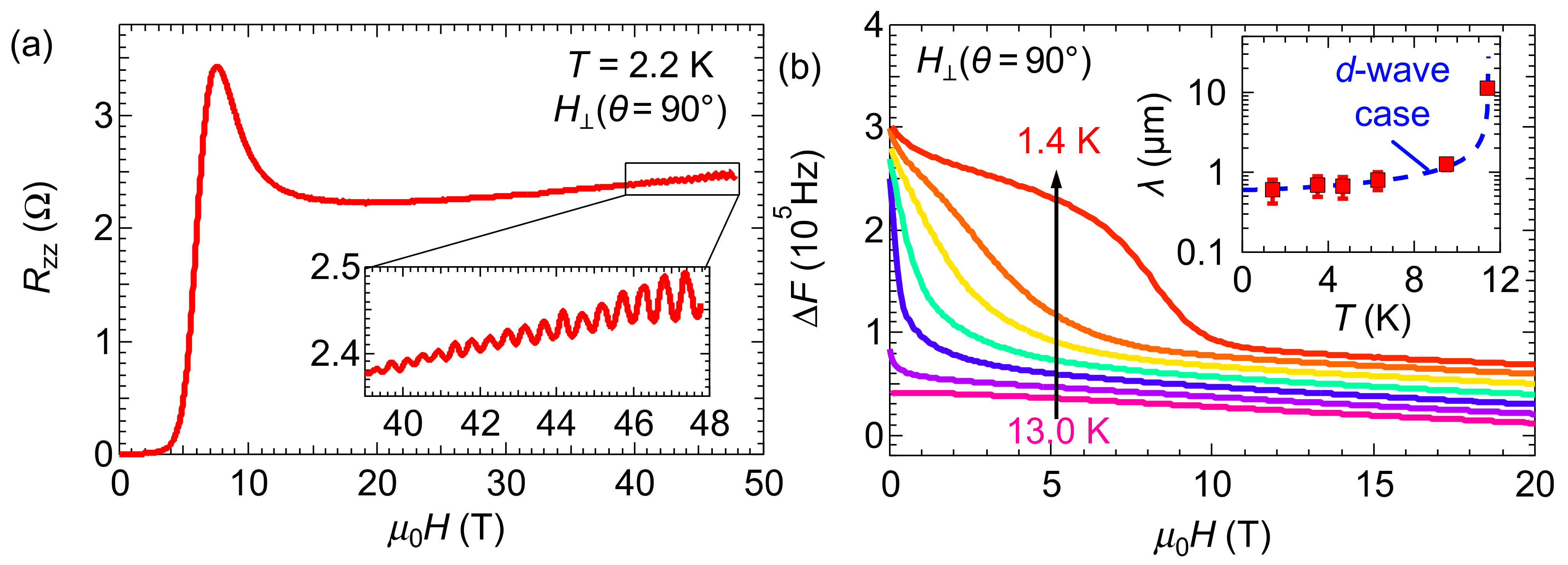
Crystals 11 01358 g002 550
Figure 2. (a) Magnetoresistance at 2.2 K in a perpendicular field (θ = 90°). The inset is the enlarged plot above 40 T to make the quantum oscillation clearer. (b) Shift of the penetration depth ΔF at various temperatures as a function of field when θ = 90°. For clarity, the datasets include offsets. The inset is the temperature dependence of the penetration depth obtained by the Equations (1) and (2). The blue dashed curve indicates behavior for simple d-wave superconductivity.
Figure 2. (a) Magnetoresistance at 2.2 K in a perpendicular field (θ = 90°). The inset is the enlarged plot above 40 T to make the quantum oscillation clearer. (b) Shift of the penetration depth ΔF at various temperatures as a function of field when θ = 90°. For clarity, the datasets include offsets. The inset is the temperature dependence of the penetration depth obtained by the Equations (1) and (2). The blue dashed curve indicates behavior for simple d-wave superconductivity.
Crystals 11 01358 g002
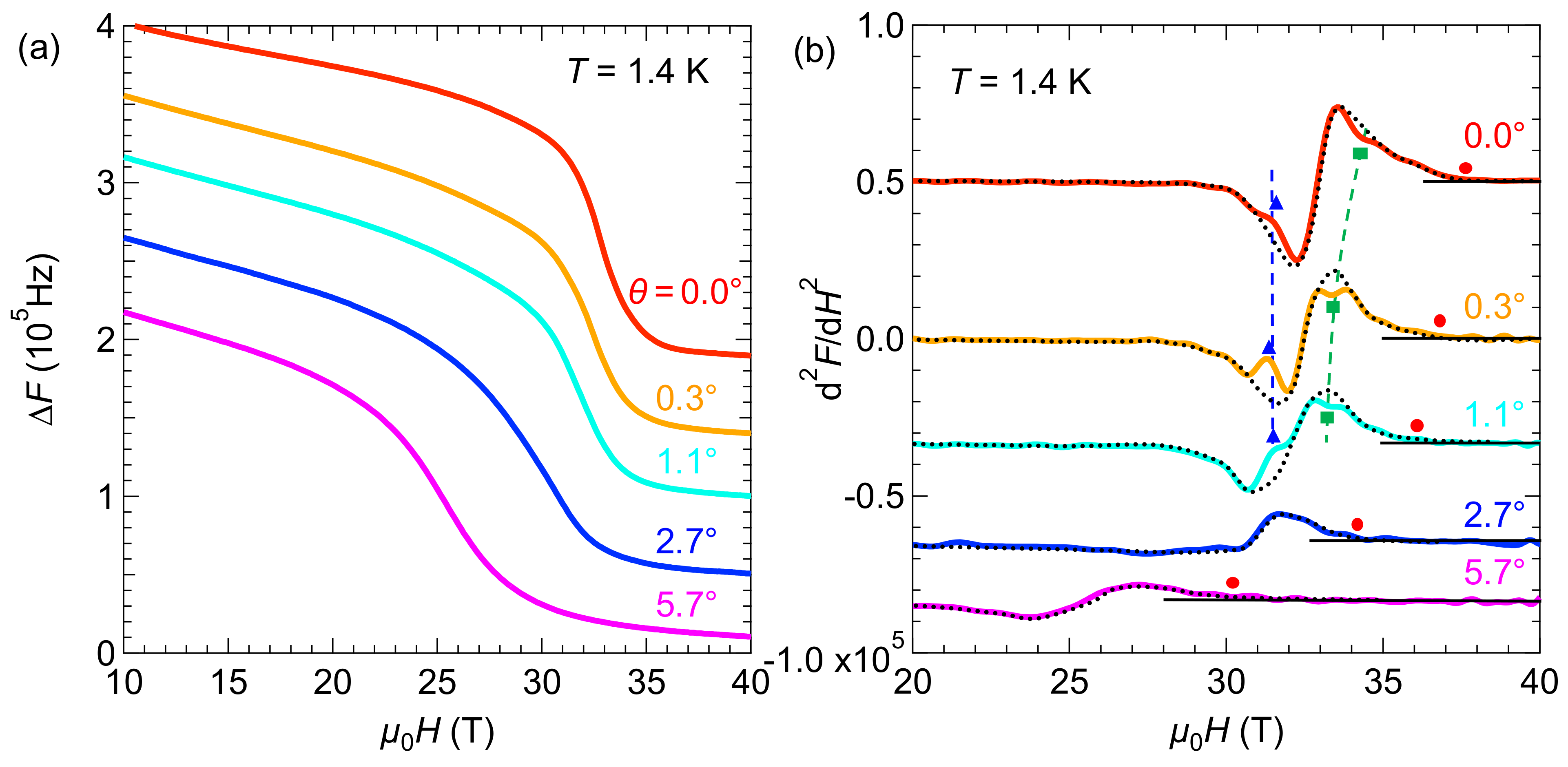
Crystals 11 01358 g003 550
Figure 3. (a) Magnetic-field dependence of ΔF at 1.4 K with changing field angle θ. (b) Second derivative of (a) d2F/dH2 as a function of field. The black solid lines and the red dots show the background of the normal state and Hc2. The blue triangles and green squares indicate the anomalous fields of d2F/dH2. The black dotted, blue dashed, and green dashed curves are eye guides.
Figure 3. (a) Magnetic-field dependence of ΔF at 1.4 K with changing field angle θ. (b) Second derivative of (a) d2F/dH2 as a function of field. The black solid lines and the red dots show the background of the normal state and Hc2. The blue triangles and green squares indicate the anomalous fields of d2F/dH2. The black dotted, blue dashed, and green dashed curves are eye guides.
Crystals 11 01358 g003
Crystals 11 01358 g004 550
Figure 4. (a) ΔF (θ = 0°) as a function of field at various temperatures. (b) Magnetic-field dependence of d2F/dH2. The symbols and curves are described using the same definitions as those used in Figure 3b.
Figure 4. (a) ΔF (θ = 0°) as a function of field at various temperatures. (b) Magnetic-field dependence of d2F/dH2. The symbols and curves are described using the same definitions as those used in Figure 3b.
Crystals 11 01358 g004
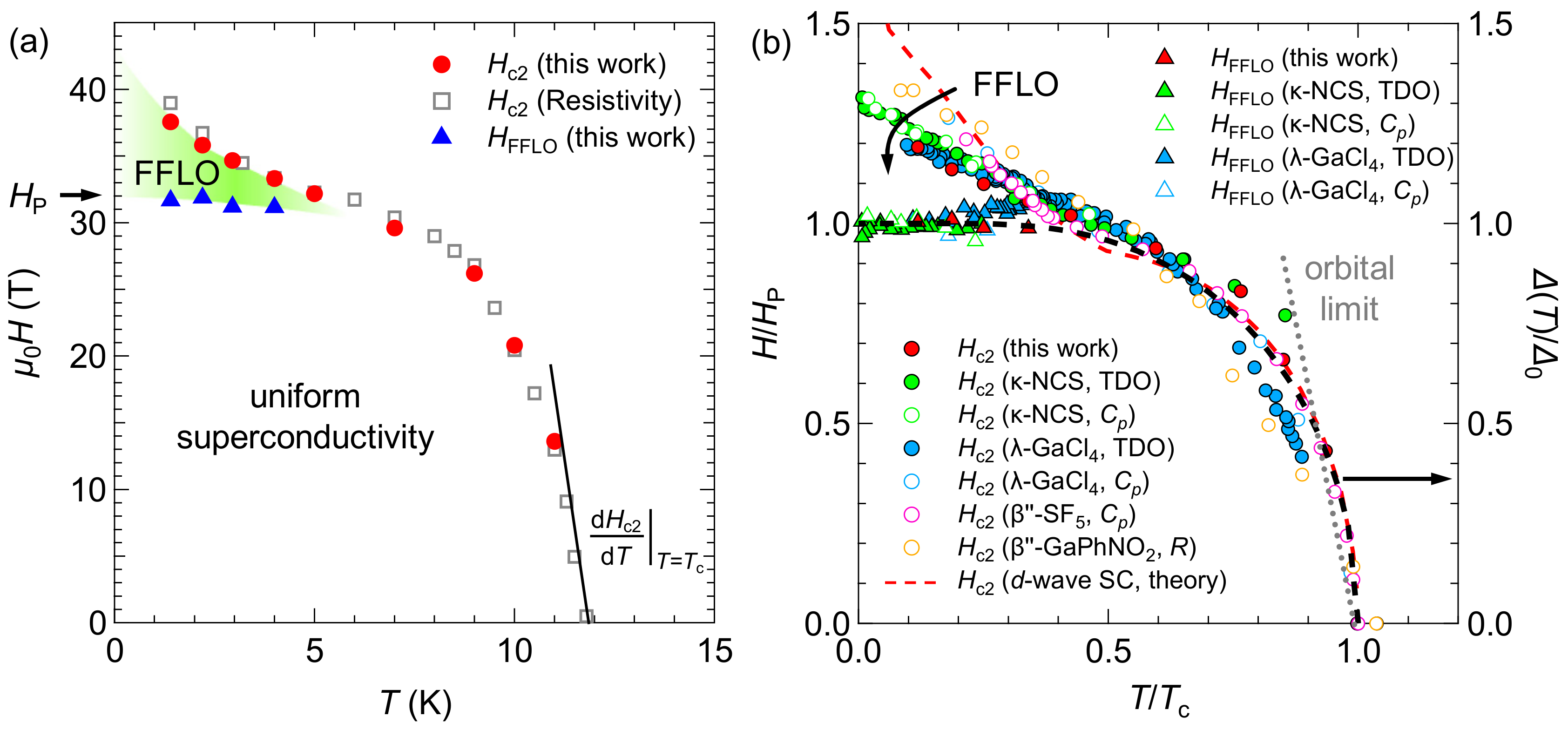
Crystals 11 01358 g005 550
Figure 5. (a) H-T superconducting phase diagram of κ-Br in parallel fields. The gray boxes are the reported Hc2 data [21]. The solid line indicates the slope of the Hc2 curve near Tc at 0 T. The light green region above HP is the FFLO state. (b) Superconducting phase diagram scaled by HP and Tc, H/HP vs. T/Tc. The circles and triangles represent Hc2 and HFFLO, respectively. The color of the symbols denotes the material. The filled symbols are taken from the TDO measurements [23,26,27], whereas the unfilled symbols are from other measurements [25,39,44,45]. The dotted gray line represents an example of the temperature dependence of Horb, which is higher than Hc2 at low temperatures. The red dotted curve is a simple theoretical calculation [9] of Hc2 for the FFLO state with d-wave superconducting symmetry. The black dashed curve (right axis) is the temperature dependence of the reduced BCS-type superconducting gap Δ(T)/Δ0.
Figure 5. (a) H-T superconducting phase diagram of κ-Br in parallel fields. The gray boxes are the reported Hc2 data [21]. The solid line indicates the slope of the Hc2 curve near Tc at 0 T. The light green region above HP is the FFLO state. (b) Superconducting phase diagram scaled by HP and Tc, H/HP vs. T/Tc. The circles and triangles represent Hc2 and HFFLO, respectively. The color of the symbols denotes the material. The filled symbols are taken from the TDO measurements [23,26,27], whereas the unfilled symbols are from other measurements [25,39,44,45]. The dotted gray line represents an example of the temperature dependence of Horb, which is higher than Hc2 at low temperatures. The red dotted curve is a simple theoretical calculation [9] of Hc2 for the FFLO state with d-wave superconducting symmetry. The black dashed curve (right axis) is the temperature dependence of the reduced BCS-type superconducting gap Δ(T)/Δ0.
Crystals 11 01358 g005
Table
Table 1. Reported HFFLO and calculated HP with parameters characterizing the FFLO state. The abbreviations of the material names are described in the main text. The shown HP is estimated by the Equation (3) and the parameters shown here, which are typical values taking into account sample dependence, etc. For the estimation of the values of g*/g, the Wilson’ ratio RW, calculated by γ and χP, is also used to compare with g*/g determined by angle-dependent quantum oscillations. The values of α are taken from heat capacity measurements.
Table 1. Reported HFFLO and calculated HP with parameters characterizing the FFLO state. The abbreviations of the material names are described in the main text. The shown HP is estimated by the Equation (3) and the parameters shown here, which are typical values taking into account sample dependence, etc. For the estimation of the values of g*/g, the Wilson’ ratio RW, calculated by γ and χP, is also used to compare with g*/g determined by angle-dependent quantum oscillations. The values of α are taken from heat capacity measurements.
MaterialTc (K)g*/gαHP (T)HFFLO (T)Refs.
κ-Br11.71.33.33131–32[17,19,20,21,42,53,54]
κ-NCS9.01.32.92121–22[17,19,22,23,24,25,42,55]
λ-GaCl44.71.02.1109–10[26,39,46,56,57,58]
Β″-SF54.31.02.19.59–10[27,40,41,44,59,60,61]
β″-GaPhNO24.80.82.51616[45,48,62]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Imajo, S.; Kindo, K. The FFLO State in the Dimer Mott Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Crystals 2021, 11, 1358. https://doi.org/10.3390/cryst11111358

AMA Style

Imajo S, Kindo K. The FFLO State in the Dimer Mott Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Crystals. 2021; 11(11):1358. https://doi.org/10.3390/cryst11111358

Chicago/Turabian Style

Imajo, Shusaku, and Koichi Kindo. 2021. "The FFLO State in the Dimer Mott Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br" Crystals 11, no. 11: 1358. https://doi.org/10.3390/cryst11111358

APA Style

Imajo, S., & Kindo, K. (2021). The FFLO State in the Dimer Mott Organic Superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br. Crystals, 11(11), 1358. https://doi.org/10.3390/cryst11111358

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop