Reduced Thermal Conductivity in Ultrafast Laser Heated Silicon Measured by Time-Resolved X-ray Diffraction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment
2.2. Analysis and Modeling
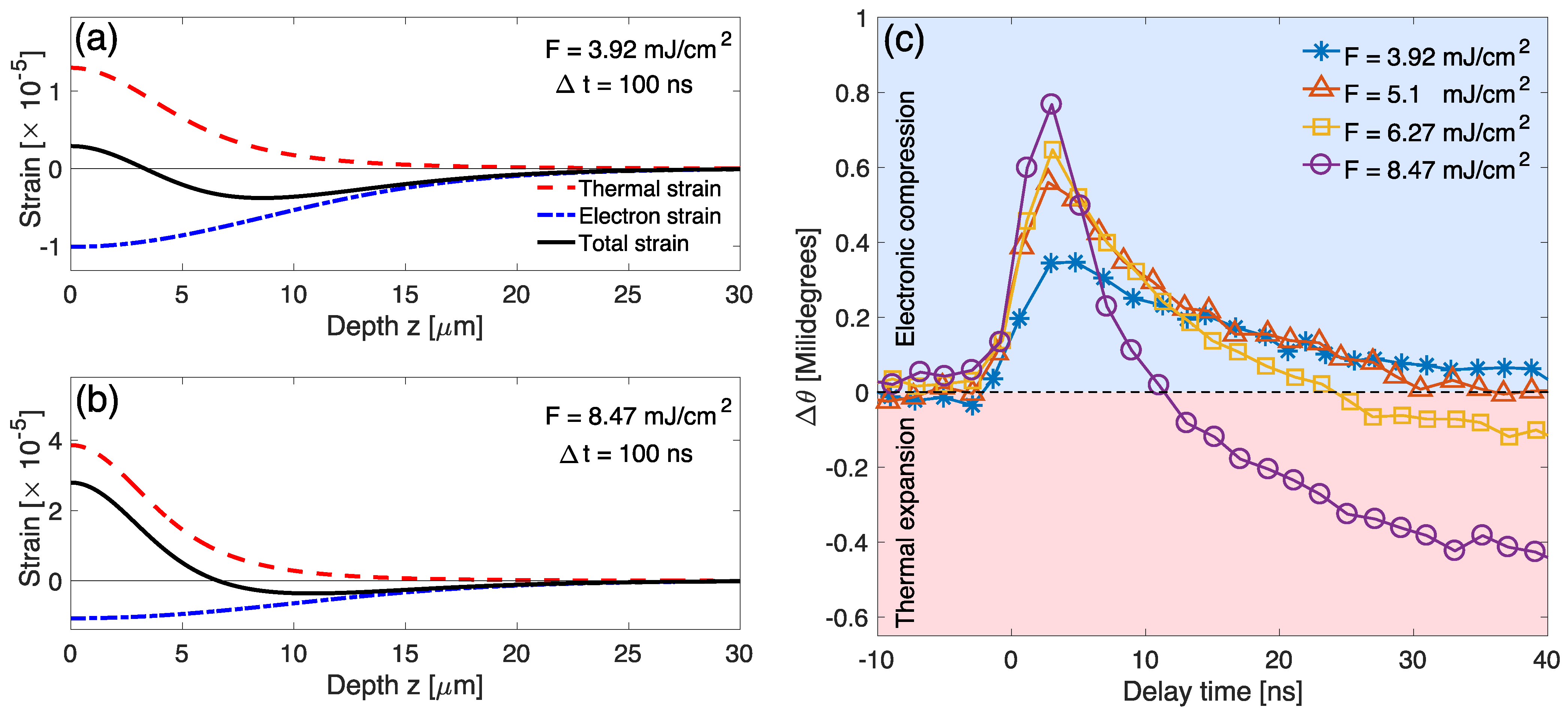
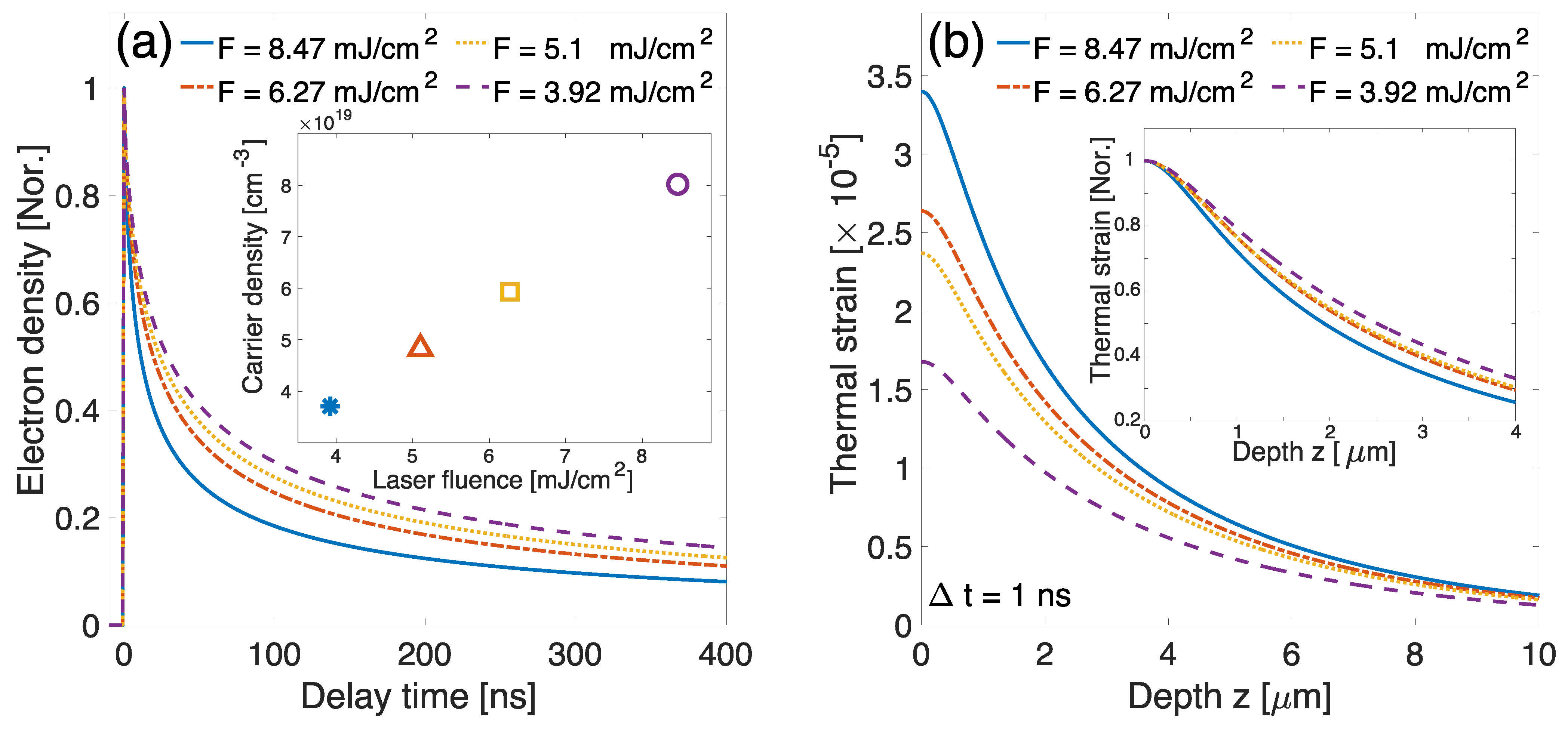
3. Results
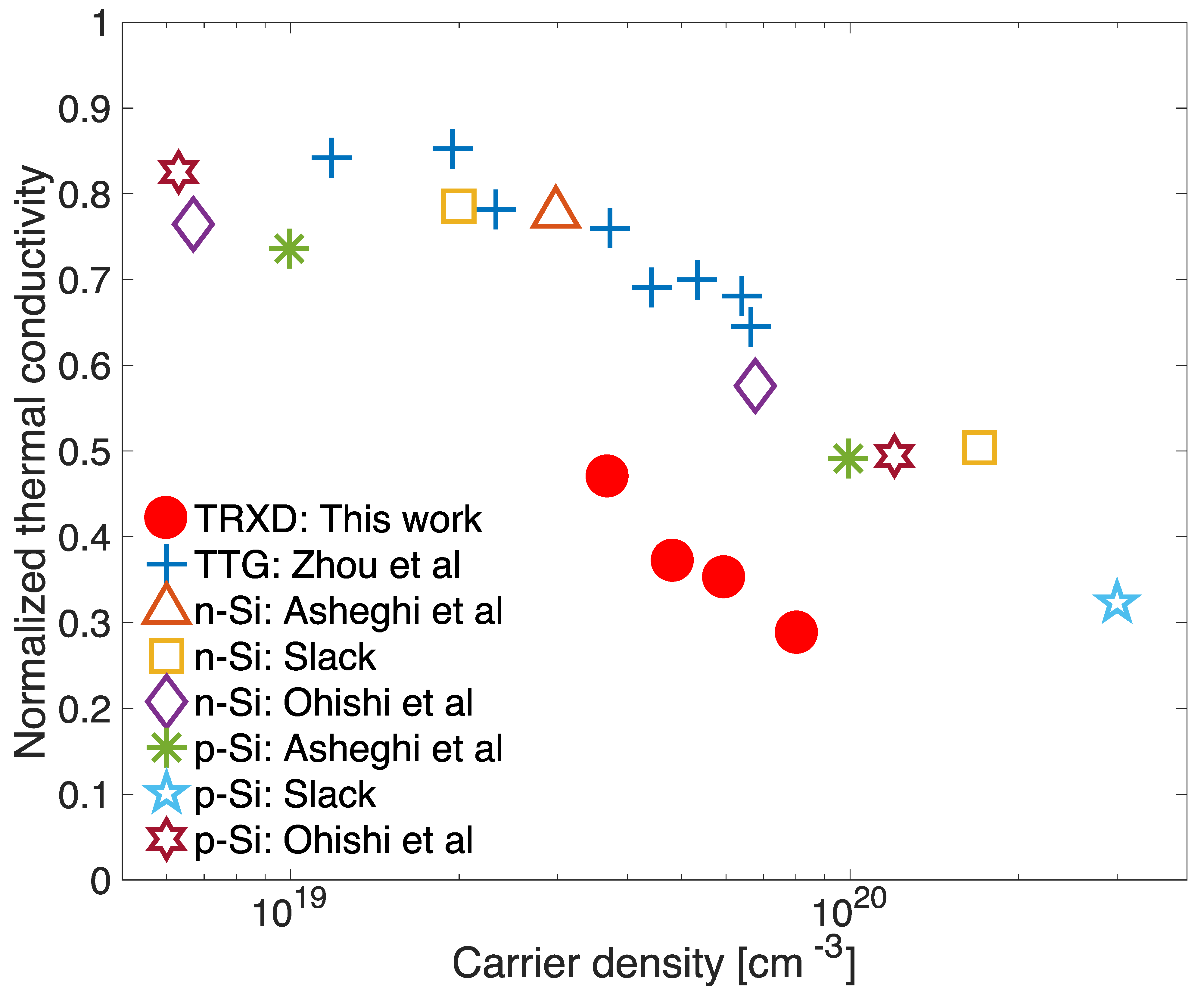
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Balestra, F.; Cristoloveanu, S.; Benachir, M.; Brini, J.; Elewa, T. Double-gate silicon-on-insulator transistor with volume inversion: A new device with greatly enhanced performance. IEEE Electron Device Lett. 1987, 8, 410–412. [Google Scholar] [CrossRef]
- Walsh, S.T.; Boylan, R.L.; McDermott, C.; Paulson, A. The semiconductor silicon industry roadmap: Epochs driven by the dynamics between disruptive technologies and core competencies. Technol. Forecast. Soc. Chang. 2005, 72, 213–236. [Google Scholar] [CrossRef]
- Khang, D.Y.; Jiang, H.; Huang, Y.; Rogers, J.A. A Stretchable Form of Single-Crystal Silicon for High-Performance Electronics on Rubber Substrates. Science 2006, 311, 208–212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, J.; Wang, A.; Green, M.A.; Ferrazza, F. 19.8% efficient “honeycomb” textured multicrystalline and 24.4% monocrystalline silicon solar cells. Appl. Phys. Lett. 1998, 73, 1991–1993. [Google Scholar] [CrossRef]
- Notomi, M.; Shinya, A.; Mitsugi, S.; Kira, G.; Kuramochi, E.; Tanabe, T. Optical bistable switching action of Si high-Q photonic-crystal nanocavities. Opt. Express 2005, 13, 2678–2687. [Google Scholar] [CrossRef] [PubMed]
- Agnese, R.; Ahmed, Z.; Anderson, A.J.; Arrenberg, S.; Balakishiyeva, D.; Basu Thakur, R.; Bauer, D.A.; Billard, J.; Borgland, A.; Brandt, D.; et al. Silicon Detector Dark Matter Results from the Final Exposure of CDMS II. Phys. Rev. Lett. 2013, 111, 251301. [Google Scholar] [CrossRef]
- Siemens, M.E.; Li, Q.; Yang, R.; Nelson, K.A.; Anderson, E.H.; Murnane, M.M.; Kapteyn, H.C. Quasi-ballistic thermal transport from nanoscale interfaces observed using ultrafast coherent soft X-ray beams. Nat. Mater. 2010, 9, 26–30. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Zeng, L.; Minnich, A.J.; Dresselhaus, M.S.; Chen, G. Spectral mapping of thermal conductivity through nanoscale ballistic transport. Nat. Nanotechnol. 2015, 10, 701–706. [Google Scholar] [CrossRef]
- Zhou, J.; Shin, H.D.; Chen, K.; Song, B.; Duncan, R.A.; Xu, Q.; Maznev, A.A.; Nelson, K.A.; Chen, G. Direct observation of large electron–phonon interaction effect on phonon heat transport. Nat. Commun. 2020, 11, 6040. [Google Scholar] [CrossRef]
- Koh, Y.K.; Cahill, D.G. Frequency dependence of the thermal conductivity of semiconductor alloys. Phys. Rev. B 2007, 76, 075207. [Google Scholar] [CrossRef] [Green Version]
- Da Cruz, C.A.; Li, W.; Katcho, N.A.; Mingo, N. Role of phonon anharmonicity in time-domain thermoreflectance measurements. Appl. Phys. Lett. 2012, 101, 083108. [Google Scholar] [CrossRef]
- Regner, K.T.; Sellan, D.P.; Su, Z.; Amon, C.H.; McGaughey, A.J.H.; Malen, J.A. Broadband phonon mean free path contributions to thermal conductivity measured using frequency domain thermoreflectance. Nat. Commun. 2013, 4, 1640. [Google Scholar] [CrossRef] [Green Version]
- Regner, K.T.; Freedman, J.P.; Malen, J.A. Advances in Studying Phonon Mean Free Path Dependent Contributions to Thermal Conductivity. Nanoscale Microscale Thermophys. Eng. 2015, 19, 183–205. [Google Scholar] [CrossRef]
- Sheu, Y.M.; Lee, S.H.; Wahlstrand, J.K.; Walko, D.A.; Landahl, E.C.; Arms, D.A.; Reason, M.; Goldman, R.S.; Reis, D.A. Thermal transport in a semiconductor heterostructure measured by time-resolved X-ray diffraction. Phys. Rev. B 2008, 78, 045317. [Google Scholar] [CrossRef]
- Lee, S.; Jo, W.; DiChiara, A.; Holmes, T.; Santowski, S.; Cho, Y.; Landahl, E. Probing Electronic Strain Generation by Separated Electron-Hole Pairs Using Time-Resolved X-ray Scattering. Appl. Sci. 2019, 9, 4788. [Google Scholar] [CrossRef] [Green Version]
- Jo, W.; Landahl, E.C.; DiChiara, A.D.; Walko, D.A.; Lee, S. Measuring femtometer lattice displacements driven by free carrier diffusion in a polycrystalline semiconductor using time-resolved X-ray scattering. Appl. Phys. Lett. 2018, 113, 032107. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Williams, G.J.; Campana, M.I.; Walko, D.A.; Landahl, E.C. Picosecond X-ray strain rosette reveals direct laser excitation of coherent transverse acoustic phonons. Sci. Rep. 2016, 6, 19140. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Chen, P.; Cosgriff, M.P.; Walko, D.A.; Lee, J.H.; Adamo, C.; Schaller, R.D.; Ihlefeld, J.F.; Dufresne, E.M.; Schlom, D.G.; et al. Electronic Origin of Ultrafast Photoinduced Strain in BiFeO3. Phys. Rev. Lett. 2013, 110, 037601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schick, D.; Herzog, M.; Wen, H.; Chen, P.; Adamo, C.; Gaal, P.; Schlom, D.G.; Evans, P.G.; Li, Y.; Bargheer, M. Localized Excited Charge Carriers Generate Ultrafast Inhomogeneous Strain in the Multiferroic BiFeO3. Phys. Rev. Lett. 2014, 112, 097602. [Google Scholar] [CrossRef] [Green Version]
- Juvé, V.; Gu, R.; Gable, S.; Maroutian, T.; Vaudel, G.; Matzen, S.; Chigarev, N.; Raetz, S.; Gusev, V.E.; Viret, M.; et al. Ultrafast light-induced shear strain probed by time-resolved X-ray diffraction: Multiferroic BiFeO3 as a case study. Phys. Rev. B 2020, 102, 220303. [Google Scholar] [CrossRef]
- Von Reppert, A.; Willig, L.; Pudell, J.E.; Rössle, M.; Leitenberger, W.; Herzog, M.; Ganss, F.; Hellwig, O.; Bargheer, M. Ultrafast laser generated strain in granular and continuous FePt thin films. Appl. Phys. Lett. 2018, 113, 123101. [Google Scholar] [CrossRef] [Green Version]
- Pudell, J.; Maznev, A.A.; Herzog, M.; Kronseder, M.; Back, C.H.; Malinowski, G.; von Reppert, A.; Bargheer, M. Layer specific observation of slow thermal equilibration in ultrathin metallic nanostructures by femtosecond X-ray diffraction. Nat. Commun. 2018, 9, 3335. [Google Scholar] [CrossRef]
- Wall, S.; Yang, S.; Vidas, L.; Chollet, M.; Glownia, J.M.; Kozina, M.; Katayama, T.; Henighan, T.; Jiang, M.; Miller, T.A.; et al. Ultrafast disordering of vanadium dimers in photoexcited VO2. Science 2018, 362, 572–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zalden, P.; Quirin, F.; Schumacher, M.; Siegel, J.; Wei, S.; Koc, A.; Nicoul, M.; Trigo, M.; Andreasson, P.; Enquist, H.; et al. Femtosecond X-ray diffraction reveals a liquid–liquid phase transition in phase-change materials. Science 2019, 364, 1062–1067. [Google Scholar] [CrossRef]
- Wie, C.R.; Tombrello, T.A.; Vreeland, T. Dynamical X-ray diffraction from nonuniform crystalline films: Application to X-ray rocking curve analysis. J. Appl. Phys. 1986, 59, 3743–3746. [Google Scholar] [CrossRef] [Green Version]
- Jo, W.; Lee, S.; Eom, I.; Landahl, E.C. Synchronizing femtosecond laser with X-ray synchrotron operating at arbitrarily different frequencies. Rev. Sci. Instrum. 2014, 85, 125112. [Google Scholar] [CrossRef]
- Van de Walle, C.G. Band lineups and deformation potentials in the model-solid theory. Phys. Rev. B 1989, 39, 1871–1883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rämer, A.; Osmani, O.; Rethfeld, B. Laser damage in silicon: Energy absorption, relaxation, and transport. J. Appl. Phys. 2014, 116, 053508. [Google Scholar] [CrossRef] [Green Version]
- Williams, G.J.; Lee, S.; Walko, D.A.; Watson, M.A.; Jo, W.; Lee, D.R.; Landahl, E.C. Direct measurements of multi-photon induced nonlinear lattice dynamics in semiconductors via time-resolved X-ray scattering. Sci. Rep. 2016, 6, 39506. [Google Scholar] [CrossRef]
- Paul, W.; Warschauer, D. Optical properties of semiconductors under hydrostatic pressure—II. Silicon. J. Phys. Chem. Solids 1958, 5, 102–106. [Google Scholar] [CrossRef]
- Hu, H.; Liu, M.; Wang, Z.F.; Zhu, J.; Wu, D.; Ding, H.; Liu, Z.; Liu, F. Quantum Electronic Stress: Density-Functional-Theory Formulation and Physical Manifestation. Phys. Rev. Lett. 2012, 109, 055501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Driel, H.M. Kinetics of high-density plasmas generated in Si by 1.06- and 0.53-μm picosecond laser pulses. Phys. Rev. B 1987, 35, 8166–8176. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mater. 2002, 1, 217–224. [Google Scholar] [CrossRef]
- Anisimov, S.I.; Kapeliovich, B.L.; Perelman, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Zhurnal Eksp. Teor. Fiz. 1974, 66, 776–781. [Google Scholar]
- Ames, W.F. Numerical Solution of Partial Differential Equations: Theory, Tools and Case Studies. SIAM Rev. 1986, 28, 92. [Google Scholar] [CrossRef]
- DeCamp, M.F.; Reis, D.A.; Cavalieri, A.; Bucksbaum, P.H.; Clarke, R.; Merlin, R.; Dufresne, E.M.; Arms, D.A.; Lindenberg, A.M.; MacPhee, A.G.; et al. Transient Strain Driven by a Dense Electron-Hole Plasma. Phys. Rev. Lett. 2003, 91, 165502. [Google Scholar] [CrossRef] [Green Version]
- Young, J.F.; van Driel, H.M. Ambipolar diffusion of high-density electrons and holes in Ge, Si, and GaAs: Many-body effects. Phys. Rev. B 1982, 26, 2147–2158. [Google Scholar] [CrossRef]
- Rosling, M.; Bleichner, H.; Jonsson, P.; Nordlander, E. The ambipolar diffusion coefficient in silicon: Dependence on excess-carrier concentration and temperature. J. Appl. Phys. 1994, 76, 2855–2859. [Google Scholar] [CrossRef]
- Lundstrom, M. Fundamentals of Carrier Transport, 2nd ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Mouskeftaras, A.; Chanal, M.; Chambonneau, M.; Clady, R.; Utéza, O.; Grojo, D. Direct measurement of ambipolar diffusion in bulk silicon by ultrafast infrared imaging of laser-induced microplasmas. Appl. Phys. Lett. 2016, 108, 041107. [Google Scholar] [CrossRef] [Green Version]
- Jo, W.; Landahl, E.C.; Kim, S.; Lee, D.R.; Lee, S. Delayed auger recombination in silicon measured by time-resolved X-ray scattering. Curr. Appl. Phys. 2018, 18, 1230–1234. [Google Scholar] [CrossRef]
- Lee, S.H.; Cavalieri, A.L.; Fritz, D.M.; Swan, M.C.; Hegde, R.S.; Reason, M.; Goldman, R.S.; Reis, D.A. Generation and Propagation of a Picosecond Acoustic Pulse at a Buried Interface: Time-Resolved X-ray Diffraction Measurements. Phys. Rev. Lett. 2005, 95, 246104. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, Y.; Tanaka, Y.; Kirimura, T.; Tsukuda, N.; Kuramoto, E.; Ishikawa, T. Acoustic Pulse Echoes Probed with Time-Resolved X-ray Triple-Crystal Diffractometry. Phys. Rev. Lett. 2006, 96, 115505. [Google Scholar] [CrossRef]
- Schroder, D. Carrier lifetimes in silicon. IEEE Trans. Electron Devices 1997, 44, 160–170. [Google Scholar] [CrossRef]
- Huldt, L. Band-to-band auger recombination in indirect gap semiconductors. Phys. Status Solidi 1971, 8, 173–187. [Google Scholar] [CrossRef]
- Conradt, R.; Aengenheister, J. Minority carrier lifetime in highly doped Ge. Solid State Commun. 1972, 10, 321–323. [Google Scholar] [CrossRef]
- Okada, Y.; Tokumaru, Y. Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K. J. Appl. Phys. 1984, 56, 314–320. [Google Scholar] [CrossRef]
- Okhotin, A.S.; Pushkarskij, A.S.; Gorbachev, V.V. Thermophysical Properties of Semiconductors; Atomizdat: Moscow, Russia, 1972. [Google Scholar]
- Wortman, J.J.; Evans, R.A. Young’s Modulus, Shear Modulus, and Poisson’s Ratio in Silicon and Germanium. J. Appl. Phys. 1965, 36, 153–156. [Google Scholar] [CrossRef]
- Dziewior, J.; Schmid, W. Auger coefficients for highly doped and highly excited silicon. Appl. Phys. Lett. 1977, 31, 346–348. [Google Scholar] [CrossRef]
- Slack, G.A. Thermal Conductivity of Pure and Impure Silicon, Silicon Carbide, and Diamond. J. Appl. Phys. 1964, 35, 3460–3466. [Google Scholar] [CrossRef]
- Asheghi, M.; Kurabayashi, K.; Kasnavi, R.; Goodson, K.E. Thermal conduction in doped single-crystal silicon films. J. Appl. Phys. 2002, 91, 5079–5088. [Google Scholar] [CrossRef] [Green Version]
- Ohishi, Y.; Xie, J.; Miyazaki, Y.; Aikebaier, Y.; Muta, H.; Kurosaki, K.; Yamanaka, S.; Uchida, N.; Tada, T. Thermoelectric properties of heavily boron- and phosphorus-doped silicon. Jpn. J. Appl. Phys. 2015, 54, 071301. [Google Scholar] [CrossRef]
- Makinson, R.E.B. The thermal conductivity of metals. Math. Proc. Camb. Philos. Soc. 1938, 34, 474–497. [Google Scholar] [CrossRef]
- Klemens, P. The Lattice Component of the Thermal Conductivity of Metals and Alloys. Aust. J. Phys. 1954, 7, 57–63. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Morelli, D.T.; Meisner, G.P.; Chen, W.; Dyck, J.S.; Uher, C. Influence of electron-phonon interaction on the lattice thermal conductivity of Co1−xNixSb3. Phys. Rev. B 2002, 65, 094115. [Google Scholar] [CrossRef]
- Shi, X.; Pei, Y.; Snyder, G.J.; Chen, L. Optimized thermoelectric properties of Mo3Sb7−xTex with significant phonon scattering by electrons. Energy Environ. Sci. 2011, 4, 4086–4095. [Google Scholar] [CrossRef] [Green Version]
- Liao, B.; Qiu, B.; Zhou, J.; Huberman, S.; Esfarjani, K.; Chen, G. Significant Reduction of Lattice Thermal Conductivity by the Electron-Phonon Interaction in Silicon with High Carrier Concentrations: A First-Principles Study. Phys. Rev. Lett. 2015, 114, 115901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Q.; Zhou, J.; Liu, T.H.; Chen, G. Effect of electron-phonon interaction on lattice thermal conductivity of SiGe alloys. Appl. Phys. Lett. 2019, 115, 023903. [Google Scholar] [CrossRef]


| Parameter | Used Value | Literature Value |
|---|---|---|
| One photon absorption coefficient ( [cm−1]) | [28] | [28] |
| Two photon absorption coefficient ( [cm/GW]) | 9 [28] | 9 [28] |
| Deformation potential coefficient ( [eV/Pa]) | [30] | |
| Ambipolar diffusion coefficient ( [cm2/s]) | 2.4 | 2.5 [40] |
| Radiative recombination rate ( [cm3/s]) | [44] | [44] |
| Auger recombination rate ( [cm6/s]) | ∼ [41,44,45,46] | |
| Thermal expansion coefficient ( [C°−1] ) | [47] | [47] |
| Specific heat ( [J/gC°]) | 0.7 [48] | 0.7 [48] |
| Young’s Modulus for [100] ( [GPa]) | 130 [49] | 130 [49] |
| Bulk Modulus ( [GPa]) | 98 [49] | 98 [49] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, W.; Cho, Y.C.; Kim, S.; Landahl, E.C.; Lee, S. Reduced Thermal Conductivity in Ultrafast Laser Heated Silicon Measured by Time-Resolved X-ray Diffraction. Crystals 2021, 11, 186. https://doi.org/10.3390/cryst11020186
Jo W, Cho YC, Kim S, Landahl EC, Lee S. Reduced Thermal Conductivity in Ultrafast Laser Heated Silicon Measured by Time-Resolved X-ray Diffraction. Crystals. 2021; 11(2):186. https://doi.org/10.3390/cryst11020186
Chicago/Turabian StyleJo, Wonhyuk, Yong Chan Cho, Seongheun Kim, Eric Carl Landahl, and Sooheyong Lee. 2021. "Reduced Thermal Conductivity in Ultrafast Laser Heated Silicon Measured by Time-Resolved X-ray Diffraction" Crystals 11, no. 2: 186. https://doi.org/10.3390/cryst11020186
APA StyleJo, W., Cho, Y. C., Kim, S., Landahl, E. C., & Lee, S. (2021). Reduced Thermal Conductivity in Ultrafast Laser Heated Silicon Measured by Time-Resolved X-ray Diffraction. Crystals, 11(2), 186. https://doi.org/10.3390/cryst11020186








