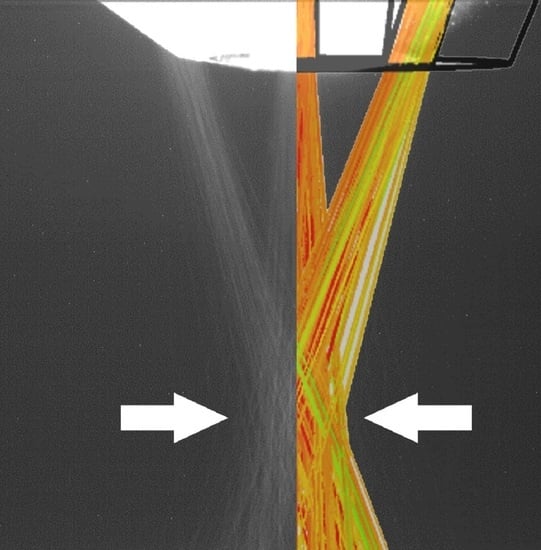
Numerical Study on Powder Stream Characteristics of Coaxial Laser Metal Deposition Nozzle
Abstract
:1. Introduction
| Ref. | Model Type | Software | Gas Flow | Powder Stream |
|---|---|---|---|---|
| Lin (2000) [2] | 2D | Fluent | k-ε model | Discrete Phase Model (DPM) |
| Pinkerton and Li (2004) [3] | mathematical model | |||
| Pan et al. (2005) [4] | 2D | Not mentioned | No gas | Stochastic model |
| Pan et al. (2006) [5] | 2D | Fluent | k-ε model | DPM |
| Zekovic et al. (2007) [6] | 3D | Fluent | k-ε model | DPM |
| Wen et al. (2009) [7] | 2D | Fluent | k-ε model | DPM |
| Tabernero et al. (2010) [8] | 3D | Fluent | k-ε model | DPM |
| Zhu et al. (2011) [9] | 2D | Fluent | k-ε model | DPM |
| Smurov et al. (2012) [10] | 2D | Not mentioned | ||
| Kovaleva et al. (2013) [11] | 2D | Not mentioned | self-created | |
| Nie et al. (2014) [12] | 2D | Fluent | k-ε model | DPM |
| Arrizubiteta et al. (2014) [13] | 3D | Fluent | k-ε model | DPM |
| Liu et al. (2016) [14] | 3D | Fluent | k-ε model | DPM |
| Zhang el al. (2016) [15] | 3D | Fluent | k-ε model | DPM |
| Koruba et al. (2018) [16] | 2D | Fluent | k-ε model | DPM |
| Ju et al. (2019) [17] | 3D | Fluent | Eulerian two-fluid models | DPM |
| Guo et al. (2020) [18] | 3D | Fluent | k-ε model | DPM |
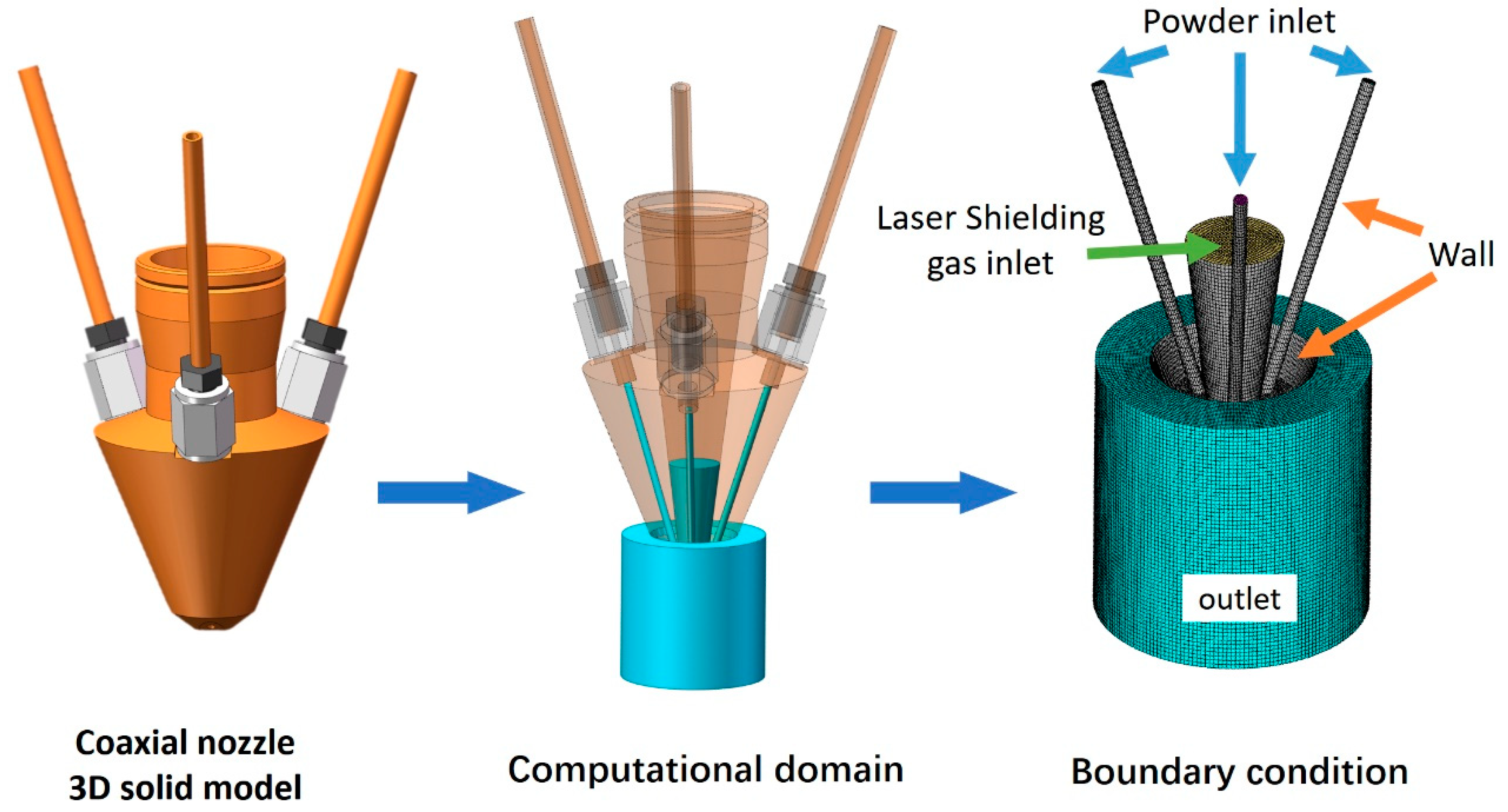
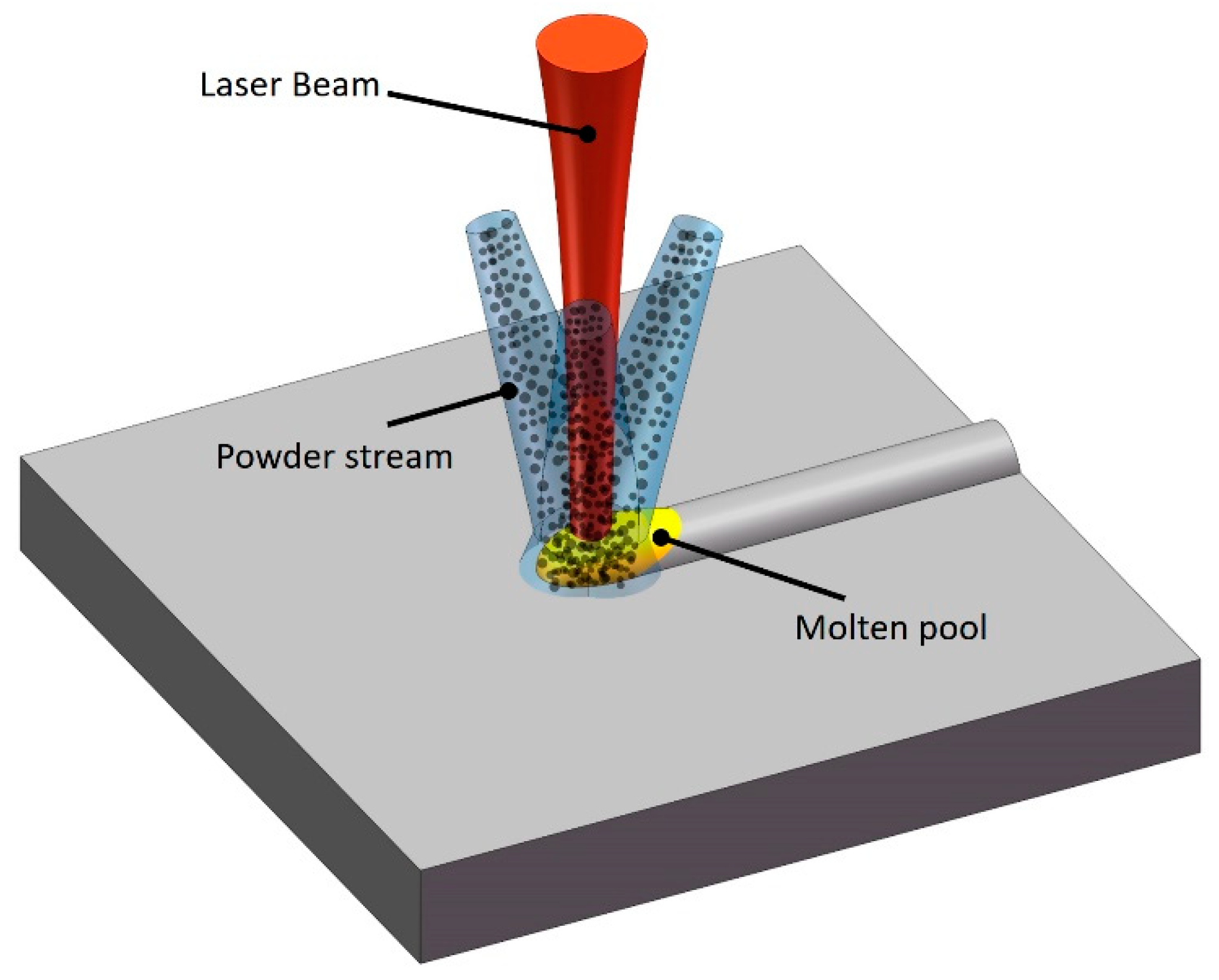
2. Research Method
3. Result and Discussion
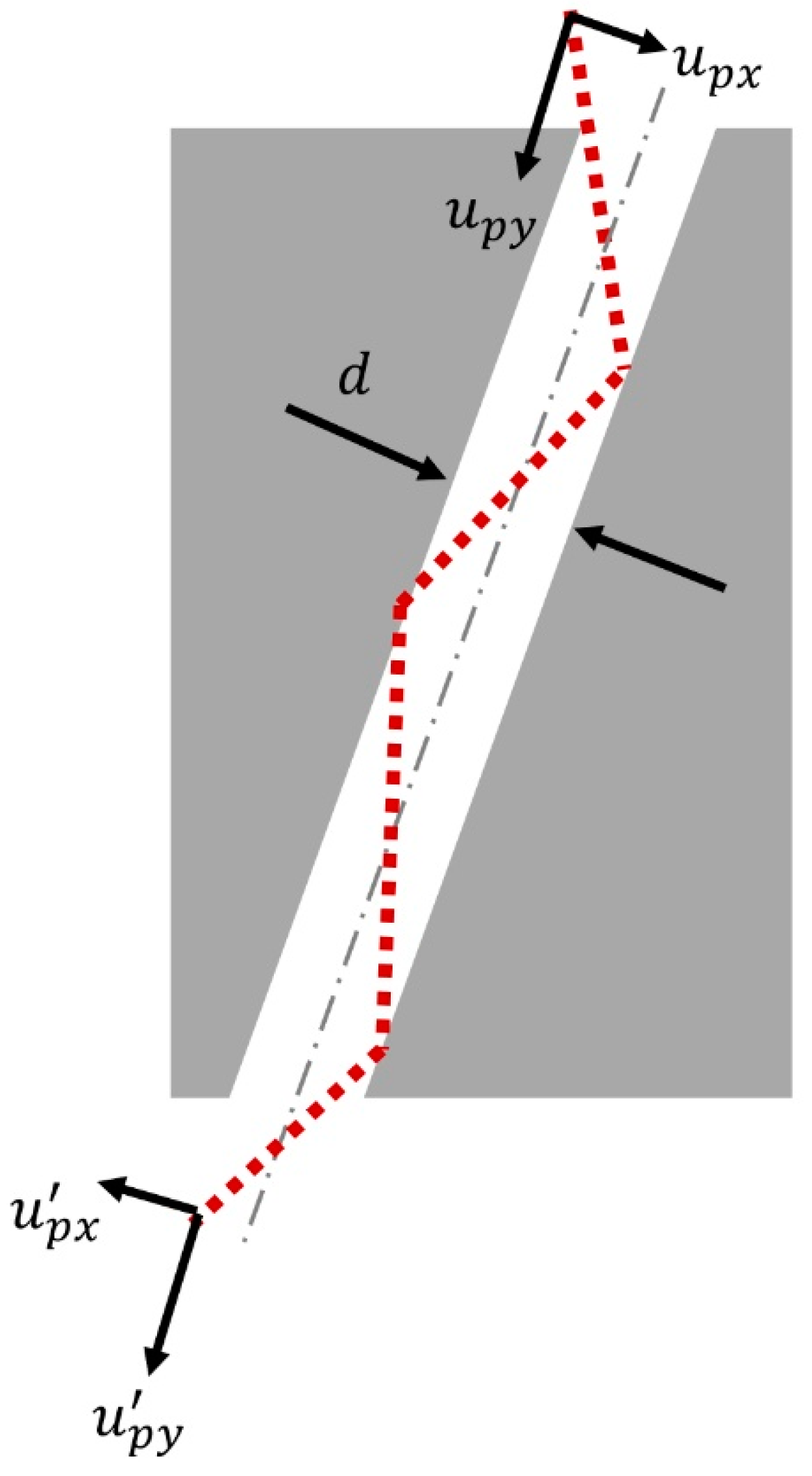
3.1. Collision between Powders and Passage Inner Wall
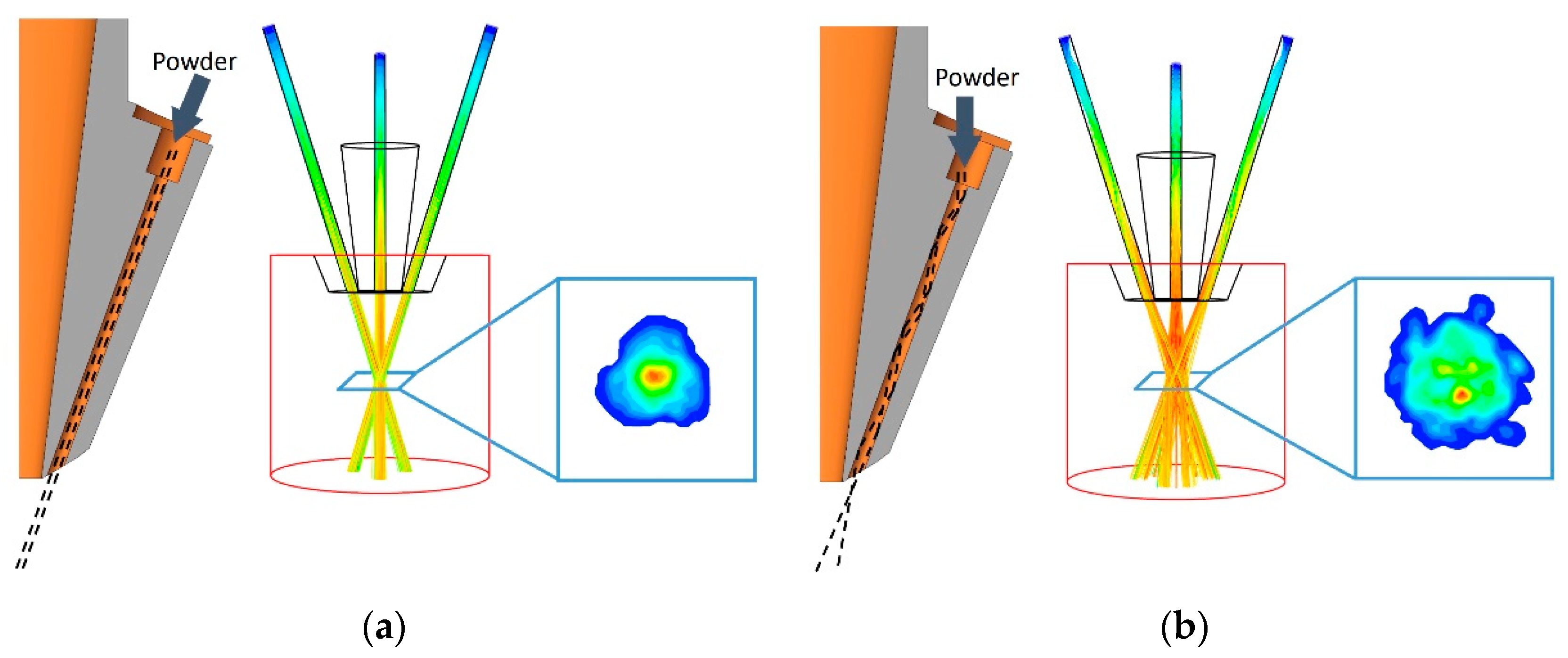
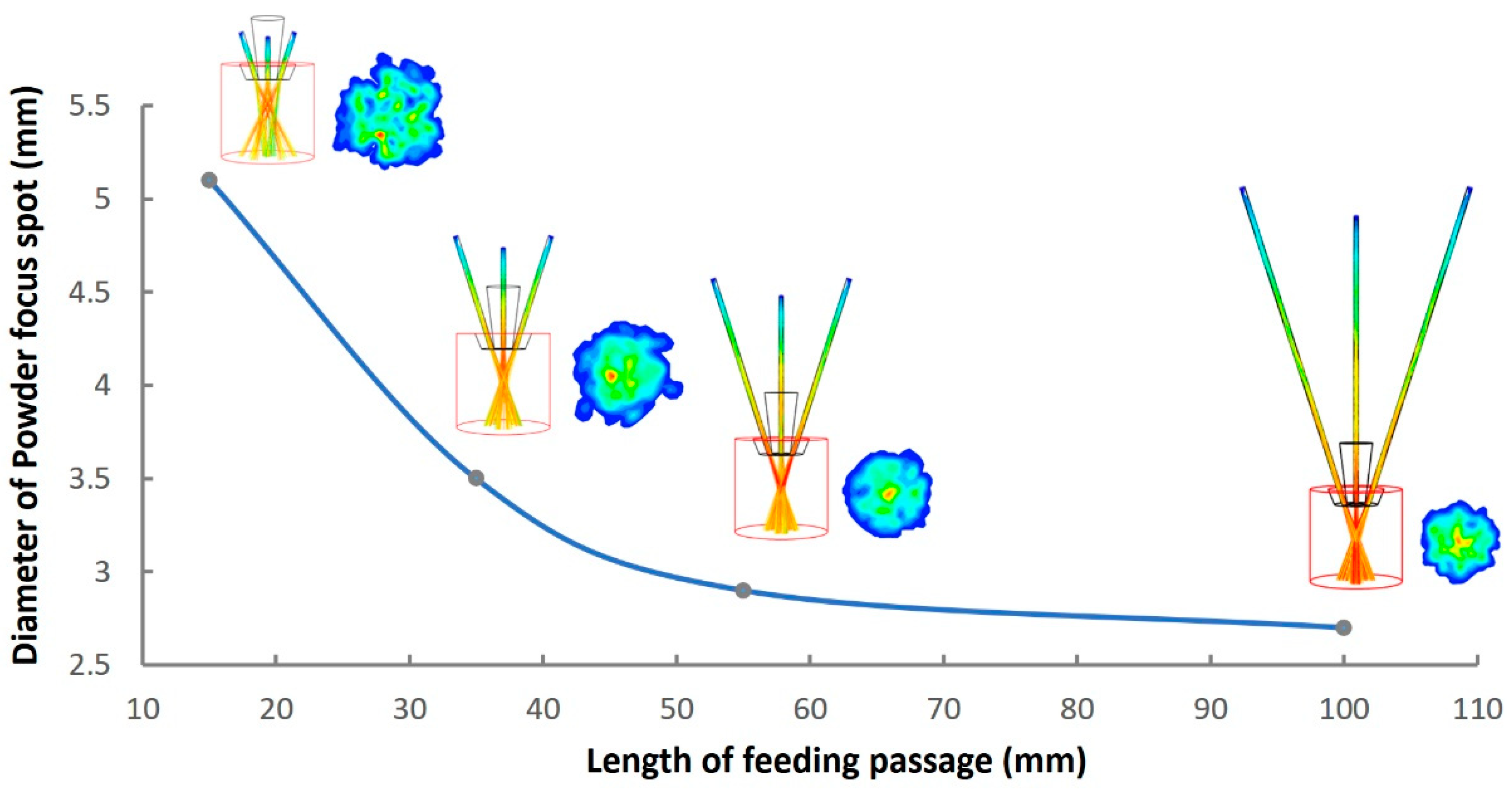
3.2. The Influence of Nozzle Structure Parameters
3.2.1. Passage Length
3.2.2. Passage Diameter
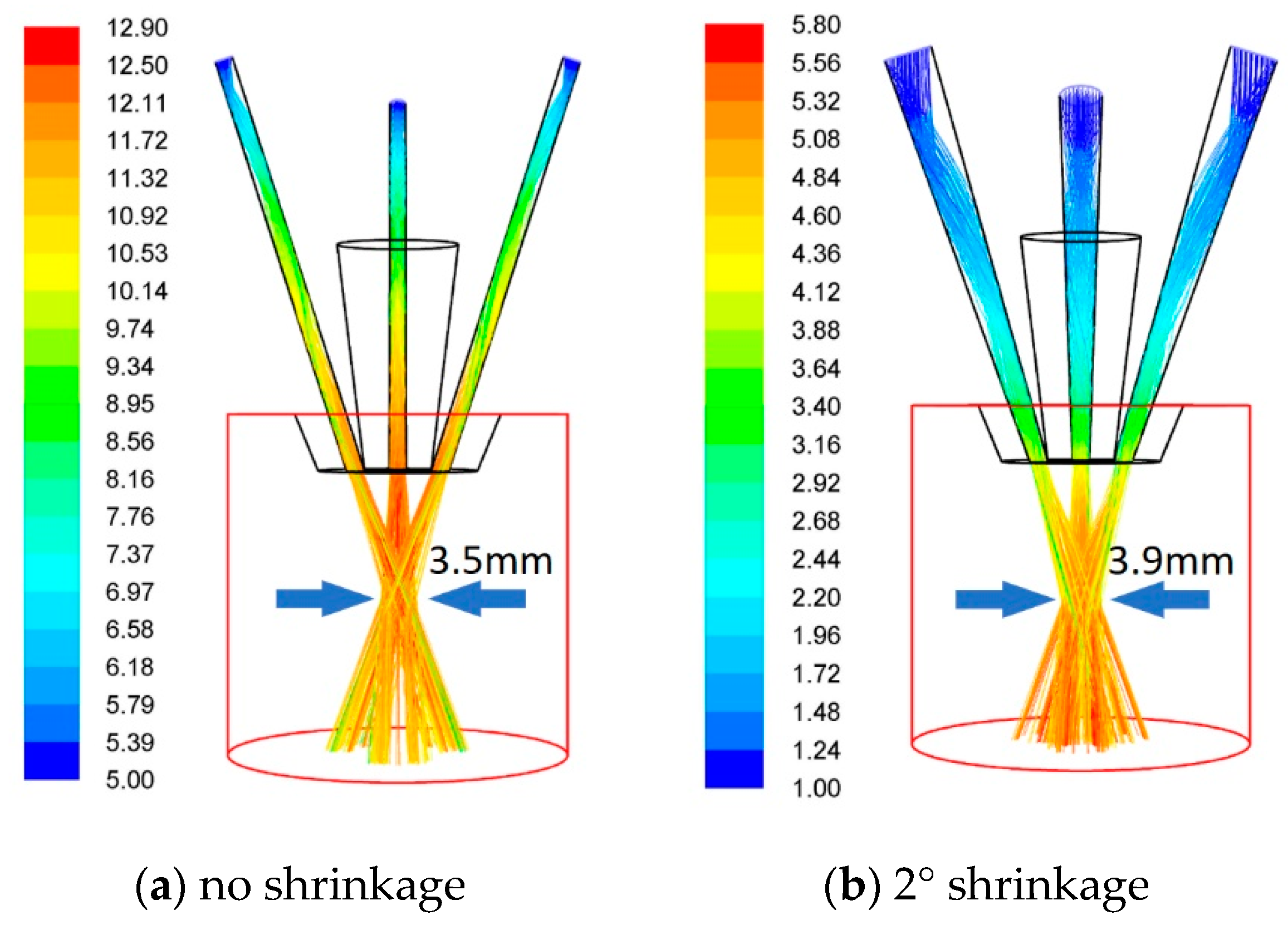
3.2.3. Passage Shrinkage
3.3. The Influence of Process Parameters
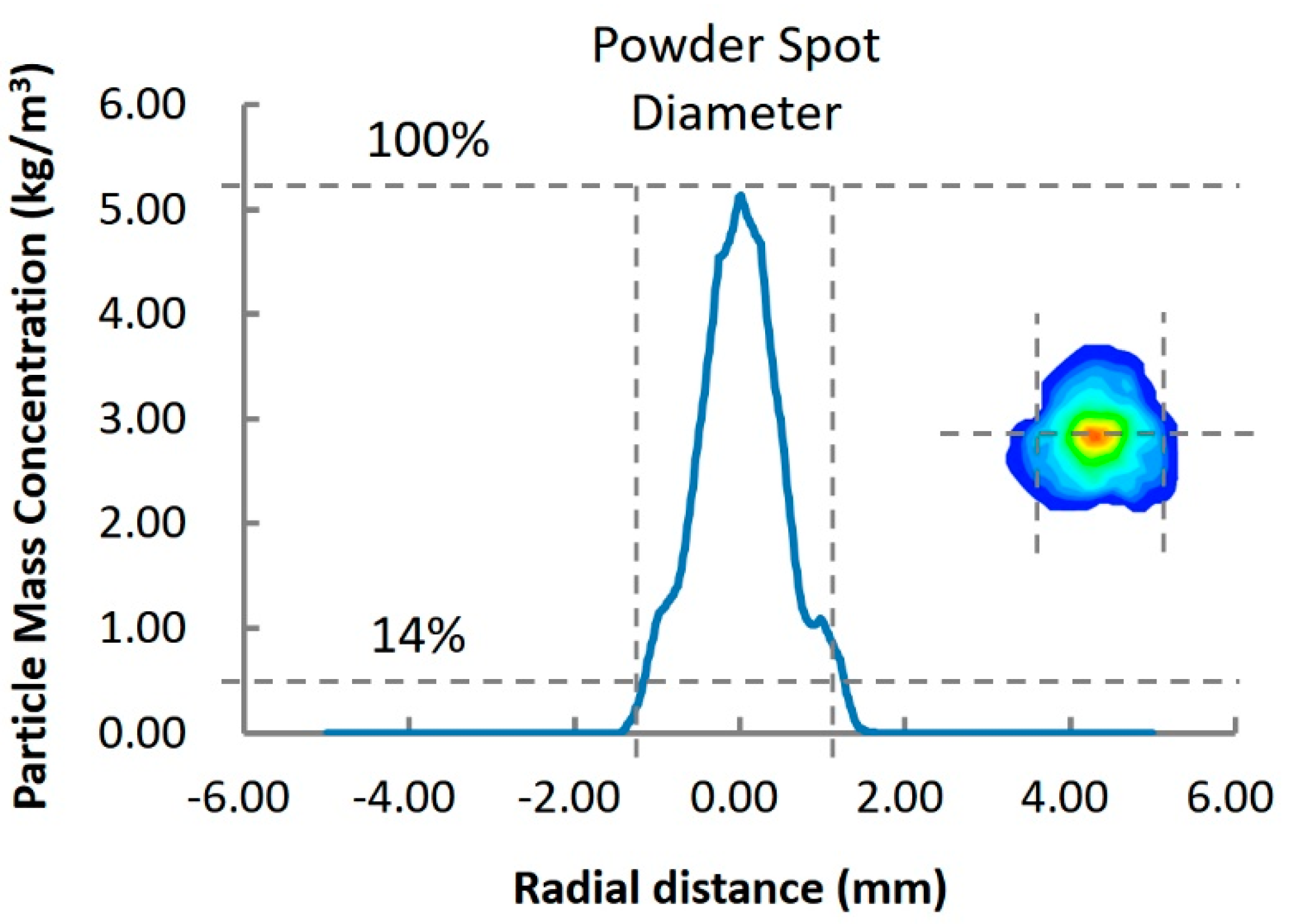
3.3.1. Particle Size Distribution
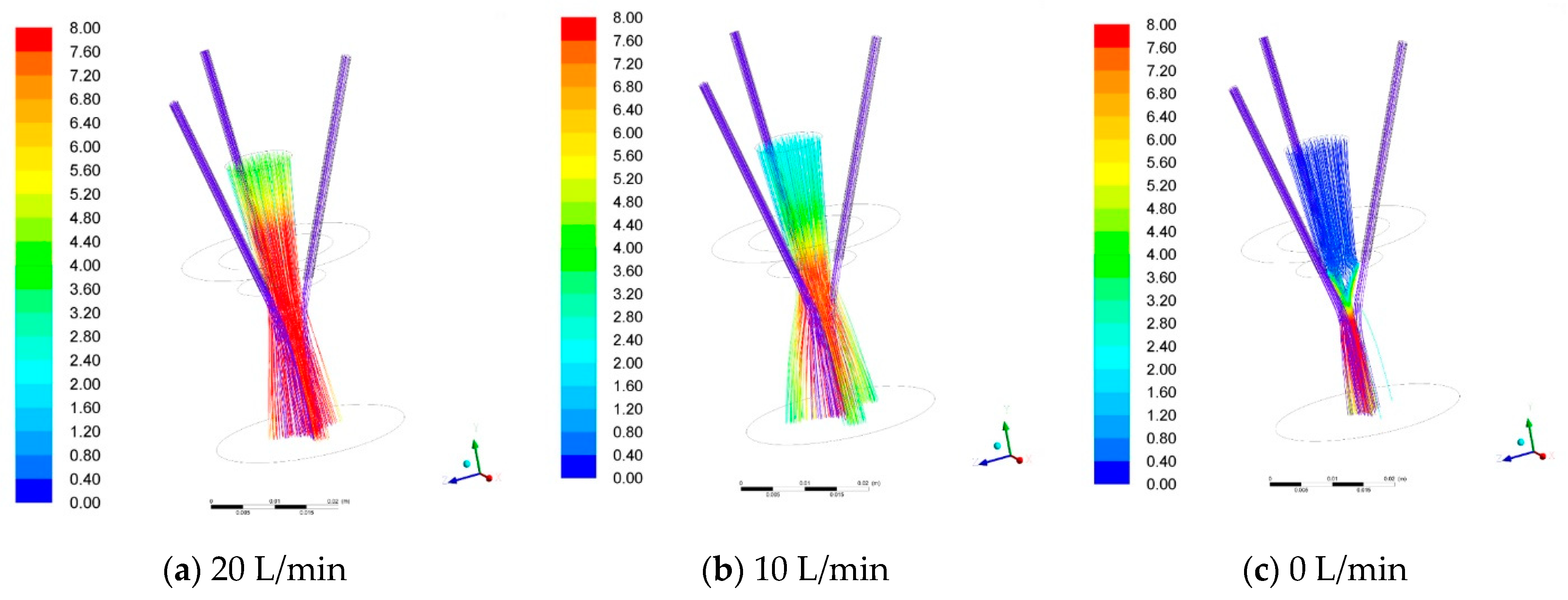
3.3.2. Inner Laser Shielding Gas
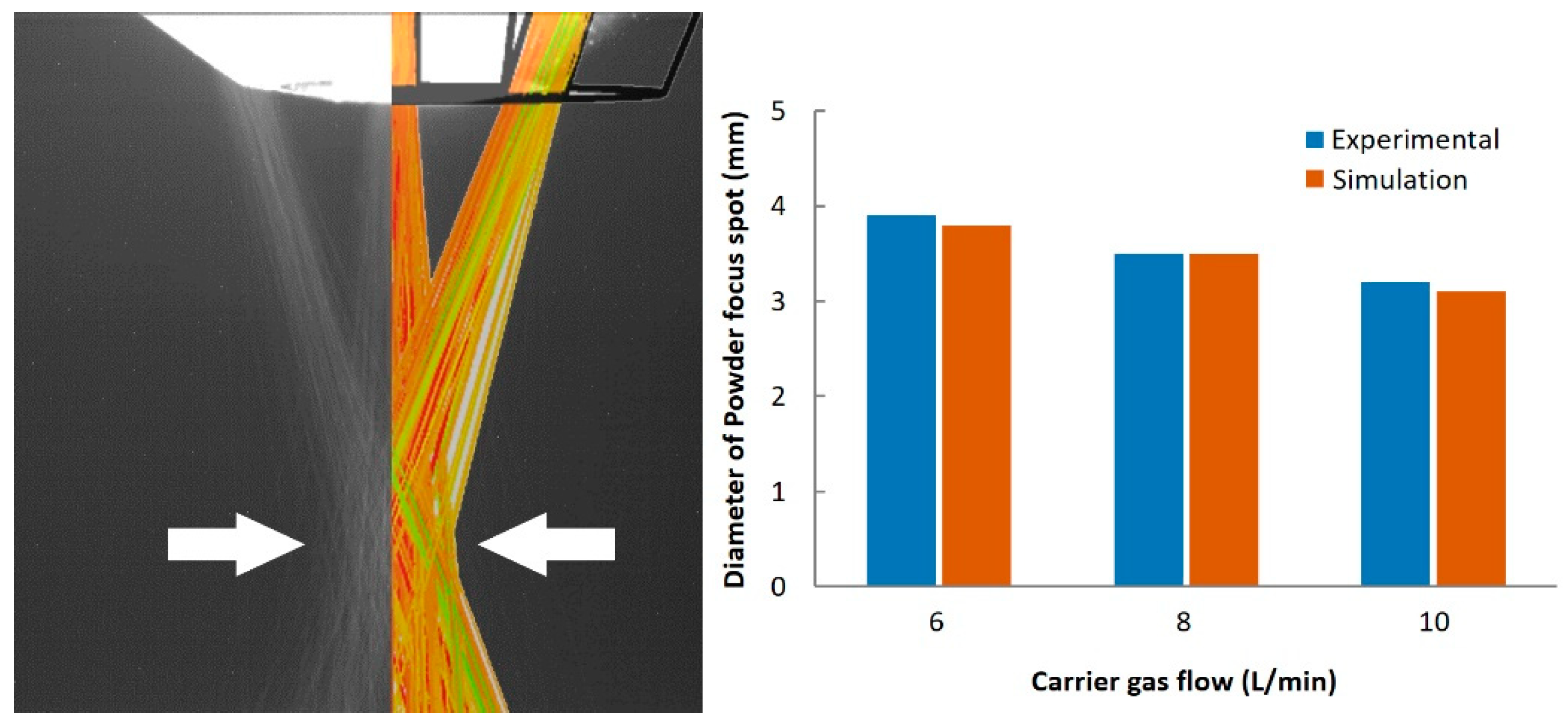
3.4. The Principle of Powder Spot Size Control
4. Conclusions
5. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tamanna, N.; Crouch, R.; Naher, S. Progress in numerical simulation of the laser cladding process. Opt. Lasers Eng. 2019, 122, 151–163. [Google Scholar] [CrossRef]
- Lin, J. Numerical simulation of the focused powder streams in coaxial laser cladding. J. Mater. Process. Technol. 2000, 105, 17–23. [Google Scholar] [CrossRef]
- Pinkerton, A.J.; Li, L. Modelling powder concentration distribution from a coaxial deposition nozzle for laser-based rapid tooling. J. Manuf. Sci. Eng. 2004, 126, 33–41. [Google Scholar] [CrossRef]
- Pan, H.; Liou, F. Numerical simulation of metallic powder flow in a coaxial nozzle for the laser aided deposition process. J. Mater. Process. Technol. 2005, 168, 230–244. [Google Scholar] [CrossRef]
- Pan, H.; Sparks, T.; Thakar, Y.D.; Liou, F. The investigation of gravity-driven metal powder flow in coaxial nozzle for laser-aided direct metal deposition process. J. Manuf. Sci. Eng. 2006, 128, 541–553. [Google Scholar] [CrossRef]
- Zekovic, S.; Dwivedi, R.; Kovacevic, R. Numerical simulation and experimental investigation of gas–powder flow from radially symmetrical nozzles in laser-based direct metal deposition. Int. J. Mach. Tools Manuf. 2007, 47, 112–123. [Google Scholar] [CrossRef]
- Wen, S.Y.; Shin, Y.C.; Murthy, J.Y.; Sojka, P.E. Modeling of coaxial powder flow for the laser direct deposition process. Int. J. Heat Mass Transf. 2009, 52, 5867–5877. [Google Scholar] [CrossRef]
- Tabernero, I.; Lamikiz, A.; Ukar, E.; De Lacalle, L.L.; Angulo, C.; Urbikain, G. Numerical simulation and experimental validation of powder flux distribution in coaxial laser cladding. J. Mater. Process. Technol. 2010, 210, 2125–2134. [Google Scholar] [CrossRef]
- Zhu, G.; Li, D.; Zhang, A.; Tang, Y. Numerical simulation of metallic powder flow in a coaxial nozzle in laser direct metal deposition. Opt. Laser Technol. 2011, 43, 106–113. [Google Scholar] [CrossRef]
- Kovaleva, I.; Kovalev, O.; Zaitsev, A.; Smurov, I. Numerical simulation and comparison of powder jet profiles different types of coaxial nozzles in direct material deposition. Phys. Procedia 2013, 41, 870–872. [Google Scholar] [CrossRef] [Green Version]
- Smurov, I.; Doubenskaia, M.; Zaitsev, A. Complex analysis of laser cladding based on comprehensive optical diagnostics and numerical simulation. Phys. Procedia 2012, 39, 743–752. [Google Scholar] [CrossRef] [Green Version]
- Nie, P.; Ojo, O.A.; Li, Z. Modeling analysis of laser cladding of a nickel-based superalloy. Surf. Coat. Technol. 2014, 258, 1048–1059. [Google Scholar] [CrossRef]
- Arrizubieta, J.I.; Tabernero, I.; Ruiz, J.E.; Lamikiz, A.; Martínez, S.; Ukar, E. Continuous coaxial nozzle design for LMD based on numerical simulation. Phys. Procedia 2014, 56, 429–438. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Qi, H.; Jiang, L. Control of crystal orientation and continuous growth through inclination of coaxial nozzle in laser powder deposition of single-crystal superalloy. J. Mater. Process. Technol. 2016, 230, 177–186. [Google Scholar] [CrossRef]
- Zhang, B.; Coddet, C. Numerical study on the effect of pressure and nozzle dimension on particle distribution and velocity in laser cladding under vacuum base on CFD. J. Manuf. Process. 2016, 23, 54–60. [Google Scholar] [CrossRef]
- Koruba, P.; Wall, K.; Reiner, J. Influence of processing gases in laser cladding based on simulation analysis and experimental tests. Procedia CIRP 2018, 74, 719–723. [Google Scholar] [CrossRef]
- Ju, H.; Zhang, Z.J.; Lin, C.X.; Liu, Z.J. Design optimization and experimental study of coaxial powder-feeding nozzle in the laser cladding process. IOP Conf. Ser. Mater. Sci. Eng. 2019, 474, 012008. [Google Scholar] [CrossRef]
- Guo, S.R.; Yin, Q.Q.; Cui, L.J.; Xiao, L.L.; Cui, Y.H.; Zheng, B.; Cao, Y.L.; Zeng, W.Z. Simulation and experimental research based on carrier gas flow rate on the influence of four-channel coaxial nozzle flow field. Meas. Control 2020, 53, 9–10. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An Investigation of Particle Trajectories in Two-Phase Flow Systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
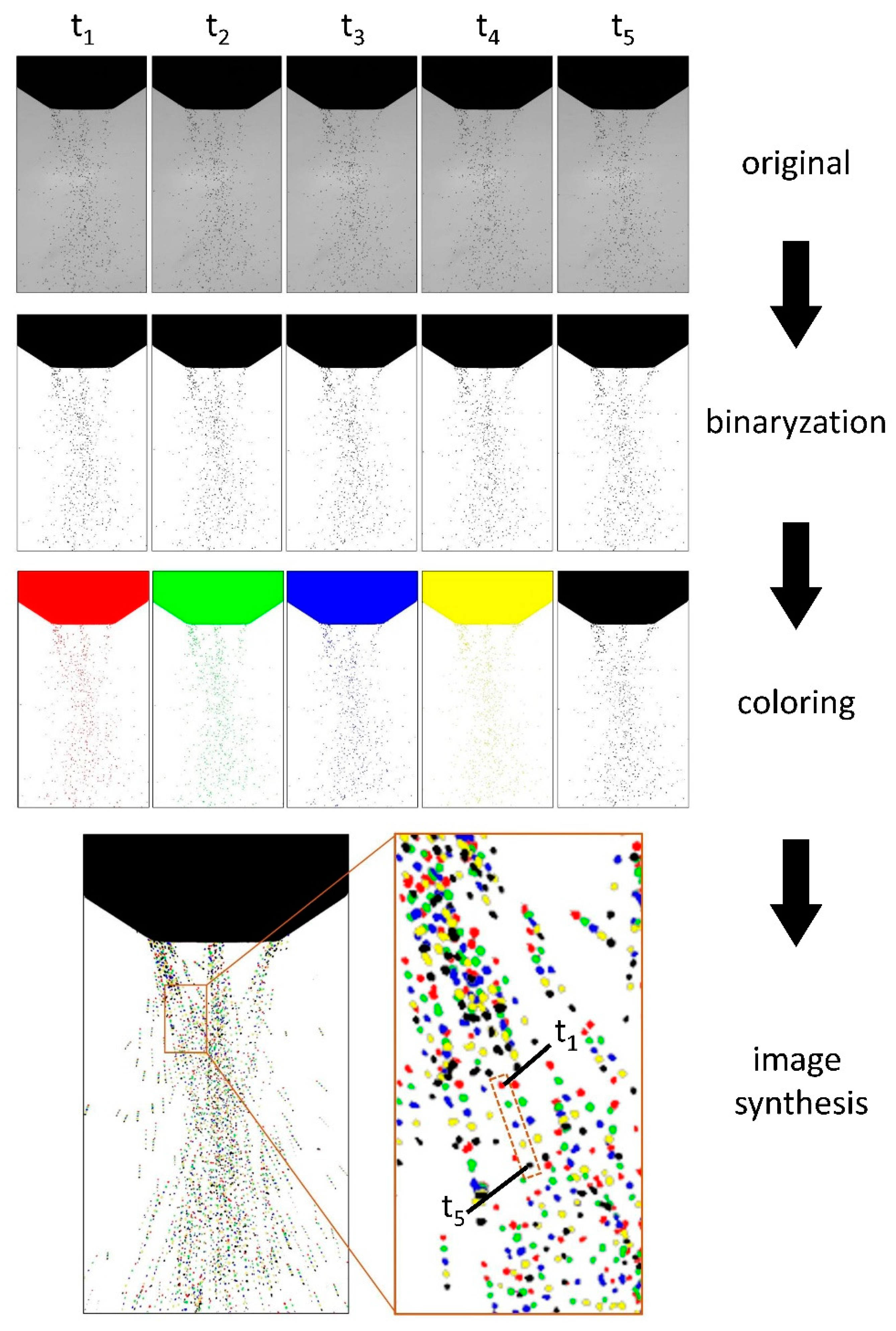
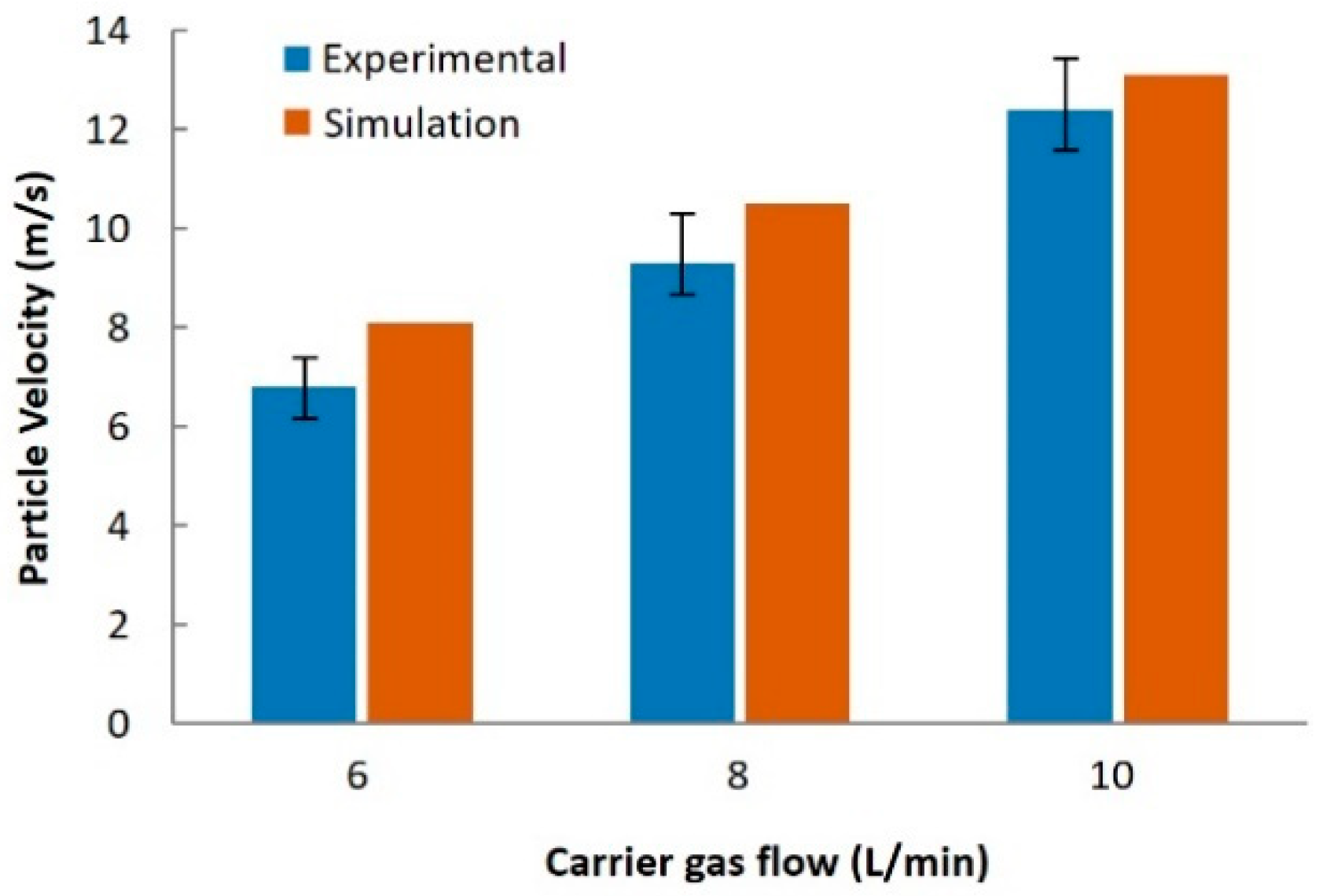



| Powder Material | Ti6Al4V |
| Powder Size | 75 μm, Spherical |
| Powder Flow Rate | 5 g/min |
| Particle Carrier Gas Flow Rate | 8 L/min |
| Inner Shielding Gas Flow Rate | 10 L/min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Huang, Y.; Zou, C.; Tao, W. Numerical Study on Powder Stream Characteristics of Coaxial Laser Metal Deposition Nozzle. Crystals 2021, 11, 282. https://doi.org/10.3390/cryst11030282
Li L, Huang Y, Zou C, Tao W. Numerical Study on Powder Stream Characteristics of Coaxial Laser Metal Deposition Nozzle. Crystals. 2021; 11(3):282. https://doi.org/10.3390/cryst11030282
Chicago/Turabian StyleLi, Liqun, Yichen Huang, Chunyu Zou, and Wang Tao. 2021. "Numerical Study on Powder Stream Characteristics of Coaxial Laser Metal Deposition Nozzle" Crystals 11, no. 3: 282. https://doi.org/10.3390/cryst11030282
APA StyleLi, L., Huang, Y., Zou, C., & Tao, W. (2021). Numerical Study on Powder Stream Characteristics of Coaxial Laser Metal Deposition Nozzle. Crystals, 11(3), 282. https://doi.org/10.3390/cryst11030282