Electro-Optic Control of Lithium Niobate Bulk Whispering Gallery Resonators: Analysis of the Distribution of Externally Applied Electric Fields
Abstract
:1. Introduction
2. Materials and Methods
3. Results
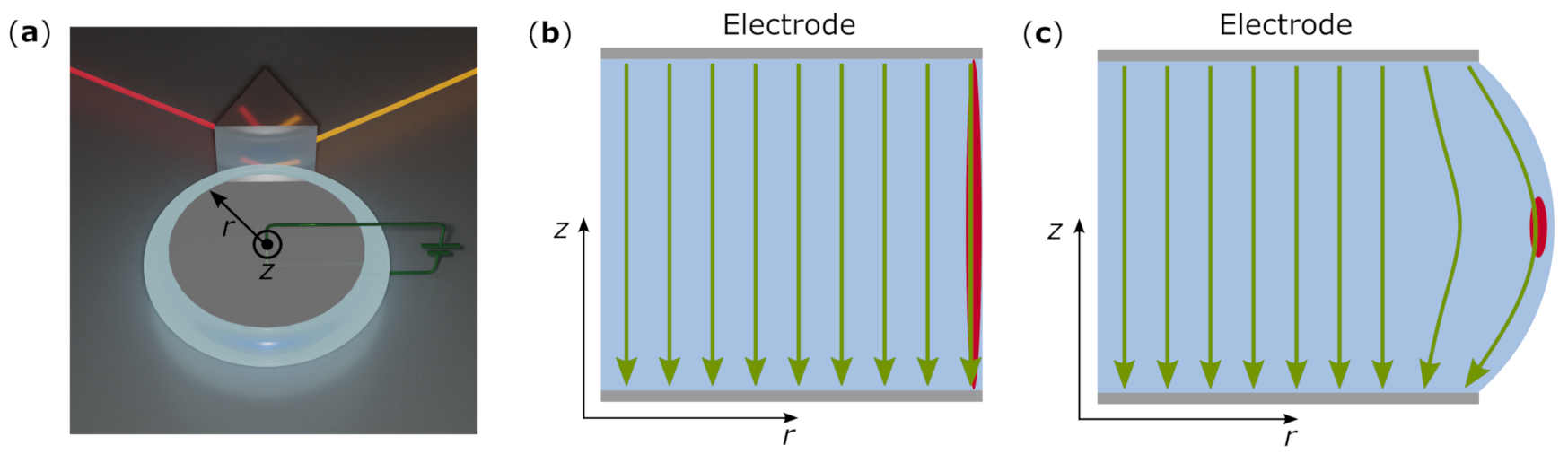
3.1. Conventional Resonator Geometry
3.2. Few-Mode Resonator
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Whispering gallery resonator | WGR |
Appendix A. Bézier Curve
References
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: Burlington, MA, USA, 2008. [Google Scholar]
- Schliesser, A.; Picqué, N.; Hänsch, T.W. Mid-infrared frequency combs. Nat. Photonics 2012, 6, 440–449. [Google Scholar] [CrossRef] [Green Version]
- Vainio, M.; Halonen, L. Mid-infrared optical parametric oscillators and frequency combs for molecular spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 4266–4294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lemos, G.B.; Borish, V.; Cole, G.D.; Ramelow, S.; Lapkiewicz, R.; Zeilinger, A. Quantum imaging with undetected photons. Nature 2014, 512, 409–412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalashnikov, D.A.; Paterova, A.V.; Kulik, S.P.; Krivitsky, L.A. Infrared spectroscopy with visible light. Nat. Photonics 2016, 10, 98–101. [Google Scholar] [CrossRef] [Green Version]
- Sowade, R.; Breunig, I.; Camara Mayorga, I.; Kiessling, J.; Tulea, C.; Dierolf, V.; Buse, K. Continuous-wave optical parametric terahertz source. Opt. Express 2009, 17, 22303. [Google Scholar] [CrossRef]
- Sowade, R.; Kießling, J.; Breunig, I. One light source—All colors. Opt. Photonik 2013, 8, 46–49. [Google Scholar] [CrossRef]
- He, Y.; Yang, Q.F.; Ling, J.; Luo, R.; Liang, H.; Li, M.; Shen, B.; Wang, H.; Vahala, K.; Lin, Q. Self-starting bi-chromatic LiNbO3 soliton microcomb. Optica 2019, 6, 1138. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Zhang, M.; Yu, M.; Zhu, R.; Hu, H.; Loncar, M. Monolithic lithium niobate photonic circuits for Kerr frequency comb generation and modulation. Nat. Commun. 2019, 10, 978. [Google Scholar] [CrossRef]
- Szabados, J.; Puzyrev, D.N.; Minet, Y.; Reis, L.; Buse, K.; Villois, A.; Skryabin, D.V.; Breunig, I. Frequency comb generation via cascaded second-order nonlinearities in microresonators. Phys. Rev. Lett. 2020, 124, 203902. [Google Scholar] [CrossRef]
- Hendry, I.; Trainor, L.S.; Xu, Y.; Coen, S.; Murdoch, S.G.; Schwefel, H.G.L.; Erkintalo, M. Experimental observation of internally pumped parametric oscillation and quadratic comb generation in a χ(2) whispering-gallery-mode microresonator. Opt. Lett. 2020, 45, 1204–1207. [Google Scholar] [CrossRef]
- Zhang, M.; Buscaino, B.; Wang, C.; Shams-Ansari, A.; Reimer, C.; Zhu, R.; Kahn, J.M.; Lončar, M. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 2019, 568, 373–377. [Google Scholar] [CrossRef]
- Rueda, A.; Sedlmeir, F.; Kumari, M.; Leuchs, G.; Schwefel, H.G.L. Resonant electro-optic frequency comb. Nature 2019, 568, 378–381. [Google Scholar] [CrossRef]
- Breunig, I. Three-wave mixing in whispering gallery resonators. Laser Photonics Rev. 2016, 10, 569–587. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Marquardt, C.; Matsko, A.B.; Schwefel, H.G.L.; Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 2016, 18, 123002. [Google Scholar] [CrossRef] [Green Version]
- Rueda, A.; Sedlmeir, F.; Collodo, M.C.; Vogl, U.; Stiller, B.; Schunk, G.; Strekalov, D.V.; Marquardt, C.; Fink, J.M.; Painter, O.; et al. Efficient microwave to optical photon conversion: An electro-optical realization. Optica 2016, 3, 597. [Google Scholar] [CrossRef]
- Minet, Y.; Reis, L.; Szabados, J.; Werner, C.S.; Zappe, H.; Buse, K.; Breunig, I. Pockels-effect-based adiabatic frequency conversion in ultrahigh-Q microresonators. Opt. Express 2020, 28, 2939–2947. [Google Scholar] [CrossRef] [PubMed]
- Savchenkov, A.A.; Ilchenko, V.S.; Matsko, A.B.; Maleki, L. High-order tunable filters based on a chain of coupled crystalline whispering gallery-mode resonators. IEEE Photonics Technol. Lett. 2005, 17, 136–138. [Google Scholar] [CrossRef]
- Fürst, J.U.; Strekalov, D.V.; Elser, D.; Lassen, M.; Andersen, U.L.; Marquardt, C.; Leuchs, G. Naturally phase-matched second-harmonic generation in a whispering-gallery-mode resonator. Phys. Rev. Lett. 2010, 104, 153901. [Google Scholar] [CrossRef] [Green Version]
- Szabados, J.; Sturman, B.; Breunig, I. Frequency comb generation threshold via second-harmonic excitation in χ(2) optical microresonators. APL Photonics 2020, 5, 116102. [Google Scholar] [CrossRef]
- Ferdous, F.; Demchenko, A.A.; Vyatchanin, S.P.; Matsko, A.B.; Maleki, L. Microcavity morphology optimization. Phys. Rev. A 2014, 90. [Google Scholar] [CrossRef]
- Grudinin, I.S.; Yu, N. Dispersion engineering of crystalline resonators via microstructuring. Optica 2015, 2, 221. [Google Scholar] [CrossRef]
- Archambeault, B.; Brench, C.; Ramahi, O.M. (Eds.) EMI/EMC Computational Modeling Handbook, 2nd ed.; The Springer International Series in Engineering and Computer Science; Springer: Boston, MA, USA, 2001; Volume 630. [Google Scholar] [CrossRef]
- Weis, R.S.; Gaylord, T.K. Lithium niobate: Summary of physical properties and crystal structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Savchenkov, A.A.; Matsko, A.B.; Yu, N. Efficient upconversion of subterahertz radiation in a high-Q whispering gallery resonator. Opt. Lett. 2009, 34, 713–715. [Google Scholar] [CrossRef] [Green Version]
- Luennemann, M.; Hartwig, U.; Panotopoulos, G.; Buse, K. Electrooptic properties of lithium niobate crystals for extremely high external electric fields. Appl. Phys. B 2003, 76, 403–406. [Google Scholar] [CrossRef]
- Tipler, P.A. College Physics; Worth: New York, NY, USA, 1987; p. 467. [Google Scholar]
- Umemura, N.; Matsuda, D.; Mizuno, T.; Kato, K. Sellmeier and thermo-optic dispersion formulas for the extraordinary ray of 5 mol.% MgO-doped congruent LiNbO3 in the visible, infrared, and terahertz regions. Appl. Opt. 2014, 53, 5726–5732. [Google Scholar] [CrossRef]
- Abarkan, M.; Aillerie, M.; Kokanyan, N.; Teyssandier, C.; Kokanyan, E. Electro-optic and dielectric properties of zirconium-doped congruent lithium–niobate crystals. Opt. Mater. Express 2014, 4, 179. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minet, Y.; Zappe, H.; Breunig, I.; Buse, K. Electro-Optic Control of Lithium Niobate Bulk Whispering Gallery Resonators: Analysis of the Distribution of Externally Applied Electric Fields. Crystals 2021, 11, 298. https://doi.org/10.3390/cryst11030298
Minet Y, Zappe H, Breunig I, Buse K. Electro-Optic Control of Lithium Niobate Bulk Whispering Gallery Resonators: Analysis of the Distribution of Externally Applied Electric Fields. Crystals. 2021; 11(3):298. https://doi.org/10.3390/cryst11030298
Chicago/Turabian StyleMinet, Yannick, Hans Zappe, Ingo Breunig, and Karsten Buse. 2021. "Electro-Optic Control of Lithium Niobate Bulk Whispering Gallery Resonators: Analysis of the Distribution of Externally Applied Electric Fields" Crystals 11, no. 3: 298. https://doi.org/10.3390/cryst11030298
APA StyleMinet, Y., Zappe, H., Breunig, I., & Buse, K. (2021). Electro-Optic Control of Lithium Niobate Bulk Whispering Gallery Resonators: Analysis of the Distribution of Externally Applied Electric Fields. Crystals, 11(3), 298. https://doi.org/10.3390/cryst11030298





