Isotope Effect in Thermal Conductivity of Polycrystalline CVD-Diamond: Experiment and Theory
Abstract
1. Introduction
2. Materials and Methods
3. Results
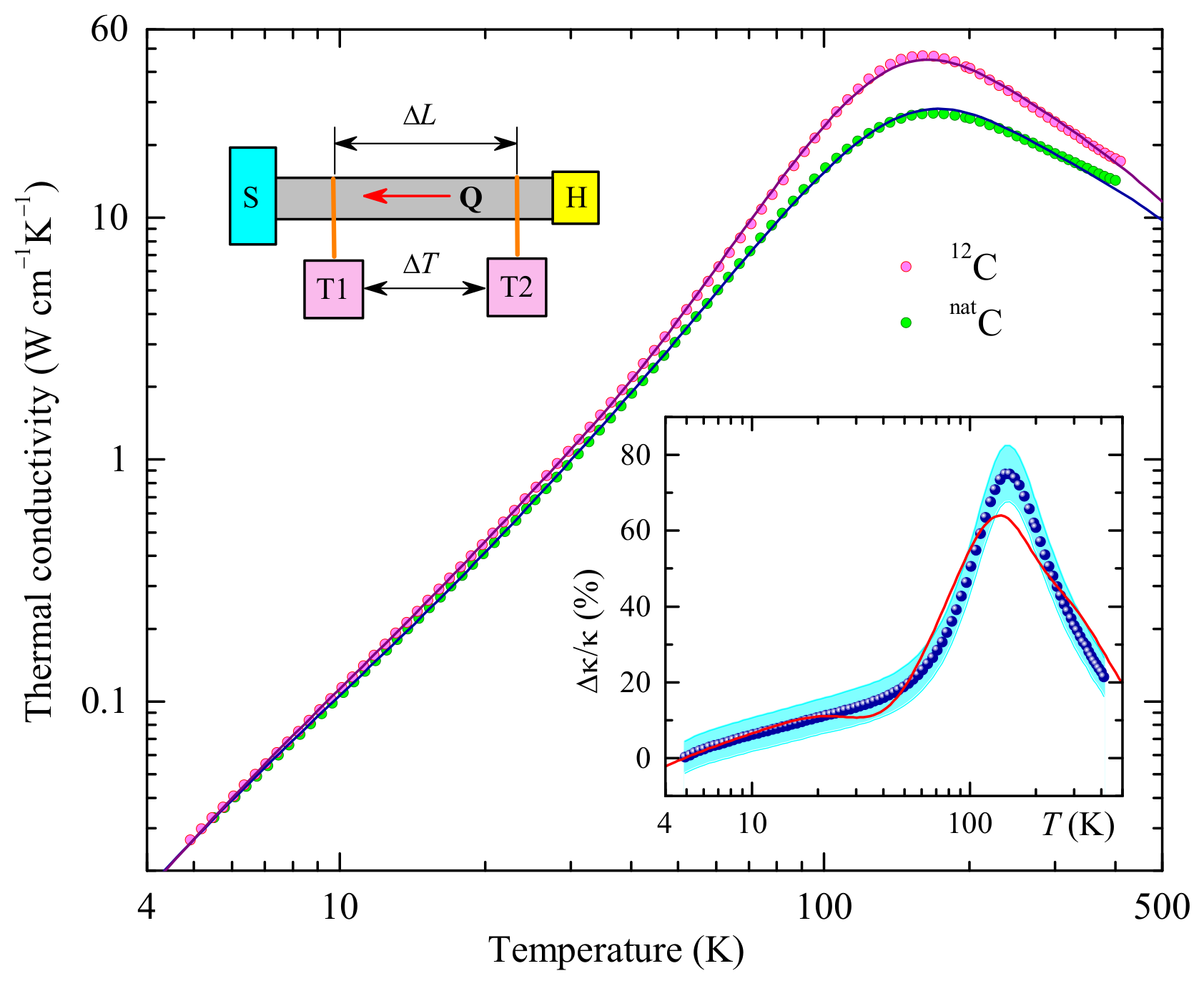
3.1. Thermal Conductivity: Experimental Data
3.2. Modeling
3.2.1. External Boundaries
3.2.2. Point Defects and C Isotopes
3.2.3. Dislocations
3.2.4. Charge Carriers Bound to Dopant Centers
3.2.5. Grain Boundaries and Intergrain Regions
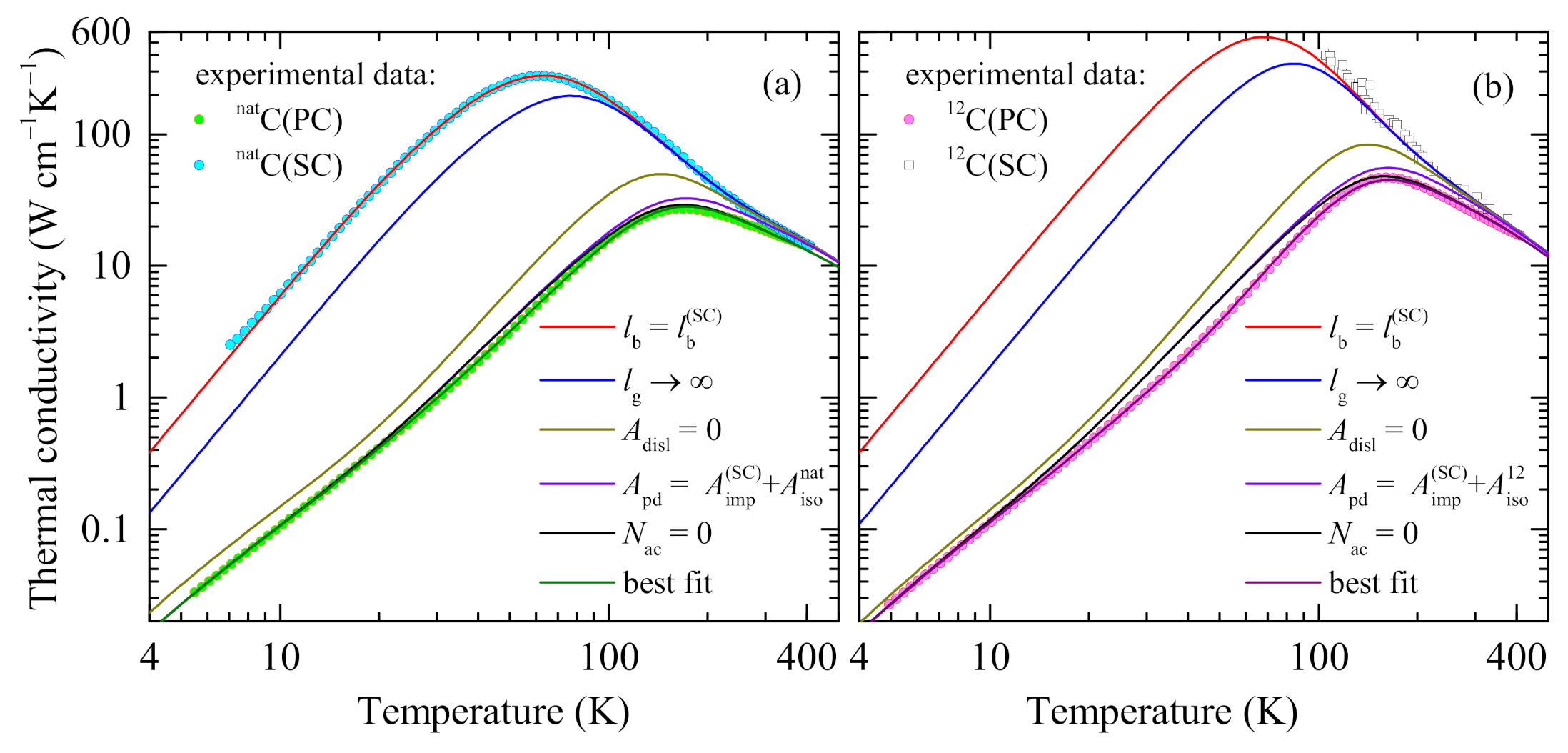
3.3. Fitting Results
4. Discussion
4.1. Scattering by Point Defects and Holes Bound to Acceptors
4.2. Scattering by Grain Boundaries and Intergrain Regions
4.3. Dislocation Scattering
4.4. Contributions of Different Scattering Processes
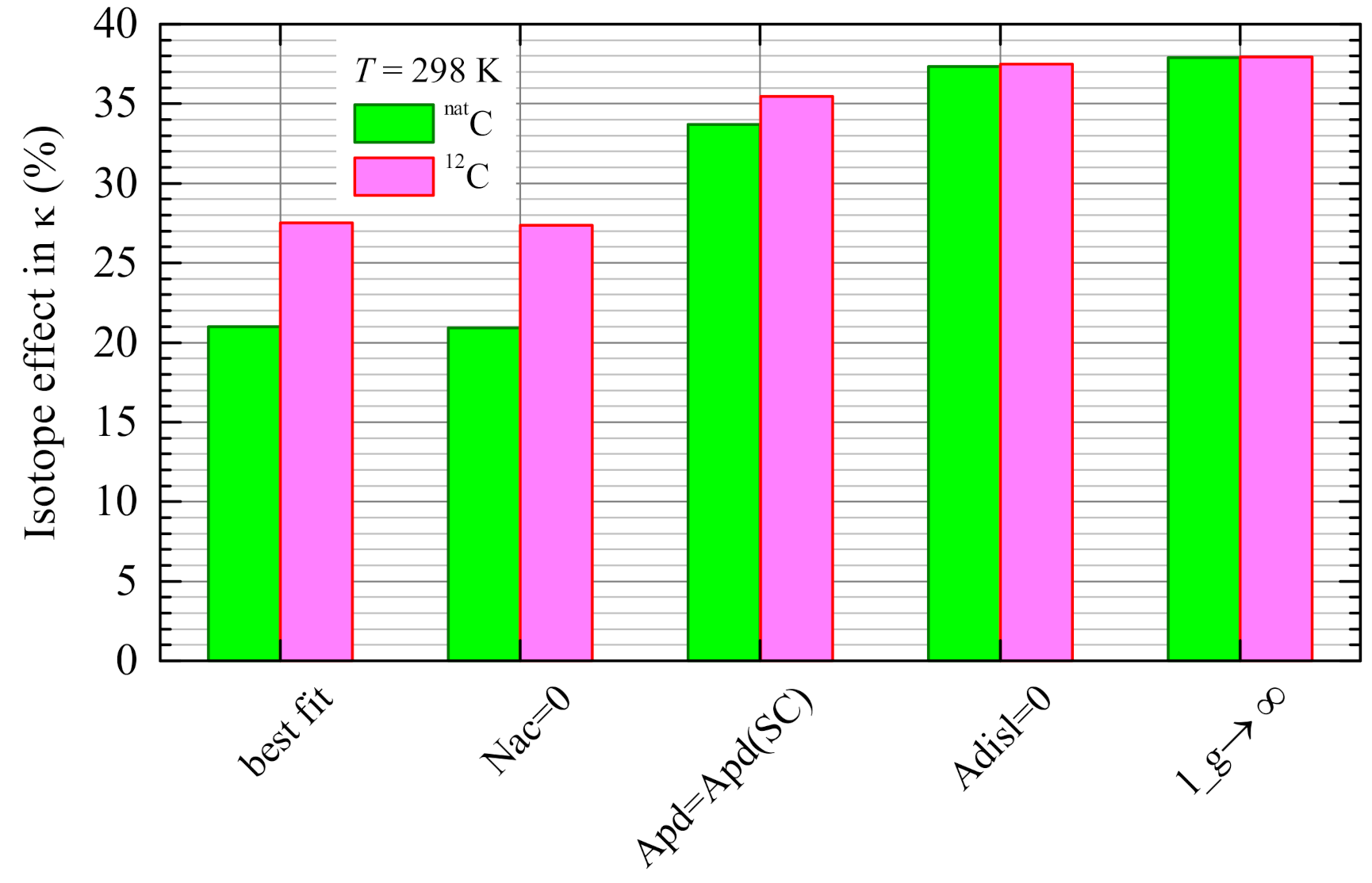
4.5. Evaluation of the Isotope Effect
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anthony, T.R.; Banholzer, W.F.; Fleischer, J.F.; Wei, L.; Kuo, P.K.; Thomas, R.L.; Pryor, R.W. Thermal diffusivity of isotopically enriched 12C diamond. Phys. Rev. B 1990, 42, 1104–1111. [Google Scholar] [CrossRef]
- Onn, D.G.; Witek, A.; Qiu, Y.Z.; Anthony, T.R.; Banholzer, W.F. Some aspects of the thermal conductivity of isotopically enriched diamond single crystals. Phys. Rev. Lett. 1992, 68, 2806–2809. [Google Scholar] [CrossRef]
- Olson, J.R.; Pohl, R.O.; Vandersande, J.W.; Zoltan, A.; Anthony, T.R.; Banholzer, W.F. Thermal conductivity of diamond between 170 and 1200 K and the isotope effect. Phys. Rev. B 1993, 47, 14850–14856. [Google Scholar] [CrossRef]
- Wei, L.; Kuo, P.K.; Thomas, R.L.; Anthony, T.R.; Banholzer, W.F. Thermal conductivity of isotopically modified single crystal diamond. Phys. Rev. Lett. 1993, 70, 3764–3767. [Google Scholar] [CrossRef]
- Nepsha, V.I.; Grinberg, V.R.; Klyuev, Y.A.; Naletov, A.M.; Bokii, G.B. Effect of 13C isotopes on the diamond thermal conduction in the approximation of the dominant role of normal phonon-scattering processes. Dokl. Akad. Nauk SSSR 1991, 317, 96–97. [Google Scholar]
- Berman, R. Thermal conductivity of isotopically enriched diamonds. Phys. Rev. B 1992, 45, 5726–5728. [Google Scholar] [CrossRef] [PubMed]
- Hass, K.C.; Tamor, M.A.; Anthony, T.R.; Banholzer, W.F. Lattice dynamics and Raman spectra of isotopically mixed diamond. Phys. Rev. B 1992, 45, 7171–7182. [Google Scholar] [CrossRef]
- Berman, R. Interpretation of the thermal conductivity of isotopically depleted diamonds. J. Phys. Chem. Solids 1998, 59, 1229–1234. [Google Scholar] [CrossRef]
- Zhernov, A.P.; Inyushkin, A.V. Kinetic coefficients in isotopically disordered crystals. Phys.–Uspekhi 2002, 45, 527–552. [Google Scholar] [CrossRef]
- Morelli, D.T.; Heremans, J.P.; Slack, G.A. Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III-V semiconductors. Phys. Rev. B 2002, 66, 195304. [Google Scholar] [CrossRef]
- Barman, S.; Srivastava, G.P. Temperature dependence of the thermal conductivity of different forms of diamond. J. Appl. Phys. 2007, 101, 123507. [Google Scholar] [CrossRef]
- Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Sparavigna, A. Influence of isotope scattering on the thermal conductivity of diamond. Phys. Rev. B 2002, 65, 064305. [Google Scholar] [CrossRef]
- Ward, A.; Broido, D.A.; Stewart, D.A.; Deinzer, G. Ab initio theory of the lattice thermal conductivity in diamond. Phys. Rev. B 2009, 80, 125203. [Google Scholar] [CrossRef]
- Fugallo, G.; Lazzeri, M.; Paulatto, L.; Mauri, F. Ab initio variational approach for evaluating lattice thermal conductivity. Phys. Rev. B 2013, 88, 045430. [Google Scholar] [CrossRef]
- Simon, R.B.; Anaya, J.; Faili, F.; Balmer, R.; Williams, G.T.; Twitchen, D.J.; Kuball, M. Effect of grain size of polycrystalline diamond on its heat spreading properties. Appl. Phys. Express 2016, 9, 061302. [Google Scholar] [CrossRef]
- Graebner, J.E.; Jin, S.; Kammlott, G.W.; Herb, J.A.; Gardinier, C.F. Large anisotropic thermal conductivity in synthetic diamond films. Nature 1992, 359, 401–403. [Google Scholar] [CrossRef]
- Graebner, J.E.; Reiss, M.E.; Seibles, L.; Hartnett, T.M.; Miller, R.P.; Robinson, C.J. Phonon scattering in chemical-vapor-deposited diamond. Phys. Rev. B 1994, 50, 3702–3713. [Google Scholar] [CrossRef]
- Anthony, T.R.; Fleischer, J.F.; Olson, J.R.; Cahil, D.G. The thermal conductivity of isotopically enriched polycrystalline diamond films. J. Appl. Phys. 1991, 69, 8122–8125. [Google Scholar] [CrossRef]
- Graebner, J.E.; Hartnett, T.M.; Miller, R.P. Improved thermal conductivity in isotopically enriched chemical vapor deposited diamond. Appl. Phys. Lett. 1994, 64, 2549–2551. [Google Scholar] [CrossRef]
- Inyushkin, A.V.; Ralchenko, V.G.; Taldenkov, A.N.; Artyukhov, A.A.; Artyukhov, A.A.; Kravets, Y.M.; Gnidoi, I.P.; Ustinov, A.L.; Bolshakov, A.P.; Popovich, A.F.; et al. Considerable increase in thermal conductivity of a polycrystalline CVD diamond upon isotope enrichment. Bull. Lebedev Phys. Inst. 2007, 34, 329–333. [Google Scholar] [CrossRef]
- Artyukhov, A.A.; Kravets, Y.M.; Artyukhov, A.A.; Bryksin, A.E.; Gnidoi, I.P.; Ustinov, A.L. Conversion of 12C enriched carbon monoxide to methane. Russ. J. Phys. Chem. 2009, 83, 1376–1379. [Google Scholar] [CrossRef]
- Nistor, S.V.; Stefan, M.; Ralchenko, V.; Khomich, A.; Schoemaker, D. Nitrogen and hydrogen in thick diamond films grown by microwave plasma enhanced chemical vapor deposition at variable H2 flow rates. J. Appl. Phys. 2000, 87, 8741–8746. [Google Scholar] [CrossRef]
- Inyushkin, A.V.; Taldenkov, A.N.; Ralchenko, V.G.; Vlasov, I.I.; Konov, V.I.; Khomich, A.V.; Khmelnitskii, R.A.; Trushin, A.S. Thermal conductivity of polycrystalline CVD diamond: Effect of annealing induced transformations of defects and grain boundaries. Phys. Stat. Sol. A 2008, 205, 2226–2232. [Google Scholar] [CrossRef]
- Inyushkin, A.V.; Taldenkov, A.N.; Ral’chenko, V.G.; Konov, V.I.; Khomich, A.V.; Khmel’nitski, R.A. Thermal conductivity of polycrystalline CVD-diamond: Experiment and theory. JETP 2008, 107, 462. [Google Scholar] [CrossRef]
- Inyushkin, A.V.; Taldenkov, A.N.; Ralchenko, V.G.; Bolshakov, A.P.; Koliadin, A.V.; Katrusha, A.N. Thermal conductivity of high purity synthetic single crystal diamonds. Phys. Rev. B 2018, 97, 144305. [Google Scholar] [CrossRef]
- McCurdy, A.K.; Maris, H.J.; Elbaum, C. Anisotropic heat conduction in cubic crystals in the boundary scattering regime. Phys. Rev. B 1970, 2, 4077–4083. [Google Scholar] [CrossRef]
- Carruthers, P. Theory of thermal conductivity of solids at low temperatures. Rev. Mod. Phys. 1961, 33, 92–138. [Google Scholar] [CrossRef]
- Klemens, P.G. The scattering of low-frequency lattice waves by static imperfections. Proc. Phys. Soc. Lond. Sec. A 1955, 68, 1113–1128. [Google Scholar] [CrossRef]
- Li, M.; Ding, Z.; Meng, Q.; Zhou, J.; Zhu, Y.; Liu, H.; Dresselhaus, M.S.; Chen, G. Nonperturbative quantum nature of the dislocation-phonon interaction. Nano Lett. 2017, 17, 1587–1594. [Google Scholar] [CrossRef]
- Sun, B.; Haunschild, G.; Polanco, C.; Ju, J.; Lindsay, L.; Koblmüller, G.; Koh, Y.K. Dislocation-induced thermal transport anisotropy in single-crystal group-III nitride films. Nat. Mater. 2019, 18, 136–140. [Google Scholar] [CrossRef]
- Li, H.; Hanus, R.; Polanco, C.A.; Zeidler, A.; Koblmüller, G.; Koh, Y.K.; Lindsay, L. GaN thermal transport limited by the interplay of dislocations and size effects. Phys. Rev. B 2020, 102, 014313. [Google Scholar] [CrossRef]
- Inyushkin, A.V.; Taldenkov, A.N.; Ralchenko, V.G.; Shu, G.; Dai, B.; Bolshakov, A.P.; Khomich, A.A.; Ashkinazi, E.E.; Boldyrev, K.N.; Khomich, A.V.; et al. Thermal conductivity of pink chemical vapor deposition diamond: Effect of phonon interaction with bound electrons of nitrogen-related centers. (to be published).
- Graebner, J.E. Thermal conductivity of diamond. In Diamond: Electronic Properties and Applications; Pan, L.S., Kania, D.R., Eds.; Springer: New York, NY, USA, 1995; Chapter 7; pp. 285–318. [Google Scholar] [CrossRef]
- Suzuki, K.; Mikoshiba, N. Effects of uniaxial stress and magnetic field on the low-temperature thermal conductivity of p-type Ge and Si. J. Phys. Soc. Jpn. 1971, 31, 44–53. [Google Scholar] [CrossRef]
- Suzuki, K.; Mikoshiba, N. Erratum: Effects of uniaxial stress and magnetic field on the low-temperature thermal conductivity of p-type Ge and Si. J. Phys. Soc. Jpn. 1972, 32, 586(E). [Google Scholar] [CrossRef]
- Singh, M.; Verma, G.S. Lattice thermal conductivity of p-type III-V semiconductors and p-Si at low temperatures. J. Phys. 1974, 35, 571–575. [Google Scholar] [CrossRef]
- Challis, L.J.; Haseler, S.C. The effect of uniaxial stress on the thermal conductivity of p-Ge. J. Phys. C 1978, 11, 4681–4694. [Google Scholar] [CrossRef]
- Klemens, P.G. Phonon scattering and thermal resistance due to grain boundaries. Int. J. Thermophys. 1994, 15, 1345–1351. [Google Scholar] [CrossRef]
- Turk, L.A.; Klemens, P.G. Phonon scattreing by impurity platelet precipitates in diamond. Phys. Rev. B 1974, 9, 4422–4428. [Google Scholar] [CrossRef]
- Berman, R.; Hudson, P.R.W.; Martinez, M. Nitrogen in diamond: Evidence from thermal conductivity. J. Phys. C 1975, 8, L430–L434. [Google Scholar] [CrossRef]
- Lang, A.R.; Pang, G. On the dilatation of diamond by nitrogen impurity aggregated in A defects. Phil. Trans. R. Soc. Lond. A 1998, 356, 1397–1419. [Google Scholar] [CrossRef]
- Ratsifaritana, C.A.; Klemens, P.G. Scattering of phonons by vacancies. Int. J. Thermophys. 1987, 8, 737–750. [Google Scholar] [CrossRef]
- Katcho, N.A.; Carrete, J.; Li, W.; Mingo, N. Effect of nitrogen and vacancy defects on the thermal conductivity of diamond: An ab initio Green’s function approach. Phys. Rev. B 2014, 90, 094117. [Google Scholar] [CrossRef]
- Dannefaer, S.; Zhu, W.; Bretagnon, T.; Kerr, D. Vacancies in polycrystalline diamond films. Phys. Rev. B 1996, 53, 1979–1984. [Google Scholar] [CrossRef] [PubMed]
- Fabis, P.M. Defect distribution modification in CVD diamond by vacuum annealing. Thin Solid Films 1996, 288, 193–197. [Google Scholar] [CrossRef]
- Graebner, J.E.; Mucha, J.A.; Baiocchi, F.A. Sources of thermal resistance in chemically vapor deposited diamond. Diam. Relat. Mater. 1996, 5, 682–687. [Google Scholar] [CrossRef]
- Wörner, E.; Pleuler, E.; Wild, C.; Koidl, P. Thermal and optical properties of high purity CVD-diamond discs doped with boron and nitrogen. Diam. Relat. Mater. 2003, 12, 744–748. [Google Scholar] [CrossRef]
- Sood, A.; Cheaito, R.; Bai, T.; Kwon, H.; Wang, Y.; Li, C.; Yates, L.; Bougher, T.; Graham, S.; Asheghi, M.; et al. Direct visualization of thermal conductivity suppression due to enhanced phonon scattering near individual grain boundaries. Nano Lett. 2018, 18, 3466–3472. [Google Scholar] [CrossRef] [PubMed]
- Ralchenko, V.G.; Inyushkin, A.V.; Shu, G.; Dai, B.; Karateev, I.A.; Bolshakov, A.P.; Khomich, A.A.; Ashkinazi, E.E.; Zavedeev, E.V.; Han, J.; et al. Thermal conductivity of diamond mosaic crystals grown by chemical vapor deposition: Thermal resistance of junctions. (to be published).
- Spiteri, D.; Anaya, J.; Kuball, M. The effects of grain size and grain boundary characteristics on the thermal conductivity of nanocrystalline diamond. J. Appl. Phys. 2016, 119, 085102. [Google Scholar] [CrossRef]
- Anaya, J.; Bai, T.; Wang, Y.; Li, C.; Goorsky, M.; Bougher, T.L.; Yates, L.; Cheng, Z.; Graham, S.; Hobart, K.D.; et al. Simultaneous determination of the lattice thermal conductivity and grain/grain thermal resistance in polycrystalline diamond. Acta Mater. 2017, 139, 215–225. [Google Scholar] [CrossRef]



| , | , | , | , | , | f, | , | |
|---|---|---|---|---|---|---|---|
| cm eV | sK | sK | m | nm | % | mm | |
| C | 6.4 (2.5) | 7.8 (0.3) | 2.2 (0.1) | 25 (3) | 1.7 (0.2) | 5.3 (0.6) | 0.91 |
| C | 17 (3) | 2.3 (0.1) | 1.1 (0.1) | 31 (2) | 1.9 (0.2) | 9.8 (0.8) | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inyushkin, A.V.; Taldenkov, A.N.; Ralchenko, V.G.; Bolshakov, A.P.; Khomich, A.V. Isotope Effect in Thermal Conductivity of Polycrystalline CVD-Diamond: Experiment and Theory. Crystals 2021, 11, 322. https://doi.org/10.3390/cryst11040322
Inyushkin AV, Taldenkov AN, Ralchenko VG, Bolshakov AP, Khomich AV. Isotope Effect in Thermal Conductivity of Polycrystalline CVD-Diamond: Experiment and Theory. Crystals. 2021; 11(4):322. https://doi.org/10.3390/cryst11040322
Chicago/Turabian StyleInyushkin, Alexander V., Alexander N. Taldenkov, Victor G. Ralchenko, Andrey P. Bolshakov, and Alexander V. Khomich. 2021. "Isotope Effect in Thermal Conductivity of Polycrystalline CVD-Diamond: Experiment and Theory" Crystals 11, no. 4: 322. https://doi.org/10.3390/cryst11040322
APA StyleInyushkin, A. V., Taldenkov, A. N., Ralchenko, V. G., Bolshakov, A. P., & Khomich, A. V. (2021). Isotope Effect in Thermal Conductivity of Polycrystalline CVD-Diamond: Experiment and Theory. Crystals, 11(4), 322. https://doi.org/10.3390/cryst11040322







