Control of the Swell by an Array of Helmholtz Resonators

Abstract

We present a theoretical and experimental study of a resonator of the Helmholtz type for the control of the swell. An experimental demonstration of the shielding effect by a belt made of evenly distributed resonators is given. We then provide in-depth analysis of the Fano resonance resulting from the interference between the dock scattering (the background) and the resonant cavity scattering. This is done thanks to space–time resolved experiments which provides the complex-valued scattering coefficients and amplitude within the resonator. We provide a one-dimensional model derived in the shallow water regime owing to asymptotic analysis. The model contains the two ingredients of the Fano resonance and allows us to exhibit the damping due to leakage. When adding heuristically the damping due to losses, it reproduces the main features of the resonance observed experimentally.

1. Introduction

Breakwaters are structures designed to create a sheltered area, protected from the wave attacks. Among the different strategies, floating breakwaters (FBW) are attractive when bottom-connected structures are not suitable, e.g., in sea area with deep waters or soft soil beds. Besides, they have less impact on the underwater fauna and flora [1,2]. The building block of such breakwaters is a rigid or flexible floating body, being either plain or partially empty. More generally, the modern design of devices able to control the energy flow of ocean waves has begun to benefit from the development of metamaterials. For instance, the propagation can be made anisotropic using varying bathymetry see e.g., [3,4,5], or it can be guided due to valley-locked transport [6]. In addition, a plethora of interesting phenomena has been proposed, such as the cancellation of the scattering by rigid obstacles and their cloaking [7,8,9,10,11,12], the perfect absorption of the wave energy in the nonlinear regime [13] and the trapping for energy harvesting using graded arrays of resonators [14,15].

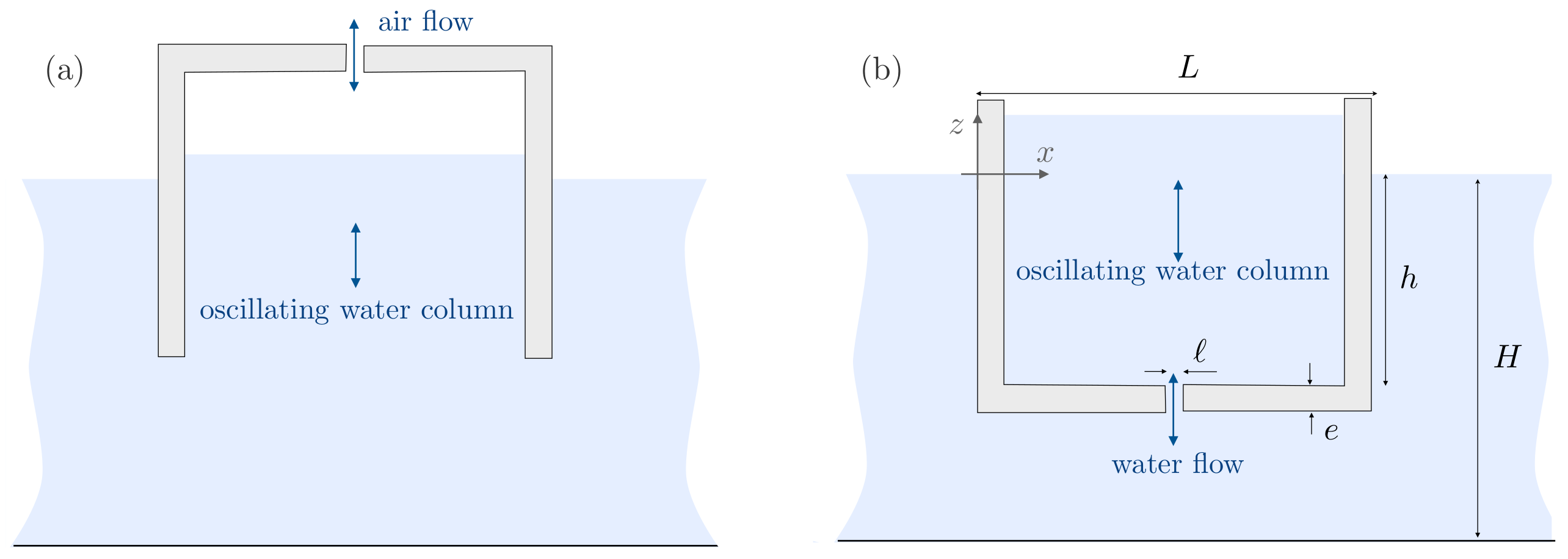
In the present study, we envision a building block based on a resonance of the Helmholtz type. It is composed of a cavity open on its upper part to the air and connected to the surrounding sea water thanks to a thin neck (Figure 1b). Amusingly, this resonant cavity is the upside down version of the oscillatory water column devices (OWC) used to collect the sea wave energy [16], see Figure 1a. To begin with, we report in Figure 2 and Figure 3 elements of the proof-of-concept of the shielding efficiency of a belt made of evenly distributed resonators. In a laboratory experiment, we have realised two rectangular belts surrounding a central target area that is to be protected. In the configuration (a) the belt is composed by cavities open to the sea by a neck (our Helmholtz resonators); in the configuration (b) it is composed by close cavities (a dock). In each case, two ping-pong balls on both sides of the belt are used to track the movements outside and inside the target area. For an incoming plane wave (blue arrow in Figure 2), video recordings evidence the efficiency of the configuration (a) to produce an unperturbed area within the belt (the videos are available in the Supplementary Materials; in these movies, top view corresponds to Figure 2a and bottom view to Figure 2b).

In Figure 3, we report illustrations of our observations. The ball on the left with middle line shown as plain lines is outside the target area. The ball on the right with middle line shown as dashed lines is inside the target area. In (a) and (b) we have selected two times during the oscillatory motion of the ball at left at its maximum and minimum vertical positions. In (a), the ball on the right in the target area remains at the same heigh as the area is efficiently sheltered by the resonant belt. In contrast for the rigid dock belt (b), the ball on the right has an oscillation motion with nearly the same amplitude as outside the target area.

In this study, we characterize the resonance responsible for the shielding effect reported above. Firstly, we present in Section 2 experimental quantitative results obtained using the Fourier Transform Profilometry (FTP) which allows for space-time resolved measurements of the free surface elevation [17,18,19]. The set-up involves an incident-guided wave on a single resonator in a rectangular duct which is analog to an incident plane wave at normal incidence on a periodic array of resonators. The significant losses within the cavity weaken the sharp variations of the resonance around the perfect reflection of the Fano curve [20]. The combined effects of the resonance and of the losses produce a low transmission when compared to that produced by a dock. In Section 3, we use a one-dimensional model governing the surface elevation outside the resonant cavity. The model obtained in a recent study [21] reduces the effect of the resonator to jump conditions applying to the surface elevation and its horizontal derivative; next it encapsulates the resonant dynamics in an equation of a harmonic oscillator forced by the incident wave with damping due to the leakage by radiation. When accounting for the inherent viscous and nonlinear losses the experimental results are qualitatively well reproduced by the model. Perspectives are drawn in concluding remarks Section 4.

Throughout the paper, in the numerics and the modelling, we consider an inviscid, incompressible fluid, and an irrotational motion in the harmonic regime with time dependence $e^{-i\omega t}$. Under these assumptions, the velocity potential $\varphi (x,z)$ satisfies

$$\left\{\begin{array}{c}{\displaystyle \Delta \varphi =0,}\hfill \\ {\displaystyle {\partial }_z\varphi (x,0)=\frac{{\omega }^2}{g}\varphi (x,0),\nabla \varphi ·{\mathit{n}}_{|\mathsf{\Gamma }}=0,}\hfill \end{array}\right.$$

(1)

with x the horizontal coordinate, z the vertical one ($z=0$ is the undisturbed free surface, $z=-$H the sea bottom) and $\mathsf{\Gamma }$ denotes the boundaries of the rigid parts of the resonator and of the sea bottom. The free surface elevation $\eta (x)$ and the velocity $\mathbf{u}=(u,v)$ are then given by

$$\mathbf{u}(\mathbf{x})=\nabla \varphi (\mathbf{x}),\eta (x)=\frac{i\omega }{g}\varphi (x,0).$$

(2)

2. Experimental Result–Effect of the Losses

To characterize the resonator, we use a single resonator in a duct. The duct is 1.5 m long and $p=6$ cm wide (along y); the water depth is set to $H=6$ cm. The cavity has the same width p as the duct and it is fixed at the free surface with an immersion depth $h=2.8$ cm; its dimensions are indicated in the Figure 4. This set-up is the equivalent of an array of resonators evenly distributed along y with spacing p for an incoming wave (along x) at normal incidence. In both cases, the solution far from the cavity region reads

$${\displaystyle \eta (x<0,\omega )=A\left(e^{ikx}+R(\omega )e^{-ikx}\right),\eta (x>L,\omega )=AT(\omega )e^{ik(x-L)},}$$

(3)

with the complex valued amplitude of the incident wave A and scattering coefficients $(R,T)$. At the frequency $\omega$ is associated the wavenumber k.

2.1. Experimental Characterization of Complex-Free Surface Elevation

Working in a duct has two advantages. Far from scattering regions, it gives rise to the propagation of a perfectly plane wave below the cut-off frequency ${\omega }_c=2\pi \sqrt{gH}/$$p\simeq 80$ rad·s${}^{-1}$ (only the mode 0 can propagate). Besides, it necessitates a relatively small volume of water hence allows for its coloration with anatase pigment rendering the free surface light diffusive (the coloration of water is visible in Figure 4). The FTP can, therefore, be implemented. It uses the field of a fringe pattern projected onto the moving free surface. The phase map between the instantaneous deformed pattern and the reference undeformed one is used to reconstruct the field of free surface elevation [17,18,19]. The fringe patterns have been recorded using a camera Photron (1024 × 1024). With a recorded window $x\in (-40,40)$ cm and $y\in (-1.5,1.5)$ cm, the spatial resolution $\delta x=\delta y=0.84$ mm is given by the pixel of the camera and the time resolution $\delta t=1/25$ s by its acquisition frequency.

Our experiments have been performed in the harmonic regime with incident waves generated by a wavemaker at the left end of the duct imposing a sinusoidal motion at frequency $\omega$ (visible in the Figure 4); 11 values within the range (9,16) rad·s${}^{-1}$ have been considered. To prevent the strong reflection at the right end of the duct we use a beach with an $8^{\circ }$ angle. The experiments have been done using a resonant cavity and for comparison using a simple dock with the same dimensions. The instantaneous fields $\eta (x,y,t)$ are stored which allows for pixel-by-pixel Fourier transforms resulting in the complex amplitude $\eta (x,y,\omega )$. To reduce the noise-to-signal ratio, we use the mean profile $\eta (x,\omega )=\frac{1}{3}{\int }_{-1.5}^{1.5}\eta (x,y,\omega )\mathrm{d}y$ which provides the amplitude ${\eta }_{\mathrm{c}}(\omega )$ in the cavity for $x\in (0,L)$ and the scattering coefficients $(R,T)$ by fitting the forms in (3) for $x<0$ and $x>L$. For the resonant open cavity, the Figure 5 shows an instantaneous free surface measurement $\eta (x,y,t)$ at an arbitrary time for the two frequencies realizing the minimum and maximum transmissions (top panels) and the mean complex profiles $\eta (x,\omega )$ (bottom panel, real part with blue lines and imaginary part with red lines); the result of the fits using (3) are shown with dashed black lines.

2.2. Experimental Evidence of Fano Resonance

Figure 6 shows $(R,T)$ and ${\eta }_{\mathrm{c}}$ against the wavelength $\lambda =2\pi /k$ obtained experimentally (circles) along with the same quantities calculated numerically (plain and dashed lines). The dashed lines in the lossless case are characteristic of a Fano resonance with striking variations of the scattering curves around the smooth curve of the dock on its own. The measurements of $(R_{\mathrm{dock}},T_{\mathrm{dock}})$ for the dock on its own (green circles) coincide with the numerics without a loss (plain green line). In contrast to the resonant, cavity-significant shifts between measurements and lossless numerics are observed. Accordingly in the numerics, we have accounted for the losses in the cavity only by adding a small complex part to the real wavenumber satisfying $ktanhkh=\frac{{\omega }^2}{g}$, namely we have considered $k\to k+i{k}_i$ (the plain lines show the best agreement for $k_i=1.5$ m${}^{-1}$). Although the losses weaken the resonance, the cavity efficiently reduces the transmission (compared to a dock) for wavelengths smaller than about 35 cm.

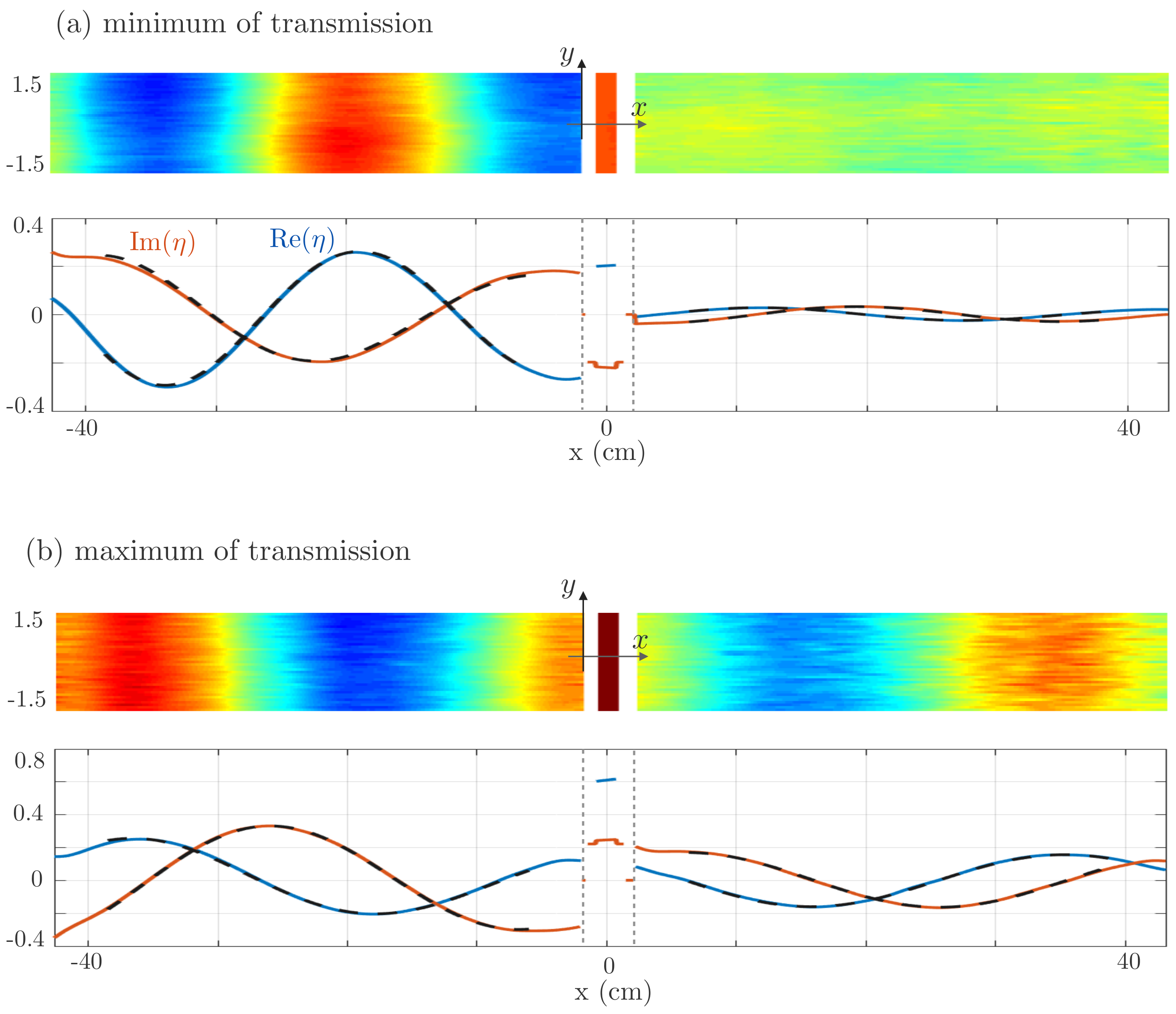
This shielding effect is further illustrated in Figure 7a where we report the 2D patterns of the velocity potential in the $(x,z)$ plane at the minimum of transmission obtained from Figure 6 (without and with losses in the cavity). For comparison, the patterns at the maximum of transmission are reported in the panels (b). The presence of losses does not much affect the resonant mechanism in which the potential inside the cavity oscillates in phase quadrature with the incoming wave to prevent the transmission while it oscillates in phase with the incoming wave to foster it.

3. One-Dimensional Model of the Resonator

In this section, we analyze our experimental and numerical results with a one-dimensional model whose derivation is detailed in [21]. The model holds for waves propagating over a small water depth and for subwavelength dimensions of the resonator; namely for $kH,kL\ll 1$, with $k=\omega /\sqrt{gH}$ in the shallow water regime. With these assumptions, asymptotic analysis allows us to reduce the actual problem to a one-dimensional problem along x which applies for the complex swell amplitude at the free surface $\eta (x)$ (the dependence of $\eta$ on $\omega$ is omitted in this section). In the harmonic regime, the reduced problem reads

$$\left\{\begin{array}{c}{\displaystyle {\partial }_{xx}\eta (x)+k^2\eta (x)=0,x\in (-\infty ,0)\cup (L,+\infty ),}\hfill \\ {\displaystyle 〚\eta 〛=H\mathcal{B}\overline{{\partial }_x\eta },〚{\partial }_x\eta 〛=-\frac{{\omega }^2{L}_{\mathrm{o}}}{g}{\eta }_{\mathrm{c}},}\hfill \end{array}\right.$$

(4)

where $〚\eta 〛=\eta (L)-\eta (0)$ is the jump of $\eta$ across the resonator (the same for $〚{\partial }_x\eta 〛$), $\overline{{\partial }_x\eta }=\frac{1}{2}\left({\partial }_x\eta (0)+{\partial }_x\eta (L)\right)$ is the mean value of ${\partial }_x\eta$ and $L_{\mathrm{o}}=(L-2e)$ is the inner width of the cavity. Next the uniform surface elevation ${\eta }_{\mathrm{c}}$ within the cavity satisfies the equation of a damped harmonic oscillator of the form

$$\left\{\begin{array}{c}{\displaystyle \left({\omega }_0^2-{\omega }^2-2i\omega ({\sigma }_{\mathrm{R}}+{\sigma }_{\mathrm{L}})\right){\eta }_{\mathrm{c}}={\omega }_0^2{\eta }_{\mathrm{inc}}(0),}\hfill \\ {\displaystyle \mathrm{where}{\omega }_0=\sqrt{\frac{g\ell }{e_{\mathrm{eff}}{L}_{\mathrm{o}}}},{\sigma }_{\mathrm{R}}=\frac{\ell }{4e_{\mathrm{eff}}}\sqrt{\frac{g}{H}}.}\hfill \end{array}\right.$$

(5)

In the above expressions, ${\omega }_0$ is the resonance frequency, ${\sigma }_{\mathrm{R}}$ the radiative damping due to the coupling of the resonator with the surrounding fluid and ${\sigma }_{\mathrm{L}}$ the damping due to the losses (viscous and nonlinear). The forcing term ${\eta }_{\mathrm{inc}}(0)$ is the surface elevation at $x=0$ associated to an incident wave ${\eta }_{\mathrm{inc}}(x)$. Eventually, aside from the geometrical parameters, the reduced models (4) and (5) involve two parameters, $\mathcal{B}$ being the blockage coefficient of the dock and $e_{\mathrm{eff}}$ being the so-called effective length of the resonator which read

$$\left\{\begin{array}{cc}{\displaystyle \mathcal{B}=\frac{L}{h^{-}}+2{\mathcal{B}}_{\mu },}\hfill & \mu =\frac{h^{-}}{H}.\hfill \\ \\ e_{\mathrm{eff}}=e+\frac{\ell }{2}\left({\mathcal{B}}_{\mu }+{\mathcal{B}}_{{\mu }_0}\right),\hfill & \mu =\frac{\ell }{L},{\mu }_0=\frac{\ell }{L_{\mathrm{o}}}\hfill \end{array}\right.$$

(6)

where ${\mathcal{B}}_{\mu }$ is a function of $\mu$ only, defined by

$${\mathcal{B}}_{\mu }=\frac{1}{\pi }\frac{({\mu }^2+1)}{\mu }log\frac{1+\mu }{1-\mu }-\frac{2}{\pi }log\frac{4\mu }{1-{\mu }^2}.$$

It is worth noting that in (5) and (6), two elements have been introduced heuristically in the result of the asymptotic analysis (see Appendix A). Firstly, we added the damping due to the losses as the analysis is performed in an inviscid fluid and linear case (the radiative damping is obtained from the asymptotic analysis). Secondly, the effective length $e_{\mathrm{eff}}$ with an added length which would appear in the analysis at a higher order (this added length accounts for boundary layer effects at both ends of the neck).

Scattering Coefficients and Amplitude within the Cavity

For an incident wave producing a surface elevation ${\eta }_{\mathrm{inc}}(x)=e^{ikx}$, the reflected and transmitted waves are written as in (3) and the solution for the uniform surface elevation in the cavity read, from (5),

$${\displaystyle {\eta }_{\mathrm{c}}(\omega )=\frac{{\omega }_0^2}{{\omega }_0^2-{\omega }^2-2i\omega \left({\sigma }_{\mathrm{R}}+{\sigma }_{\mathrm{L}}\right)}.}$$

(7)

The above result can be further used (4), and with $\frac{c{L}_{\mathrm{o}}}{gH}=\frac{4}{{\omega }_0^2\tau }$, we obtain

$$\left\{\begin{array}{c}{\displaystyle R=\frac{1}{2}\frac{{\omega }_0^2-{\omega }^2+2i\omega \left({\sigma }_{\mathrm{R}}-{\sigma }_{\mathrm{L}}\right)}{{\omega }_0^2-{\omega }^2-2i\omega \left({\sigma }_{\mathrm{R}}+{\sigma }_{\mathrm{L}}\right)}-\frac{1}{2}\frac{{\sigma }_{\mathrm{dock}}+i\omega }{{\sigma }_{\mathrm{dock}}-i\omega }\mathrm{with}{\sigma }_{\mathrm{dock}}=\frac{2}{\mathcal{B}}\sqrt{\frac{g}{H}},}\hfill \\ \\ {\displaystyle T=\frac{1}{2}\frac{{\omega }_0^2-{\omega }^2+2i\omega \left({\sigma }_{\mathrm{R}}-{\sigma }_{\mathrm{L}}\right)}{{\omega }_0^2-{\omega }^2-2i\omega \left({\sigma }_{\mathrm{R}}+{\sigma }_{\mathrm{L}}\right)}+\frac{1}{2}\frac{{\sigma }_{\mathrm{dock}}+i\omega }{{\sigma }_{\mathrm{dock}}-i\omega }}\hfill \end{array}\right.$$

(8)

which produces ${|R|}^2+{|T|}^2=1$ if ${\sigma }_{\mathrm{L}}=0$ (the system resonator+surrounding water is conservative) and ${|R|}^2+{|T|}^2<1$ otherwise. For the dock on its own, ${\eta }_{\mathrm{c}}=0$, resulting in

$$R_{\mathrm{dock}}=\frac{1}{2}-\frac{1}{2}\frac{\left({\sigma }_{\mathrm{dock}}+i\omega \right)}{\left({\sigma }_{\mathrm{dock}}-i\omega \right)},T_{\mathrm{dock}}=1-R_{\mathrm{dock}}.$$

(9)

In (7) and (8) all the parameters are explicit with $({\omega }_0,{\sigma }_{\mathrm{R}},{\sigma }_{\mathrm{dock}})$ in (5) except for ${\sigma }_{\mathrm{L}}$ which has been introduced heuristically. As in the previous section, the damping ${\sigma }_{\mathrm{L}}$ can be viewed as the small imaginary part of the complex frequency $\omega \to \omega +i{\sigma }_{\mathrm{L}}$ with ${\omega }_0\to {\omega }_0-i{\sigma }_{\mathrm{R}}$ the complex resonance frequency due to the leakage by radiation being the pole of the scattering coefficients.

The Figure 8 shows the same sequence of results as the Figure 6 for $(T,R,{\eta }_{\mathrm{c}})$ from (7) and (8). Although the overall variations of the resonance curves are well reproduced, we observe a significant shift from ${\omega }_0=11.1$ rad·s${}^{-1}$ (${\lambda }_0=38$ cm from ${\omega }^2=gktanh(kH)$) in the experiments to ${\omega }_0=16.0$ rad·s${}^{-1}$ (${\lambda }_0=$ 30 cm with $\omega =\sqrt{gH}k$ in the shallow water approximation) given by the reduced model. At these higher frequencies, the losses have been accounted for using ${\sigma }_{\mathrm{L}}=1.6$ s${}^{-1}$ to reproduce the significant attenuation of the experiments (this value is roughly twice that given by the simple correspondence ${\sigma }_{\mathrm{L}}=\sqrt{gh}{k}_i)$. The main reason for the observed discrepancy is attributable to the neck of the resonator chosen in the experiments. At the small scale of our laboratory experiments, viscous effects would destroy the resonance being too important in a very thin neck. This certainly modifies the form of the effective length $e_{\mathrm{eff}}$ in (6) as the boundary layers are weaker for a relatively large neck but they are also wider. Note also that the experiments do not fulfill the hypothesis of shallow water, with $|\lambda -{\lambda }_{\mathrm{SW}}|/|\lambda |\sim$ 20% in the considered range of frequency but this affects mainly the response of the dock on its own (from the Figure 6 and Figure 8, it is slightly underestimated).

4. Conclusions

We have presented experimental results on a resonator of the Helmholtz type in the context of water waves. As its acoustic analog, this resonator can be used as the building block of devices able to control the energy flow of the swell. When a single type of resonator is used, we have illustrated its capability to reduce the transmission up to almost zero at a single frequency. Extensions concern perfect absorption induced by losses or nonlinearities [22,23], a concept which has been already exploited in the context of water waves [13]. For applications to breakwaters, the broadband absorption obtained in acoustic devices should be transposable using a set of graded resonators [24,25].