Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions
Abstract
:1. Introduction
2. Theory
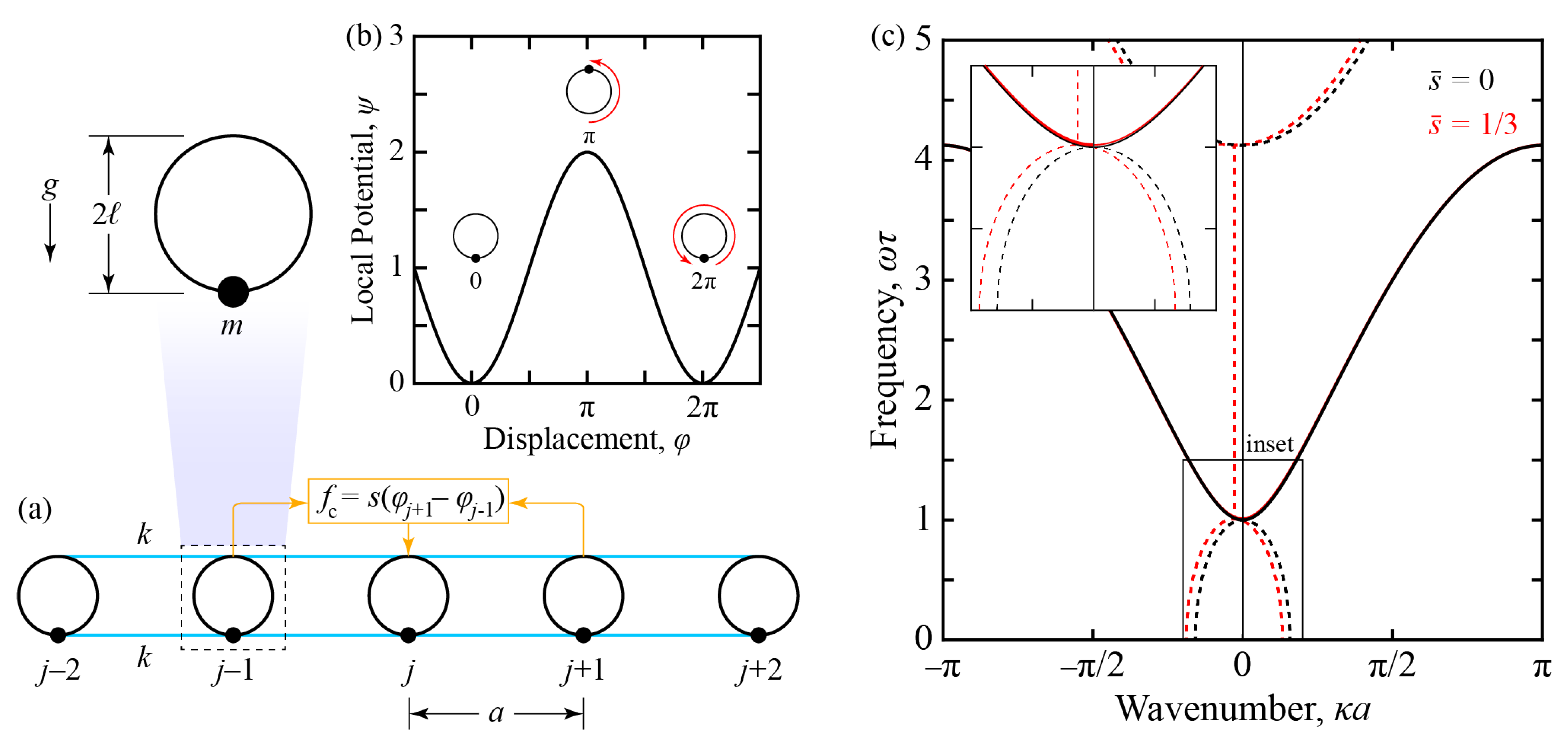
2.1. Model
2.2. Dispersion
3. Results
3.1. Simulation
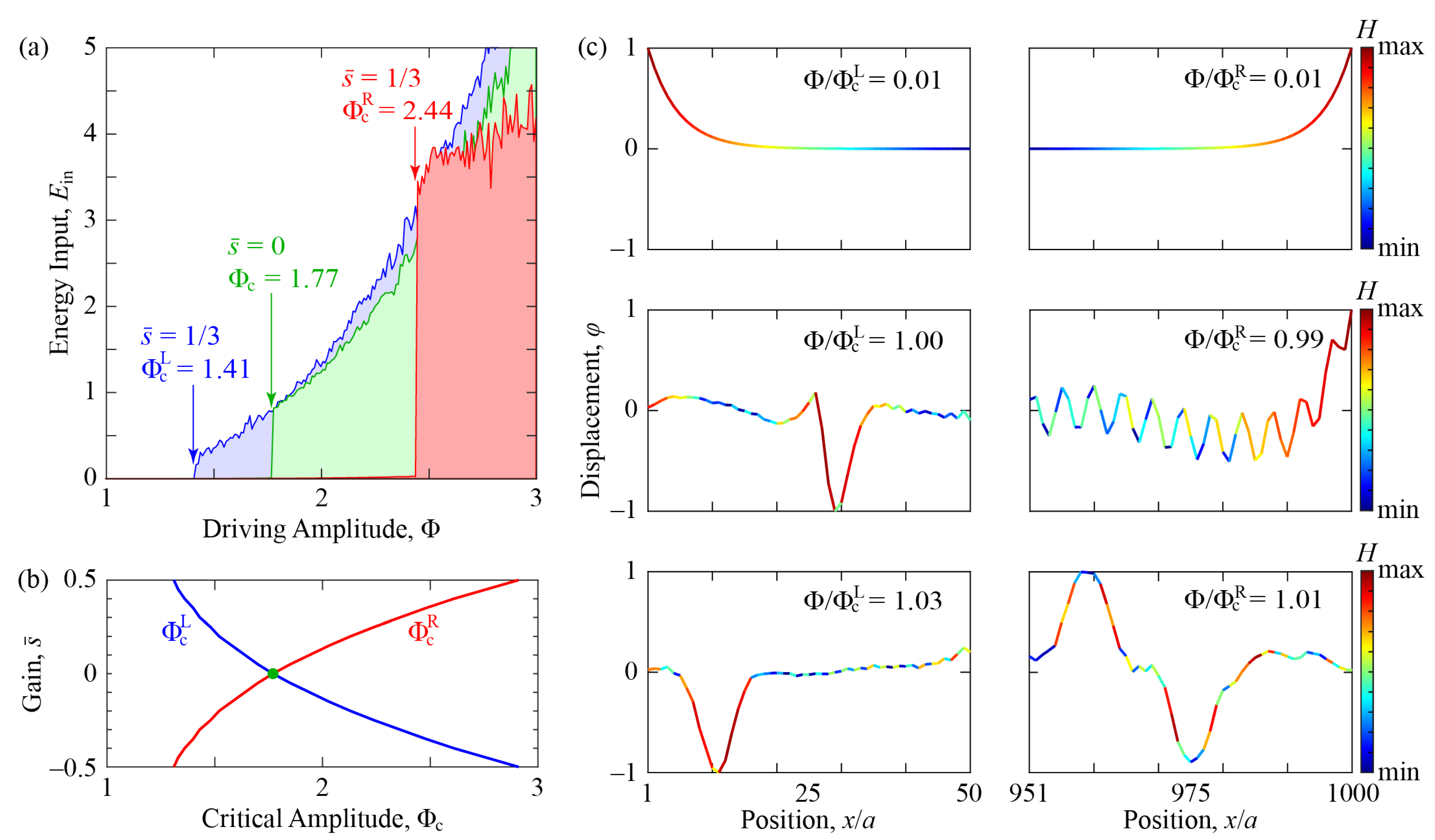
3.2. Supratransmission: One Dimension
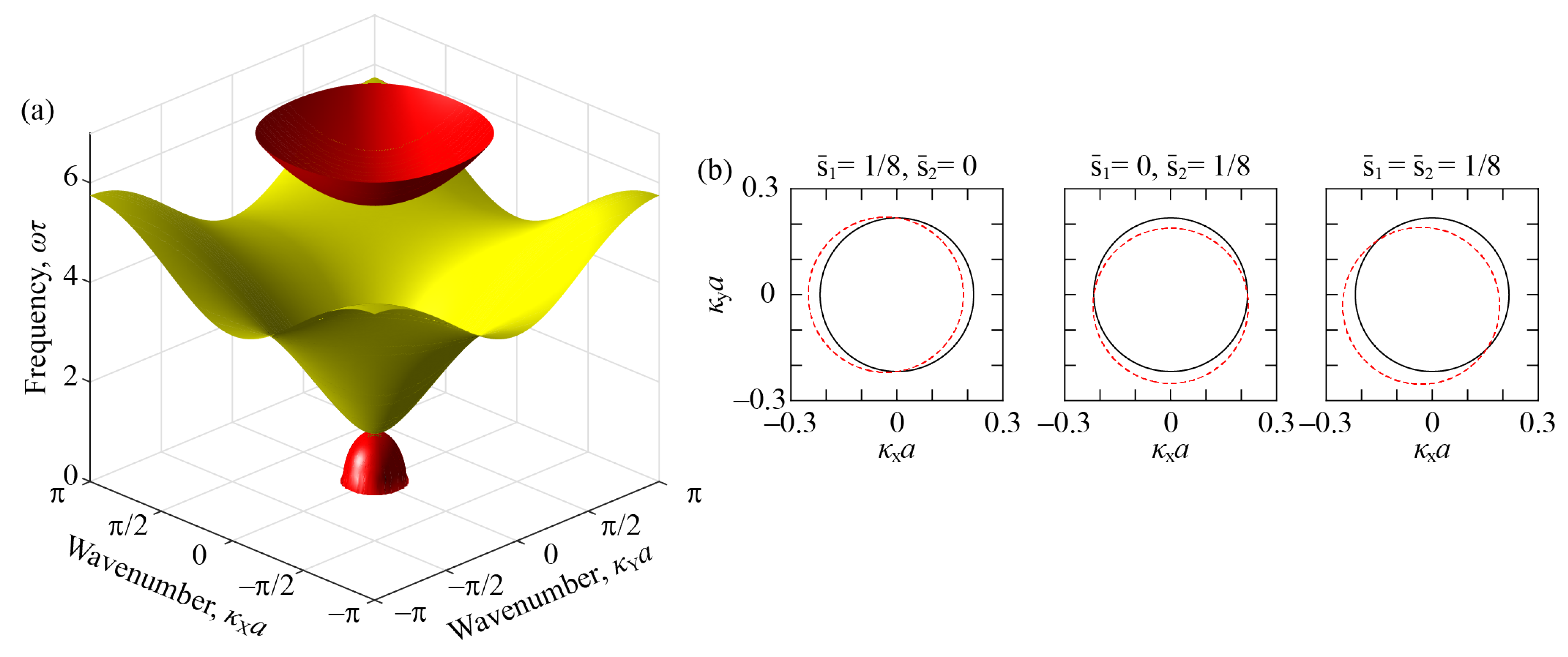
3.3. Supratransmission: Two Dimensions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.F.; Ni, X.; Feng, L.; Lu, M.H.; He, C.; Chen, Y.F. Tunable unidirectional sound propagation through a sonic-crystal-based acoustic diode. Phys. Rev. Lett. 2011, 106, 084301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhong, J.; Zhao, H.; Yang, H.; Wang, Y.; Yin, J.; Wen, J. Theoretical requirements and inverse design for broadband perfect absorption of low-frequency waterborne sound by ultrathin metasurface. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- Benichou, I.; Givli, S. Force-sensitive metamaterials for vibration mitigation and mechanical protection. Extreme Mech. Lett. 2020, 40. [Google Scholar] [CrossRef]
- Geniet, F.; Leon, J. Energy transmission in the forbidden band gap of a nonlinear chain. Phys. Rev. Lett. 2002, 89, 134102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khomeriki, R.; Lepri, S.; Ruffo, S. Nonlinear supratransmission and bistability in the Fermi-Pasta-Ulam model. Phys. Rev. E 2004, 70, 066626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macías-Díaz, J.E. Numerical study of the transmission of energy in discrete arrays of sine-Gordon equations in two space dimensions. Phys. Rev. E 2008, 77, 016602. [Google Scholar] [CrossRef] [PubMed]
- Macías-Díaz, J.E. Bistability of a two-dimensional Klein-Gordon system as a reliable means to transmit monochromatic waves: A numerical approach. Phys. Rev. E 2008, 78, 056603. [Google Scholar] [CrossRef]
- Togueu Motcheyo, A.B.; Tchawoua, C.; Tchinang Tchameu, J.D. Supratransmission induced by waves collisions in a discrete electrical lattice. Phys. Rev. E 2013, 88, 040901. [Google Scholar] [CrossRef] [PubMed]
- Yousefzadeh, B.; Phani, A.S. Energy transmission in finite dissipative nonlinear periodic structures from excitation within a stop band. J. Sound Vib. 2015, 354, 180–195. [Google Scholar] [CrossRef]
- Malishava, M. All-phononic amplification in coupled cantilever arrays based on gap soliton dynamics. Phys. Rev. E 2017, 95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geniet, F.; Leon, J. Nonlinear supratransmission. J. Phys. Condens. Matter 2003, 15, 2933–2949. [Google Scholar] [CrossRef] [Green Version]
- Macías-Díaz, J.E.; Puri, A. An application of nonlinear supratransmission to the propagation of binary signals in weakly damped, mechanical systems of coupled oscillators. Phys. Lett. A 2007, 366, 447–450. [Google Scholar] [CrossRef] [Green Version]
- Khomeriki, R.; Leon, J.; Chevriaux, D. Quantum Hall bilayer digital amplifier. Eur. Phys. J. B 2006, 49, 213–218. [Google Scholar] [CrossRef]
- Malishava, M.; Khomeriki, R. All-phononic digital transistor on the basis of gap-soliton dynamics in an anharmonic oscillator ladder. Phys. Rev. Lett. 2015, 115, 104301. [Google Scholar] [CrossRef] [Green Version]
- Nassar, H.; Yousefzadeh, B.; Fleury, R.; Ruzzene, M.; Alu, A.; Daraio, C.; Norris, A.N.; Huang, G.; Haberman, M.R. Nonreciprocity in acoustic and elastic materials. Nat. Rev. Mater. 2020, 5. [Google Scholar] [CrossRef]
- Matsuo, H.; Kitanaka, Y.; Inoue, R.; Noguchi, Y.; Miyayama, M. Switchable diode-effect mechanism in ferroelectric BiFeO3 thin film capacitors. J. Appl. Phys. 2017, 118, 114101. [Google Scholar] [CrossRef]
- Potton, R.J. Reciprocity in optics. Rep. Prog. Phys. 2004, 67, 717–754. [Google Scholar] [CrossRef]
- Kodera, T.; Sounas, D.L.; Caloz, C. Magnetless nonreciprocal metamaterial (MNM) technology: Application to microwave components. IEEE Trans. Microw. Theory Tech. 2013, 61, 1020–1042. [Google Scholar] [CrossRef]
- Liang, B.; Yuan, B.; Cheng, J.C. Acoustic diode: Rectification of acoustic energy flux in one-dimensional systems. Phys. Rev. Lett. 2009, 103, 104301. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Parker, R.G.; Yellen, B.B. Optimization of an acoustic rectifier for uni-directional wave propagation in periodic mass–spring lattices. J. Sound Vib. 2013, 332, 4876–4894. [Google Scholar] [CrossRef]
- Maznev, A.A.; Every, A.G.; Wright, O.B. Reciprocity in reflection and transmission: What is a ‘phonon diode’? Wave Motion 2013, 50, 776–784. [Google Scholar] [CrossRef] [Green Version]
- Fleury, R.; Sounas, D.L.; Haberman, M.R.; Alu, A. Nonreciprocal acoustics. Acoust. Today 2015, 11, 14–21. [Google Scholar]
- Fleury, R.; Sounas, D.L.; Sieck, C.F.; Haberman, M.R.; Alu, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 2014, 343, 516–519. [Google Scholar] [CrossRef]
- Attarzadeh, M.A.; Callanan, J.; Nouh, M. Experimental observation of nonreciprocal waves in a resonant metamaterial beam. Phys. Rev. Appl. 2020, 13, 021001. [Google Scholar] [CrossRef] [Green Version]
- Swinteck, N.; Matsuo, S.; Runge, K.; Vasseur, J.O.; Lucas, P.; Deymier, P.A. Bulk elastic waves with unidirectional backscattering-immune topological states in a time-dependent superlattice. J. Appl. Phys. 2015, 118, 063103. [Google Scholar] [CrossRef]
- Wang, Y.; Yousefzadeh, B.; Chen, H.; Nassar, H.; Huang, G.; Daraio, C. Observation of nonreciprocal wave propagation in a dynamic phononic lattice. Phys. Rev. Lett. 2018, 121, 194301. [Google Scholar] [CrossRef] [Green Version]
- Trainiti, G.; Xia, Y.; Marconi, J.; Cazzulani, G.; Erturk, A.; Ruzzene, M. Time-periodic stiffness modulation in elastic metamaterials for selective wave filtering: Theory and experiment. Phys. Rev. Lett. 2019, 122, 124301. [Google Scholar] [CrossRef] [Green Version]
- Pal, R.K.; Schaeffer, M.; Ruzzene, M. Helical edge states and topological phase transitions in phononic systems using bi-layered lattices. J. Appl. Phys. 2016, 119, 084305. [Google Scholar] [CrossRef] [Green Version]
- Souslov, A.; van Zuiden, B.C.; Bartolo, D.; Vitelli, V. Topological sound in active-liquid metamaterials. Nat. Phys. 2017, 13, 1091–1094. [Google Scholar] [CrossRef]
- Rosa, M.I.N.; Ruzzene, M. Dynamics and topology of non-Hermitian elastic lattices with non-local feedback control interactions. New J. Phys. 2020, 22, 053004. [Google Scholar] [CrossRef]
- Liang, B.; Guo, X.S.; Tu, J.; Zhang, D.; Cheng, J.C. An acoustic rectifier. Nat. Mat. 2010, 9, 989–992. [Google Scholar] [CrossRef] [PubMed]
- Popa, B.I.; Cummer, S.A. Non-reciprocal and highly nonlinear active acoustic metamaterials. Nat. Commun. 2014, 5, 4398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raney, J.R.; Nadkarni, N.; Daraio, C.; Kochmann, D.M.; Lewis, J.A.; Bertoldi, K. Stable propagation of mechanical signals in soft media using stored elastic energy. Proc. Natl. Acad. Sci. USA 2016, 113, 9722–9727. [Google Scholar] [CrossRef] [Green Version]
- Nadkarni, N.; Arrieta, A.F.; Chong, C.; Kochmann, D.M.; Daraio, C. Unidirectional transition waves in bistable lattices. Phys. Rev. Lett. 2016, 116, 244501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hwang, M.; Arrieta, A.F. Solitary waves in bistable lattices with stiffness grading: Augmenting propagation control. Phys. Rev. E 2018, 98, 042205. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Frazier, M.J. Transition waves in multi-stable metamaterials with space-time modulated potentials. Appl. Phys. Lett. 2020, 117, 151901. [Google Scholar] [CrossRef]
- Wu, Z.; Zheng, Y.; Wang, K.W. Metastable modular metastructures for on-demand reconfiguration of band structures and nonreciprocal wave propagation. Phys. Rev. E 2018, 97, 022209. [Google Scholar] [CrossRef] [Green Version]
- Brandenbourger, M.; Locsin, X.; Lerner, E.; Coulais, C. Non-reciprocal robotic metamaterials. Nat. Commun. 2019, 10, 4608. [Google Scholar] [CrossRef]
- Frenkel, Y.I.; Kontorova, T. On the theory of plastic deformation and twinning. J. Phys. 1939, 1, 137–149. [Google Scholar]
- Perring, J.K.; Skyrme, T.H.R. A model unified field equation. Nucl. Phys. 1962, 31. [Google Scholar] [CrossRef]
- Josephson, B.D. Supercurrents through barriers. Adv. Phys. 1965, 14, 419–451. [Google Scholar] [CrossRef]
- Kopidakis, G.; Aubry, S. Discrete breathers and delocalization in nonlinear disordered systems. Phys. Rev. Lett. 2000, 84, 3236–3239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maniadis, P.; Kopidakis, G.; Aubry, S. Energy dissipation threshold and self-induced transparency in systems with discrete breathers. Phys. D 2006, 216, 121–135. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, K.W. On the wave propagation analysis and supratransmission prediction of a metastable modular metastructure for non-reciprocal energy transmission. J. Sound Vib. 2019, 458. [Google Scholar] [CrossRef] [Green Version]
- Macías-Díaz, J.E.; Motcheyo, A.B.T. Energy transmission in nonlinear chains of harmonic oscillators with long-range interactions. Results Phys. 2020, 18. [Google Scholar] [CrossRef]
- Leon, J. Nonlinear supratransmission as a fundamental instability. Phys. Lett. A 2003, 319, 130–136. [Google Scholar] [CrossRef] [Green Version]
- Leon, J.; Spire, A. Gap soliton formation by nonlinear supratransmission in Bragg media. Phys. Lett. A 2004, 327, 474–480. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pechac, J.E.; Frazier, M.J. Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions. Crystals 2021, 11, 94. https://doi.org/10.3390/cryst11020094
Pechac JE, Frazier MJ. Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions. Crystals. 2021; 11(2):94. https://doi.org/10.3390/cryst11020094
Chicago/Turabian StylePechac, Jack E., and Michael J. Frazier. 2021. "Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions" Crystals 11, no. 2: 94. https://doi.org/10.3390/cryst11020094
APA StylePechac, J. E., & Frazier, M. J. (2021). Non-Reciprocal Supratransmission in Mechanical Lattices with Non-Local Feedback Control Interactions. Crystals, 11(2), 94. https://doi.org/10.3390/cryst11020094





