Measuring Complex Refractive Indices of a Nanometer-Thick Superconducting Film Using Terahertz Time-Domain Spectroscopy with a 10 Femtoseconds Pulse Laser

Abstract

Superconducting thin films are widely applied in various fields, including switching devices, because of their phase transition behaviors in relation to temperature changes. Therefore, it is important to quantitatively determine the optical constant of a superconducting material in the thin-film state. We performed a terahertz time-domain spectroscopy, based on a 10 femtoseconds pulse laser, to measure the optical constant of a superconducting GdBa₂Cu₃O_7−x (GdBCO) thin film in the terahertz region. We then estimated the terahertz refractive indices of the 70 nm-thick GdBCO film using a numerical extraction process, even though the film thickness was approximately 1/10,000 times smaller than the terahertz wavelength range of 200 μm to 1 mm. The resulting refractive indices of the GdBCO thin film were consistent with the theoretical results using the two-fluid model. Our work will help to further understand the terahertz optical properties of superconducting thin films with thicknesses under 100 nm, as well as provide a standard platform for characterizing the optical properties of thin films without the need of Kramers–Kronig transformation at the terahertz frequencies.

1. Introduction

Because of their high conductivity, noble-metal films are most commonly used in various applications, such as metamaterials and sensing devices in the terahertz region [1,2,3,4,5,6,7,8]. Recently, many studies have been carried out in order to develop new switching devices combined with phase transition materials modulated via external stimuli, such as temperature and electrical voltage [9,10,11,12]. In addition, superconducting materials are widely applied in the field of switching devices because of their phase transition below the critical temperature T_c [13,14,15,16,17]. In the terahertz frequency region, such materials are much more promising for developing metamaterials and switching devices because the superconductor properties remain robust and well-maintained [18]. Furthermore, it is important to ensure that the superconducting property is well maintained in the desired thin film form, because superconductors are used in the form of thin films in most terahertz applications [19,20].

One advantage of employing time-domain spectroscopy is that the optical constants of a target material can be determined via a transmission or reflection experiment without the need of Kramers–Kronig transformation, because the amplitude and phase information can be obtained simultaneously [21]. Of these, analysis of the results is relatively simpler in the transmission experiment than in the reflection experiment. In the case of a thick substrate there is a sufficient phase difference; hence, the refractive index can be easily obtained. However, phase retardation of a terahertz-transparent thin film is not sufficient, and the refractive index is difficult to obtain owing to the pulse width resolution of the probe beam [22]. In contrast, because the film in a metal has a sufficiently large refractive index, the phase difference can be distinguished even in the case of a thin film. Therefore, the complex refractive index of the metal sample can be determined [23,24,25]. More specifically, if $nd/c>PW$, where n is the real part of the refractive index of the material, d is the thickness, c is the speed of light, and PW is the pulse width of the probe beam, we can estimate the complex refractive indices of the material. For example, a probe beam with a pulse width of 10 fs can be used to analyze a material with the optical path (=$nd$) of 3 μm. In many terahertz time-domain spectroscopy studies, lasers with a pulse width of about 100 fs were used [19,26,27]. The corresponding resolution of the optical path by the 100 fs pulse is about 30 μm, which is too long to directly measure any change in the phase of the terahertz pulse through the thin film with a short optical path ($nd/c\ll PW$). One study estimated the complex conductivities of metal thin films with a thicknesses of 10 to 30 nm, using a laser with a pulse width of 12 fs [28]. In the case of a conducting material, it would be relatively easier to estimate its refractive index, even within the form of thin films, but we need one more procedure to accurately estimate complex refractive indices of superconductor thin films, which retain relatively low refractive indices below T_c.

In this work, we introduced a method for measuring the complex refractive indices of a target material using terahertz time-domain spectroscopy combined with a numerical extraction process. Consistent with previous studies, we double-checked the complex refractive indices of an optically thick insulating substrate (undoped silicon and LaAlO₃) and metallic thin films [25,27,29,30]. Based on our ability to analyze the refractive indices of both insulating and conducting materials, we estimated the terahertz refractive indices of a 70 nm-thick superconducting GdBa₂Cu₃O_7−x (GdBCO) thin film with a critical temperature of around 90 K in a broad temperature range of 20–180 K.

2. Experimental Method

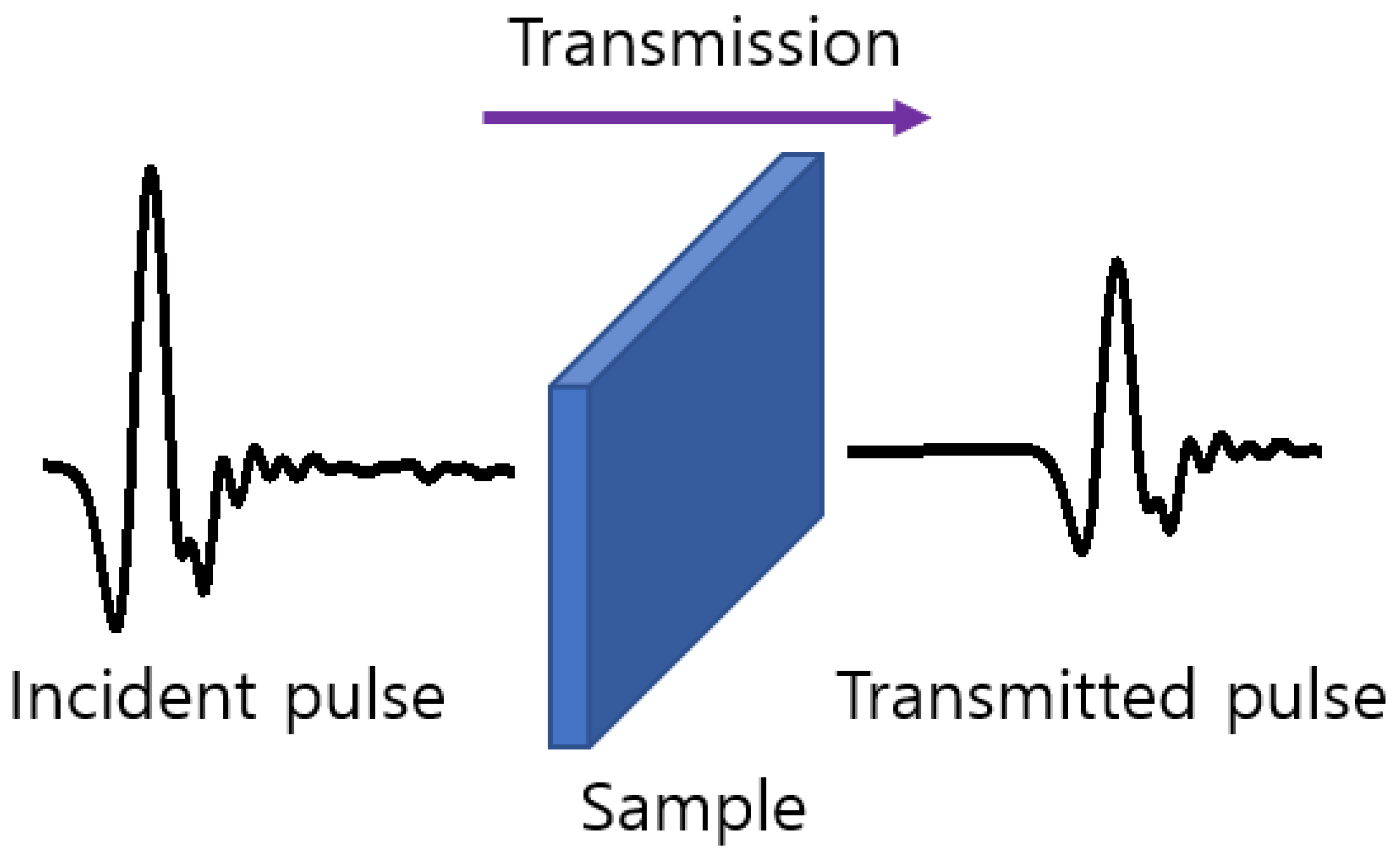
2.1. Terahertz Time-Domain Spectroscopy

To experimentally determine the complex refractive indices of the samples, terahertz time-domain spectroscopy was performed (Figure 1). A terahertz pulse with a single-cycle picosecond pulse was generated from a commercial GaAs emitter (Tera-SED3, Laser Quantum, Stockport, UK), illuminated with a Ti:sapphire laser pulse train with the center wavelength of 780 nm, repetition rate of 75.1 MHz, and pulse width of 10 fs (Synergy, Spectra-Physics, Andover, MA, USA). For the detection, we used the electro-optic sampling method with a 1 mm-thick ZnTe crystal [31], and the resulting signal-to-noise ratio (SNR) is 5000:1. As mentioned in the introduction, the 10 fs probe pulse in the electro-optic sampling method has limited to an optical path resolution of 3 um.

2.2. Sample Fabrication

Silver thin films with thicknesses of 15, 30 and 50 nm, which are sub-skin depth in the terahertz region, were deposited via e-beam evaporation onto a 500 μm-thick undoped silicon substrate. The deposition conditions for the silver thin film included a degree of vacuum less than 5.0 × 10⁻⁶ Torr and deposition rate of 1 Å/s. Additionally, a 70 nm-thick GdBCO thin film was deposited onto a 500 μm-thick single-crystal LaAlO₃ (LAO) substrate using pulsed laser deposition (KrF excimer laser, LPX pro240, 248 nm, Coherent, Santa Clara, USA). The deposition conditions for the GdBCO thin film were optimized for the best epitaxial quality as follows: GdBCO was synthesized at 780 °C under the partial O₂ pressure of 350 mTorr with the laser energy of 130 mJ/pulse; subsequently, oxygen annealing was performed at 500 mTorr and 500 °C for 1 h. As shown in Figure 2, the GdBCO film thickness is 70$\pm$6 nm confirmed by scanning electron microscope (SEM).

3. Analytical Method

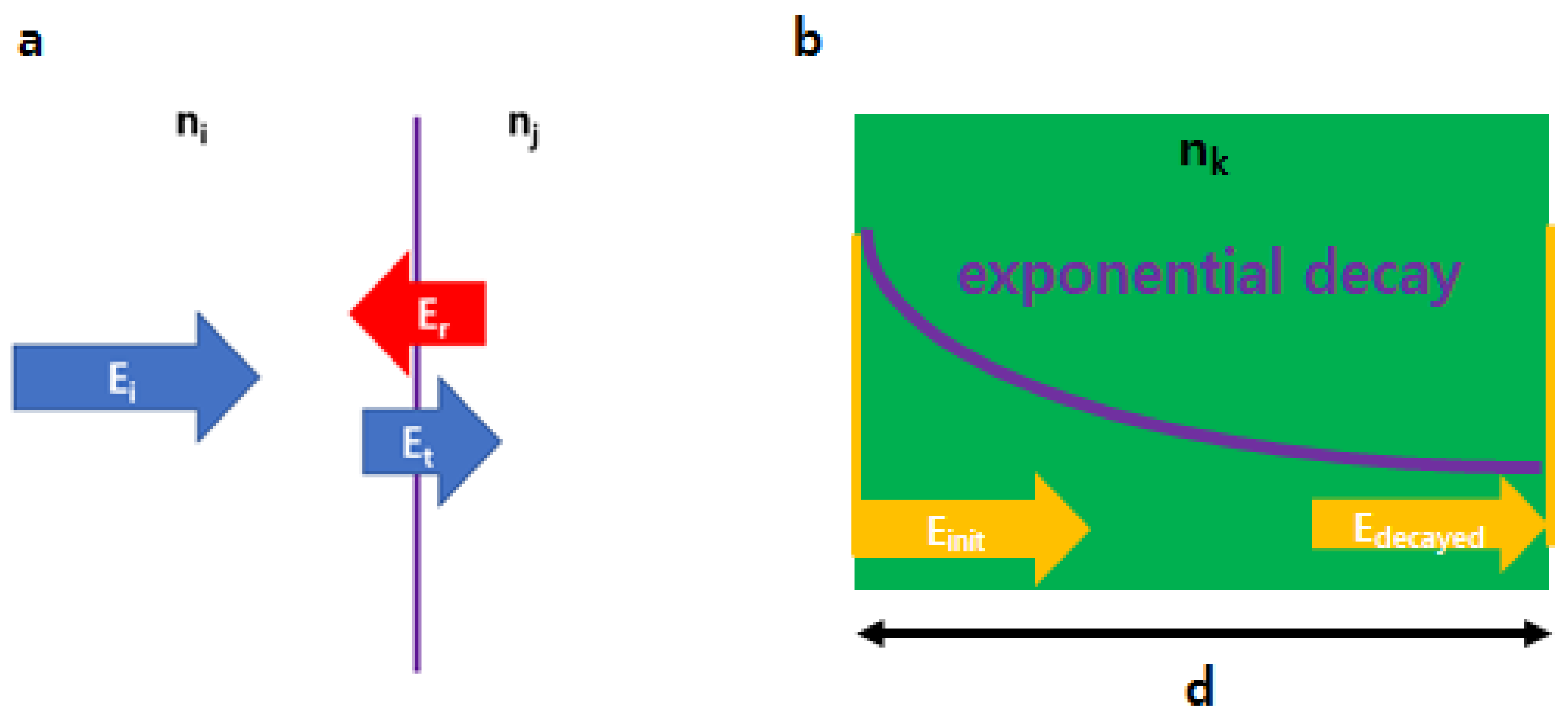
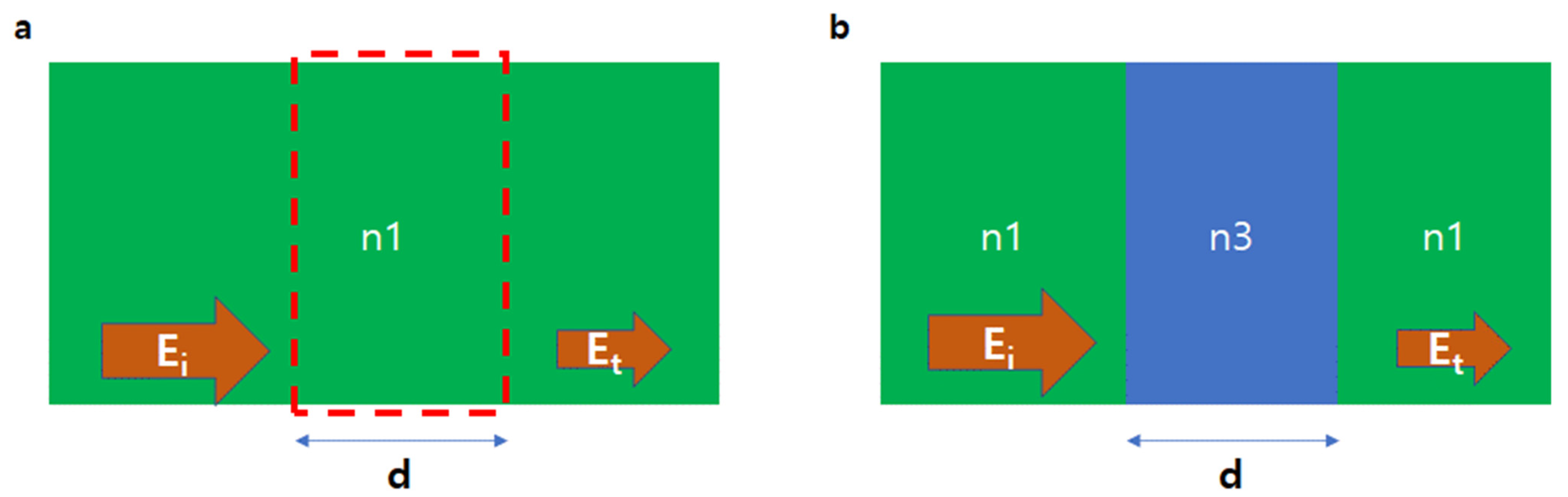
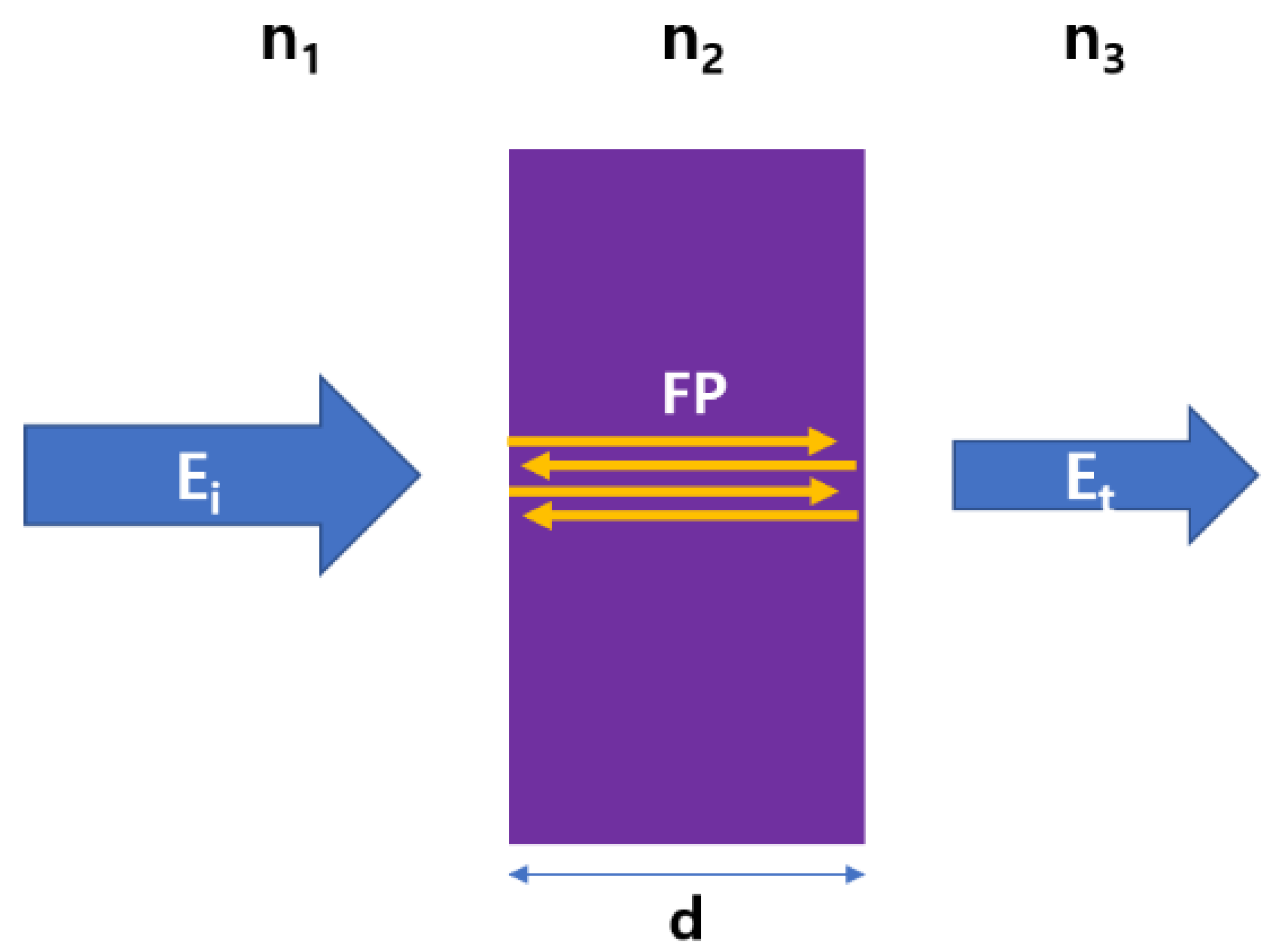
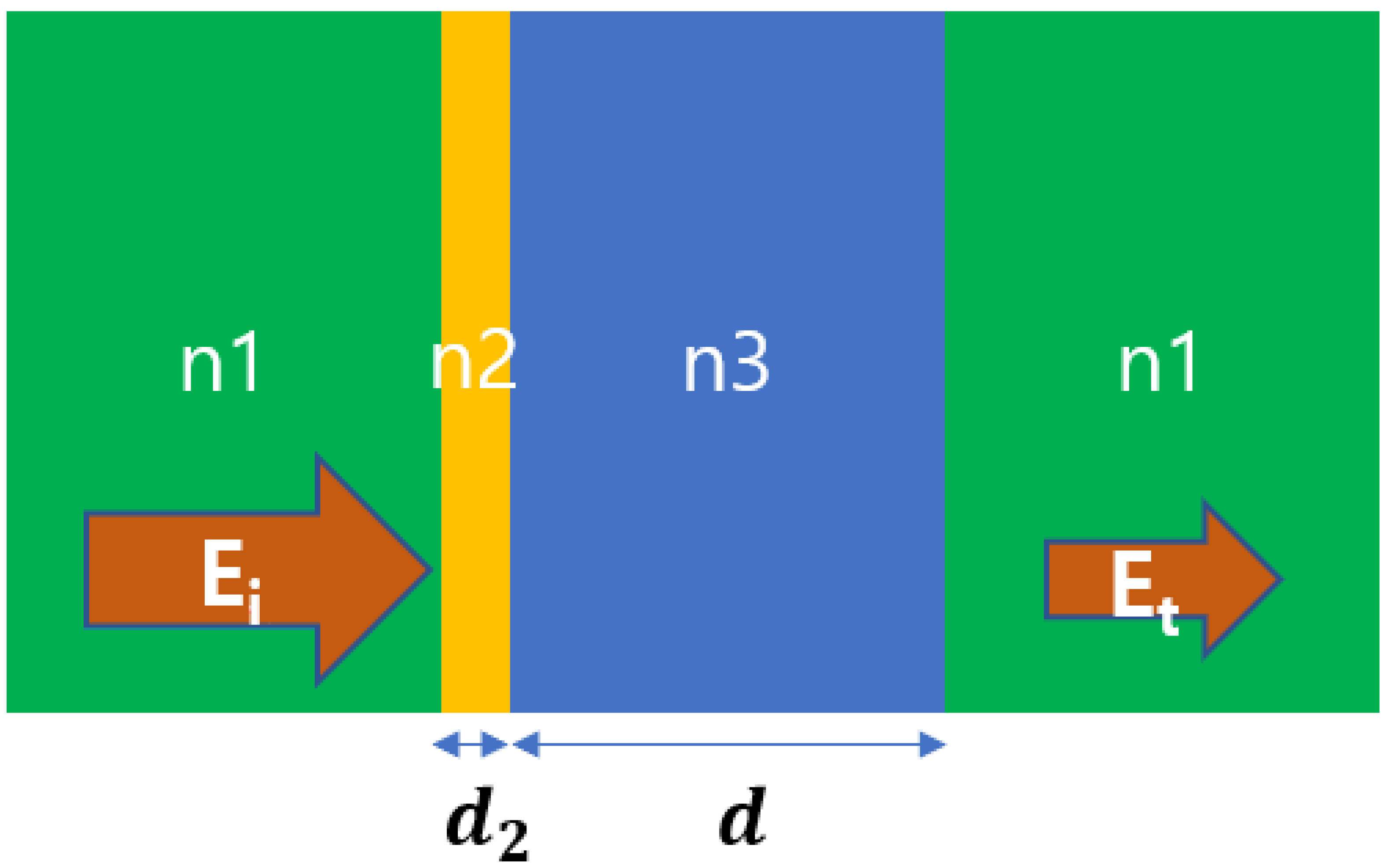
3.1. Transmission Coefficients of Bulk and Thin Film Samples

Using the Fresnel equation, we can obtain the transmission and reflection of light of the media using the refractive index, and vice versa. As shown in Figure 3, the Fresnel equation is defined as follows [32].

When the electric field is normally incident to material j from i, the Fresnel coefficients are:

$$r_{ij}=\frac{n_j-n_i}{n_i+n_j},$$

(1)

$$t_{ij}=\frac{2n_i}{n_i+n_j}.$$

(2)

The electric field of light passing through the interface is given by:

$$E_t=E_i{t}_{ij}.$$

(3)

When the electric field passes through the inside of the medium, the electric field is exponentially decayed as follows

$$E_{decayed}=E_{init}{\mathsf{e}}^{i{k}_{k}d}$$

(4)

where $k_k$ is a wavevector in the medium, expressed as:

$$k_k=2\pi {\tilde{n}}_k/\lambda$$

(5)

According to Equations (4) and (5), it can be seen that the real part of the refractive index mainly contributes to the phase changes, and the imaginary part of the refractive index mainly contributes to the amplitude changes. Using these relationships, the transmitted electric fields for the bulk and thin film samples can be calculated as follows.

In time-domain spectroscopy experiments, the first and multiple signals for bulk samples, such as single crystals, can be distinguished from the time data. Therefore, there is no need to consider multiple reflections.

In the experiment, the case was first measured with only the aperture, and then the sample was measured. Subsequently, the data measured on the sample was divided by the data measured with only the aperture. For the transmitted electric field of the aperture case, as shown in Figure 4a, the sample thickness was considered.

$$E_{\mathrm{ref}}=E_i{t}_{11}{t}_{11}{\mathrm{e}}^{i{k}_{1}d}$$

(6)

The transmitted electric field of the sample (Figure 4b) is given by:

$$E_{\mathrm{sub}}=E_i{t}_{13}{t}_{31}{\mathrm{e}}^{i{k}_{3}d}.$$

(7)

Thus, the transmission coefficient of the bulk sample is:

$$t_{\mathrm{sub}}=E_{\mathrm{sub}}/E_{\mathrm{ref}}=t_{13}{t}_{31}{\mathrm{e}}^{i\left(k_3-k_1\right)d}/t_{11}{t}_{11}=t_{13}{t}_{31}{\mathrm{e}}^{i\left(k_3-k_1\right)d},$$

(8)

For thin films, the terms reflected from the interface (so-called multiple reflections or Fabry–Perot interference) must be considered as the multiple reflections, and the first signal cannot be distinguished from the time data. Thin films are generally deposited onto substrates, and the interfaces of the materials are shown in Figure 5.

Fabry–Perot interference is defined as the multiple reflections that occur at both interfaces of a thin sample, as shown in Equation (9).

$$FP={\displaystyle \sum }_p{\left(r_{12}{r}_{23}{\mathsf{e}}^{2i{k}_{2}d}\right)}^p=\frac{1}{1-r_{12}{r}_{23}{\mathsf{e}}^{2i{k}_{2}d}}$$

(9)

Thus, the transmitted electric field through the thin sample can be established as:

$$E_t=E_i{t}_{12}{t}_{23}\times FP.$$

(10)

In the experiment, the situation will be as shown in Figure 6.

Typical data processing for calculating the transmission coefficient in an experiment involves dividing the transmitted signal through the thin film on the substrate (Figure 6) by that of the substrate only (Figure 4b). Therefore, the transmission coefficient of the thin film is given by:

$$t_{\mathrm{film}}=E_{\mathrm{film}}/E_{\mathrm{sub}}=t_{12}{t}_{23}{t}_{31}{\mathrm{e}}^{i{k}_2{d}_2}{\mathrm{e}}^{i{k}_{3}d}\times FP/t_{13}{t}_{31}{\mathrm{e}}^{i{k}_{3}d}=\frac{t_{12}{t}_{23}}{t_{13}}{\mathrm{e}}^{i{k}_2{d}_2}\times FP.$$

(11)

3.2. Numerical Method

Most of the materials used as a substrate have very little absorption in the terahertz region. In particular, when the refractive index of the substrate is $n_3=N_3+i{K}_3$, the K₃ value is very small compared with the N₃ value. Then, the following approximation can be obtained [33]:

$$t_{\mathrm{sub}}=t_{13}{t}_{31}{\mathsf{e}}^{i\left(k_3-k_1\right)d}=\frac{4n_1\left(N_3+i{K}_3\right)}{{\left(n_1+N_3+i{K}_3\right)}^2}{\mathrm{e}}^{i\left(k_3-k_1\right)d}\approx \frac{4n_1{N}_3}{{\left(n_1+N_3\right)}^2}{\mathrm{e}}^{i\left(k_3-k_1\right)d}.$$

(12)

The transmitted electric field can be expressed as Equation (13), including the amplitude and phase components.

$$t_{\mathrm{sub}}=\left|t\right|{\mathsf{e}}^{-i\varnothing }$$

(13)

Combining Equations (12) and (13) provides the following:

$$\angle t_{\mathrm{sub}}=\varnothing =-\left[N_3-n_1\right]\frac{\omega d}{c},$$

(14)

$$ln \left|t_{\mathrm{sub}}\right|=ln \left[\frac{4n_1{N}_3}{n_1+N_3}\right]-K_3\frac{\omega d}{c}.$$

(15)

Therefore, the equations for the refractive indices of thick and insulating materials can be obtained, respectively, as:

$$N_3=n_1-\frac{c}{\omega d}\varnothing ,$$

(16)

$$K_3=\frac{c}{\omega d}\left\{ln \left[\frac{4n_1{N}_3}{n_1+N_3}\right]-ln \left|t_{\mathrm{sub}}\right|\right\}.$$

(17)

These values are almost correct; however, to improve the accuracy, these values are used as the initial value, and the numerical method is performed to determine the result faster and more accurately, as shown in Figure 7. We used the fsolve function in MATLAB for our analysis. The fsolve function is an optimization tool that finds the optimal solution using the Levenberg–Marquardt algorithm [34,35]. Using the optimization tool, we finally obtained the most accurate refractive indices, which were perfectly matched with the amplitude and phase of the transmitted signal through the sample.

In the case of conducting samples, the n and $\kappa$ values of the complex refractive index are generally comparable in the terahertz frequencies. For this reason, to set an appropriate initial value when calculating the numerical solution, the refractive indices are considered to be n =$\kappa$ when the refractive index of the film is ${\tilde{n}}_{film}=n+i\kappa$. If n =$\kappa$, we can assume that there is only one variable. Therefore, Equation (18) was established, which can be solved using only the amplitude data.

$$\left|\frac{t_{12}{t}_{23}}{t_{13}}\times FP\right|=\left|\frac{E_{\mathrm{film}}}{E_{\mathrm{sub}}}\right|$$

(18)

Following this, a reasonable solution of the complex refractive index can be obtained using the same optimization tool with this initial value.

$$\frac{t_{12}{t}_{23}}{t_{13}}\times FP=\frac{E_{\mathrm{film}}}{E_{\mathrm{sub}}}$$

(19)

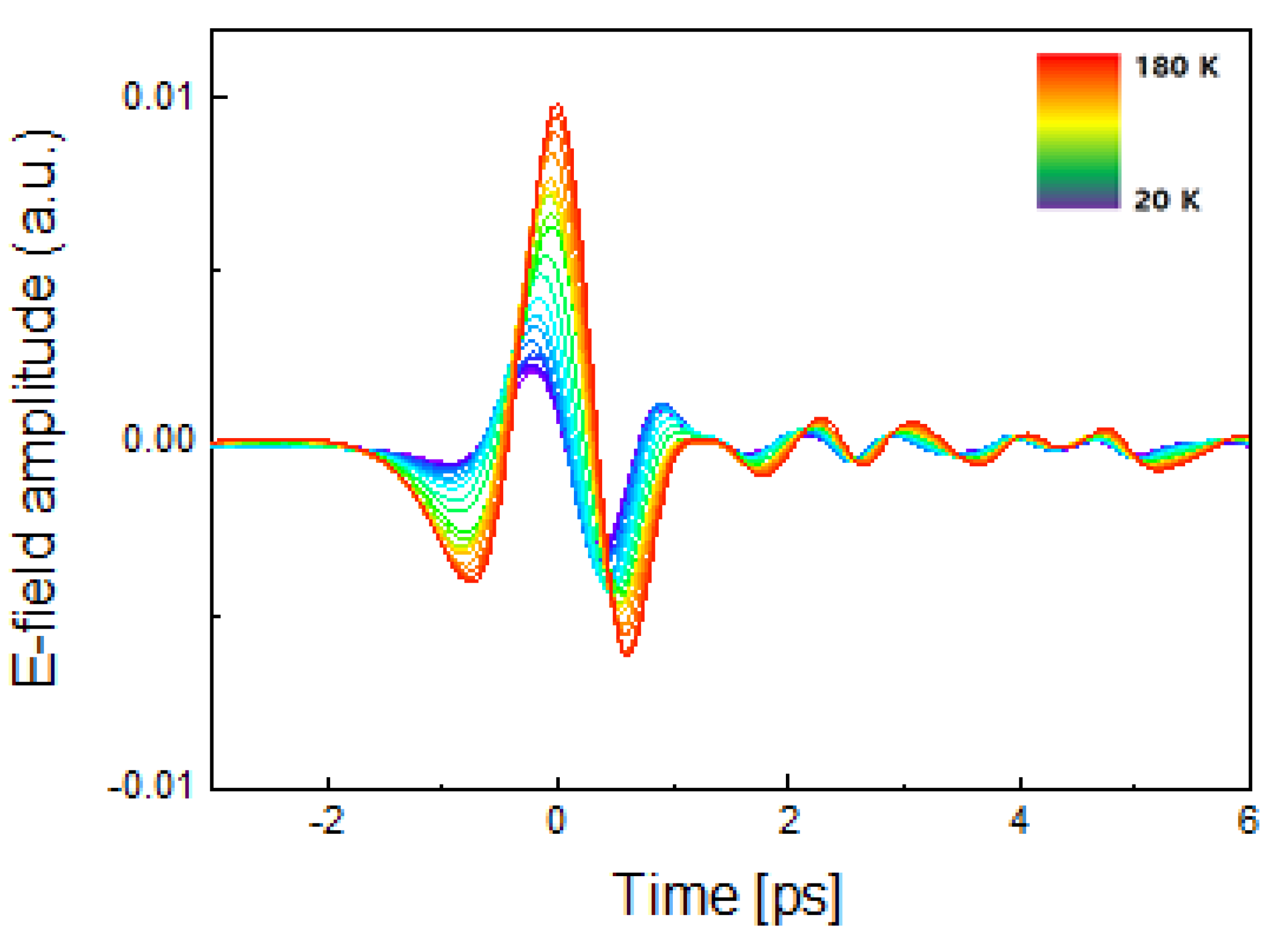
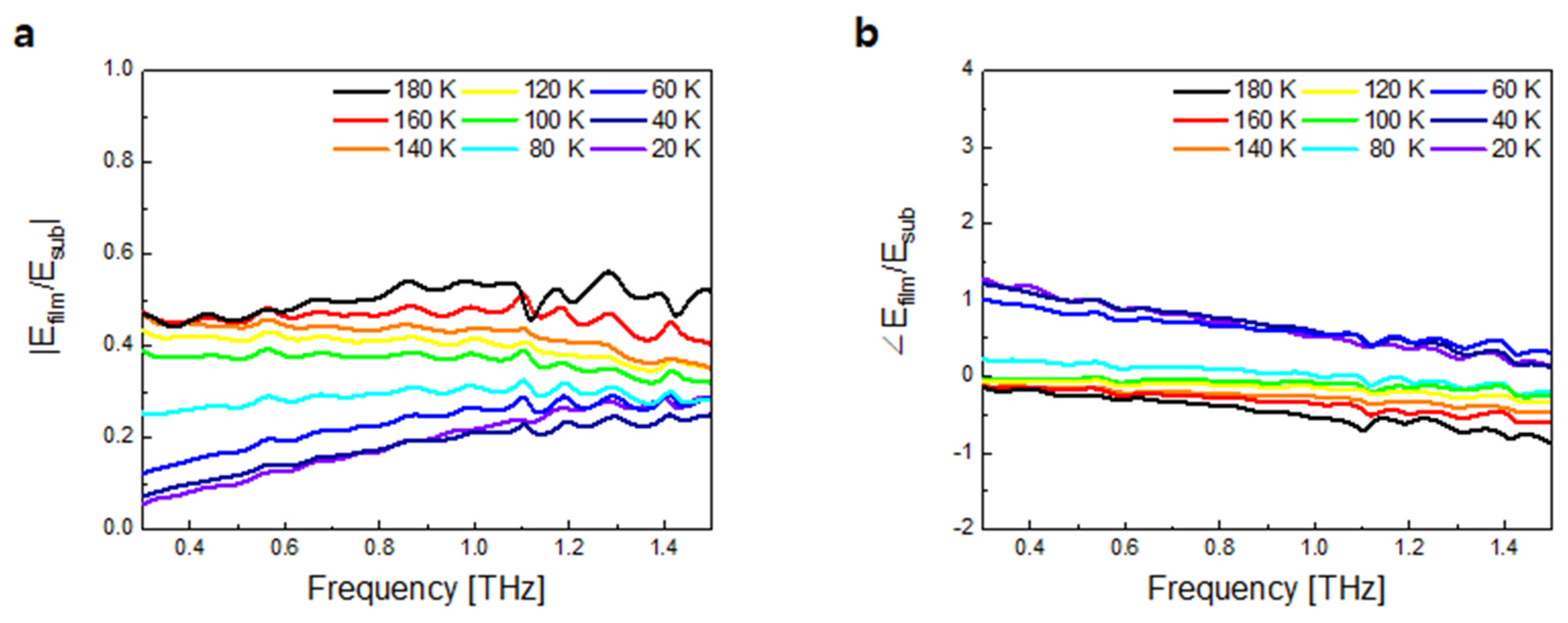
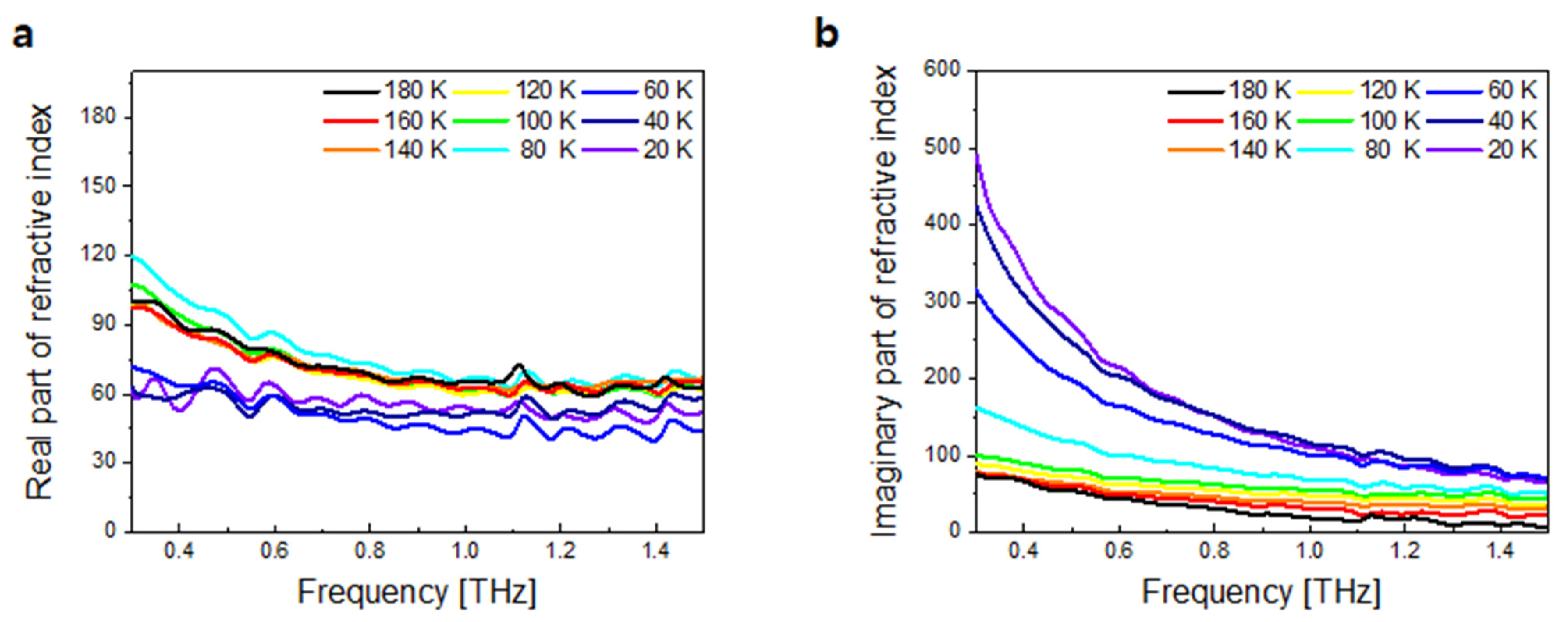
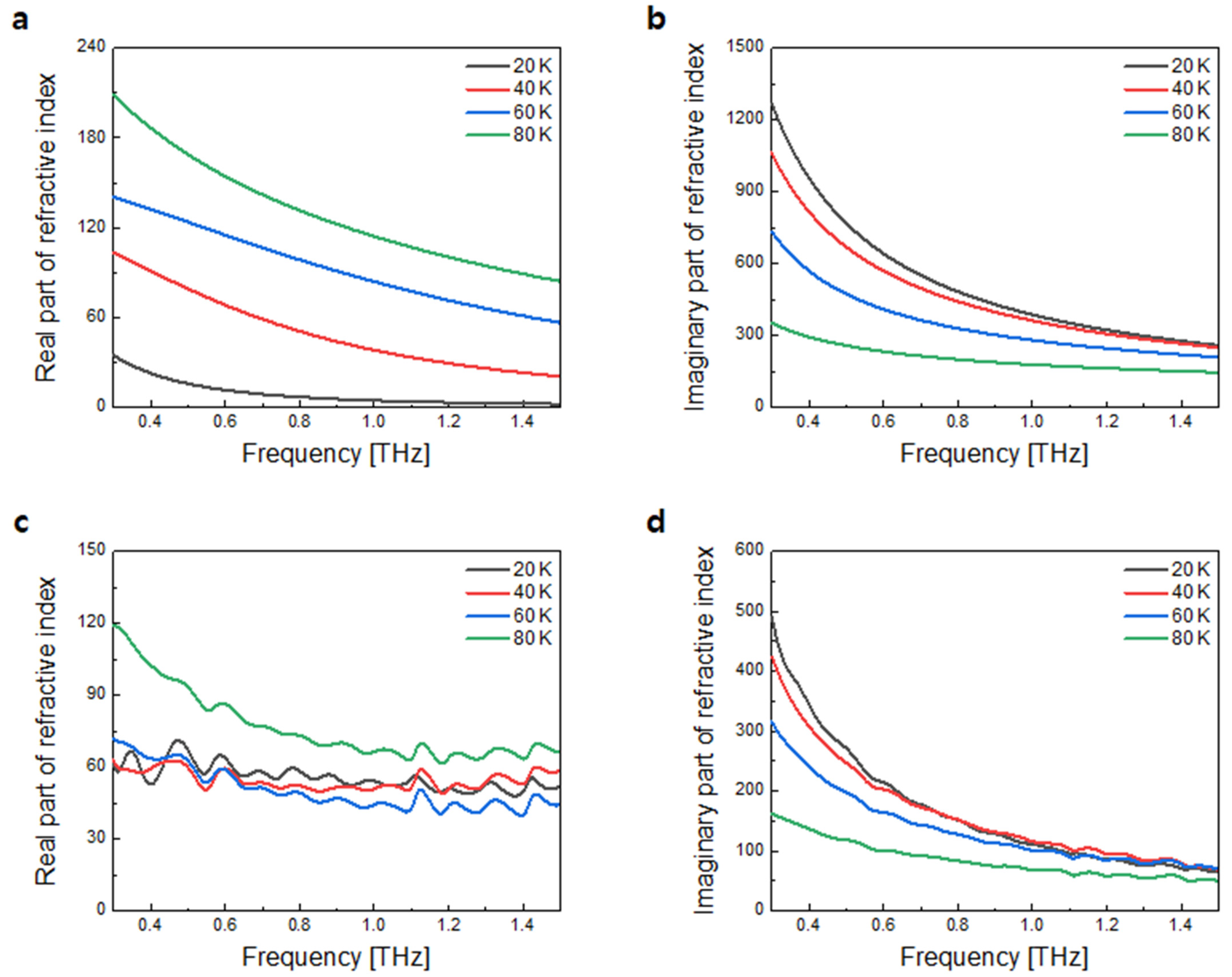
4. Results and Discussions

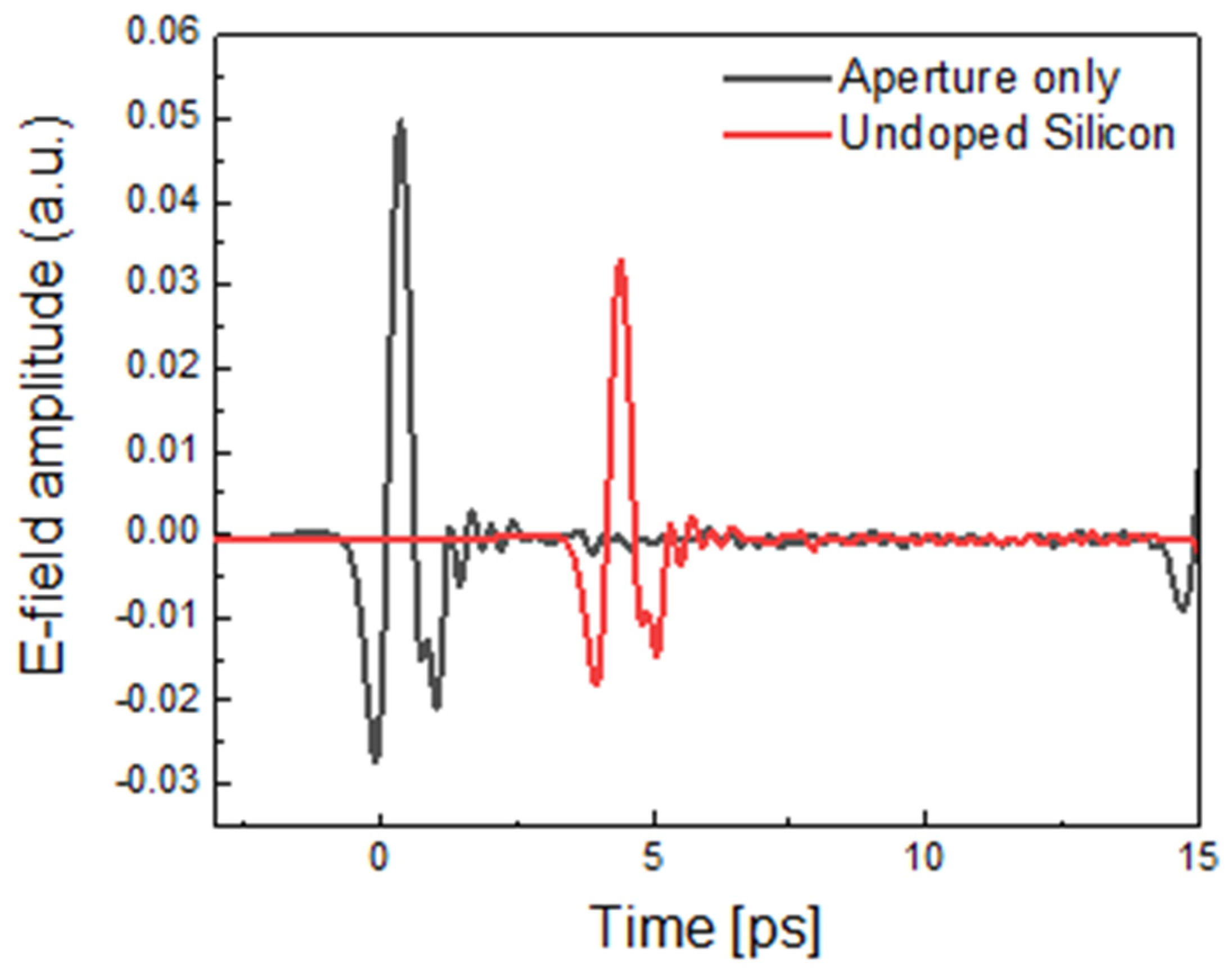
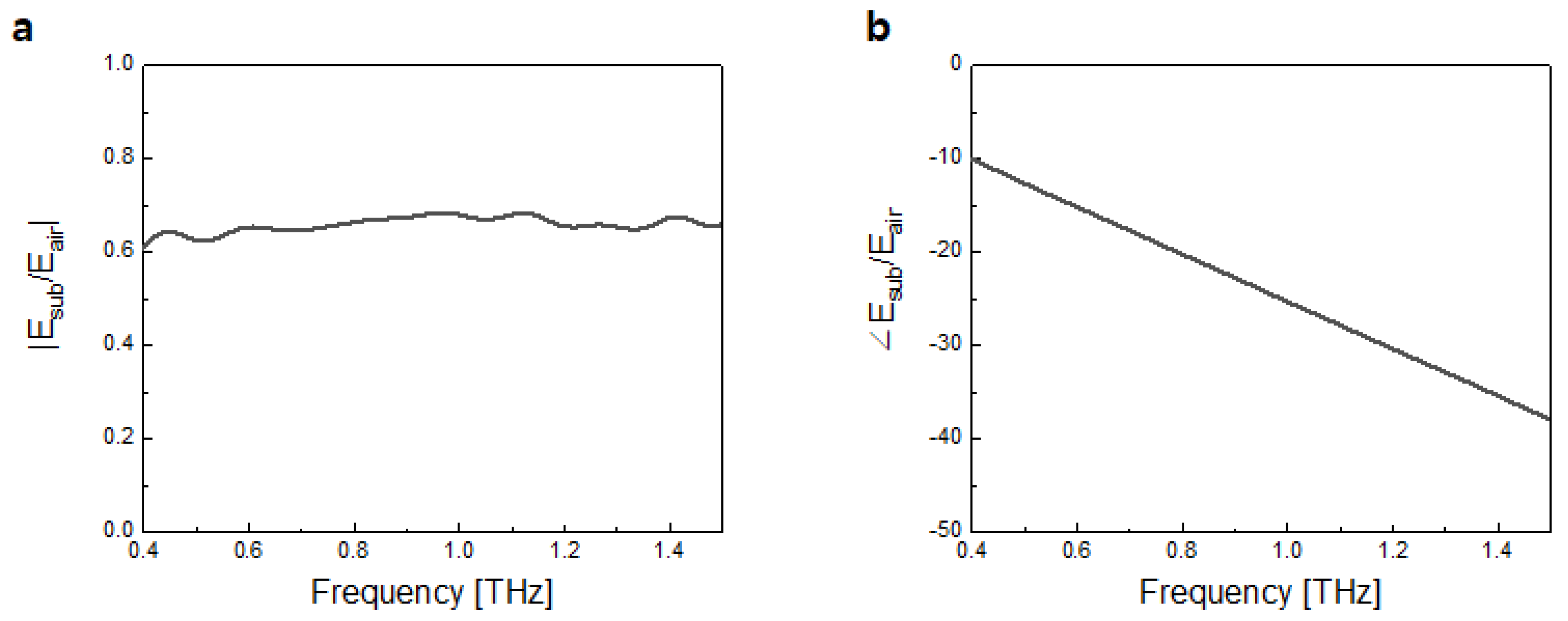
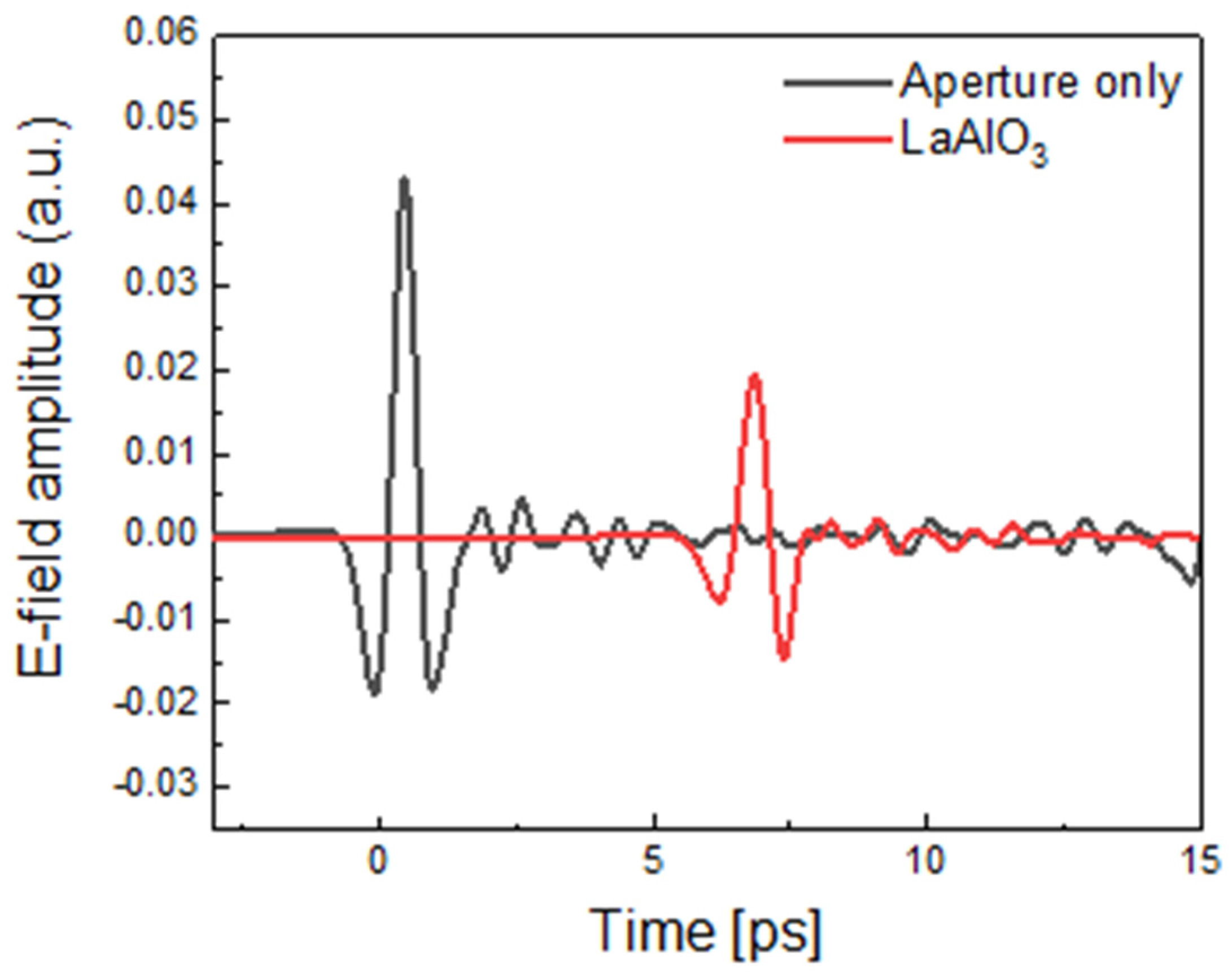
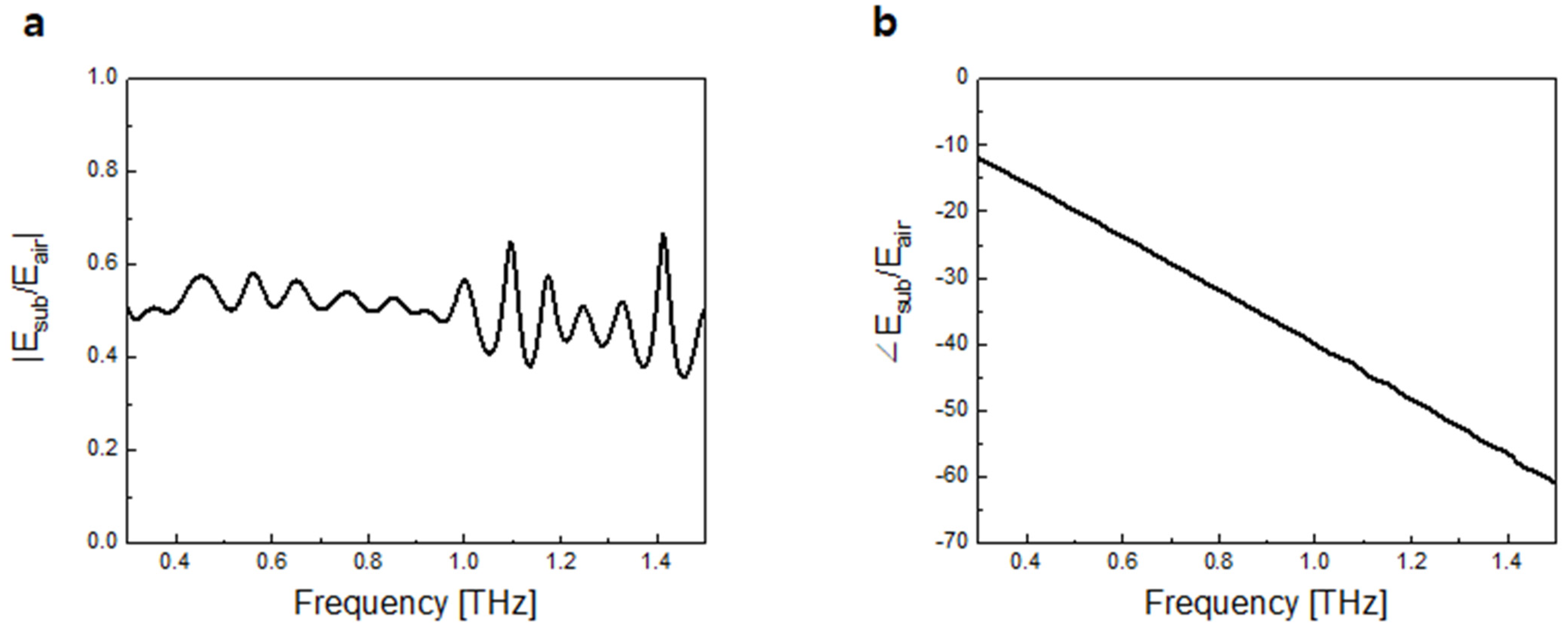
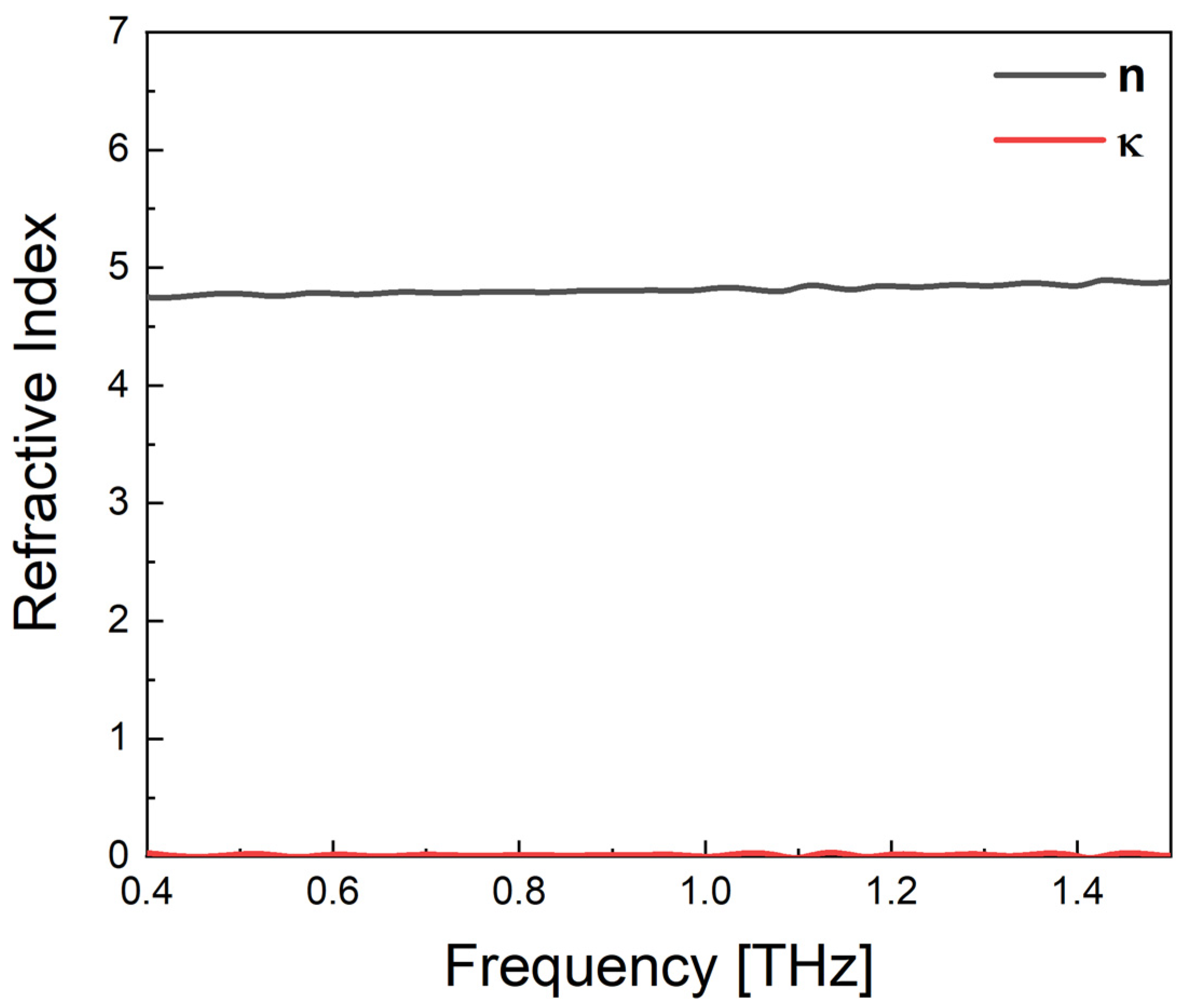
4.1. Undoped Silicon and Single Crystal LaAlO₃

Silicon wafers are one of the most commonly used substrates. In Section 4.2, an undoped silicon wafer (2000 Ω) was used as a substrate for the silver thin films. The time data of the terahertz transmitted through the aperture and the Si wafer are shown in Figure 8, and the normalized Fourier transform data are shown in Figure 9. By substituting the amplitude and phase of the Fourier transform data into Equations (16) and (17), the refractive index values can be obtained. Using these as an initial value, we obtained the numerical solution of Equation (6) to determine the refractive indices, as shown in Figure 10 ($n\approx 3.4,\kappa \approx 0.005$). This result is consistent with the generally known refractive indices of high resistivity: float-zone silicon [29].

A 500 μm-thick single-crystal LAO was used to deposit the GdBCO film. Usually an SrTiO₃ (STO) substrate is used, but in the terahertz region transmission is very low, owing to the influence of its phonon, thus an STO is not suitable [36,37]. The time data of the transmission through the aperture and LAO are shown in Figure 11, and the normalized Fourier transform data are shown in Figure 12. Meanwhile, Figure 13 presents the refractive indices of LAO, obtained using the same method as that used to calculate the refractive indices of the Si wafer. Therefore, we obtained the refractive indices of LAO ($n=4.8,\kappa \approx 0.01$). This result is consistent with the generally known refractive indices of single crystal LAO [30].

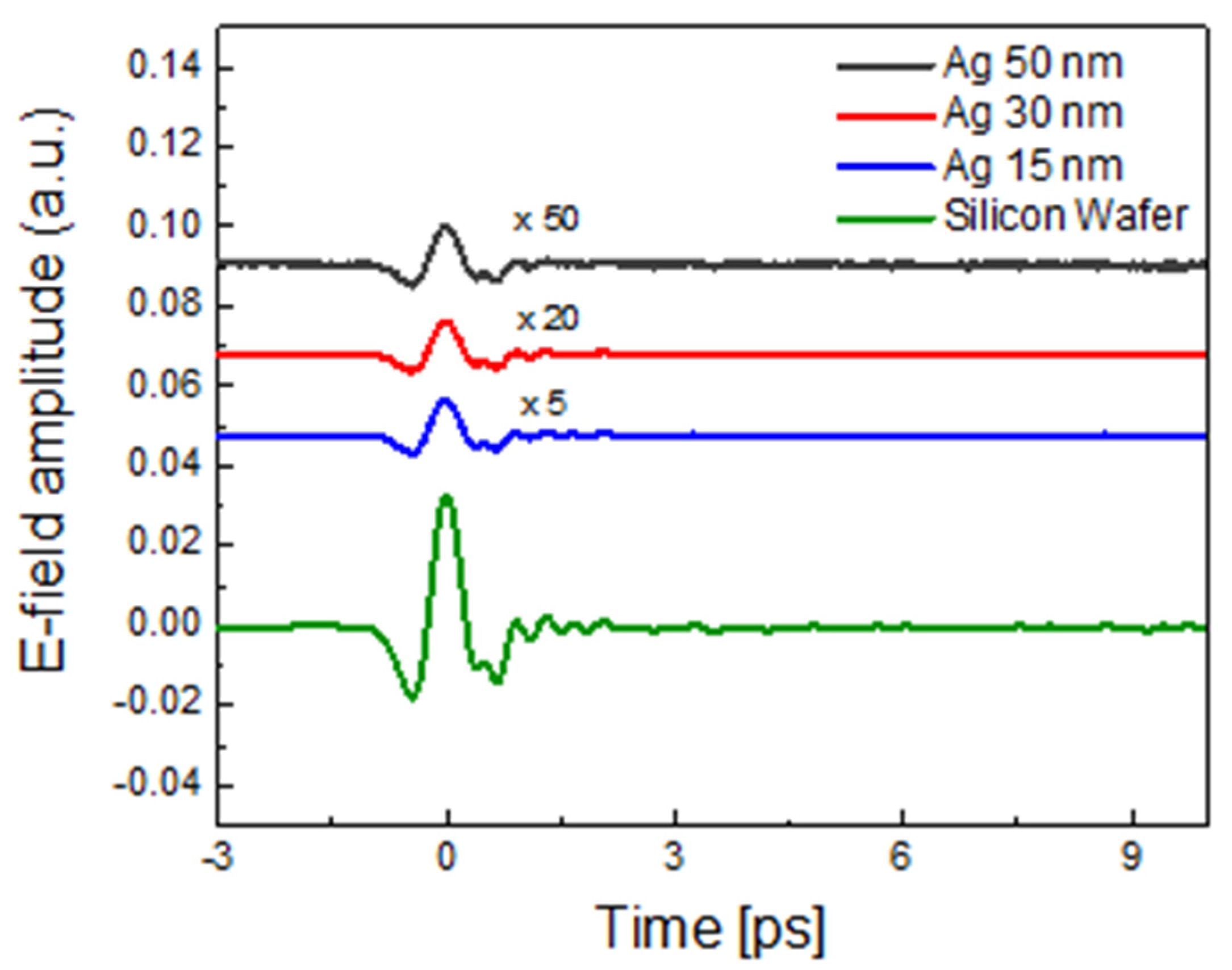
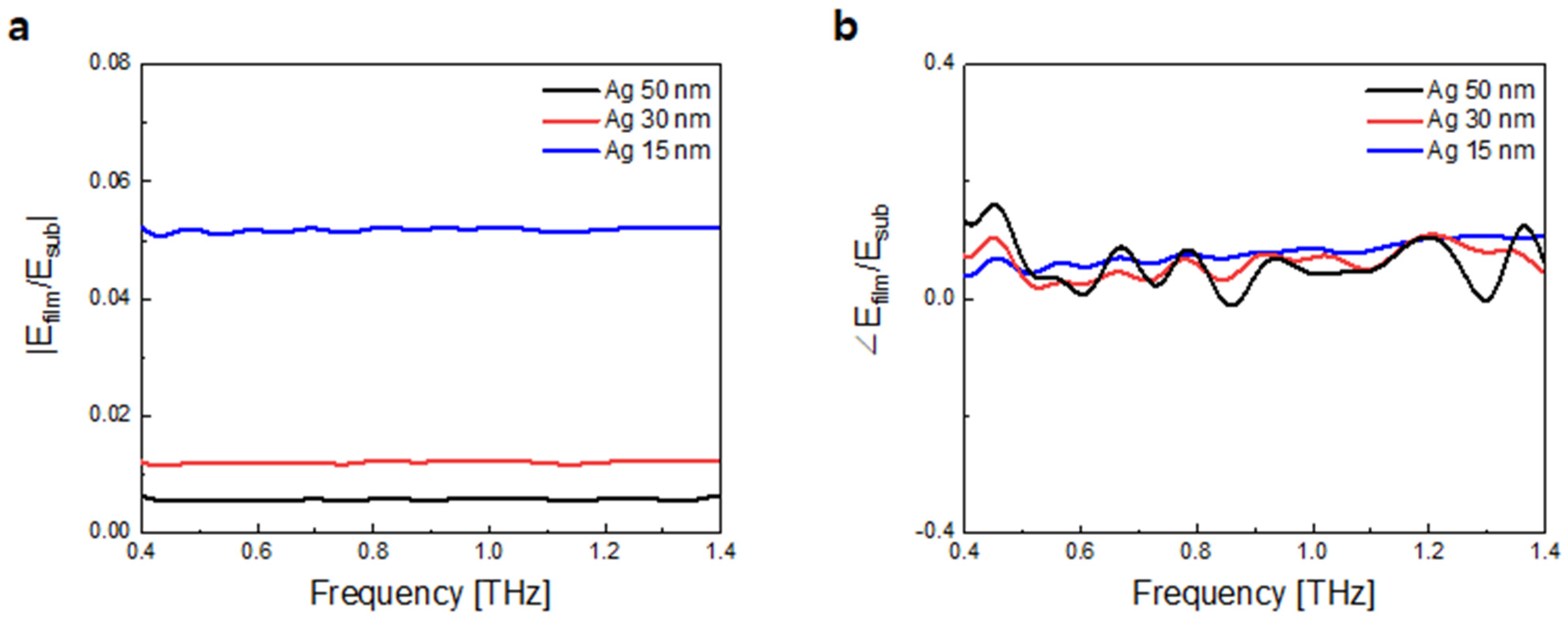
4.2. Silver Thin Films

Silver is a noble metal with very high conductivity. Thus, it is widely applied in the field of metamaterials and plasmonics as a perfect metal in the terahertz and lower frequency region. Noble metals have very large refractive indices in the terahertz region, so even if it is thin, the optical path is large enough. As a result, there is no problem in estimating the refractive index, even with the form of the thin film. Figure 14 shows the measured time trace data of the silver films and the substrate. Using the data in Figure 15, obtained from the Fourier transform of the data in Figure 14, the refractive indices of the silver thin film can be estimated, as shown in Figure 16, by applying the numerical extraction method presented in Section 3.

The simple Drude model for conductors is useful for describing the properties of metals in the low-frequency region. The Drude model dielectric function is given by

$$\tilde{\epsilon }\left(\omega \right)={\mathsf{\epsilon }}_{\infty }-\frac{{\omega }_p^2}{{\omega }^2+i\omega {\omega }_{\tau }}={\tilde{n}}^2.$$

(20)

where ${\omega }_p=1.37\times {10}^{16} \mathrm{Hz}$ and ${\omega }_{\tau }=27.4\times {10}^{12} \mathrm{Hz}$ are the Drude parameters of a bulk silver [38].

As shown in Figure 16, it is possible to estimate the refractive indices of the sub-50 nm-thick silver films, which are in a sub-skin depth region. It can be observed that the feature for this thin film tends to differ from that of bulk metal. Compared with the n and $\kappa$ values extracted from the Drude model of the bulk characteristic, it is apparent that both these values decrease as the film becomes even thinner. In particular, $\kappa$ decreases relatively more. In addition, the refractive indices of the 15 nm-thick silver film are approximately half that of the bulk. It should be noted that the terahertz transmittance through the metal film of the sub-skin depth thickness increases even more as its thickness decreases, because the refractive indices of the metal film also decline with the decreasing thickness. As the optical path of the silver thin film with a thickness of 15 nm is approximately 400 × 15 nm = 6 μm, the refractive indices of the silver film as thin as 10 nm can be experimentally extracted accurately. The estimated indices of n and $\kappa$ in the sub-skin depth thick silver films are qualitatively consistent with previous results [25,27].

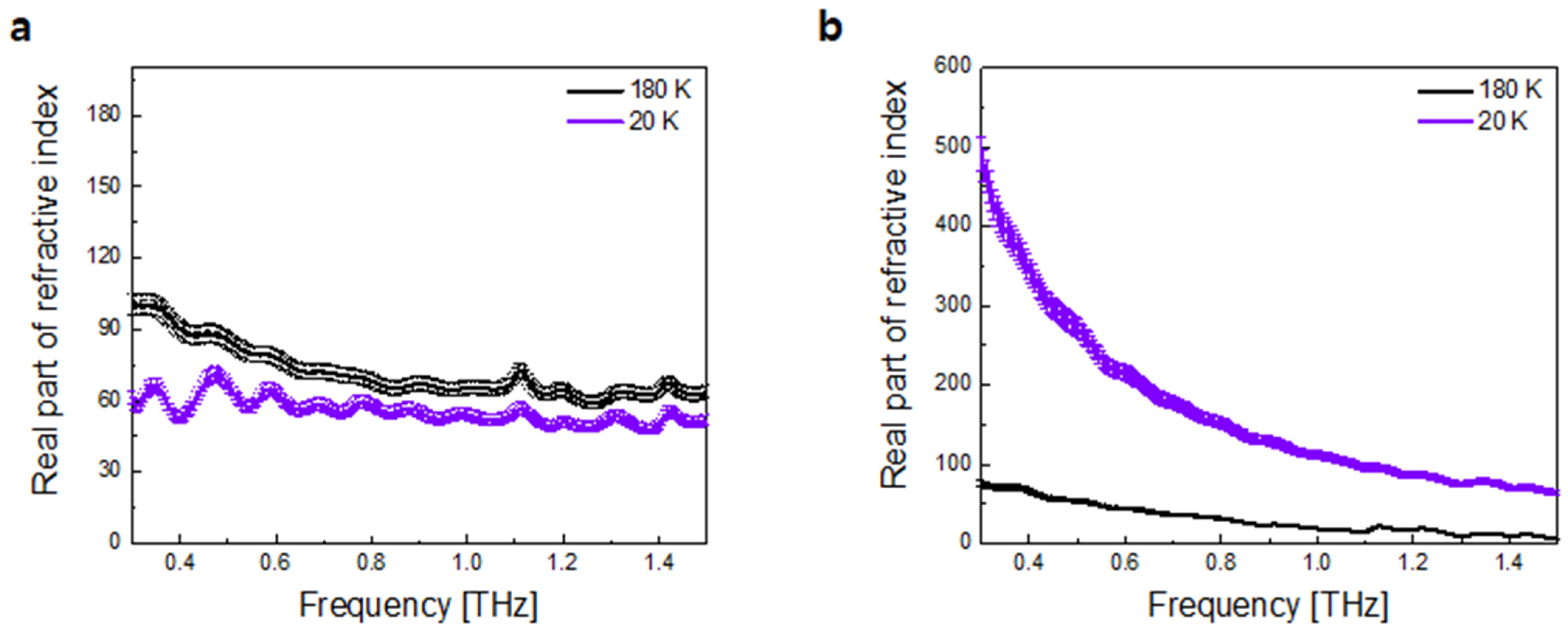
4.3. GdBCO Thin Film

GdBCO is a high-T_c cuprate superconducting material with a T_c of about 90 K. Such materials are more intriguing in various fields because they exhibit phase transition characteristics at moderately high temperatures. We measured transmitted signals through the 70 nm-thick GdBCO film on the LAO substrate in the temperature range between 20 and 180 K (Figure 17). By Fourier-transforming the time-domain data, we obtained the transmitted amplitude and phase spectra for the sample and a bare substrate. For normalization of the measured spectra, we used a reference signal for the bare LAO substrate. We obtained the normalized transmitted amplitude and phase spectra as the ratio between the measured data for the sample and the bare substrate, as shown in Figure 18. Using the same method as was used for the analysis of the silver thin films described in Section 4.2., we estimated the refractive indices of the GdBCO thin film at the selected temperatures, as shown in Figure 19.

As shown in Figure 19, the GdBCO thin films exhibit a Drude feature above T_c, like a general conducting material, and superconducting features at temperatures below T_c. We will further explain the details of the two-fluid model in the following paragraph.

To analyze the optical properties of the superconducting thin film, a two-fluid model was used (Figure 20a,b). The two-fluid model is similar to the Drude model, except that it explains the conductivity characteristics of a superconductor such that the ratio of carriers (normal electrons and superconducting electrons) changes with temperature [39]. The two-fluid model conductivity is expressed as follows

$$\tilde{\sigma }={\sigma }_1+i{\sigma }_2,$$

(21)

$${\sigma }_1=\frac{n{e}^2}{m^{*}}\frac{f_n\left(T\right)\omega \tau }{1+{\omega }^2{\tau }^2}={\omega }_p^2{\epsilon }_0\frac{f_n\left(T\right)\tau }{1+{\omega }^2{\tau }^2} ,$$

(22)

$${\sigma }_2=\frac{n{e}^2}{m^{*}}\left[\frac{f_n\left(T\right)\omega \tau }{1+{\omega }^2{\tau }^2}+\frac{f_s\left(T\right)}{\omega }\right]={\omega }_p^2{\epsilon }_0\left[\frac{f_n\left(T\right)\omega \tau }{1+{\omega }^2{\tau }^2}+\frac{f_s\left(T\right)}{\omega }\right],$$

(23)

where $f_n$ and $f_s$ are ratios of the normal and superconducting carriers, respectively, given by

$$f_n\left(T\right)+f_s\left(T\right)=1,$$

(24)

$$f_s\left(T\right)={\left(1-t^{\gamma }\right)}^2,$$

(25)

$$f_n\left(T\right)=1-f_s\left(T\right),$$

(26)

where $\tau$ and $t$ are the relaxation time and the reduced temperature T/T_c, respectively, and $\gamma$ is an empirical parameter.

$$\frac{1}{\tau }=\frac{1}{\tau \left(1\right)}\frac{t}{1+\alpha \left(t^{1-\gamma }-t\right)}$$

(27)

$$t=\frac{T}{T_{\mathrm{c}}}$$

(28)

Here, $\alpha =10$, $\gamma =1.5$, $T_{\mathrm{c}}=90 \mathsf{K}$, ${\omega }_p=2\times {10}^{15} \mathrm{Hz}$, and $\tau \left(1\right)=3.57\times {10}^{-14}\mathsf{s}$. The superconductivity emerges on the CuO₂ plane in cuprate superconductors. The A site ion (Y, Gd), located in between two CuO₂ layers, plays the role of the insulating layer. The two-fluid model is based on normal and superconducting carriers, and since the two-fluid model has been mainly applied for YBa₂Cu₃O₇ (YBCO), we used the parameters of YBCO, which is similar to the GdBCO [40], in the analysis using the two-fluid model [41].

The complex dielectric function is expressed as:

$$\tilde{\epsilon }\left(\omega \right)={\tilde{n}}^2={\mathsf{\epsilon }}_{\infty }+\frac{i\tilde{\sigma }}{\omega {\epsilon }_0}.$$

(29)

The complex refractive index is given by:

$$\tilde{n}=n+i\kappa =\sqrt{\tilde{\epsilon }}.$$

(30)

In the time data of Figure 17, the tendency of the terahertz transient appears at an earlier delay time, as the temperature decrease is contrary to the belief that the conductivity increases and the refractive index increases as the temperature decreases. This is because, as the temperature decreases, the real part of the refractive index decreases, which shortens the optical path. In addition, the imaginary part of the refractive index will greatly affect the amplitude of the exponential term in the Fresnel coefficient. However, as it also exists in the term outside the exponential, it may affect the optical path, although it is less than the real part of the refractive index. As shown in Figure 20, the 70 nm-thick superconducting GdBCO film exhibited qualitatively similar properties. However, the reason why the quantitative values are different not only owes to the use of the YBCO parameters, but also the GdBCO film, which is too thin to sustain the quality of bulk [37,42]. Moreover, contrary to the theory (Figure 20a,b), there was no significant difference in the real part of the refractive index from 20 to 60 K throughout the experiment (Figure 20c,d). The pulse width of the probe beam was approximately 10 fs; therefore, it was difficult to distinguish the time delay when the optical path was less than 3 μm. As the thickness of the thin film is 70 nm and the real part of the refractive index is approximately 50, the optical path is approximately 3.5 µm, which is close to the resolution limit. Therefore, it is difficult to accurately estimate a refractive index value that is smaller than this. However, as previously mentioned, the imaginary part of the refractive index corresponds more with amplitude, so it would be qualitatively good agreement with the results obtained by the two-fluid model.

In the experiment, the SNR is 5000:1. Therefore, it hardly affects the error in the estimated values, and the most critical error is the uncertainty in the thickness of the GdBCO film, as shown in the SEM image in Figure 2. Accordingly, the refractive index and the related error bars that can occur due to the thickness at the highest and lowest temperatures are shown in Figure 21. The error of the refractive indices due to the thickness uncertainty of about $\pm$10% is about $\pm$5%.

In summary, we experimentally estimated the refractive indices of a 70 nm-thick superconducting GdBCO film via transmission-type terahertz time-domain spectroscopy combined with the numerical extraction method. Although many studies were performed with superconducting thin films, especially in the terahertz and lower frequency regions, they were limited to analysis of the actual index of refraction of the superconducting thin film, where its thickness is in the sub-skin depth region. Our terahertz time-domain spectroscopy, based on the 10-fs pulse laser, showed a great possibility of estimating the terahertz dielectric constants of sub-100 nm thick superconducting films, even in the superconducting state. In addition, this technique, combined with the numerical extraction method, can be applied to experimentally analyze the terahertz optical properties of various thin film materials with the one-shot measurement.