Modeling Interactions of Iron Atoms Encapsulated in Nanotubes
Abstract
:1. Introduction
2. Computational Details
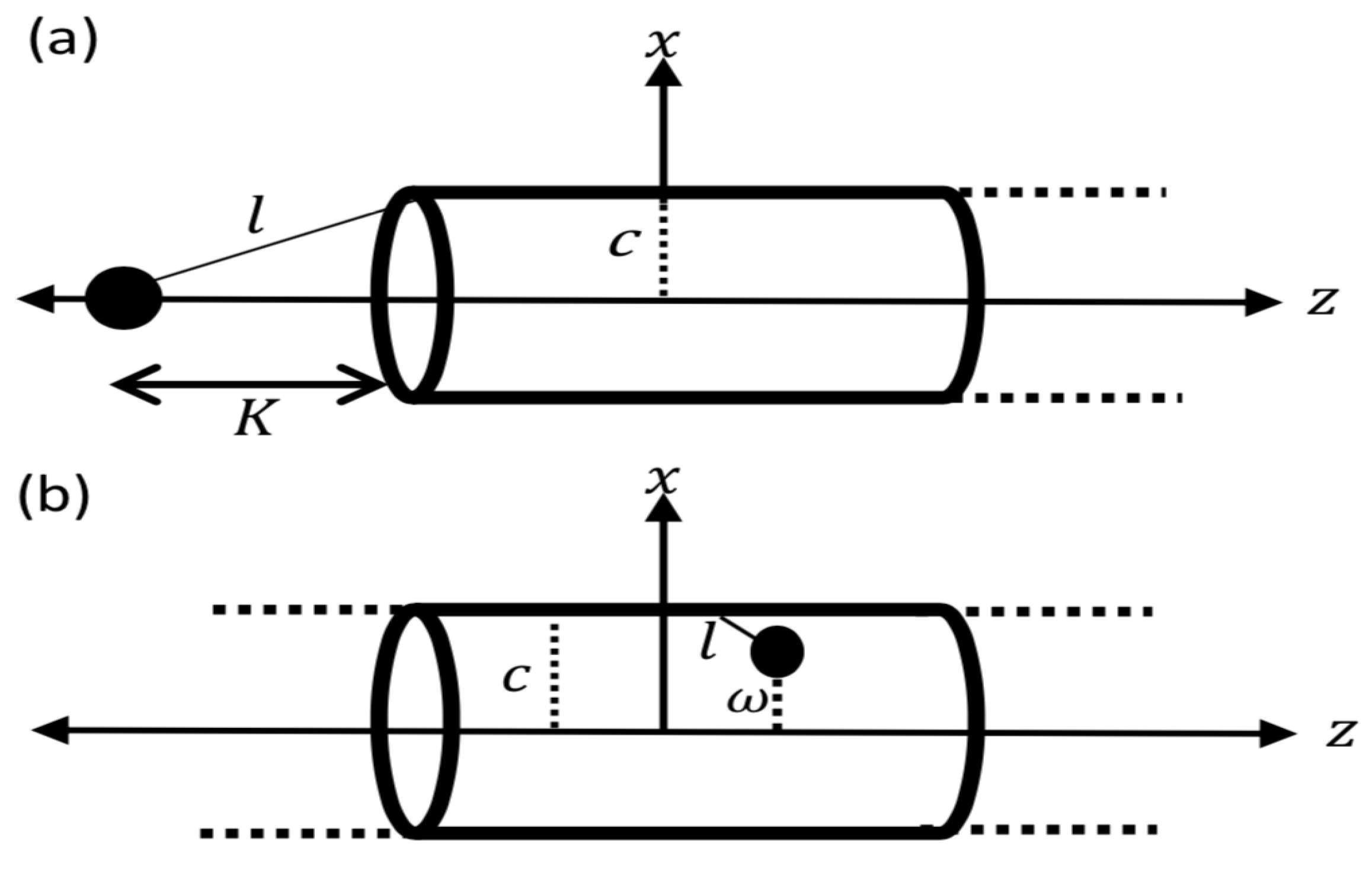
2.1. Suction Energy of Fe Atom Entering Nanotube
2.2. An Equilibrium Offset Position of Fe Atom Inside Nanotube
3. Numerical Results and Discussion
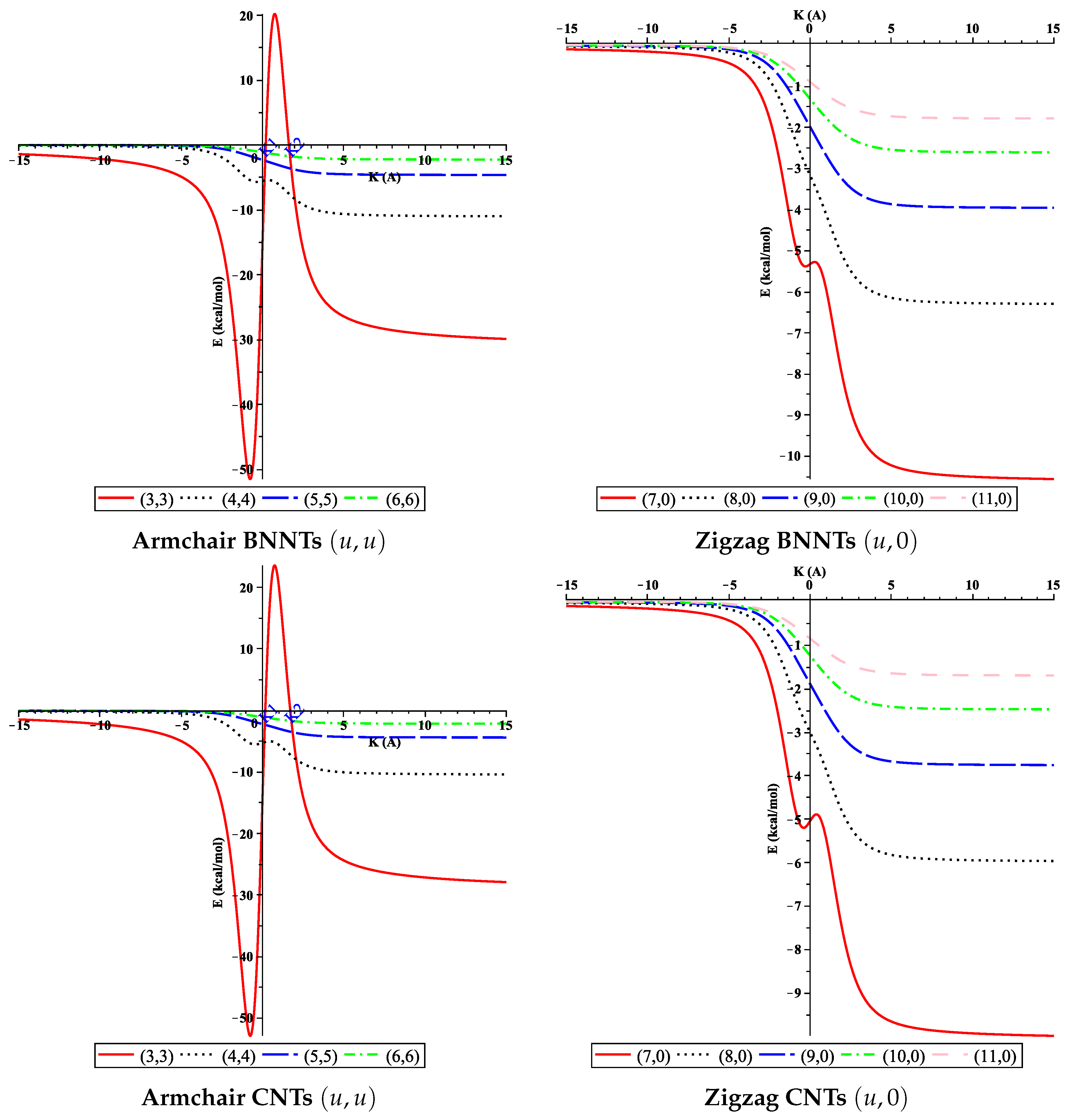
3.1. Suction Energy
3.2. An Equilibrium Offset
4. Summary
Funding
Data Availability Statement
Conflicts of Interest
References
- Dresselhaus, M.S.; Dresselhaus, G.; Avouris, P. Carbon Nanotubes: Synthesis, Structure, Properties and Applications; Springer: Berlin, Germany, 2001; Volume 80. [Google Scholar]
- Dolati, S.; Fereidoon, A.; Kashyzadeh, K.R. A Comparison Study between Boron nitride Nanotubes and Carbon Nanotubes. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 2250–2459. [Google Scholar]
- Vovushaab, H.; Sanyal, B. Adsorption of nucleobases on 2D transition-metal dichalcogenides and graphene sheet: A first principles density functional theory study. RSC Adv. 2015, 5, 67427. [Google Scholar] [CrossRef]
- Alshehri, M.H.; Duraihem, F.Z.; Aba Oud, M.A. Instability and translocation through nanopores of DNA interacting with single-layer materials. RSC Adv. 2020, 10, 36962. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Liu, Y.; Zhao, J. Boosting sensitivity of boron nitride nanotube (BNNT) to nitrogen dioxide by Fe encapsulation. J. Mol. Graph. Model. 2014, 51, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Munizaga, V.; Garcia, G.; Bringa, E.; Weissmann, M.; Ramirez, R.; Kiwi, M. Atomistic simulation of soldering iron filled carbon nanotubes. Comput. Mater. Sci. 2014, 92, 457–463. [Google Scholar] [CrossRef]
- Cheng, J.; Zou, X.P.; Zhu, G.; Wang, M.F.; Su, Y.; Yang, G.Q.; Lü, X.M. Synthesis of iron-filled carbon nanotubes with a great excess of ferrocene and their magnetic properties. Solid State Commun. 2009, 149, 1619–1622. [Google Scholar] [CrossRef]
- Munizaga, V.; Ramirez, R.; Kiwi, M.; Garcia, G. Mechanical properties of iron filled carbon nanotubes: Numerical simulations. J. Appl. Phys. 2017, 121, 234303. [Google Scholar] [CrossRef] [Green Version]
- Monteiro, A.O.; Cachim, P.B.; Costa, P.M.F.J. Mechanics of filled carbon nanotubes. Diam. Relat. Mater. 2014, 44, 11–25. [Google Scholar] [CrossRef]
- Kang, Y.-J.; Choi, J.; Moon, C.-Y.; Chang, K.J. Electronic and magnetic properties of single-wall carbon nanotubes filled with iron atoms. Phys. Rev. B 2005, 71, 115441. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, A.K.; Kumari, K.N. Electronic and Magnetic Properties of Iron Clusters Encapsulated in Carbon Nanotubes. Bull. Pure Appl. Sci. Phys. 2020, 39, 218–223. [Google Scholar] [CrossRef]
- Horga, F.I.; Mañanes, A.; López, M.J.; Alonso, J.A. Electronic and magnetic properties of Fe clusters inside finite zigzag single-wall carbon nanotubes. Phys. Rev. B 2013, 87, 085402. [Google Scholar] [CrossRef]
- Wang, S.-F.; Zhang, J.-M.; Xu, K.-W. Structural, electronic and magnetic properties of Fe nanowires encapsulated in boron nitride nanotubes. Physica B 2010, 405, 1035–1039. [Google Scholar] [CrossRef]
- Xie, Y.; Huo, Y.-P.; Zhang, J.-M. Magnetic properties and electronic structures of hcp Fe, Co and Ni nanowires encapsulated in a zigzag (12, 0) BN nanotube. Physica B 2012, 407, 2136–2140. [Google Scholar] [CrossRef]
- Fathalian, A.; Jalilian, J.; Shahidi, S. First principle study of the electronic and magnetic properties of a single iron atomic chain encapsulated in boron nitrite nanotubes. Solid State Commun. 2011, 151, 1635–1639. [Google Scholar] [CrossRef]
- Koi, N.; Okua, T.; Nishijima, M. Fe nanowire encapsulated in boron nitride nanotubes. Solid State Commun. 2005, 136, 342–345. [Google Scholar] [CrossRef]
- Wang, S.-F.; Chen, L.-Y.; Zhang, Y.; Zhang, J.-M.; Xu, K.-W. Magnetic and electronic properties of a single iron atomic chain encapsulated in carbon nanotubes: A first-principles study. J. Mol. Struct. Theochem. 2010, 962, 108–112. [Google Scholar] [CrossRef]
- Rappi, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skid, W.M. UFF, a full periodic table force field formolecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Alshehri, M.H. Modelling of Nickel Atoms Interacting with Single-Walled Nanotubes. Adv. Math. Phys. 2019, 2019, 8240587. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 6th ed.; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Erdelyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume 1. [Google Scholar]

| Interaction | A (Å6 kcal/mol) | B (Å12 kcal/mol) |
|---|---|---|
| C-Fe | 230.724747 | 360,215.204700 |
| BN-Fe | 242.024836 | 384,731.550600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, M.H. Modeling Interactions of Iron Atoms Encapsulated in Nanotubes. Crystals 2021, 11, 845. https://doi.org/10.3390/cryst11080845
Alshehri MH. Modeling Interactions of Iron Atoms Encapsulated in Nanotubes. Crystals. 2021; 11(8):845. https://doi.org/10.3390/cryst11080845
Chicago/Turabian StyleAlshehri, Mansoor H. 2021. "Modeling Interactions of Iron Atoms Encapsulated in Nanotubes" Crystals 11, no. 8: 845. https://doi.org/10.3390/cryst11080845
APA StyleAlshehri, M. H. (2021). Modeling Interactions of Iron Atoms Encapsulated in Nanotubes. Crystals, 11(8), 845. https://doi.org/10.3390/cryst11080845