Next Article in Journal
Identifying a Unique Communication Mechanism of Thermochromic Liquid Crystal Printing Ink
Next Article in Special Issue
The Effect of Specimen Size and Test Procedure on the Creep Behavior of ME21 Magnesium Alloy
Previous Article in Journal
Localization of Native Mms13 to the Magnetosome Chain of Magnetospirillum magneticum AMB-1 Using Immunogold Electron Microscopy, Immunofluorescence Microscopy and Biochemical Analysis
Previous Article in Special Issue
Effect of High Pressure and Temperature on the Evolution of Si Phase and Eutectic Spacing in Al-20Si Alloys
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 11
Issue 8
10.3390/cryst11080875
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Thermal Convection in the Core of Ganymede Inferred from Liquid Eutectic Fe-FeS Electrical Resistivity at High Pressures

by
Joshua A. H. Littleton
*,
Richard A. Secco
and
Wenjun Yong
Department of Earth Sciences, University of Western Ontario, London, ON N6A5B7, Canada
*
Author to whom correspondence should be addressed.
Crystals 2021, 11(8), 875; https://doi.org/10.3390/cryst11080875
Submission received: 24 June 2021 / Revised: 22 July 2021 / Accepted: 26 July 2021 / Published: 28 July 2021
(This article belongs to the Special Issue Properties of Transition Metals and Their Compounds at Extreme Conditions)
Browse Figures
Versions Notes

Abstract

:
The core of Ganymede is suggested to be mainly Fe but with a significant proportion of S. Effects of S as a core constituent are freezing-point depression, allowing for a molten core at relatively low core temperatures, and modification of transport properties that can influence the dynamo and thermal evolution. The electrical resistivity of solid and liquid Fe-FeS (~24–30 wt.% S) was measured up to 5 GPa and thermal conductivity was calculated using the Wiedemann–Franz law. These first well-constrained experimental data on near eutectic Fe-FeS compositions showed intermediate values of electrical and thermal conductivities compared to the end-members. Eutectic temperatures were delineated from the solid to liquid transition, inferred from sharp changes in electrical resistivity, at each pressure. Combined with thermal models, our calculated estimates of the adiabatic heat flow of a molten Fe-FeS eutectic composition core model of Ganymede showed that thermal convection is permissible.

1. Introduction

The dipolar magnetic field of Ganymede may be produced by internal convection of a liquid iron (Fe) outer core, similar to Earth’s geodynamo [1]. Convective motions in liquid cores may be derived from two broad sources: (i) thermal and (ii) compositional [2]. The former requires heat transfer out of the core exceeding the heat transferred by conduction of the core. The latter is related to the gradual cooling of the core and consequent inner core formation, and density contrasts between precipitated core chemical species and residual liquid (e.g., Fe snow or FeS floatation) [3,4,5]. While Ganymede is believed to have a predominantly Fe core, it has been suggested that the core is composed of more sulfur (S) compared to other terrestrial Fe cores [3,6,7,8,9,10]. A significant effect due to the presence of S as a core element is freezing-point depression. For instance, the eutectic temperature (T) in the Fe-FeS system at 1 atm is ~1260 K, approximately 600 K lower than the melting T of Fe [11]. Impurities and more abundant elemental constituents may also affect transport properties such as electrical resistivity (ρ) and thermal conductivity (κ) [12], which are two critical parameters in magnetic field generation via planetary body dynamos.
Experimental investigations of ρ and κ of Fe (e.g., [13,14,15,16,17,18,19]) and FeS [16,20,21] at core conditions have shown varying degrees of agreement and consistency. However, typical estimates of the S content in the core of Ganymede, based on internal structure and magnetic field generation models, are adjacent to the Fe-FeS eutectic [3,4,5,9,10,22]. If core S composition is eutectic or eutectic-adjacent (i.e., within a few weight percent), this may allow the core of Ganymede to be molten and permit thermally driven convection at relatively low core T (<1400 K) that can power a dynamo-produced magnetic field. In this work, we measured ρ of eutectic-adjacent Fe-FeS in both solid and liquid states at pressures (P) up to 5 GPa. The measured results were used to delineate the P-dependent eutectic T and to calculate κ and adiabatic heat flow (Qa) to determine if thermal convection is permissible in a molten, eutectic-adjacent S composition core of Ganymede constrained to a low core T.

2. Materials and Methods

Fe and FeS powders were purchased from ESPI Metals (99.95% purity) and Alfa Aesar (99.98% purity), respectively, and were mixed together to attain an S content close to the eutectic composition (Table 1) [23]. All experiments were conducted in a 1000-ton cubic anvil press, as described by Secco [24]. A three-sectioned cubic P cell design and four-wire electrical resistance technique using Type S (platinum (Pt) and rhodium (Rh) alloy) thermocouples for all experiments were the same as those used and described by Littleton et al. [21]. Experimental specifications remained largely the same, with two minor alterations: (i) the highest T reached was ~1430 K since the liquidus T’s are considerably lower for the Fe-FeS system investigated than for FeS; and (ii) P- and T-dependent contributions to the measured voltage from tungsten (W) disks placed between the thermocouple junctions and powder mixture sample were accounted for [25] since these contributions were proportionally larger and non-negligible compared to measurements of FeS under similar conditions.

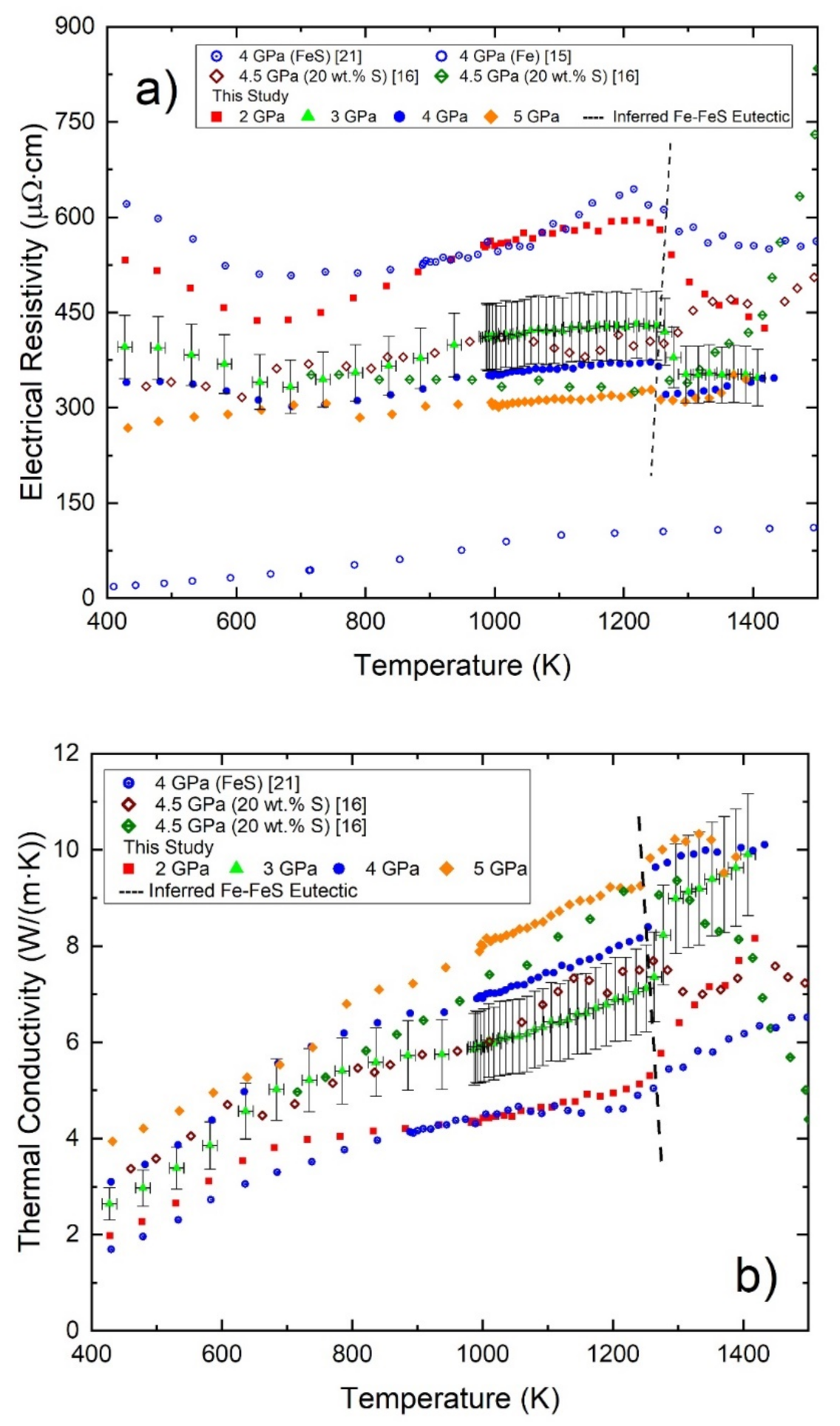
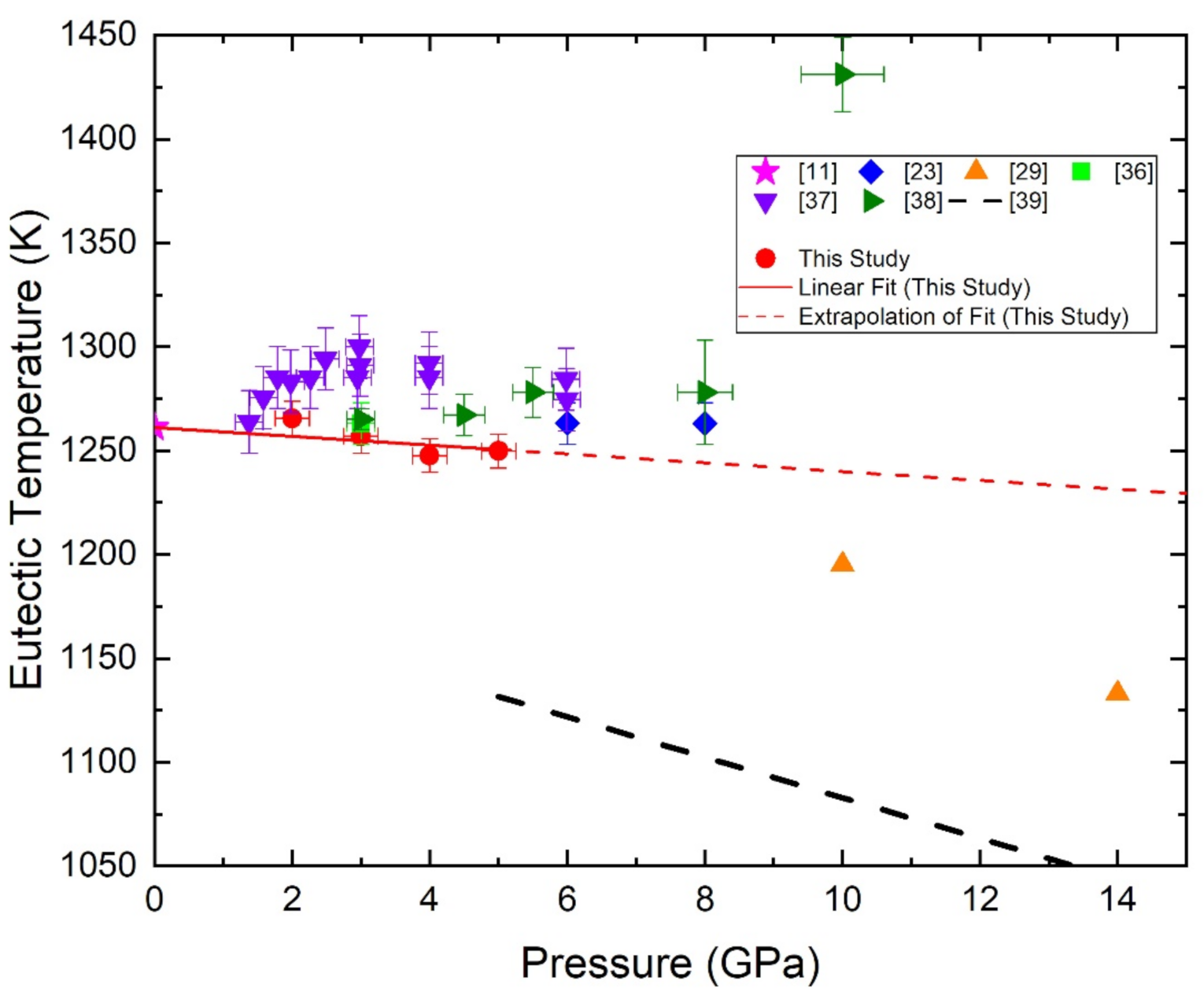
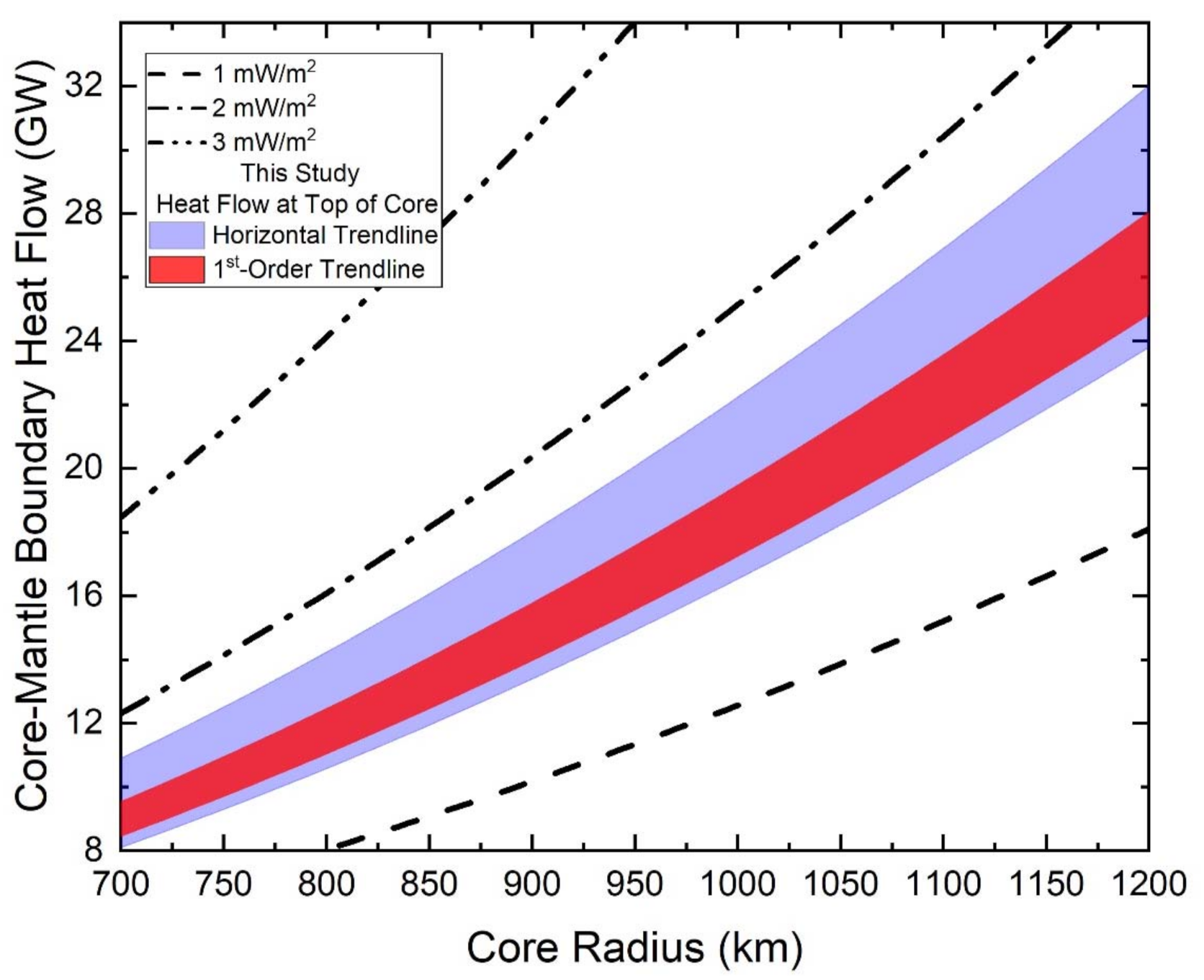
3. Results and Discussion

Figure 1a,b show measured values of ρ and calculated values of κ of Fe-FeS, respectively, up to 5 GPa and ~1430 K from this study. Also shown are ρ and κ values of FeS [21], Fe-FeS (20 wt.% S) [16], and Fe [15] from previous studies for comparison. Fe-FeS was observed to have intermediate values of ρ compared to the end-members. This result was expected since the addition of electrically conductive Fe to FeS should decrease ρ, or equivalently the addition of semiconducting FeS to Fe should increase ρ. The Wiedemann–Franz law (WFL), κ = L·T/ρ, using a Lorenz number (L) equal to the theoretical Sommerfeld value (2.445·10−8 W·Ω·K−2), was used to calculate the electronic component of κ. Similarly, as expected, the results showed that Fe-FeS is more thermally conductive than FeS but less so than Fe.
The results of this study showed the T-coefficient of ρ, (∂ρ/∂T)P, from room T up to a few hundred degrees increased as a function of increasing P. The T-coefficient was most negative at 2 GPa, which gradually became shallower with each P increment until 5 GPa, at which a shallow positive T-coefficient was observed. The negative T-coefficient for 2–4 GPa is consistent with the trends observed for FeS IV, the hexagonal phase of FeS, at similar conditions [21]; however, the positive T-coefficient at 5 GPa is a behavior more comparable to a metallic electrical conductor (e.g., [15,16,17,26,27,28]). One interpretation is that Fe-FeS behavior changes to become more conductor-like with increasing P at low T. Alternatively, as discussed later, this observation may be the result of the sample containing the largest proportion of Fe to account for the P-dependency of the eutectic composition [23]. Below the eutectic T at our experimental P, the binary system exhibits a two-phase solid-state regime (Fe + FeS) [11,29]. We doubt this observation is related to a solid-state phase transition since the reported P conditions at which other solid-state phases (e.g., Fe3S, Fe3S2) have been observed well exceed ours (>10 GPa) [29,30,31,32,33,34]. Two sets of low T measurements of Fe 20 wt.% S at 4.5 GPa reported by Pommier [16] are more similar to our observations at 5 GPa. Those results show, however, conflicting solid-state trends as one exhibits a positive T-coefficient while the other is negative. With continued heating and increasing T, the T-coefficient of ρ at all P is positive and approaches a nearly linear trend at T leading up to the transition from solid to liquid states. These T-dependencies are also consistent with the trends observed for FeS V [16,21], the Ni-As-type phase of FeS, and Fe [14,15,16,17,19].
The T-dependent trends leading up to the eutectic T observed in this study are in good agreement with those measured by Pommier [16] who also showed, in full context of that study, that ρ and κ of Fe-FeS had intermediate values of the end-members. With the expectation that 20 wt.% S is more electrically conductive than our higher S contents, as discussed later, the measured values of ρ and κ are also in good agreement within reported error ranges up to the eutectic T. At T above the eutectic, the measured values differ considerably, with high T measurements at 4.5 GPa approaching values as large as 3000 μΩ·cm while values of ρ in this study remain nearly a magnitude less. The corresponding values of κ calculated via the WFL are expectedly low by comparison to this work. Similar observations and comparisons to Pommier [16] were made in the FeS investigations by Littleton et al. [21] in which they suggested that a possible explanation for the rapidly increasing values of ρ was apparent incomplete liquid confinement and reduced thermocouple/electrode chemical integrity. For the 4.5 GPa experiment by Pommier [16] that utilized molybdenum (Mo) electrodes and Type-C (tungsten (W)-rhenium (Re) alloys) thermocouples, a post-experiment cross-section SEM image of the same sample clearly showed and annotated liquid migration and complete dissolution of the electrodes. We echo the same interpretation as Littleton et al. [21] for these investigations on Fe-FeS.
A representative post-experiment cross-section is shown in Figure 2a,b. Figure 2a shows an image of the cross-section of the 4 GPa pressure cell centered on the sample and Figure 2b shows a back-scattered electron image of the same sample. Tabulated electron microprobe results of 15 locations correspond to labeled sites on the Figure 2b image. The bulk of the sample retained an Fe-S composition and the bulk of the W disks and arms of the Type-S TC wires retained high chemical purity. After normalizing the Fe and S content values, the microprobe analyses were used to determine an average S-content (wt.% S) of the samples: 29.56 ± 0.05 (2 GPa); 26.17 ± 0.05 (3 GPa); 25.68 ± 0.07 (4 GPa); 23.76 ± 0.06 (5 GPa). For comparison, estimates of the P-dependent eutectic composition of the Fe-FeS system, using the equation reported by Buono and Walker [23], are (wt. % S): 28.0 (2 GPa); 26.5 (3 GPa); 25.1 (4 GPa); 23.8 (5 GPa), suggesting our sample compositions are eutectic or eutectic-adjacent.
In this study, the abrupt decrease of ρ following the near linear trends is indicative of T exceeding the eutectic T and a state change of the sample from solid to partially liquid. The decrease of ρ at the solidus is consistent with other Fe alloys (e.g., [28,35]) and FeS [21]. Compared to FeS, the decrease is significantly sharper. Although fast heating rate and high measurement frequency were also used here, the difference in the sharpness of this transition is due to a sample composition in the proximity of the eutectic. An exception, however, are the 2 GPa results that show a broader and more gradual decrease similar to FeS. This could be attributed to the composition of the sample being the most S-rich and furthest from the eutectic, resulting in a larger partial melting region. In other words, the more gradual decrease of ρ reflects the gradual production of liquid with increasing T past the eutectic. While previous works have investigated a broader range of S contents [16,20], our results are the first well-constrained experimental data on near eutectic compositions in the Fe-FeS system.
A line was drawn on Figure 1a to estimate the eutectic T at each P where the resistivity trend began to decrease. Immediately left of and right of the line represent the last solid and initial liquid state measurement of the sample, respectively. For the 5 GPa experiment, the results do not show an observable partial melting region. This may indicate that the S content is either very close to or at the eutectic composition. Thus, the measurement immediately to the right of the line represents the initial measurement of a completely liquid state sample. Figure 3 compares the eutectic T estimates of this study to prior works at high P. Our results are in good agreement with several prior studies at similar P conditions and indicate that the eutectic T up to 5 GPa does not deviate far from the eutectic at 1 atm. Moreover, our results indicate a negative P-dependency of the eutectic T, a trend also reported by Fei et al. [29] and Morard et al. [39] at higher P. However, we note that our P-dependent trend is shallower by comparison. The difference in the trends could be related to the methodology used for determining the eutectic T. Fei et al. [29] determined eutectic melting on the basis of quenched textures and chemical mapping, while Morard et al. [39] used in situ X-ray diffraction. Moreover, Buono and Walker [23] asserted that the presence of hydrogen, from the breakdown of trapped water within the sample material and/or sample enclosure, may be responsible for the significant eutectic T depression in the Fe-FeS system observed by Fei et al. [29] and Morard et al. [39].
Estimates of P within the core of Ganymede range from ~5 GPa at the core–mantle boundary (CMB) to ~11 GPa at its center and T at the CMB span ~1250–2100 K [3,5,7,9,10]. We adopted the same procedure to calculate adiabatic heat flow (Qa) at the top of Ganymede’s core as Littleton et al. [21], although for the current study two linear fits to interpolate and extrapolate values of ρ at 5 GPa between 1250 and 1450 K were used, as shown in the Appendix (Figure A1). A positive linear fit (with (∂ρ/∂T)P > 0 μΩ∙cm/K) was used to account for all measurements at T above the estimated eutectic T, while a horizontal linear fit (with (∂ρ/∂T)P = 0 μΩ∙cm/K and with ρ = 315 μΩ∙cm) was used to account for all measurements excluding the highest two temperatures. These were excluded because they may indicate the onset of deteriorating thermocouple integrity and W contamination.
Qa on the core side of the CMB was calculated using Equation (1) below:
Qa = −4πr2 κ(∂T/∂r)a
where (∂T/∂r)a is the adiabatic thermal gradient adopted from Breuer et al. [40]. Figure 4 shows Qa at the top of the core with radius varying between 700 and 1200 km and with a CMB T from 1250 to 1450 K and P of 5 GPa alongside estimates of the heat flow through the CMB for comparison. The specified T range was chosen to allow for an entirely molten core. Our estimates of Qa using a horizontal linear model ranged from ~8 GW for a CMB T of 1250 K and core radius of 700 km up to ~32 GW for a CMB T of 1450 K and core radius of 1200 km. These heat flow estimates are similar in magnitude to those reported by Littleton et al. [21] for a molten FeS core, which ranged from ~11 GW up to ~37 GW. However, it is important to note that the estimates of this study are for a significantly cooler molten core allowed by a eutectic-adjacent S composition. For instance, if the horizontal linear fit were extrapolated to a core T between 1600 and 1700 K used by Littleton et al. [21], the lower-bound and upper-bound Qa in the core would be ~13 GW and ~44 GW, respectively. The heat flow in the core using the positive linear fit is more constrained than the horizontal linear fit, with estimates of Qa ranging from ~8 GW up to ~28 GW. This result is due to the competing effects of increasing T and ρ, which are directly proportional and inversely proportional to κ, respectively, via the WFL.
Estimates of the heat flux out of the core and through the CMB of Ganymede range from ~1 to 6 mW/m2 [3,4,5,10]. Both the linear and horizontal models showed that thermal convection of a molten Fe-FeS core at relatively low core T is permissible provided the heat flux on the mantle-side of the CMB exceeds ~ 1.5 mW/m2. Littleton et al. [21] showed that thermal convection can carry up to one-third of the heat load to the CMB for a heat transfer of 3 mW/m2 through the CMB in a Ganymede core of liquid FeS. The results of this study for a Ganymede core of near eutectic Fe-FeS show a similar heat load proportion that can be carried by thermal convection for our core model, especially when the difference in core T estimates are taken into account. Thus, our results indicate that thermal convection is permissible for the majority of the 1250–1450 K T-range and may be a source of energy to power an internal core dynamo to produce the magnetic field of Ganymede. We note that with respect to P and T, these estimates of convective heat load represent a lower bound. Based on the trends observed in this study and other investigations on the Fe-FeS system [16], increasing P will result in decreased values of ρ and increased values of κ and Qa. Similarly, based on the results of this study, the net effect of increasing T will also result in increased values of κ and Qa. Acting singly or together, both effects produce a more thermally conductive core and could potentially diminish the effectiveness of, or completely shut down, heat transfer by thermal convection. For instance, extrapolated core heat flow values (~13–44 GW) of our horizontal linear fit applied to a 1600–1700 K liquid core model [21] suggest that the heat load carried by thermal convection to the CMB can be reduced to one-fifth for a heat transfer of 3 mW/m2 through the CMB. With respect to S content, these estimates provide information for a middle-ground core composition between the lower (FeS) and upper (Fe) bounds. Core thermal conductivity is expected to increase as composition becomes more Fe-rich and decrease as composition becomes more FeS-rich in other core composition models.
We note the absence of consensus regarding the P-dependence of the eutectic T in this system. A linear or non-linear increase (e.g., [38,41]) or decrease (e.g., [29,39] and this study) of the eutectic T can significantly change the lowest-bound T that allows for an entirely molten Fe-FeS core of Ganymede and, consequently, constrains the effectiveness of thermally driven convection as a heat transport mechanism. A higher eutectic T than reported here would result in a core that is more thermally conductive since the lower-bound of Qa increases and thus decreases reliance on thermally driven convection to power an internal dynamo. Conversely, a lower eutectic T would result in a core that is less thermally conductive since the lower-bound of Qa decreases and thus increases reliance on thermally driven convection. A CMB pressure of 5 GPa is the lowest expected value. If pressure increases at the CMB, the eutectic composition shifts towards the Fe-end of the binary system and ρ is expected to decrease while κ and Qa are expected to increase. The uncertain behavior of the eutectic T implies the lower-bound T for either Fe or FeS crystallization regimes is uncertain. Beyond this, it is difficult to precisely describe the extent of the effect of the uncertain eutectic T on both crystallization regimes (bottom-up or top-down) and chemical- or buoyancy-driven convection. This is due to the non-linearity of the liquidus boundaries with increasing P, which marks the onset of crystallization. An increased or decreased eutectic T may widen or shrink the T range between the liquidus and solidus but may have little to no significant effect on the liquidus T for some compositions.

4. Conclusions

The presence of S as an element in the Fe-rich core of Ganymede can allow for an entirely molten core at relatively low core T due to freezing-point depression, while also affecting core transport properties influencing magnetic field generation via an internal dynamo. This study provided measurements of the ρ of Fe-FeS with eutectic-adjacent S-contents in solid and liquid states at P from 2–5 GPa, where the transition from solid to liquid states was inferred from measurements of ρ. The phase transition was used for delineation of the eutectic T of the Fe-FeS system, which showed a small negative P-dependency. Our results are the first well-constrained experimental data on near eutectic compositions in this binary system. The electronic component of κ was calculated via the WFL using the measured values of ρ, and was subsequently used to estimate Qa on the core-side of Ganymede’s CMB. The results showed that both ρ and κ had intermediate values between the end-members of the system, and that thermal convection may be permissible in the core to transport heat and act as a dynamo energy source.

Author Contributions

Conceptualization, R.A.S.; methodology, J.A.H.L., R.A.S. and W.Y.; validation, R.A.S.; formal analysis, J.A.H.L.; investigation, J.A.H.L. and W.Y.; resources, R.A.S.; data curation, J.A.H.L.; writing—original draft preparation, J.A.H.L.; writing—review and editing, R.A.S. and W.Y.; supervision, R.A.S.; project administration, R.A.S.; funding acquisition, R.A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Canada Foundation for Innovation (11860) and Natural Sciences and Engineering Research Council of Canada (RGPIN-2018-05021).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are openly available in Mendeley Data at doi:10.17632/4zphh54798.1 [42].

Acknowledgments

We thank Jonathan Jacobs for help with machining of experimental components and two anonymous reviewers for providing insightful and constructive criticisms that helped improve the quality of this manuscript.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A

The following figure (Figure A1) shows the values and function used to interpolate the value of electrical resistivity at temperatures between 1250 K and 1450 K. The interpolated and extrapolated values were used to calculate the adiabatic conductive heat flow at the top of the core of Ganymede.
Crystals 11 00875 g0a1 550
Figure A1. A first-order polynomial (red) was fitted to eight measurements and a horizontal line (315 μΩ·cm; blue) was fitted to six measurements of the 5 GPa experiment. Both fits were used to interpolate and extrapolate the values of electrical resistivity for temperatures from 1250 K to 1450 K. The values obtained from these fits were used to calculate the adiabatic conductive heat flow for the core of Ganymede described in the main text.
Figure A1. A first-order polynomial (red) was fitted to eight measurements and a horizontal line (315 μΩ·cm; blue) was fitted to six measurements of the 5 GPa experiment. Both fits were used to interpolate and extrapolate the values of electrical resistivity for temperatures from 1250 K to 1450 K. The values obtained from these fits were used to calculate the adiabatic conductive heat flow for the core of Ganymede described in the main text.
Crystals 11 00875 g0a1

References

  1. Connerney, J.E.P. Planetary Magnetism. In Treatise on Geophysics, 1st ed.; Spohn, T., Schubert, G., Eds.; Elsevier Ltd.: Amsterdamn, The Netherlands, 2007; Volume 10, pp. 243–280. [Google Scholar]
  2. Olson, P. Mantle control of the geodynamo: Consequences of top-down regulation. Geochem. Geophys. Geosyst. 2016, 17, 1935–1956. [Google Scholar] [CrossRef] [Green Version]
  3. Hauck II, S.A.; Aurnou, J.M.; Dombard, A.J. Sulfur’s impact on core evolution and magnetic field generation on Ganymede. J. Geophys. Res. Planet. 2006, 111, E09008. [Google Scholar] [CrossRef] [Green Version]
  4. Rückriemen, T.; Breuer, D.; Spohn, T. The Fe snow regime in Ganymede’s core: A deep-seated dynamo below a stable snow zone. J. Geophys. Res. Planet. 2015, 120, 1095–1118. [Google Scholar] [CrossRef] [Green Version]
  5. Rückriemen, T.; Breuer, D.; Spohn, T. Top-down freezing in a Fe-FeS core and Ganymede’s present-day magnetic field. Icarus 2018, 307, 172–196. [Google Scholar] [CrossRef]
  6. Schubert, G.; Zhang, K.; Kivelson, M.G.; Anderson, J.D. The magnetic field and internal structure of Ganymede. Nature 1996, 384, 544–545. [Google Scholar] [CrossRef]
  7. Sohl, F.; Spohn, T.; Breuer, D.; Nagel, K. Implications from Galileo observations on the interior structure and chemistry of the Galilean satellites. Icarus 2002, 157, 101–119. [Google Scholar] [CrossRef]
  8. Scott, H.P.; Williams, Q.; Ryerson, F.J. Experimental constraints on the chemical evolution of large icy satellites. Earth Planet. Sci. Lett. 2002, 203, 399–412. [Google Scholar] [CrossRef]
  9. Bland, M.T.; Showman, A.P.; Tobie, B. The production of Ganymede’s magnetic field. Icarus 2008, 198, 384–399. [Google Scholar] [CrossRef]
  10. Kimura, J.; Nakagawa, T.; Kurita, K. Size and compositional constraints of Ganymede’s metallic core for driving an active dynamo. Icarus 2009, 202, 216–224. [Google Scholar] [CrossRef]
  11. Kubaschewski, I. Iron-Sulphur. In IRON—Binary Phase Diagrams; Springer: Berlin/Heidelberg, Germany; Düsseldorf, Germany, 1982; pp. 125–128. [Google Scholar]
  12. Gomi, H.; Yoshino, T. Impurity resistivity of fcc and hcp Fe-based alloys: Thermal stratification at the top of the core of super-Earths. Front. Earth Sci. 2018, 6, 217. [Google Scholar] [CrossRef]
  13. Konôpková, Z.; McWilliams, R.S.; Gómez-Pérez, N.; Goncharov, A.F. Direct measurement of thermal conductivity of solid iron at planetary core conditions. Nature 2016, 534, 99–101. [Google Scholar] [CrossRef]
  14. Ohta, K.; Kuwayama, Y.; Hirose, K.; Shimizu, K.; Ohishi, Y. Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature 2016, 534, 95–98. [Google Scholar] [CrossRef]
  15. Silber, R.E.; Secco, R.A.; Yong, W.; Littleton, J.A.H. Electrical resistivity of liquid Fe to 12 GPa: Implications for heat flow in cores of terrestrial bodies. Sci. Rep. 2018, 8, 10758. [Google Scholar] [CrossRef] [Green Version]
  16. Pommier, A. Influence of sulfur on the electrical resistivity of a crystallizing core in small terrestrial bodies. Earth Planet. Sci. Lett. 2018, 496, 37–46. [Google Scholar] [CrossRef]
  17. Yong, W.; Secco, R.A.; Littleton, J.A.H.; Silber, R.E. The iron invariance: Implications for thermal convection in Earth’s core. Geophys. Res. Lett. 2019, 46, 11065–11070. [Google Scholar] [CrossRef]
  18. Hsieh, W.-P.; Goncharov, A.F.; Labrosse, S.; Holtgrewe, N.; Lobanov, S.S.; Chuvashova, I.; Deschamps, F.; Lin, J.-F. Low thermal conductivity of iron-silicon alloys at Earth’s core conditions with implications for the geodynamo. Nat. Commun. 2020, 11, 3332. [Google Scholar] [CrossRef]
  19. Ezenwa, I.C.; Yoshino, T. Martian core heat flux: Electrical resistivity and thermal conductivity of liquid Fe at Martian core P-T conditions. Icarus 2021, 360, 114367. [Google Scholar] [CrossRef]
  20. Manthilake, G.; Chantel, J.; Monteux, J.; Andrault, D.; Bouhifd, M.A.; Casanova, N.B.; Boulard, E.; Guignot, N.; King, A.; Itie, J.P. Thermal conductivity of FeS and its implications for Mercury’s long-sustaining magnetic field. J. Geophys. Res. Planet. 2019, 124, 2359–2368. [Google Scholar] [CrossRef]
  21. Littleton, J.A.H.; Secco, R.A.; Yong, W. Electrical resistivity of FeS at high pressures and temperatures: Implications of thermal transport in the core of Ganymede. J. Geophys. Res. Planet. 2021, 126, e2020JE006793. [Google Scholar] [CrossRef]
  22. Kuskov, O.L.; Kronrod, V.A. Core sizes and internal structure of Earth’s and Jupiter’s satellites. Icarus 2001, 151, 204–227. [Google Scholar] [CrossRef]
  23. Buono, A.S.; Walker, D. H, not O or pressures, causes eutectic T depression in the Fe-FeS system to 8 GPa. Meteorit. Planet. Sci. 2015, 50, 547–554. [Google Scholar] [CrossRef]
  24. Secco, R.A. High p,T physical property studies of Earth’s interior: Thermoelectric power of solid and liquid Fe up to 6.4 GPa. Can. J. Phys. 1995, 73, 287–294. [Google Scholar] [CrossRef]
  25. Littleton, J.A.H.; Secco, R.A.; Yong, W.; Berrada, M. Electrical resistivity and thermal conductivity of W and Re up to 5 GPa and 2300 K. J. Appl. Phys. 2019, 125, 135901. [Google Scholar] [CrossRef]
  26. Pommier, A. Experimental investigations of the effect of nickel on the electrical resistivity of Fe-Ni and Fe-Ni-S alloys under pressure. Am. Mineral. 2020, 105, 1069–1077. [Google Scholar] [CrossRef]
  27. Silber, R.E.; Secco, R.A.; Yong, W.; Littleton, J.A.H. Heat Flow in Earth’s Core From Invariant Electrical Resistivity of Fe-Si on the Melting Boundary to 9 GPa: Do Light Elements Matter? J. Geophys. Res. Solid Earth 2019, 124, 5521–5543. [Google Scholar] [CrossRef]
  28. Berrada, M.; Secco, R.A.; Yong, W.; Littleton, J.A.H. Electrical resistivity measurements of Fe-Si with implications for the early lunar dynamo. J. Geophys. Res. Planet. 2020, 125, e2020JE006380. [Google Scholar] [CrossRef]
  29. Fei, Y.; Bertka, C.M.; Finger, L.W. High-Pressure Iron-Sulfur Compound, Fe3S, and Melting Relations in the Fe-FeS System. Science 1997, 275, 1621–1623. [Google Scholar] [CrossRef]
  30. Fei, Y.; Li, J.; Bertka, C.M.; Prewitt, C.T. Structure type and bulk modulus of Fe3S, a new iron-sulfur compound. Am. Mineral. 2000, 85, 1830–1833. [Google Scholar] [CrossRef]
  31. Li, J.; Fei, Y.; Mao, H.K.; Hirose, K.; Shieh, S.R. Sulfur in the Earth’s inner core. Earth Planet. Sci. Lett. 2001, 193, 509–514. [Google Scholar] [CrossRef]
  32. Stewart, A.J.; Schmidt, M.W.; van Westrenen, W.; Liebske, C. Mars: A new core-crystallization regime. Science 2007, 316, 1323–1325. [Google Scholar] [CrossRef] [Green Version]
  33. Morard, G.; Andrault, D.; Guignot, N.; Sanloup, C.; Mezouar, M.; Petitgirard, S.; Fiquet, G. In situ determination of Fe-Fe3S phase diagram and liquid structural properties up to 65 GPa. Earth Planet. Sci. Lett. 2008, 272, 620–626. [Google Scholar] [CrossRef]
  34. Kamada, S.; Terasaki, H.; Ohtani, E.; Sakai, T.; Kikegawa, T.; Ohishi, Y.; Hirao, N.; Sata, N.; Kondo, T. Phase relationships of the Fe-FeS system in conditions up to the Earth’s outer core. Earth Planet. Sci. Lett. 2010, 293, 94–100. [Google Scholar] [CrossRef]
  35. Pommier, A.; Leinenweber, K.; Tran, T. Mercury’s thermal evolution controlled by an insulating liquid outermost core? Earth Planet. Sci. Lett. 2019, 517, 125–134. [Google Scholar] [CrossRef]
  36. Brett, R.; Bell, P.M. Melting relations in the Fe-rich portion of the system Fe-FeS at 30 kb pressure. Earth Planet. Sci. Lett. 1969, 6, 479–482. [Google Scholar] [CrossRef]
  37. Ryzhenko, B.; Kennedy, G.C. The effect of pressure on the eutectic in the system Fe-FeS. Am. J. Sci. 1973, 273, 803–810. [Google Scholar] [CrossRef]
  38. Usselman, T.M. Experimental approach to the state of the core: Part, I. The liquidus relations of the Fe-rich portion of the Fe-Ni-S system from 30 to 100 kb. Am. J. Sci. 1975, 275, 278–290. [Google Scholar] [CrossRef]
  39. Morard, G.; Sanloup, C.; Fiquet, G.; Mezouar, M.; Rey, N.; Poloni, R.; Beck, P. Structure of eutectic Fe-FeS melts to pressures up to 17 GPa: Implications for planetary cores. Earth Planet. Sci. Lett. 2007, 262, 128–139. [Google Scholar] [CrossRef]
  40. Breuer, D.; Rückriemen, T.; Spohn, T. Iron snow, crystal floats, and inner-core growth: Modes of core solidification and implications for dynamos in terrestrial planets and moons. Prog. Earth Planet. Sci. 2015, 2, 39. [Google Scholar] [CrossRef] [Green Version]
  41. Boehler, R. Fe-FeS eutectic temperatures to 620 kbar. Phys. Earth Planet. Inter. 1996, 96, 181–186. [Google Scholar] [CrossRef]
  42. Littleton, J.A.H.; Secco, R.A.; Yong, W. Thermal Convection in The Core of Ganymede Inferred from Liquid Eutectic Fe-FeS Electrical Resistivity at High Pressures; [dataset]; Mendeley Data; Elsevier: Amsterdam, The Netherlands, 2020; Version 1. [Google Scholar] [CrossRef]
Crystals 11 00875 g001 550
Figure 1. (a) Measured electrical resistivity of Fe-FeS at pressures of 2–5 GPa as a function of temperature. Sulfur contents (wt. %) of the samples at each pressure are: 29.56 ± 0.05 (2 GPa); 26.17 ± 0.05 (3 GPa); 25.68 ± 0.07 (4 GPa); 23.76 ± 0.06 (5 GPa). Results of this study are compared to three previous studies and include end-member compositions. The dashed line indicates the transition from solid to molten states and was used to delineate eutectic temperatures. (b) Electronic components of thermal conductivity as a function of temperature of Fe-FeS calculated from the electrical resistivity measurements using the Wiedemann–Franz law and the Sommerfeld value of the Lorenz number. Results of this study are compared to two previous studies. Data of the pure Fe end-member are not shown for scaling purposes (>12 W·m−1·K−1). The dashed line indicates the transition from solid to partially molten states.
Figure 1. (a) Measured electrical resistivity of Fe-FeS at pressures of 2–5 GPa as a function of temperature. Sulfur contents (wt. %) of the samples at each pressure are: 29.56 ± 0.05 (2 GPa); 26.17 ± 0.05 (3 GPa); 25.68 ± 0.07 (4 GPa); 23.76 ± 0.06 (5 GPa). Results of this study are compared to three previous studies and include end-member compositions. The dashed line indicates the transition from solid to molten states and was used to delineate eutectic temperatures. (b) Electronic components of thermal conductivity as a function of temperature of Fe-FeS calculated from the electrical resistivity measurements using the Wiedemann–Franz law and the Sommerfeld value of the Lorenz number. Results of this study are compared to two previous studies. Data of the pure Fe end-member are not shown for scaling purposes (>12 W·m−1·K−1). The dashed line indicates the transition from solid to partially molten states.
Crystals 11 00875 g001
Crystals 11 00875 g002 550
Figure 2. (a) Cross-sectional view of the post-experiment 4 GPa pressure cell; (b) backscattered electron image of the sample from (a) at a different depth due to additional grinding and polishing required for electron microprobe analysis. Results of the microprobe are tabulated.
Figure 2. (a) Cross-sectional view of the post-experiment 4 GPa pressure cell; (b) backscattered electron image of the sample from (a) at a different depth due to additional grinding and polishing required for electron microprobe analysis. Results of the microprobe are tabulated.
Crystals 11 00875 g002
Crystals 11 00875 g003 550
Figure 3. Experimentally determined eutectic temperatures of the Fe-FeS system as a function of pressure. The results of this work are compared to several previous works [11,23,29,36,37,38,39].
Figure 3. Experimentally determined eutectic temperatures of the Fe-FeS system as a function of pressure. The results of this work are compared to several previous works [11,23,29,36,37,38,39].
Crystals 11 00875 g003
Crystals 11 00875 g004 550
Figure 4. Calculated adiabatic heat flow at the core–mantle boundary (CMB) of Ganymede of a fully molten eutectic-adjacent core at 5 GPa. The differently dashed lines each represent different estimates of the heat flow through the CMB [3,4,5,10]. The shaded regions represent all values of calculated heat flow values on the core-side of the CMB. The lighter blue and darker red shaded regions are calculated values using a horizontal and linear fitting trendline, as shown in the Supporting Information section. The CMB temperature ranges from 1250 K at the bottom to 1450 K at the top of the shaded regions of this study. Propagated uncertainty for the calculations ranges from ~1 to 1.5% of the reported values.
Figure 4. Calculated adiabatic heat flow at the core–mantle boundary (CMB) of Ganymede of a fully molten eutectic-adjacent core at 5 GPa. The differently dashed lines each represent different estimates of the heat flow through the CMB [3,4,5,10]. The shaded regions represent all values of calculated heat flow values on the core-side of the CMB. The lighter blue and darker red shaded regions are calculated values using a horizontal and linear fitting trendline, as shown in the Supporting Information section. The CMB temperature ranges from 1250 K at the bottom to 1450 K at the top of the shaded regions of this study. Propagated uncertainty for the calculations ranges from ~1 to 1.5% of the reported values.
Crystals 11 00875 g004
Table
Table 1. Values of targeted eutectic Fe-FeS sample compositions and post-experiment analysis results of sample compositions for each pressure in this study. Post-experiment sample compositions are noted to be either Fe-rich or FeS-rich relative to the target pressure-dependent eutectic composition.
Table 1. Values of targeted eutectic Fe-FeS sample compositions and post-experiment analysis results of sample compositions for each pressure in this study. Post-experiment sample compositions are noted to be either Fe-rich or FeS-rich relative to the target pressure-dependent eutectic composition.
Pressure (GPa)Target Eutectic Composition
(wt.% S)		Sample Composition (Post-Experiment)
(wt.% S)		Relative Location Adjacent to Eutectic
228.029.56 ± 0.05FeS-rich
326.526.17 ± 0.05Fe-rich
425.125.68 ± 0.07FeS-rich
523.823.76 ± 0.06Fe-rich
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Littleton, J.A.H.; Secco, R.A.; Yong, W. Thermal Convection in the Core of Ganymede Inferred from Liquid Eutectic Fe-FeS Electrical Resistivity at High Pressures. Crystals 2021, 11, 875. https://doi.org/10.3390/cryst11080875

AMA Style

Littleton JAH, Secco RA, Yong W. Thermal Convection in the Core of Ganymede Inferred from Liquid Eutectic Fe-FeS Electrical Resistivity at High Pressures. Crystals. 2021; 11(8):875. https://doi.org/10.3390/cryst11080875

Chicago/Turabian Style

Littleton, Joshua A. H., Richard A. Secco, and Wenjun Yong. 2021. "Thermal Convection in the Core of Ganymede Inferred from Liquid Eutectic Fe-FeS Electrical Resistivity at High Pressures" Crystals 11, no. 8: 875. https://doi.org/10.3390/cryst11080875

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop