Investigation of Mid-Infrared Broadband Second-Harmonic Generation in Non-Oxide Nonlinear Optic Crystals
Abstract
1. Introduction
2. Materials and Theories
2.1. BPM and GV Matching for Broadband SHG
2.2. Effective Nonlinearities
2.3. Spatial Walk-Off
3. Simulations and Discussion
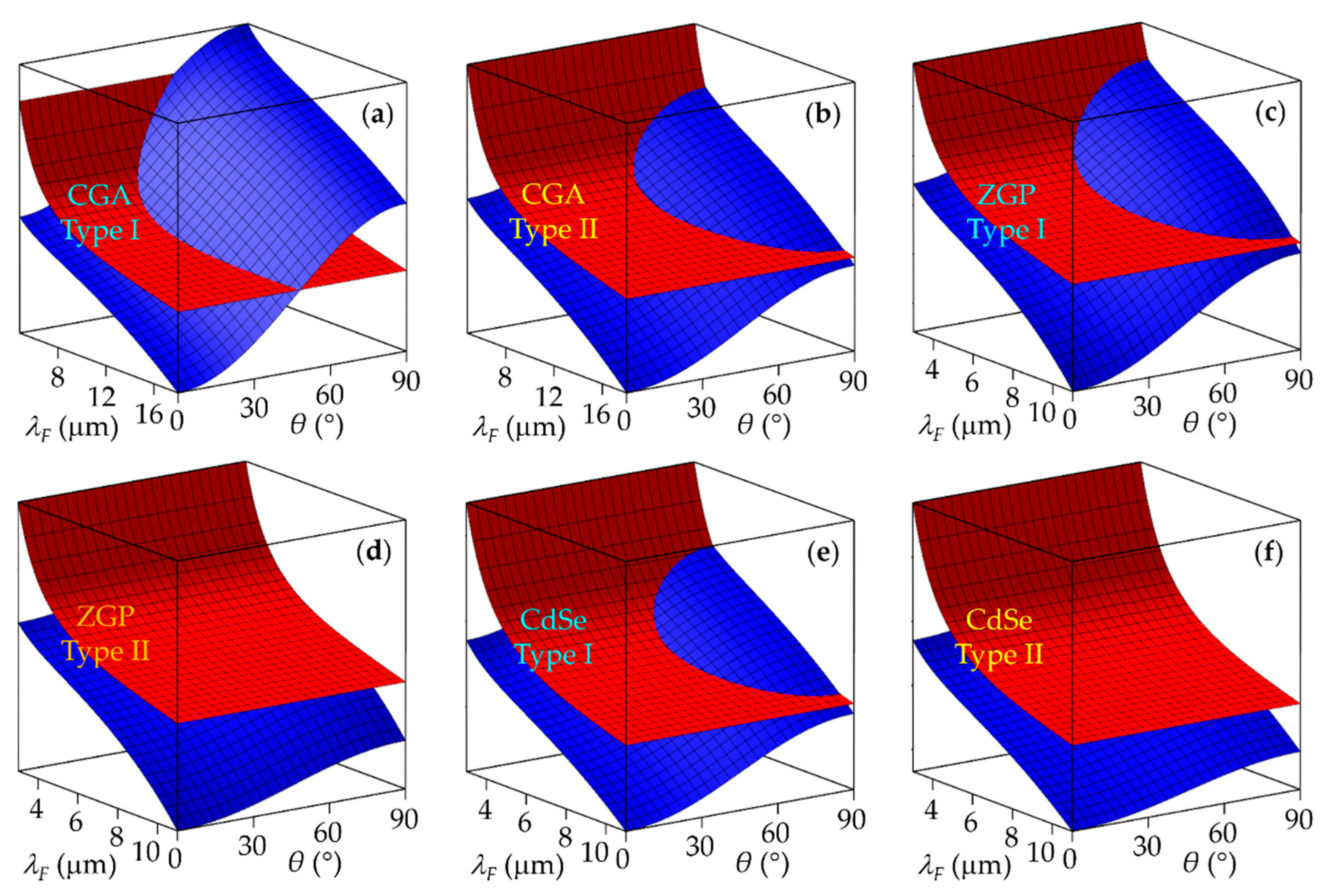
3.1. Broadband SHG in Uniaxial Chalcopyrite and Defect Chalcopyrite Crystals
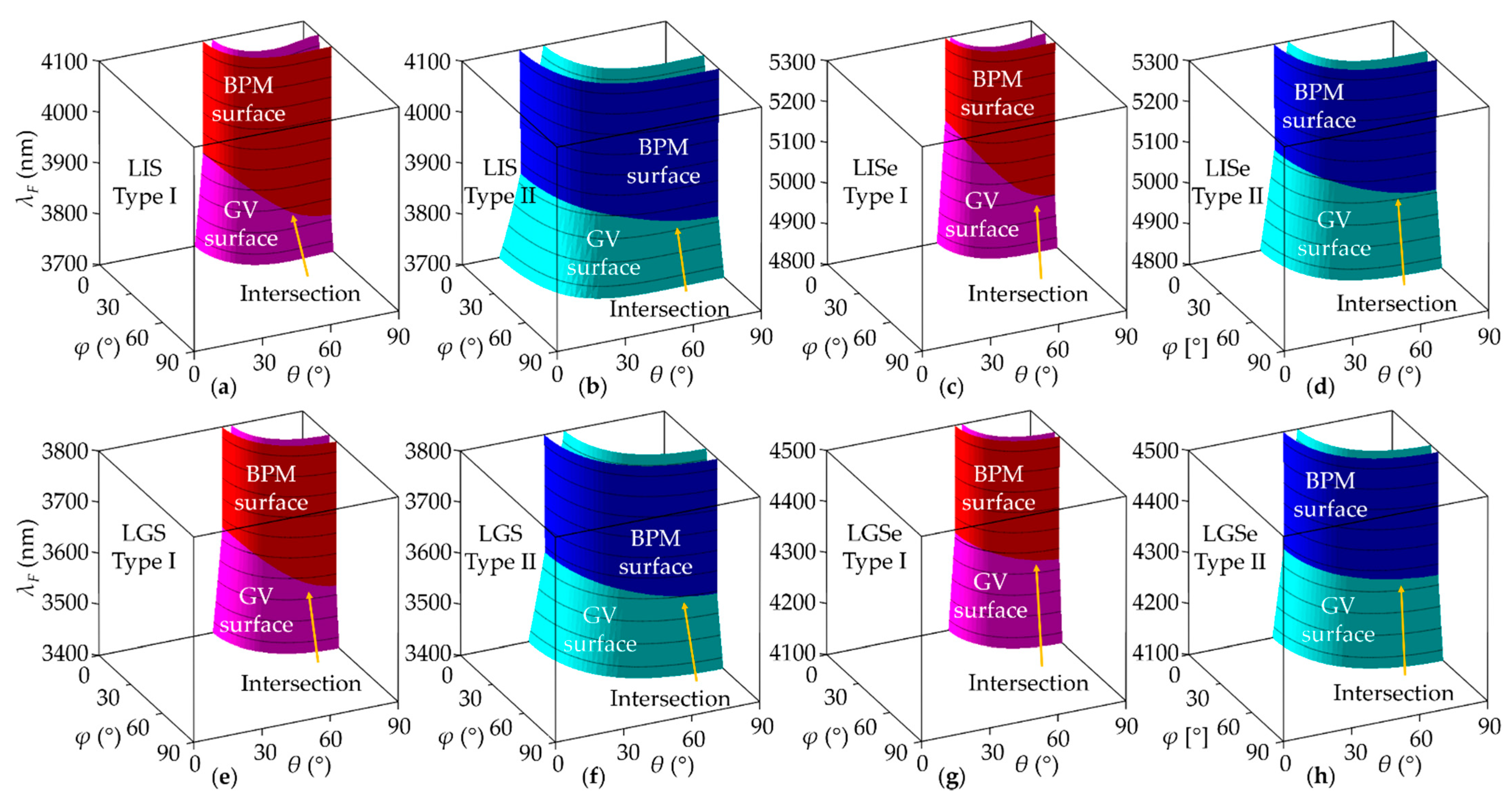
3.2. Broadband SHG in Biaxial Orthorhombic Ternary Chalcogenides
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krier, A. Mid-Infrared Semiconductor Optoelectronics; Springer: London, UK, 2006; pp. 595–738. [Google Scholar]
- Ebrahim-Zadeh, M.; Sorokina, I.T. Mid-Infrared Coherent Sources and Applications; Springer: Dordrecht, The Netherlands, 2008; pp. 467–621. [Google Scholar]
- Pereira, M.F.; Shulika, O. Terahertz and Mid Infrared Radiation; Springer: Dordrecht, The Netherlands, 2011; pp. 1–194. [Google Scholar]
- Schunemann, P.G.; Zawilski, K.T.; Pomeranz, L.A.; Creeden, D.J.; Budni, P.A. Advances in nonlinear optical crystals for mid-infrared coherent sources. J. Opt. Soc. Am. B 2016, 33, D36–D43. [Google Scholar] [CrossRef]
- Luo, X.; Li, Z.; Guo, Y.; Yao, J.; Wu, Y. Recent progress on new infrared nonlinear optical materials with application prospect. J. Solid State Chem. 2019, 270, 674–687. [Google Scholar] [CrossRef]
- O’Connor, M.V.; Watson, M.A.; Shepherd, D.P.; Hanna, D.C.; Price, J.H.V.; Malinowski, A.; Nilsson, J.; Broderick, N.G.R.; Richardson, D.J.; Lefort, L. Synchronously pumped optical parametric oscillator driven by a femtosecond mode-locked fiber laser. Opt. Lett. 2002, 27, 1052–1054. [Google Scholar] [CrossRef][Green Version]
- Kumar, S.C.; Samanta, G.K.; Ebrahim-Zadeh, M. High-power, single-frequency, continuous-wave second-harmonic-generation of ytterbium fiber laser in PPKTP and MgO:sPPLT. Opt. Express 2009, 17, 13711–13726. [Google Scholar] [CrossRef]
- Kokabee, O.; Esteban-Martin, A.; Ebrahim-Zadeh, M. Efficient, high-power, ytterbium-fiber-laser-pumped picosecond optical parametric oscillator. Opt. Lett. 2010, 35, 3210–3212. [Google Scholar] [CrossRef]
- Kumar, S.C.; Ebrahim-Zadeh, M. High-power, fiber-laser-pumped, picosecond optical parametric oscillator based on MgO:sPPLT. Opt. Express 2011, 19, 26660–26665. [Google Scholar] [CrossRef] [PubMed]
- Andriukaitis, G.; Balčiūnas, T.; Ališauskas, S.; Pugžlys, A.; Baltuška, A.; Popmintchev, T.; Chen, M.-C.; Murnane, M.M.; Kapteyn, H.C. 90 GW peak power few-cycle mid-infrared pulses from an optical parametric amplifier. Opt. Lett. 2011, 36, 2755–2757. [Google Scholar] [CrossRef] [PubMed]
- Petrov, V. Parametric down-conversion devices: The coverage of the mid-infrared spectral range by solid-state laser sources. Opt. Mat. 2012, 34, 536–554. [Google Scholar] [CrossRef]
- Petrov, V. Frequency down-conversion of solid-state laser sources to the mid-infrared spectral range using non-oxide nonlinear crystals. Prog. Quantum Electron. 2015, 42, 1–106. [Google Scholar] [CrossRef]
- Zahedpour, S.; Hancock, S.W.; Milchberg, H.M. Ultrashort infrared 2.5–11 μm pulses: Spatiotemporal profiles and absolute nonlinear response of air constituents. Opt. Lett. 2019, 44, 843–846. [Google Scholar] [CrossRef]
- Ionin, A.A.; Kinyaevskiy, I.O.; Klimachev, Y.M.; Kotkov, A.A.; Kozlov, A.Y.; Sagitova, A.M.; Sinitsyn, D.V.; Rulev, O.A.; Badikov, V.V.; Badikov, D.V. Frequency conversion of mid-IR lasers into the long-wavelength domain of 12–20 μm with AgGaSe2, BaGa2GeSe6 and PbIn6Te10 nonlinear crystals. Opt. Express 2019, 27, 24353–24361. [Google Scholar] [CrossRef]
- Kumar, S.C.; Schunemann, P.G.; Zawilski, K.T.; Ebrahim-Zadeh, M. Advances in ultrafast optical parametric sources for the mid-infrared based on CdSiP2. J. Opt. Soc. Am. B 2016, 33, D44–D56. [Google Scholar] [CrossRef]
- Ferdinandus, M.R.; Gengler, J.J.; Averett, K.L.; Zawilski, K.T.; Schunemann, P.G.; Liebig, C.M. Nonlinear optical measurements of CdSiP2 at near and mid-infrared wavelengths. Opt. Mater. Express 2020, 10, 2066–2074. [Google Scholar] [CrossRef]
- Popien, S.; Beutler, M.; Rimke, I.; Badikov, D.; Badikov, V.; Petrov, V. Femtosecond Yb-fiber laser synchronously pumped HgGa2S4 optical parametric oscillator tunable in the 4.4- to 12-μm range. Opt. Eng. 2018, 57, 111802. [Google Scholar] [CrossRef]
- Liu, G.-Y.; Chen, Y.; Yao, B.-Q.; Wang, R.; Yang, K.; Yang, C.; Mi, S.; Dai, T.-Y.; Duan, X.-M. 3.5 W long-wave infrared ZnGeP2 optical parametric oscillator at 9.8 µm. Opt. Lett. 2020, 45, 2347–2350. [Google Scholar] [CrossRef]
- Liu, G.; Mi, S.; Yang, K.; Wei, D.; Li, J.; Yao, B.; Yang, C.; Dai, T.; Duan, X.; Tian, L.; et al. 161 W middle infrared ZnGeP2 MOPA system pumped by 300 W-class Ho:YAG MOPA system. Opt. Lett. 2021, 46, 82–85. [Google Scholar] [CrossRef]
- Nam, S.-H.; Fedorov, V.; Mirov, S.; Hong, K.-H. Octave-spanning mid-infrared femtosecond OPA in a ZnGeP2 pumped by a 2.4 μm Cr:ZnSe chirped-pulse amplifier. Opt. Express 2020, 28, 32403–32414. [Google Scholar] [CrossRef]
- Qian, C.; Yu, T.; Liu, J.; Jiang, Y.; Wang, S.; Shi, X.; Ye, X.; Chen, W. A High-Energy, Narrow-Pulse-Width, Long-Wave Infrared Laser Based on ZGP Crystal. Crystals 2021, 11, 656. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, G.; Yang, C.; Yao, B.; Wang, R.; Mi, S.; Yang, K.; Dai, T.; Duan, X.; Ju, Y. 1 W, 10.1 μm, CdSe optical parametric oscillator with continuous-wave seed injection. Opt. Lett. 2020, 45, 2119–2122. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, C.; Liu, G.; Yao, B.; Wang, R.; Yang, K.; Mi, S.; Dai, T.; Duan, X.; Ju, Y. 11 µm, high beam quality idler-resonant CdSe optical parametric oscillator with continuous-wave injection-seeded at 2.58 μm. Opt. Express 2020, 28, 17056–17063. [Google Scholar] [CrossRef]
- Wang, S.; Dai, S.; Jia, N.; Zong, N.; Li, C.; Shen, Y.; Yu, T.; Qiao, J.; Gao, Z.; Peng, Q.; et al. Tunable 7–12 μm picosecond optical parametric amplifier based on a LiInSe2 mid-infrared crystal. Opt. Lett. 2017, 42, 2098–2101. [Google Scholar] [CrossRef]
- Smetanin, S.N.; Jelínek, M.; Kubeček, V.; Kurus, A.F.; Vedenyapin, V.N.; Lobanov, S.I.; Isaenko, L.I. 50-µJ level, 20-picosecond, narrowband difference-frequency generation at 4.6, 5.4, 7.5, 9.2, and 10.8 μm in LiGaS2 and LiGaSe2 at Nd:YAG laser pumping and various crystalline Raman laser seedings. Opt. Mater. Express 2020, 10, 1881–1890. [Google Scholar] [CrossRef]
- Chen, B.-H.; Wittmann, E.; Morimoto, Y.; Baum, P.; Riedle, E. Octave-spanning single-cycle middle-infrared generation through optical parametric amplification in LiGaS2. Opt. Express 2019, 27, 21306–21318. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.J.; Liu, S.; Parmigiani, F.; Ibsen, M.; Petropoulos, P.; Gallo, K.; Richardson, D.J. OTDM to WDM format conversion based on quadratic cascading in a periodically poled lithium niobate waveguide. Opt. Express 2010, 18, 10282–10288. [Google Scholar] [CrossRef]
- Barh, A.; Rodrigo, P.J.; Meng, L.; Pedersen, C.; Tidemand-Lichtenberg, P. Parametric upconversion imaging and its applications. Adv. Opt. Photon. 2019, 11, 952–1019. [Google Scholar] [CrossRef]
- Tan, S.; Wei, X.; Li, B.; Lai, Q.T.K.; Tsia, K.K.; Wong, K.K.Y. Ultrafast optical imaging at 2.0 μm through second-harmonic-generation-based time-stretch at 1.0 μm. Opt. Lett. 2018, 43, 3822–3825. [Google Scholar] [CrossRef] [PubMed]
- Petrov, V.; Ghotbi, M.; Kokabee, O.; Esteban-Martin, A.; Noack, F.; Gaydardzhiev, A.; Nikolov, I.; Tzankov, P.; Buchvarov, I.; Miyata, K.; et al. Femtosecond nonlinear frequency conversion based on BiB3O6. Laser Photon. Rev. 2010, 4, 53–98. [Google Scholar] [CrossRef]
- Feigelson, R.S.; Route, R.K. Recent developments in the growth of chalcopyrite crystals for nonlinear infrared applications. Opt. Eng. 1987, 26, 113–119. [Google Scholar] [CrossRef]
- Barnes, N.P.; Gettemy, D.J.; Hietanen, J.R.; Lannini, R.A. Parametric amplification in AgGaSe2. Appl. Opt. 1989, 28, 5162–5168. [Google Scholar]
- Zawilski, K.T.; Schunemann, P.G.; Pollak, T.C.; Zelmon, D.E.; Fernelius, N.C.; Hopkins, F.K. Growth and characterization of large CdSiP2 single crystals. J. Cryst. Growth 2010, 312, 1127–1132. [Google Scholar] [CrossRef]
- Schunemann, P.G.; Pollak, T.M. Synthesis and growth of HgGa2S4 crystals. J. Cryst. Growth 1997, 174, 278–282. [Google Scholar] [CrossRef]
- Ewbank, M.D.; Newman, P.R.; Mota, N.L.; Lee, S.M.; Wolfe, W.L.; DeBell, A.G.; Harrison, W.A. The temperature dependence of optical and mechanical properties of Tl3AsSe3. J. Appl. Phys. 1980, 51, 3848–3852. [Google Scholar] [CrossRef]
- Vodopyanov, K.L.; Kulevskii, L.A.; Voevodin, V.G.; Gribenyukov, A.I.; Allakhverdiev, K.R.; Kerimov, T.A. High efficiency middle IR parametric superradiance in ZnGeP2 and GaSe crystals pumped by an erbium laser. Opt. Commun. 1991, 83, 322–326. [Google Scholar] [CrossRef]
- Byer, R.L.; Kildal, H.; Feigelson, R.S. CdGeAs2—A new nonlinear crystal phasematchable at 10.6 μm. Appl. Phys. Lett. 1971, 19, 237–240. [Google Scholar] [CrossRef]
- Finsterbusch, K.; Bayer, A.; Zacharias, H. Tunable, narrow-band picosecond radiation in the mid-infrared by difference frequency mixing in GaSe and CdSe. Appl. Phys. B 2004, 79, 457–462. [Google Scholar] [CrossRef]
- Kato, K.; Umemura, N. Sellmeier and thermo-optic dispersion formulas for LiInS2. Appl. Opt. 2014, 53, 7998–8001. [Google Scholar] [CrossRef]
- Petrov, V.; Zondy, J.-J.; Bidault, O.; Isaenko, L.; Vedenyapin, V.; Yelisseyev, A.; Chen, W.; Tyazhev, A.; Lobanov, S.; Marchev, G.; et al. Optical, thermal, electrical, damage, and phase-matching properties of lithium selenoindate. J. Opt. Soc. Am. B 2010, 27, 1902–1927. [Google Scholar] [CrossRef]
- Isaenko, L.; Yelisseyev, A.; Lobanov, S.; Titov, A.; Petrov, V.; Zondy, J.-J.; Krinitsin, P.; Merkulov, A.; Vedenyapin, V.; Smirnova, J. Growth and properties of LiGaX2 (X = S, Se, Te) single crystals for nonlinear optical applications in the mid-IR. Cryst. Res. Technol. 2003, 38, 379–387. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 4th ed.; Academic Press: San Diego, CA, USA, 2020; pp. 72–79. [Google Scholar]
- Kato, K.; Petrov, V.; Umemura, N. Sellmeier and thermo-optic dispersion formulas for LiInSe2. Appl. Opt. 2014, 53, 1063–1066. [Google Scholar] [CrossRef]
- Kato, K.; Miyata, K.; Isaenko, L.; Lobanov, S.; Vedenyapin, V.; Petrov, V. Phase-matching properties of LiGaS2 in the 1.025–10.5910 μm spectral range. Opt. Lett. 2017, 42, 4363–4366. [Google Scholar] [CrossRef] [PubMed]
- Miyata, K.; Petrov, V.; Kato, K. Phase-matching properties of LiGaSe2 for SHG and SFG in the 1.026–10.5910 μm range. Appl. Opt. 2017, 56, 6126–6129. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007; pp. 30–33. [Google Scholar]
- Midwinter, J.E.; Warner, J. The effects of phase matching method and of uniaxial crystal symmetry on the polar distribution of second-order non-linear optical polarization. Brit. J. Appl. Phys. 1965, 16, 1135–1142. [Google Scholar] [CrossRef]
- Dmitriev, V.G.; Nikogosyan, D.N. Effective nonlinearity coefficients for three-wave interactions in biaxial crystals of mm2 point group symmetry. Opt. Comm. 1993, 95, 173–182. [Google Scholar] [CrossRef]
- Gehr, R.J.; Kimmel, M.W.; Smith, A.V. Simultaneous spatial and temporal walk-off compensation in frequency-doubling femtosecond pulses in β-BaB2O4. Opt. Lett. 1998, 23, 1298–1300. [Google Scholar] [CrossRef] [PubMed]
- Zondy, J.-J.; Touahri, D.; Acef, O. Absolute value of the d36 nonlinear coefficient of AgGaS2: Prospect for a low-threshold doubly resonant oscillator-based 3:1 frequency divider. J. Opt. Soc. Am. B 1997, 14, 2481–2497. [Google Scholar] [CrossRef]
- Roberts, D.A. Simplified characterization of uniaxial and biaxial nonlinear optical crystals: A plea for standardization of nomenclature and conventions. IEEE J. Quantum Electron. 1992, 28, 2057–2074. [Google Scholar] [CrossRef]
- Kemlin, V.; Boulanger, B.; Petrov, V.; Segonds, P.; Ménaert, B.; Schunneman, P.G.; Zawilski, K.T. Nonlinear, dispersive, and phase-matching properties of the new chalcopyrite CdSiP2 [Invited]. Opt. Mater. Express 2011, 1, 1292–1300. [Google Scholar] [CrossRef]
- Rotermund, F.; Petrov, V. Mercury thiogallate mid-infrared femtosecond optical parametric generator pumped at 1.25 μm by a Cr: Forsterite regenerative amplifier. Opt. Lett. 2000, 25, 746–748. [Google Scholar] [CrossRef]
- Feichtner, J.D.; Roland, G.W. Optical properties of a new nonlinear optical material: Tl3AsSe3. Appl. Opt. 1972, 11, 993–998. [Google Scholar] [CrossRef]
- Tanaka, E.; Kato, K. Second-harmonic and sum-frequency generation in CdGeAs2. In MRS Symposium Proceedings; McDaniel, D.L., Jr., Manasreh, M.O., Miles, R.H., Sivananthan, S., Eds.; Materials Research Society: Warrendale, PA, USA, 1998; Volume 484, pp. 475–479. [Google Scholar]
- Kato, K. Second-harmonic and sum-frequency generation in ZnGeP2. Appl. Opt. 1997, 36, 2506–2510. [Google Scholar] [CrossRef]
- Fossier, S.; Salaün, S.; Mangin, J.; Bidault, O.; Thénot, I.; Zondy, J.-J.; Chen, W.; Rotermund, F.; Petrov, V.; Petrov, P.; et al. Optical, vibrational, thermal, electrical, damage, and phase-matching properties of lithium thioindate. J. Opt. Soc. Am. B 2004, 21, 1981–2007. [Google Scholar] [CrossRef]
- Petrov, V.; Yelisseyev, A.; Isaenko, L.; Lobanov, S.; Titov, A.; Zondy, J.-J. Second harmonic generation and optical parametric amplification in the mid-IR with orthorhombic biaxial crystals LiGaS2 and LiGaSe2. Appl. Phys. B 2004, 78, 543–546. [Google Scholar] [CrossRef]
- Kim, I.; Lee, D.; Lee, K.J. Study of type II SPDC in lithium niobate for high spectral purity photon pair generation. Crystals 2021, 11, 406. [Google Scholar] [CrossRef]
- Brehat, F.; Wyncke, B. Calculation of double-refraction walk-off angle along the phase-matching directions in nonlinear biaxial crystals. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 1891–1898. [Google Scholar] [CrossRef]
- Lee, D.; Kim, I.; Lee, K.J. Investigation of 1064-nm pumped type II SPDC in potassium niobate for generation of high spectral purity photon pairs. Crystals 2021, 11, 599. [Google Scholar] [CrossRef]
- Bai, Y.; Bandyopadhyay, N.; Tsao, S.; Slivken, S.; Razeghi, M. Room temperature quantum cascade lasers with 27% wall plug efficiency. Appl. Phys. Lett. 2011, 98, 181102. [Google Scholar] [CrossRef]
- Lyakh, A.; Maulini, R.; Tsekoun, A.; Go, R.; Patel, C.K.N. Tapered 4.7 μm quantum cascade lasers with highly strained active region composition delivering over 4.5 watts of continuous wave optical power. Opt. Express 2012, 20, 4382–4388. [Google Scholar] [CrossRef]
- Maulini, R.; Lyakh, A.; Tsekoun, A.; Kumar, C.; Patel, N. λ~7.1 μm quantum cascade lasers with 19% wallplug efficiency at room temperature. Opt. Express 2011, 19, 17203–17211. [Google Scholar] [CrossRef]
- Lu, Q.Y.; Bai, Y.; Bandyopadhyay, N.; Slivken, S.; Razeghi, M. Room-temperature continuous wave operation of distributed feedback quantum cascade lasers with watt-level power output. Appl. Phys. Lett. 2010, 97, 231119. [Google Scholar] [CrossRef]
- Lu, Q.Y.; Bai, Y.; Bandyopadhyay, N.; Slivken, S.; Razeghi, M. 2.4 W room temperature continuous wave operation of distributed feedback quantum cascade lasers. Appl. Phys. Lett. 2011, 98, 181106. [Google Scholar] [CrossRef]
- Lee, B.G.; Zhang, H.A.; Pfluegl, C.; Diehl, L.; Belkin, M.A.; Fischer, M.; Wittmann, A.; Faist, J.; Capasso, F. Broadband distributed-feedback quantum cascade laser array operating from 8.0 to 9.8 μm. IEEE Photon. Technol. Lett. 2009, 21, 914–916. [Google Scholar] [CrossRef]
- Hugi, A.; Maulini, R.; Faist, J. External cavity quantum cascade laser. Semicond. Sci. Technol. 2010, 25, 083001. [Google Scholar] [CrossRef]
- Maulini, R.; Beck, M.; Faist, J.; Gini, E. Broadband tuning of external cavity bound-to-continuum quantum-cascade lasers. Appl. Phys. Lett. 2004, 84, 1659. [Google Scholar] [CrossRef]
- Fedorov, V.V.; Mirov, S.B.; Gallian, A.; Badikov, D.V.; Frolov, M.P.; Korostelin, Y.V.; Kozlovsky, V.I.; Landman, A.I.; Podmar’kov, Y.P.; Akimov, V.A.; et al. 3.77–5.05-μm tunable solid-state lasers based on Fe2+-doped ZnSe crystals operating at low and room temperatures. IEEE J. Quantum Electron. 2006, 42, 907. [Google Scholar] [CrossRef]
- Firsov, K.N.; Gavrishchuk, E.M.; Kazantsev, S.Y.; Kononov, I.G.; Rodin, S.A. Increasing the radiation energy of ZnSe:Fe2+ laser at room temperature. Laser Phys. Lett. 2014, 11, 085001. [Google Scholar] [CrossRef]
- Velikanov, S.D.; Gavrishchuk, E.M.; Zaretsky, N.A.; Zakhryapa, A.V.; Ikonnikov, V.B.; Kazantsev, S.Y.; Kononov, I.G.; Maneshkin, A.A.; Mashkovskii, D.A.; Saltykov, E.V.; et al. Repetitively pulsed Fe:ZnSe laser with an average output power of 20 W at room temperature of the polycrystalline active element. Quantum Electron. 2017, 47, 303. [Google Scholar] [CrossRef]
- Kozlovsky, V.I.; Akimov, V.A.; Frolov, M.P.; Korostelin, Y.V.; Landman, A.I.; Martovitsky, V.P.; Mislavskii, V.V.; Podmar’kov, Y.P.; Skasyrsky, Y.K.; Voronov, A.A. Room-temperature tunable midinfrared lasers on transition-metal doped II-VI compound crystals grown from vapor phase. Phys. Status Solidi B 2010, 247, 1553. [Google Scholar] [CrossRef]
- Cui, Y.; Huang, W.; Wang, Z.; Wang, M.; Zhou, Z.; Li, Z.; Gao, S.; Wang, Y.; Wang, P. 4.3 μm fiber laser in CO2-filled hollow-core silica fibers. Optica 2019, 6, 951–954. [Google Scholar] [CrossRef]
- Wittmann, A.; Hugi, A.; Gini, E.; Hoyler, N.; Faist, J. Heterogeneous high-performance quantum-cascade laser sources for broad-band tuning. IEEE J. Quantum Electron. 2008, 44, 1083–1088. [Google Scholar] [CrossRef]
- Takaoka, E.; Kato, K.; Umemura, N. Thermo-optic dispersion formula for AgGaS2. Appl. Opt. 1999, 38, 4577–4580. [Google Scholar] [CrossRef]
- Komine, H.; Fukumoto, J.M.; Long, W.H.; Stappaerts, E.A. Noncritically phase matched mid-infrared generation in AgGaSe2. IEEE J. Sel. Top. Quant. Electron. 1995, 1, 44–49. [Google Scholar] [CrossRef]
- Kato, K.; Petrov, V.; Umemura, N. Phase-matching properties of yellow color HgGa2S4 for SHG and SFG in the 0.944–10.5910 μm range. Appl. Opt. 2016, 55, 3145–3148. [Google Scholar] [CrossRef] [PubMed]
- Takaoka, E.; Kato, K. Temperature phase-matching properties for harmonic generation in GaSe. Jpn. J. Appl. Phys. 1999, 38, 2755–2759. [Google Scholar] [CrossRef]
- Zelmon, D.E.; Hanning, E.A.; Schunemann, P.G. Refractive-index measurements and Sellmeier coefficients for zinc germanium phosphide from 2 to 9 μm with implications for phase matching in optical frequency-conversion devices. J. Opt. Soc. Am. B 2001, 18, 1307–1310. [Google Scholar] [CrossRef]
- Bhar, G.C. Refractive index interpolation in phase-matching. Appl. Opt. 1976, 15, 305–307. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.Q.; Hoffman, A.J.; Escarra, M.D.; Franz, K.J.; Khurgin, J.B.; Dikmelik, Y.; Wang, X.; Fan, J.-Y.; Gmachl, C.F. Highly power-efficient quantum cascade lasers. Nat. Photon. 2010, 4, 95. [Google Scholar] [CrossRef]
- Bai, Y.; Slivken, S.; Kuboya, S.; Darvish, S.R.; Razeghi, M. Quantum cascade lasers that emit more light than heat. Nat. Photon. 2010, 4, 99. [Google Scholar] [CrossRef]
- Cathabard, O.; Teissier, R.; Devenson, J.; Baranov, A.N. InAs-based distributed feedback quantum cascade lasers. Electron. Lett. 2009, 45, 1028. [Google Scholar] [CrossRef]
- M Squared Lasers Limited. Available online: https://www.m2lasers.com/firefly-ir.html (accessed on 7 July 2021).
- Fedorov, V.Y.; Tzortzakis, S. Optimal wavelength for two-color filamentation-induced terahertz sources. Opt. Express 2018, 26, 31150–31159. [Google Scholar] [CrossRef]
- Koulouklidis, A.D.; Gollner, C.; Shumakova, V.; Fedorov, V.Y.; Pugžlys, A.; Baltuška, A.; Tzortzakis, S. Observation of extremely efficient terahertz generation from mid-infrared two-color laser filaments. Nat. Commun. 2020, 11, 292. [Google Scholar] [CrossRef]
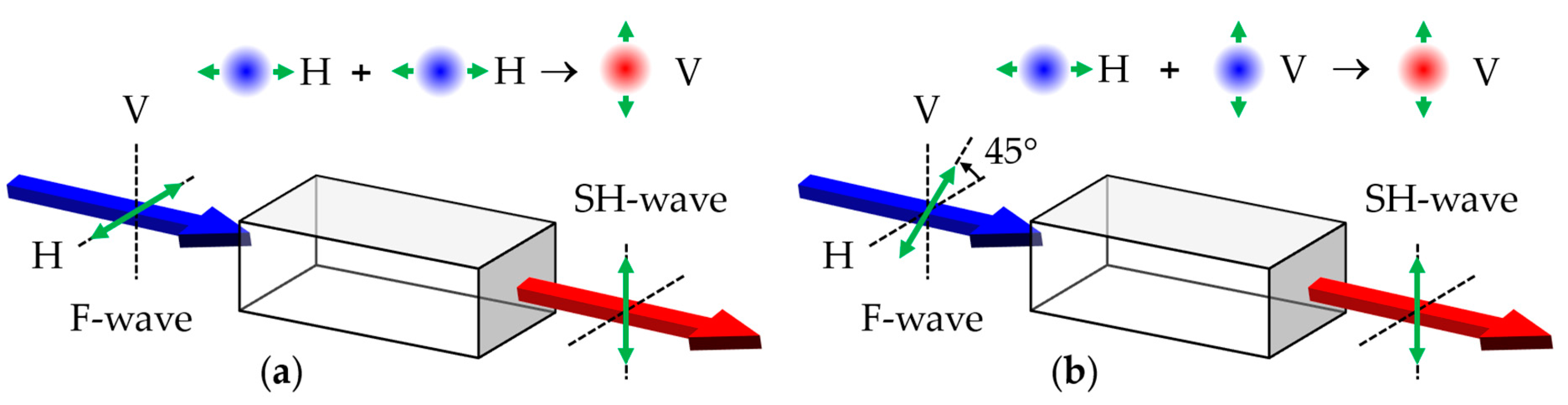




| Crystals | Birefringence | Crystal System | Point Group | Transparency |
|---|---|---|---|---|
| AgGaS2 (AGS) | Negative uniaxial | Tetragonal | 0.45–13 µm [31] | |
| AgGaSe2 (AGSe) | 0.71–19 µm [32] | |||
| CdSiP2 (CSP) | 0.66–6.5 µm [33] | |||
| HgGa2S4 (HGS) | 0.55–11 µm [34] | |||
| Tl3AsSe3 (TASe) | Trigonal | 1.26–17 µm [35] | ||
| GaSe | Hexagonal | 0.65–18 µm [36] | ||
| CdGeAs2 (CGA) | Positive uniaxial | Tetragonal | 2.4–18 µm [37] | |
| ZnGeP2 (ZGP) | 0.74–12 µm [36] | |||
| CdSe | Hexagonal | 0.8–20 µm [38] | ||
| LiInS2 (LIS) | Negative biaxial | Orthorhombic | 0.4 μm–12 µm [39] | |
| LiInSe2 (LISe) | 0.5 μm–12 µm [40] | |||
| LiGaS2 (LGS) | 0.32 μm–11.6 µm [41] | |||
| LiGaSe2 (LGSe) | 0.37 μm–13.2 µm [41] |
| Type | Condition | Negative Uniaxial | Positive Uniaxial |
|---|---|---|---|
| Type I | BPM | ||
| GV matching | |||
| Type II | BPM | ||
| GV matching |
| Type | Condition | Negative Biaxial |
|---|---|---|
| Type I | BPM | |
| GV matching | ||
| Type II | BPM | |
| GV matching |
| Crystals | Point Group | dil Component (pm/V) | BPM Type | deff Expression 1 |
|---|---|---|---|---|
| AGS | d36 = 13.7 (@ λF = 2.53 µm [50]) | Type I | ||
| Type II | ||||
| AGSe | d36 = 33 (@ λF = 2.3 µm [51]) | Type I | ||
| Type II | ||||
| CSP | d36 = 84.5 (@ λF = 4.56 µm [52]) | Type I | ||
| Type II | ||||
| HGS | d36 = 31.5, d31 = 10.5 (@ λF = 1.064 µm [53]) | Type I | ||
| Type II | ||||
| TASe | d22 = 32, d31 = 20 (@ λF = 10.6 µm [54]) | Type I | ||
| Type II | ||||
| GaSe | d22 = 54 (@ λF = 10.6 µm [51]) | Type I | ||
| Type II | ||||
| CGA | d36 = 186 (@ λF = 5.2955 µm [55]) | Type I | ||
| Type II | ||||
| ZGP | d36 = 70 (@ λF = 5.2955 µm [56]) | Type I | ||
| Type II | ||||
| CdSe | d31 = 18 (@ λF = 10.6 µm [51]) | Type I | 0 | |
| Type II |
| Crystals | Point Group | dil Components (pm/V) 1 |
|---|---|---|
| LIS | d31 = 7.2 ± 0.4, d32 = 5.7 ± 0.6, d33 = −16 ± 4 (@ λF = 2.53 µm [57]) | |
| LISe | d31 = 11.78 ± 5%, d32 = 8.17 ± 10%, d33 = −16 ± 25% (@ λF = 2.53 µm [40]) | |
| LGS | d31 =5.8, d32 = 5.1, d33 = −10.7 (@ λF = 2.53 µm [58]) | |
| LGSe | d31 = 9.9, d32 = 7.7, d33 = −18.2 (@ λF = 2.53 µm [58]) |
| Crystals | BPM Type | λF (nm) | λSH (nm) | θBPM (°) | |deff| (pm/V) 1 | w (°) | ΔλF (nm) |
|---|---|---|---|---|---|---|---|
| AGS [76] | Type I | 4386.04 | 2193.02 | 31.92 | 7.5 | 1.16 | 488.69 |
| Type II | 4373.83 | 2186.92 | 48.87 | 13.5 | 1.27 | 484.71 | |
| AGSe [77] | Type I | 6224.24 | 3112.12 | 39.93 | 21.5 | 0.70 | 870.19 |
| Type II | 6271.35 | 3135.67 | 67.21 | 23.2 | 0.50 | 868.39 | |
| CSP [52] | Type I | 5315.10 | 2657.55 | 42.36 | 57.5 | 0.53 | 697.04 |
| Type II | 5270.76 | 2635.38 | 74.35 | 43.2 | 0.27 | 669.20 | |
| HGS [78] | Type I | 4438.55 | 2219.28 | 35.16 | 27.2 | 0.94 | 506.49 |
| Type II | 4412.72 | 2206.36 | 54.18 | 31.2 | 0.93 | 506.54 | |
| TASe [35] | Type I | 9076.20 | 4538.10 | 17.95 | 18.6 | 2.12 | 1122.97 |
| Type II | 9140.37 | 4570.18 | 25.64 | 24.7 | 2.79 | 1145.78 | |
| GaSe [79] | Type I | 5625.28 | 2812.64 | 10.57 | 52.5 | 2.99 | 760.91 |
| Type II | 5620.10 | 2810.05 | 15.08 | 48.2 | 4.12 | 760.70 | |
| CGA [55] | Type I | 9474.36 | 4737.18 | 32.13 | 163.6 | −1.33 | 1164.03 |
| Type II | 9474.36 | 4737.18 | 48.44 | 135.9 | −1.49 | 1164.24 | |
| ZGP [80] | Type I | 6006.92 | 3003.46 | 45.75 | 70.0 | −0.70 | 644.54 |
| Type II | - | - | - | - | - | - | |
| CdSe [81] | Type I | 6380.33 | 3190.17 | 53.04 | 0 | −0.44 | - |
| Type II | - | - | - | - | - | - |
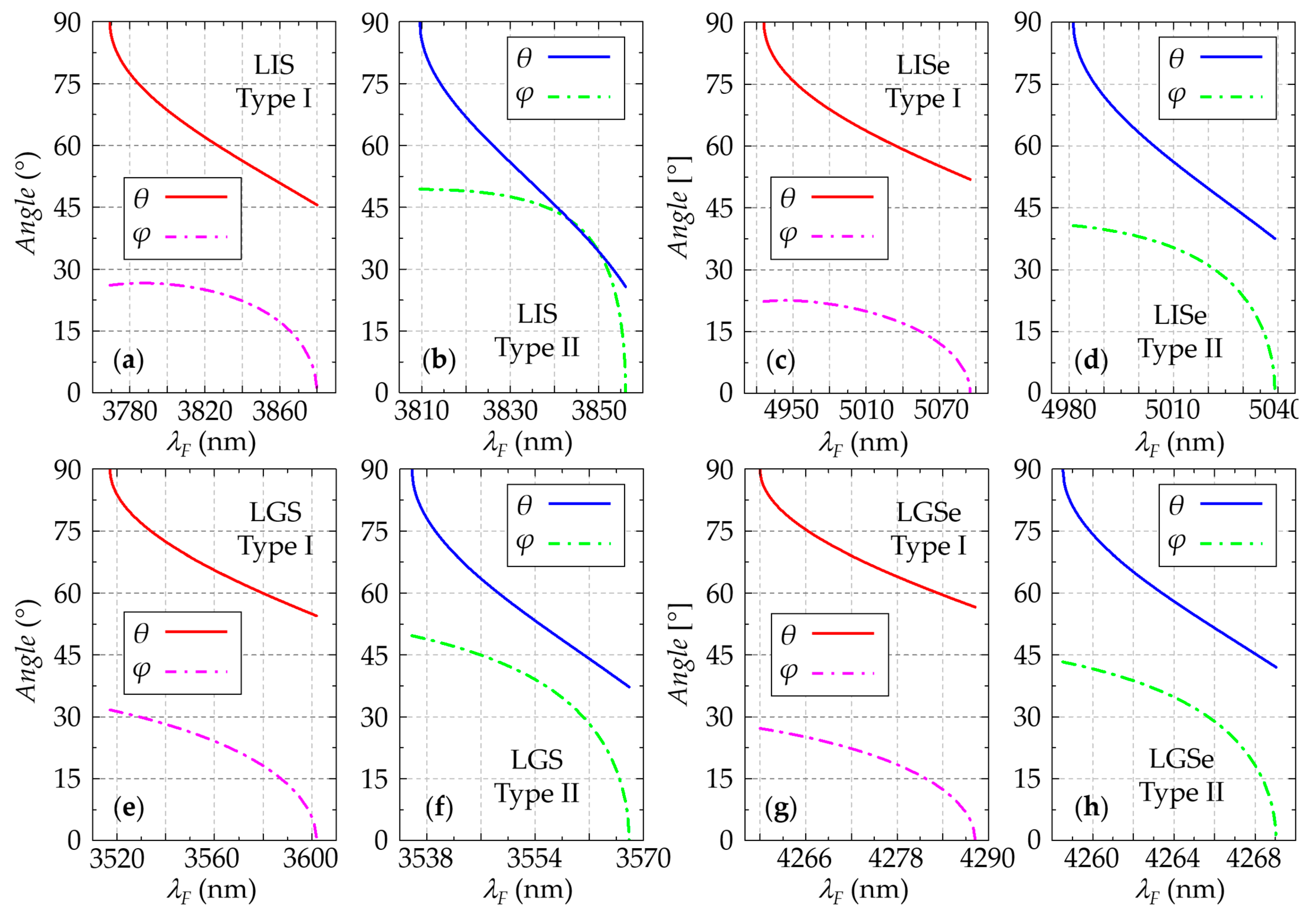
| Crystals | BPM Type | λF Range (nm) | λSH Range (nm) | φ Range (°) | θ Range (°) |
|---|---|---|---|---|---|
| LIS [39] | Type I | 3769.29—3879.91 | 1884.64—1939.95 | 26.10—0.00 | 90.00—45.57 |
| Type II | 3809.60—3856.09 | 1904.80—1928.04 | 49.39—0.00 | 90.00—25.75 | |
| LISe [43] | Type I | 4926.06—5095.49 | 2463.03—2547.75 | 22.31—0.00 | 90.00—51.91 |
| Type II | 4981.24—5039.20 | 2490.62—2519.60 | 40.71—0.00 | 90.00—37.53 | |
| LGS [44] | Type I | 3517.15—3601.95 | 1758.58—1800.98 | 31.69—0.00 | 90.00—54.48 |
| Type II | 3535.79—3567.88 | 1767.90—1783.94 | 49.69—0.00 | 90.00—37.22 | |
| LGSe [45] | Type I | 4259.98—4288.26 | 2129.99—2144.13 | 27.21—0.00 | 90.00—56.60 |
| Type II | 4258.53—4269.03 | 2129.26—2134.52 | 43.32—0.00 | 90.00—42.01 |
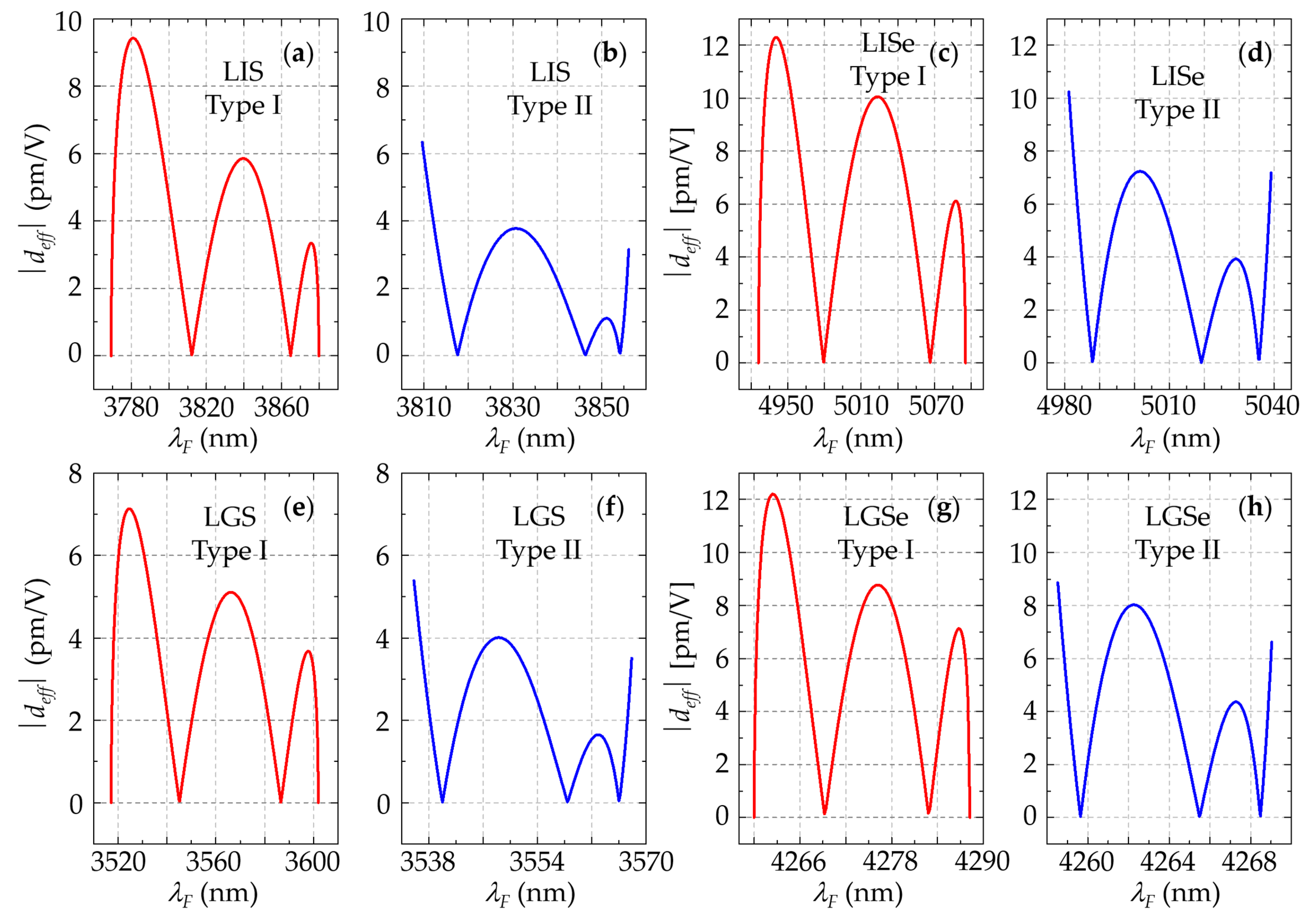
| Crystals | BPM Type | λF (nm) | λSH (nm) | φ (°) | θ (°) | |deff| (pm/V) 1 | w (°) | ΔλF (nm) |
|---|---|---|---|---|---|---|---|---|
| LIS | Type I | 3781.02 | 1890.51 | 26.58 | 76.84 | 9.4 | 0.86 | 402.05 |
| Type II | 3809.60 | 1904.80 | 49.39 | 90.00 | 6.3 | 0.94 | 410.30 | |
| LISe | Type I | 4940.40 | 2470.20 | 22.55 | 78.97 | 12.3 | 0.82 | 629.79 |
| Type II | 4981.24 | 2490.62 | 40.71 | 90.00 | 10.2 | 1.01 | 648.12 | |
| LGS | Type I | 3524.58 | 1762.29 | 30.67 | 80.07 | 7.1 | 1.03 | 369.30 |
| Type II | 3535.79 | 1767.90 | 49.69 | 90.00 | 5.4 | 1.11 | 375.76 | |
| LGSe | Type I | 4262.46 | 2131.23 | 26.41 | 80.65 | 12.2 | 1.06 | 488.26 |
| Type II | 4258.53 | 2129.26 | 43.32 | 90.00 | 8.9 | 1.25 | 491.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, I.; Lee, D.; Lee, K.J. Investigation of Mid-Infrared Broadband Second-Harmonic Generation in Non-Oxide Nonlinear Optic Crystals. Crystals 2021, 11, 921. https://doi.org/10.3390/cryst11080921
Kim I, Lee D, Lee KJ. Investigation of Mid-Infrared Broadband Second-Harmonic Generation in Non-Oxide Nonlinear Optic Crystals. Crystals. 2021; 11(8):921. https://doi.org/10.3390/cryst11080921
Chicago/Turabian StyleKim, Ilhwan, Donghwa Lee, and Kwang Jo Lee. 2021. "Investigation of Mid-Infrared Broadband Second-Harmonic Generation in Non-Oxide Nonlinear Optic Crystals" Crystals 11, no. 8: 921. https://doi.org/10.3390/cryst11080921
APA StyleKim, I., Lee, D., & Lee, K. J. (2021). Investigation of Mid-Infrared Broadband Second-Harmonic Generation in Non-Oxide Nonlinear Optic Crystals. Crystals, 11(8), 921. https://doi.org/10.3390/cryst11080921






