Effect of Graphene on Ice Polymorph
Abstract
:1. Introduction
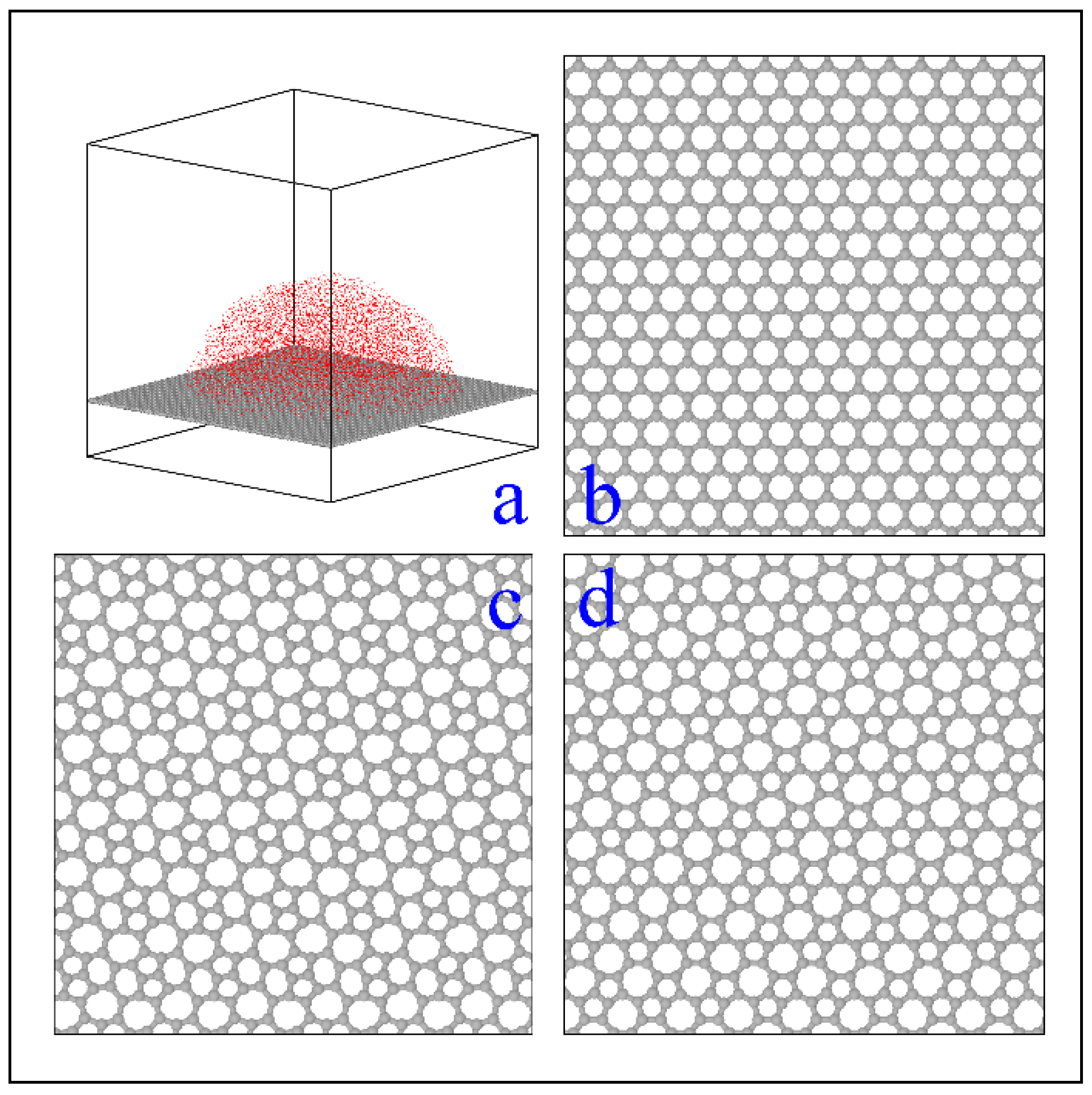
2. Methods
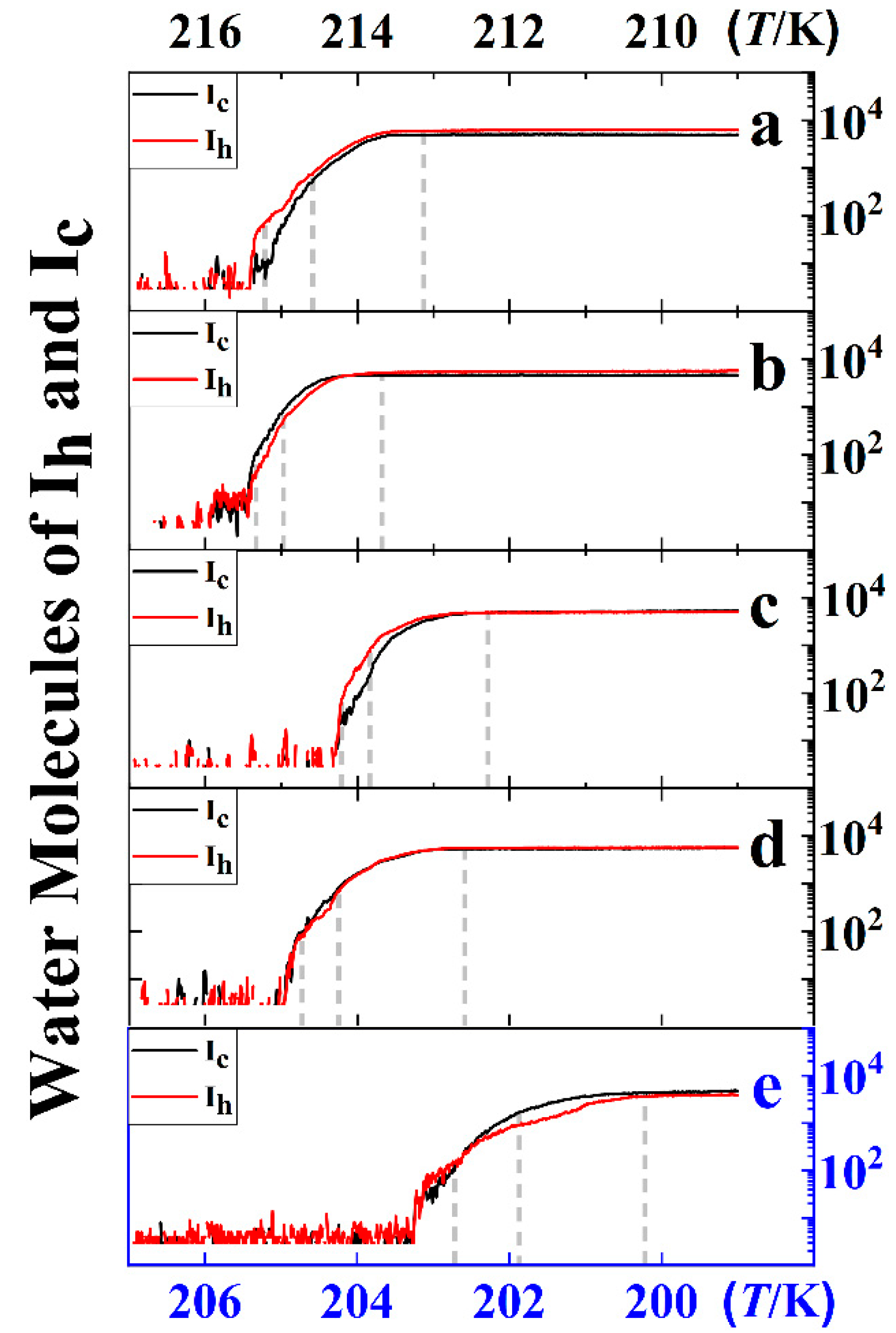
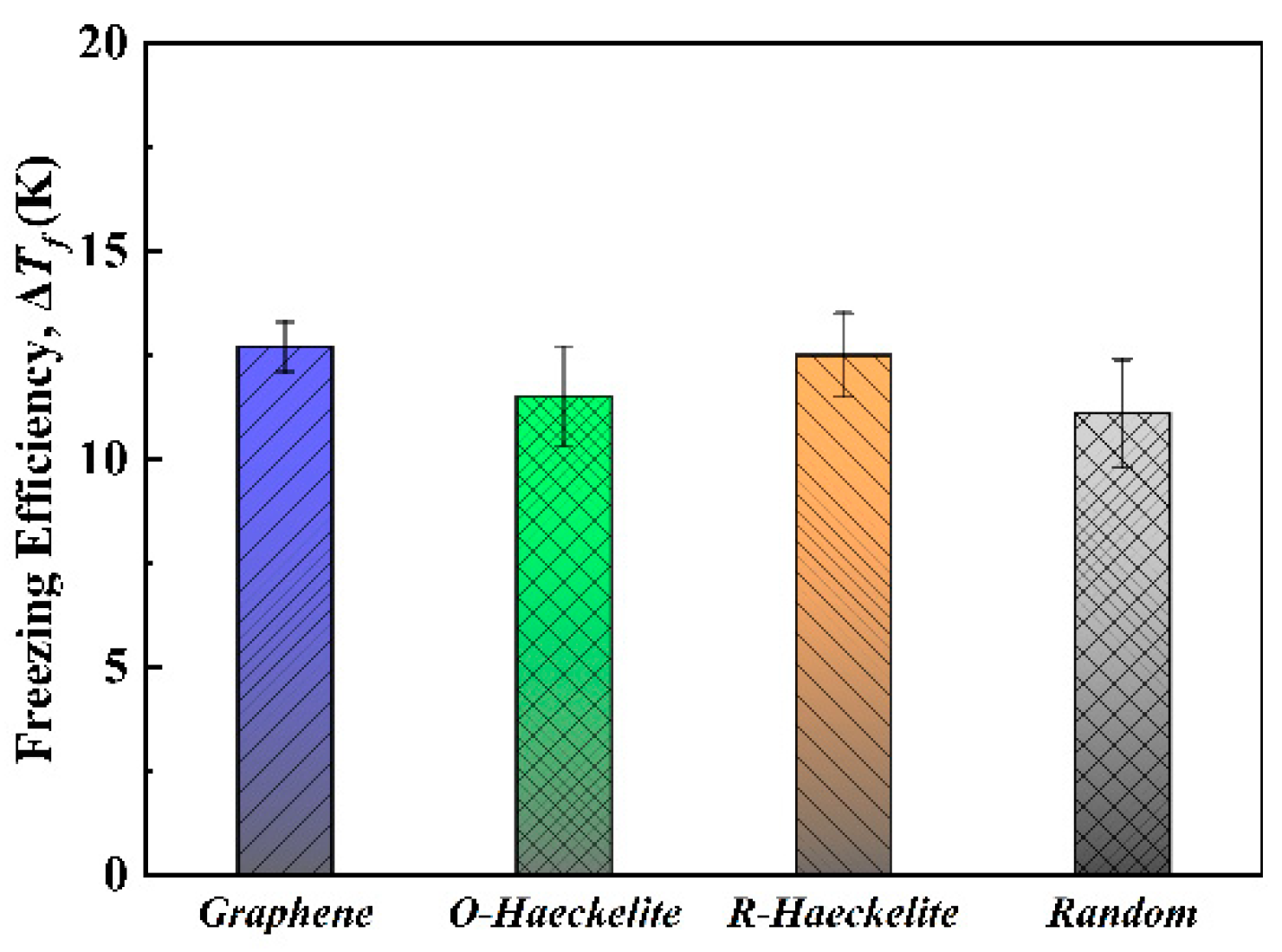
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hudait, A.; Moberg, D.R.; Qiu, Y.; Odendahl, N.; Paesani, F.; Molinero, V. Preordering of water is not needed for ice recognition by hyperactive antifreeze proteins. Proc. Natl. Acad. Sci. USA 2018, 115, 8266–8271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, J.Y.; Patey, G.N. Heterogeneous Ice Nucleation Induced by Electric Fields. J. Phys. Chem. Lett. 2011, 2, 2555–2559. [Google Scholar] [CrossRef]
- Herbert, R.J.; Murray, B.J.; Dobbie, S.J.; Koop, T. Sensitivity of liquid clouds to homogenous freezing parameterizations. Geophys. Res. Lett. 2015, 42, 1599–1605. [Google Scholar] [CrossRef] [PubMed]
- Hudait, A.; Molinero, V. What Determines the Ice Polymorph in Clouds? J. Am. Chem. Soc. 2016, 138, 8958–8967. [Google Scholar] [CrossRef] [PubMed]
- Lupi, L.; Hudait, A.; Peters, B.; Grünwald, M.; Mullen, R.G.; Nguyen, A.H.; Molinero, V. Role of stacking disorder in ice nucleation. Nature 2017, 551, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Malkin, T.L.; Murray, B.J.; Salzmann, C.G.; Molinero, V.; Pickering, S.J.; Whale, T.F. Stacking disorder in ice I. Phys. Chem. Chem. Phys. 2015, 17, 60–76. [Google Scholar] [CrossRef] [Green Version]
- Moore, E.B.; Molinero, V. Is it cubic? Ice crystallization from deeply supercooled water. Phys. Chem. Chem. Phys. 2011, 13, 20008–20016. [Google Scholar] [CrossRef]
- Sosso, G.C.; Tribello, G.A.; Zen, A.; Pedevilla, P.; Michaelides, A. Ice formation on kaolinite: Insights from molecular dynamics simulations. J. Chem. Phys. 2016, 145, 211927. [Google Scholar] [CrossRef] [Green Version]
- Thurmer, K.; Nie, S. Formation of hexagonal and cubic ice during low-temperature growth. Proc. Natl. Acad. Sci. USA 2013, 110, 11757–11762. [Google Scholar] [CrossRef] [Green Version]
- Kuhs, W.F.; Sippel, C.; Falenty, A.; Hansen, T.C. Extent and relevance of stacking disorder in “ice I(c)”. Proc. Natl. Acad. Sci. USA 2012, 109, 21259–21264. [Google Scholar] [CrossRef] [Green Version]
- Shilling, J.E.; Tolbert, M.A.; Toon, O.B.; Jensen, E.J.; Murray, B.J.; Bertram, A.K. Measurements of the vapor pressure of cubic ice and their implications for atmospheric ice clouds. Geophys. Res. Lett. 2006, 33, 17. [Google Scholar] [CrossRef] [Green Version]
- Hansen, T.C.; Koza, M.M.; Lindner, P.; Kuhs, W.F. Formation and annealing of cubic ice: II. Kinetic study. J. Phys. Cond. Matt. 2008, 20, 285105. [Google Scholar] [CrossRef]
- Morishige, K.; Uematsu, H. The proper structure of cubic ice confined in mesopores. J. Chem. Phys. 2005, 122, 44711. [Google Scholar] [CrossRef] [PubMed]
- Malkin, T.L.; Murray, B.J.; Brukhno, A.V.; Anwar, J.; Salzmann, C.G. Structure of ice crystallized from supercooled water. Proc. Natl. Acad. Sci. USA 2012, 109, 1041–1045. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.Y.; Du, N. Zero-sized effect of nano-particles and inverse homogeneous nucleation. Principles of freezing and antifreeze. J. Biol. Chem. 2004, 279, 6124–6131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Liu, X.Y. Control of ice nucleation: Freezing and antifreeze strategies. Chem. Soc. Rev. 2018, 47, 7116–7139. [Google Scholar] [CrossRef]
- Lary, D.; Shallcross, D.; Toumi, R. Carbonaceous aerosols and their potential role in atmospheric chemistry. J. Geophys. Res. 1999, 104, 15929–15940. [Google Scholar] [CrossRef] [Green Version]
- Lupi, L.; Kastelowitz, N.; Molinero, V. Vapor deposition of water on graphitic surfaces: Formation of amorphous ice, bilayer ice, ice I, and liquid water. J. Chem. Phys. 2014, 141, 18C508. [Google Scholar] [CrossRef]
- Penner, J.; Eddleman, H.; Novakov, T. Towards the development of a global inventory for black carbon emissions. Atmos. Environ. Part A Gen. Top. 1993, 27, 1277–1295. [Google Scholar] [CrossRef]
- Lupi, L.; Hudait, A.; Molinero, V. Heterogeneous nucleation of ice on carbon surfaces. J. Am. Chem. Soc. 2014, 136, 3156–3164. [Google Scholar] [CrossRef]
- Lupi, L.; Molinero, V. Does hydrophilicity of carbon particles improve their ice nucleation ability? J. Phys. Chem. A 2014, 118, 7330–7337. [Google Scholar] [CrossRef]
- Cabriolu, R.; Li, T. Ice nucleation on carbon surface supports the classical theory for heterogeneous nucleation. Phys. Rev. E 2015, 91, 052402. [Google Scholar] [CrossRef] [Green Version]
- Whale, T.F.; Rosillo-Lopez, M.; Murray, B.J.; Salzmann, C.G. Ice nucleation properties of oxidized carbon nanomaterials. J. Phys. Chem. Lett. 2015, 6, 3012–3016. [Google Scholar] [CrossRef]
- Bi, Y.; Cabriolu, R.; Li, T. Heterogeneous ice nucleation controlled by the coupling of surface crystallinity and surface hydrophilicity. J. Phys. Chem. C 2016, 120, 1507–1514. [Google Scholar] [CrossRef] [Green Version]
- Terrones, H.; Terrones, M.; Hernández, E. New metallic allotropes of planar and tubular carbon. Phys. Rev. Lett. 2000, 84, 1716. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Molinero, V.; Moore, E.B. Water Modeled As an Intermediate Element between Carbon and Silicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, J.C.; Molinero, V. Crystallization, melting, and structure of water nanoparticles at atmospherically relevant temperatures. J. Am. Chem. Soc. 2012, 134, 6650–6659. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zeng, X.C. Wetting and interfacial properties of water nanodroplets in contact with graphene and monolayer boron–nitride sheets. ACS Nano 2012, 6, 2401–2409. [Google Scholar] [CrossRef]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces; Interscience: New York, NY, USA, 1967; Volume 15. [Google Scholar]
- Nguyen, A.H.; Molinero, V. Identification of Clathrate Hydrates, Hexagonal Ice, Cubic Ice, and Liquid Water in Simulations: The CHILL+ Algorithm. J. Phys. Chem. B 2015, 119, 9369–9376. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Mod. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Cox, S.J.; Raza, Z.; Kathmann, S.M.; Slater, B.; Michaelides, A. The microscopic features of heterogeneous ice nucleation may affect the macroscopic morphology of atmospheric ice crystals. Faraday Disc. 2013, 167, 389–403. [Google Scholar] [CrossRef] [Green Version]
- Xue, H.; Lu, Y.; Geng, H.; Dong, B.; Wu, S.; Fan, Q.; Zhang, Z.; Li, X.; Zhou, X.; Wang, J. Hydroxyl Groups on the Graphene Surfaces Facilitate Ice Nucleation. J. Phys. Chem. Lett. 2019, 10, 2458–2462. [Google Scholar] [CrossRef]
- Li, T.; Donadio, D.; Russo, G.; Galli, G. Homogeneous ice nucleation from supercooled water. Phys. Chem. Chem. Phys. 2011, 13, 19807–19813. [Google Scholar] [CrossRef] [PubMed]
- Pozzo, M.; Alfe, D.; Lacovig, P.; Hofmann, P.; Lizzit, S.; Baraldi, A. Thermal expansion of supported and freestanding graphene: Lattice constant versus interatomic distance. Phys. Rev. Lett. 2011, 106, 135501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Zhu, C.; Liu, K.; Jiang, Y.; Song, Y.; Francisco, J.S.; Zeng, X.C.; Wang, J. Distinct ice patterns on solid surfaces with various wettabilities. Proc. Natl. Acad. Sci. USA 2017, 114, 11285–11290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, A.H.; Koc, M.A.; Shepherd, T.D.; Molinero, V. Structure of the Ice–Clathrate Interface. J. Phys. Chem. C 2015, 119, 4104–4117. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Kang, Y.; Liang, L.J.; Liu, Y.C.; Wu, T.; Wang, Q. Peptide encapsulation regulated by the geometry of carbon nanotubes. Biomaterials 2014, 35, 1771–1778. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.-C.; Shen, J.-W.; Gubbins, K.E.; Moore, J.D.; Wu, T.; Wang, Q. Diffusion dynamics of water controlled by topology of potential energy surface inside carbon nanotubes. Phys. Rev. B 2008, 77, 125438. [Google Scholar] [CrossRef]
- Cox, S.J.; Kathmann, S.M.; Purton, J.A.; Gillan, M.J.; Michaelides, A. Non-hexagonal ice at hexagonal surfaces: The role of lattice mismatch. Phys. Chem. Chem. Phys. 2012, 14, 7944–7949. [Google Scholar] [CrossRef]
- Qiu, Y.; Hudait, A.; Molinero, V. How Size and Aggregation of Ice-Binding Proteins Control Their Ice Nucleation Efficiency. J. Am. Chem. Soc. 2019, 141, 7439–7452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roudsari, G.; Reischl, B.; Pakarinen, O.H.; Vehkamäki, H. Atomistic Simulation of Ice Nucleation on Silver Iodide (0001) Surfaces with Defects. J. Phys. Chem. C 2019, 124, 436–445. [Google Scholar] [CrossRef]
- Zielke, S.A.; Bertram, A.K.; Patey, G.N. A Molecular Mechanism of Ice Nucleation on Model AgI Surfaces. J. Phys. Chem. B 2015, 119, 9049–9055. [Google Scholar] [CrossRef] [PubMed]
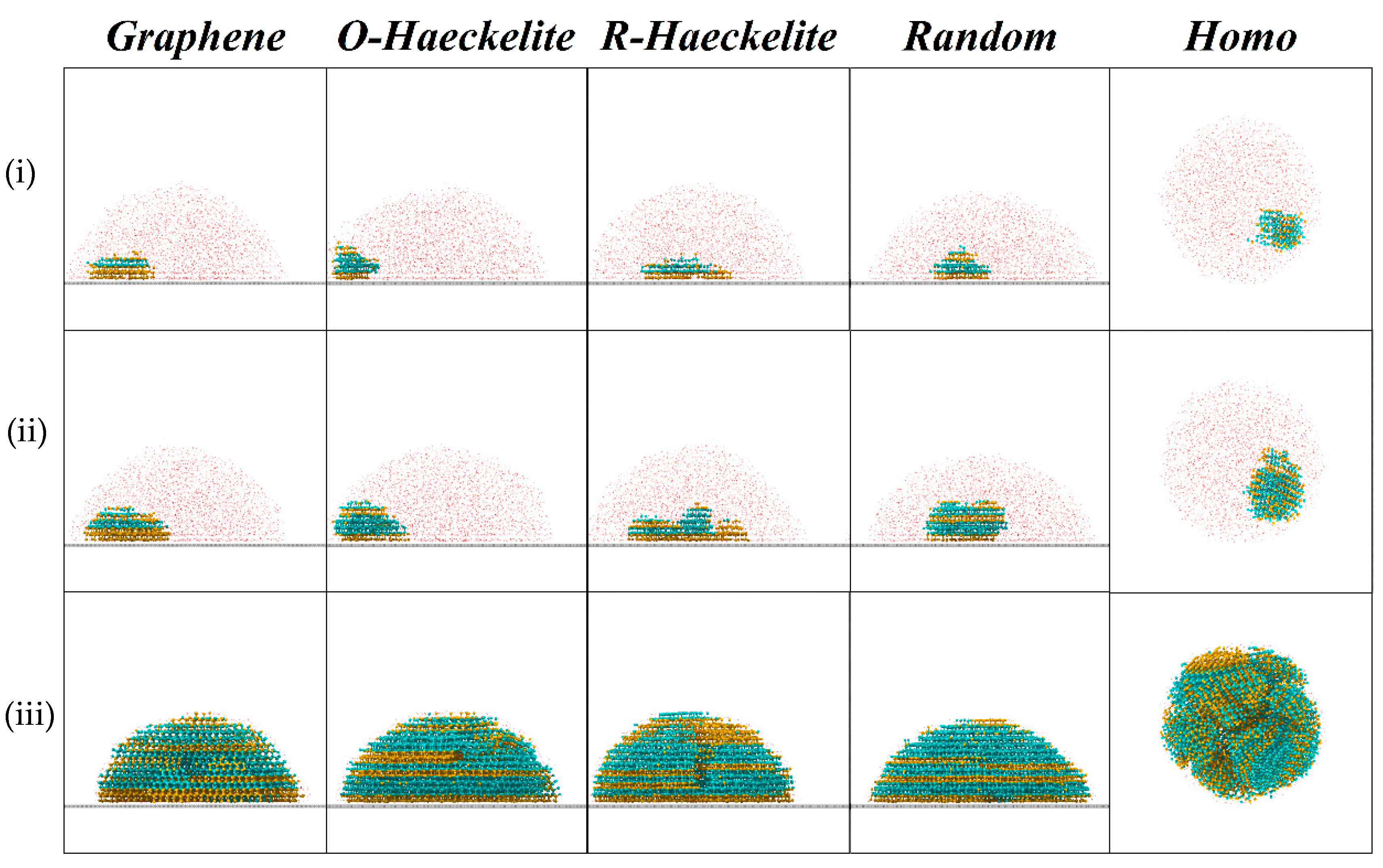
| Substrate | Graphene | O-Haeckelite | R-Haeckelite | Random | Homo |
|---|---|---|---|---|---|
| Cubicity/% | 28.4 ± 2.5 | 41.2 ± 1.9 | 42.9 ± 2.3 | 42.6 ± 2.8 | 52.5 ± 1.3 |
| 34.2 ± 2.9 | 45.2 ± 4.5 | 44.0 ± 3.7 | 45.5 ± 3.9 | 53.9 ± 1.6 | |
| 53.4 ± 1.8 | 55.3 ± 1.5 | 56.5 ± 1.5 | 55.0 ± 1.7 | 58.2 ± 0.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, C.; Lu, H.; Xu, Q.; Liu, T.; Patil, A.; Wu, J.; de Vries, R.; Zuilhof, H.; Zhang, Z. Effect of Graphene on Ice Polymorph. Crystals 2021, 11, 1134. https://doi.org/10.3390/cryst11091134
Zheng C, Lu H, Xu Q, Liu T, Patil A, Wu J, de Vries R, Zuilhof H, Zhang Z. Effect of Graphene on Ice Polymorph. Crystals. 2021; 11(9):1134. https://doi.org/10.3390/cryst11091134
Chicago/Turabian StyleZheng, Chuanbao, Hao Lu, Quanming Xu, Tianyi Liu, Aniruddha Patil, Jianyang Wu, Renko de Vries, Han Zuilhof, and Zhisen Zhang. 2021. "Effect of Graphene on Ice Polymorph" Crystals 11, no. 9: 1134. https://doi.org/10.3390/cryst11091134
APA StyleZheng, C., Lu, H., Xu, Q., Liu, T., Patil, A., Wu, J., de Vries, R., Zuilhof, H., & Zhang, Z. (2021). Effect of Graphene on Ice Polymorph. Crystals, 11(9), 1134. https://doi.org/10.3390/cryst11091134






