Modeling Hardness Evolution during the Post-Welding Heat Treatment of a Friction Stir Welded 2050-T34 Alloy
Abstract
:1. Introduction
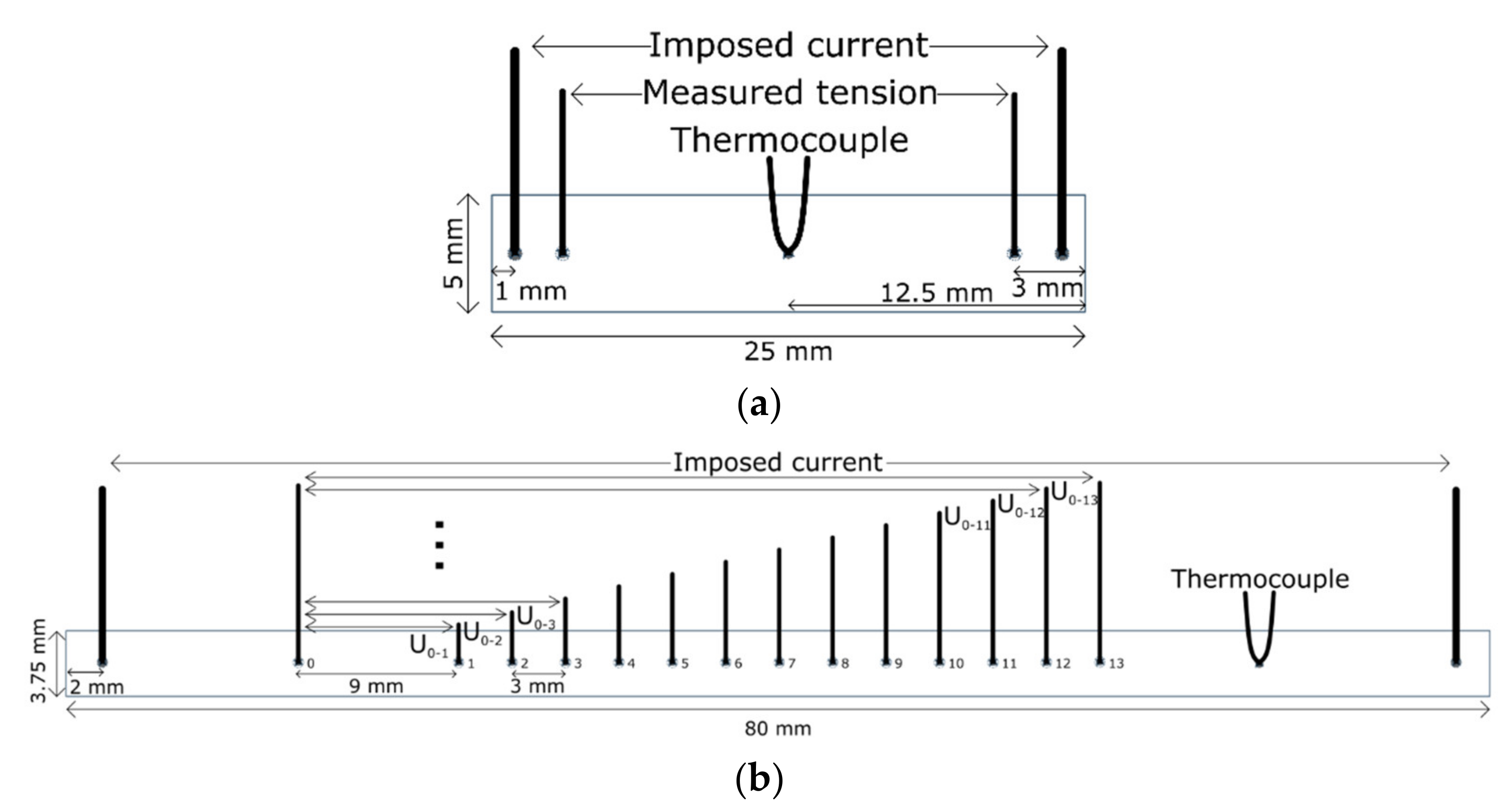
2. Materials and Methods
3. Experimental Results
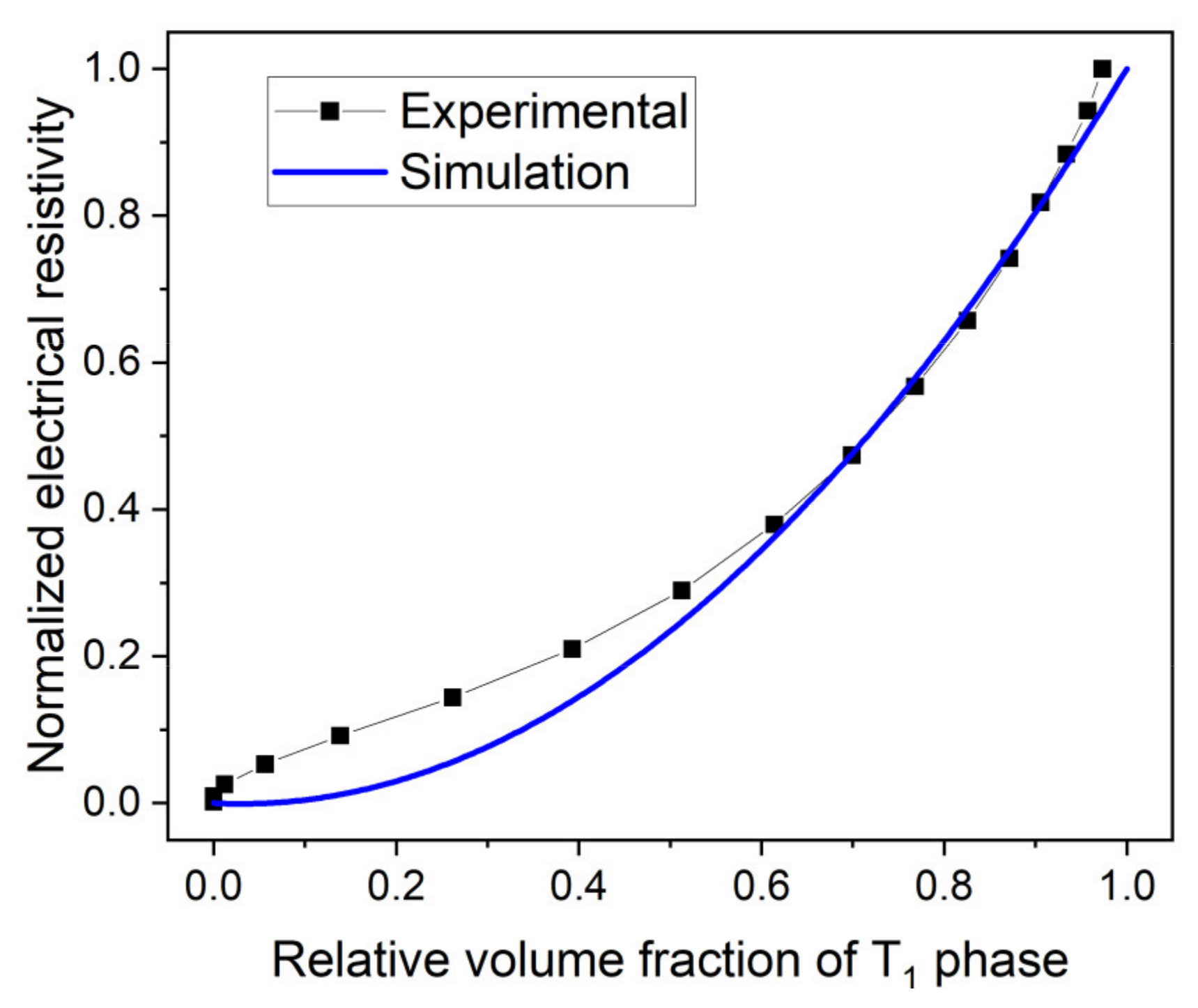
3.1. Monitoring T1 Precipitate Evolution Using Electrical Resistivity Measurement
3.2. Kinetics of Precipitation of the T1 Phase during Post-Welding Heat Treatment
4. Modeling
4.1. Original Constitutive Model
4.1.1. Dislocations
4.1.2. Solid Solution
4.1.3. Clusters
4.1.4. T1 Precipitates
4.1.5. Yield Strength
4.1.6. Summary and Material Constants
4.1.7. Comparison to Experimental Values
4.2. Revised Version of the Model
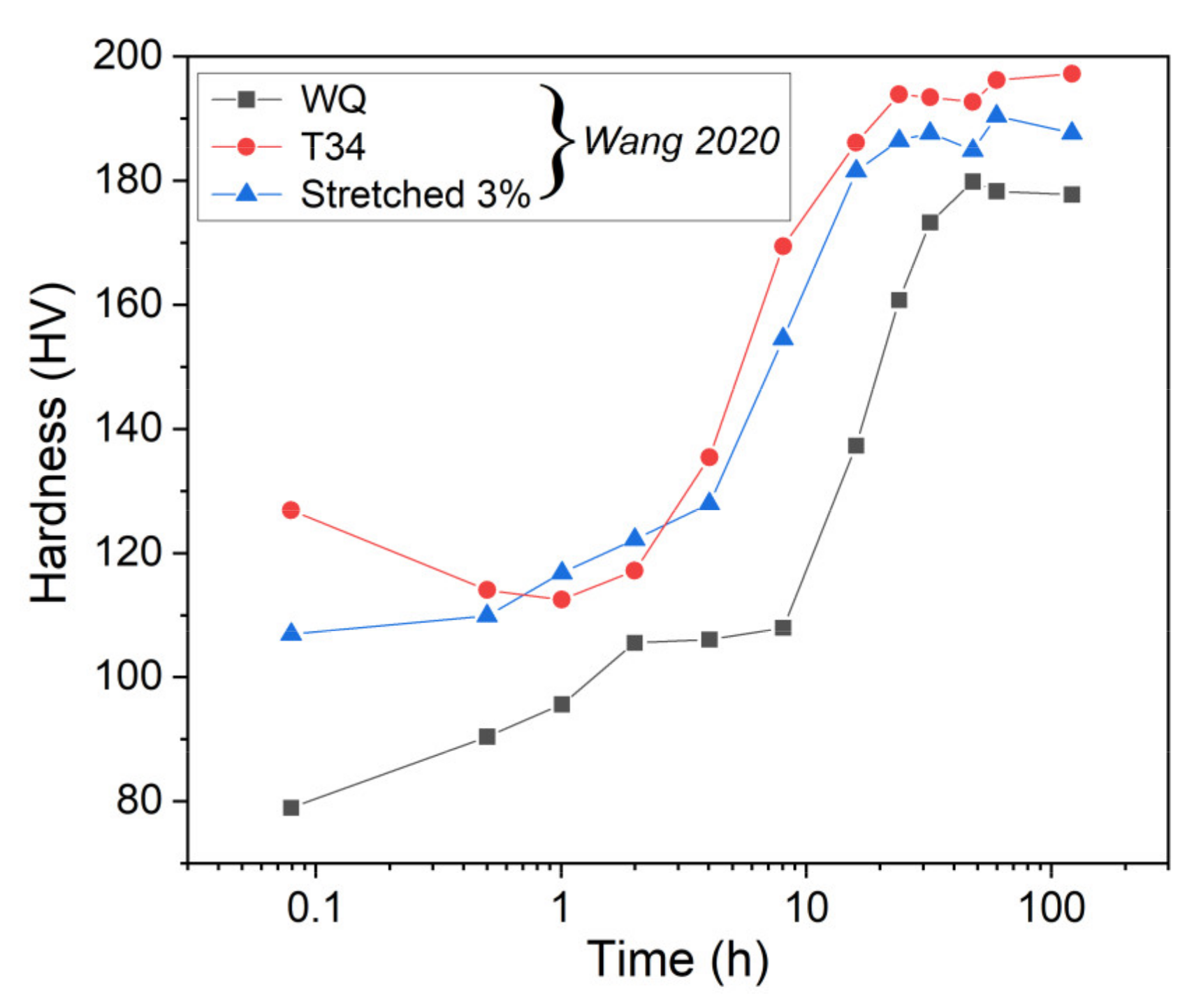
4.2.1. Influence of Pre-Treatments
4.2.2. Simulations with the Original Model
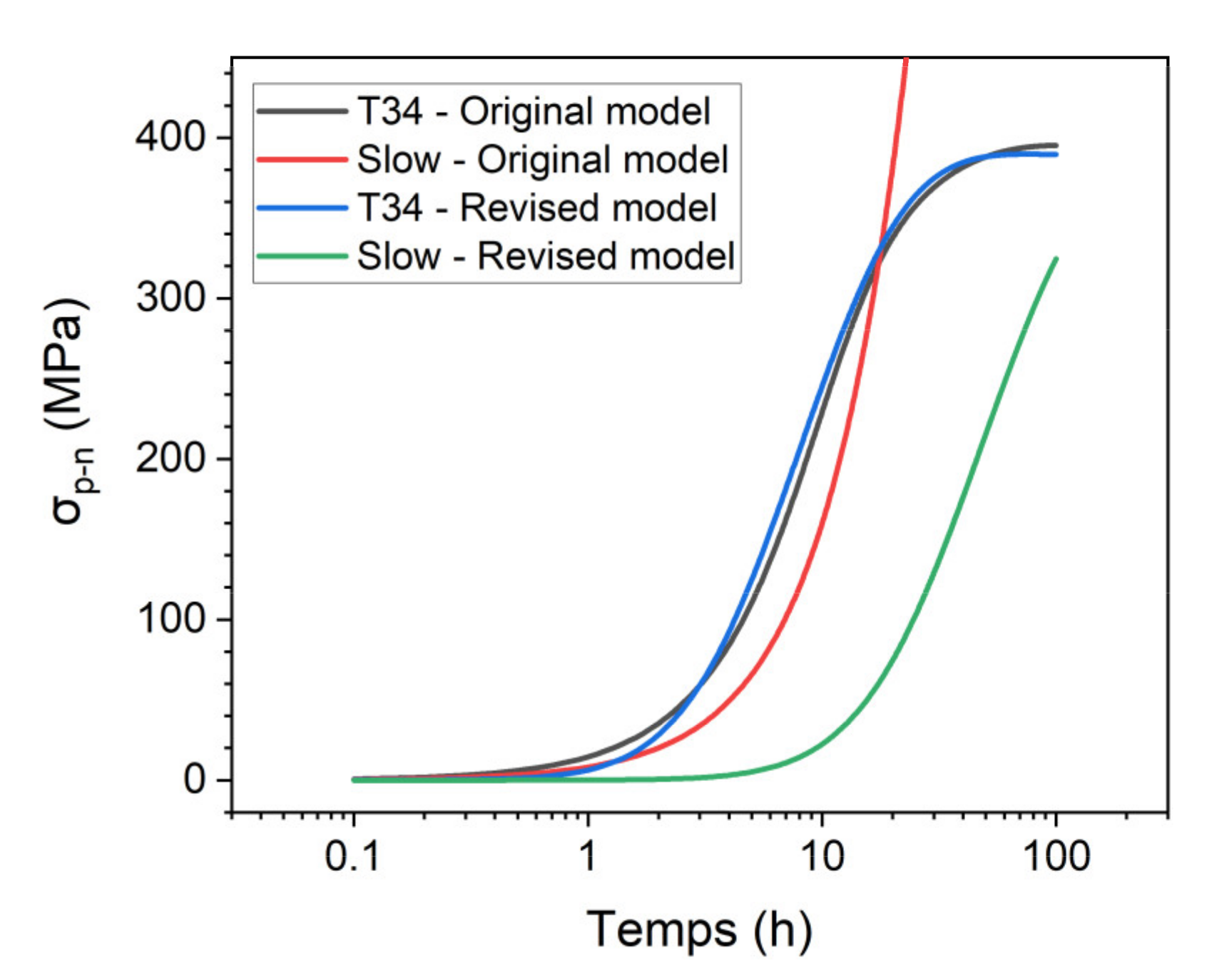
4.2.3. Revised Model
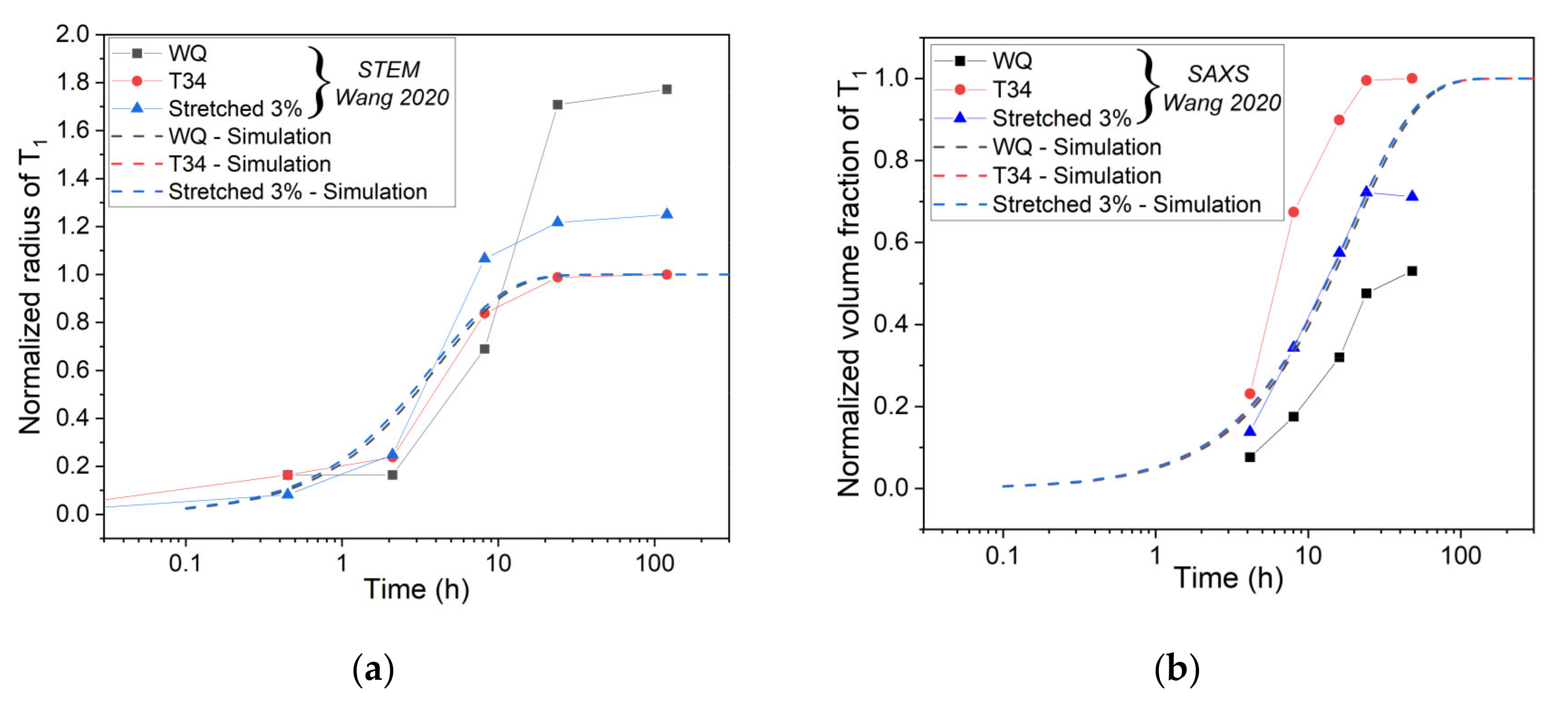
Normalized Volume Fraction of the T1 Phase
Normalized Radius of the T1 Precipitates
Strength Contribution of the T1 Precipitates
5. Application to FSW
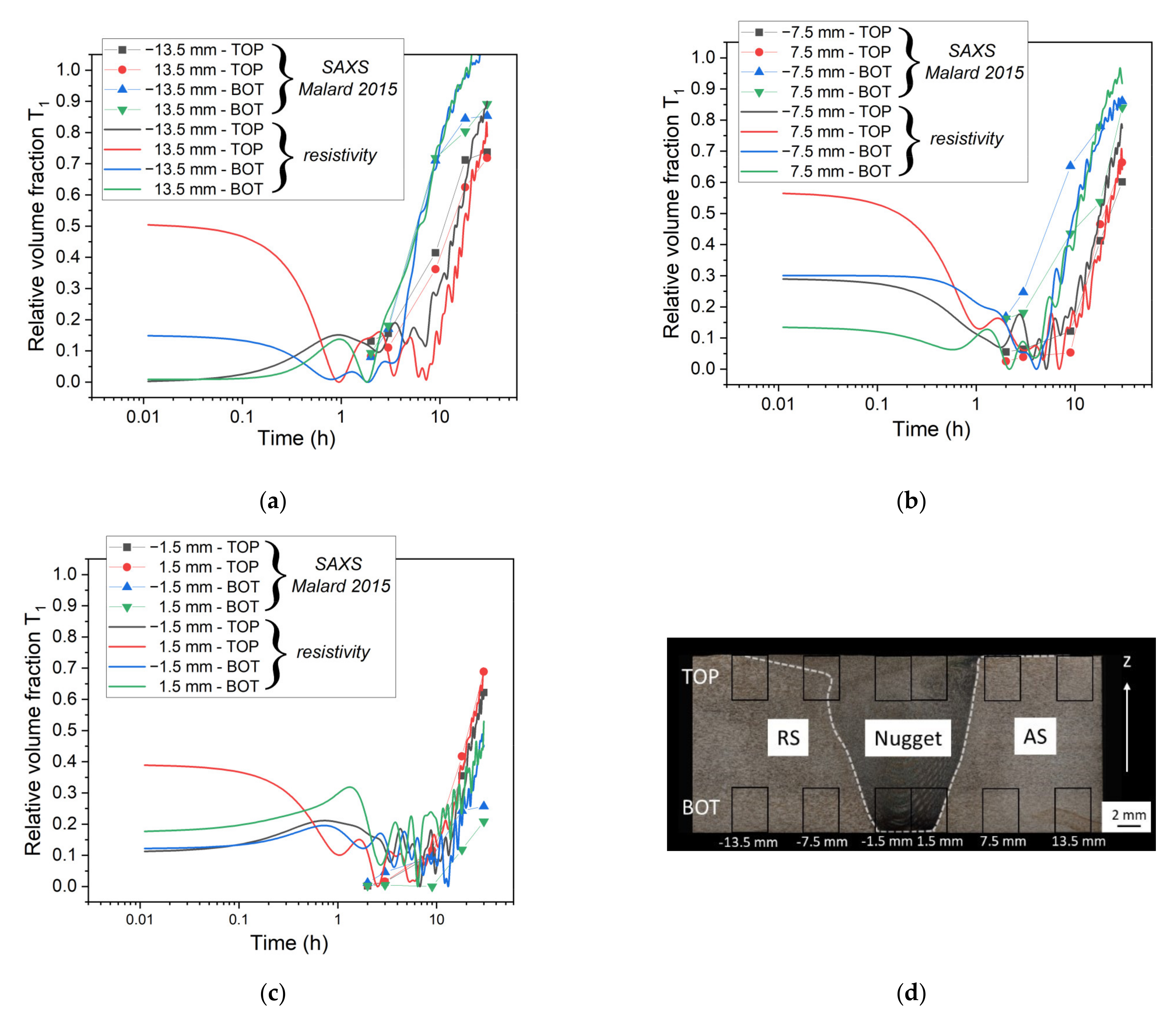
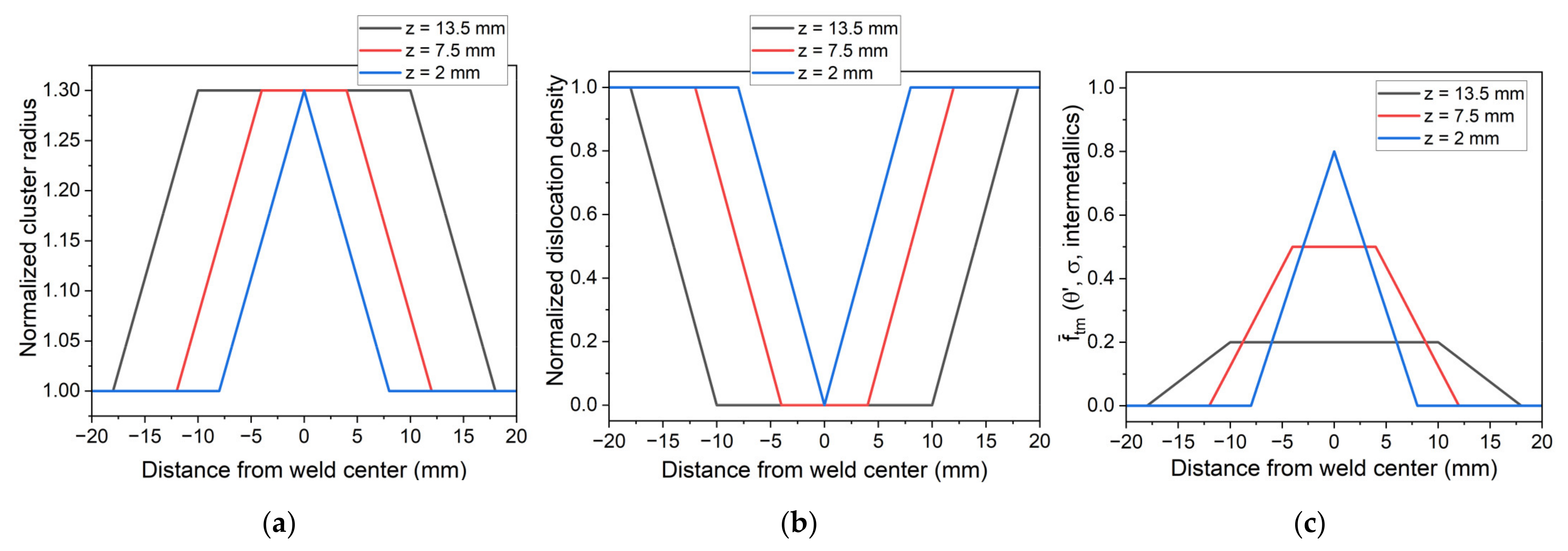
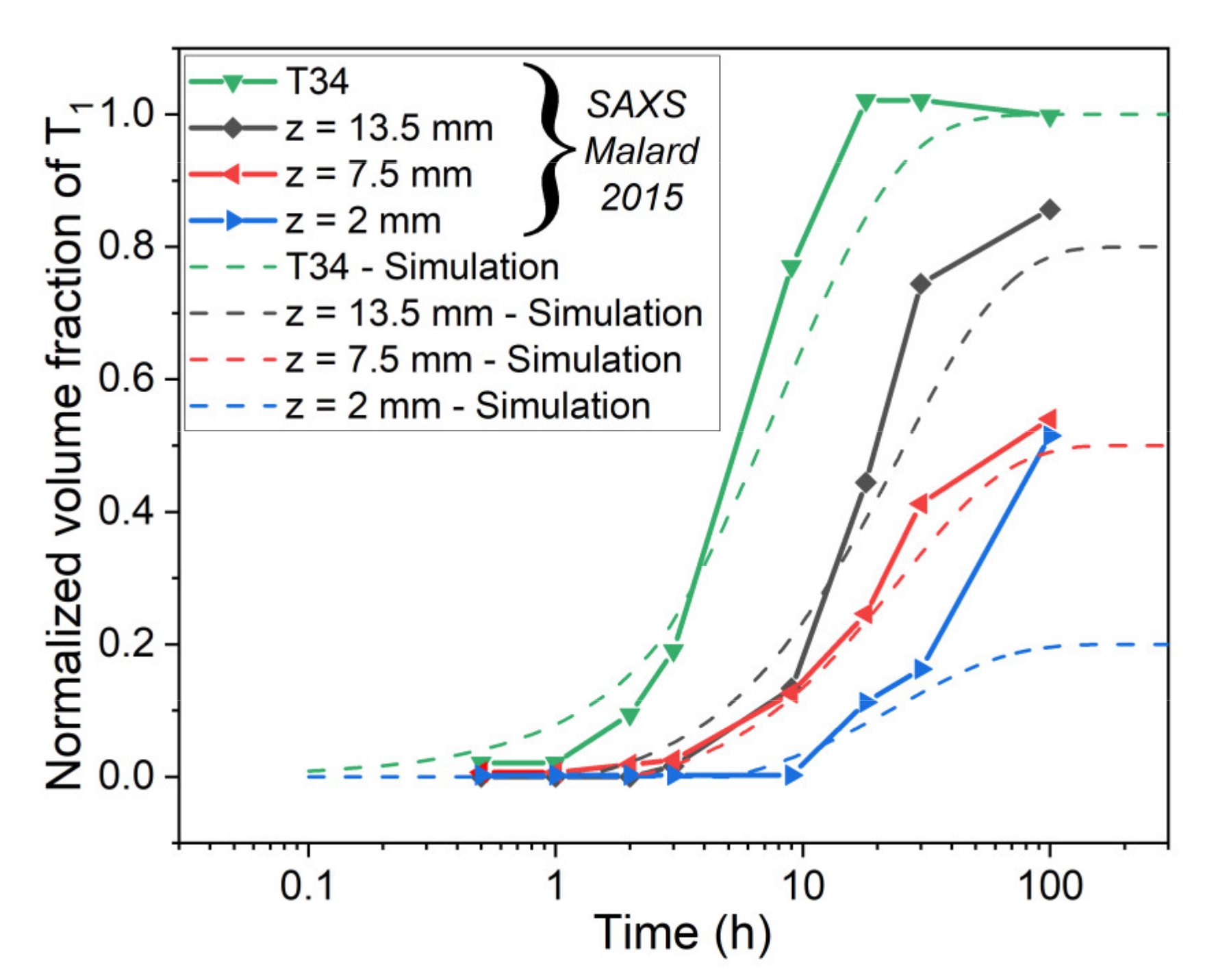
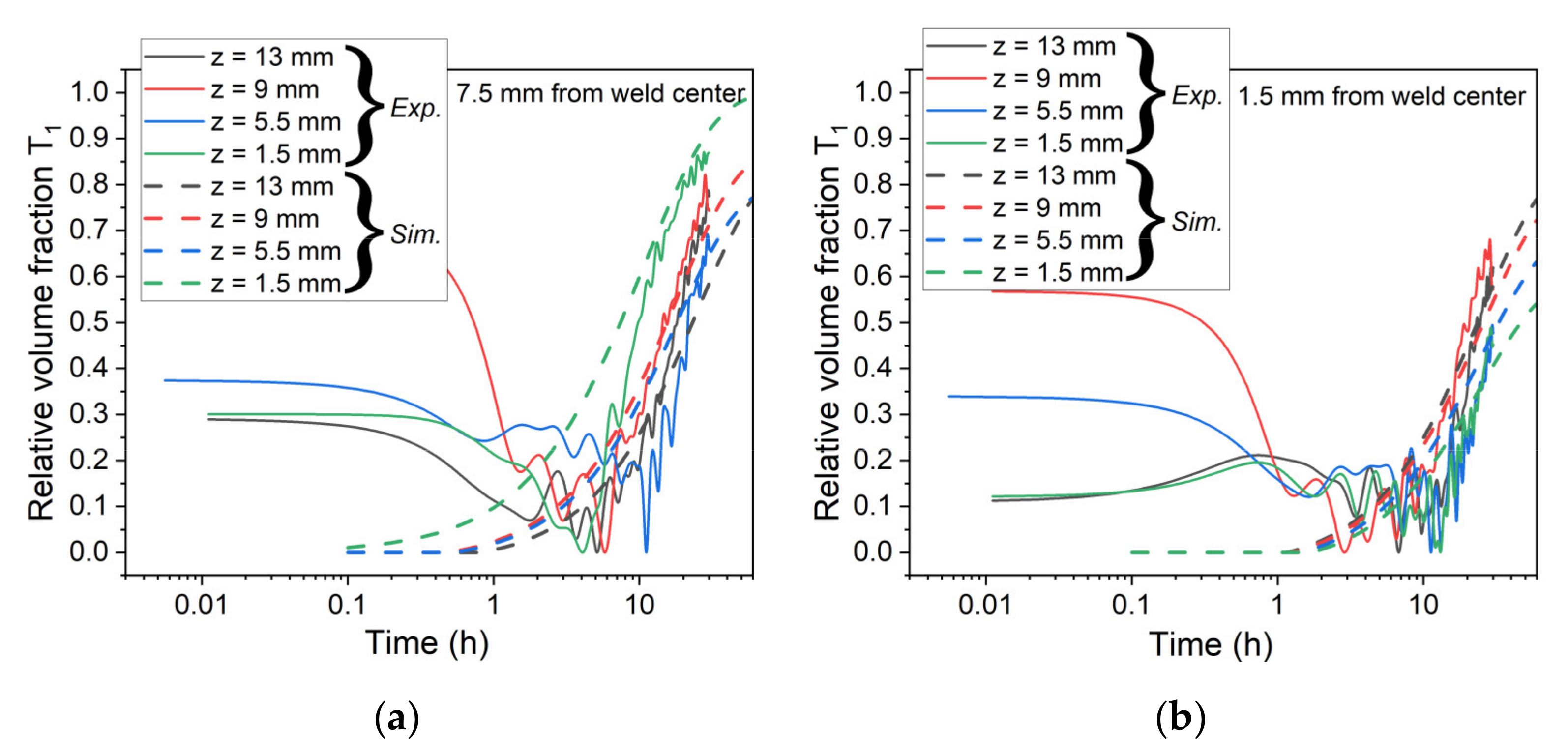
5.1. Simulation of Post-Weld Heat Treatment by Using the SAXS Data from [6]
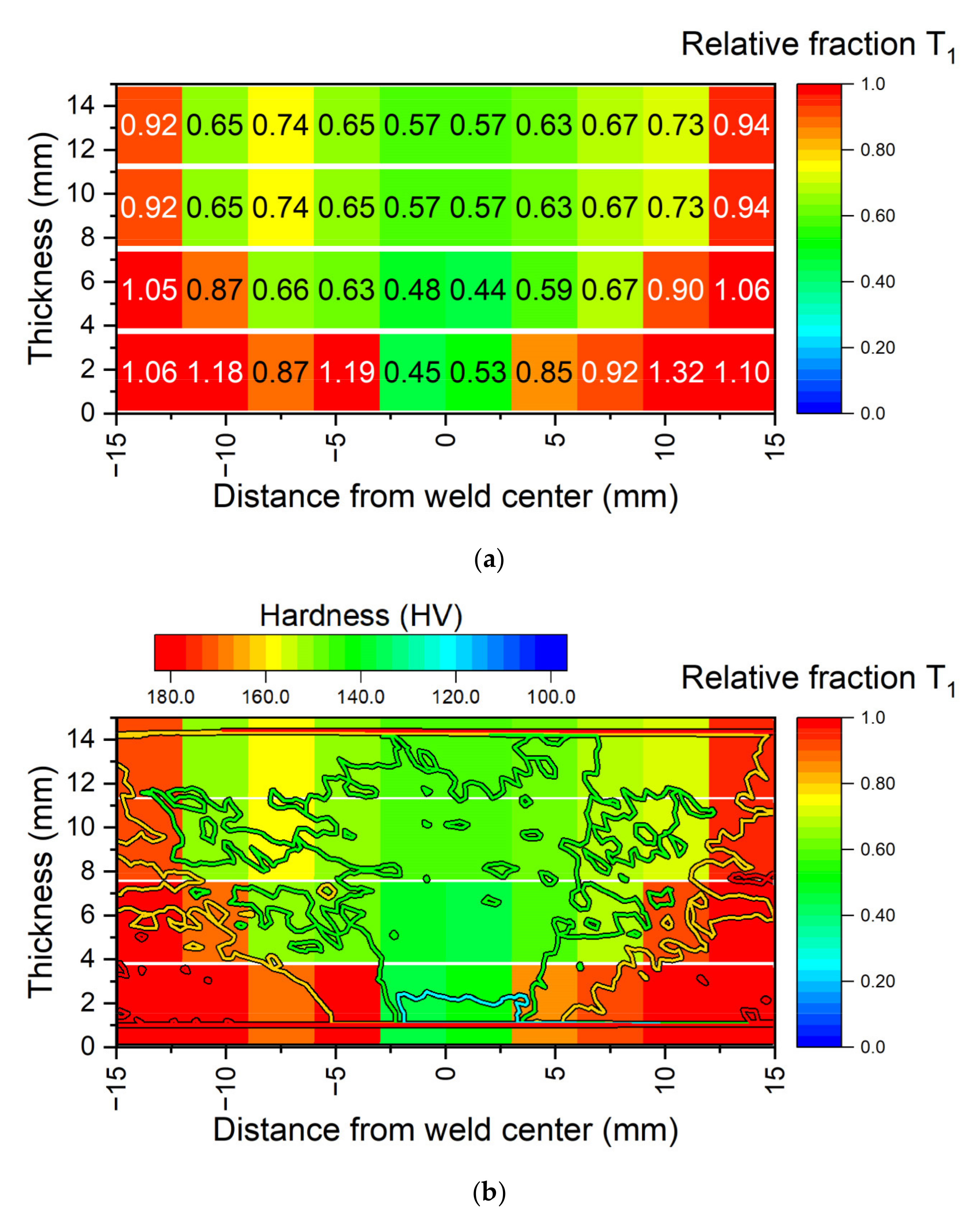
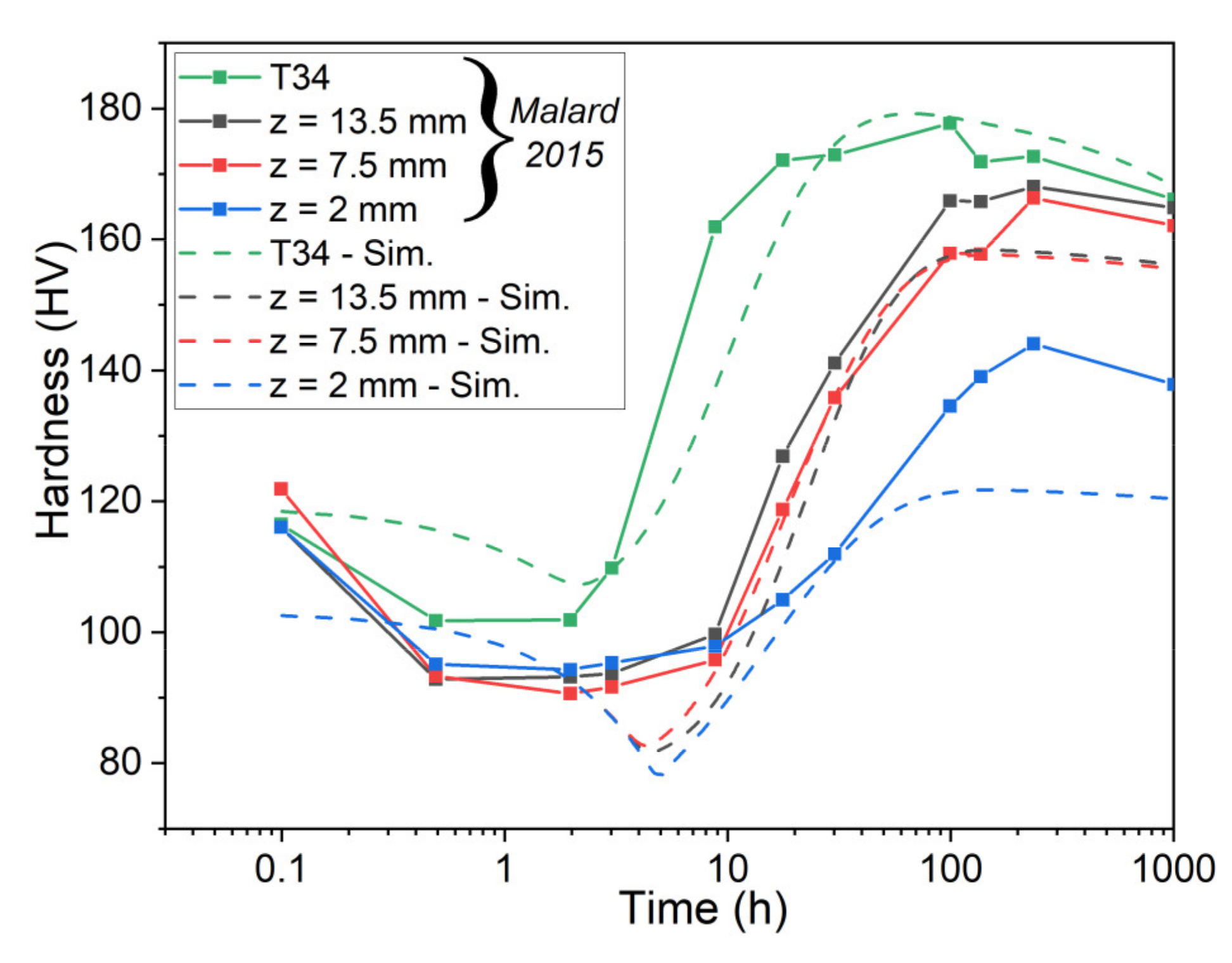
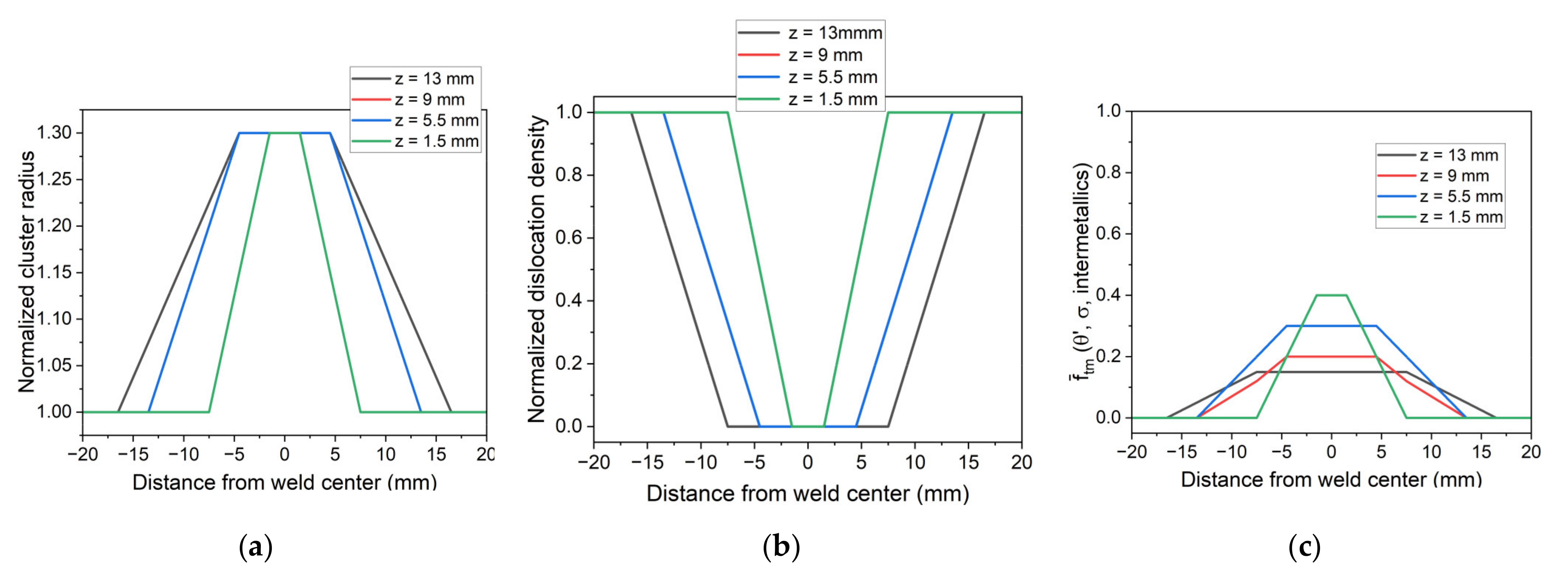
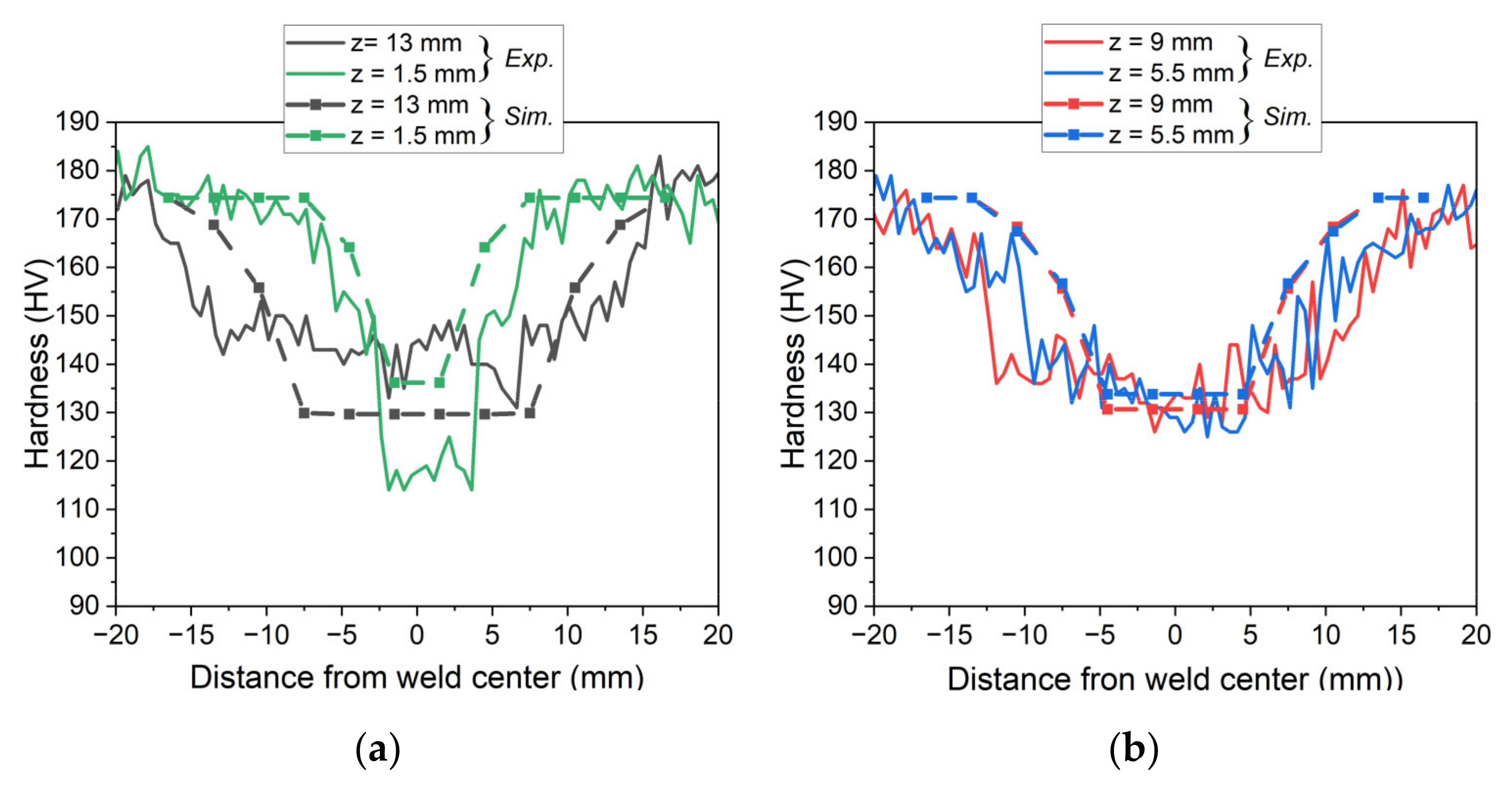
5.2. Simulation of Post-Weld Heat Treatment by Using Electrical Resistivity
6. Conclusions
- Characterization by electrical resistivity has been performed on the unwelded material and on FSW samples to follow the precipitation kinetics of the T1 phase during heat treatment at 155 °C. Results on FSW samples are consistent with data from the literature obtained by other techniques such as SAXS or DSC. Moreover, the softened zone in the nugget corresponds to the lower fraction of the T1 phase obtained in electrical resistivity. This technique was thus found adequate for mapping T1 precipitation.
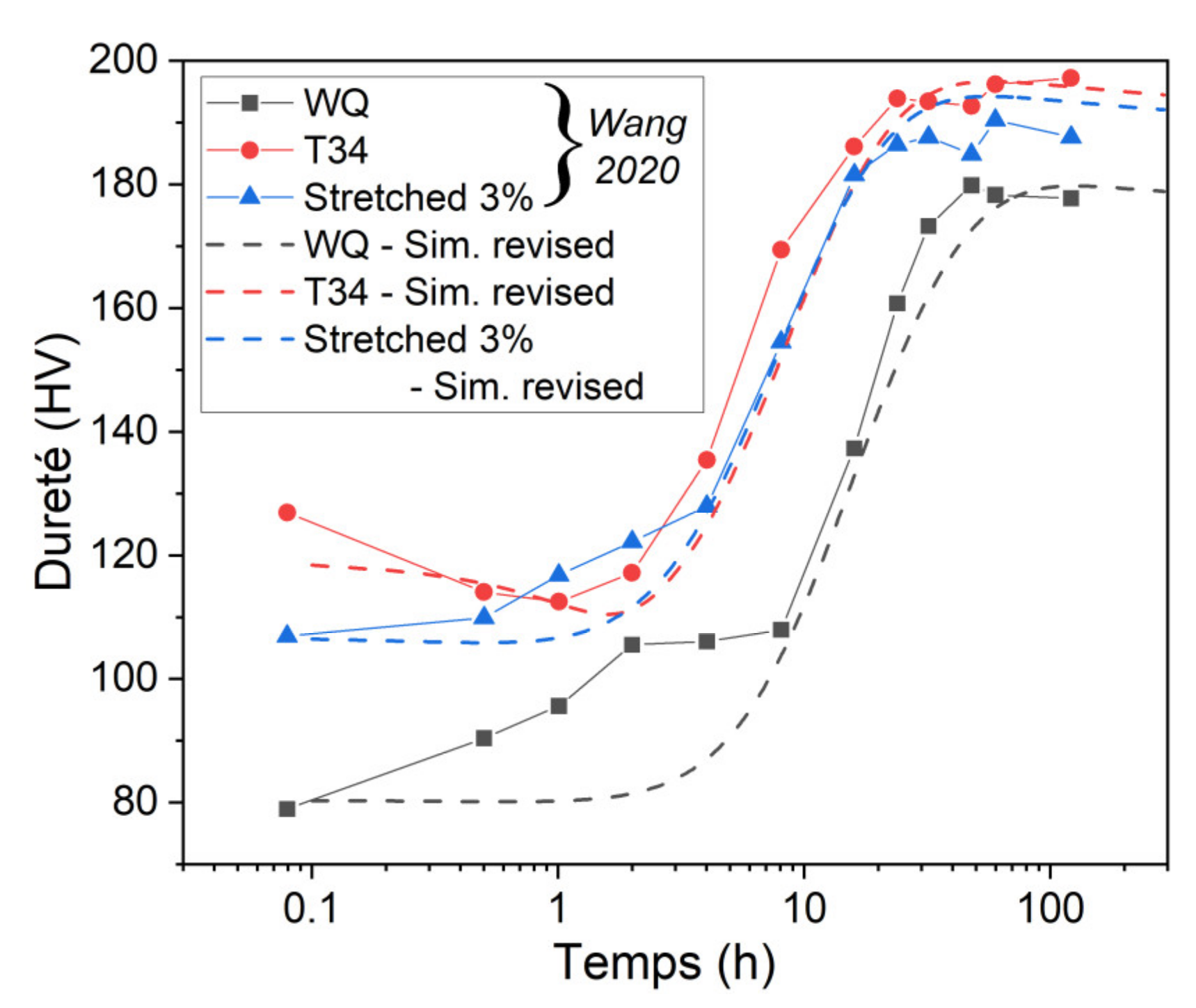
- The original constitutive model has been revised to predict the yield strength evolution during the aging of AA2050 with different initial tempers. With several modifications, the model provides proper simulations of the evolution of normalized volume fraction, normalized precipitate radius, and hardness for the different initial states.
- To simulate the evolution of the relative volume fraction of the T1 phase and hardness in the different zones of FSW samples during post-welding heat treatment, it was chosen to impose the initial state of the material across the weld joint.
- By using experimental data from the literature to impose the initial state, a good agreement concerning the evolution of relative volume fraction until 30 h at 155 °C was found. The simulated hardness was also found to be close to experimental data but was underestimated before and after this 30 h of heat treatment.
- Finally, the resistivity measurements were used to impose the initial state of the material on the different zones of FSW samples. Despite some observed discrepancies on the top and bottom of the weld joint, the revised numerical model captures the overall hardness profile after the post-weld heat treatment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, R.S.; Sidhar, H. Friction Stir Welding of 2xxx Aluminum Alloys Including Al-Li Alloys; Elsevier Science, Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar] [CrossRef]
- Ahmed, M.M.Z.; Wynne, B.P.; Rainforth, W.M.; Addison, A.; Martin, J.P.; Therasgill, P.L. Effect of tool geometry and heat input on the hardness, grain structure, and crystallographic texture of thick-section friction stir-welded aluminium. Metall. Mat. Trans. A 2019, 50, 271–284. [Google Scholar] [CrossRef]
- Hou, W.; Ding, Y.; Huang, G.; Huda, N.; Shah, L.H.; Piao, Z.; Shen, Y.; Shen, Z.; Gerlich, A. The role of pin eccentricity in friction stir welding of Al-Mg-Si alloy sheets: Microstructural evolution and mechanical properties. Int. J. Adv. Manuf. Technol. 2022, 121, 7661–7675. [Google Scholar] [CrossRef]
- Proton, V.; Alexis, J.; Andrieu, E.; Delfosse, J.; Deschamps, A.; De Geuser, F.; Lafont, M.C.; Blanc, C. The influence of artificial ageing on the corrosion behaviour of a 2050 aluminium–copper–lithium alloy. Corros. Sci. 2014, 80, 494–502. [Google Scholar] [CrossRef] [Green Version]
- Sidhar, H.; Mishra, R.S.; Reynolds, A.P.; Baumman, J.A. Impact of thermal management on post weld heat treatment efficacy in friction stir welded 2050-T3 alloy. J. Alloys Compd. 2017, 722, 330–338. [Google Scholar] [CrossRef]
- Malard, B.; De Geuser, F.; Deschamps, A. Microstructure distribution in an AA2050 T34 friction stir weld and its evolution during post-welding heat treatment. Acta Mater. 2015, 101, 90–100. [Google Scholar] [CrossRef] [Green Version]
- De Geuser, F.; Malard, B.; Deschamps, A. Microstructure mapping of a friction stir welded AA2050 Al–Li–Cu in the T8 state. Phil. Mag. 2014, 94, 1451–1462. [Google Scholar] [CrossRef]
- Yan, Y.; Peguet, L.; Gharbi, O.; Deschamps, A.; Hutchinson, C.R.; Kairy, S.K.; Birbilis, N. On the corrosion, electrochemistry and microstructure of Al-Cu-Li alloy AA2050 as a function of ageing. Materialia 2018, 1, 25–36. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Lin, J. Experimental investigation and modelling of yield strength and work hardening behaviour of artificially aged Al-Cu-Li alloy. Mater. Des. 2019, 183, 108121. [Google Scholar] [CrossRef]
- Avettand-Fenoel, M.-N.; Taillard, R. Heterogeneity of the Nugget Microstructure in a Thick 2050 Al Friction-Stirred Weld. Metall. Mat. Trans. A 2015, 46, 300–314. [Google Scholar] [CrossRef]
- Wang, X.; Shao, W.; Jiang, J.; Li, G.; Wang, X.; Zhen, L. Quantitative analysis of the influences of pre-treatments on the microstructure evolution and mechanical properties during artificial ageing of an Al–Cu–Li–Mg–Ag alloy. Mater. Sci. Eng. A 2020, 782, 139253. [Google Scholar] [CrossRef]
- Milkereit, B.; Kessler, O.; Schick, C. Recording of continuous cooling precipitation diagrams of aluminium alloys. Thermochim. Acta 2009, 492, 73–78. [Google Scholar] [CrossRef]
- Entringer, J.; Reimann, M.; Norman, A.; dos Santos, J.F. Influence of Cu/Li ratio on the microstructure evolution of bobbin-tool friction stir welded Al–Cu–Li alloys. J. Mater. Res. Technol. 2019, 8, 2031–2040. [Google Scholar] [CrossRef]
- Milagre, M.X.; Mogili, N.V.; Donatus, U.; Giorjao, R.A.R.; Terada, M.; Araujo, J.V.S.; Machado, C.S.C.; Costa, I. On the microstructure characterization of the AA2098-T351 alloy welded by FSW. Mater. Char. 2018, 140, 233–246. [Google Scholar] [CrossRef]
- Thompson, G.E.; Noble, B. Resistivity of Al-Cu-Li alloys during T1 (Al2CuLi) Precipitation. Metal Sci. J. 1973, 7, 32–35. [Google Scholar] [CrossRef]
- Yamamoto, A. Resistivity study of aging in Al-Li-Cu alloys. Mat. Trans. JIM 1995, 36, 1447. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.K.; Robinson, J.S. Effect of silver on precipitation response of Al–Li–Cu–Mg alloys. Mater. Sci. Technol. 2008, 24, 1369–1377. [Google Scholar] [CrossRef]
- Khan, A.K.; Robinson, J.S. Effect of cold compression on precipitation and conductivity of an Al–Li–Cu alloy. J. Microsc. 2008, 232, 534–538. [Google Scholar] [CrossRef]
- Buck, O.; Brasche, L.J.H.; Shield, J.E.; Bracci, D.J.; Jiles, D.C.; Chumbley, L.S. Nondestructive detection of the T1 phase in Al–Li alloy. Scripta Met. 1989, 23, 183–187. [Google Scholar] [CrossRef]
- Jiang, F.; Zhang, H. Non-isothermal precipitation kinetics and its effect on hot working behaviors of an Al–Zn–Mg–Cu alloy. J. Mater. Sci. 2018, 53, 2830–2843. [Google Scholar] [CrossRef]
- Ceresara, S.; Giarda, A.; Sanchéz, A. Annealing of vacancies and ageing in Al-Li alloys. Philo. Mag. 1977, 35, 97–110. [Google Scholar] [CrossRef]
- Noble, B.; Thompson, G.E. Precipitation Characteristics of Aluminium-Lithium Alloys. Metal Sci. J. 1971, 5, 114–120. [Google Scholar] [CrossRef]
- Kocks, U.F. Laws for Work-Hardening and Low-Temperature Creep. J. Eng. Mater. Technol. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Cassada, W.A.; Shiflet, G.J.; Starke, E.A. Mechanism of AI2CuLi (T1) Nucleation and Growth. Met. Trans. A 1991, 22, 287–297. [Google Scholar] [CrossRef]
- Shercliff, H.R.; Ashby, M.F. A process model for age hardening of aluminium alloys—I. The model. Acta Metal. Mater. 1990, 38, 1789–1802. [Google Scholar] [CrossRef]
- Proton, V. Caractérisation et Compréhension du Comportement en Corrosion de Structures en Alliage D’aluminium-cuivre-lithium 2050 Assemblées par Friction Stir Welding (FSW). Ph.D. Thesis, Institut National Polytechnique de Toulouse, Université de Toulouse, Toulouse, France, 2012. [Google Scholar]
- Chung, T.-F.; Yang, Y.-L.; Hsiao, C.-N.; Li, W.-C.; Huang, B.-M.; Tsao, C.-S.; Shi, Z.; Lin, J.; Fischione, P.E.; Ohmura, T.; et al. Morphological evolution of GP zones and nanometer-sized precipitates in the AA2050 aluminium alloy. Int. J. Lightweight Mater. Manuf. 2018, 1, 142–156. [Google Scholar] [CrossRef]
- Xu, X.; WU, G.; Zhang, L.; Tong, X.; Zhang, X.; Sun, J.; Li, L.; Xiong, X. Effects of heat treatment and pre-stretching on the mechanical properties and microstructure evolution of extruded 2050 Al–Cu–Li alloy. Mater. Sci. Eng. A 2022, 845, 143236. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Lin, J.; Yang, Y.L.; Rong, Q.; Huang, B.M.; Chung, T.F.; Tsao, C.S.; Yang, J.R.; Balint, D.S. A unified constitutive model for asymmetric tension and compression creep-ageing behaviour of naturally aged Al-Cu-Li alloy. Int. J. Plast. 2017, 89, 130–149. [Google Scholar] [CrossRef]




| Dislocations | Solid Solution | Clusters |
|---|---|---|
| Precipitates | Yield Strength | |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 0.1 | 0.045 | 8 × 10−5 | |||
| 6.5 | 120 | 0.3 | |||
| 100 | 0.185 | 0.05 | |||
| 0.05 | 52 | 36.3 | |||
| 0.316 | 0.238 | 0.06 | |||
| 1.28 | 1 | 9.5 | |||
| 0.08 | 1.05 | 0.22 |
| Normalized Variable | T34 | Stretched 3% | WQ |
|---|---|---|---|
| Cluster radius | 1 | 0 | 0 |
| Cluster volume fraction | 0.032 | 0 | 0 |
| Dislocation density | 1 | 1 | 0 |
| Solid solution concentration | 0.978 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galisson, S.; Carron, D.; Le Masson, P.; Stamoulis, G.; Feulvarch, E.; Surdon, G. Modeling Hardness Evolution during the Post-Welding Heat Treatment of a Friction Stir Welded 2050-T34 Alloy. Crystals 2022, 12, 1543. https://doi.org/10.3390/cryst12111543
Galisson S, Carron D, Le Masson P, Stamoulis G, Feulvarch E, Surdon G. Modeling Hardness Evolution during the Post-Welding Heat Treatment of a Friction Stir Welded 2050-T34 Alloy. Crystals. 2022; 12(11):1543. https://doi.org/10.3390/cryst12111543
Chicago/Turabian StyleGalisson, Sébastien, Denis Carron, Philippe Le Masson, Georgios Stamoulis, Eric Feulvarch, and Gilles Surdon. 2022. "Modeling Hardness Evolution during the Post-Welding Heat Treatment of a Friction Stir Welded 2050-T34 Alloy" Crystals 12, no. 11: 1543. https://doi.org/10.3390/cryst12111543





