Study of the Thermal Properties and Lattice Disorder Effects in CdTe–Based Crystals: CdBeTe, CdMnTe, and CdZnTe
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Thermal Parameters Determination
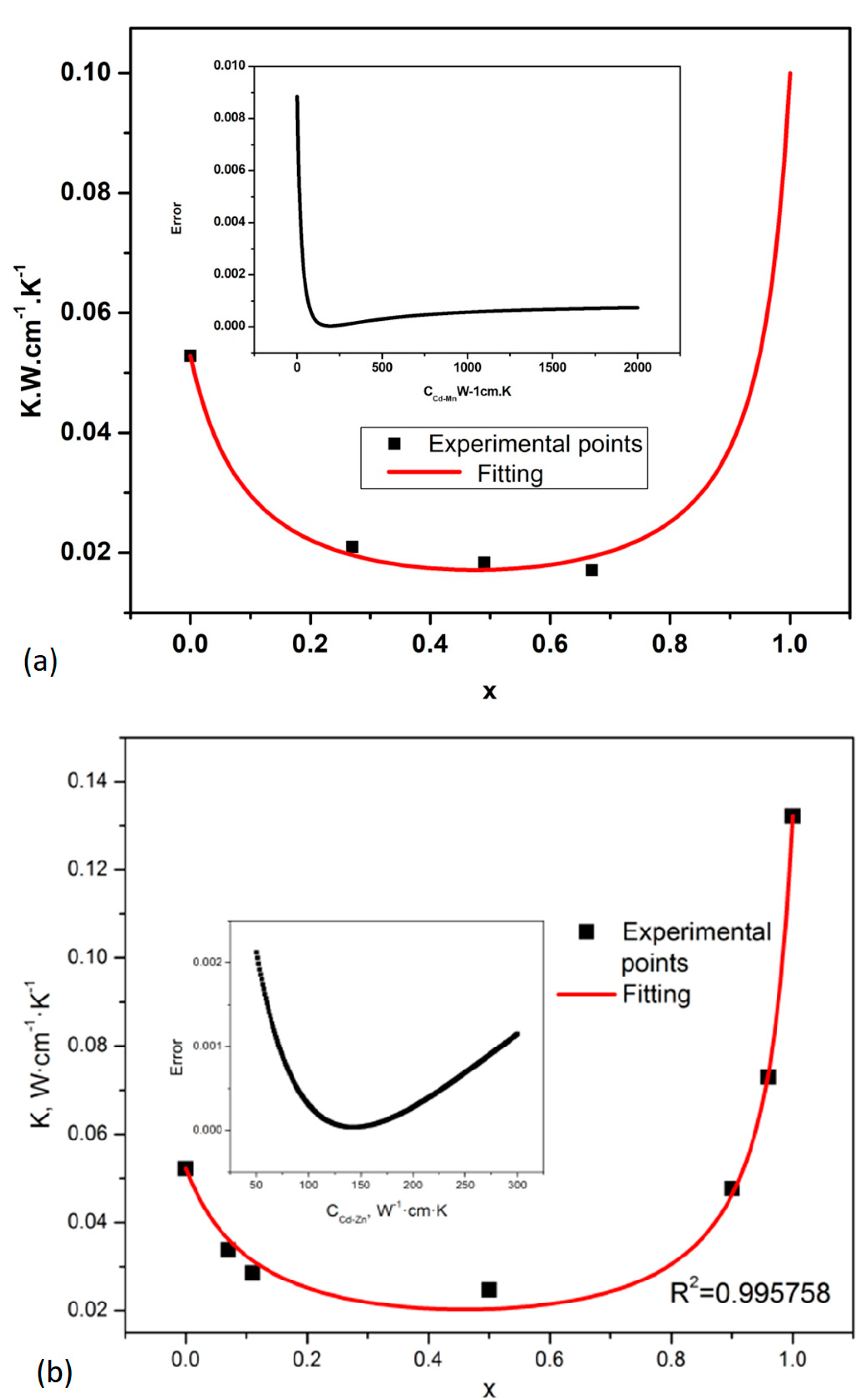
3.2. Thermal Resistivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, X.; Roushan, M.; Zhang, R.; Peng, J.; Zeng, H.; Li, J. Tuning and Enhancing White Light Emission of II–VI Based Inorganic–Organic Hybrid Semiconductors as Single–Phased Phosphors. Chem. Mater. 2012, 24, 1710–1717. [Google Scholar] [CrossRef]
- Ehinger, M.; Koch, C.; Korn, M.; Albert, D.; Nürnberger, J.; Hock, V.; Faschinger, W.; Landwehr, G. High quantum efficiency II–VI photodetectors for the blue and blue–violet spectral range. Appl. Phys. Lett. 1998, 73, 3562. [Google Scholar] [CrossRef]
- Ishibashi, A. Blue–Green Laser Diodes. IEEE J. Sel. Top. Quantum Electron. 1995, 1, 741. [Google Scholar] [CrossRef]
- Isshiki, M.; Wang, J. Wide–Bandgap II–VI Semiconductors: Growth and Properties. In Springer Handbook of Electronic and Photonic Materials; Springer Handbooks; Kasap, S., Capper, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 365–384. [Google Scholar]
- Zyoud, S.H.; Zyoud, A.H.; Ahmed, N.M.; Abdelkader, A.F.I. Numerical Modelling Analysis for Carrier Concentration Level Optimization of CdTe Heterojunction Thin Film–Based Solar Cell with Different Non–Toxic Metal Chalcogenide Buffer Layers Replacements: Using SCAPS–1D Software. Crystals 2021, 11, 1454. [Google Scholar] [CrossRef]
- Lin, Y.; Qin, Q.; Wang, X.; Chen, J.; Li, L.; Jiang, J.; He, Y.; Wang, X.; Zhao, P.; Yuan, S. Effect of Annealing on the Structure of Composite Passivation Films Prepared by Magnetron Sputtering Deposition on the Surface of HgCdTe. Crystals 2022, 12, 983. [Google Scholar] [CrossRef]
- Szeles, C.; Soldner, S.A.; Vydrin, S.; Graves, J.; Bale, D.S. CdZnTe Semiconductor Detectors for Spectroscopic X–ray Imaging. IEEE Trans. Nucl. Sci. 2008, 55, 572. [Google Scholar] [CrossRef]
- Park, S.; Kim, H. Growth and Fabrication Method of CdTe and Its Performance As a Radiation. J. Korean Phys. Soc. 2015, 66, 27–30. [Google Scholar] [CrossRef]
- Roy, U.N.; Bolotnikov, A.E.; Camarda, G.S.; Cui, Y.; Hossain, A.; Lee, K.; Lee, W.; Tappero, R.; Yang, G.; Gul, R. High compositional homogeneity of CdTexSe1−x crystals grown by the Bridgman method. APL Mater. 2015, 3, 026102. [Google Scholar] [CrossRef]
- Yim, W.M.; Dismukes, J.P.; Stofko, E.J.; Paff, R.J. Synthesis and some properties of BeTe, BeSe and BeS. J. Phys. Chem. Solids 1972, 33, 501. [Google Scholar] [CrossRef]
- Waag, A.; Fischer, F.; Lugauer, H.J.; Litz, T.; Laubender, J.; Lunz, U.; Zehnder, U.; Ossau, W.; Gerhardt, T.; Landwehr, G. Molecular–beam epitaxy of beryllium chalcogenide based thin films and quantum well structures. J. Appl. Phys. 1996, 792, 792–796. [Google Scholar] [CrossRef]
- Nagelstraßer, M.; Dröge, H.; Steinrück, H.P.; Fischer, F.; Litz, T.; Waag, A.; Landwehr, G.; Fleszar, A.; Hanke, W. Band structure of BeTe: A combined experimental and theoretical study. Phys. Rev. B 1998, 58, 10394. [Google Scholar] [CrossRef]
- Strzałkowski, K. The composition effect on the thermal and optical properties across CdZnTe crystals. J. Phys. D Appl. Phys. 2016, 49, 435106. [Google Scholar] [CrossRef]
- Theurich, G.; Hill, N.A. First–principles approach to spin–orbit coupling in dilute magnetic semiconductors. Phys. Rev. B 2002, 66, 115208. [Google Scholar] [CrossRef]
- Strzałkowski, K.; Firszt, F.; Marasek, A. Thermal Diffusivity, Effusivity, and Conductivity of CdMnTe Mixed Crystals. Int. J. Thermophys. 2014, 35, 2140–2149. [Google Scholar] [CrossRef][Green Version]
- Dong, J.; Sun, F.; Tang, H.; Hayashi, K.; Li, H.; Shang, P.; Miyazaki, Y.; Li, J. Reducing Lattice Thermal Conductivity of MnTe by Se Alloying toward High Thermoelectric Performance. ACS Appl. Mater. Interfaces 2019, 11, 28221–28227. [Google Scholar] [CrossRef]
- Yang, G.; Gu, G.; Bolotnikov, A.E.; Cui, Y.; Camarda, G.S.; Hossain, A. Structural, electrical, and optical properties of CdMnTe crystals grown by modified floating–zone technique. Electr. Mater. Lett. 2015, 11, 500–504. [Google Scholar] [CrossRef]
- Zaiour, A.; Charara, J.; Hamdoun, B.; Hamié, A.; Hage–ali, M. Electrical Properties Study of Three Highly Purified CdTe Ingots. Phys. Procedia. 2014, 55, 470–475. [Google Scholar] [CrossRef][Green Version]
- Kamieniecki, E. Effect of charge trapping on effective carrier lifetime in compoundsemiconductors: High resistivity CdZnTe. J. Appl. Phys. 2014, 116, 193702. [Google Scholar] [CrossRef]
- Chirtoc, M.; Mihilescu, G. Theory of the photopyroelectric method for investigation of optical and thermal materials properties. Phys. Rev. B 1989, 40, 9606–9617. [Google Scholar] [CrossRef]
- Maliński, M.; Chrobak, Ł. Investigations and modeling aspects of the influence of the high energy and high dose implantation on the optical and transport parameters of implanted layers in silicon. Phys. B Condens. Matter 2020, 578, 411851. [Google Scholar] [CrossRef]
- Chrobak, Ł.; Korte, D.; Budasheva, H.; Maliński, M.; Rodič, P.; Milošev, I.; Janta–Lipińska, S. Investigations of the Thermal Parameters of Hybrid Sol–Gel Coatings Using Nondestructive Photothermal Techniques. Energies 2022, 15, 4122. [Google Scholar] [CrossRef]
- Bale, D.S.; Szeles, C. Electron transport and charge induction in cadmium zinc telluride detectors with space charge build up under intense x–ray irradiation. J. Appl. Phys. 2010, 107, 114512. [Google Scholar] [CrossRef]
- Adachi, S. Lattice thermal conductivity of group–IV and III–V semiconductor alloys. J. Appl. Phys. 2007, 102, 063502. [Google Scholar] [CrossRef]
- Firszt, F.; Łegowski, S.; Meczynska, H.; Szatkowski, J.; Paszkowicz, W.; Godwod, K. Growth and characterisation of Zn1−xBexSe mixed crystals. J. Cryst. Growth 1998, 184/185, 1335. [Google Scholar] [CrossRef]
- Strzalkowski, K.; Dadarlat, D.; Streza, M.; Firszt, F. On the optimization of experimental parameters in photopyroelectric investigation of thermal diffusivity of solids. Thermochim. Acta 2015, 614, 232–238. [Google Scholar] [CrossRef]
- Strzałkowski, K. Effect of lattice disorder on the thermal conductivity of ZnBeSe, ZnMgSe and ZnBeMgSe crystals. Mater. Chem. Phys. 2015, 163, 453–459. [Google Scholar] [CrossRef]
- Degheidy, A.R.; Elkenany, E.B.; Madkour, M.A.K.; Ahmed AbuAli, M. Temperature dependence of phonons and related crystal properties in InAs, InP and InSb zinc–blende binary compounds. Comput. Condens. Matter 2018, 16, e00308. [Google Scholar] [CrossRef]
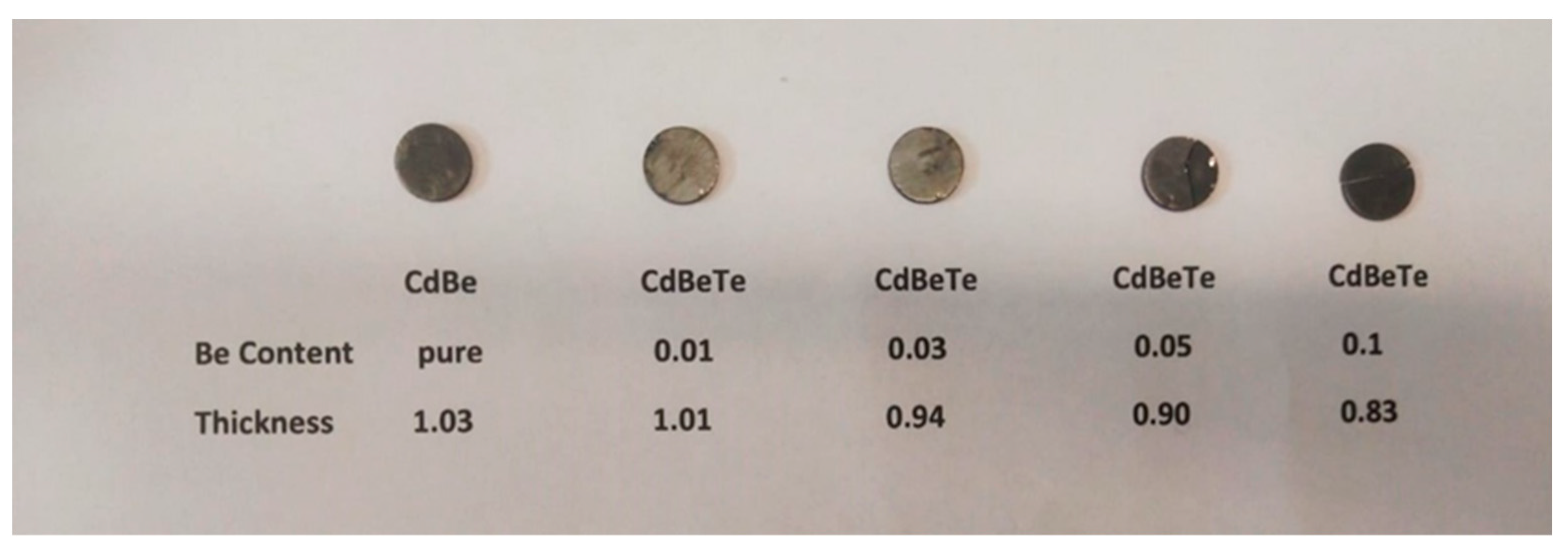

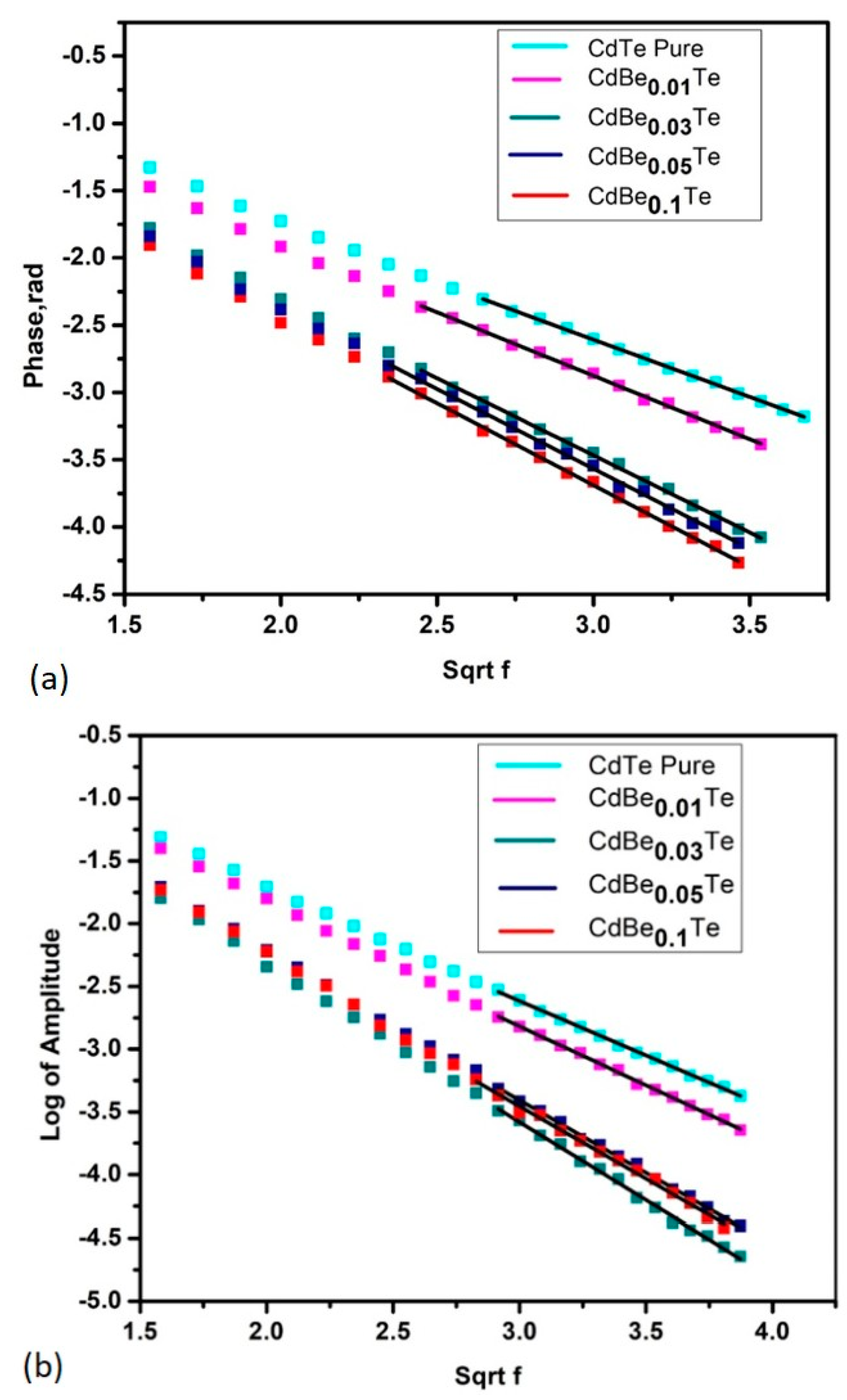
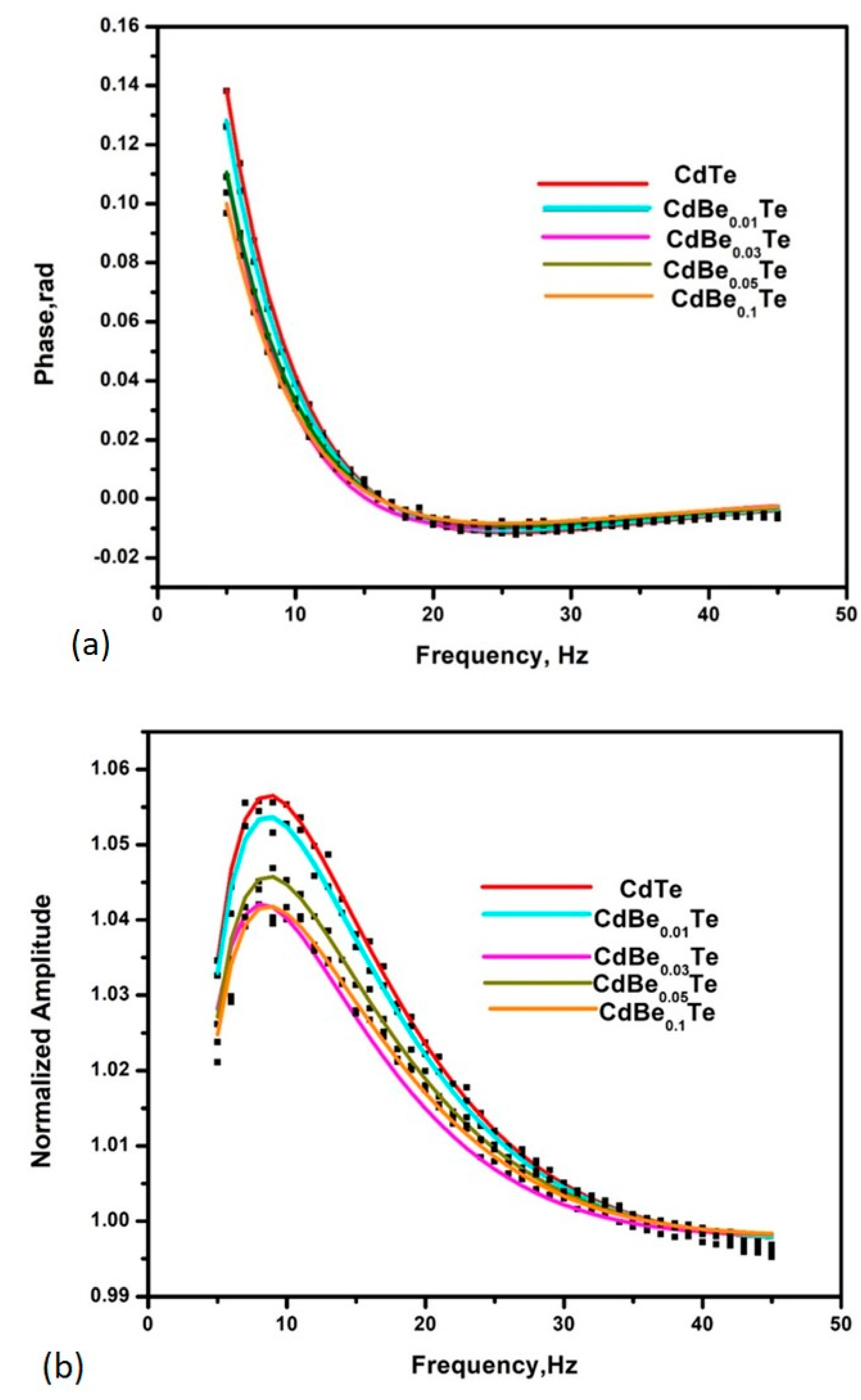

| Crystal Composition x | Thermal Diffusivity (m2·s−1) ×10−6 | Thermal Effusivity (W·s1/2·m−2·K−1) | R2 (Effusivity from the Phase) | Thermal Conductivity (W·m−1·K−1) |
|---|---|---|---|---|
| 0 | 4.629 ± 0.019 | 2656.0 ± 53.5 | 0.998 | 5.714 ± 0.0.127 |
| 0.01 | 3.64 ± 0.045 | 2323.8 ± 36.4 | 0.995 | 4.437 ± 0.097 |
| 0.03 | 2.112 ± 0.109 | 1725.8 ± 8.7 | 0.982 | 2.516 ± 0.078 |
| 0.05 | 1.946 ± 0.006 | 1730.0 ± 28.6 | 0.990 | 2.413 ± 0.043 |
| 0.10 | 1.592 ± 0.030 | 1613.8 ± 19.3 | 0.977 | 1.998 ± 0.043 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, D.; Strzałkowski, K.; Abouais, A.; Alaoui-Belghiti, A. Study of the Thermal Properties and Lattice Disorder Effects in CdTe–Based Crystals: CdBeTe, CdMnTe, and CdZnTe. Crystals 2022, 12, 1555. https://doi.org/10.3390/cryst12111555
Singh D, Strzałkowski K, Abouais A, Alaoui-Belghiti A. Study of the Thermal Properties and Lattice Disorder Effects in CdTe–Based Crystals: CdBeTe, CdMnTe, and CdZnTe. Crystals. 2022; 12(11):1555. https://doi.org/10.3390/cryst12111555
Chicago/Turabian StyleSingh, Diksha, Karol Strzałkowski, Ali Abouais, and Amine Alaoui-Belghiti. 2022. "Study of the Thermal Properties and Lattice Disorder Effects in CdTe–Based Crystals: CdBeTe, CdMnTe, and CdZnTe" Crystals 12, no. 11: 1555. https://doi.org/10.3390/cryst12111555
APA StyleSingh, D., Strzałkowski, K., Abouais, A., & Alaoui-Belghiti, A. (2022). Study of the Thermal Properties and Lattice Disorder Effects in CdTe–Based Crystals: CdBeTe, CdMnTe, and CdZnTe. Crystals, 12(11), 1555. https://doi.org/10.3390/cryst12111555








