The Correspondence Theory and Its Application to NiTi Shape Memory Alloys
Abstract
:1. Introduction
2. Toward a Change of Paradigm to Understand the Crystallography of Martensite?
2.1. The Phenomenological Theory of Martensite Crystallography
2.2. The Hidden Algebraic Structure of Variants
3. Crystallography for Phase Transformations
3.1. Directions and Planes
3.2. The Transformation Matrices
3.3. The Algebraic Structure of the Variants with Their Operators
4. The Main Principles of the Correspondence Theory
4.1. Compatibility by Symmetry Preservation
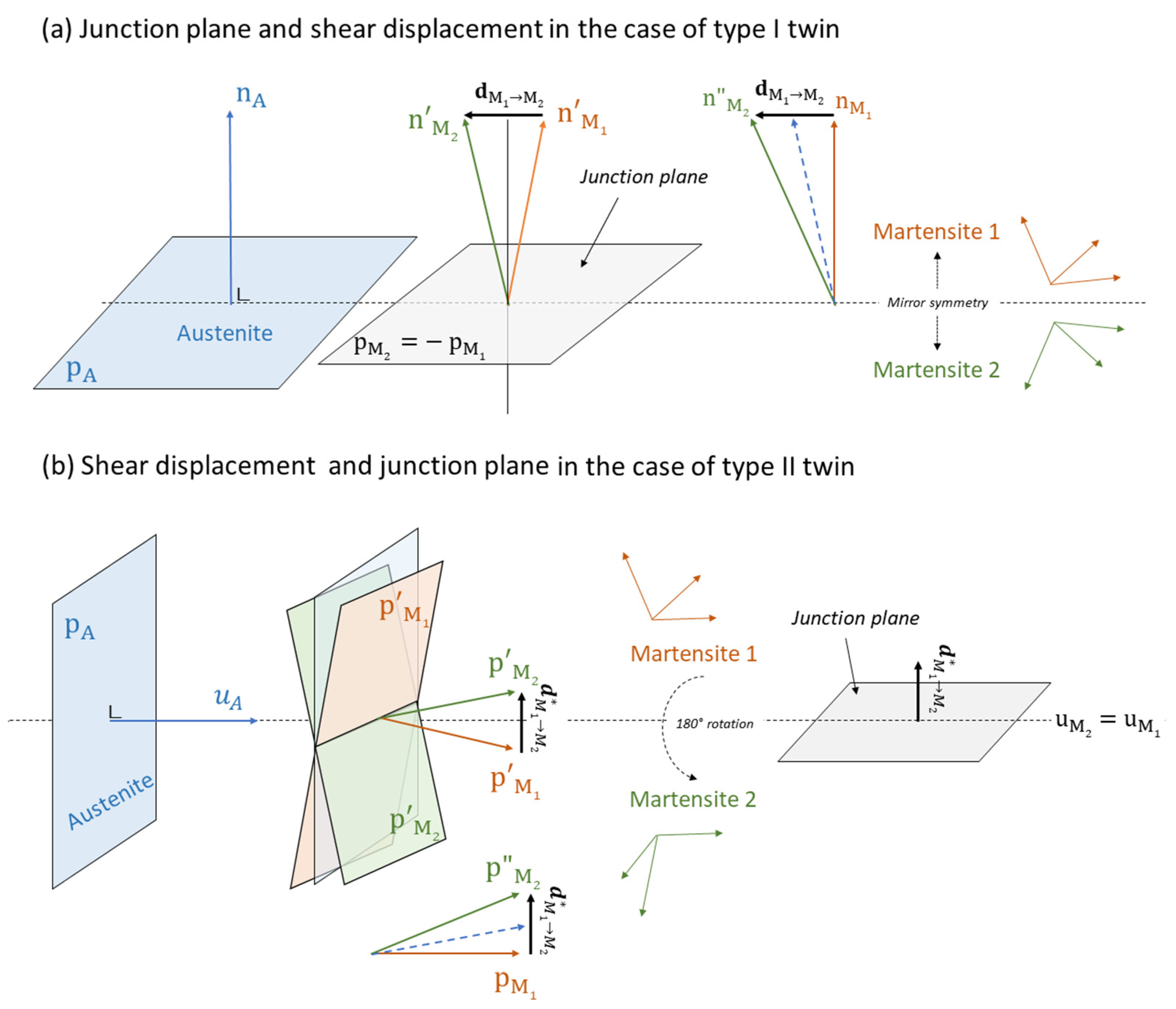
4.2. Junction Planes for Variants Linked by a Parent Reflection Symmetry
4.3. Junction Planes for Variants Linked by a Parent 180° Rotation Symmetry
4.4. Junction Planes for Variants Not Linked by a Two-Fold Parent Symmetry
5. Application of the Correspondence Theory to the Junction Planes in NiTi Alloys
5.1. The Variants and the Operators
5.2. Prediction of the Junction Planes and Closing-Gap ORs
5.3. Comparison with PTMC
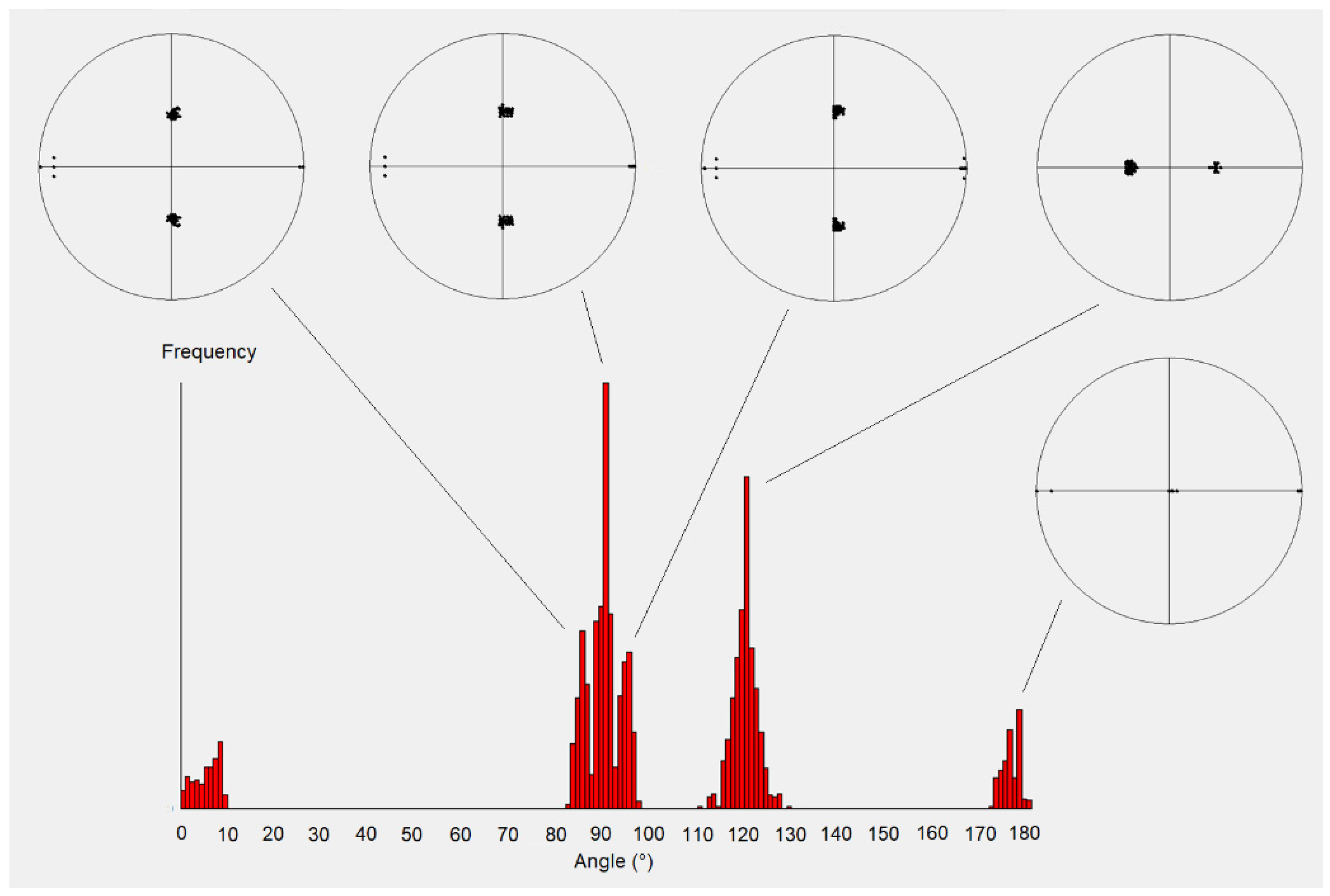
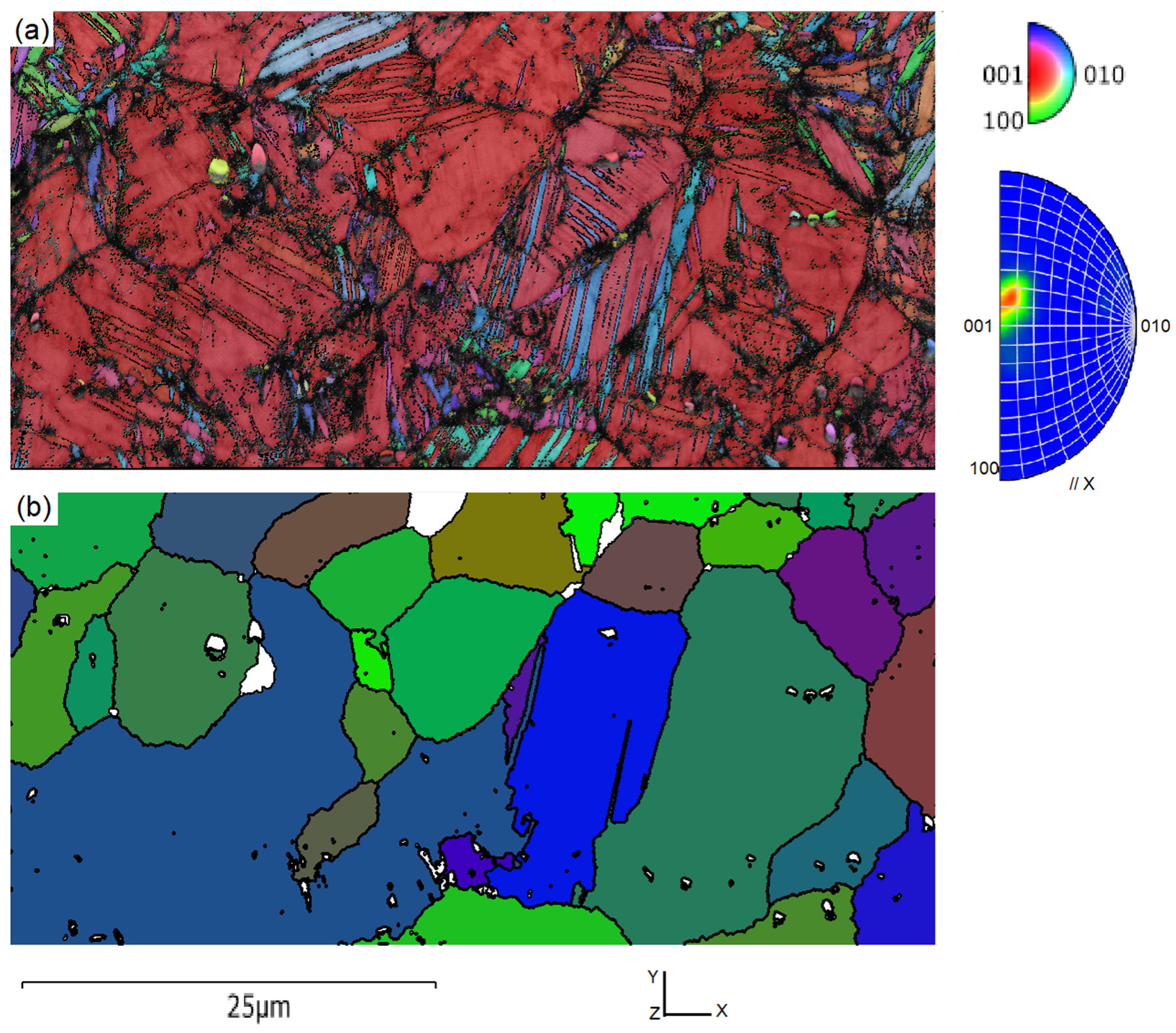
5.4. TKD Observations of the Junction Planes in NiTi Alloys
6. Discussion
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. How to Cook Cosets and Double Cosets
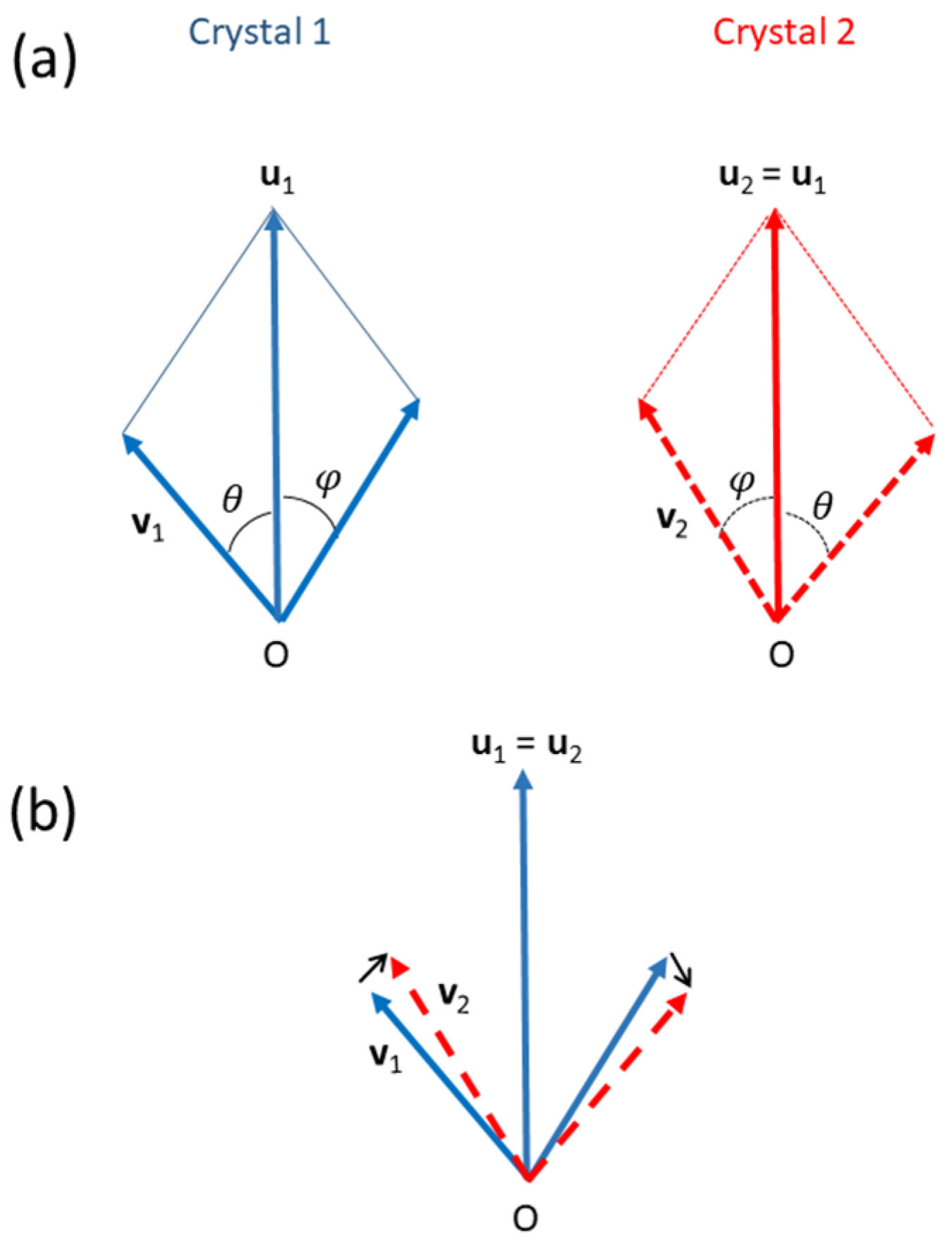
Appendix B. Illustration of the Correspondence Theory with a Simple 2D Example
| Correspondence | Orientation | Distortion |
|---|---|---|
| Intersection subgroups | ||
| Variants (from simple cosets) | ||
| Operators (from double cosets) | ||
| With Their Geometrical Elements | Operators as Set of Equivalent Arrows (Source Variant → Target Variant) | |||
|---|---|---|---|---|
| , | ||||
| , |
Appendix C. Additional TKD Map and Junction Planes


References
- Buehler, W.J.; Gilfrich, J.W.; Wiley, R.C. Effect of Low-Temperature Phase Changes on the Mechanical Properties of Alloys near Composition TiNi. J. Appl. Phys. 1963, 34, 1473–1477. [Google Scholar] [CrossRef]
- Bhattacharya, K. Microstructure of Martensite. In Why It Forms and How It Gives Rise to the Shape-Memory Effect, 1st ed.; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mat. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Chowdhury, P.; Sehitoglu, H. Deformation physics of shape memory alloys—Fundamentals at atomistic frontier. Prog. Mater. Sci. 2017, 88, 49–88. [Google Scholar] [CrossRef]
- Otsuka, K.; Sawamura, T.; Shimizu, K. Crystal structure and internal defects of equiatomic TiNi martensite. Phys. Stat. Sol. 1971, 5, 457–470. [Google Scholar] [CrossRef]
- Knowles, K.M.; Smith, D.A. The crystallography of the martensitic transformation in equiatomic nickel-titanium. Acta Metall. 1981, 29, 101–110. [Google Scholar] [CrossRef]
- Nishida, M.; Nishiura, T.; Kawano, H.; Inamura, T. Self-accommodation of B19’ martensite in Ti-Ni shape memory alloys-Part I. Morphological and crystallographic studies of the variant selection rules. Philos. Mag. 2012, 92, 2215–2223. [Google Scholar] [CrossRef]
- Nishida, M.; Okunishi, E.; Nishiura, T.; Kawano, H.; Inamura, T.; Li, S.; Hara, T. Self-accommodation of B19’ martensite in Ti-Ni shape memory alloys-Part II. Characteristic interface structures between habit plane variants. Philos. Mag. 2012, 92, 2234–2246. [Google Scholar] [CrossRef]
- Šittner, P.; Molnárová, O.; Kadeřávek, L.; Tyc, O.; Heller, L. Deformation twinning in martensite affecting functional behavior of NiTi shape memory alloys. Materialia 2020, 9, 100506. [Google Scholar] [CrossRef]
- Waitz, T. The self-accommodated morphology of martensite in nanocrystalline NiTi shape memory alloys. Acta Mater. 2005, 53, 2273–2283. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, Z.L. Twinning and detwinning of <011> type II twin in shape memory alloy. Acta Mater. 2003, 51, 5529–5543. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, Z.L. The rational Nature of Type II Twin in NiTi Shape Memory Alloy. J. Intell. Mater. Struct. 2006, 17, 1083–1090. [Google Scholar] [CrossRef]
- Ye, J.; Mishra, R.K.; Pelton, A.R.; Minor, A.M. Direct observation of the NiTi martensitic phase transformation in nanoscale volumes. Acta Mater. 2010, 58, 490–498. [Google Scholar] [CrossRef]
- Ii, S.; Yamauchi, K.; Maruhashi, Y.; Nishida, M. Direct evidence of correlation between {20-1}B19′ and {114}B2 deformation twins in Ti–Ni shape memory alloy. Scr. Mater. 2003, 49, 723–727. [Google Scholar] [CrossRef]
- Šittner, P.; Sedlák, P.; Seiner, H.; Sedmák, P.; Pilch, J.; Delville, R.; Heller, L.; Kadeřávek, L. On the coupling between martensitic transformation and plasticity in NiTi: Experiments and continuum based modelling. Prog. Mater. Sci. 2018, 98, 249–298. [Google Scholar] [CrossRef]
- Laplanche, G.; Birk, T.; Schneider, S.; Frenzel, J.; Eggeler, G. Effect of temperature and texture on the reorientation of martensite variants in NiTi shape memory alloys. Acta Mater. 2017, 127, 143–152. [Google Scholar] [CrossRef]
- Xiao, Y.; Zeng, P.; Lei, L.; Zhang, Y. In situ observation on temperature dependence of martensitic transformation and plastic deformation in superelastic NiTi shape memory alloy. Mater. Des. 2017, 134, 111–120. [Google Scholar] [CrossRef]
- Hsu, W.-N.; Polatidis, E.; Šmíd, M.; Casati, N.; Van Petegem, S.; Van Swygenhoven, H. Load path change on superelastic NiTi alloys: In situ synchrotron XRD and SEM DIC. Acta Mater. 2018, 144, 874–883. [Google Scholar] [CrossRef]
- Hsu, W.-N.; Polatidis, E.; Šmíd, M.; Van Petegem, S.; Casati, N.; Van Swygenhoven, H. Deformation and degradation of superelastic NiTi under multiaxial loading. Acta Mater. 2019, 167, 149–158. [Google Scholar] [CrossRef]
- Polatidis, E.; Šmíd, M.; Kuběna, I.; Hsu, W.-N.; Laplanche, G.; Van Swygenhoven, H. Deformation mechanisms in a superelastic NiTi alloy: An in-situ high resolution digital image correlation study. Mater. Des. 2020, 191, 108622. [Google Scholar] [CrossRef]
- Keller, R.R.; Geiss, R.H. Transmission EBSD from 10 nm domains in a scanning electron microscope. J. Microsc. 2012, 245, 245–251. [Google Scholar] [CrossRef]
- Trimby, T. Orientation mapping of nanostructured materials using transmission Kikuchi diffraction in the scanning electron microscope. Ultramicrosc 2012, 120, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S. Feature of Transmission EBSD and its application. JOM 2013, 65, 1254–1263. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. What EBSD and TKD tell us about the crystallography of the martensitic B2-B19′ transformation in NiTi shape memory alloys. Crystals 2020, 10, 562. [Google Scholar] [CrossRef]
- Bowles, J.S.; Mackenzie, J.K. The crystallography of martensitic transformations I. Acta Metall. 1954, 2, 129–137. [Google Scholar] [CrossRef]
- Bowles, J.S.; Mackenzie, J.K. The crystallography of martensitic transformations II. Acta Metall. 1954, 2, 138–147. [Google Scholar] [CrossRef]
- Wechsler, M.S.; Liebermann, D.S.; Read, T.A. On the theory of the formation of martensite. Trans. AIME 1953, 197, 1503–1515. [Google Scholar]
- Christian, J. Applications of the phenomenological theories of martensite I–II. J. Inst. Met. 1956, 84, 386–394. [Google Scholar]
- Bain, E.C.; Dunkirk, N. The nature of martensite. Trans. AIME 1924, 70, 25–47. [Google Scholar]
- Bhadeshia, H.K.D.H. Worked Examples in the Geometry of Crystals, 2nd ed.; The Institute of Metals: London, UK, 1987. [Google Scholar]
- Wayman, C.M. Shear transformations and microstructures. Metallography 1975, 8, 105–130, republished in Mater. Charact. 1997, 39, 235–260. [Google Scholar] [CrossRef]
- Duparc, O.B.M.H. A review of some elements for the history of mechanical twinning centred on its German origins until Otto Mügge’s K1 and K2 invariant plane notation. J. Mater. Sci. 2016, 52, 4182–4196. [Google Scholar] [CrossRef]
- Mügge, O. Ueber Homogene Deformationen (einfache Schiebungen) an den Triklinen Doppelsalzen BaCdCl4.4aq., Neues Jahrbuch für Mineralogie, Geologie und Palaeontologie Beilage-Band. 1889. Available online: https://www.phase-trans.msm.cam.ac.uk/2001/geometry2/Geometry.pdf (accessed on 22 November 2021).
- Kihô, H. The Crystallographic Aspect of the Mechanical Twinning in Metals. J. Phys. Soc. Jpn. 1954, 9, 739–747. [Google Scholar] [CrossRef]
- Jaswon, M.A.; Dove, D.B. The Crystallography of Deformation Twinning. Acta Cryst. 1960, 13, 232–240. [Google Scholar] [CrossRef] [Green Version]
- Bilby, B.A.; Crocker, A.G. The Theory of the Crystallography of Deformation Twinning. Proc. R. Soc. Lond. Ser. A 1965, 288, 240–255. [Google Scholar]
- Bevis, M.; Crocker, A.G. Twinning Shears in Lattices. Proc. R. Soc. Lond. Ser. A 1968, 304, 123–134. [Google Scholar]
- Cahn, R.W. Twinned Crystals. Adv. Phys. 1954, 3, 363–445. [Google Scholar] [CrossRef]
- Christian, J.W.; Mahajan, S. Deformation Twinning. Prog. Mater. Sci. 1995, 39, 1–157. [Google Scholar] [CrossRef]
- Gupta, S.P.; Johnson, A.A. Morphology and crystallography of beta’ martensite in TiNi alloys. Trans. Jpn. Inst. Metals. 1973, 14, 292–302. [Google Scholar] [CrossRef] [Green Version]
- Sinclair, R. Origin of stacking faults in NiTi martensite. AIP Conf. 1979, 53, 269. [Google Scholar]
- Nishida, M.; Yamauchi, K.; Itai, I.; Ohgi, H.; Chiba, A. High resolution electron microscopy studies of twin boundary structure in B19’ martensite in the Ti-Ni shape memory alloy. Acta Metall. Mater. 1995, 43, 1229–1234. [Google Scholar] [CrossRef]
- Mohammed, A.S.K.; Sehitoglu, H. Modeling the interface structure of type II boundary in B19’ NiTi from an atomistic and topological standpoint. Acta Mater. 2020, 183, 93–109. [Google Scholar] [CrossRef]
- Miyazaki, S.; Kimura, S.; Otsuka, K.; Suzuki, Y. The habit plane and transformation strains associated with martensitic transformation in Ti-Ni single crystals. Scr. Metall. 1984, 18, 883–888. [Google Scholar] [CrossRef]
- Miyazaki, S.; Otsuka, K.; Wayman, C.M. The shape memory mechanism associated with the martensitic transformation in Ti-Ni alloys-I. Self-accommodation. Acta Metall. 1989, 37, 1873–1884. [Google Scholar] [CrossRef]
- Ball, J.M.; James, R.D. Finite phase mixtures as minimizers of energy. Arch. Ration. Mech. Anal. 1987, 100, 13–52. [Google Scholar] [CrossRef]
- Pitteri, M.; Zanzotto, G. Generic and non-generic cubic-to-monoclinic transitions and their twins. Acta Mater. 1998, 46, 225–237. [Google Scholar] [CrossRef]
- Pitteri, M.; Zanzotto, G. Continuum Models for Phase Transitions and Twinning in Crystals; Chapman & Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hane, K.F.; Shield, T.W. Microstructure in the cubic to monoclinic transition in titanium-nickel shape memory alloys. Acta Mater. 1999, 47, 2603–2617. [Google Scholar] [CrossRef]
- Inamura, T.; Nishiura, T.; Kawano, H.; Hosoda, H.; Nishida, M. Self-accommodation of B19’ martensite in Ti-Ni shape memory alloys-Part III. Analysis of habit plane variant clusters by the geometrically nonlinear theory. Philos. Mag. 2012, 92, 2247–2263. [Google Scholar] [CrossRef]
- Gu, H.; Bumke, L.; Chluba, C.; Quandt, E.; James, R.D. Phase engineering and supercompatibility of shape memory alloys. Mater. Todays 2018, 21, 265–277. [Google Scholar] [CrossRef]
- Song, Y.; Chen, X.; Dabade, V.; Shield, T.W.; James, R.D. Enhanced reversibility and unusual microstructure of a phase-transforming material. Nature 2013, 502, 85–88. [Google Scholar] [CrossRef]
- Chen, X.; Liu, T.; Li, R.; Liu, J.; Zhao, Y. Molecular dynamics simulation on the shape memory effect and superelasticity in NiTi shape memory alloy. Comput. Mater. Sci. 2018, 146, 61–69. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; An, Q. Structural origin of reversible martensitic transformation and reversible twinning in NiTi shape memory alloy. Acta Mater. 2020, 199, 240–252. [Google Scholar] [CrossRef]
- Janovec, V. Group analysis of domains and domain pairs. Czech. J. Phys. B 1972, 22, 975–994. [Google Scholar] [CrossRef]
- Janovec, V.; Hahn, T.; Klapper, H. International Tables for Crystallography; Authier, A., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; Volume D, pp. 377–391. [Google Scholar]
- Cayron, C. Groupoid of orientational variants. Acta Cryst. 2006, 62, 21–40. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. GenOVa: A computer program to generate orientational variants. J. Appl. Cryst. 2007, 40, 1179–1182. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Cryst. 2007, 40, 1183–1188. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C.; Barcelo, F.; de Carlan, Y. The mechanisms of the fcc–bcc martensitic transformation revealed by pole figures. Acta Mater. 2010, 58, 1395–1402. [Google Scholar] [CrossRef]
- Cayron, C. One-step model of the face-centred-cubic to body-centred-cubic martensitic transformation. Acta Cryst. 2013, 69, 498–509. [Google Scholar] [CrossRef]
- Cayron, C. Continuous atomic displacements and lattice distortion during fcc–bcc martensitic transformation. Acta Mater. 2015, 96, 189–202. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. Angular distortive matrices of phase transitions in the fcc-bcc-hcp system. Acta Mater. 2016, 111, 417–441. [Google Scholar] [CrossRef] [Green Version]
- Baur, A.P.; Cayron, C.; Logé, R. {225}γ habit planes in martensitic steels: From the PTMC to a continuous model. Sci. Rep. 2017, 7, 40938. [Google Scholar] [CrossRef] [PubMed]
- Baur, A.P.; Cayron, C.; Logé, R. Variant selection in surface martensite. J. Appl. Cryst. 2017, 50, 1646–1652. [Google Scholar] [CrossRef] [Green Version]
- Baur, A.P.; Cayron, C.; Logé, R. Variant selection in Fe-2Ni-1.8C under bending. Crystals 2018, 8, 474. [Google Scholar] [CrossRef] [Green Version]
- Larcher, M.N.D.; Cayron, C.; Blatter, A.; Soulignac, R.; Logé, R. EBSD Study of Variant Selection during Ordering Phase Transformation in L10-type Red Gold Alloy. J. Appl. Cryst. 2019, 52, 1202–1213. [Google Scholar] [CrossRef]
- Larcher, M.N.D.; Cayron, C.; Blatter, A.; Soulignac, R.; Logé, R. The thermally activated distortion with amplification effect and related variant selection in red gold alloys. Acta Mater. 2020, 198, 242–256. [Google Scholar] [CrossRef]
- Cayron, C. The transformation matrices (Distortion, orientation, correspondence), their continuous forms and their variants. Acta Cryst. 2019, 75, 411–437. [Google Scholar]
- Jaswon, M.A.; Wheeler, J.A. Atomic Displacements in the Austenite-Martensite Transformation. Acta Cryst. 1948, 1, 216–224. [Google Scholar] [CrossRef]
- Cayron, C. Complements to Mügge and Friedel’s theory of twinning. Metals 2020, 10, 231. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C.; Logé, R. Evidence of new twinning modes in magnesium questioning the shear paradigm. J. Appl. Cryst. 2018, 51, 809–817. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. Shifting the shear paradigm in the crystallographic models of displacive transformations in metals and alloys. Crystals 2018, 8, 181. [Google Scholar] [CrossRef] [Green Version]
- Cayron, C. The weak plane and weak twins. in preparation.
- Cayron, C. Hard-sphere displacive model of extension twinning in magnesium. Mater. Des. 2017, 119, 361–375. [Google Scholar] [CrossRef] [Green Version]
- Christian, J.W. Deformation by Moving Interfaces. Metall. Trans. A 1982, 13, 509–538. [Google Scholar] [CrossRef]



| Correspondence | Orientation | Distortion |
|---|---|---|
| Intersection subgroups | ||
| Variants (from simple cosets) | ||
| Number of variants (Lagrange’s formula) | ||
| 12 | 12 | 12 |
| Operators (from double cosets) | ||
| Number of operators (Burnside’s formula) | ||
| 7 | 7 | 7 |
| B2 Symmetries in the Double Cosets | |||
|---|---|---|---|
| Disorient. | Matrices | Geometrical Elements | |
| , , , | |||
| , , , | |||
| , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , , , | |||
| , | |||
| , , , | |||
| , , , | |||
| , , | |||
| , , , | |||
| Reflection Junction Plane (Type I) | Rotational Junction Plane (Type II and Weak) | Shear Amplitude | |
|---|---|---|---|
| or | s = 0.2389 | ||
| s = 0.3096 | |||
| s = 0.1422 | |||
| s = 0.2804 | |||
| no solution | sg = 0.2911 | ||
| Op. | OR | Deviation from AQ OR |
|---|---|---|
| 1.43° | ||
| 8.23° | ||
| )B2 and | 2.21° | |
| and | 8.88° | |
| )B2 and | 8.11° | |
| and | 2.15° | |
| )B2 and | 7.93° | |
| and | 3.94° | |
| case 1: | 7.04° | |
| case 2: and | 3.45° |
| Closing-Gap Disorientation | Junction Planes CT | Shear | Junction Planes PTMC | Name in PTMC | Shear | |
|---|---|---|---|---|---|---|
(from C1) | C1: , C2: | 0.2385 | C1: , C2: | S1, A | 0.2385 | |
(from I) | t.I: t.II: W: | 0.3096 | t.I: t.II: | S3, D/C | 0.3096 | |
(from W) | t.I: t.II: W: | 0.1422 | t.I: t.II: | S4, C/D | 0.1423 | |
(from W) | t.I: t.II: W: | 0.2804 | t.I: t.II: | S2, B | 0.2804 | |
| W: | 0.2912 | no solution | S5 | no value | ||
| S6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cayron, C. The Correspondence Theory and Its Application to NiTi Shape Memory Alloys. Crystals 2022, 12, 130. https://doi.org/10.3390/cryst12020130
Cayron C. The Correspondence Theory and Its Application to NiTi Shape Memory Alloys. Crystals. 2022; 12(2):130. https://doi.org/10.3390/cryst12020130
Chicago/Turabian StyleCayron, Cyril. 2022. "The Correspondence Theory and Its Application to NiTi Shape Memory Alloys" Crystals 12, no. 2: 130. https://doi.org/10.3390/cryst12020130






