A LiNbO3 Integrated Optics Sensor for Measurement of Pulsed Current
Abstract
:1. Introduction
2. Sensor Principles and Fabrication
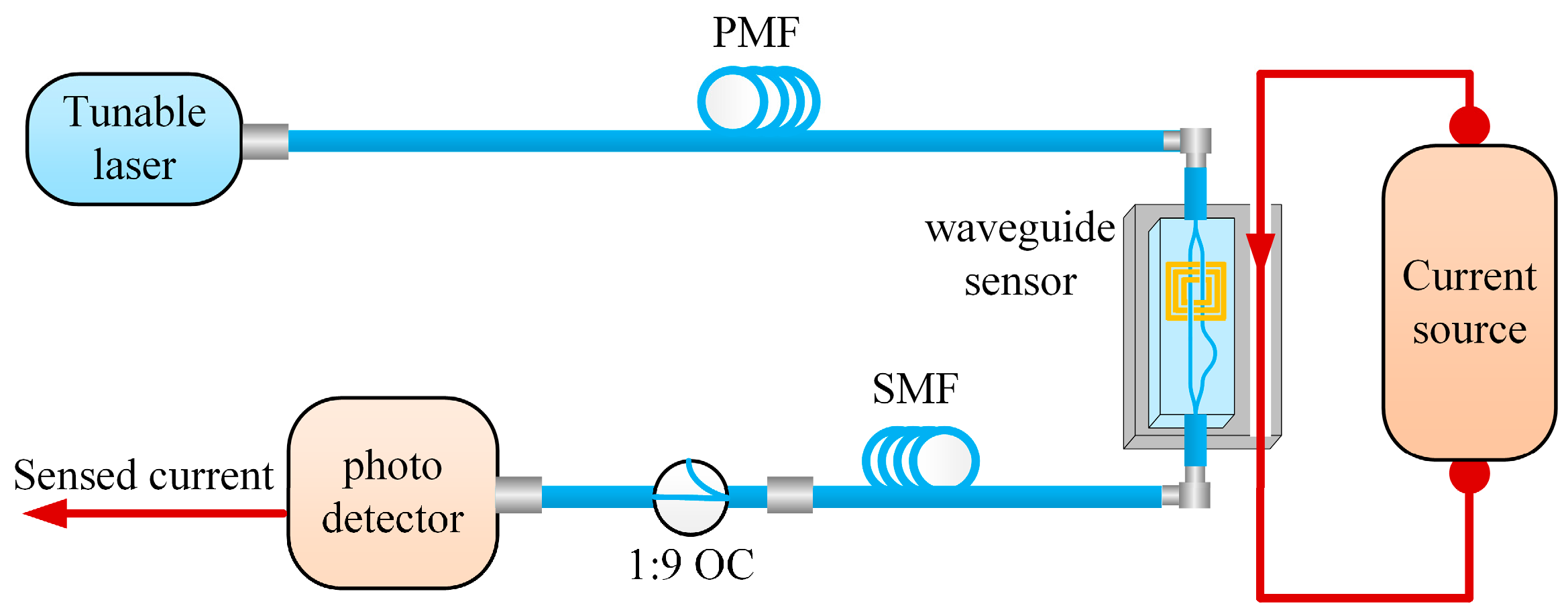
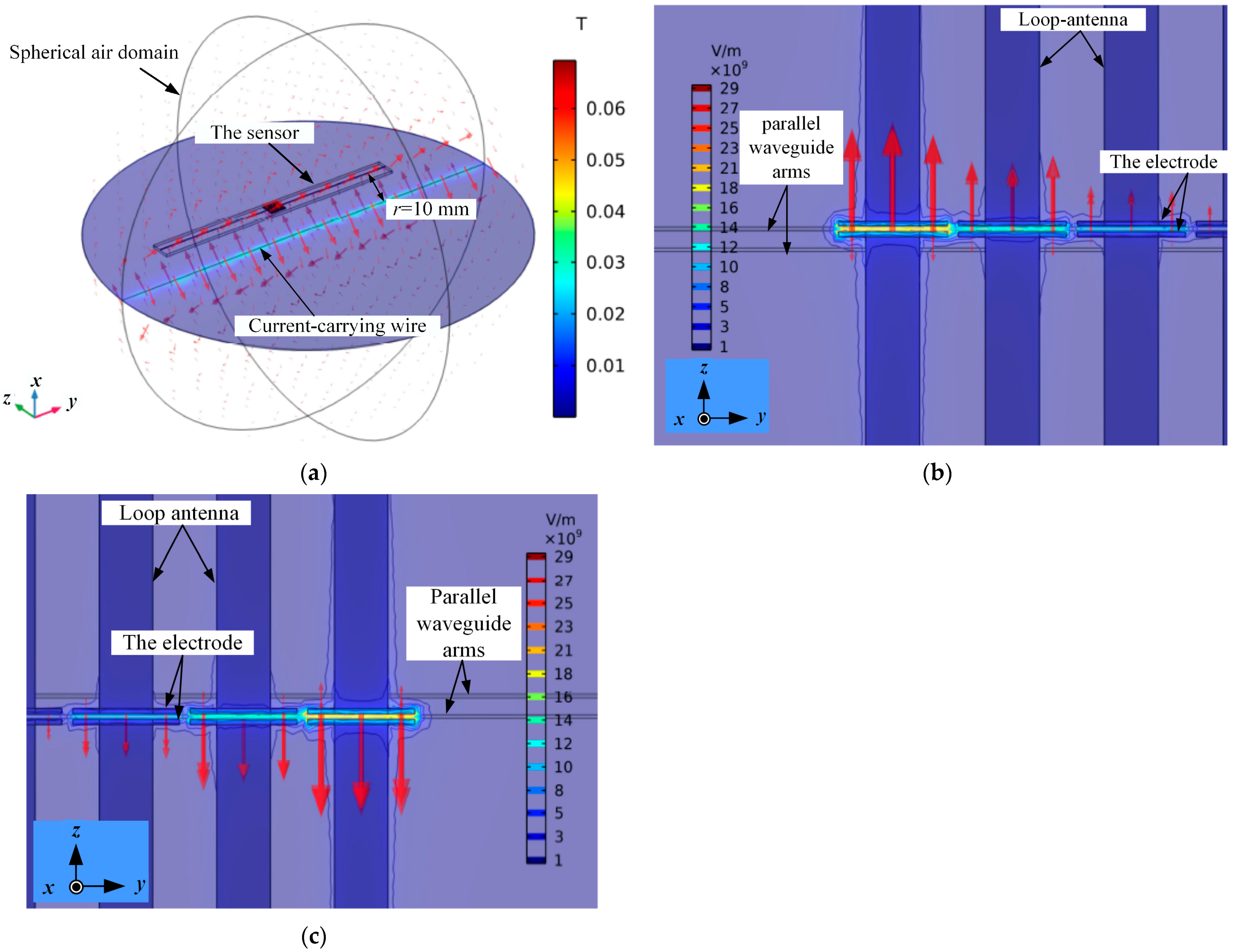
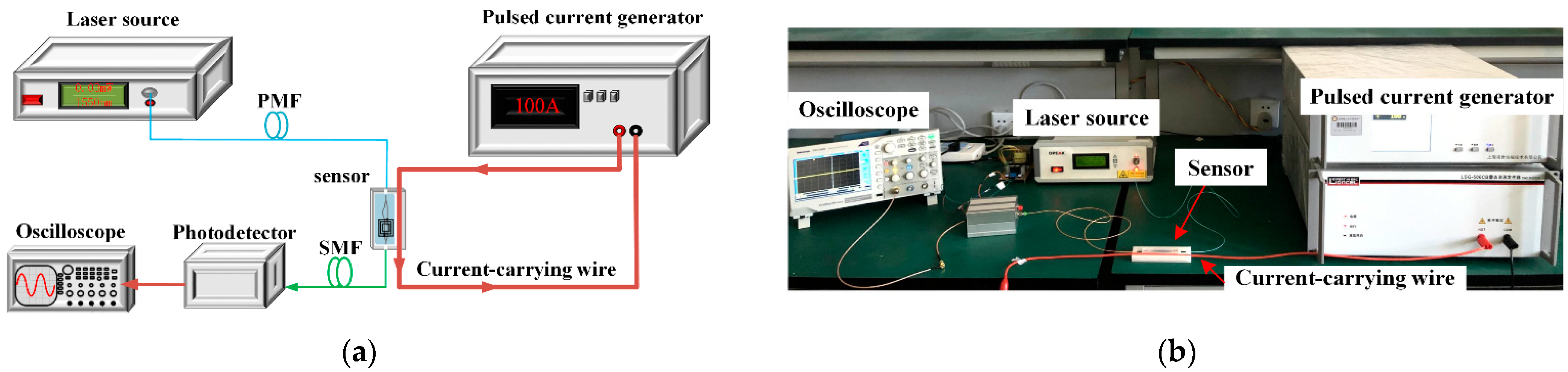
2.1. Sensing System
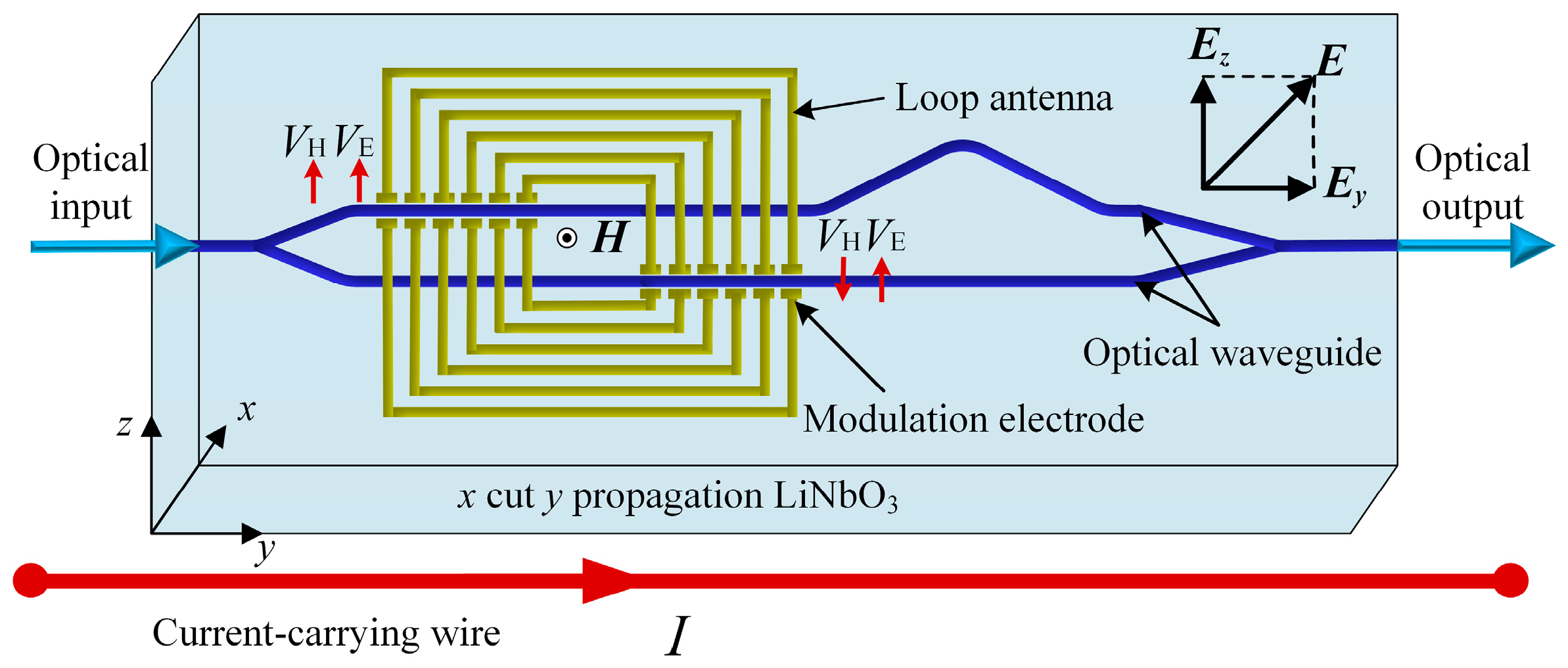
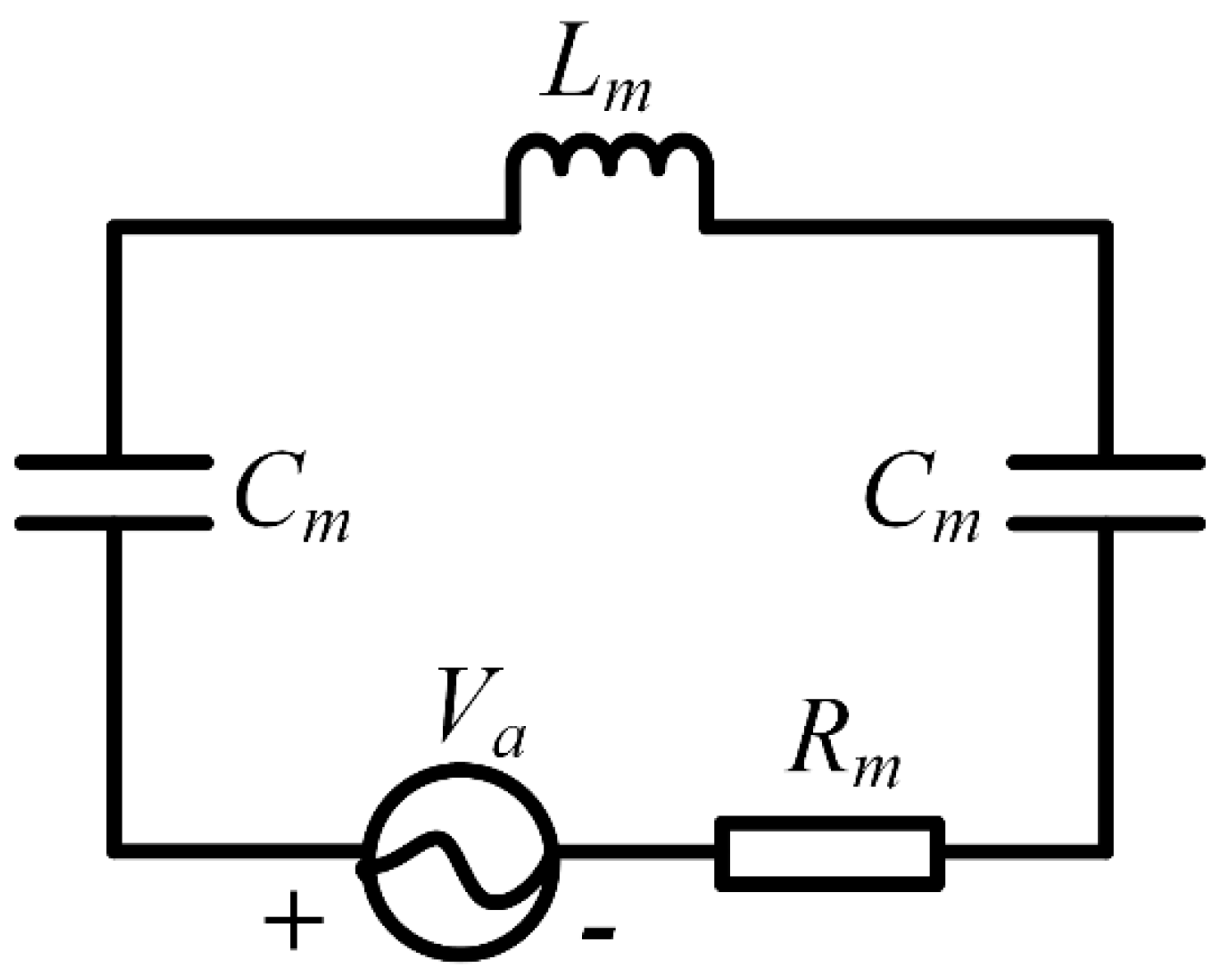
2.2. Sensor Structure and Operation Principles
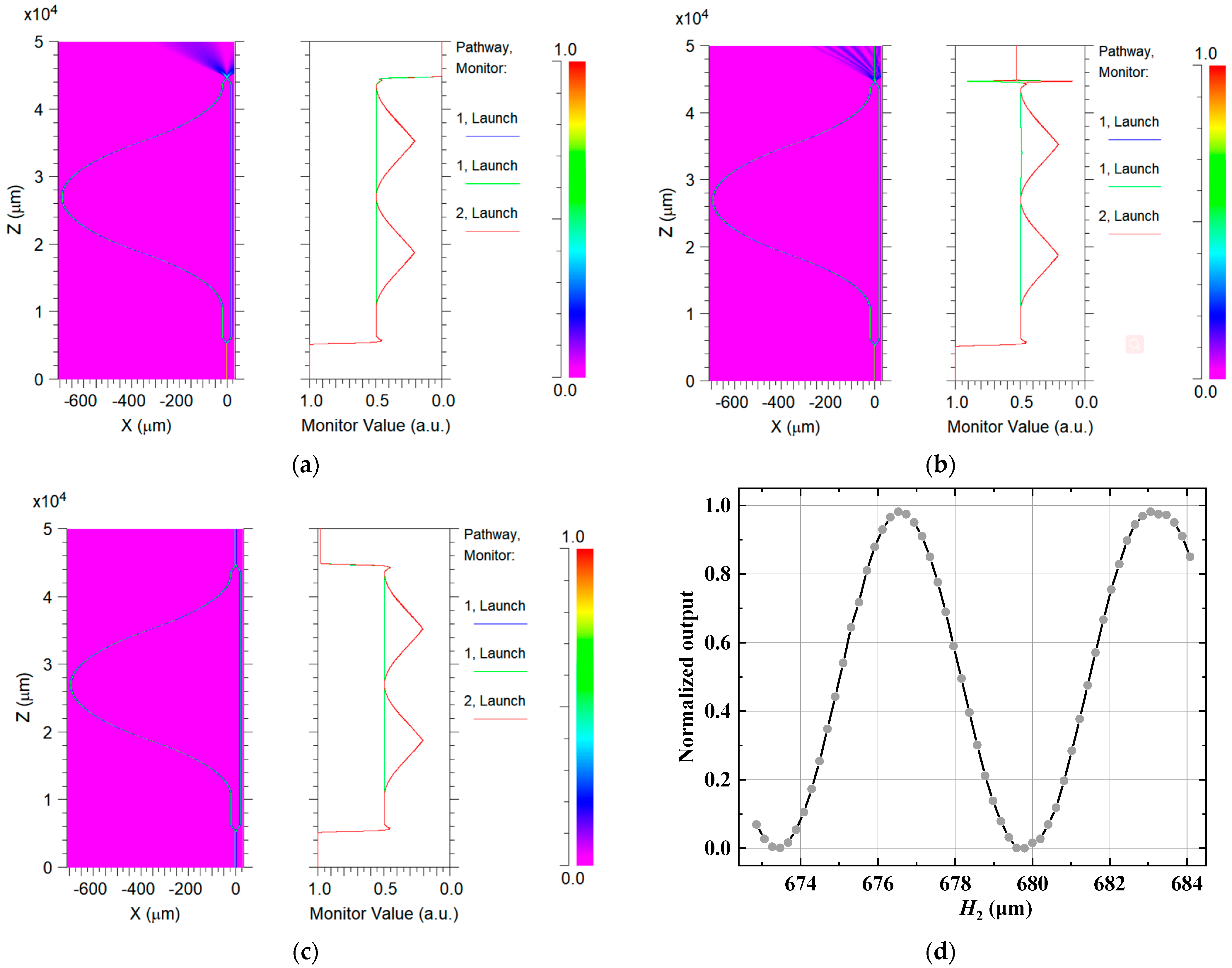
2.3. Sensor Design and Fabrication
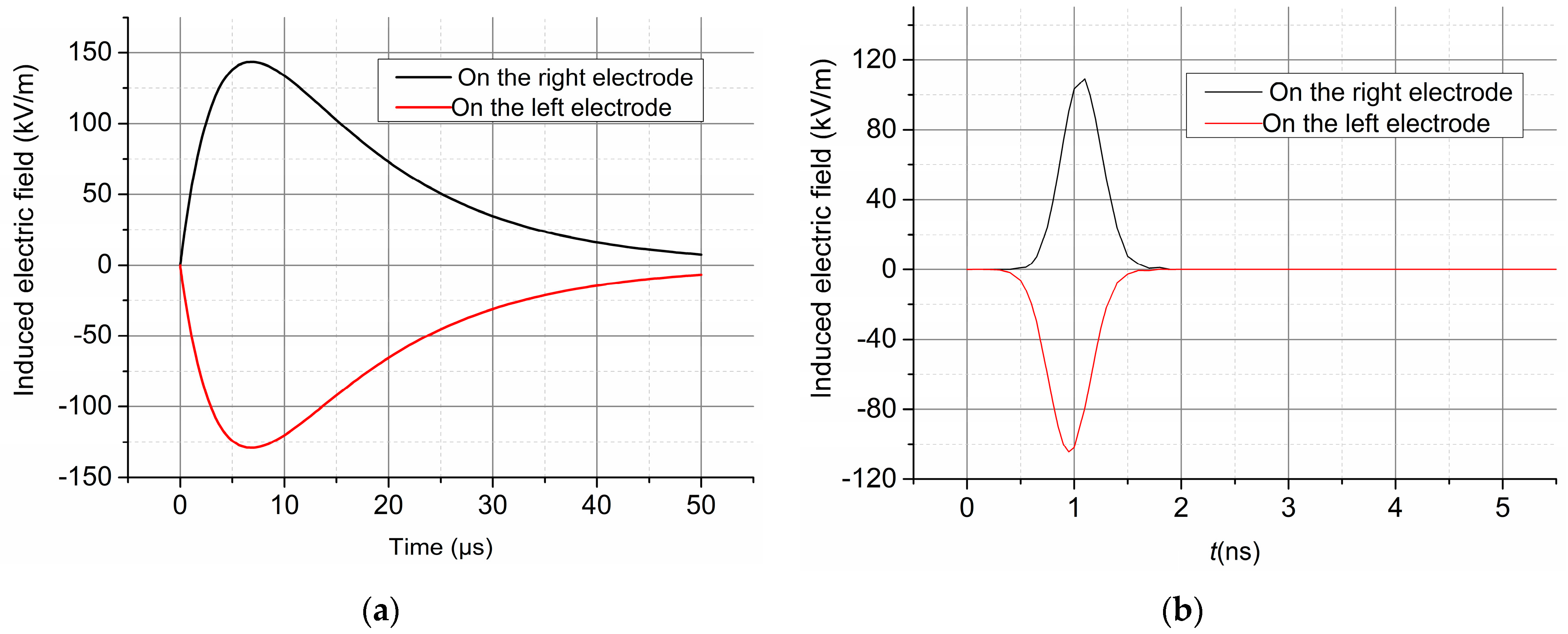
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, W.; Mao, C.; Lu, J. Study of the Virtual Instrumentation Applied to Measure Pulsed Heavy Currents. IEEE Trans. Instrum. Meas. 2005, 54, 284–288. [Google Scholar] [CrossRef]
- Ziegler, S.; Woodward, R.C.; Iu, H.H.-C.; Borle, L.J. Current Sensing Techniques: A Review. IEEE Sens. J. 2009, 9, 354–376. [Google Scholar] [CrossRef]
- Pellinen, D.G.; Di Capua, M.S.; Sampayan, S.E.; Gerbracht, H.; Wang, M. Rogowski coil for measuring fast, high-level pulsed currents. Rev. Sci. Instrum. 1980, 51, 1535–1540. [Google Scholar] [CrossRef]
- Ramboz, J.D. Machinable rogowski coil, design, and calibration. IEEE Trans. Instrum. Meas. 1996, 45, 511–515. [Google Scholar] [CrossRef]
- Gerasimov, A.I. Wide-Range Inductive Sensors of Currents with Nanosecond Rise Times for Measuring Parameters of High-Current Pulses (Review). Instrum. Exp. Tech. 2002, 45, 147–161. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, F.; Zhang, Q.; Zhong, H. Design and construction of a Rogowski Coil for measuring wide pulsed current. IEEE Sens. J. 2011, 11, 123–130. [Google Scholar] [CrossRef]
- Zhang, W.; Sohid, S.B.; Wang, F.; Cui, H.; Holzinger, B. High-Bandwidth Combinational Rogowski Coil for SiC MOSFET Power Module. IEEE Trans. Power Electron. 2022, 37, 4397–4405. [Google Scholar] [CrossRef]
- Fu, S.; Deng, E.; Peng, C.; Zhang, G.; Zhao, Z.; Cui, X. Method of Turns Arrangement of Noncircular Rogowski Coil with Rectangular Section. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Hasegawa, K.; Takahara, S.; Tabata, S.; Tsukuda, M.; Omura, I. A new output current measurement method with tiny PCB sensors capable of being embedded in an IGBT module. IEEE Trans. Power Electron. 2017, 32, 1707–1712. [Google Scholar] [CrossRef] [Green Version]
- Hasegawa, K.; Sho, S.; Tsukuda, M.; Omra, I.; Ichiki, M.; Kato, T. Output-Current Measurement of a PWM Inverter with a Tiny PCB Rogowski Sensor Integrated into an IGBT Module. In Proceedings of the IEEE Energy Conversion Congress and Exposition, ECCE, Baltimore, MD, USA, 29 September–3 October 2019; pp. 5707–5711. [Google Scholar] [CrossRef]
- Bayarkhuu, B.; Bat-Ochir, B.; Hasegawa, K.; Tsukuda, M.; Dugarjav, B.; Omura, I. Analog Basis, Low-Cost Inverter Output Current Sensing with Tiny PCB Coil Implemented inside IPM. In Proceedings of the 2019 31st International Symposium on Power Semiconductor Devices and ICs (ISPSD), Shanghai, China, 19–23 May 2019; pp. 251–254. [Google Scholar] [CrossRef]
- Gu, P.Y.; Chen, Q.; Li, H.B.; Hu, C.; Gong, H.; Jiao, Y. PCB Rogowski Coils for 300 kA Current Measurement on a Multi-Split Conductor. IEEE Sens. J. 2019, 19, 6786–6794. [Google Scholar] [CrossRef]
- Belal, M.; Song, Z.; Jung, Y.; Brambilla, G.; Newson, T.P. Optical fiber microwire current sensor. Opt. Lett. 2010, 35, 3045. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Dong, Y.; Leeson, J.; Chen, L.; Bao, X. High sensitivity optical fiber current sensor based on polarization diversity and a Faraday rotation mirror cavity. Appl. Opt. 2011, 50, 924–929. [Google Scholar] [CrossRef] [PubMed]
- Bohnert, K.; Gabus, P.; Nehring, J.; Brändle, H. Temperature and vibration insensitive fiber-optic current sensor. J. Lightwave Technol. 2002, 20, 267–276. [Google Scholar] [CrossRef]
- Liu, T.; Han, J.; Hu, H. Optical Current Sensor with Dual-Wavelength Configuration for Improving Temperature Robustness. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Hu, H.; Huang, J.; Xia, L.; Yan, Z.; Peng, S. The compensation of long-term temperature induced error in the all fiber current transformer through optimizing initial phase delay in λ/4 wave plate. Microw. Opt. Technol. Lett. 2019, 61, 1769–1773. [Google Scholar] [CrossRef]
- Muller, G.M.; Frank, A.; Yang, L.; Gu, X.; Bohnert, K. Temperature Compensation of Interferometric and Polarimetric Fiber-Optic Current Sensors with Spun Highly Birefringent Fiber. J. Lightwave Technol. 2019, 37, 4507–4513. [Google Scholar] [CrossRef]
- Huang, Y.; Xia, L.; Pang, F.; Yuan, Y.; Ji, J. Self-Compensative Fiber Optic Current Sensor. J. Lightwave Technol. 2021, 39, 2187–2193. [Google Scholar] [CrossRef]
- Jia, Q.; Han, Q.; Liang, Z.; Cheng, Z.; Hu, H.; Wang, S.; Ren, K.; Jiang, J.; Liu, T. Temperature Compensation of Optical Fiber Current Sensors with a Static Bias. IEEE Sens. J. 2022, 22, 352–356. [Google Scholar] [CrossRef]
- Mora, J.; Díez, A.; Cruz, J.L.; Andrés, M.V. Magnetostrictive sensor interrogated by fiber gratings for DC-current and temperature discrimination. IEEE Photonics Technol. Lett. 2000, 12, 1680–1682. [Google Scholar] [CrossRef]
- Satpathi, D.; Moore, J.A.; Ennis, M.G. Design of a Terfenol-D based fiber-optic current transducer. IEEE Sens. J. 2005, 5, 1057–1065. [Google Scholar] [CrossRef]
- Cremonezi, A.O.; Ferreira, E.C.; Filho, A.J.B.; Dias, J.A.S. A fiber bragg grating RMS current transducer based on the magnetostriction effect using a terfenol-D toroidal-shaped modulator. IEEE Sens. J. 2013, 13, 683–690. [Google Scholar] [CrossRef]
- De Nazaré, F.V.B.; Werneck, M.M. Compact optomagnetic Bragg-grating-based current sensor for transmission lines. IEEE Sens. J. 2015, 15, 100–109. [Google Scholar] [CrossRef]
- Dante, A.; Lopez, J.D.; Carvalho, C.C.; Allil, R.C.D.S.B.; Werneck, M.M. A Compact FBG-Based Magnetostrictive Optical Current Sensor with Reduced Mass of Terfenol-D. IEEE Photonics Technol. Lett. 2019, 31, 1461–1464. [Google Scholar] [CrossRef]
- Lopez, J.D.; Dante, A.; Bacurau, R.M.; Cremonezi, A.O.; Mok, R.W.; Carvalho, C.C.; Allil, R.C.D.S.B.; Ferreira, E.C.; Werneck, M.M. Fiber-Optic Current Sensor Based on FBG and Optimized Magnetostrictive Composite. IEEE Photonics Technol. Lett. 2019, 31, 1987–1990. [Google Scholar] [CrossRef]
- Lopez, J.D.; Dante, A.; Cremonezi, A.O.; Bacurau, R.M.; Carvalho, C.C.; Allil, R.C.D.S.B.; Ferreira, E.C.; Werneck, M.M. Fiber-Optic Current Sensor Based on FBG and Terfenol-D with Magnetic Flux Concentration for Enhanced Sensitivity and Linearity. IEEE Sens. J. 2020, 20, 3572–3578. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Q.; Ge, W.; Li, L. A Temperature-Insensitive AC Current Sensor Based on Two Opposite Bias Magnetic Circuits. IEEE Photonics Technol. Lett. 2016, 28, 2724–2727. [Google Scholar] [CrossRef]
- Han, J.; Hu, H.; Wang, H.; Zhang, B.; Song, X.; Ding, Z.; Zhang, X.; Liu, T. Temperature-Compensated Magnetostrictive Current Sensor Based on the Configuration of Dual Fiber Bragg Gratings. J. Lightwave Technol. 2017, 35, 4910–4915. [Google Scholar] [CrossRef]
- Xiao, D.; Wang, G.; Yu, F.; Liu, S.; Shao, L.; Wang, C.; Fu, H.; Shum, P.P.; Ye, T.; Wang, W. Highly Stable and Precise Demodulation of an FBG-Based Optical Current Sensor Using a Dual-Loop Optoelectronic Oscillator. J. Lightwave Technol. 2021, 39, 5962–5972. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, C.; Zhao, Z. Design and Application of Integrated Optics Sensor for Measurement of Intense Pulsed Electric Field. J. Lightwave Technol. 2019, 37, 1440–1448. [Google Scholar] [CrossRef]
- Suzuki, E.; Arakawa, S.; Ota, H.; Arai, K.I.; Sato, R. Optical magnetic field probe with a loop antenna element doubly loaded with electrooptic crystals. IEEE Trans. Electromagn. Compat. 2004, 46, 641–647. [Google Scholar] [CrossRef]
- Alferness, R.C. Waveguide Electrooptic Modulators. IEEE Trans. Microw. Theory Tech. 1982, 30, 1121–1137. [Google Scholar] [CrossRef]
- Lu, H.; Li, Y.; Zhang, J. Design and Analysis of Broadband LiNbO3 Optical Waveguide Electric Field Sensor with Tapered Antenna. Sensors 2021, 21, 3672. [Google Scholar] [CrossRef] [PubMed]
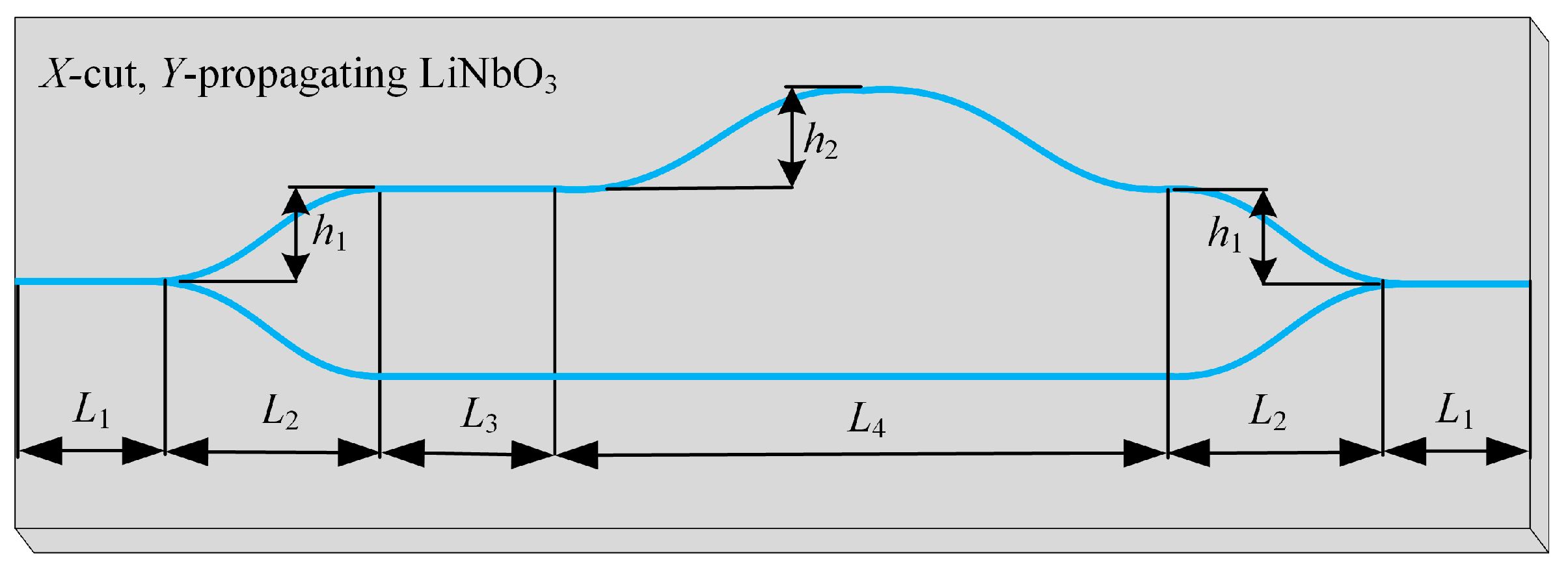
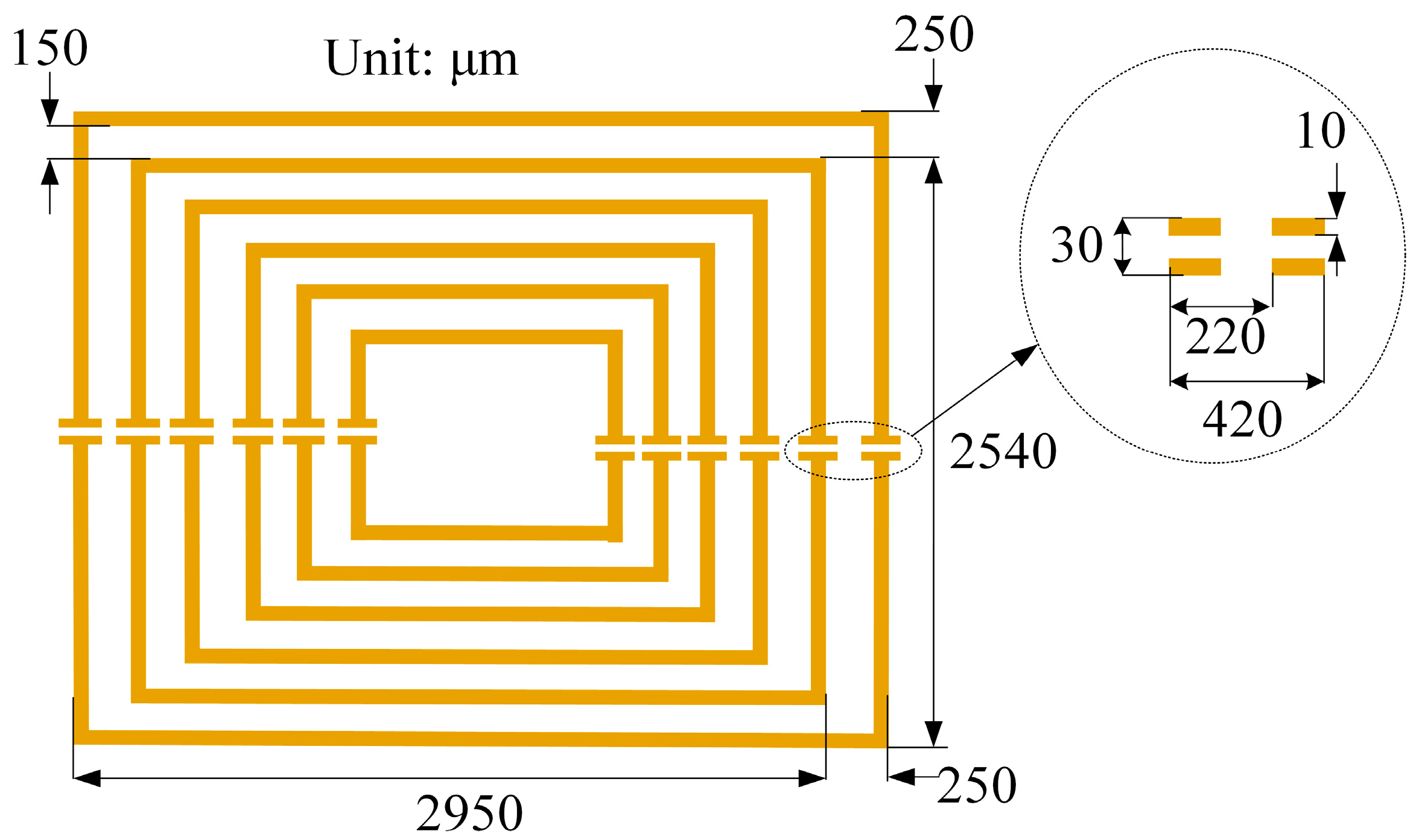



| L1 (μm) | L2 (μm) | L3 (μm) | L4 (μm) | h1 (μm) | h2 (μm) |
|---|---|---|---|---|---|
| 5000 | 1500 | 4000 | 33,000 | 11 | 676.5 |
| Pulsed Current /A | Pearson CT | Optical Waveguide Sensor | ||
|---|---|---|---|---|
| Tf/µs | Td/µs | Tf/µs | Td/µs | |
| 100 | 7.54 | 18.96 | 7.13 | 18.53 |
| 1000 | 7.34 | 19.08 | 6.87 | 20.18 |
| 2000 | 7.21 | 20.97 | 7.13 | 19.94 |
| 3300 | 7.09 | 22.38 | 6.88 | 20.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, Q.; Li, Y.; Zhang, J. A LiNbO3 Integrated Optics Sensor for Measurement of Pulsed Current. Crystals 2022, 12, 265. https://doi.org/10.3390/cryst12020265
Zhang J, Li Q, Li Y, Zhang J. A LiNbO3 Integrated Optics Sensor for Measurement of Pulsed Current. Crystals. 2022; 12(2):265. https://doi.org/10.3390/cryst12020265
Chicago/Turabian StyleZhang, Jiahong, Qinkai Li, Yingna Li, and Jing Zhang. 2022. "A LiNbO3 Integrated Optics Sensor for Measurement of Pulsed Current" Crystals 12, no. 2: 265. https://doi.org/10.3390/cryst12020265





