3.1. Linear Waveguides
The light guiding within an electrically induced and controlled NLC waveguide is based on total internal reflection from two regions within the NLC layer with a different spatial distribution of the molecules [
13,
14,
29]. When there is no voltage applied, the NLC molecules are uniformly oriented in a planar configuration (along the
z-axis) over the whole volume of the sample. As the voltage increases (above the Freedericksz threshold value), molecules reorient out of plane towards the electric field lines to homeotropic orientation.
Figure 3a presents the orientation of molecules in a uniform NLC cell characterized by the planar molecular alignment of a thickness equal to 12 μm, the same as the thickness of the analyzed NLC structures. The reorientation is induced by a uniform electric field; however, the final position of molecules depends, among others, on anchoring conditions, liquid crystal elasticity and applied voltage, as it is sketched for 6CHBT NLC for U = 1.2 V— black square, 1.5 V—gray circle, 2.0 V—light gray triangle, 2.5 V—magenta hexagon, 7.0 V—violet hexagon, and 20.0 V—purple star. As the molecules reorient out of plane, the refractive index for the input beam linearly polarized along with
x increases according to
, where:
is the angle between the long axis and
yz-plane, and
and
are ordinary and extraordinary refractive indices, respectively, as is plotted in
Figure 3b. In contrast, in the regions without electrodes, molecules maintain a planar orientation. Therefore, in a non-uniform electric field induced by structured electrodes, a transverse modulation of the refractive index is obtained. NLC cells with structured electrodes resemble a graded waveguide structure for a linearly polarized input beam with TM (along with
x-axis) polarization.
Without an electric field, the NLC molecules maintain planar orientation and the TM-beam propagates along the z-axis and diffracts as it does in isotropic media, with the refractive index . For a driving voltage above the Freedericksz threshold value, the molecules reorient under the electrode, increasing the angle . As a result, the refractive index for the TM-polarized beam increases, and a waveguide channel is formed.
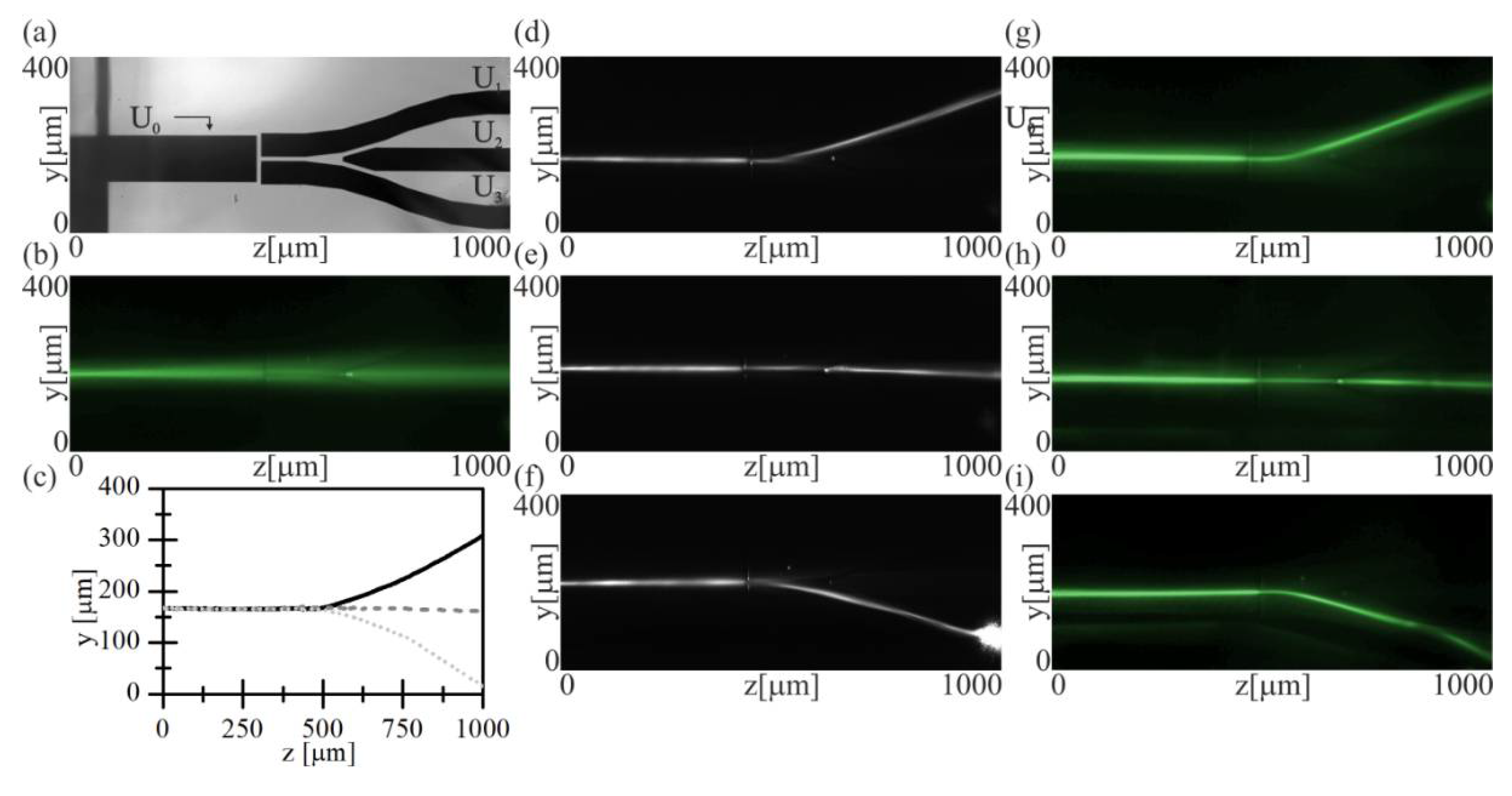
The laser beam propagation in the designed structure with a straight electrode is shown in
Figure 3c–e. The linearly polarized input beam along the
x-axis beam at λ = 532 nm is launched into the NLC sample in the region of the stripe-shaped electrode. Without the external voltage (U = 0), the light beam diffracts, increasing its width with propagation distance (
Figure 3c). In the output plane (
xy), this is visible as a broad illuminated region along the
y-axis, confirming the beam diffraction in the
yz-plane. Along the
x-axis, the beam does not diffract significantly due to its limited thickness. Applying a voltage of (U = 2.3 V) causes a reorientation of the NLC molecules and thus an increase in the refractive index in this region, which consequently leads to the excitation of the waveguide channel (
Figure 3d). The intensity distribution at the cell output is approximately Gaussian, characterized by partial ellipticity. The approximate diameter of the modal field is
and
, measured as FWHM values. Increasing the voltage up to 7 V widens the waveguide in both
x and
y directions due to further reorientation and saturation, and nonlocality of NLC molecules, respectively (
Figure 3e). The beam output profile becomes irregular and corresponds to a mix of higher-order guiding modes. Therefore, the induced waveguide starts to support more and more higher-order modes.
The mean width of a beam as a function of biasing voltage on electrodes of a width equal to 5 and 10 μm is plotted and presented in
Figure 3f. The beam is the narrowest for a biasing voltage of about
, then, as the voltage increases, the mean width of a beam increases as well. Biasing voltage of 7 V results in irregular optical field distribution at the output. It indicates that propagation is realized as a superposition of higher-order modes.
An electrically induced waveguide also supports different wavelengths. The propagation of the visible beam at λ = 642 nm (
Figure 3g) and infrared one λ = 1064 nm (
Figure 3h) is recorded for a U = 1.8 V biasing voltage. Furthermore, NLC waveguides are not limited to straight geometry. An example is presented in
Figure 4, where there are sketched arch-shaped electrodes of different sizes (left panel,
Figure 4a) and a combination of three arch electrodes (left panel,
Figure 4b). The propagation of a TM-polarized beam of a wavelength λ = 532 in a single arch-shaped channel and beam splitting at three different combined NLC arch-shaped electrically induced waveguides (driving voltage U = 2.3 V) are shown in
Figure 4a,b (right panels). The possibility of beam splitting between more guiding channels makes it possible to design and perform novel photonics devices for integrated optical circuits.
3.1.1. Waveguide Formation Times
One of the important issues and also one of the significant drawbacks is the dynamics of the waveguide channel formation. Due to the fact that reorientation involves, in general, the rotation of the molecules, it is a relatively slow process. The relationship between the response time and the dynamic rotational viscosity
and the cell thickness
d is directly proportional:
. From this relation, the larger the dynamic rotational viscosity, the slower the response time, but the thickness is even more critical in determining the response time, as it is squared with the response time, which can be defined as the time that a certain region of an NLC cell takes to turn from on to off or vice versa. NLC with a low rotational viscosity favors a rapid switching using an electric field. For a specific NLC, the value of the viscosity cannot be changed freely; however, the electrical driving signal can be optimized to maximize the overall performance of the structure. In order to determine the formation time of the induced waveguide structure, the setup, as shown in
Figure 1b, is used. The waveguide formation time is defined as the time from the moment the voltage is switched on until the transverse beam profile at a given propagation distance does not change and is more or less the same as the input beam profile. In an experiment, a more convenient way is to use a photodetector at the output of the waveguide. The criterion for the waveguide formation time that is measured is a time from beam coupling to the input to a moment when the electric signal at the photodetector reaches 0.9 times its maximum value. Generation of a waveguide channel requires a voltage just above the Frederiks threshold value. Such a voltage value forces the molecules to reorient, thus providing a change in refractive index
sufficient to guide the light beam. However, in this case (relatively small voltage value), the reorientation time of molecules is on the order of hundreds of milliseconds (for the 12
thick cell).
The obtained NLC waveguide formation times are presented in
Figure 5a. The reorientation time is estimated from a sequence of images taken by a CCD camera operating at a recording rate of 30 fps, i.e., the measurement resolution is 33 ms. No significant differences are observed in NLC cells with and without alignment layers at the bottom and top surfaces. However, the arrangement of all molecules towards the propagation direction seems to be a better approach to the reorientation process and slightly increases the response times of the molecules.
The reorientation rate directly depends on the amplitude of the driving voltage. For a driving voltage with an amplitude higher than the threshold value, the reorientation process occurs significantly faster than for voltages of the order of the threshold value. On the other hand, as shown already in
Figure 3a, higher voltages are disadvantageous because they induce too high reorientation (and thus a change in refractive index) and promote/support higher-order modes. Therefore, we propose a solution of using two voltages: a high overdrive voltage to achieve fast molecule reorientations and a voltage to ensure single-mode waveguide maintenance. The duration time of this high amplitude driving voltage must be precisely determined. It is important to reduce the amplitude of a voltage to the optimum value needed for waveguide formation at a specific time. An overdriving voltage duration that is too short will not result in a sufficient reorientation angle to induce waveguide formation. On the other hand, when the duration of the overdriving voltage is too long, the molecules will reorient too much, and the induced waveguide becomes highly multimodal.
To determine the overdrive voltage duration, a typical configuration with two crossed polarizers and a planar NLC cell with the optical axis oriented at 45° to the polarizers’ axis is used. Without an electric field, an NLC cell placed between crossed polarizers acts as a wave plate and brightens the field of view. As the voltage is switched on, the molecules start to reorient, and the phase delay between ordinary and extraordinary wave components changes. As a result, the intensity of a beam transmitted through the optical system varies in time. It stabilizes at a certain level depending on the final position of the molecules for a given voltage. Transmitted light intensity reaches the successive minima and maxima, finally reaching zero for the entirely reoriented molecules almost to a homeotropic texture. The number of oscillations increases with the NLC birefringence and cell thickness.
The oscillatory character of these changes for U = 2.1 V (the voltage value for which single-mode waveguide is formed) is presented in
Figure 5b. In the measurements intended to determine the duration time of high overdriving voltage, a reorientation time is defined as the time from when the voltage is turned on until the intensity of the transmitted beam reaches 0.1 times its maximum value. From this, the reorientation times are determined for different overdriving voltages and plotted in
Figure 5c. The line fitted to the experimental data is exponentially decreasing, and further increasing the voltage above a few tens of volts does not significantly reduce the reorientation time.
The waveguide induction time measurements are investigated as a function of overdriving voltage of duration, and amplitude presented in
Figure 5b. The experiment is performed in the same experimental setup as in
Figure 2a. A sinusoidal overdriving voltage of frequency 10 kHz and a precisely determined duration and amplitude, after which the voltage dropped to a value of U = 2.1 V, are applied to the NLC cell. The waveguide formation time is defined as the time that elapses from the voltage on until the electric signal generated on the photodetector reaches 0.9 times its maximum.
The application of a high overdrive voltage made it possible to shorten a switching time by two orders of magnitude. The best result is obtained for U
ovr = 21.2 V, and the formation time corresponds to 2.2 ms. The impact of a short duration voltage with high amplitude (2.2 ms; 21.2 V) is presented in
Figure 5d.
3.1.2. Splitting Structures
Since the beam trajectory coincides with the shape of the electrodes, it is possible to design more complex electro-optical circuits designed for optical switching. The Y-splitter design is the simplest element to implement light splitting or switching.
Figure 6a shows a top view image of the designed Y-splitter. It consists of three individual electrodes with a width of 10 μm each, namely, (1), (2) and (3), as marked on the photo, which allows for independent voltage control in each branch. The length of the first electrode to the forking (splitting) is equal to 600 μm; the angle between the second and third electrode is equal to 7° and the length of these electrodes is equal to 600 μm; thus, the distance between the output electrode (the “fork” width) is 50 μm. The voltages applied to the input electrode and two output electrodes are labelled as U
1, U
2, and U
3, respectively. The visible dark stripe perpendicular to the input electrode is used to supply the voltage and does not affect the beam propagation.
Figure 6b–d shows the propagation result of linearly polarized TM infrared beam λ = 1064 nm in the fabricated structure. The first electrode, supplied with a voltage U
1 = 2.1 V is used to induce the input channel. Applying a voltage to the top electrode (U
2 = 2.1 V; U
3 = 0 V) induces the upper channel and the beam follows the direction (
Figure 6b), while applying a voltage to the third electrode (U
2 = 0 V; U
3 = 2.1 V) switches the beam into the lower channel (
Figure 6c). Applying the same voltage to all three electrodes (U
1 = U
2 = U
3 = 2.1 V) excites three waveguide channels in the medium, and the laser beam propagates along these channels (
Figure 6c). The light is captured by a single input waveguide and then undergoes splitting/forking with approximately equal intensities due to the electrode geometry.
Figure 6e,f shows the corresponding intensity distribution in the lower and upper channels at a distance of 800 μm for different voltages, illustrating the principle operation of the structure.
3.2. Nonlinear Waveguides
In a nonlinear case, an intense light beam in an NLC medium can propagate with a constant width at a propagation distance exceeding the Rayleigh range multiple times. For the TM-polarized beam, the generation of nematicon requires proper alignment direction. The strongest nonlinear response of the molecules is when molecules are oriented in the direction of the
k vector. For a non-threshold reorientation of molecules in the presence of a light beam and avoiding the Freedericksz threshold effect, the initial pretilt of molecules is induced by an external electric field (
Figure 7a). Without an electric field, molecules are subjected to a threshold, and, for the TM-polarized beam, diffraction is observed (
Figure 7b). In the presence of an electric field, molecules tend to reorient towards the x-direction. The beam propagates in the form of spatial soliton (nematicon) and preserves its width at a distance of a few millimeters (
Figure 7c).
As described in the introduction part, in the nonlinear case, a light beam with sufficiently high intensity can propagate in NLC medium, with a constant width over distances many times the Rayleigh range, in the form of a so-called nematicon.
The alignment layers ensure planar orientation in the
yz-plane with initial molecular anchoring at
with respect to the
z-axis (
Figure 7a). Indium/tin oxide (ITO) thin transparent electrodes deposited on the inner side of the NLC cell are applied to provide an adjustable low-frequency electric field for the out-of-
yz-plane reorientation of the molecules. The NLC cell under consideration has been infiltrated with 6CHBT NLC and the linear polarized TM (along
x-axis) light beam at λ = 1064 nm with optical power P = 1.5 mW has been focused to the waist of several micrometers and then launched into the NLC cell with its k vector oriented along the
z-axis, as schematically presented in
Figure 7a.
Figure 7b presents an experimental photo of light beam propagation without an external electric field. As one can clearly see, the light beam diffracts. Without an external electric field, the reorientation is subjected to a threshold value much higher than the 1.5 mW. When a sufficiently high voltage is applied to the ITO electrodes, the NLC molecules are reoriented in the
xz-plane, changing, thus, the director orientation. Indeed, by applying an electrical bias of 1.6 V (1 kHz), the self-trapped beam of TM-polarization is induced (
Figure 7c). The beam propagates in the form of a nematicon and preserves its width at a distance of 2 mm.
Among other possibilities of controll light propagation in NLC structures [
30,
31,
32,
33], bycombining the propagation of the nematicon with the properties of structures with specially designed electrodes as described in
Section 3.1, we obtain a configuration for changing the propagation direction of the nematicon in a Y-shaped geometry, as presented in
Figure 8a. It is composed of one initial electrode of a width of 100 μm and two electrodes of a thickness equal to 50 μm with a short gap between them. The width of a cell is 50 μm. The amplitude of the driving voltage on each electrode can be controlled independently. The propagation direction of the nematicon between the upper (U
1) and lower (U
2) electrodes can be change by applying the voltage to the proper electrodes. To generate nematicon in the area designated by the initial electrode (U
0), a TM-polarized IR beam of initial width w
0 = 2.5 μm and optical power P = 1.5 mW is coupled to the middle part of the NLC cell. For the biasing voltage, the U
0 = 2.1 V beam forms a nematicon that propagates along the z-axis. Depending on the voltages U
1 and U
2, a nematicon is redirected to the upper or lower part of the NLC cell, as presented in
Figure 8b,c. Trajectories of the nematicon that propagates in the case of U
0 = 2.1 V and U
1 = 2.1 V or U
2 = 2.1 V are plotted in
Figure 8d. After propagation over a 1 mm distance, the spatial separation of a beam exceeds 300 mm, which may be advantageous for the application of the structure in integrated optical circuits. More NLC cells can be combined to obtain guiding/switching structures or decouple the beam from the NLC cell.