Picosecond Pulsed-Periodic High-Peak Power Nd:YAG Laser Operationally Controlled by KTP-Based Pockels Cell
Abstract
:1. Introduction
2. Materials and Methods
2.1. KTP Family Crystals for PCs and Second Harmonic Conversion Efficiency
2.2. KTP Pockels Cell
2.3. Second and Third Harmonics Measurements
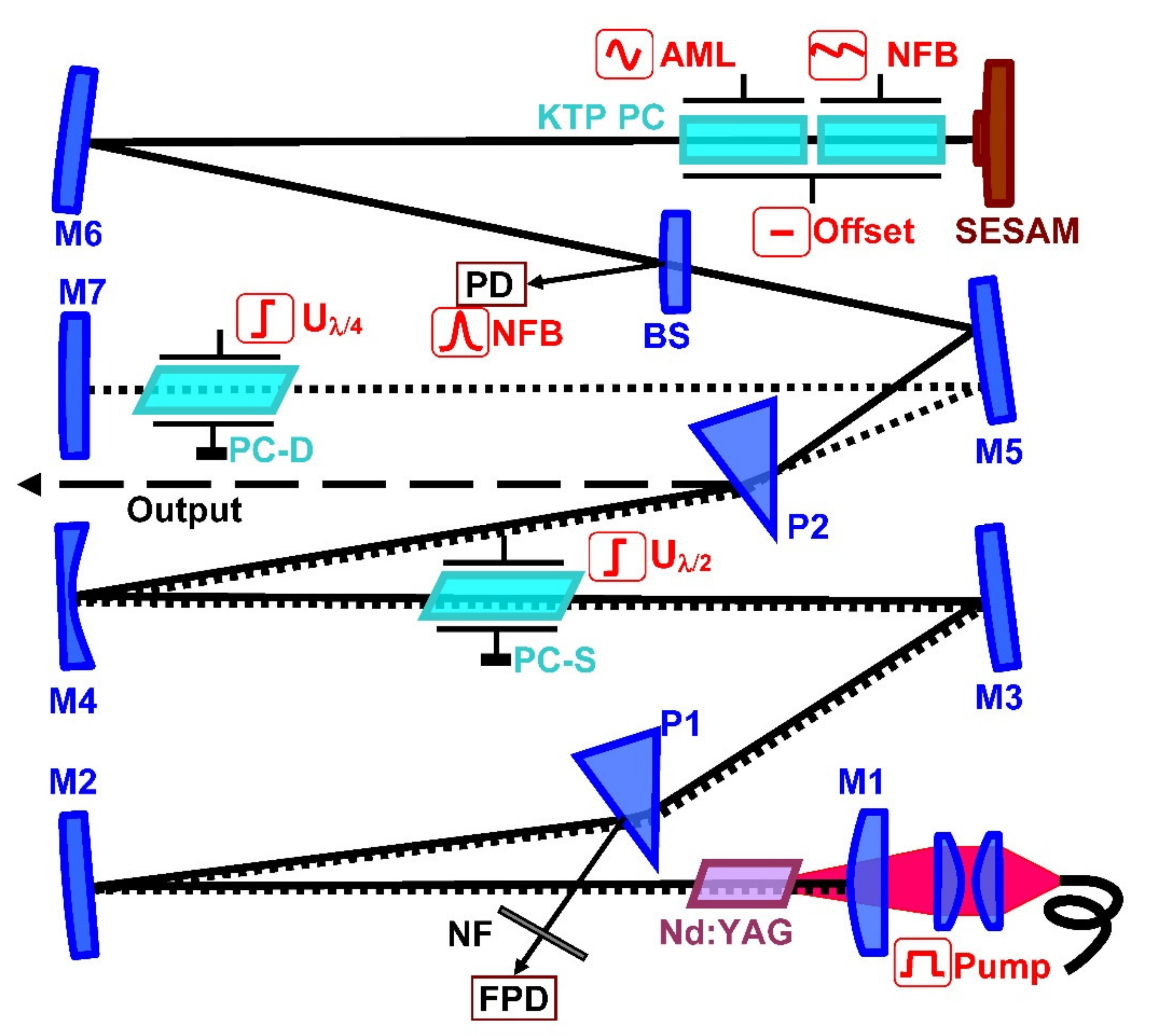
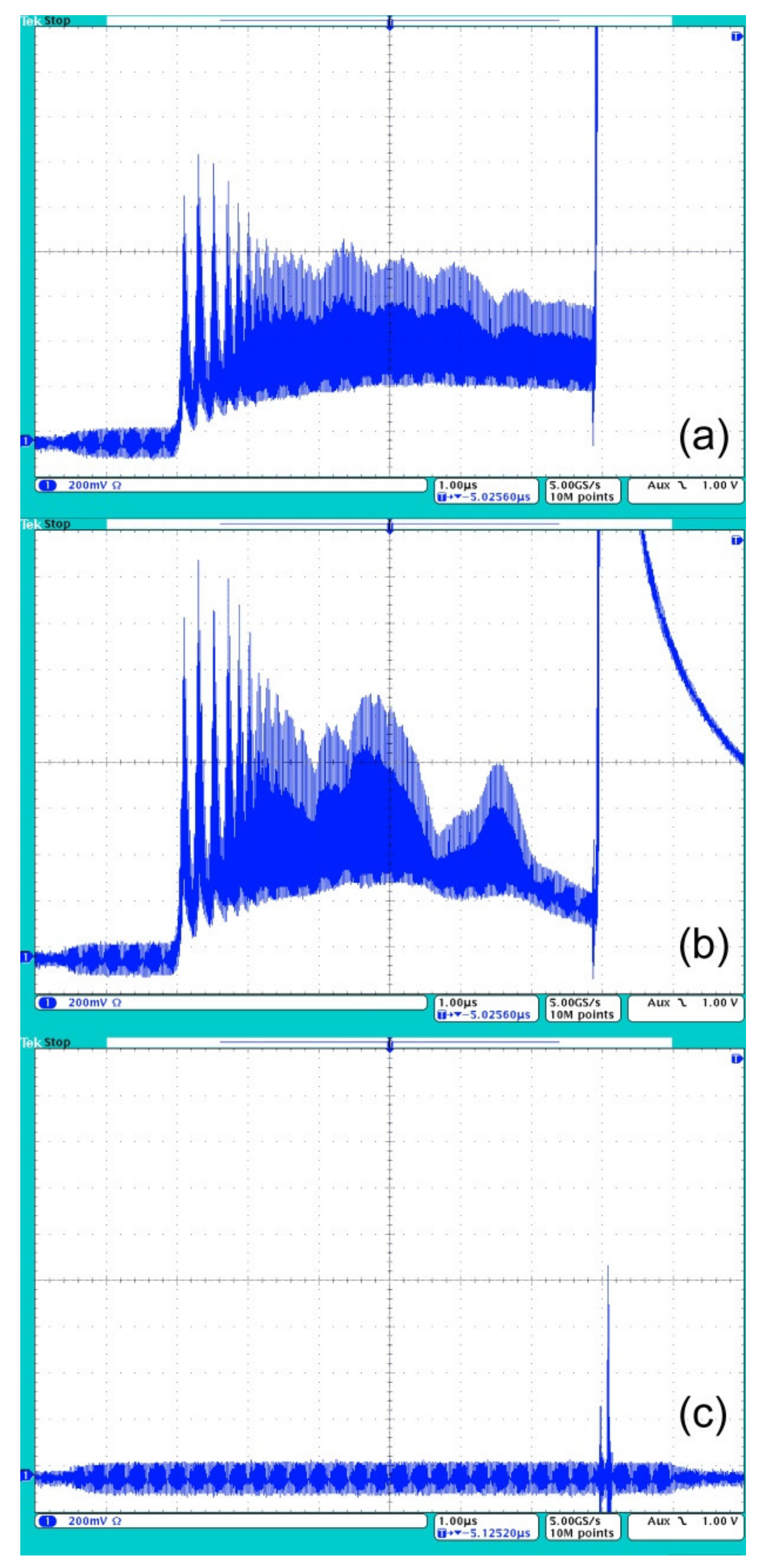
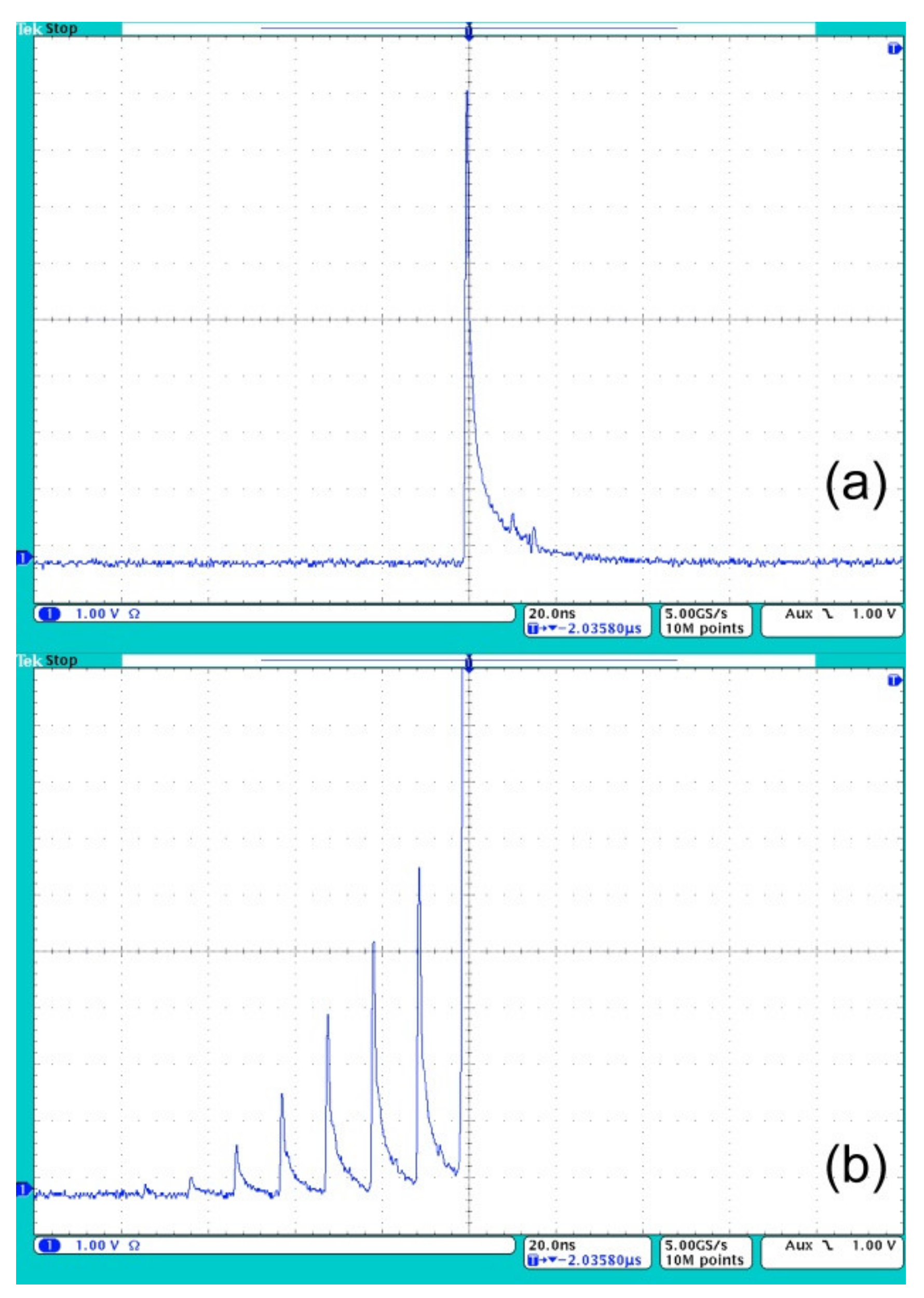
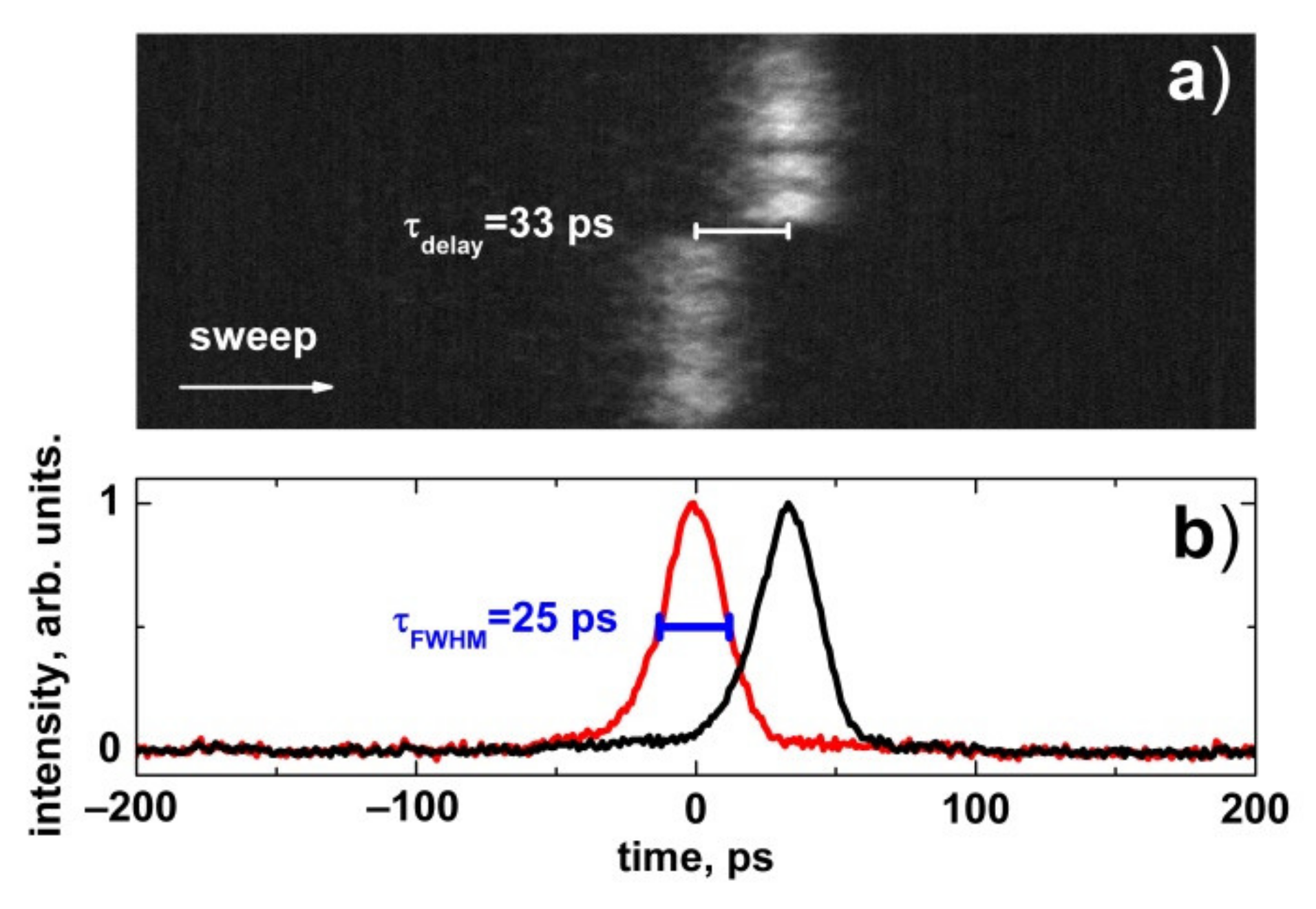
2.4. Pulsed-Periodic Picosecond Laser Scheme and Operation Control
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Montello, A.; Nishihara, M.; Rich, J.W.; Adamovich, I.V.; Lempert, W.R. Picosecond CARS measurements of nitrogen rotational/translational and vibrational temperature in a nonequilibrium Mach 5 flow. Exp. Fluids 2013, 54, 1422. [Google Scholar] [CrossRef]
- Seeger, T.; Kiefer, J.; Leipertz, A.; Patterson, B.D.; Kliewer, C.J.; Settersten, T.B. Picosecond time-resolved pure-rotational coherent anti-Stokes Raman spectroscopy for N2 thermometry. Opt. Lett. 2009, 34, 3755–3757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arakcheev, V.G.; Kireev, V.V.; Morozov, V.B.; Olenin, A.N.; Tunkin, V.G.; Valeev, A.A.; Yakovlev, D.V. Collisionally induced dephasing and rotational energy transfer in CO2 Fermi dyad “blue” Q-branch 1388 cm−1. J. Raman Spectrosc. 2007, 38, 1046–1051. [Google Scholar] [CrossRef]
- Intartaglia, R.; Bagga, K.; Brandi, F. Study on the productivity of silicon nanoparticles by picosecond laser ablation in water: Towards gram per hour yield. Opt. Express 2014, 22, 3117–3127. [Google Scholar] [CrossRef]
- Scotti, G.; Trusheim, D.; Kanninen, P.; Naumenko, D.; Shulz-Ruhtenberg, M.; Snitka, V.; Kallio, T.; Franssila, S. Picosecond laser ablation for silicon micro fuel cell fabrication. J. Micromech. Microeng. 2013, 23, 055021. [Google Scholar] [CrossRef] [Green Version]
- Vereshchagin, A.K.; Vereshchagin, K.A.; Morozov, V.B.; Tunkin, V.G. Non-collinear optical parametric amplifier for time-resolved broadband picosecond CARS. J. Raman Spectrosc. 2014, 45, 507–514. [Google Scholar] [CrossRef]
- Gacheva, E.I.; Poteomkin, A.K.; Mironov, S.Y.; Zelenogorskii, V.V.; Khazanov, E.A.; Yushkov, K.B.; Chizhikov, A.I.; Molchanov, V.Y. Fiber laser with random-access pulse train profiling for a photoinjector driver. Phot. Res. 2017, 5, 293–298. [Google Scholar] [CrossRef]
- Petrarca, M.; Martyanov, M.; Divall, M.S.; Luchinin, G. Study of the powerful Nd:YLF laser amplifiers for the CTF3 photoinjectors. IEEE J. Quantum Electron. 2011, 47, 306–313. [Google Scholar] [CrossRef] [Green Version]
- Seeber, G. Laser Ranging. In Satellite Geodesy, 2nd ed.; Walter de Gruyter: Berlin, Germany, 2003; Chapter 8; pp. 405–442. [Google Scholar]
- Gourine, B. French transportable laser ranging station: Positioning campaigns for satellite altimeter calibration missions in occidental Mediterranean Sea. Larhyss J. 2013, 12, 57–69. [Google Scholar] [CrossRef]
- Dickey, J.O.; Bender, P.L.; Faller, J.E.; Newhall, X.X.; Ricklefs, R.L.; Ries, J.G.; Shelus, P.J.; Veillet, C.; Whipple, A.L.; Wiant, J.R.; et al. Lunar laser ranging: A continuing legacy of the Apollo Program. Science 1994, 265, 482–490. [Google Scholar] [CrossRef] [Green Version]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Progress in Lunar laser ranging tests of relativistic gravity. Phys. Rev. Lett. 2004, 93, 261101. [Google Scholar] [CrossRef] [Green Version]
- Mourou, G.; Stancampiano, C.V.; Antonetti, A.; Orszag, A. Picosecond microwave pulses generated with a subpicosecond laser-driven semiconductor switch. Appl. Phys. Lett. 1981, 39, 295–296. [Google Scholar] [CrossRef]
- Vergne, B.; Couderc, V.; Barthelemy, A.; Lalande, M.; Bertrand, V.; Gontier, D. High-power bipolar picosecond pulse generation using optically activated travelling wave generator. Microw. Opt. Technol. Lett. 2006, 48, 1645–1648. [Google Scholar] [CrossRef]
- Chung, C.; Lin, Y.; Wu, K.; Tai, W.; Chu, S.; Lee, Y.; Hwu, Y.; Lee, Y. Coherent anti-Stokes Raman scattering microscopy using a single-pass picoseconds supercontinuum-seeded optical parametric amplifier. Opt. Express 2010, 18, 6116–6122. [Google Scholar] [CrossRef]
- Kawakami, R.; Sawada, K.; Sato, A.; Hibi, T.; Kozawa, Y.; Sato, S.; Yokoyama, H.; Nemoto, T. Visualizing hippocampal neurons with in vivo two-photon microscopy using a 1030 nm picosecond pulse laser. Sci. Rep. 2013, 3, 1014. [Google Scholar] [CrossRef] [Green Version]
- Dierickx, C. Using normal and high pulse coverage with picosecond laser treatment of wrinkles and acne scarring: Long term clinical observations. Lasers Surg. Med. 2017, 50, 51–55. [Google Scholar] [CrossRef] [Green Version]
- Reiter, O.; Atzmony, L.; Akerman, L.; Levi, A.; Kershenovich, R.; Lapidoth, M.; Mimouni, D. Picosecond lasers for tattoo removal: A systematic review. Lasers Med. Sci. 2016, 31, 1397–1405. [Google Scholar] [CrossRef]
- Geerling, G.; Roider, J.; Schmidt-Erfurt, U.; Nahen, K.; El-Hifnawi, E.-S.; Laqua, H.; Vogel, A. Initial clinical experience with the picosecond Nd:YLF laser for intraocular therapeutic applications. Br. J. Ophthalmol. 1998, 82, 504–509. [Google Scholar] [CrossRef]
- Lindstrom, R.L. (Ed.) Textbook of Refractive Laser Assisted Cataract Surgery (ReLACS); Springer: New York, NY, USA, 2013; pp. 1–278. [Google Scholar] [CrossRef]
- Petersen, H.; Tavakoli, F.; Kruber, S.; Muenscher, A.; Gliese, A.; Hansen, N.; Uschold, S.; Eggert, D.; Robertson, W.; Gosau, T.; et al. Comparative study of wound healing in rat skin following incision with a novel picosecond infrared laser (PIRL) and different surgical modalities. Lasers Surg. Med. 2016, 48, 385–391. [Google Scholar] [CrossRef] [Green Version]
- Koechner, W. Solid-State Laser Engineering, 6th ed.; Springer: New York, NY, USA, 2006; pp. 534–586. [Google Scholar] [CrossRef]
- Agnesi, A.; Pirzio, F. High gain solid-state amplifiers for picosecond pulses. In Advances in Solid-State Lasers: Development and Applications; Grishin, M., Ed.; Intech: Rijeka, Croatia, 2010; pp. 213–238. [Google Scholar] [CrossRef] [Green Version]
- Osterink, L.M.; Foster, J.D. A mode-locked Nd:YAG laser. J. Appl. Phys. 1968, 39, 4163–4165. [Google Scholar] [CrossRef]
- Zaporozhchenko, V.A.; Tylets, N.A. Time locking of optical pulses to an external signal in pulsed lasers with active mode locking. Quantum Electron. 1996, 26, 512–516. [Google Scholar] [CrossRef]
- Minamikawa, T.; Tanimoto, N.; Hashimoto, M.; Araki, T.; Kobayashi, M.; Fujita, K.; Kawata, S. Jitter reduction of two synchronized picosecond mode-locked lasers using balanced cross-correlator with two-photon detectors. Appl. Phys. Lett. 2006, 89, 191101. [Google Scholar] [CrossRef]
- Brito Cruz, C.H.; De Martini, F.; Fragnito, H.L.; Palange, E. Picosecond pulse generation by intracavity nonlinear compression in self-injected Nd:YAG laser. Opt. Commun. 1982, 40, 298–301. [Google Scholar] [CrossRef]
- Komarov, K.P.; Kuch’yanov, A.S.; Ugozhaev, V.D. Steady-state ultrashort pulses generated by passive mode locking of a solid-state laser with an active feedback. Sov. J. Quantum Electron. 1986, 16, 520–524. [Google Scholar] [CrossRef]
- Del Corno, A.; Gabetta, G.; Reali, G.C.; Kubecek, V.; Marek, J. Active-passive mode-locked Nd:YAG laser with passive negative feedback. Opt. Lett. 1990, 15, 734–736. [Google Scholar] [CrossRef] [PubMed]
- Burneika, K.; Grigonis, R.; Piskarskas, A.; Sinkyavichius, G.; Sirutkaitis, V. A subpicosecond high-stable neodymium-phosphate-glass laser with passive mode locking and negative feedback. Sov. J. Quantum Electron. 1988, 18, 1034–1035. [Google Scholar] [CrossRef]
- Val’shin, A.M.; Gordienko, V.M.; Krayushkin, S.V.; Platonenko, V.T.; Popov, V.K. Yttrium aluminate sources of ultrashort radiation pulses with a controlled resonator Q factor. Sov. J. Quantum Electron. 1986, 16, 1125–1127. [Google Scholar] [CrossRef]
- Heinz, P.; Kriegleder, W.; Laubereau, A. Feedback control of an actively-passively mode-locked Nd:Glass laser. Appl. Phys. A 1987, 43, 209–212. [Google Scholar] [CrossRef]
- Heinz, P.; Laubereau, A. Stable generation of subpicosecond pulses by feedback-controlled mode locking of a Nd:Glass laser. J. Opt. Soc. Am. B 1989, 6, 1574–1578. [Google Scholar] [CrossRef]
- Murray, J.E.; Lowdermilk, W.H. Nd:YAG regenerative amplifier. J. Appl. Phys. B 1980, 51, 3548–3555. [Google Scholar] [CrossRef]
- Zayhowski, J.J. Passively Q-switched microchip lasers. In Solid-State Lasers and Applications; Sennaroglu, A., Ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2007; pp. 1–76. [Google Scholar]
- Keller, U.; Weingarten, K.J.; Kärtner, F.X.; Kopf, D.; Braun, B.; Jung, I.D.; Fluck, R.; Honninger, C.; Matuschek, N.; Der Au, J.A. Semiconductor saturable absorber mirrors (SESAM’s) for femtosecond to nanosecond pulse generation in solid-state lasers. IEEE. Sel. Top. Quantum Electron. 1996, 2, 1077–1079. [Google Scholar] [CrossRef] [Green Version]
- Keller, U. Recent development in compact ultrafast lasers. Nature 2003, 424, 831–838. [Google Scholar] [CrossRef]
- Keller, U. Ultrafast solid-state laser oscillators: A success story for the last 20 years with no end in sight. Appl. Phys. B 2010, 100, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Karnaukhov, A.A.; Morozov, V.B.; Olenin, A.N.; Yakovlev, D.V. Precise synchronization of qcw pumped active-passive mode locked picosecond lasers. In Journal of Physics: Conference; IOP Publishing: Bristol, UK, 2013; Volume 414, p. 012027. [Google Scholar] [CrossRef] [Green Version]
- Palese, S.; Schilling, L.; Wang, X.D.; Dwayne Miller, R.J.; Guo, Z.; Brown, D. Frequency modulated mode locking of a diode laser pumped Nd: LiYF4 laser utilizing a KTiOPO4 phase modulator. Appl. Phys. Lett. 2007, 61, 2257–2259. [Google Scholar] [CrossRef]
- Mazur, M.M.; Mazur, L.I.; Sirotkin, A.A.; Ryabinin, A.V.; Shorin, V.N. Acousto-optic modulators of high-power laser radiation on the basis of KGW and KYW crystals. Quantum Electron. 2020, 50, 957–961. [Google Scholar] [CrossRef]
- Liu, J.; Xu, G.; Liu, F.; Kityk, I.; Liu, X.; Zhen, Z. Recent advances in polymer electro-optic modulators. RSC Adv. 2015, 5, 15784–15794. [Google Scholar] [CrossRef]
- Chen, A.; Murphy, E. Broadband Optical Modulators: Science, Technology, and Applications; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2012; p. 568. [Google Scholar]
- Rukin, S.N. Pulsed power technology based on semiconductor opening switches: A review. Rev. Sci. Instrum. 2020, 91, 011501. [Google Scholar] [CrossRef]
- Kesar, A.S. A compact, 10-kV, 2-ns risetime pulsed-power circuit based on off-the-shelf components. IEEE Trans. Plasma Sci. 2018, 46, 594–597. [Google Scholar] [CrossRef]
- Dwayne Miller, R.J.; Bonner, C.; Palese, S.; Pereyra, A.; Schling, L.; Walmsley, A.; Wang, D.; Guo, Z. Development and applications of electro-optics for high power systems. In Diode Pumping of Average-Power Solid State Lasers; International Society for Optics and Photonics: Bellingham, WA, USA, 1993; Volume 1865, pp. 100–110. [Google Scholar] [CrossRef]
- Bierlein, J.D.; Vanherzeele, H. Potassium titanyl phosphate: Properties and new applications. J. Opt. Soc. Am. B 1989, 6, 622–633. [Google Scholar] [CrossRef]
- Ebbers, C.A.; Velsko, S.P. High average power KTiOPO4 electrooptic Q-switch. Appl. Phys. Lett. 1995, 67, 4593–4595. [Google Scholar] [CrossRef]
- Roth, M.; Tseitlin, M.; Angert, N. Oxide crystals for electro-optic Q-switching of lasers. Glass Phys. Chem. 2005, 31, 86–95. [Google Scholar] [CrossRef]
- Rusov, V.A.; Serebryakov, V.A.; Kaplun, A.B.; Gorshakov, A.V. Using modulators based on KTP crystals in Nd:YAG lasers with high mean power. J. Opt. Technol. 2009, 76, 325–331. [Google Scholar] [CrossRef]
- Rusov, V.A.; Zakharova, N.A.; Kaplun, A.B.; Meshalkin, A.B.; Gorshakov, A.V. Study of the electrical-conductivity kinetics of KTP crystals used in the modulators of solid-state lasers. J. Opt. Technol. 2013, 80, 532–536. [Google Scholar] [CrossRef]
- Rusov, V.A.; Doroganov, S.V.; Kalintseva, N.A.; Narivonchik, A.S.; Skvortsov, D.V.; Serebryakov, V.A. Electro-optical modulators based on KTP crystals for high-power lasers in the mid-IR region. J. Opt. Technol. 2016, 83, 716–721. [Google Scholar] [CrossRef]
- Johnson, C.K.M.; Eden, D.D. Solid state modulation and demodulation of light with information from five television channels simultaneously. Proc. IEEE 1965, 53, 402–403. [Google Scholar] [CrossRef]
- Gorbunkov, M.V.; Konyashkin, A.V.; Kostryukov, P.V.; Morozov, V.B.; Olenin, A.N.; Rusov, V.A.; Telegin, L.S.; Tunkin, V.G.; Shabalin, Y.V.; Yakovlev, D.V. Pulsed-diode-pumped, all-solid-state, electro-optically controlled picosecond Nd:YAG lasers. Quantum Electron. 2005, 35, 2–6. [Google Scholar] [CrossRef]
- Mikheev, N.G.; Morozov, V.B.; Olenin, A.N.; Yakovlev, D.V. Picosecond lasers with the dynamical operation control. In Saratov Fall Meeting 2015: Third International Symposium on Optics and Biophotonics and Seventh Finnish-Russian Photonics and Laser Symposium (PALS); International Society for Optics and Photonics: Bellingham, WA, USA, 2016; Volume 9917, p. 99170A. [Google Scholar] [CrossRef]
- Mikheev, N.G.; Morozov, V.B.; Olenin, A.N.; Tunkin, V.G.; Yakovlev, D.V. Picosecond pulsed high-peak-power lasers. In Progress in Photon Science; Springer Series in Chemical Physics 119; Yamanouchi, K., Tunik, S., Makarov, V., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 63–87. [Google Scholar] [CrossRef]
- Morozov, V.B.; Olenin, A.N.; Tunkin, V.G.; Yakovlev, D.V. Operation conditions for a picosecond laser with an aberration thermal lens under longitudinal pulsed diode pumping. Quantum Electron. 2011, 41, 508–514. [Google Scholar] [CrossRef]
- Halliburton, L.E.; Scripsick, M.P. Mechanisms and point defects responsible for the formation of gray tracks in KTP. In Solid State Lasers and Nonlinear Crystals; International Society for Optics and Photonics: Bellingham, WA, USA, 1995; Volume 2379, pp. 235–244. [Google Scholar] [CrossRef]
- Zhanga, Q.; Fenga, G.; Hana, J.; Li, B.; Zhub, Q.; Xieb, X. High repetition rate laser pulse induced damage in KTP crystal: Gray-tracking and catastrophic damage. Optik 2011, 122, 1313–1318. [Google Scholar] [CrossRef]
- Scripsic, M.P.; Edwards, G.J.; Halliburton, L.E.; Belt, R.F.; Loiacono, G.M. Effect of crystal growth on Ti3+ centers in KTiOPO4. J. Appl. Phys. 1994, 76, 773–776. [Google Scholar] [CrossRef]
- Martin, M.J.; Bravo, D.; Sole, R.; Diaz, F.; Lopez, F.J.; Zaldo, C. Thermal reduction of KTiOPO4 single crystals. J. Appl. Phys. 1994, 76, 7510–7518. [Google Scholar] [CrossRef]
- Boulanger, B.; Rousseau, I.; Fève, J.P.; Maglione, M.; Menaert, B.; Marnier, G. Optical studies of laser-induced gray-tracking in KTP. IEEE J. Quantum Electron. 1999, 35, 281–286. [Google Scholar] [CrossRef] [Green Version]
- Dmitriev, V.G.; Gurzadyan, G.G.; Nikogosyan, D.N. Handbook of Nonlinear Optical Crystals, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1997; p. 413. [Google Scholar]
- Nikogosyan, D.N. Nonlinear Optical Crystals: A Complete Surway; Springer Since + Business Media Inc.: New York, NY, USA, 2005; p. 427. [Google Scholar]
- Fève, J.P.; Boulanger, B.; Guillien, Y. Efficient energy conversion for cubic third-harmonic generation that is phase matched in KTiOPO4. Opt. Lett. 2000, 25, 1373–1375. [Google Scholar] [CrossRef]
- Hansson, G.; Karlsson, H.; Wang, S.; Laurell, F. Transmission measurements in KTP and isomorphic compounds. Appl. Opt. 2000, 39, 5058–5069. [Google Scholar] [CrossRef]
- Pasiskavicius, V.; Canalias, C.; Laurell, F. High efficient stimulated Raman scattering of picosecond pulses in KTiOPO4. Appl. Phys. Lett. 2006, 88, 041110. [Google Scholar] [CrossRef]
- Vereshchagin, K.A.; Morozov, V.B.; Tunkin, V.G. Broadband noncollinear optical parametric amplification under low-frequency picosecond pump in homogeneous KTP crystal. J. Raman Spectrosc. 2018, 49, 1116–1127. [Google Scholar] [CrossRef]
- Red Optronics. KTP Crystal (KTiOPO4). Available online: http://www.redoptronics.com/KTP-crystal.html (accessed on 5 August 2021).
- EKSMA. KTP—Potassium Titanyl Phosphate. Available online: https://eksmaoptics.com/out/media/EKSMA_Optics_KTP_Crystals.pdf (accessed on 5 August 2021).
- CASIX. KTP Crystals. Available online: https://www.casix.com/products/crystal-products/non-linear-optical-crystals/ktp-crystal.shtml (accessed on 5 August 2021).
- Oseledchik, Y.S.; Pisarevsky, A.I.; Prosvirnin, A.L.; Starshenko, V.V.; Svitanko, N.V. Nonlinear optical properties of the flux grown RbTiOPO4 crystal. Opt. Mater. 1994, 3, 237–242. [Google Scholar] [CrossRef]
- Raicol Crystals. Nonlinear, Electrooptic Crystals and Elements. Available online: https://raicol.com/wp-content/uploads/catalog.pdf (accessed on 5 August 2021).
- Antsygin, V.D.; Mamrashev, A.A.; Nikolaev, N.A.; Potaturkin, O.I.; Kaplun, A.B. Terahertz optical properties of potassium titanyl phosphate crystals. Opt. Exp. 2014, 22, 25436–25443. [Google Scholar] [CrossRef]
- Raicol Crystals. RTP EO Devices. Available online: https://raicol.com/wp-content/uploads/rtp-eo-devices-updated-format.pdf (accessed on 5 August 2021).
- Gentec-EO. Beamage User Manual. USB 3.0 Beam Profiling Cameras. Available online: https://downloads.gentec-eo.com/prod/4a790cf9/103680-Manual-Beamage-Rev-20.pdf (accessed on 5 August 2021).
- Roth, M.; Angert, N.; Tseitlin, M.; Alexandrovski, A. On the optical quality of KTP crystals for nonlinear optical and electro-optic application. Opt. Mater. 2001, 16, 131–136. [Google Scholar] [CrossRef]
- Vazhinsky, O.T.; Vazhinskaya, K.S.; Pargachev, I.A.; Serebrennikov, L.Y.; Krakovsky, V.A. Thermo- and mechanically stable electro-optic Q-switches based on the RKTP crystal. Phys. Procedia 2017, 86, 170–175. [Google Scholar] [CrossRef]
- Wang, X.D.; Basseras, P.; Miller, R.J.D.; Vanherzeele, H. Investigation of KTiOPO4 electro-optic amplitude modulator. Appl. Phys. Lett. 1991, 59, 519–521. [Google Scholar] [CrossRef]
- Crystal Laser. RTP Electro-Optic Assemblies. Rubidium Titanyle Phosphate-RTiOPO4. Available online: https://www.cristal-laser.com/upload/produit_fiche/lg_1_1607619420_Fiche_RTP_assies_V3.pdf (accessed on 5 August 2021).
- Lasermetrics. Series 1147-RTP Electro-Optic Modulators and Q-Switches. Available online: http://lasermetrics.com/pdf/1147.pdf (accessed on 5 August 2021).
- Hildenbrand, A.; Wagner, F.R.; Natoli, J.-Y.; Commandré, V.; Albrecht, H.; Théodore, F. Laser damage investigation in nonlinear crystals: Study of KTiOPO4 (KTP) and RbTiOPO4 (RTP) crystals. Proc. SPIE 2008, 6998, 699815. [Google Scholar] [CrossRef]
- Pargachev, I.A.; Serebrennikov, L.Y.; Mandel, A.E.; Krakowsky, V.A.; Shandarov, S.M.; Shvartzman, G.I. Electro-optic modulators of laser radiation on the basis of high-resistance KTP crystals. Dokladi TUSURa. 2011, 24, 116–118. (In Russian) [Google Scholar]
- Koval, V.V.; Kornev, A.F.; Rusov, V.A. Comparison of Pockels cell based on X-cut and Y-cut KTP crystals under intense picosecond radiation. In Proceedings of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020. [Google Scholar] [CrossRef]
- Stephany, I.E. Piezo-optic resonances in crystals of the dihydrogen phosphate type. J. Opt. Soc. Am. 1965, 55, 136–142. [Google Scholar] [CrossRef]
- Belouet, C. DKDP crystals for use in the TITUS tube. Philips Technol. Rev. 1980, 39, 50–61. [Google Scholar]
- Kuzovkova, T.A.; Medvedev, S.K.; Nilov, E.V.; Frolov, S.V. Suppression of acoustic vibrations in electrooptic Q switches. Sov. J. Quantum Electron. 1991, 18, 1124–1127. [Google Scholar] [CrossRef]
- Kuzovkova, T.A.; Medvedev, S.K.; Nilov, E.V.; Frolov, S.V. Electrooptical modulator of laser quality with stable contrast. Instr. Exp. Technol. 1992, 1, 161–164. [Google Scholar]
- Georgiev, K.; Rusov, V.; Gagarsky, S.; Trifonov, A.; Buchvarov, I. High Energy, kHz-Repetition Rate, Q-Switched Nd:YAG Laser, Using an Electro-Optical Modulator and Variable Reflectivity Mirror, in Laser Congress 2019 (ASSL, LAC, LS&C), OSA Technical Digest 2019, p. JTh3A, 28. Available online: https://www.osapublishing.org/abstract.cfm?URI=LSC-2019-JTh3A.28 (accessed on 5 August 2021).






| Crystal, Ref | 1/cm | 1/cm | pm/V | pm/V | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| KTP [68] | 1.7400 | 1.7787 | 1.7469 | 1.7924 | 1.8304 | 1.8873 | −443 | 767 | 4.35 | 2.54 | 8.8 |
| KTP [69] | 1.7404 | 1.7797 | 1.7479 | 1.7897 | 1.8296 | 1.8877 | −112 | 625 | 3.9 | 1.95 | 125 |
| KTP [70] | 1.7377 | 1.7780 | 1.7453 | 1.7886 | 1.8297 | 1.8887 | −130 | 673 | 4.35 | 2.54 | 78 |
| RTP [71,72] | 1.7652 | 1.8067 | 1.7749 | 1.8205 | 1.8536 | 1.9160 | −738 | 318 | 4.1 | 3.3 | 0.29 |
| X-Cut KTP PC | Y-Cut KTP PC | X-Cut RTP PC | Y-Cut RTP PC | |
|---|---|---|---|---|
| SH | (1.1 ± 0.3) × 102 | 1 | 4 to 50 | 2 to 90 |
| TH | (0.9 ± 0.2) × 10−3 | (4 ± 1) × 10−6 | 5 × 10−7 to 10−3 | 10−7 to 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morozov, V.; Olenin, A.; Tunkin, V.; Yakovlev, D.; Rusov, V.; Gorchakov, A.; Doroganov, S. Picosecond Pulsed-Periodic High-Peak Power Nd:YAG Laser Operationally Controlled by KTP-Based Pockels Cell. Crystals 2022, 12, 368. https://doi.org/10.3390/cryst12030368
Morozov V, Olenin A, Tunkin V, Yakovlev D, Rusov V, Gorchakov A, Doroganov S. Picosecond Pulsed-Periodic High-Peak Power Nd:YAG Laser Operationally Controlled by KTP-Based Pockels Cell. Crystals. 2022; 12(3):368. https://doi.org/10.3390/cryst12030368
Chicago/Turabian StyleMorozov, Vyacheslav, Andrey Olenin, Vladimir Tunkin, Dmitry Yakovlev, Vladimir Rusov, Alexander Gorchakov, and Sergei Doroganov. 2022. "Picosecond Pulsed-Periodic High-Peak Power Nd:YAG Laser Operationally Controlled by KTP-Based Pockels Cell" Crystals 12, no. 3: 368. https://doi.org/10.3390/cryst12030368
APA StyleMorozov, V., Olenin, A., Tunkin, V., Yakovlev, D., Rusov, V., Gorchakov, A., & Doroganov, S. (2022). Picosecond Pulsed-Periodic High-Peak Power Nd:YAG Laser Operationally Controlled by KTP-Based Pockels Cell. Crystals, 12(3), 368. https://doi.org/10.3390/cryst12030368





