A Multi-Objective Identification of DEM Microparameters for Brittle Materials
1. Introduction
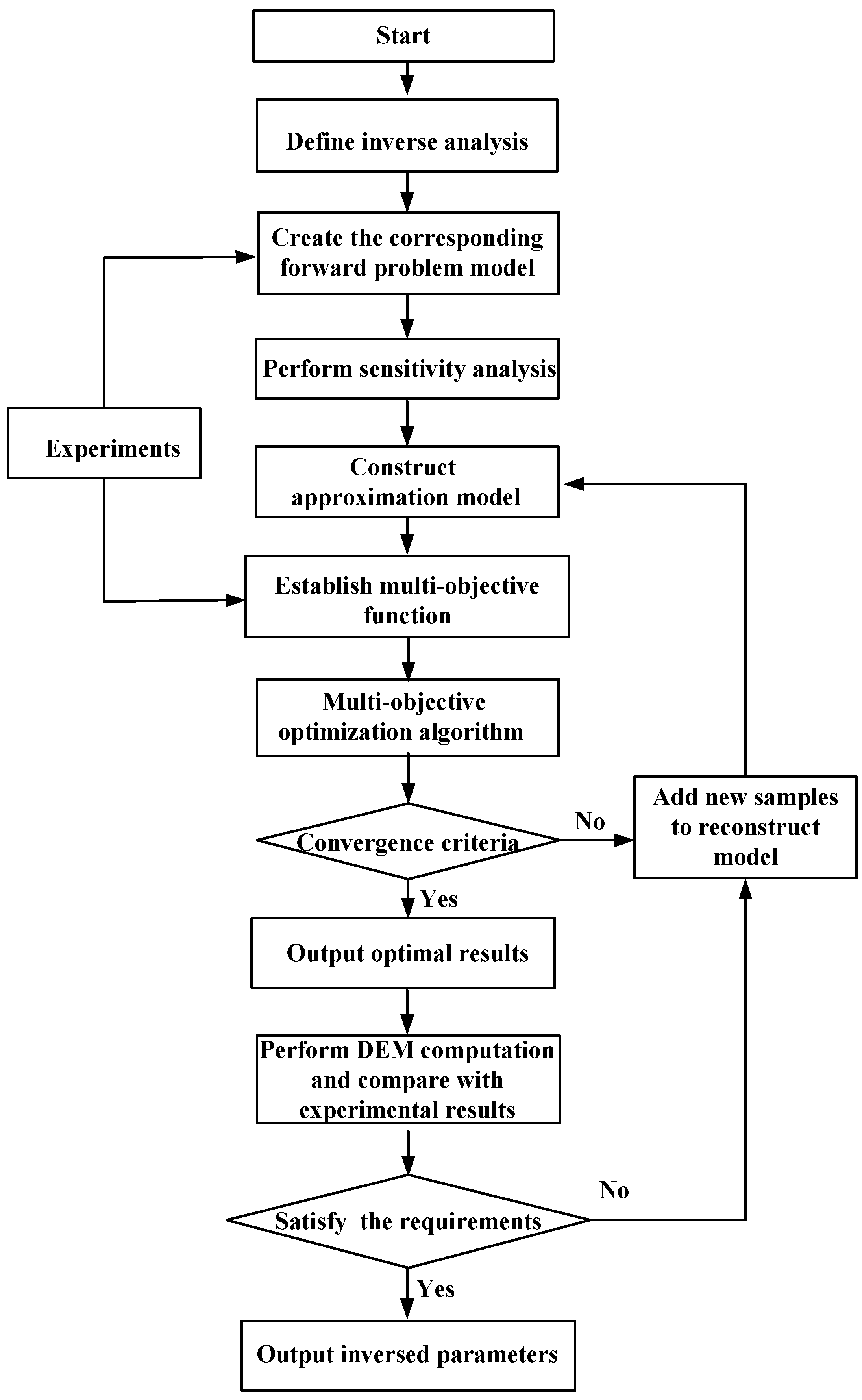
2. Multi-Objective Identification Technique
3. DEM Microparameters Identification for Granite
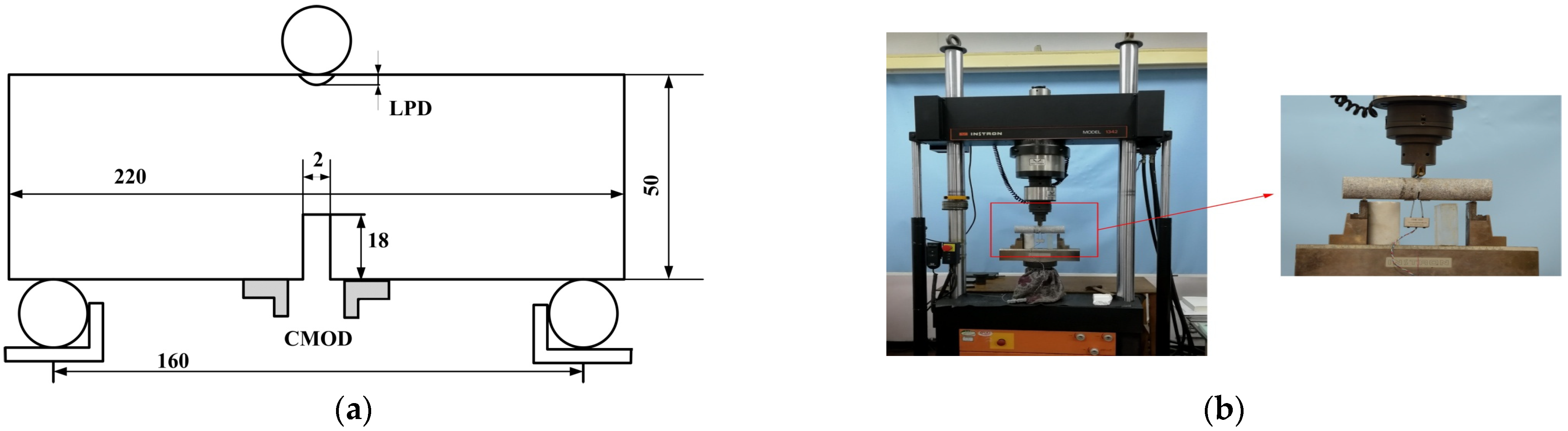
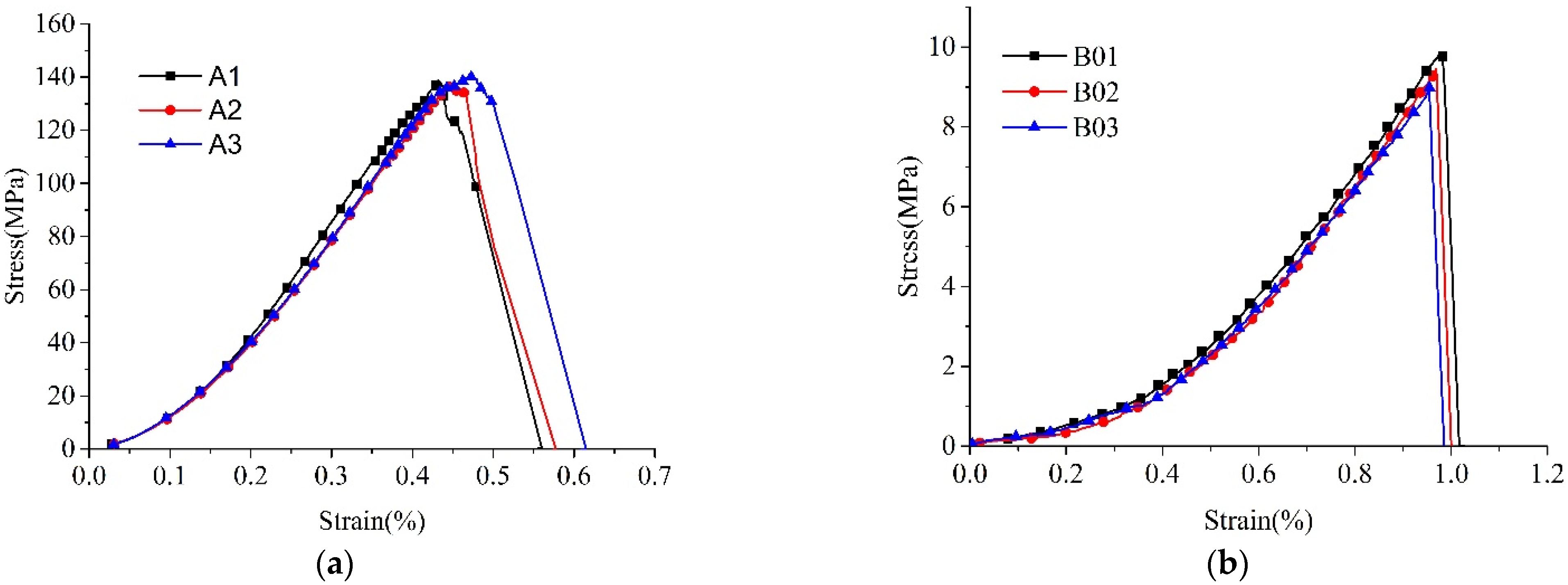
3.1. Experimental Measurement
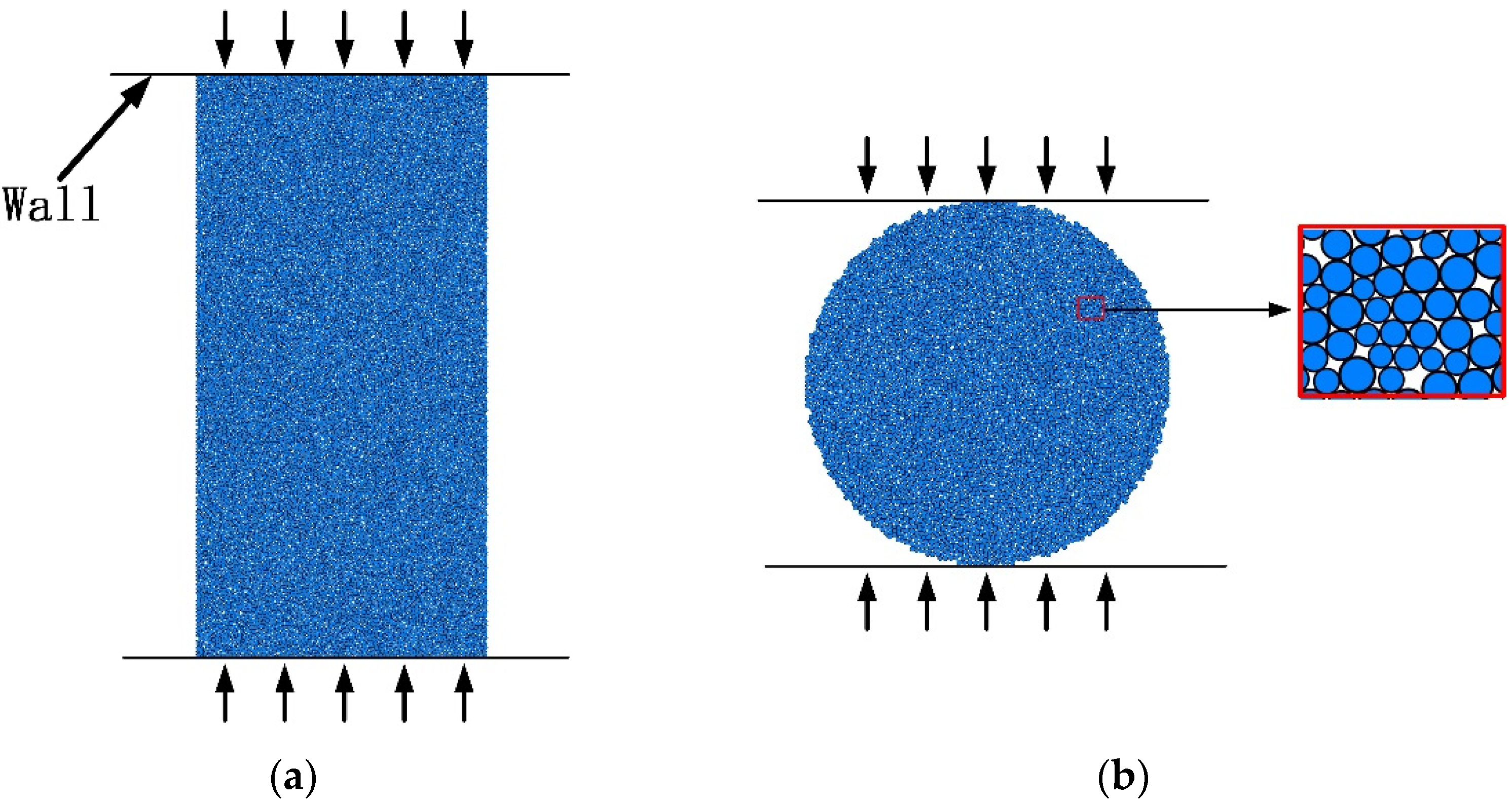
3.2. DEM Model and Its Microparameters
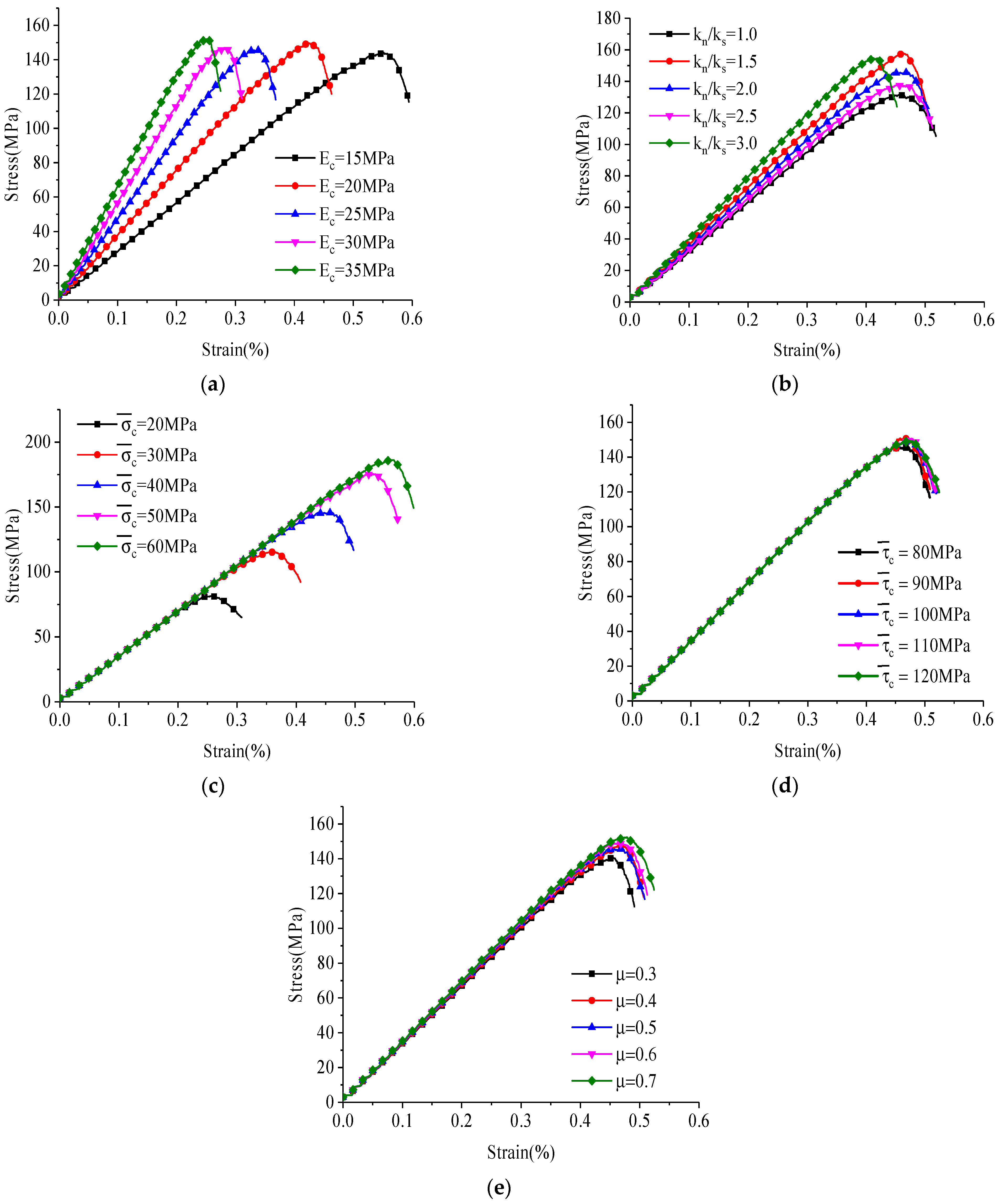
3.3. Parameter Sensitivity Analysis
3.4. Approximation Model Technique
3.5. Micro Multi-Objective Genetic Algorithm (µMOGA)
4. Results and Discussion
4.1. Results
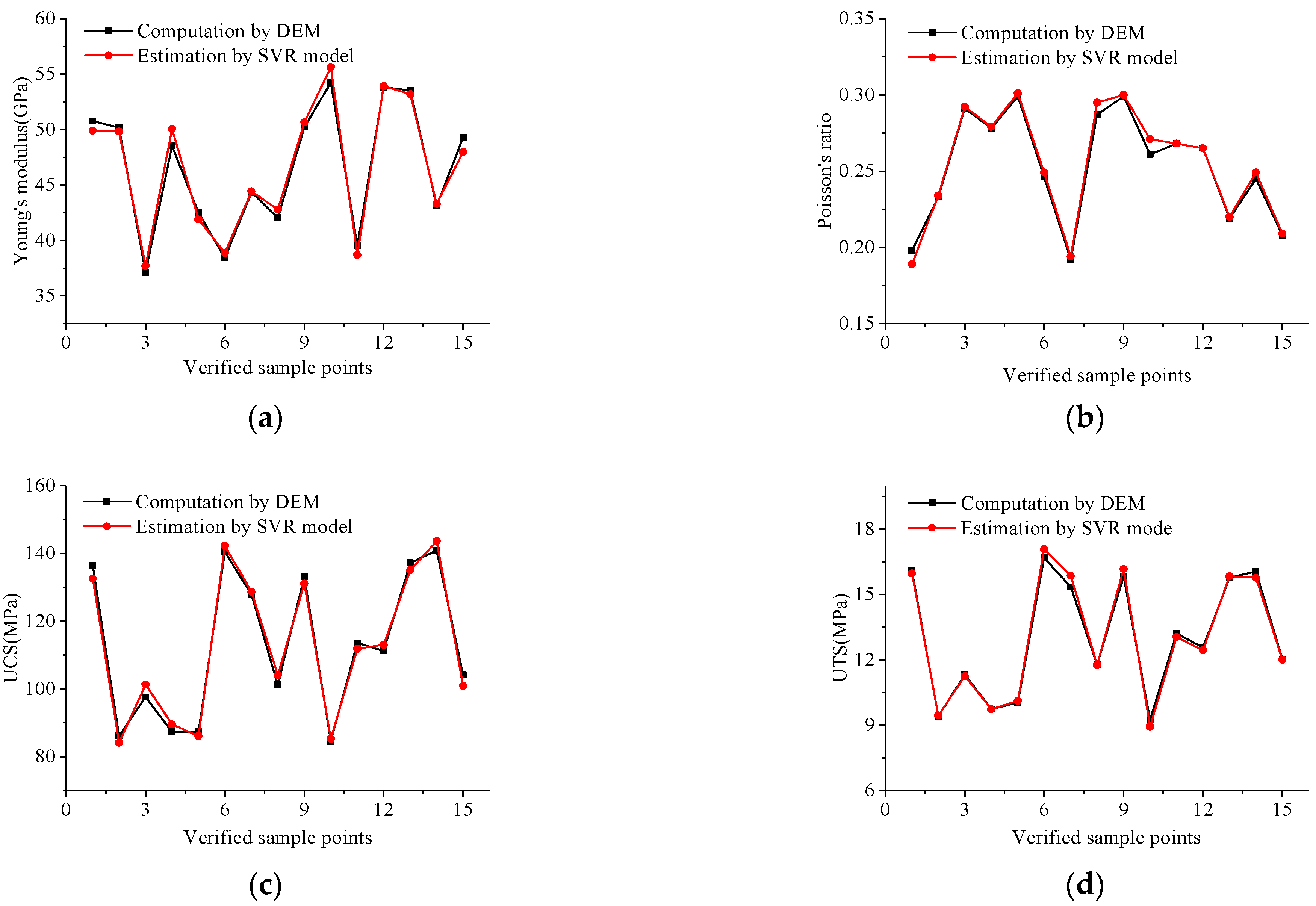
4.2. Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Sinnott, M.D.; Cleary, P.W. The effect of particle shape on mixing in a high shear mixer. Comput. Part. Mech. 2016, 3, 477–504. [Google Scholar] [CrossRef]
- Alian, M.; Ein-Mozaffari, F.; Upreti, S.R. Analysis of the mixing of solid particles in a plowshare mixer via discrete element method (DEM). Powder Technol. 2015, 274, 77–87. [Google Scholar] [CrossRef]
- Müller, P.; Tomas, J. Simulation and calibration of granules using the discrete element method. Particuology 2014, 12, 40–43. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, T.; Dai, F.; Jiang, M.; Zhou, G.G. DEM analyses of rock block shape effect on the response of rockfall impact against a soil buffering layer. Eng. Geol. 2019, 249, 60–70. [Google Scholar] [CrossRef]
- Van Wyk, G.; Els, D.; Akdogan, G.; Bradshaw, S.; Sacks, N. Discrete element simulation of tribological interactions in rock cutting. Int. J. Rock Mech. Min. Sci. 2014, 65, 8–19. [Google Scholar] [CrossRef]
- Wang, Y.; Tonon, F. Discrete Element Modeling of Drop Tests. Rock Mech. Rock Eng. 2012, 45, 863–869. [Google Scholar] [CrossRef]
- Karampinos, E.; Hadjigeorgiou, J.; Hazzard, J.; Turcotte, P. Discrete element modelling of the buckling phenomenon in deep hard rock mines. Int. J. Rock Mech. Min. Sci. 2015, 80, 346–356. [Google Scholar] [CrossRef]
- Espada, M.; Muralha, J.; Lemos, J.V.; Jiang, Q.; Feng, X.-T.; Fan, Q.; Fan, Y. Safety Analysis of the Left Bank Excavation Slopes of Baihetan Arch Dam Foundation Using a Discrete Element Model. Rock Mech. Rock Eng. 2018, 51, 2597–2615. [Google Scholar] [CrossRef]
- Scholtès, L.; Donzé, F.-V. A DEM model for soft and hard rocks: Role of grain interlocking on strength. J. Mech. Phys. Solids 2013, 61, 352–369. [Google Scholar] [CrossRef]
- Fakhimi, A. Application of slightly overlapped circular particles assembly in numerical simulation of rocks with high friction angles. Eng. Geol. 2004, 74, 129–138. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar] [CrossRef] [Green Version]
- Aster, R.; Borchers, B. Parameter Estimation and Inverse Problem; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Han, X.; Liu, G.R. Computational Inverse Technique for Material Characterization of Functionally Graded Materials. AIAA J. 2003, 41, 288–295. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Benvenuti, L.; Kloss, C.; Pirker, S. Identification of DEM simulation parameters by Artificial Neural Networks and bulk experiments. Powder Technol. 2016, 291, 456–465. [Google Scholar] [CrossRef]
- Coetzee, C. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Do, H.; Aragón, A.M.; Schott, D.L. A calibration framework for discrete element model parameters using genetic algorithms. Adv. Powder Technol. 2018, 29, 1393–1403. [Google Scholar] [CrossRef]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Tawadrous, A.S.; DeGagné, D. Prediction of uniaxial compression PFC3D model micro-properties using artificial neural net-works. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 1953–1962. [Google Scholar] [CrossRef]
- Kazerani, T. Effect of micromechanical parameters of microstructure on compressive and tensile failure process of rock. Int. J. Rock Mech. Min. Sci. 2013, 64, 44–55. [Google Scholar] [CrossRef]
- Do, H.Q.; Aragón, A.M.; Schott, D.L. Automated discrete element method calibration using genetic and optimization algo-rithms. EPJ Web Conf. EDP Sci. 2017, 140, 15011. [Google Scholar] [CrossRef]
- De Simone, M.; Souza, L.M.; Roehl, D. Estimating DEM microparameters for uniaxial compression simulation with genetic programming. Int. J. Rock Mech. Min. Sci. 2019, 118, 33–41. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Chiandussi, G.; Codegone, M.; Ferrero, S.; Varesio, F.E. Comparison of multi-objective optimization methodologies for engineering applications. Comput. Math. Appl. 2012, 63, 912–942. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Han, X.; Liu, G.; Jiang, C.; Zhao, Z. An efficient multi-objective optimization method for black-box functions using sequential approximate technique. Appl. Soft Comput. 2012, 12, 14–27. [Google Scholar] [CrossRef]
- Milani, A.; Dabboussi, W.; Nemes, J.; Abeyaratne, R. An improved multi-objective identification of Johnson–Cook material parameters. Int. J. Impact Eng. 2009, 36, 294–302. [Google Scholar] [CrossRef]
- Papon, A.; Riou, Y.; Dano, C.; Hicher, P.-Y. Single-and multi-objective genetic algorithm optimization for identifying soil parameters. Int. J. Numer. Anal. Methods Géoméch. 2011, 36, 597–618. [Google Scholar] [CrossRef] [Green Version]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Jiang, S.; Li, X.; Tan, Y.; Liu, H.; Xu, Z.; Chen, R. Discrete element simulation of SiC ceramic with pre-existing random flaws under uniaxial compression. Ceram. Int. 2017, 43, 13717–13728. [Google Scholar] [CrossRef]
- Yang, B.; Jiao, Y. A study on the effects of micro-parameters on macro-properties for specimens created by bonded particles. Eng. Comput. 2006, 23, 607–631. [Google Scholar] [CrossRef]
- Clarke, S.M.; Griebsch, J.H.; Simpson, T.W. Analysis of Support Vector Regression for Approximation of Complex Engineering Analyses. J. Mech. Des. 2004, 127, 1077–1087. [Google Scholar] [CrossRef]
- Peter, G.; Bradley, J. Optimal Design of Experiments: A Case Study Approach; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Liu, G.P.; Han, X. A micro multi-objective genetic algorithm for multi-objective optimizations. In Proceedings of the Fourth China-Japan-Korea Joint Symposium on Optimization of Structural and Mechanical Systems, Kunming, China, 6–9 November 2006. [Google Scholar]









(kg/m3) | (GPa) | (MPa) | (MPa) | (MPa·m1/2) | |
|---|---|---|---|---|---|
| 2622 | 41.5 | 0.23 | 138.8 | 9.5 | 1.057 |
| No. | μ | ||||
|---|---|---|---|---|---|
| 1 | 15 | 1 | 20 | 80 | 0.3 |
| 2 | 20 | 1.5 | 30 | 90 | 0.4 |
| 3 | 30 | 2.5 | 50 | 110 | 0.6 |
| 4 | 35 | 3 | 60 | 120 | 0.7 |
| Number | Computational Responses | ||||||
|---|---|---|---|---|---|---|---|
| (GPa) | (MPa) | (GPa) | (MPa) | (MPa) | |||
| 1 | 20.03 | 2.92 | 36.30 | 35.14 | 0.300 | 119.37 | 14.4 |
| 2 | 26.00 | 2.87 | 28.24 | 45.94 | 0.296 | 99.08 | 11.47 |
| 3 | 29.18 | 2.77 | 21.64 | 52.07 | 0.298 | 79.61 | 8.93 |
| 4 | 27.86 | 1.85 | 24.85 | 53.83 | 0.224 | 100.2 | 11.24 |
| 5 | 21.51 | 2.39 | 22.32 | 39.5 | 0.267 | 84.93 | 9.56 |
| 6 | 23.74 | 1.51 | 25.34 | 47.6 | 0.186 | 103.55 | 12.22 |
| 7 | 25.23 | 2.19 | 29.19 | 47.07 | 0.252 | 110.9 | 12.66 |
| 8 | 29.41 | 1.94 | 31.26 | 56.37 | 0.231 | 122.75 | 13.91 |
| 9 | 21.18 | 1.77 | 29.93 | 41.14 | 0.214 | 116.3 | 13.62 |
| 10 | 28.99 | 1.83 | 38.62 | 56.04 | 0.221 | 145.69 | 17.27 |
| 11 | 27.61 | 2.13 | 30.40 | 51.91 | 0.247 | 117.2 | 13.34 |
| 12 | 24.09 | 1.67 | 39.03 | 47.38 | 0.205 | 146.03 | 18.07 |
| 13 | 21.84 | 2.41 | 32.42 | 39.93 | 0.268 | 115.52 | 13.55 |
| 14 | 24.95 | 2.23 | 39.49 | 46.26 | 0.257 | 141.31 | 16.89 |
| 15 | 25.55 | 2.62 | 23.58 | 46.2 | 0.282 | 86.47 | 9.8 |
| 16 | 20.80 | 2.68 | 34.82 | 37.16 | 0.288 | 119.87 | 14.24 |
| 17 | 26.94 | 2.51 | 26.04 | 48.77 | 0.277 | 97.78 | 10.9 |
| 18 | 22.09 | 1.56 | 33.35 | 44.08 | 0.193 | 130.77 | 15.84 |
| 19 | 24.59 | 1.64 | 35.87 | 48.65 | 0.201 | 137.11 | 16.87 |
| 20 | 26.03 | 1.97 | 21.24 | 49.63 | 0.232 | 86.87 | 9.47 |
| 21 | 22.58 | 2.27 | 24.20 | 41.71 | 0.258 | 92.09 | 10.38 |
| 22 | 23.08 | 2.57 | 23.27 | 41.79 | 0.279 | 85.65 | 9.7 |
| 23 | 27.27 | 2.06 | 32.98 | 51.43 | 0.243 | 125.93 | 14.45 |
| 24 | 22.90 | 2.84 | 37.65 | 40.45 | 0.297 | 128.38 | 15.17 |
| 25 | 28.64 | 2.73 | 26.76 | 51.15 | 0.289 | 97.3 | 11.02 |
| 26 | 29.81 | 2.99 | 37.01 | 52.15 | 0.303 | 125.06 | 14.73 |
| 27 | 28.11 | 2.30 | 34.40 | 51.81 | 0.260 | 127.06 | 14.61 |
| 28 | 23.48 | 2.02 | 20.22 | 44.53 | 0.237 | 81.45 | 8.96 |
| 29 | 26.52 | 1.73 | 31.51 | 51.86 | 0.211 | 123.04 | 14.55 |
| 30 | 20.45 | 2.47 | 27.65 | 37.08 | 0.272 | 100.86 | 11.53 |
| Number | Input Parameter | ||
|---|---|---|---|
| 1 | 25.67 | 1.62 | 34.20 |
| 2 | 26.37 | 1.97 | 21.07 |
| 3 | 20.90 | 2.75 | 27.67 |
| 4 | 26.86 | 2.53 | 23.18 |
| 5 | 24.16 | 2.91 | 24.70 |
| 6 | 20.48 | 2.10 | 38.20 |
| 7 | 22.21 | 1.55 | 32.23 |
| 8 | 23.56 | 2.69 | 28.55 |
| 9 | 28.56 | 2.89 | 39.27 |
| 10 | 29.25 | 2.27 | 21.44 |
| 11 | 21.67 | 2.42 | 31.62 |
| 12 | 29.36 | 2.37 | 29.66 |
| 13 | 27.77 | 1.82 | 35.00 |
| 14 | 22.94 | 2.08 | 36.83 |
| 15 | 25.18 | 1.71 | 25.91 |
| Parameters | A | B | C | D |
|---|---|---|---|---|
| (GPa) | 23.3 | 20.9 | 21.7 | 22.2 |
| 2.43 | 2.09 | 2.23 | 2.19 | |
| (MPa) | 32.5 | 33.4 | 34.5 | 32.5 |
| 0.258 | 0.224 | 0.196 | 0.175 | |
| 0.113 | 0.118 | 0.128 | 0.141 |
| Responses | A | B | C | D | Experiment |
|---|---|---|---|---|---|
| (GPa) | 42.3 | 39.3 | 40.4 | 40.4 | 41.5 |
| 0.248 | 0.244 | 0.249 | 0.249 | 0.23 | |
| (MPa) | 117.2 | 125.5 | 125.2 | 115.4 | 138.8 |
| (MPa) | 10.47 | 10.51 | 10.66 | 10.78 | 9.5 |
| 0.254 | 0.213 | 0.209 | 0.194 | ||
| 0.102 | 0.107 | 0.122 | 0.135 |
| Response | DEM Calculation | Experiment | Relative Error |
|---|---|---|---|
| (MPa·m1/2) | 1.152 | 1.057 | 8.98% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Wang, X.; Xiao, X.; Hu, C.; Peng, R.; Wang, Y. A Multi-Objective Identification of DEM Microparameters for Brittle Materials. Crystals 2022, 12, 387. https://doi.org/10.3390/cryst12030387
Chen R, Wang X, Xiao X, Hu C, Peng R, Wang Y. A Multi-Objective Identification of DEM Microparameters for Brittle Materials. Crystals. 2022; 12(3):387. https://doi.org/10.3390/cryst12030387
Chicago/Turabian StyleChen, Rui, Xu Wang, Xiangwu Xiao, Congfang Hu, Ruitao Peng, and Yong Wang. 2022. "A Multi-Objective Identification of DEM Microparameters for Brittle Materials" Crystals 12, no. 3: 387. https://doi.org/10.3390/cryst12030387
APA StyleChen, R., Wang, X., Xiao, X., Hu, C., Peng, R., & Wang, Y. (2022). A Multi-Objective Identification of DEM Microparameters for Brittle Materials. Crystals, 12(3), 387. https://doi.org/10.3390/cryst12030387






