Self-Diffusion of Individual Adsorbed Water Molecules at Rutile (110) and Anatase (101) TiO2 Interfaces from Molecular Dynamics
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussions
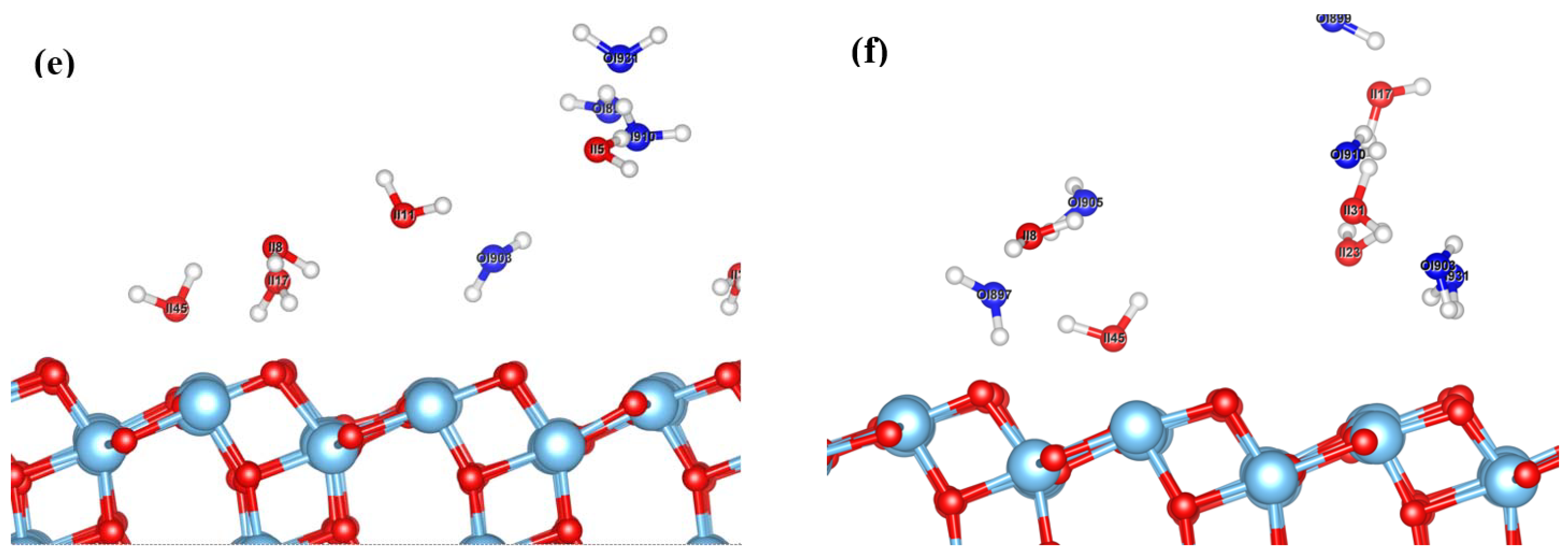
3.1. Dynamic Interfacial Structure and Layers Identification
3.2. Diffusivity and Mobility of Adsorbed Water Layers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fujishima, A.; Honda, K. Electrochemical Photolysis of Water at a Semiconductor Electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Henderson, M.A. A surface science perspective on TiO2 photocatalysis. Surf. Sci. Rep. 2011, 66, 185–297. [Google Scholar] [CrossRef]
- Bourikas, K.; Kordulis, C.; Lycourghiotis, A. Titanium Dioxide (Anatase and Rutile): Surface Chemistry, Liquid–Solid Interface Chemistry, and Scientific Synthesis of Supported Catalysts. Chem. Rev. 2014, 114, 9754–9823. [Google Scholar] [CrossRef]
- Park, N.-G.; van de Lagemaat, J.; Frank, A.J. Comparison of Dye-Sensitized Rutile- and Anatase-Based TiO2 Solar Cells. J. Phys. Chem. B 2000, 104, 8989–8994. [Google Scholar] [CrossRef] [Green Version]
- Pang, C.L.; Lindsay, R.; Thornton, G. Structure of Clean and Adsorbate-Covered Single-Crystal Rutile TiO2 Surfaces. Chem. Rev. 2013, 113, 3887–3948. [Google Scholar] [CrossRef]
- Kavan, L.; Grätzel, M.; Gilbert, S.E.; Klemenz, C.; Scheel, H.J. Electrochemical and Photoelectrochemical Investigation of Single-Crystal Anatase. J. Am. Chem. Soc. 1996, 118, 6716–6723. [Google Scholar] [CrossRef]
- Zhao, Z.-Y.; Li, Z.; Zou, Z. Surface properties and electronic structure of low-index stoichiometric anatase TiO2 surfaces. J. Phys. Condens. Matter 2010, 22, 175008. [Google Scholar] [CrossRef]
- Zhang, H.; Banfield, J.F. Thermodynamic analysis of phase stability of nanocrystalline titania. J. Mater. Chem. 1998, 8, 2073–2076. [Google Scholar] [CrossRef]
- Ranade, M.R.; Navrotsky, A.; Zhang, H.Z.; Banfield, J.; Elder, S.H.; Zaban, A.; Borse, P.; Kulkarni, S.K.; Doran, G.; Whitfield, H.J. Energetics of nanocrystalline TiO2. Proc. Natl. Acad. Sci. USA 2002, 99, 6476–6481. [Google Scholar] [CrossRef] [Green Version]
- Pang, C.L.; Lindsay, R.; Thornton, G. Chemical reactions on rutile TiO2 (110). Chem. Soc. Rev. 2008, 37, 2328–2353. [Google Scholar] [CrossRef]
- Mattioli, G.; Filippone, F.; Caminiti, R.; Bonapasta, A.A. Short Hydrogen Bonds at the Water/TiO2 (Anatase) Interface. J. Phys. Chem. C 2008, 112, 13579–13586. [Google Scholar] [CrossRef]
- Kumar, N.; Neogi, S.; Kent, P.R.C.; Bandura, A.; Kubicki, J.; Wesolowski, D.J.; Cole, D.; Sofo, J. Hydrogen Bonds and Vibrations of Water on (110) Rutile. J. Phys. Chem. C 2009, 113, 13732–13740. [Google Scholar] [CrossRef]
- Russo, D.; Teixeira, J.; Kneller, L.; Copley, J.R.D.; Ollivier, J.; Perticaroli, S.; Pellegrini, E.; Gonzalez, M.A. Vibrational Density of States of Hydration Water at Biomolecular Sites: Hydrophobicity Promotes Low Density Amorphous Ice Behavior. J. Am. Chem. Soc. 2011, 133, 4882–4888. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Fenter, P.; Cheng, L.; Sturchio, N.C.; Bedzyk, M.J.; Předota, M.; Bandura, A.; Kubicki, J.D.; Lvov, S.N.; Cummings, P.T.; et al. Ion Adsorption at the Rutile−Water Interface: Linking Molecular and Macroscopic Properties. Langmuir 2004, 20, 4954–4969. [Google Scholar] [CrossRef] [PubMed]
- Parez, S.; Předota, M.; Machesky, M. Dielectric Properties of Water at Rutile and Graphite Surfaces: Effect of Molecular Structure. J. Phys. Chem. C 2014, 118, 4818–4834. [Google Scholar] [CrossRef]
- Předota, M.; Bandura, A.; Cummings, P.; Kubicki, J.; Wesolowski, D.J.; Chialvo, A.; Machesky, M.L. Electric Double Layer at the Rutile (110) Surface. 1. Structure of Surfaces and Interfacial Water from Molecular Dynamics by Use of ab Initio Potentials. J. Phys. Chem. B 2004, 108, 12049–12060. [Google Scholar] [CrossRef]
- Předota, M.; Zhang, Z.; Fenter, P.; Wesolowski, D.J.; Cummings, P. Electric Double Layer at the Rutile (110) Surface. 2. Adsorption of Ions from Molecular Dynamics and X-ray Experiments. J. Phys. Chem. B 2004, 108, 12061–12072. [Google Scholar] [CrossRef]
- Předota, M.; Cummings, P.; Wesolowski, D.J. Electric Double Layer at the Rutile (110) Surface. 3. Inhomogeneous Viscosity and Diffusivity Measurement by Computer Simulations. J. Phys. Chem. C 2007, 111, 3071–3079. [Google Scholar] [CrossRef]
- Mamontov, E.; Wesolowski, D.J.; Vlcek, L.; Cummings, P.T.; Rosenqvist, J.; Wang, W.; Cole, D.R. Dynamics of Hydration Water on Rutile Studied by Backscattering Neutron Spectroscopy and Molecular Dynamcis Simulation. J. Phys. Chem. C 2008, 112, 12334–12341. [Google Scholar] [CrossRef]
- Mamontov, E.; Vlcek, L.; Wesolowski, D.J.; Cummings, P.T.; Rosenqvist, J.; Wang, W.; Cole, D.R.; Anovitz, L.M.; Gasparovic, G. Suppression of the dynamic transition in surface water at low hydration levels: A study of water on rutile. Phys. Rev. E 2009, 79, 051504. [Google Scholar] [CrossRef] [PubMed]
- English, N.J.; Waldron, C.J. Perspectives on external electric fields in molecular simulation: Progress, prospects and challenges. Phys. Chem. Chem. Phys. 2015, 17, 12407–12440. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.J.; English, N.J. Influence of external static and oscillating electric fields on self-diffusion of water from molecular dynamics. J. Mol. Liq. 2020, 327, 114788. [Google Scholar] [CrossRef]
- Nandi, P.K.; English, N.J. Role of hydration layer in dynamical crossover in proteins: Insights from translational self-diffusivity. J. Phys. Chem. B 2016, 120, 12031. [Google Scholar] [CrossRef]
- Agosta, L.; Brandt, E.G.; Lyubartsev, A.P. Diffusion and reaction pathways of water near fully hydrated TiO2 surfaces from ab initio molecular dynamics. J. Chem. Phys. 2017, 147, 024704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swope, W.C.; Andersen, C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium con-stants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- O’carroll, D.; Martinez-Gonzalez, J.A.; English, N.J. Coherency spectral analysis of interfacial water at TiO2 surfaces. Mol. Simul. 2020, 48, 1–10. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Wu, Y.; Tepper, H.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503. [Google Scholar] [CrossRef] [PubMed]
- Mahoney, M.W.; Jorgensen, W.L. Diffusion constant of the TIP5P model of liquid water. J. Chem. Phys. 2001, 114, 363. [Google Scholar] [CrossRef] [Green Version]
- Fernández, R.G.; Abascal, J.; Vega, C. The melting point of ice Ih for common water models calculated from direct coexistence of the solid-liquid interface. J. Chem. Phys. 2006, 124, 144506. [Google Scholar] [CrossRef] [PubMed]
- Kavathekar, R.S.; Dev, P.; English, N.J.; MacElroy, J. Molecular dynamics study of water in contact with the TiO2 rutile-110, 100, 101, 001 and anatase-101, 001 surface. Mol. Phys. 2011, 109, 1649–1656. [Google Scholar] [CrossRef] [Green Version]
- Kavathekar, R.S.; English, N.J.; MacElroy, J.M.D. Study of Translational, Librational and Intra-molecular Motion of Adsorbed Liquid Monolayers at Various TiO2 Interfaces. Mol. Phys. 2011, 109, 2645–2654. [Google Scholar] [CrossRef]
- Kavathekar, R.S.; English, N.J.; MacElroy, J. Spatial distribution of adsorbed water layers at the TiO2 rutile and anatase interfaces. Chem. Phys. Lett. 2012, 554, 102–106. [Google Scholar] [CrossRef]
- English, N.J.; Kavathekar, R.S.; MacElroy, J.M.D. Hydrogen Bond Dynamical Properties of Absorbed Liquid Water Monolayers with Various TiO2 Interfaces. Mol. Phys. 2012, 110, 2919–2925. [Google Scholar] [CrossRef]
- English, N.J. Diffusivity and Mobility of Adsorbed Water Layers at TiO2 Rutile and Anatase Interfaces. Crystals 2015, 6, 1. [Google Scholar] [CrossRef] [Green Version]
- Matsui, M.; Akaogi, M. Molecular Dynamics Simulation of the Structural and Physical Properties of the Four Polymorphs of TiO2. Mol. Simul. 1991, 6, 239–244. [Google Scholar] [CrossRef]
- Bandura, A.V.; Kubicki, J.D. Derivation of Force Field Parameters for TiO2−H2O Systems from ab Initio Calculations. J. Phys. Chem. B 2003, 107, 11072–11081. [Google Scholar] [CrossRef]
- Futera, Z.; English, N.J. Exploring Rutile (110) and Anatase (101) TiO2 Water Interfaces by Reactive Force-Field Simulations. J. Phys. Chem. C 2017, 121, 6701–6711. [Google Scholar] [CrossRef]
- Reinhardt, A.; Doye, J.P.K.; Noya, E.G.; Vega, C. Local order parameters for use in driving homogeneous ice nucleation with all-atom models of water. J. Chem. Phys. 2012, 137, 194504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-Orientational Order in Liquids and Glasses. Phys. Rev. B 1983, 28, 784. [Google Scholar] [CrossRef]
- O’Carroll, D.; English, N.J. Self-ordering water molecules at TiO2 interfaces: Advances in structural classification. J. Chem. Phys. 2020, 153, 064502. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Structure and Hydrogen Bond Dynamics of Water-Dimethyl Sulfoxide Mixtures by Computer Simulations. J. Chem. Phys. 1993, 98, 8160. [Google Scholar] [CrossRef] [Green Version]
- Lechner, W.; Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 2008, 129, 114707. [Google Scholar] [CrossRef]
- Onda, K.; Li, B.; Zhao, J.; Jordan, K.D.; Yang, J.; Petek, H. Wet electrons at the H2O/TiO2 (110) surface. Science 2005, 308, 1154–1158. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Li, Z.; Zou, Z. Structure and properties of water on the anatase TiO2 101 surface: From single-molecule adsorption to interface formation. J. Phys. Chem. C 2012, 116, 11054–11061. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, C.; Huang, L. Molecular Dynamics Simulation of First-Adsorbed Water Layer at Titanium Dioxide Surfaces. J. Chem. Eng. Data 2018, 63, 2420–2429. [Google Scholar] [CrossRef]
- Lamanna, R.; Delmelle, M.; Cannistraro, S. Role of hydrogen-bond cooperativity and free-volume fluctuations in the non-Arrhenius behavior of water self-diffusion: A continuity-of-states model. Phys. Rev. E 1994, 49, 2841–2850. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, A.A.; Kolesnikov, A.I.; Ross, N.L.; Boerio-Goates, J.; Woodfield, B.F.; Li, G.; Navrotsky, A. Dynamics of Water Confined on a TiO2 (Anatase) Surface. J. Phys. Chem. A 2007, 111, 12584–12588. [Google Scholar] [CrossRef]
- Spencer, E.C.; Levchenko, A.A.; Ross, N.; Kolesnikov, A.; Boerio-Goates, J.; Woodfield, B.F.; Navrotsky, A.; Li, G. Inelastic Neutron Scattering Study of Confined Surface Water on Rutile Nanoparticles. J. Phys. Chem. A 2009, 113, 2796–2800. [Google Scholar] [CrossRef]
- Nosaka, A.Y.; Fujiwara, T.; Yagi, H.; Akutsu, H.; Nosaka, Y. Characteristics of Water Adsorbed on TiO2 Photocatalytic Systems with Increasing Temperature as Studied by Solid-State1H NMR Spectroscopy. J. Phys. Chem. B 2004, 108, 9121–9125. [Google Scholar] [CrossRef]
- Rastogi, A.; Suresh, A.K.; Ghosh, S.J. Thermodynamics: Physical Chemistry of Aqueous Systems; InTech: London, UK, 2011; pp. 351–364. [Google Scholar]
- McDonnell, K.A.; Wadnerkar, N.; English, N.J.; Rahman, M.; Dowling, D. Photo-active and optical properties of bismuth ferrite (BiFeO3): An experimental and theoretical study. Chem. Phys. Lett. 2013, 572, 78–84. [Google Scholar] [CrossRef]
- Ghaani, M.R.; Kusalik, P.G.; English, N.J. Massive generation of metastable bulk nanobubbles in water by external electric fields. Sci. Adv. 2020, 6, eaaz0094. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.; Forester, T.R. DL-POLY-2.0: A general-purpose parallel molecular dynamics simulation package. J. Mol. Graph. 1996, 14, 136–141. [Google Scholar] [CrossRef]
- Sang, L.; Zhang, Y.; Wang, J.; Zhao, Y.; Chen, Y. Correlation of the depletion layer with the Helmholtz layer in the anatase TiO2–H2O interface via molecular dynamics simulations. Phys. Chem. Chem. Phys. 2016, 18, 15427–15435. [Google Scholar] [CrossRef] [PubMed]
- Andrade, M.F.C.; KoHsin, Y.; Zhang, L.; Car, R.; Selloni, A. Free energy of proton transfer at the water-TiO2 interface from: Ab initio deep potential molecular dynamics. Chem. Sci. 2020, 11, 2335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gala, F.; Agosta, L.; Zollo, G. Water Kinetics and Clustering on the (101) TiO2 Anatase Surface. J. Phys. Chem. C 2016, 120, 450–456. [Google Scholar] [CrossRef]

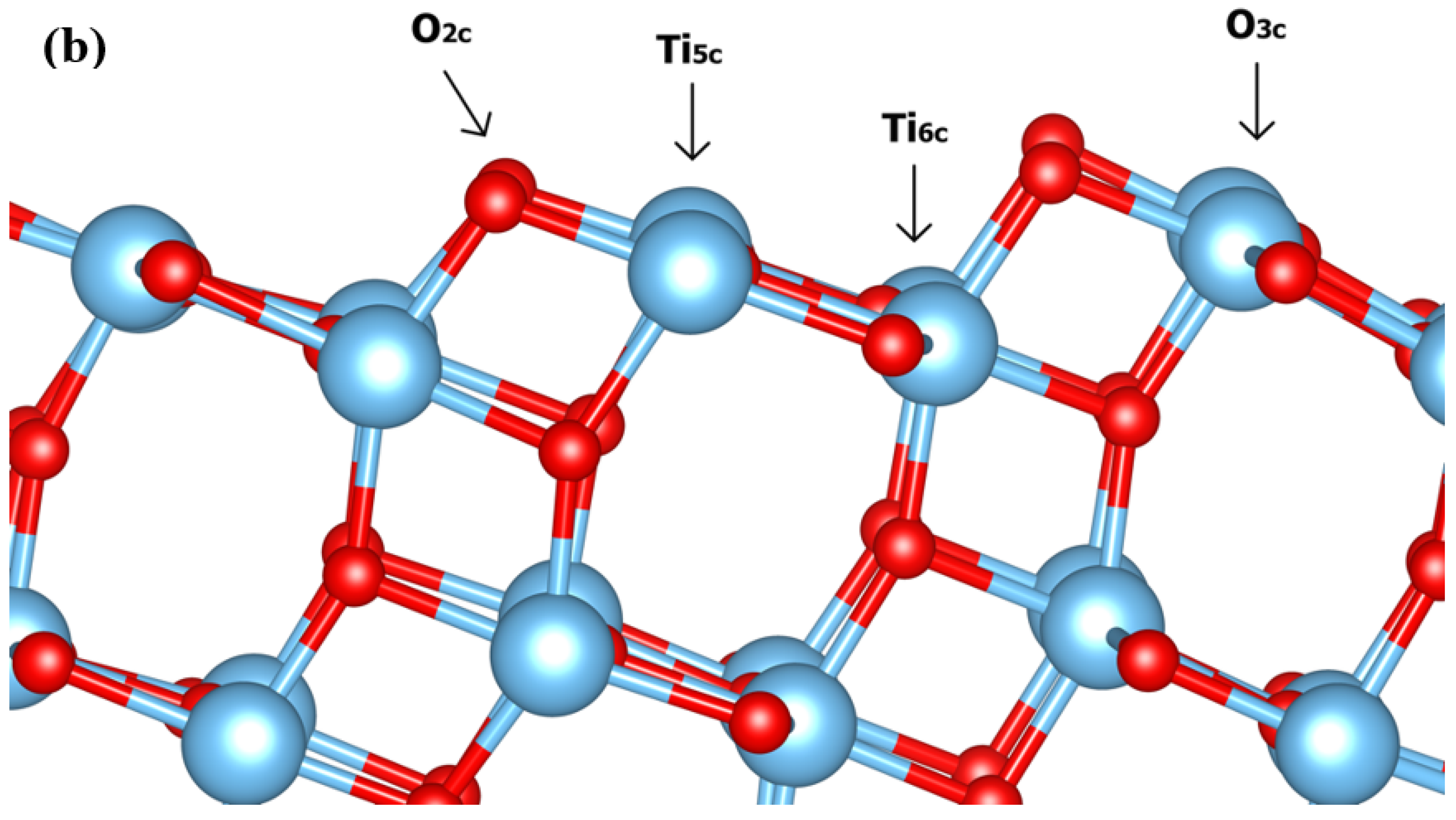
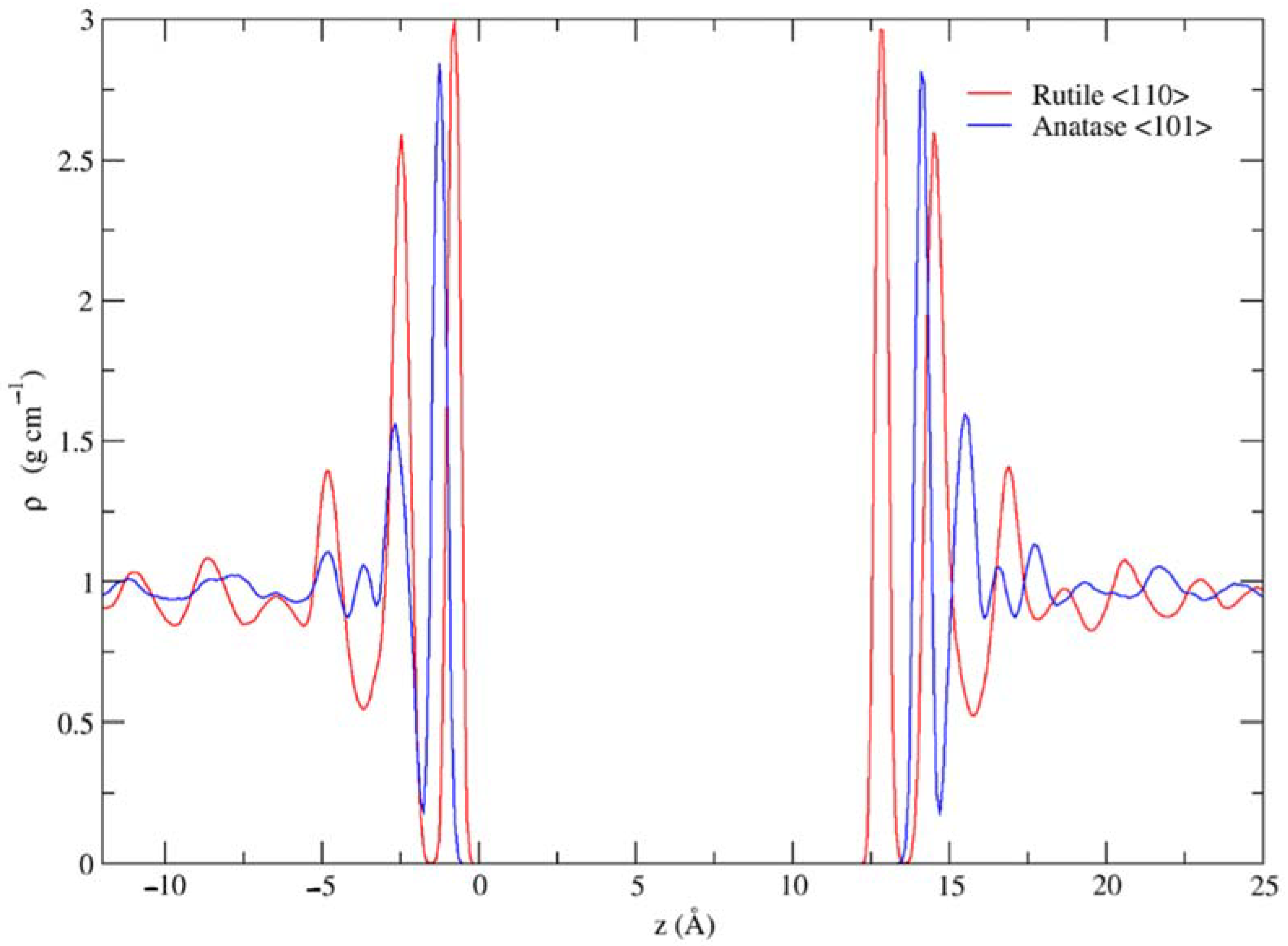
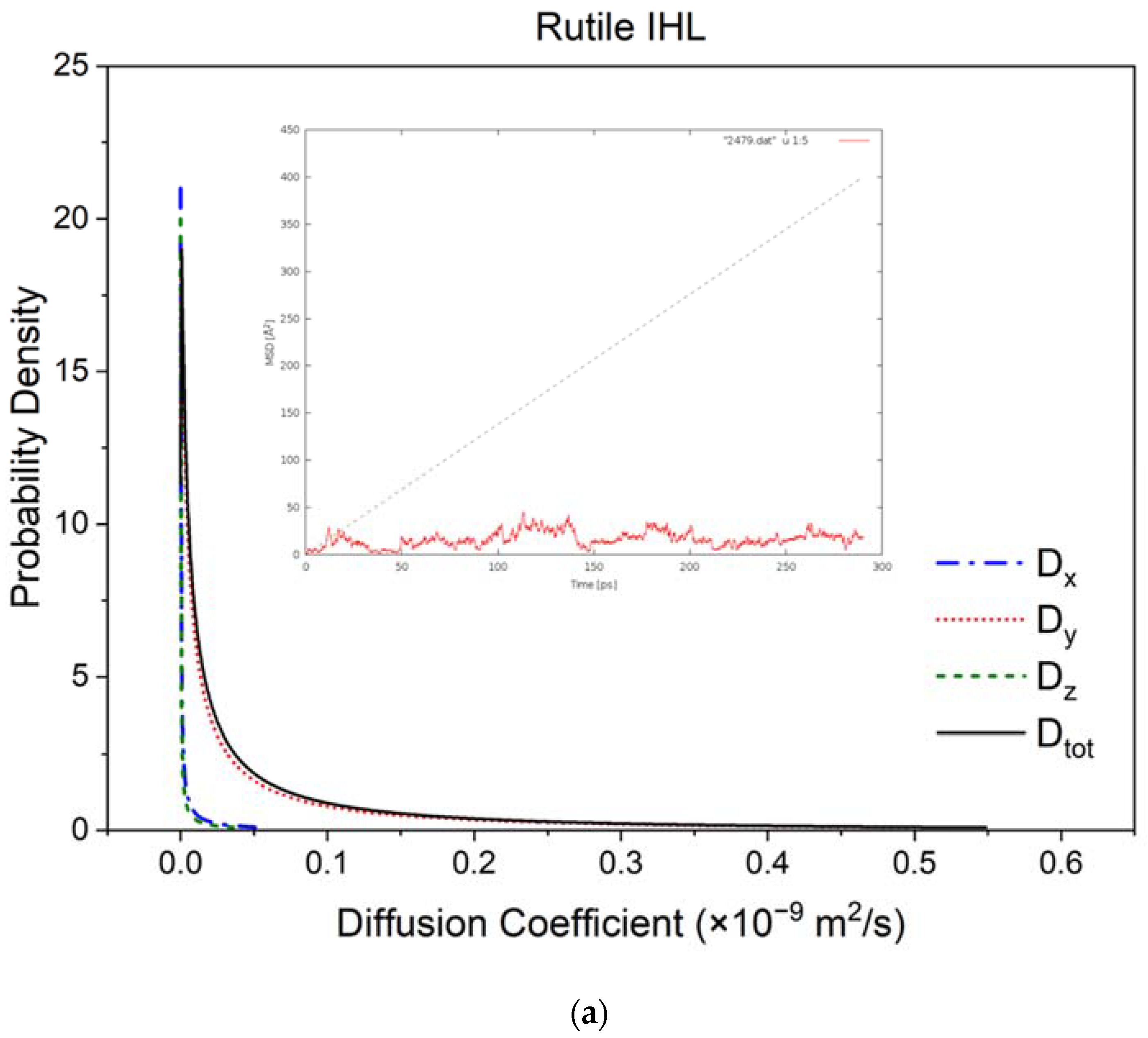


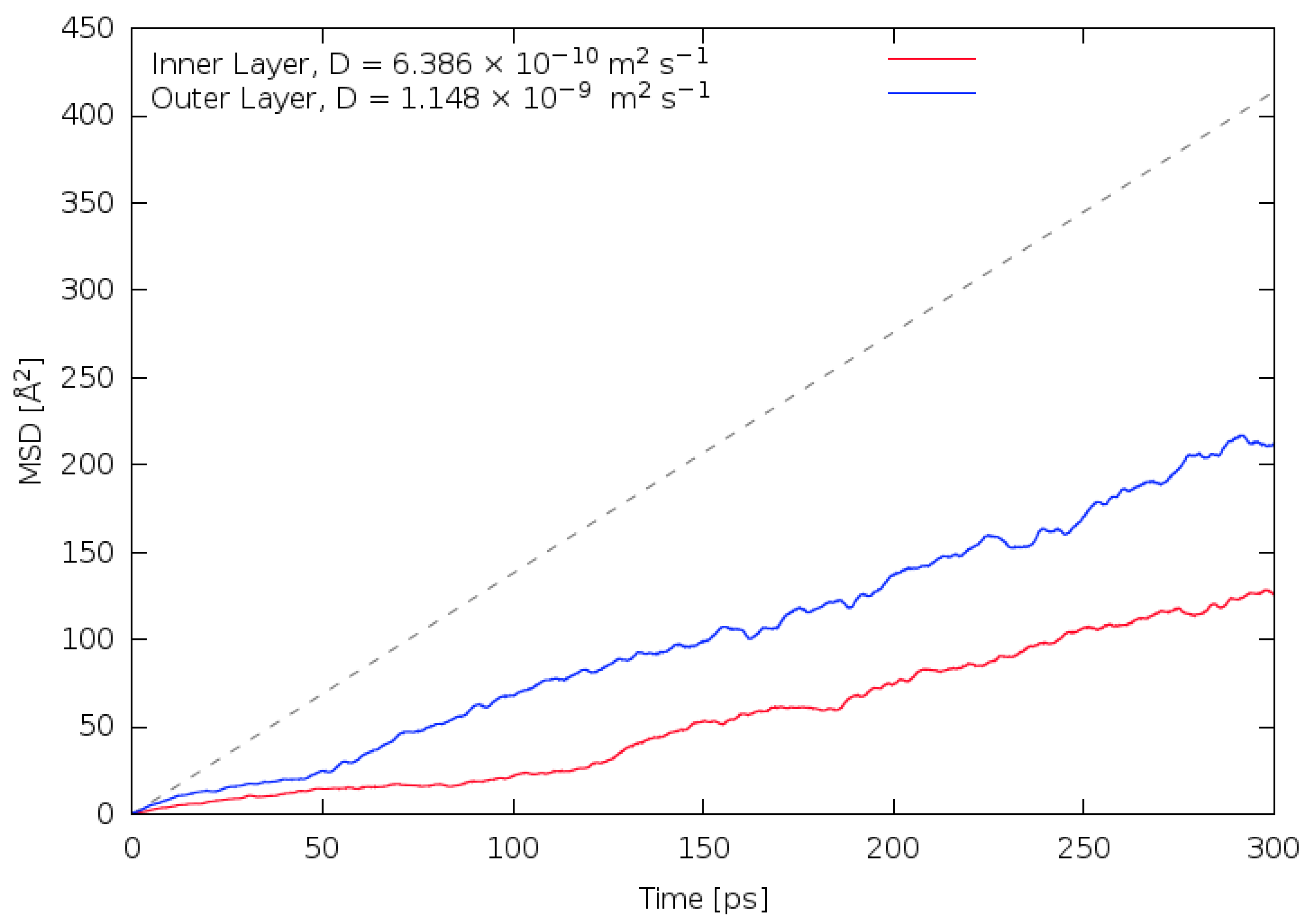

| Surface | x, y, z (Å) | NTiO2 | NH2O | T (K) |
|---|---|---|---|---|
| Anatase (101) [31] | 26.495, 40.956, 69.873 | 448 | 2000 | 298 K |
| Rutile (110) [31] | 23.624, 45.381, 69.450 | 448 | 2000 | 298 K |
| Bulk water | 30.00, 30.00, 30.00 | 0 | 826 | 298 K |
| Surface | IHL | OHL |
|---|---|---|
| Rutile (110) | 0.025, 0.027, 0.020 | 0.512, 0.545, 0.327 |
| Anatase (101) | 0.514, 0.522, 0.322 | 0.731, 0.720, 0.541 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boyd, S.J.; O’Carroll, D.; Krishnan, Y.; Long, R.; English, N.J. Self-Diffusion of Individual Adsorbed Water Molecules at Rutile (110) and Anatase (101) TiO2 Interfaces from Molecular Dynamics. Crystals 2022, 12, 398. https://doi.org/10.3390/cryst12030398
Boyd SJ, O’Carroll D, Krishnan Y, Long R, English NJ. Self-Diffusion of Individual Adsorbed Water Molecules at Rutile (110) and Anatase (101) TiO2 Interfaces from Molecular Dynamics. Crystals. 2022; 12(3):398. https://doi.org/10.3390/cryst12030398
Chicago/Turabian StyleBoyd, Stephanie J., Dáire O’Carroll, Yogeshwaran Krishnan, Run Long, and Niall J. English. 2022. "Self-Diffusion of Individual Adsorbed Water Molecules at Rutile (110) and Anatase (101) TiO2 Interfaces from Molecular Dynamics" Crystals 12, no. 3: 398. https://doi.org/10.3390/cryst12030398
APA StyleBoyd, S. J., O’Carroll, D., Krishnan, Y., Long, R., & English, N. J. (2022). Self-Diffusion of Individual Adsorbed Water Molecules at Rutile (110) and Anatase (101) TiO2 Interfaces from Molecular Dynamics. Crystals, 12(3), 398. https://doi.org/10.3390/cryst12030398








