Fabrication of Q-Carbon Nanostructures, Diamond and Their Composites with Wafer-Scale Integration
Abstract
:1. Introduction
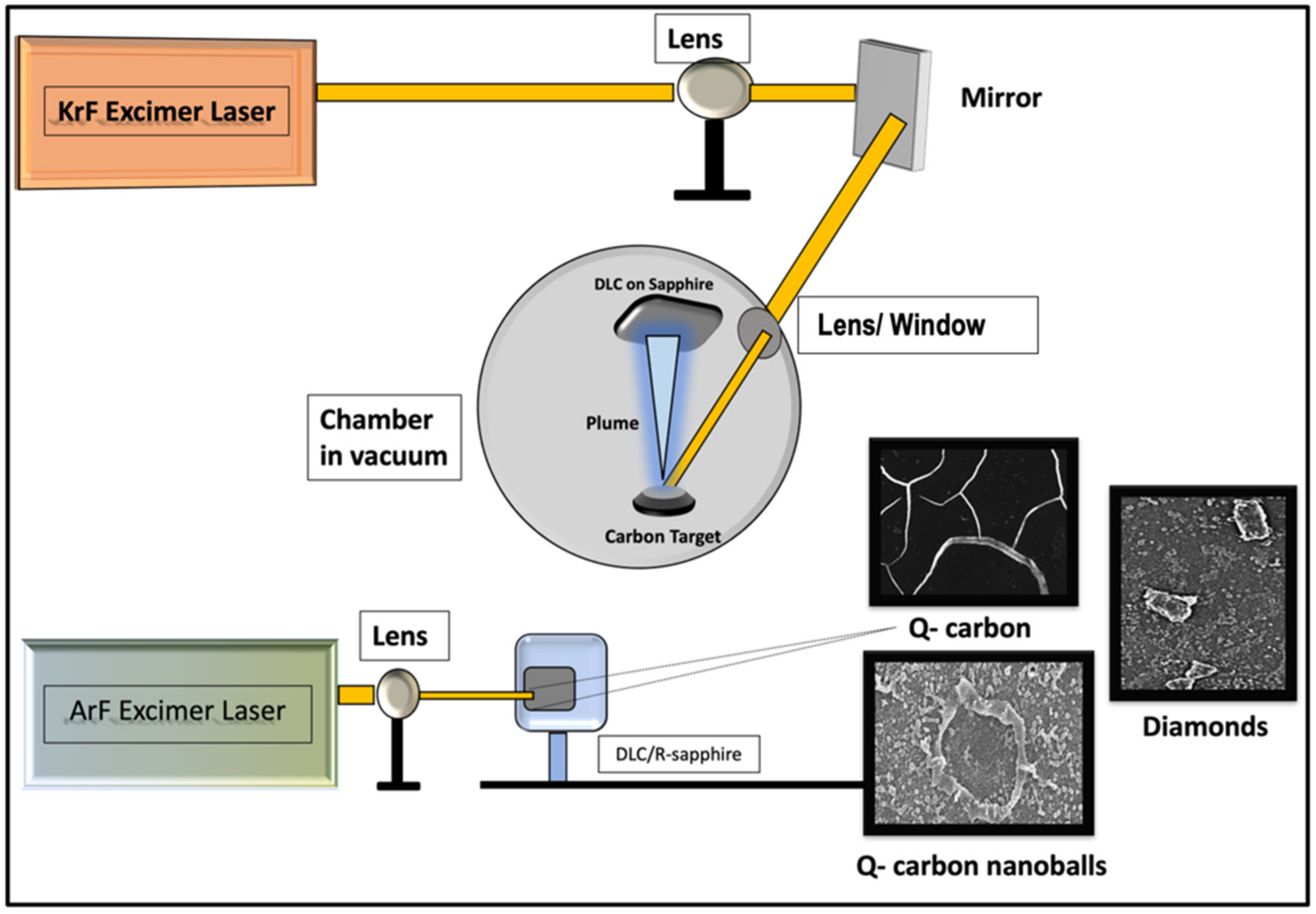
2. Experiment Section
3. Results and Discussions
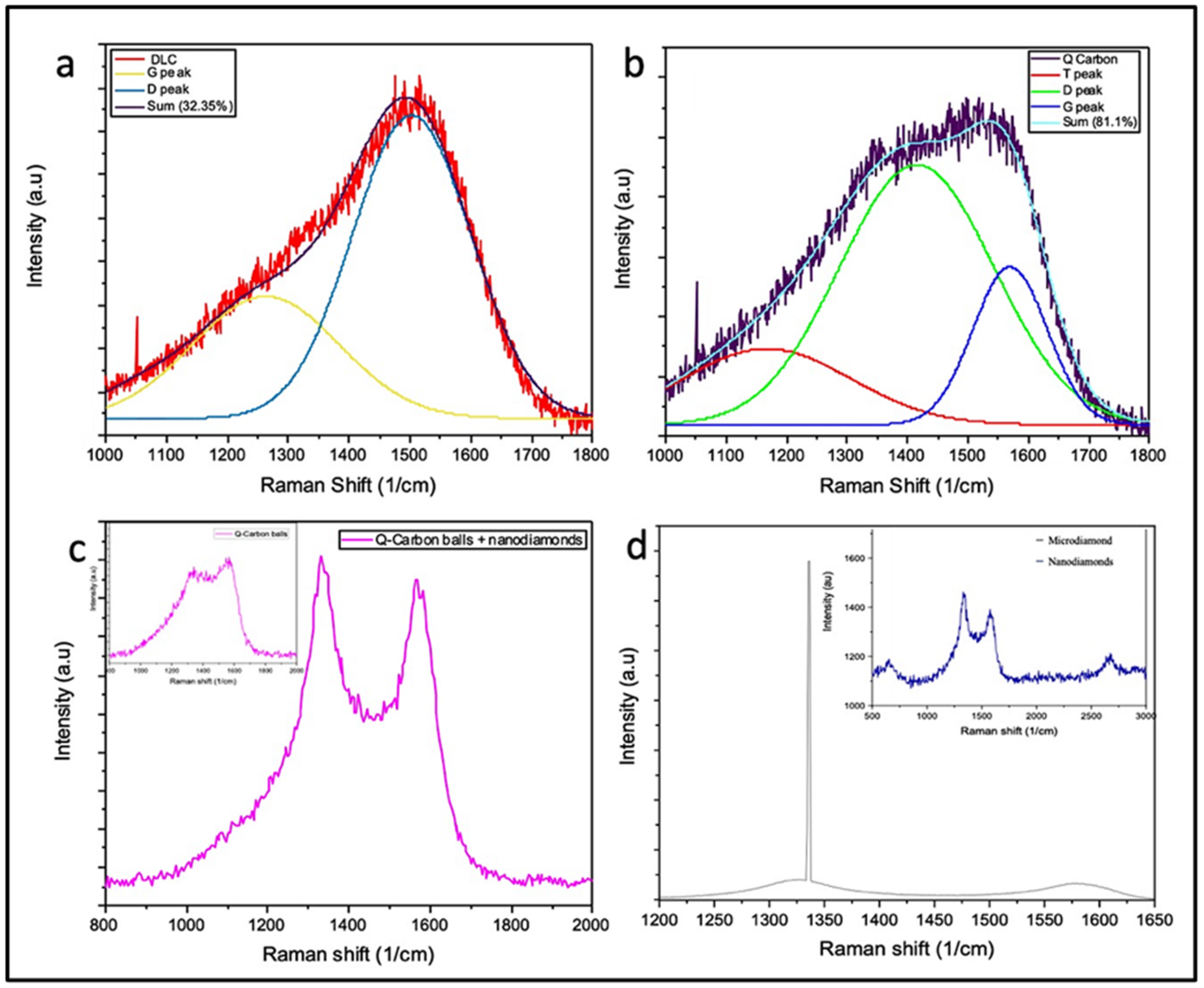
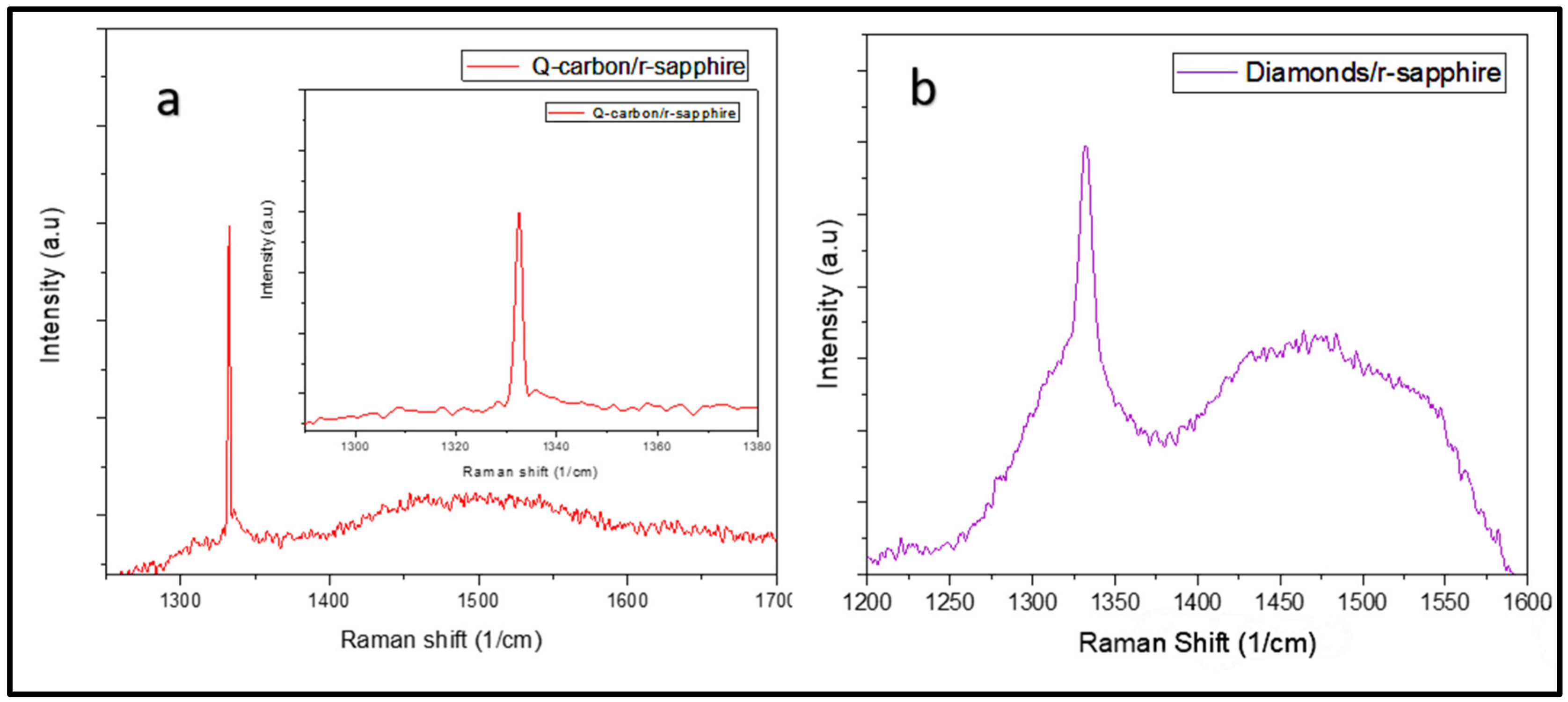
3.1. Formation of Structures by PLA
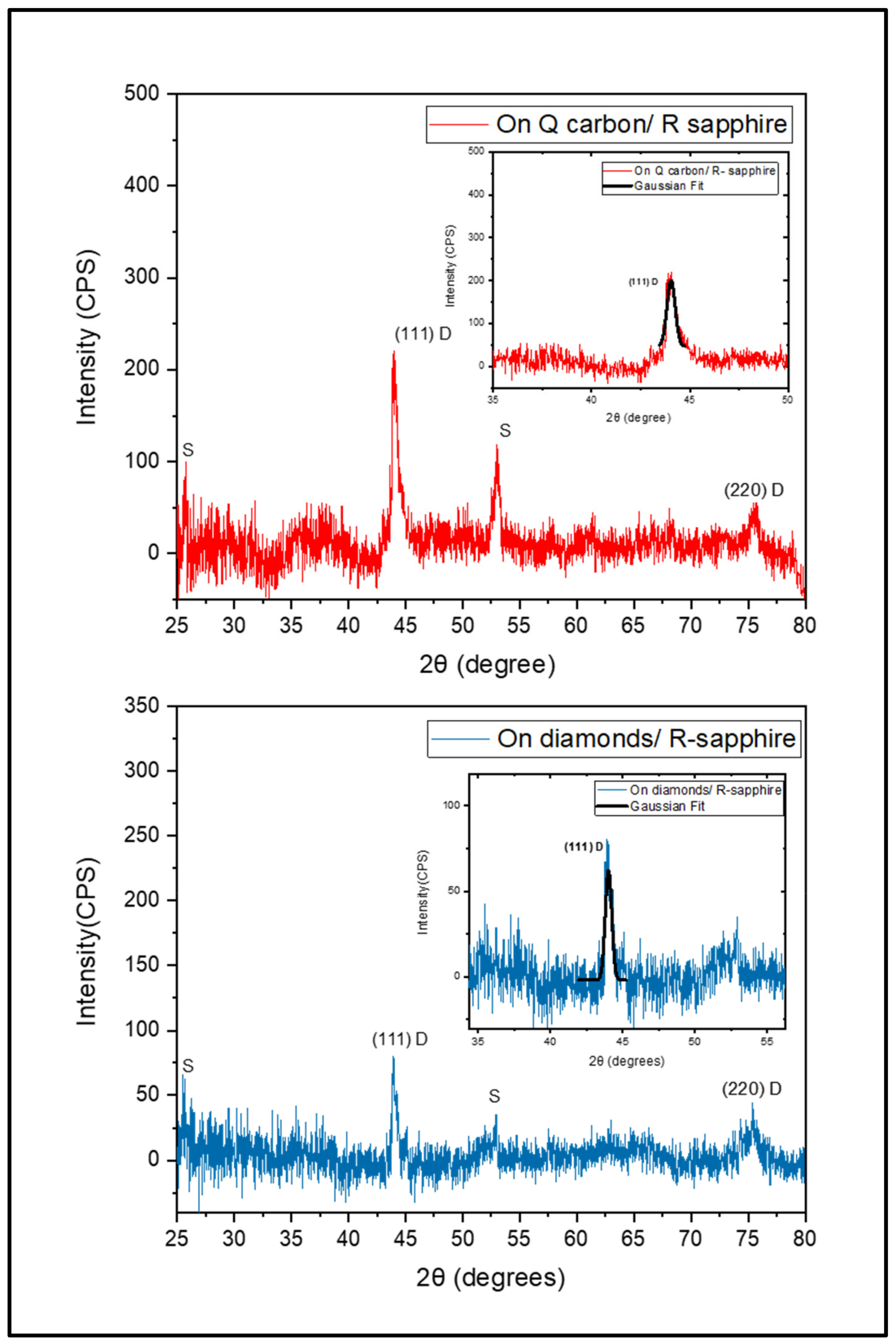
3.2. HFCVD Samples Analysis: Formation of Nano- to Microdiamonds on R-Sapphire
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Narayan, J.; Bhaumik, A.; Gupta, S.; Haque, A.; Sachan, R. Progress in Q-carbon and related materials with extraordinary properties. Mater. Res. Lett. 2018, 6, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Haque, A.; Narayan, J. Stability of electron field emission in Q-carbon. MRS Commun. 2018, 8, 1343–1351. [Google Scholar] [CrossRef]
- Narayan, J.; Joshi, P.; Smith, J.; Gao, W.; Weber, W.J.; Narayan, R.J. Q-carbon as a new radiation-resistant material. Carbon 2022, 186, 253–261. [Google Scholar] [CrossRef]
- May, P.W. Diamond Thin Films: A 21st-Century Material. Philos. Trans. R. Soc. Lond. Ser. A 2000, 358, 473–495. [Google Scholar] [CrossRef]
- Bray, K.; Kato, H.; Previdi, R.; Sandstrom, R.; Ganesan, K.; Ogura, M.; Makino, T.; Yamasaki, S.; Magyar, A.P.; Toth, M.; et al. Single Crystal Diamond Membranes for Nanoelectronics. Nanoscale 2018, 10, 4028–4035. [Google Scholar] [CrossRef] [Green Version]
- Nunn, N.; Torelli, M.; McGuire, G.; Shenderova, O. Nanodiamond: A high impact nanomaterial. Curr. Opin. Solid State Mater. Sci. 2017, 21, 1–9. [Google Scholar] [CrossRef]
- Bundy, F.P.; Bassett, W.A.; Weathers, M.S.; Hemley, R.J.; Mao, H.U.; Goncharov, A.F. The pressure-temperature phase and transformation diagram for carbon; updated through 1994. Carbon 1996, 34, 141–153. [Google Scholar] [CrossRef]
- Das, D.; Singh, R.N. A review of nucleation, growth and low temperature synthesis of diamond thin films. Int. Mater. Rev. 2007, 52, 29–64. [Google Scholar] [CrossRef]
- Sachan, R.; Hachtel, J.A.; Bhaumik, A.; Moatti, A.; Prater, J.; Idrobo, J.C.; Narayan, J. Emergence of shallow energy levels in B-doped Q-carbon: A high-temperature superconductor. Acta Mater. 2019, 174, 153–159. [Google Scholar] [CrossRef]
- Sun, Y.P.; Zhou, B.; Lin, Y.; Wang, W.; Fernando, K.A.S.; Pathak, P.; Meziani, M.J.; Harruff, B.A.; Wang, X.; Wang, H.; et al. Quantum-sized carbon dots for bright and colorful photoluminescence. J. Am. Chem. Soc. 2006, 128, 7756. [Google Scholar] [CrossRef]
- Cui, L.; Ren, X.; Sun, M.; Liu, H.; Xia, L. Carbon Dots: Synthesis, Properties and Applications. Nanomaterials 2021, 11, 3419. [Google Scholar] [CrossRef] [PubMed]
- Narayan, J.; Larson, B.C. Domain epitaxy: A unified paradigm for thin film growth. J. Appl. Phys. 2003, 93, 278–285. [Google Scholar] [CrossRef]
- Gupta, S.; Sachan, R.; Bhaumik, A.; Narayan, J. Enhanced mechanical properties of Q-carbon nanocomposites by nanosecond pulsed laser annealing. Nanotechnology 2018, 29, 45LT02. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Sachan, R.; Bhaumik, A.; Pant, P.; Narayan, J. Undercooling driven growth of Q-carbon, diamond, and graphite. MRS Commun. 2018, 8, 533–540. [Google Scholar] [CrossRef]
- Riley, P.R.; Joshi, P.; Khosla, N.; Narayan, J.; Narayan, R. Formation of Q-Carbon with Wafer Scale Integration. SSRN 2022, 1–26. [Google Scholar] [CrossRef]
- Joshi, P.; Gupta, S.; Haque, A.; Narayan, J. Fabrication of ultrahard Q-carbon nanocoatings on AISI 304 and 316 stainless steels and subsequent formation of high-quality diamond films. Diam. Relat. Mater. 2020, 104, 107742. [Google Scholar] [CrossRef]
- Gupta, S.; Bhaumik, A.; Sachan, R.; Narayan, J. Structural Evolution of Q-carbon and Nanodiamonds. JOM 2018, 70, 450–455. [Google Scholar] [CrossRef]
- Yoshinaka, H.; Inubushi, S.; Wakita, T.; Yokoya, T.; Muraoka, Y. Formation of Q-carbon by adjusting sp3 content in diamond-like carbon films and laser energy density of pulsed laser annealing. Carbon 2020, 167, 504–511. [Google Scholar] [CrossRef]
- Singh, R.K.; Narayan, J. A novel method for simulating laser-solid interactions in semiconductors and layered structures. Mater. Sci. Eng. B 1989, 3, 217–230. [Google Scholar] [CrossRef]
- Narayan, J.; Bhaumik, A.; Gupta, S.; Joshi, P.; Riley, P.; Narayan, R.J. Formation of self-organized nano-and micro-diamond rings. Mater. Res. Lett. 2021, 9, 300–307. [Google Scholar] [CrossRef]
- Zhao, T.C.; Yuan, J.L.; Deng, Q.F.; Feng, K.P.; Xu, W. Contrast Experiments in Dielectrophoresis Polishing (DEPP)/Chemical Mechanical Polishing (CMP) of Sapphire Substrate. Appl. Sci. 2019, 9, 3704. [Google Scholar] [CrossRef] [Green Version]
- Aida, H.; Doi, T.; Takeda, H.; Katakura, H.; Kim, S.-W.; Koyama, K.; Yamazaki, T.; Uneda, M. Ultraprecision CMP for sapphire, GaN, and SiC for advanced optoelectronics materials. Curr. Appl. Phys. 2012, 12, S41–S46. [Google Scholar] [CrossRef]
- Xu, L.; Zou, C.; Shi, X.; Pan, G.; Luo, G.; Zhou, Y. Fe-Nx/C assisted chemical–mechanical polishing for improving the removal rate of sapphire. Appl. Surf. Sci. 2015, 343, 115–120. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photonics 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Liang, J.; Nakamura, Y.; Zhan, T.; Ohno, Y.; Shimizu, Y.; Katayama, K.; Watanabe, T.; Yoshida, H.; Nagai, Y.; Wang, H.; et al. Fabrication of high-quality GaAs/diamond heterointerface for thermal management applications. Diam. Relat. Mater. 2021, 111, 108207. [Google Scholar] [CrossRef]
- Singh, R.K.; Narayan, J. Pulsed-laser evaporation technique for deposition of thin films: Physics and theoretical model. Phys. Rev. B 1990, 41, 8843. [Google Scholar] [CrossRef] [PubMed]
- Steinbeck, J.; Dresselhaus, G.; Dresselhaus, M.S. The properties of liquid carbon. Int. J. Thermophys. 1990, 11, 789–796. [Google Scholar] [CrossRef]
- Narayan, J.; Khosla, N. Self-organization of amorphous Q-carbon and Q-BN nanoballs. Carbon 2022, 192, 301–307. [Google Scholar] [CrossRef]
- Liz-Marzán, L.M.; Mulvaney, P. The assembly of coated nanocrystals. J. Phys. Chem. B 2003, 107, 7312–7326. [Google Scholar] [CrossRef]
- Joshi, P.; Riley, P.R.; Denning, W.; Shukla, S.; Khosla, N.; Narayan, J.; Narayan, R. Laser-patterned carbon coatings on flexible and optically transparent plastic substrates for advanced biomedical sensing and implant applications. J. Mater. Chem. C 2022, 10, 2965–2975. [Google Scholar] [CrossRef]
- Panda, M.; Krishnan, R.; Ravindran, T.R.; Das, A.; Mangamma, G.; Dash, S.; Tyagi, A.K. Spectroscopic studies on diamond like carbon films synthesized by pulsed laser ablation. AIP Conf. Proc. 2016, 1731, 080040. [Google Scholar]
- Dennison, J.R.; Holtz, M.; Swain, G. Raman spectroscopy of carbon materials. Spectroscopy 1996, 11, 38–45. [Google Scholar]
- Zhang, Y.; Li, Z.; Kim, P.; Zhang, L.; Zhou, C. Anisotropic hydrogen etching of chemical vapor deposited graphene. ACS Nano 2012, 6, 126–132. [Google Scholar] [CrossRef] [PubMed]
- Haubner, R.; Lux, B. Deposition of ballas diamond and nano-crystalline diamond. Int. J. Refract. Met. Hard Mater. 2002, 20, 93–100. [Google Scholar] [CrossRef]
- Bühlmann, S.; Blank, E.; Haubner, R.; Lux, B. Characterization of ballas diamond depositions. Diam. Relat. Mater. 1999, 8, 194–201. [Google Scholar] [CrossRef]
- Narayan, J. Recent progress in thin film epitaxy across the misfit scale. Acta Mater. 2013, 61, 2703–2724. [Google Scholar] [CrossRef]
- Kuo, C.T.; Lin, C.R.; Lien, H.M. Origins of the residual stress in CVD diamond films. Thin Solid Film. 1996, 290, 254–259. [Google Scholar] [CrossRef]
- Haubner, R.; Rudigier, M. Raman characterisation of diamond coatings using different laser wavelengths. Phys. Procedia 2013, 46, 71–78. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, N.G.; Abramof, E.; Leite, N.F.; Corat, E.J.; Trava-Airoldi, V.J. Analysis of residual stress in diamond films by X-ray diffraction and micro-Raman spectroscopy. J. Appl. Phys. 2002, 91, 2466–2472. [Google Scholar] [CrossRef] [Green Version]
- Fox, B.A.; Stoner, B.R.; Malta, D.M.; Ellis, P.J.; Glass, R.C.; Sivazlian, F.R. Epitaxial nucleation, growth, and characterization of highly oriented,(100)-textured diamond films on silicon. Diam. Relat. Mater. 1994, 3, 382–387. [Google Scholar] [CrossRef]
- Gruen, D.M. Nanocrystalline diamond films. Annu. Rev. Mater. Sci. 1999, 29, 211–259. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosla, N.; Narayan, J. Fabrication of Q-Carbon Nanostructures, Diamond and Their Composites with Wafer-Scale Integration. Crystals 2022, 12, 615. https://doi.org/10.3390/cryst12050615
Khosla N, Narayan J. Fabrication of Q-Carbon Nanostructures, Diamond and Their Composites with Wafer-Scale Integration. Crystals. 2022; 12(5):615. https://doi.org/10.3390/cryst12050615
Chicago/Turabian StyleKhosla, Nayna, and Jagdish Narayan. 2022. "Fabrication of Q-Carbon Nanostructures, Diamond and Their Composites with Wafer-Scale Integration" Crystals 12, no. 5: 615. https://doi.org/10.3390/cryst12050615
APA StyleKhosla, N., & Narayan, J. (2022). Fabrication of Q-Carbon Nanostructures, Diamond and Their Composites with Wafer-Scale Integration. Crystals, 12(5), 615. https://doi.org/10.3390/cryst12050615





