Symplectic Method for the Thin Piezoelectric Plates
Abstract
:1. Introduction
2. Hamilton Canonical Equations
3. Symplectic Analysis
4. Symplectic Solutions of a Thin Piezoelectric Plate with Full Edges Simply Supported
4.1. Eigensolutions of a Thin Piezoelectric Plate
4.2. Expansion of Eigenfunctions
4.3. Analytical Solutions of Thin Piezoelectric Plate
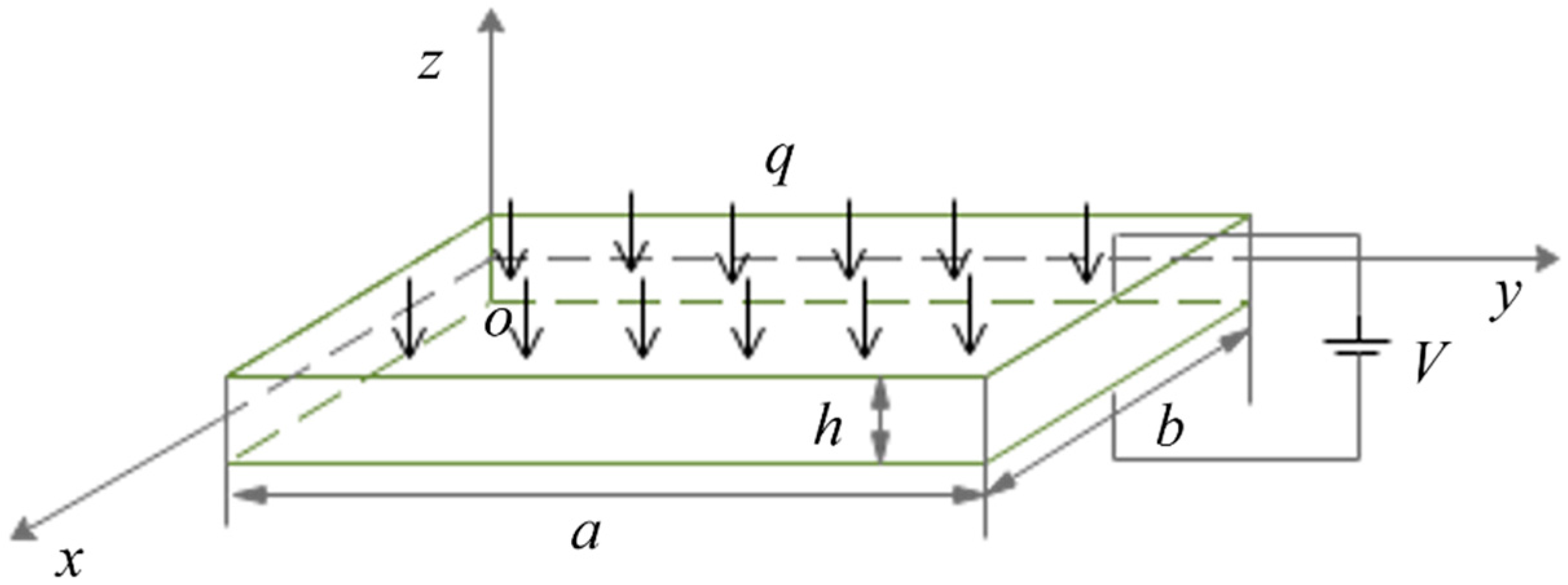
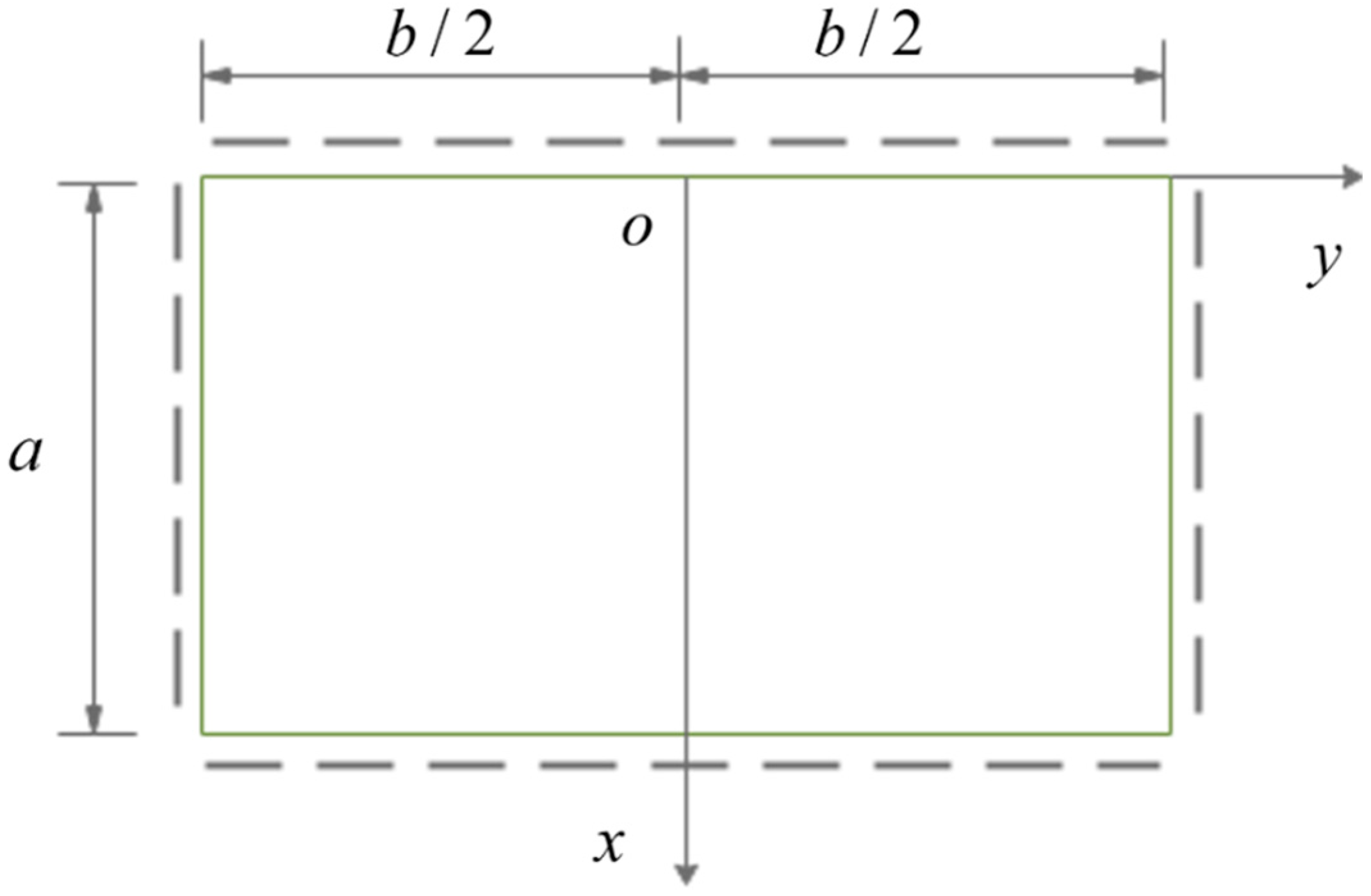
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matko, V.; Milanovič, M. Detection principles of temperature compensated oscillators with reactance influence on piezoelectric resonator. Sensors 2020, 20, 802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matko, V.; Milanovič, M. Temperature-compensated capacitance-frequency converter with high resolution. Sens. Actuators A Phys. 2014, 220, 262–269. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Chen, X.F. Application of piezoelectric actuator in series nano-positioning stage. Sci. Prog. 2019, 103, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gohari, H.D.; Zarastvand, M.R.; Talebitooti, R.; Loghmani, A.; Omidpanah, M. Radiated sound control from a smart cylinder subjected to piezoelectric uncertainties based on sliding mode technique using self-adjusting boundary layer. Aerosp. Sci. Technol. 2020, 106, 106141. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. A review approach for sound propagation prediction of plate constructions. Arch. Comput. Methods Eng. 2020, 28, 2817–2843. [Google Scholar] [CrossRef]
- Dunn, M.L.; Wienecke, H.A. Green’s functions for transversely isotropic piezoelectric solids. Int. J. Solids Struct. 1996, 33, 4571–4581. [Google Scholar] [CrossRef]
- Hill, L.R. Three-dimensional piezoelectric boundary elements. AIAA J. 1998, 36, 102. [Google Scholar] [CrossRef]
- Ding, H.J.; Xu, R.Q.; Chen, W.Q. Free vibration of transversely isotropic piezoelectric circular cylindrical panels. Int. J. Mech. Sci. 2002, 44, 191–206. [Google Scholar] [CrossRef]
- Zhong, W.; Williams, F.W. Physical interpretation of the symplectic orthogonality of the eigensolutions of a hamiltonian or symplectic matrix. Comput. Struct. 1993, 49, 749–750. [Google Scholar] [CrossRef]
- Yao, W.A.; Zhong, W.X.; Lim, C.W. Symplectic Elasticity; World Scientific: Singapore, 2009. [Google Scholar]
- Xu, X.S.; Gu, Q.; Leung, A.Y.T.; Zhen, J.J. A symplectic eigensolution method in transversely isotropic piezoelectric cylindrical media. J. Zhejiang Univ. Sci. A 2005, 6, 922–927. [Google Scholar]
- Gu, Q.; Xu, X.S.; Leung, A.Y.T. Application of Hamiltonian system for two-dimensional transversely isotropic piezoelectric media. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2005, 6, 915–921. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Xu, X.S.; Gu, Q.; Leung, C.; Zheng, J.J. The boundary layer phenomena in two-dimensional transversely isotropic piezoelectric media by exact symplectic expansion. Int. J. Numer. Methods Eng. 2007, 69, 2381–2408. [Google Scholar] [CrossRef]
- Xu, X.S.; Leung, A.Y.T.; Gu, Q.; Yang, H.; Zheng, J.J. 3D symplectic expansion for piezoelectric media. Int. J. Numer. Methods Eng. 2008, 74, 1848–1871. [Google Scholar] [CrossRef]
- Xu, X.S.; Tong, Z.Z.; Rong, D.L.; Cheng, X.H.; Xu, C.H.; Zhou, Z.H. Fracture analysis of magnetoelectroelastic bimaterials with imperfect interfaces by symplectic expansion. Appl. Math. Mech. 2017, 38, 1043–1058. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, R.; Liu, Y.M.; Tian, B. On new symplectic approach for exact bending solutions of moderately thick rectangular plates with two opposite edges simply supported. Int. J. Solids Struct. 2009, 46, 2506–2513. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Li, R. Exact bending analysis of fully clamped rectangular thin plates subjected to arbitrary loads by new symplectic approach. Mech. Res. Commun. 2009, 36, 707–714. [Google Scholar] [CrossRef]
- Li, R.; Zhong, Y. On a new symplectic geometry method for exact bending solutions of orthotropic rectangular plates with two opposite sides clamped. Acta Mech. 2011, 216, 333–343. [Google Scholar] [CrossRef]
- Zhang, K.; Ge, M.H.; Zhao, C.; Deng, Z.C.; Xu, X.J. Free vibration of nonlocal Timoshenko beams made of functionally graded materials by Symplectic method. Compos. Part B Eng. 2019, 156, 174–184. [Google Scholar] [CrossRef]
- Xu, C.H.; Rong, D.L.; Zhou, Z.H.; Deng, Z.C.; Lim, C.W. Vibration and buckling characteristics of cracked natural fiber reinforced composite plates with corner point-supports. Eng. Struct. 2020, 214, 110614. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Mao, S.G. A symplectic Galerkin method for non-linear vibration of beams and plates. J. Sound Vib. 1995, 183, 475–491. [Google Scholar] [CrossRef]
- Jia, J.F.; Lai, A.D.; Li, T.; Zhou, Z.H.; Xu, X.S.; Lim, C.W. A symplectic analytical approach for free vibration of orthotropic cylindrical shells with stepped thickness under arbitrary boundary conditions. Thin-Walled Struct. 2022, 171, 108696. [Google Scholar] [CrossRef]
- Bisegna, P.; Maceri, F. A consistent theory of thin piezoelectric plates. J. Intell. Mater. Syst. Struct. 1996, 7, 372–389. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N.; Abramson, H.N. Book Reviews—Theory of Elasticity (3rd ed.). ASME J. Appl. Mech. 1970, 37, 888. [Google Scholar] [CrossRef]
- Zhao, M.H.; Qian, C.F.; Lee, S.W.R.; Tong, P.; Suemasu, H.; Zhang, T.Y. Electro-elastic analysis of piezoelectric laminated plates. Adv. Compos. Mater. 2007, 16, 63–81. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L. Vibration and buckling analysis of a piezoelectric nanoplate considering surface effects and in-plane constraints. R. Soc. Lond. Proc. Ser. A 2012, 468, 3458–3475. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Ke, L.L.; Wang, Y.S.; Yang, J.; Kitipornchai, S. Thermo-electro-mechanical vibration of piezoelectric nanoplates based on the nonlocal theory. Compos. Struct. 2013, 106, 167–174. [Google Scholar] [CrossRef]
- Ding, H.J.; Chen, W.Q. Three Dimensional Problems of Piezoelasticity; Nova Science Publishers: Huntington, NY, USA, 2001. [Google Scholar]

| Present | 1.0 | 1 | 0.00410935 |
| 3 | 0.0040588 | ||
| 5 | 0.00406297 | ||
| ref. [24] | 1 | - | 0.004062 |
| 1 | 3 | 5 | 7 | 9 | 11 | |
|---|---|---|---|---|---|---|
| −8.44573 | −8.43419 | −8.43454 | −8.43450 | −8.43450 | −8.43450 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Li, L.; Chen, A. Symplectic Method for the Thin Piezoelectric Plates. Crystals 2022, 12, 681. https://doi.org/10.3390/cryst12050681
Fan J, Li L, Chen A. Symplectic Method for the Thin Piezoelectric Plates. Crystals. 2022; 12(5):681. https://doi.org/10.3390/cryst12050681
Chicago/Turabian StyleFan, Junjie, Lianhe Li, and Alatancang Chen. 2022. "Symplectic Method for the Thin Piezoelectric Plates" Crystals 12, no. 5: 681. https://doi.org/10.3390/cryst12050681






