Elastic Metagratings with Simultaneous Modulation of Reflected and Transmitted Waves
Abstract
:1. Introduction
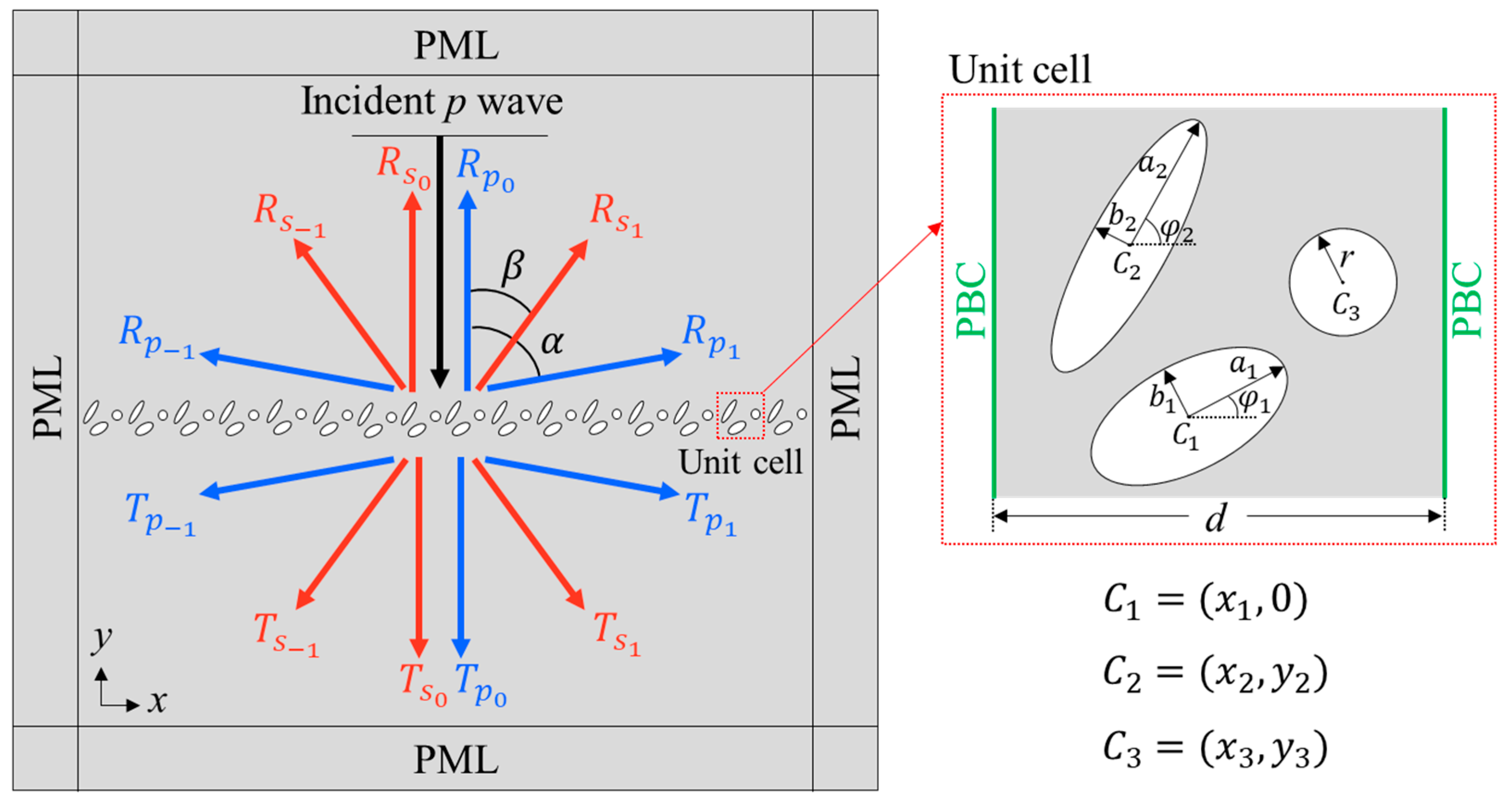
2. Analysis of Grating Diffraction
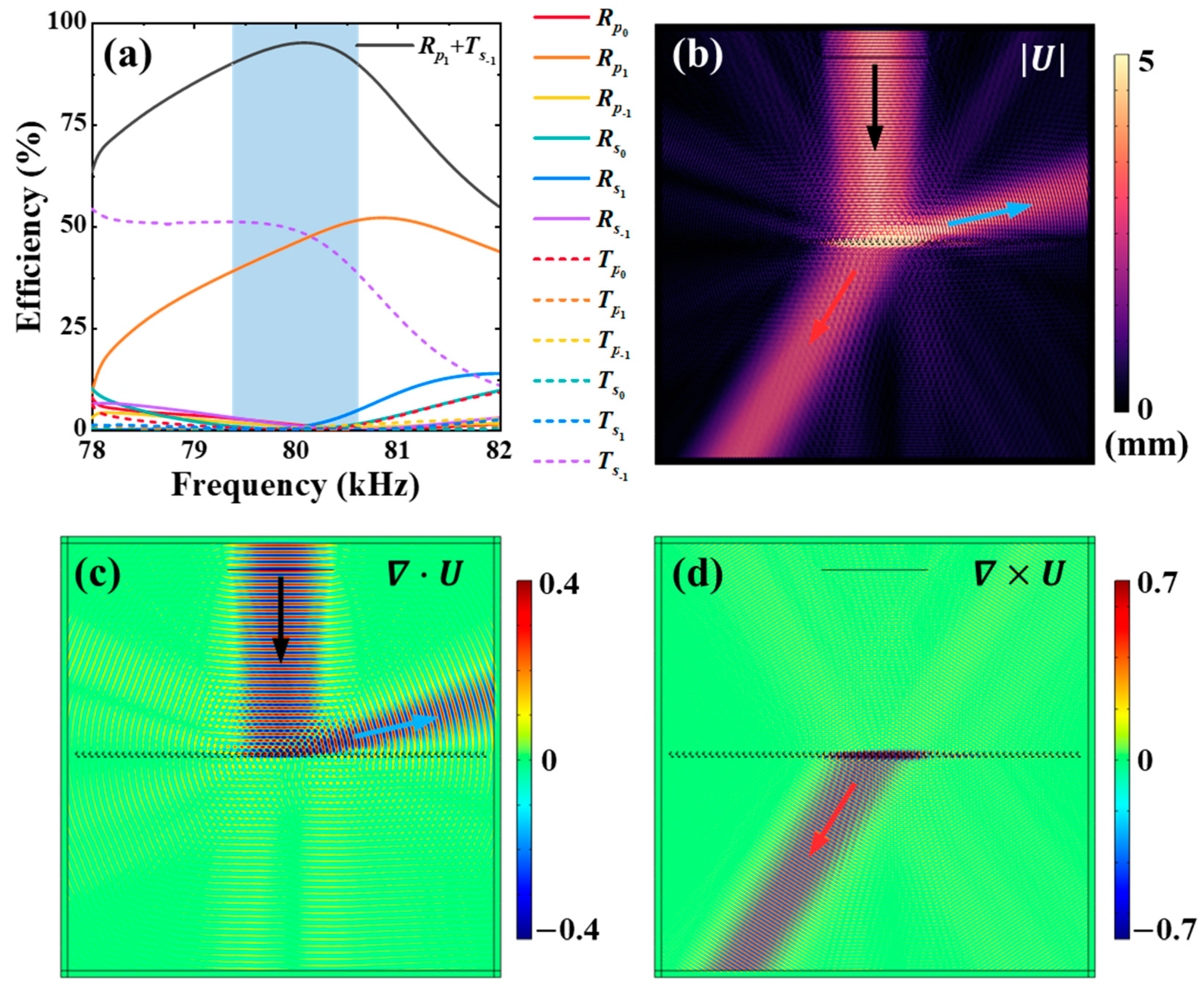
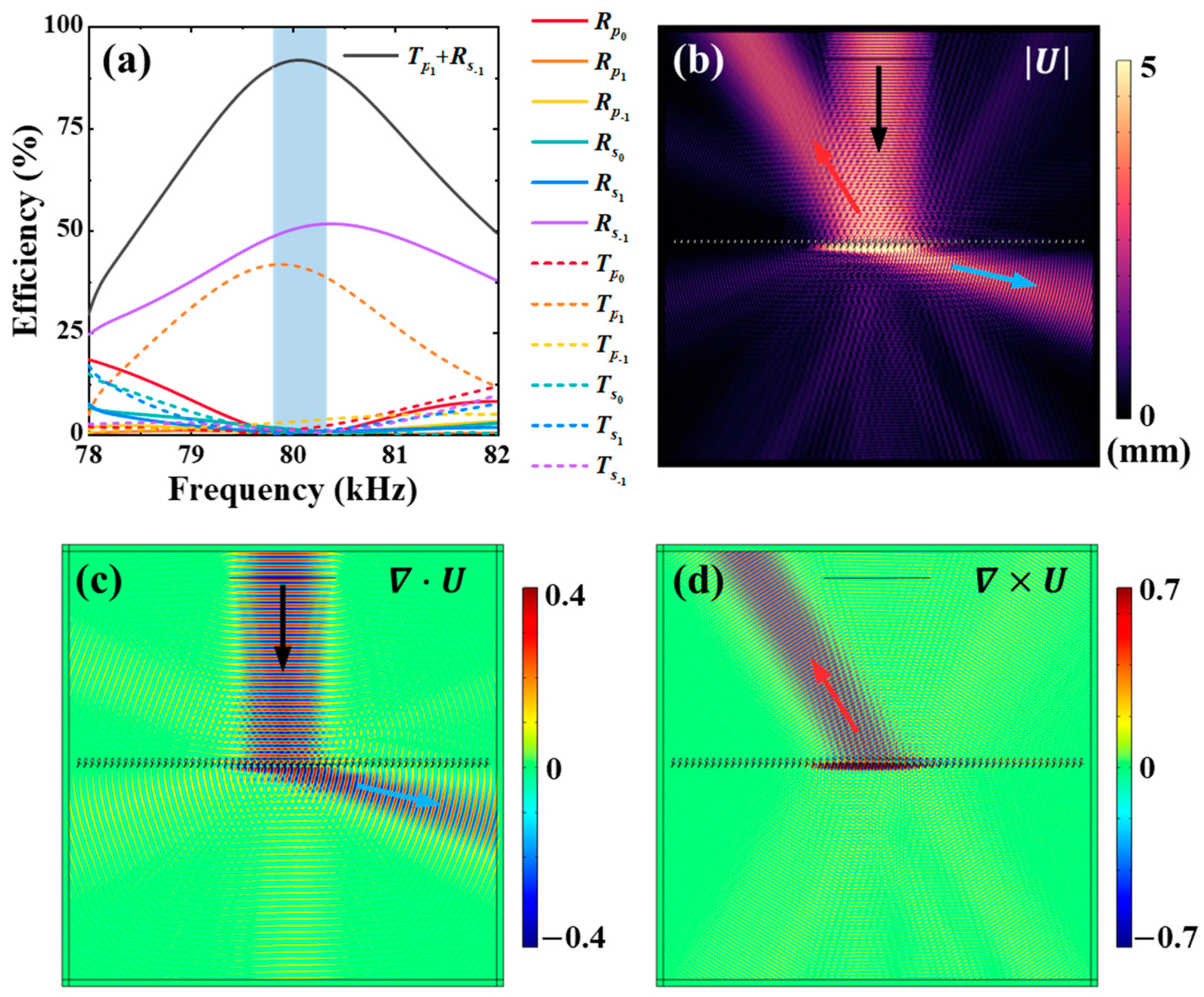
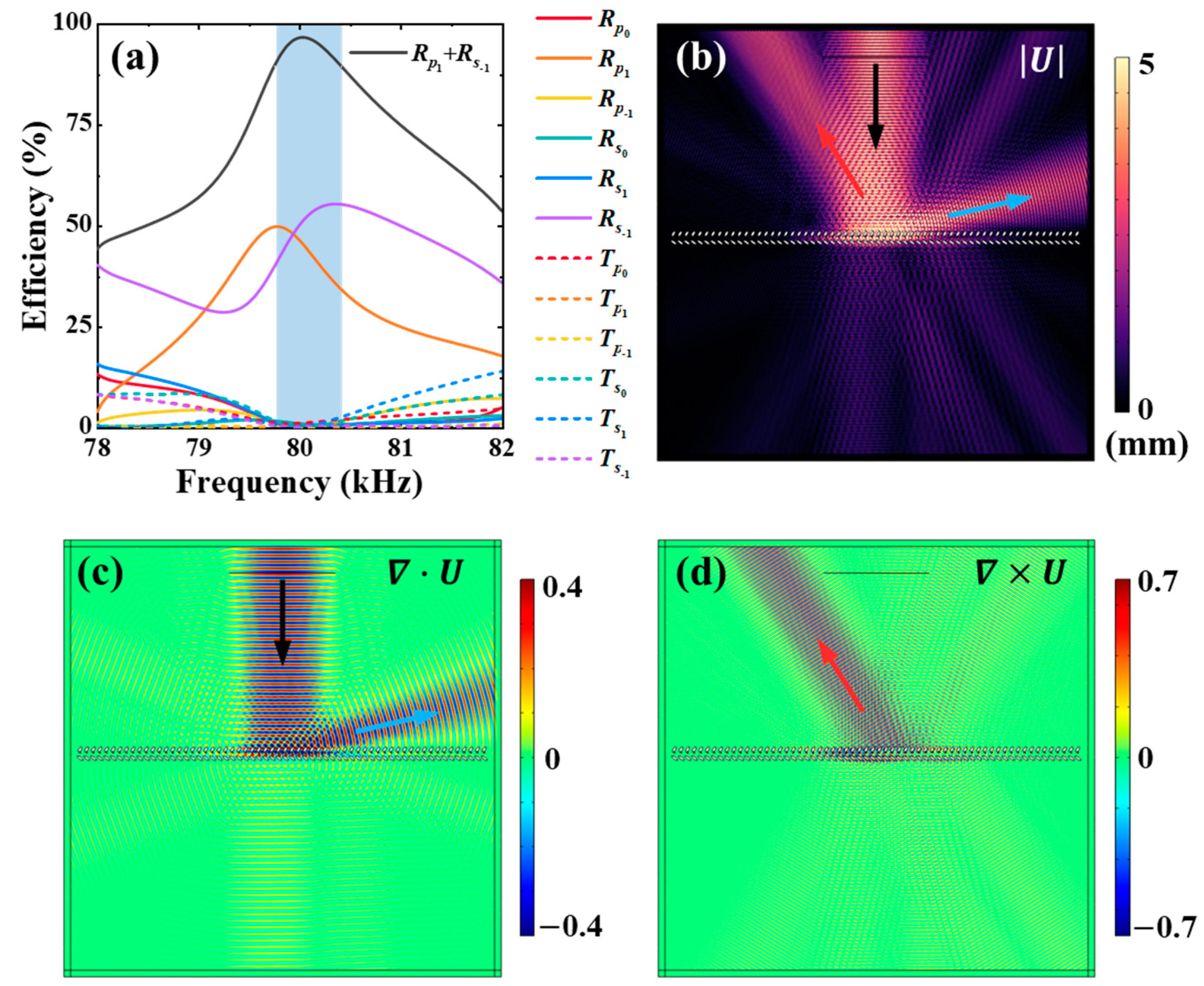
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Assouar, B.; Liang, B.; Wu, Y.; Li, Y.; Cheng, J.C.; Jing, Y. Acoustic metasurfaces. Nat. Rev. Mater. 2018, 3, 460–472. [Google Scholar] [CrossRef] [Green Version]
- Mei, J.; Wu, Y. Controllable transmission and total reflection through an impedance-matched acoustic metasurface. New J. Phys. 2014, 16, 123007. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, C.; Yuan, B.G.; Wu, D.J.; Wei, Q.; Liu, X.J. Ultra-sparse metasurface for high reflection of low-frequency sound based on artificial Mie resonances. Nat. Mater. 2015, 14, 1013–1019. [Google Scholar] [CrossRef]
- Tang, K.; Qiu, C.; Ke, M.; Lu, J.; Ye, Y.; Liu, Z. Anomalous refraction of airborne sound through ultrathin metasurfaces. Sci. Rep. 2014, 4, 6517. [Google Scholar] [CrossRef] [Green Version]
- Tang, K.; Qiu, C.; Lu, J.; Ke, M.; Liu, Z. Focusing and directional beaming effects of airborne sound through a planar lens with zigzag slits. J. Appl. Phys. 2015, 117, 024503. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Rubio, A.; Tretyakov, S.A. Acoustic metasurfaces for scattering-free anomalous reflection and refraction. Phys. Rev. B 2017, 96, 125409. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Shen, C.; Díaz-Rubio, A.; Tretyakov, S.A.; Cummer, S.A. Systematic design and experimental demonstration of bianisotropic metasurfaces for scattering-free manipulation of acoustic wavefronts. Nat. Commun. 2018, 9, 1342. [Google Scholar] [CrossRef]
- Guo, X.; Gusev, V.E.; Bertoldi, K.; Tournat, V. Manipulating acoustic wave reflection by a nonlinear elastic metasurface. J. Appl. Phys. 2018, 123, 124901. [Google Scholar] [CrossRef]
- Zhou, H.T.; Fu, W.X.; Wang, Y.F.; Wang, Y.S. High-efficiency Ultrathin Nonlocal Waterborne Acoustic Metasurface. Phy. Rev. Appl. 2021, 15, 044046. [Google Scholar] [CrossRef]
- Zhou, H.T.; Fu, W.X.; Li, X.S.; Wang, Y.F.; Wang, Y.S. Loosely coupled reflective impedance metasurfaces: Precise manipulation of waterborne sound by topology optimization. Mech. Syst. Signal. Process. 2022, 177, 109228. [Google Scholar] [CrossRef]
- Danila, O.; Manaila-Maximean, D. Bifunctional metamaterials using spatial phase gradient architectures: Generalized reflection and refraction considerations. Materials 2021, 14, 2201. [Google Scholar] [CrossRef] [PubMed]
- Danila, O. Polyvinylidene fluoride-based metasurface for high-quality active switching and spectrum shaping in the terahertz g-band. Polymers 2021, 13, 1860. [Google Scholar] [CrossRef] [PubMed]
- Esfahlani, H.; Karkar, S.; Lissek, H.; Mosig, J.R. Acoustic carpet cloak based on an ultrathin metasurface. Phys. Rev. B 2016, 94, 014302. [Google Scholar] [CrossRef] [Green Version]
- Qi, S.; Li, Y.; Assouar, B. Acoustic focusing and energy confinement based on multilateral metasurfaces. Phys. Rev. Appl. 2017, 7, 054006. [Google Scholar] [CrossRef]
- Xie, H.; Hou, Z. Nonlocal Metasurface for Acoustic Focusing. Phys. Rev. Appl. 2021, 15, 034054. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [Green Version]
- Ra’Di, Y.; Sounas, D.L.; Alù, A. Metagratings: Beyond the Limits of Graded Metasurfaces for Wave Front Control. Phys. Rev. Lett. 2017, 119, 067404. [Google Scholar] [CrossRef]
- Epstein, A.; Rabinovich, O. Unveiling the Properties of Metagratings via a Detailed Analytical Model for Synthesis and Analysis. Phys. Rev. Appl. 2017, 8, 054037. [Google Scholar] [CrossRef] [Green Version]
- Torrent, D. Acoustic anomalous reflectors based on diffraction grating engineering. Phys. Rev. B 2018, 98, 060101. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Fang, X.; Li, Y.; Assouar, B. Highly Efficient Acoustic Metagrating with Strongly Coupled Surface Grooves. Phys. Rev. Appl. 2019, 12, 034021. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Shen, C.; Cao, Y.; Gao, L.; Chen, H.; Chan, C.T.; Cummer, S.A.; Xu, Y. Reversal of transmission and reflection based on acoustic metagratings with integer parity design. Nat. Commun. 2019, 10, 2326. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.; Mei, J. Metagratings for Waterborne Sound: Various Functionalities Enabled by an Efficient Inverse Design Approach. Phys. Rev. Appl. 2020, 14, 044003. [Google Scholar] [CrossRef]
- Chiang, Y.K.; Oberst, S.; Melnikov, A.; Quan, L.; Marburg, S.; Alù, A.; Powell, D.A. Reconfigurable Acoustic Metagrating for High-Efficiency Anomalous Reflection. Phys. Rev. Appl. 2020, 13, 064067. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Liu, X. Modulation of acoustic waves by a broadband metagrating. Sci. Rep. 2019, 9, 7271. [Google Scholar] [CrossRef]
- Ni, H.; Fang, X.; Hou, Z.; Li, Y.; Assouar, B. High-efficiency anomalous splitter by acoustic meta-grating. Phys. Rev. B 2019, 100, 104104. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Mei, J. Acoustic Metagrating Circulators: Nonreciprocal, Robust, and Tunable Manipulation with Unitary Efficiency. Phys. Rev. Appl. 2021, 15, 064002. [Google Scholar] [CrossRef]
- Fan, L.; Mei, J. Multifunctional Waterborne Acoustic Metagratings: From Extraordinary Transmission to Total and Abnormal Reflection. Phys. Rev. Appl. 2021, 16, 044029. [Google Scholar] [CrossRef]
- He, J.; Jiang, X.; Ta, D.; Wang, W. Experimental demonstration of underwater ultrasound cloaking based on metagrating. Appl. Phys. Lett. 2020, 117, 091901. [Google Scholar] [CrossRef]
- Zhao, D.; Ye, Y.; Xu, S.; Zhu, X.; Yi, L. Broadband and wide-angle negative reflection at a phononic crystal boundary. Appl. Phys. Lett. 2014, 104, 043503. [Google Scholar]
- Yang, Y.; Jia, H.; Bi, Y.; Zhao, H.; Yang, J. Experimental demonstration of an acoustic asymmetric diffraction grating based on passive parity-time-symmetric medium. Phys. Rev. Appl. 2019, 12, 034040. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Jia, H.; Wang, S.; Zhang, P.; Yang, J. Diffraction control in a non-Hermitian acoustic grating. Appl. Phys. Lett. 2020, 116, 213501. [Google Scholar] [CrossRef]
- Kim, S.Y.; Lee, W.; Lee, J.S.; Kim, Y.Y. Longitudinal wave steering using beam-type elastic metagratings. Mech. Syst. Signal Process. 2021, 156, 107688. [Google Scholar] [CrossRef]
- Packo, P.; Norris, A.N.; Torrent, D. Inverse grating problem: Efficient design of anomalous flexural wave reflectors and refractors. Phys. Rev. Appl. 2019, 11, 014023. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Semperlotti, F. Anomalous refraction of acoustic guided waves in solids with geometrically tapered metasurfaces. Phys. Rev. Lett. 2016, 117, 034302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Liang, Z.; Liu, F.; Diba, O.; Lamb, A.; Li, J. Source illusion devices for flexural lamb waves using elastic metasurfaces. Phys. Rev. Lett. 2017, 119, 034301. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Nassar, H.; Hu, G.; Huang, G. A programmable metasurface for real time control of broadband elastic rays. Smart Mater. Struct. 2018, 27, 115011. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Xu, Y.; Assouar, B.; Yang, Z. Asymmetric flexural wave transmission based on dual-layer elastic gradient metasurfaces. Appl. Phys. Lett. 2018, 113, 183506. [Google Scholar] [CrossRef]
- Cao, L.; Yang, Z.; Xu, Y.; Fan, S.W.; Zhu, Y.; Chen, Z.; Vincent, B.; Assouar, B. Disordered elastic metasurfaces. Phys. Rev. Appl. 2020, 13, 014054. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, W.; Park, C.I.; Oh, J.H. Elastic wave energy entrapment for reflectionless metasurface. Phys. Rev. Appl. 2020, 13, 054036. [Google Scholar] [CrossRef]
- Chaplain, G.J.; De Ponti, J.M.; Aguzzi, G.; Colombi, A.; Craster, R.V. Topological rainbow trapping for elastic energy harvesting in graded Su-Schrieffer-Heeger systems. Phys. Rev. Appl. 2020, 14, 054035. [Google Scholar] [CrossRef]
- Yuan, S.M.; Chen, A.L.; Cao, L.; Zhang, H.W.; Fan, S.W.; Assouar, B.; Wang, Y.S. Tunable multifunctional fish-bone elastic metasurface for the wavefront manipulation of the transmitted in-plane waves. J. Appl. Phys. 2020, 128, 224502. [Google Scholar] [CrossRef]
- Ruan, Y.; Liang, X.; Hu, C. Retroreflection of flexural wave by using elastic metasurface. J. Appl. Phys. 2020, 128, 045116. [Google Scholar] [CrossRef]
- Li, B.; Hu, Y.; Chen, J.; Su, G.; Liu, Y.; Zhao, M.; Li, Z. Efficient asymmetric transmission of elastic waves in thin plates with lossless metasurfaces. Phys. Rev. Appl. 2020, 14, 054029. [Google Scholar] [CrossRef]
- Zheng, M.; Park, C.I.; Liu, X.; Zhu, R.; Hu, G.; Kim, Y.Y. Non-resonant metasurface for broadband elastic wave mode splitting. Appl. Phys. Lett. 2020, 116, 171903. [Google Scholar] [CrossRef]
- Rong, J.; Ye, W.; Zhang, S.; Liu, Y. Frequency-coded passive multifunctional elastic metasurfaces. Adv. Funct. Mater. 2020, 30, 2005285. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Zhu, R.; Huang, G. An active meta-layer for optimal flexural wave absorption and cloaking. Mech. Syst. Signal Process. 2021, 149, 107324. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, W.; Khelif, A.; Djafari-Rouhani, B. Elastic metasurfaces for deep and robust subwavelength focusing and imaging. Phys. Rev. Appl. 2021, 15, 024005. [Google Scholar] [CrossRef]
- Lin, Z.; Tol, S. Elastic metasurfaces for full wavefront control and low-frequency energy harvesting. J. Vib. Acoust. 2021, 143, 061005. [Google Scholar]
- Li, X.S.; Wang, Y.F.; Wang, Y.S. Sparse binary metasurfaces for steering the flexural waves. Extreme Mech. Lett. 2022, 52, 101675. [Google Scholar]
- Su, X.; Lu, Z.; Norris, A.N. Elastic metasurfaces for splitting SV- and P-waves in elastic solids. J. Appl. Phys. 2018, 123, 091701. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Su, X.; Pennec, Y.; Jing, Y.; Liu, X.; Hu, N. Wavefront steering of elastic shear vertical waves in solids via a composite-plate-based metasurface. J. Appl. Phys. 2018, 124, 164505. [Google Scholar] [CrossRef] [Green Version]
- Ahn, B.; Lee, H.; Lee, J.S.; Kim, Y.Y. Topology optimization of metasurfaces for anomalous reflection of longitudinal elastic waves. Comput. Methods Appl. Mech. Eng. 2019, 357, 112582. [Google Scholar] [CrossRef]
- Rong, J.; Ye, W. Multifunctional elastic metasurface design with topology optimization. Acta Mater. 2020, 185, 382–399. [Google Scholar] [CrossRef]
- Spägele, C.; Tamagnone, M.; Kazakov, D.; Ossiander, M.; Piccardo, M.; Capasso, F. Multifunctional wide-angle optics and lasing based on supercell metasurfaces. Nat. Commun. 2021, 12, 3787. [Google Scholar] [CrossRef] [PubMed]


| Mesh Size | |||
|---|---|---|---|
| 1.26 | 1.22 | 1.22 | |
| 46.24 | 46.09 | 45.97 | |
| 0.82 | 0.90 | 0.83 | |
| 0.05 | 0.05 | 0.05 | |
| 0.61 | 0.57 | 0.59 | |
| 0.96 | 0.98 | 0.99 | |
| 0.01 | 0.01 | 0.01 | |
| 0.13 | 0.12 | 0.12 | |
| 0.51 | 0.54 | 0.58 | |
| 0.09 | 0.08 | 0.09 | |
| 0.44 | 0.45 | 0.45 | |
| 48.88 | 48.98 | 49.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, J.; Fan, L.; Hong, X. Elastic Metagratings with Simultaneous Modulation of Reflected and Transmitted Waves. Crystals 2022, 12, 901. https://doi.org/10.3390/cryst12070901
Mei J, Fan L, Hong X. Elastic Metagratings with Simultaneous Modulation of Reflected and Transmitted Waves. Crystals. 2022; 12(7):901. https://doi.org/10.3390/cryst12070901
Chicago/Turabian StyleMei, Jun, Lijuan Fan, and Xiaobin Hong. 2022. "Elastic Metagratings with Simultaneous Modulation of Reflected and Transmitted Waves" Crystals 12, no. 7: 901. https://doi.org/10.3390/cryst12070901
APA StyleMei, J., Fan, L., & Hong, X. (2022). Elastic Metagratings with Simultaneous Modulation of Reflected and Transmitted Waves. Crystals, 12(7), 901. https://doi.org/10.3390/cryst12070901






