Room-Temperature 181Ta(TiO2): An e-γ TDPAC Study
Abstract
:1. Introduction
1.1. State of the Art (181Ta(TiO2) γ−γ TDPAC Spectroscopy)
1.2. Physics and Properties of Rutile TiO2
1.3. Motivation for Applying the e−γ TDPAC Spectroscopy to the TiO2 Material
2. Time Differential Perturbed Angular Correlations
3. Experimental Setup
3.1. Implantation of 181Hf Isotope at the Bonn Radioisotope Separator
3.2. Data Accquisition of 181Ta(TiO2) γ−γ and e−γ TDPAC Spectroscopy
3.3. X-ray Diffraction of the 181Ta(TiO2) Sample after the γ−γ and e−γ TDPAC Spectroscopy
4. Results
4.1. γ−γ TDPAC Spectroscopy Setup
4.2. e−γ TDPAC Spectroscopy Setup
4.3. X-ray Diffraction of the 181Ta(TiO2) Sample after the γ−γ and e−γ TDPAC Spectroscopy
5. Discussion
5.1. γ−γ TDPAC Spectroscopy Setup
5.2. e−γ TDPAC Spectroscopy Setup Compared with γ−γ TDPAC Spectroscopy Setup
5.3. X-ray Diffraction of the 181Ta(TiO2) Sample after the γ−γ and e−γ TDPAC Spectroscopy
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. A Discussion on Ion Implantation Damage to Our TiO2 Sample
Appendix A.1. Literature Review of Ion Implantation Damage to the Host Semiconductor
Appendix A.2. Discussion Pertaining to the Degree of Annealing, with Relevant TDPAC Results Attached
| R(t) Signal | Fundamental Frequency (Mrad/s) | Asymmetry Parameter | (1020 V/m2) | Delta Lorentzian (%) | Chi Squared | Theta (deg) | Phi (deg) | Additive Constant |
|---|---|---|---|---|---|---|---|---|
| U_1 | 763 (4) | 0.53 (1) | 142.0 ± 0.7 a ± 3.0 b | 6.6 (7) | 0.98 | 0 (6) | 37.8 (4) | −0.018 (2) |
| U_2 | 766.31 (7) | 0.525 (7) | 142.48 ± 0.01 a ± 3.02 b | 6.0 (2) | 1.20 | 0.0 (4) | 37.9 (2) | −0.005 (1) |
| U_3 | 759.7 (1) | 0.519 (4) | 141.255 ± 0.002 a ± 2.993 b | 6.0 (2) | 1.40 | 0 (2) | 37.9 (2) | −0.000 (1) |
| Average | 763 (4) | 0.53 (1) | 141.9 ± 0.7 c | 6.2 (8) | N.A. | N.A. | N.A. | N.A. |
| R(t) Signal | Fundamental Frequency (Mrad/s) | Asymmetry Parameter | (1020 V/m2) | Delta Lorentzian (%) | Chi Squared | Theta (Deg) | Phi (Deg) | Additive Constant (Fixed) |
|---|---|---|---|---|---|---|---|---|
| A_1 | 762 (2) | 0.548 (4) | 141.6 ± 0.4 a ± 3.0 b | 1.1 (3) | 0.83 | 45 (3) | 58.8 (7) | −0.0398 |
| A_2 | 760 (2) | 0.548 (4) | 142.3 ± 0.3 a ± 3.0 b | 1.0 (2) | 0.83 | 43 (3) | 57.9 (6) | −0.0398 |
| A_3 | 763.0 (8) | 0.543 (2) | 141.9 ± 0.2 a ± 3.0 b | 0.9 (1) | 0.94 | 45 (1) | 58.5 (3) | −0.0398 |
| A_4 | 762.9 (5) | 0.543 (1) | 141.85 ± 0.09 a ± 3.01 b | 0.95 (7) | 1.30 | 45.7 (8) | 58.5 (2) | −0.0398 |
| A_5 | 762.4 (5) | 0.543 (1) | 141.75 ± 0.09 a ± 3.00 b | 1.04 (7) | 1.37 | 45.9 (8) | 58.4 (2) | −0.0398 |
| Average | 762 (3) | 0.545 (6) | 141.07 ± 0.5 c | 1.0 (4) | N.A. | N.A. | N.A. | N.A. |
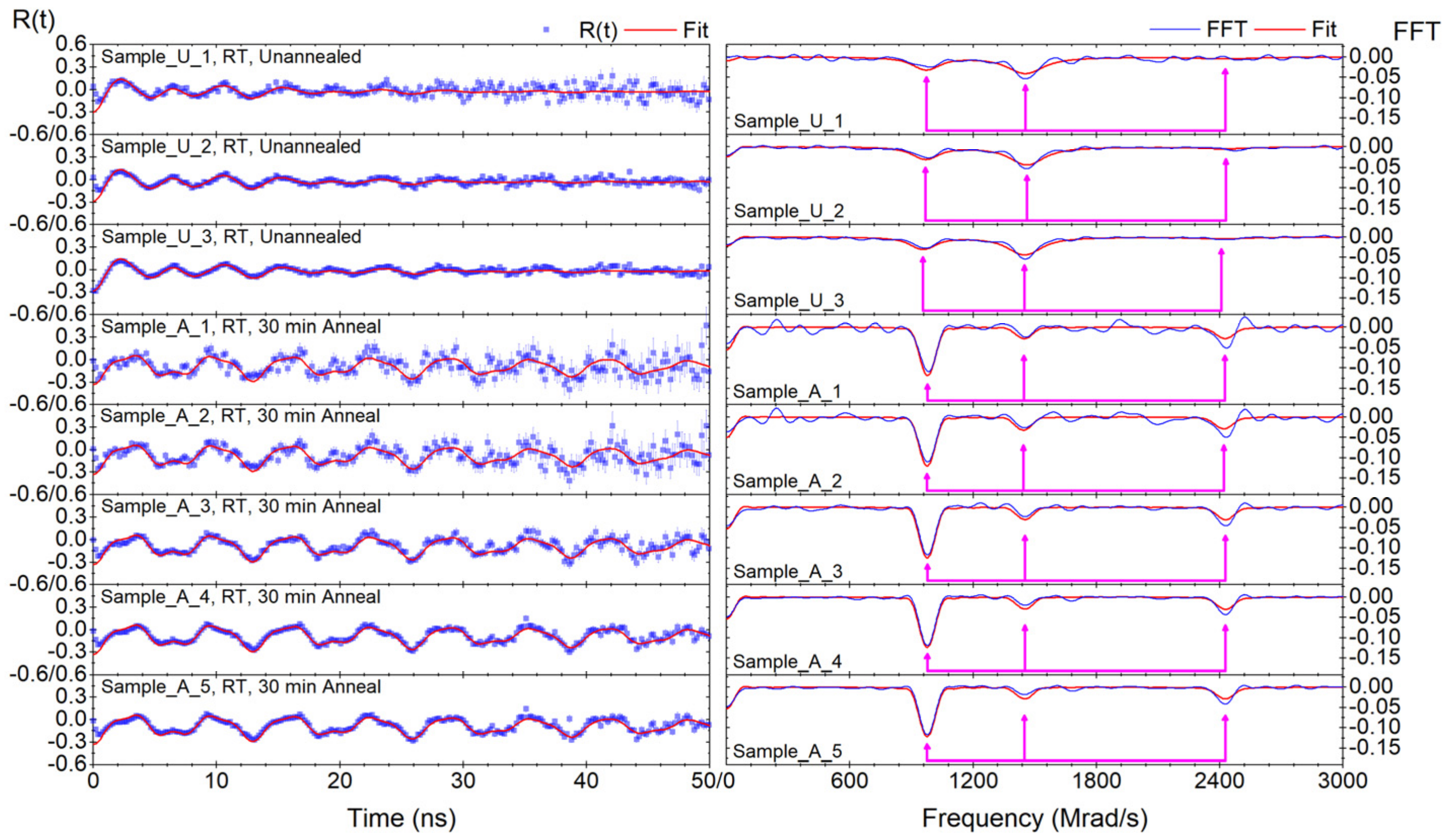
| Annealing Time (mins) | Fundamental Frequency (Mrad/s) | Asymmetry Parameter | (1020 V/m2) | Delta Lorentzian (%) |
|---|---|---|---|---|
| 0 (3 samples) | 763 (4) | 0.53 (1) | 141.9 (7) | 6.2 (8) |
| 30 (5 samples) | 762 (3) | 0.545 (6) | 141.7 (5) | 1.0 (4) |
| 315 (13 samples) | 765 (2) | 0.54 (1) | 142.2 (4) | 0.05 ± 0.19 a |
Appendix B. Geometry between the Different Detector Planes
References
- Greenwood, N.N.; Earnshaw, A. Chapter 21: “Titanium, Zirconium and Hafnium”. In Chemistry of the Elements, 2nd ed.; Butterworth Heinemann: Oxford, UK, 1998; pp. 954–975. ISBN 0750633654. [Google Scholar]
- Hanaor, D.A.H.; Sorrell, C.C. Review of the anatase to rutile phase transformation. J. Mater. Sci. 2011, 46, 855–874. [Google Scholar] [CrossRef] [Green Version]
- Fujishima, A.; Honda, K. Electrochemical Photolysis of Water at a Semiconductor Electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Hanaor, D.A.H.; Sorrell, C.C. Sand Supported Mixed-Phase TiO2 Photocatalysts for Water Decontamination Application. Adv. Eng. Mater. 2014, 16, 248–254. [Google Scholar] [CrossRef] [Green Version]
- Dumbuya, H.; Grimes, P.E.; Lynch, S.; Ji, K.; Brahmachary, M.; Zheng, Q.; Bouez, C.; Wangari-Talbot, J. Impact of iron-oxide containing formulations against visible light-induced skin pigmentation in skin of color individuals. J. Drugs Dermatol. 2020, 19, 712–717. [Google Scholar] [CrossRef]
- Gázquez, M.J.; Moreno, S.M.P.; Bolívar, J.P. Chapter 9: “TiO2 as white pigment and valorization of the waste coming from its production”. In Metal Oxides Series: Titanium Dioxide (TiO2) and Its Applications, 1st ed.; Parrino, F., Palmisano, L., Eds.; Elsevier Academic Press: Amsterdam, The Netherlands, 2021; pp. 311–335. ISBN 9780128199602. [Google Scholar]
- Adams, J.M.; Catchen, G.L. Anomalous crystal chemistries of the 111In → 111Cd and 181Hf → 181Ta probes in rutile TiO2 studied using perturbed-angular-correlation spectroscopy. Phys. Rev. B 1994, 50, 1264. [Google Scholar] [CrossRef]
- Darriba, G.N.; Errico, L.A.; Eversheim, P.D.; Fabricus, G.; Rentería, M. First-principles and time-differential γ−γ perturbed-angular-correlation spectroscopy study of structural and electronic properties of Ta-doped TiO2 semiconductor. Phys. Rev. B 2009, 79, 115213, Erratum in Phys. Rev. B 2011, 84, 239903. https://doi.org/10.1103/PhysRevB.84.239903. [Google Scholar] [CrossRef]
- Das, S.K.; Thakare, S.V.; Butz, T. The nuclear quadrupole interaction at 111Cd and 181Ta sites in anatase and rutile TiO2: A TDPAC study. J. Phys. Chem. Solids 2009, 70, 778–781. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, D.; Das, S.K.; Thakare, S.V.; Nabhiraj, P.Y.; Menon, R.; Bhandari, R.K.; Krishnan, K. Study of surface-bulk mass transport and phase transformation in nano-TiO2 using hyperfine interaction technique. J. Phys. Chem. Solids 2010, 71, 983–987. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, D.; Das, S.K.; Thakare, S.V. Simultaneous measurement of electric field gradient both at 111Cd and 181Ta sites in a single perturbed γ−γ angular correlation measurement. J. Radioanal. Nucl. Chem. 2017, 313, 677–682. [Google Scholar] [CrossRef]
- Banerjee, D.; Guin, R.; Das, S.K.; Thakare, S.V. Effect of γ-dose on the crystal structure and leaching behavior of TiO2 matrix labeled with 181Hf/181Ta tracer. J. Radioanal. Nucl. Chem. 2011, 290, 119–121. [Google Scholar] [CrossRef]
- Schell, J.; Lupascu, D.C.; Carbonari, A.W.; Mansano, R.D.; Ribeiro Junior, I.S.; Dang, T.T.; Anusca, I.; Trivedi, H.; Johnston, K.; Vianden, R. Ion implantation in titanium dioxide thin films studied by perturbed angular correlations. Int. J. Appl. Phys. 2017, 121, 145302. [Google Scholar] [CrossRef]
- Schell, J. Investigation of Hyperfine Parameters in Pure and 3D Transition Metal Doped SnO2 and TiO2 by Means of Perturbed Gamma–Gamma Angular Correlation Spectroscopy. Ph.D. Thesis, São Paulo University, São Paulo, Brazil, 2015. [Google Scholar]
- Martucci, T.; Ramos, J.M.; Carbonari, A.W.; Silva, A.S.; Saxena, R.N. Investigation of electric quadrupole interaction in TiO2 by means of perturbed gamma-gamma angular correlation spectroscopy. In Proceedings of the 2011 International Nuclear Atlantic Conference, Belo Horizonte, Brazil, 24–28 October 2011; Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/43/046/43046289.pdf (accessed on 7 March 2022).
- Dimesso, L. Pechini Processes: An Alternate Approach of the Sol–Gel Method, Preparation, Properties, and Applications. In Handbook of Sol-Gel Science and Technology, 1st ed.; Klein, L., Aparicio, M., Jitianu, A., Eds.; Springer: Cham, Switzerland, 2018; pp. 1–22. ISBN 9783319194547. [Google Scholar] [CrossRef]
- Ribeiroa, P.C.; Figueiredo de Melo da Costa, A.C.; Goldschmidt Aliaga Kiminami, R.H.; Sasaki, J.M.; Lira, H.L. Synthesis of TiO2 by the Pechini Method and Photocatalytic Degradation of Methyl Red. Mater. Res. 2013, 16, 468–472. [Google Scholar] [CrossRef]
- Schell, J.; Zyabkin, D.; Lupascu, D.C.; Hofsäss, H.C.; Karabasov, M.O.; Welker, A.; Schaaf, P. A hyperfine look at Titanium Dioxide. AIP Adv. 2019, 9, 085208. [Google Scholar] [CrossRef] [Green Version]
- Aroyo, M.I. (Ed.) Vol. A, Ch. 7.1: Space Group 136. In International Tables for Crystallography, Volume A, 6th Edition, Space-group Symmetry; Wiley: Chichester, UK, 2006; ISBN 978-0-470-97423-0. Available online: https://it.iucr.org/Ab/ch7o1v0001/sgtable7o1o136/ (accessed on 4 April 2022).
- Rutile (TiO2, C4) Structure: A2B_tP6_136_f_a. In Encyclopedia of Crystallographic Prototypes. Available online: http://aflowlib.org/prototype-encyclopedia/A2B_tP6_136_f_a.html (accessed on 4 April 2022).
- Titanium Dioxide (Rutile) TiO2, Shinkosha. Available online: https://www.shinkosha.com/english/product/epi_substrate/epi_substrate_03/ (accessed on 7 March 2022).
- Maity, P.; Mohammed, O.F.; Katsiev, K. Study of the Bulk Charge Carrier Dynamics in Anatase and Rutile TiO2 Single Crystals by Femtosecond Time Resolved Spectroscopy. J. Phys. Chem. C 2018, 122, 8925–8932. [Google Scholar] [CrossRef] [Green Version]
- Grundmann, M. Chapter 8: “Transport” and Chapter 10: “Recombination” In The Physics of Semiconductors: An Introduction Including Nanophysics and Applications, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 278–281, 343–346. ISBN 978-3-319-23879-1. [Google Scholar]
- Gehring, A.; Selberherr, S. Chapter 9: “Tunnelling Models for Semiconductor Device Simulation”. In Handbook of Theoretical and Computational Nanotechnology; American Scientific Publishers: Valencia, CA, USA, 2006; Volume 10, Available online: https://www.iue.tuwien.ac.at/pdf/ib_2006/BC2006_Gehring_1.pdf (accessed on 7 March 2022).
- Woolcot, T.; Teobaldi, G.; Pang, C.L.; Beglitis, N.S.; Fisher, A.J.; Hofer, W.A.; Thornton, G. Scanning Tunneling Microscopy Contrast Mechanisms for TiO2. Phys. Rev. Lett. 2012, 109, 156105. [Google Scholar]
- Adachi, Y.; Brndiar, J.; Wen, H.F.; Zhang, Q.Z.; Miyazaki, M.; Thakur, S.; Sugawara, Y.; Sang, H.Q.; Li, Y.J.; Štich, I.; et al. Electron dynamics of tip-tunable oxygen species on TiO2 surface. Commun. Mater. 2021, 2, 71. [Google Scholar] [CrossRef]
- Thomas, A.G.; Flavell, W.R.; Mallick, A.K.; Kumarasinghe, A.R.; Tsoutsou, D.; Khan, N.; Chatwin, C.; Rayner, S.; Smith, G.C. Comparison of the electronic structure of anatase and rutile TiO2 single-crystal surfaces using resonant photoemission and X-ray absorption spectroscopy. Phys. Rev. B 2007, 75, 035105. [Google Scholar] [CrossRef]
- Zhu, H.X.; Zhou, P.X.; Li, X.; Liu, J.-M. Electronic structures and optical properties of rutile TiO2 with different point defects from DFT+U calculations. Phys. Lett. A 2014, 378, 2719–2724. [Google Scholar] [CrossRef]
- Perron, H.; Domain, C.; Roques, J.; Drot, R.; Simoni, E.; Catalette, H. Optimization of accurate rutile TiO2 (110), (100), (101) and (001) surface models from periodic DFT calculations. Theor. Chem. Acc. 2007, 117, 565–574. [Google Scholar] [CrossRef] [Green Version]
- Rühle, S.; Cahen, D. Electron Tunnelling at TiO2/Substrate Interface Can Determine Dye-Sensitized Solar Cell Performance. J. Phys. Chem. B 2004, 108, 17946–17951. [Google Scholar] [CrossRef]
- Barbosa, M.B.; Correia, J.G.; Lorenz, K.; Vianden, R.; Araújo, J.P. Studying electronic properties in GaN without using electrical contacts using γ−γ vs e−−γ Perturbed Angular Correlations. Sci. Rep. 2019, 9, 15734. [Google Scholar] [CrossRef]
- Schell, J.; Lupascu, D.C.; Correia, J.G.; Carbonari, A.W.; Deicher, M.; Barbosa, M.B.; Mansano, R.D.; Johnston, K.; Ribeiro, I.S., Jr. ISOLDE collaboration “In and Cd as defect traps in titanium dioxide”. Hyperfine Interact. 2017, 238, 2. [Google Scholar] [CrossRef]
- Schatz, G.; Weidinger, A. Chapter 2: “Electromagnetic Properties and Nuclear Decay. Chapter 3: “Hyperfine Interactions. Chapter 5: “Perturbed γ−γ Angular Correlation (PAC). In Nuclear Condensed Matter Physics: Nuclear Methods and Applications; Wiley: Chichester, UK, 1996; pp. 3–32, 63–99. ISBN 0471954799. [Google Scholar]
- Steffen, R.M.; Alder, K. Chapter 13: “Extranuclear perturbations of angular distributions and correlations”. In The Electromagnetic Interaction in Nuclear Spectroscopy, 1st ed.; Hamilton, W.D., Ed.; North-Holland Publishing Company Ltd.: Oxford, UK, 1975; pp. 583–643. ISBN 0720402751. [Google Scholar]
- Butz, T. Analytic perturbation functions for static interactions in perturbed angular correlation of γ rays. Hyperfine Interact. 1989, 52, 189–228. [Google Scholar] [CrossRef]
- Johnston, K.; Schell, J.; Correia, J.G.; Deicher, M.; Gunnlaugsson, H.P.; Fenta, A.S.; David-Bosne, E.; Costa, A.R.G.; Lupascu, D.C. “The solid state physics programme at ISOLDE: Recent developments and perspectives. J. Phys. G Nucl. Part. Phys. 2017, 44, 104001. [Google Scholar] [CrossRef]
- Marschick, G.; Schell, J.; Stöger, B.; Gonçalves, J.N.; Karabasov, M.O.; Zyabkin, D.; Welker, A.; Escobar, C.M.; Gärtner, D.; Efe, I.; et al. Multiferroic bismuth ferrite: Perturbed angular correlation studies on its ferroic α−β phase transition. Phys. Rev. B 2020, 102, 224110. [Google Scholar] [CrossRef]
- Jancso, A.; Correia, J.G.; Gottberg, A.; Schell, J.; Stachura, M.; Szunyogh, D.; Pallada, S.; Lupascu, D.C.; Kowalska, M.; Hemmingsen, L. TDPAC and β-NMR applications in chemistry and biochemistry. J. Phys. G Nucl. Part. Phys. 2017, 44, 064003. [Google Scholar] [CrossRef]
- Balogh, R.K.; Gyurcsik, B.; Hunyadi-Gulyás, É.; Schell, J.; Thulstrup, P.W.; Hemmingsen, L.; Jancsó, A. C-terminal Cysteines of CueR Act as Auxiliary Metal Site Ligands upon Hg-II Binding—A Mechanism to Prevent Transcriptional Activation by Divalent Metal Ions? Chem. Eur. J. 2019, 25, 15030–15035. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.-C. Nuclear Data Sheets for A = 181. Nucl. Data Sheets 2005, 106, 367–600. [Google Scholar] [CrossRef]
- Catherall, R.; Andreazza, W.; Breitenfeldt, M.; Dorsival, A.; Focker, G.J.; Gharsa, T.P.; Giles, T.J.; Grenard, J.-L.; Locci, F.; Martins, P. The ISOLDE facility. J. Phys. G: Nucl. Part. Phys. 2017, 44, 094002. [Google Scholar] [CrossRef] [Green Version]
- Schell, J.; Schaff, P.; Lupascu, D.C. Perturbed angular correlations at ISOLDE: A 40 years young technique. AIP Adv. 2017, 7, 105017. [Google Scholar] [CrossRef] [Green Version]
- Marques, J.G.; Correia, J.G.; Melo, A.A.; da Silva, M.F.; Soares, J.C. ISOLDE Collaboration (CERN). A four-detector spectrometer for e−γ PAC on-line with the ISOLDE-CERN isotope separator. Nucl. Instrum. Methods Phys. Res. Sect. B 1995, 99, 645–648. [Google Scholar] [CrossRef] [Green Version]
- Kleinheinz, P.; Samuelsson, L.; Vukanović, R.; Siegbahn, K. A four-detector electron directional correlation spectrometer. Nucl. Instrum. Methods. 1965, 32, 1–27. [Google Scholar] [CrossRef]
- Nagl, M.A.; Barbosa, M.B.; Vetter, U.; Correia, J.G.; Hofsäss, H.C. A new tool for the search of nuclides with properties suitable for nuclear solid state physics based on the Evaluated Nuclear Structure Data Files. Nucl. Instrum. Methods Phys. Res. A 2013, 726, 17–30. [Google Scholar] [CrossRef]
- Lupascu, D.C.; Habenicht, S.; Lieb, K.-P.; Neubauer, M.; Uhrmacher, M.; Wenzel, T. Relaxation of electronic defects in pure and doped La2O3 observed by perturbed angular correlations. Phys. Rev. B 1996, 871, 871. [Google Scholar] [CrossRef]
- Forker, M.; Krien, K.; Reuschenbach, F. e−−γ TDPAC measurements of the magnetic and electric hyperfine interaction of 181Ta implanted in terbium. Hyperfine Interact. 1981, 9, 255–259. [Google Scholar] [CrossRef]
- Krien, K.; Forker, M.; Reuschenbach, F.; Trzcinski, R. “The magnetic hyperfine field and the electric field gradient at 181Ta impurities in Gd metal. Hyperfine Interact. 1979, 7, 19–27. [Google Scholar] [CrossRef]
- Soares, J.C.; Krien, K.; Freitag, K. Magnetic hyperfine fields at Ta in Co and Fe hosts measured by the e−−γ time-differential perturbed angular-correlation method. Hyperfine Interact. 1975, 1, 45–53. [Google Scholar] [CrossRef]
- Krien, K.; Bibiloni, A.G.; Freitag, K.; Soares, J.C.; Vianden, R. Measurements of the Magnetic Hyperfine Fields at Hg in Fe, Co, and Ni Hosts by the e−−γ Time-Differential Perturbed-Angular-Correlation Method. Phys. Rev. B 1973, 8, 2248. [Google Scholar] [CrossRef]
- Butz, T.; Lerf, A. Comment on “Mössbauer studies of the 6.2 keV γ rays of 181Ta in Ta-dichalcogenides. Phys. Lett. A 1983, 97, 217–218. [Google Scholar] [CrossRef]
- Wegner, T. Calculated Perturbed Angular Correlations for 111In Doped Cubic Single Crystals. Hyperfine Interact. 1985, 23, 179–210. [Google Scholar] [CrossRef]
- Correia, J.G.; C2TN, DECN, Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal; European Organization for Nuclear Research (CERN), 1211 Geneva, Switzerland. Qk(e−) anisotropy attenuation coefficients consider electron (back)scattering on sample and spectrometer geometry acceptance solid angle determined with the esP2P4 program that was built on purpose and integrates modified versions of Penelope and penEasy programs. Personal communication, 2019. [Google Scholar]
- Baró, J.; Sempau, J.; Fernández-Varea, J.M.; Salvat, F. PENELOPE: An algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl. Instrum. Methods Phys. Res. Sect. B 1995, 100, 31–46. [Google Scholar] [CrossRef]
- Crystals GmbH. Available online: https://crystal-gmbh.com/ (accessed on 18 January 2022).
- Freitag, K. A facility for ion implantation in samples colder than 0.5 K. Radiat. Eff. 1979, 44, 185. [Google Scholar] [CrossRef]
- Rutile Mineral Data. Available online: http://webmineral.com/data/Rutile.shtml#.YeYHc_7MIQ9 (accessed on 18 January 2022).
- Jäger, M.; Iwig, K.; Butz, T. A compact digital time differential perturbed angular correlation-spectrometer using field programmable gate arrays and various timestamp algorithms. Rev. Sci. Instrum. 2011, 82, 065105. [Google Scholar] [CrossRef]
- Raghavan, R.S.; Raghavan, P. A new method for differential perturbed angular correlation measurements. Nucl. Instrum. Methods 1971, 92, 435–437. [Google Scholar] [CrossRef]
- Horta, J.; Silva, D. Interlude, Copyright (2000–2002) from Leipzig University © JL; Leipzig University: Leipzig, Germany, 2002. [Google Scholar]
- Correia, J.G. Correia, for GFIT19 and N. P. Barradas for NNFIT Programs. In PAC MANual; Lisbon, Portugal, 1992. [Google Scholar]
- Barradas, N.P. NNFit the PAC MANual; Lisabon, Portugal, 1992. [Google Scholar]
- Barradas N., P.; Rots, M.; Melo, A.A.; Soares, J.C. Magnetic anisotropy and temperature dependence of the hyperfine fields of 111Cd in single-crystalline cobalt. Phys. Rev. B 1993, 47, 8763. [Google Scholar] [CrossRef]
- Nightmare (MDI). Version RC 3 (1.2.0.247): Copyright (2005–2010) from the Group Reiner Vianden and (2008-2010) Ronan Nédélec; Bonn University: Bonn, Germany, 2010. [Google Scholar]
- Correia, J.G.; C2TN, DECN, Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal; European Organization for Nuclear Research (CERN), 1211 Geneva, Switzerland. Details for γ Akk coefficients. Obtained with program multiAkk (J.G. Correia and J.G. Marques) that generates angular correlation coefficients (bk)Akk’(bk’). Multiple gamma—gamma and electron-gamma nuclear cascades. The program further includes gamma finite size (gamma) attenuations coefficients Qkk’ which were analytically calculated. Personal communication, 2019. [Google Scholar]
- Hager, R.S.; Seltzer, E.C. Internal conversion tables, part II: Directional and polarization particle parameters for Z = 30 to Z = 103. Nucl. Data Sheets A 1968, 4, 397–641. [Google Scholar] [CrossRef]
- Hager, R.S.; Seltzer, E.C. Internal conversion tables, part I: K-, L-, M- Shell conversion coefficients for Z = 30 to Z = 103. Nucl. Data Sheets A 1968, 4, 1–235. [Google Scholar] [CrossRef]
- Rose, M.E. The Analysis of Angular Correlation and Angular Distribution Data. Phys. Rev. 1953, 91, 610. [Google Scholar] [CrossRef]
- Empyrean, the Intelligent Diffractometer by Malvern Panalytical. Available online: https://www.malvernpanalytical.com/en/products/product-range/empyrean-range/empyrean (accessed on 17 June 2022).
- Guo, X.Y.; Xu, D.P.; Ding, Z.H.; Su, W.H. Preparation and Raman Spectrum of Rutile Single Crystals using Floating Zone Method. Chin. Phys. Lett. 2006, 23, 1645. [Google Scholar] [CrossRef]
- Müller, G.; Friedrich, J. Crystal Growth, Bulk: Methods. In Encyclopedia of Condensed Matter Physics, 1st ed.; Bassani, F., Liedl, G.L., Wyder, P., Eds.; Elsevier Academic Press: Amsterdam, The Netherlands, 2007; pp. 269–270. ISBN 978-0-12-369401-0. [Google Scholar]
- Power Diffraction Data of Rutile. Available online: https://rruff.info/Rutile/R060745 (accessed on 18 June 2022).
- RRUFF™ Project. Available online: https://rruff.info/about/about_general.php (accessed on 18 June 2022).
- Gibbons, J.F. Ion implantation in semiconductors—Part I: Range distribution theory and experiments. Proc. IEEE 1972, 56, 259–319. [Google Scholar] [CrossRef]
- Metropolis, N. The Beginning of the Monte Carlo Method; Volume is a Special Issue Dedicated to Stanislaw Ulam; LANL Publications: Los Alamos County, NM, USA, 1987; Volume 15, pp. 124–130. Available online: https://library.lanl.gov/la-pubs/00326866.pdf (accessed on 11 April 2022).
- Gibbons, J.F. Ion implantation in semiconductors—Part II: Damage production and annealing. Proc. IEEE 1972, 60, 1062–1096. [Google Scholar] [CrossRef]


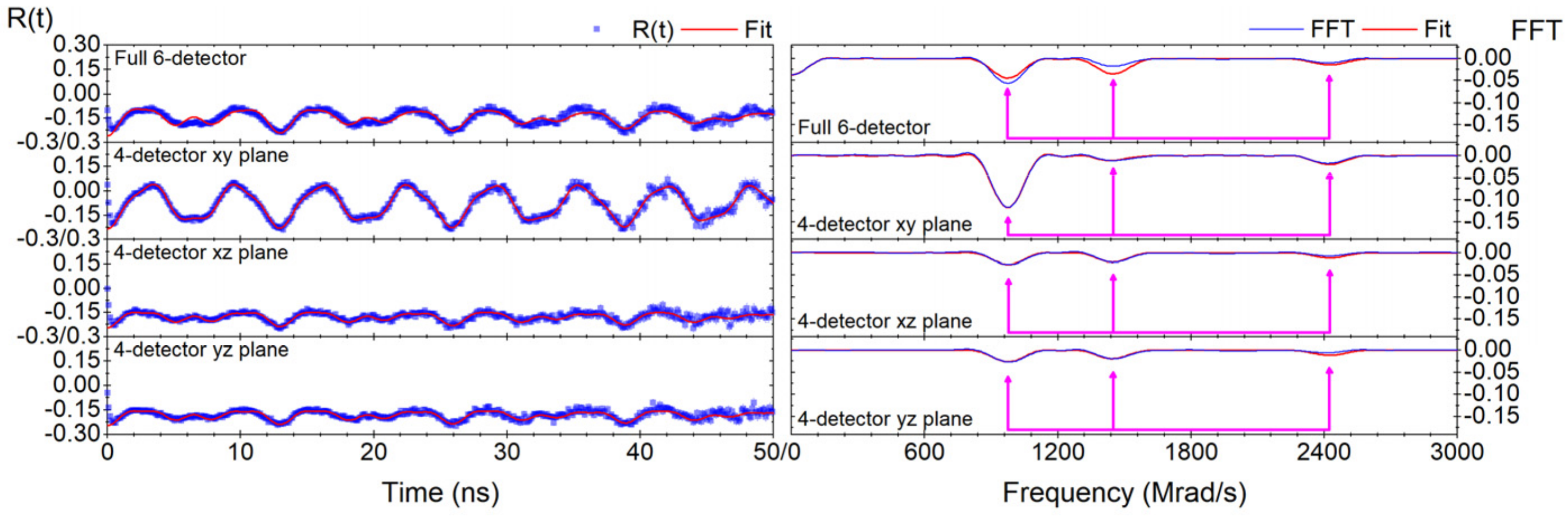

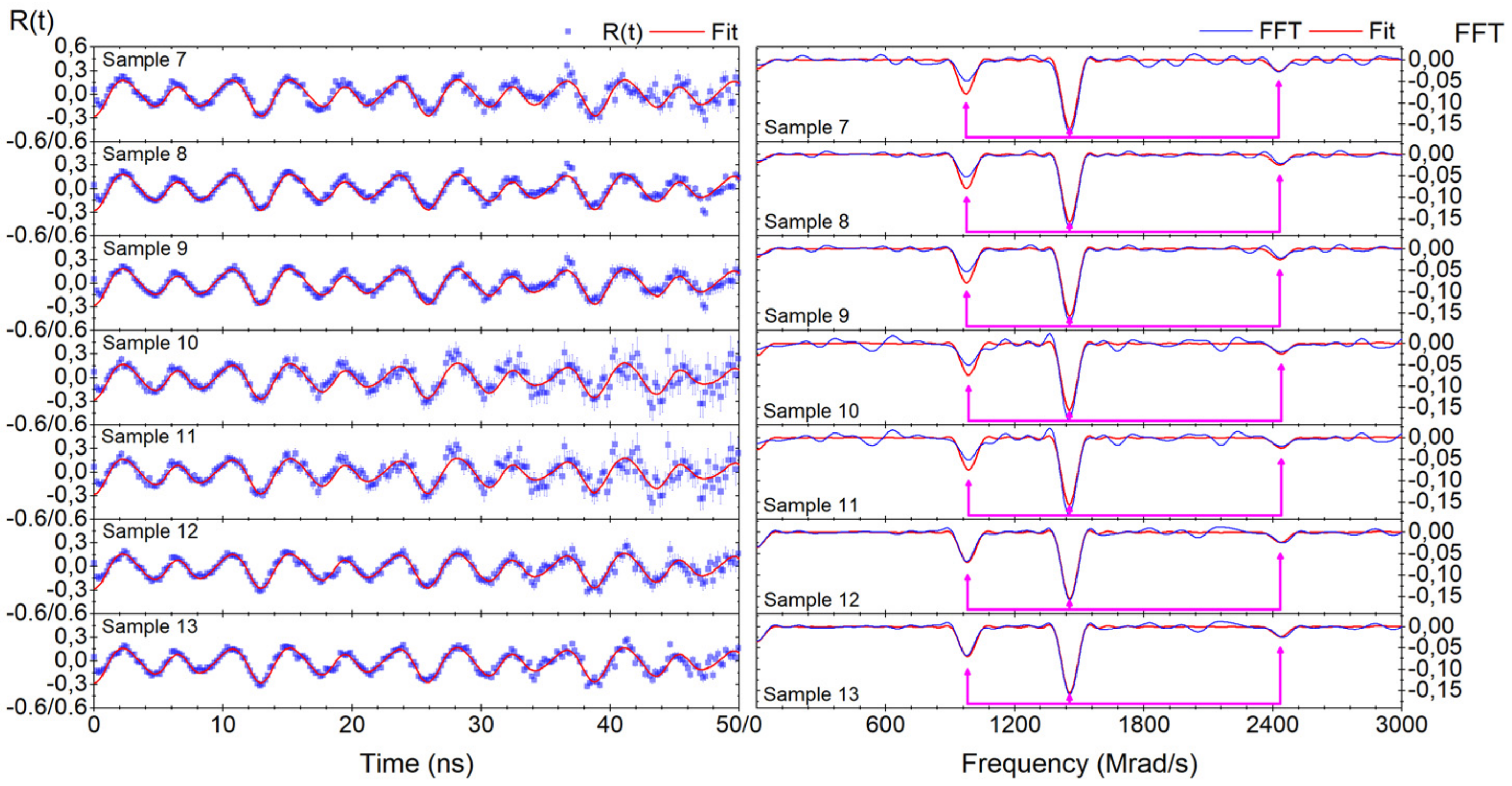
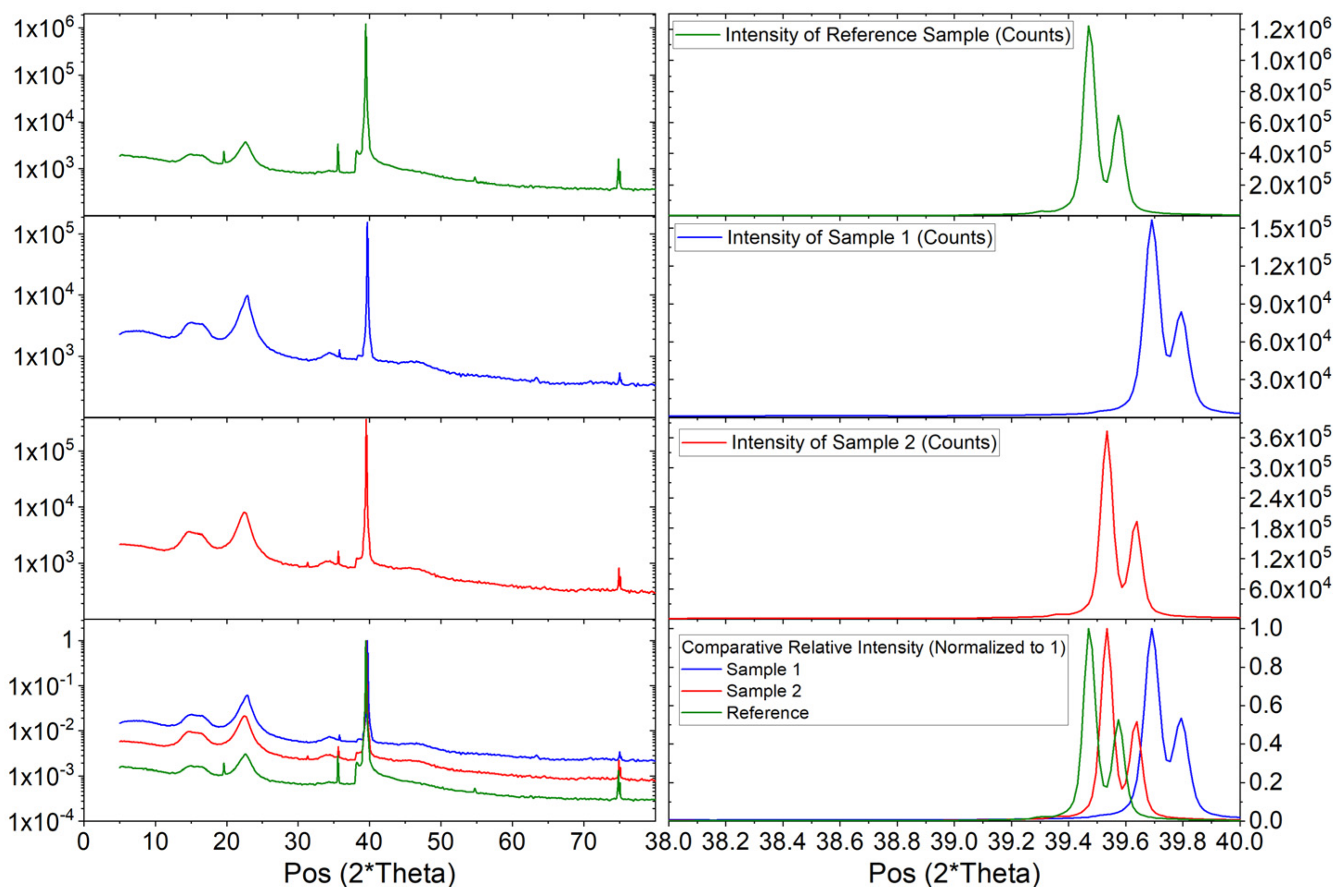
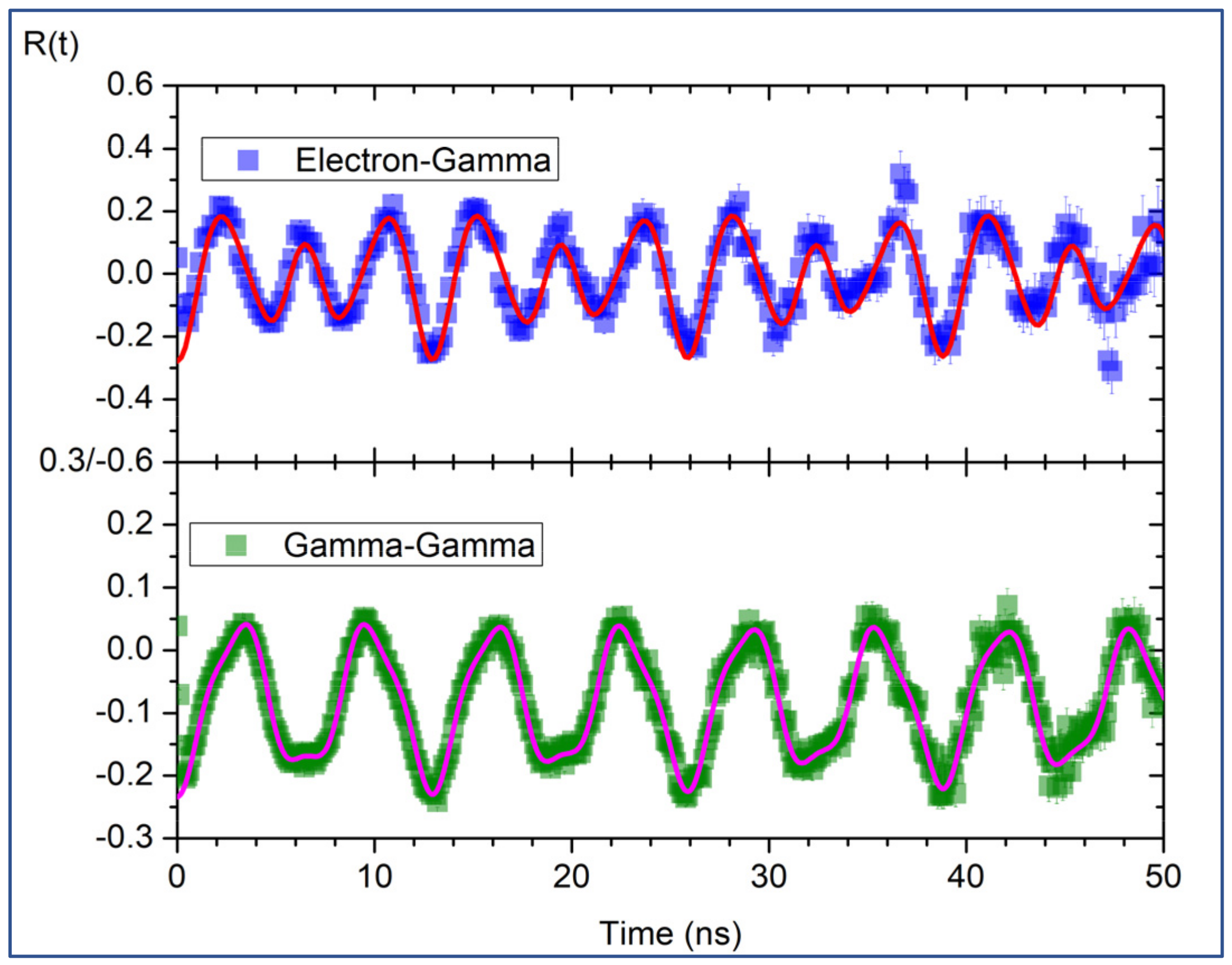
| Geometry | Fundamental Frequency (Mrad/s) | Asymmetry Parameter | (1020 V/m2) | Delta Lorentzian (%) | Chi Squared | Theta (Deg) | Phi (Deg) | Multiplicative Constant | Additive Constant |
|---|---|---|---|---|---|---|---|---|---|
| Six-detectors | 762.0 (4) | 0.540 (1) | 141.68 ± 0.07 a ± 3.00 b | 0.94 (5) | 3.5 | N.A. | N.A. | 0.692 (5) | −0.1111 (4) |
| Four-detector x-y plane | 761.8 (2) | 0.542 (1) | 141.64 ± 0.04 a ± 3.00 b | 0.17 (3) | 0.77 | 64.4 (5) | 47.1 (3) | 0.719 (5) | −0.0817 (5) |
| Four-detector x-z plane | 761.9 (7) | 0.545 (2) | 141.7 ± 0.1 a ± 3.0 b | 0.49 (9) | 0.79 | 28.6 (8) | 45.8 (3) | 0.314 (7) | −0.1795 (5) |
| Four-detector y-z plane | 761.5 (6) | 0.544 (2) | 141.6 ± 0.1 a ± 3.0 b | 0.46 (8) | 0.96 | 29.5 (7) | 46.3 (4) | 0.300 (6) | −0.1843 (4) |
| Average | 762 (1) | 0.543 (3) | 141.6 ± 0.2 c | N.A. | N.A. | N.A. | N.A. | N.A. | N.A. |
| R(t) Signal | Fundamental Frequency (Mrad/s) | Asymmetry Parameter | (1020 V/m2) | Delta Lorentzian (%) | Chi Squared | Phi (Deg) | Additive Constant (Fixed) |
|---|---|---|---|---|---|---|---|
| 1 | 765.0 (5) | 0.549 (3) | 142.23 ± 0.09 a ± 3.01 b | 0.03 (6) | 0.72 | 37.8 (4) | 0.0187 |
| 2 | 765.6 (3) | 0.546 (2) | 142.35 ± 0.06 a ± 3.02 b | 0.04 (6) | 0.99 | 37.9 (2) | 0.0187 |
| 3 | 765.6 (3) | 0.546 (2) | 142.35 ± 0.06 a ± 3.02 b | 0.04 (6) | 0.99 | 37.9 (2) | 0.0187 |
| 4 | 764.4 (3) | 0.543 (2) | 142.12 ± 0.06 a ± 3.01 b | 0.02 (2) | 0.89 | 37.5 (2) | 0.0187 |
| 5 | 764.4 (3) | 0.543 (2) | 142.12 ± 0.06 a ± 3.01 b | 0.02 (2) | 0.89 | 37.5 (2) | 0.0187 |
| 6 | 764.4 (3) | 0.543 (2) | 142.12 ± 0.06 a ± 3.01 b | 0.02 (2) | 0.89 | 37.5 (2) | 0.0187 |
| 7 | 763.8 (7) | 0.536 (4) | 142.0 ± 0.1 a ± 3.0 b | 0.04 (9) | 0.73 | 38.6 (5) | 0.0085 |
| 8 | 764.6 (4) | 0.539 (2) | 142.17 ± 0.08 a ± 3.01 b | 0.09 (6) | 0.85 | 38.8 (3) | 0.0085 |
| 9 | 764.6 (4) | 0.539 (2) | 142.17 ± 0.08 a ± 3.01 b | 0.09 (6) | 0.85 | 38.8 (3) | 0.0085 |
| 10 | 765 (1) | 0.552 (5) | 142.2 ± 0.2 a ± 3.0 b | 0.07 (1) | 0.60 | 37.2 (7) | 0.0085 |
| 11 | 765 (1) | 0.552 (5) | 142.2 ± 0.2 a ± 3.0 b | 0.07 (1) | 0.60 | 37.2 (7) | 0.0085 |
| 12 | 765.1 (5) | 0.544 (3) | 142.3 ± 0.1 a ± 3.0 b | 0.06 (7) | 0.71 | 36.3 (3) | 0.0085 |
| 13 | 765.1 (5) | 0.544 (3) | 142.3 ± 0.1 a ± 3.0 b | 0.06 (7) | 0.71 | 36.3 (3) | 0.0085 |
| Average | 765 (2) | 0.54 (1) | 142.2 ± 0.4 c | 0.05 ± 0.19 d | N.A. | 38 (1) | 0.0085 |
| Sample and Peak Number | Angle (2 × Deg) | d-Spacing (Angstrom) | Observed Intensity (Counts) | (2 × Deg) | Background Intensity (Counts) | Crystallite Size (Angstrom) | Micro-Strain (%) |
|---|---|---|---|---|---|---|---|
| Reference Sample, Peak 1 | 39.4731 | 2.28104 | 1,264,663 | 0.0468 | 4616.40 | 29,652 | 0.003846 |
| Reference Sample, Peak 2 | 39.5760 | 2.28100 | 612,150 | 0.0468 | 4647.93 | 29,735 | 0.003846 |
| Sample 1, Peak 1 | 39.6912 | 2.26901 | 152,133 | 0.0624 | 1421.86 | 29,672 | 0.003823 |
| Sample 1, Peak 2 | 39.7943 | 2.26900 | 76,443 | 0.0468 | 1427.01 | 29,756 | 0.003813 |
| Sample 2, Peak 1 | 39.5332 | 2.27771 | 378,807 | 0.0468 | 2202.72 | 29,658 | 0.003840 |
| Sample 2, Peak 2 | 39.6359 | 2.27769 | 182,428 | 0.0468 | 2227.21 | 29,741 | 0.003829 |
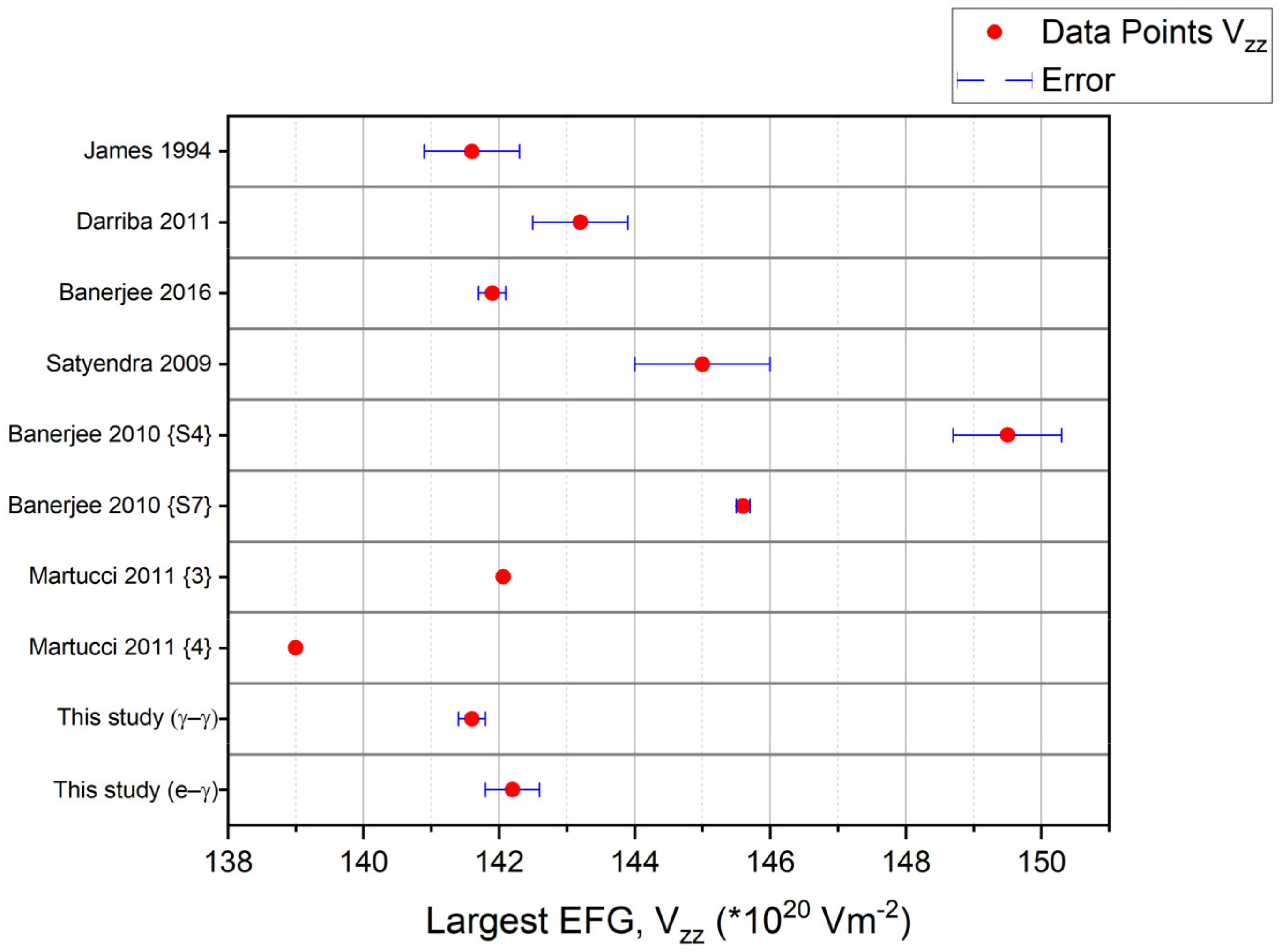
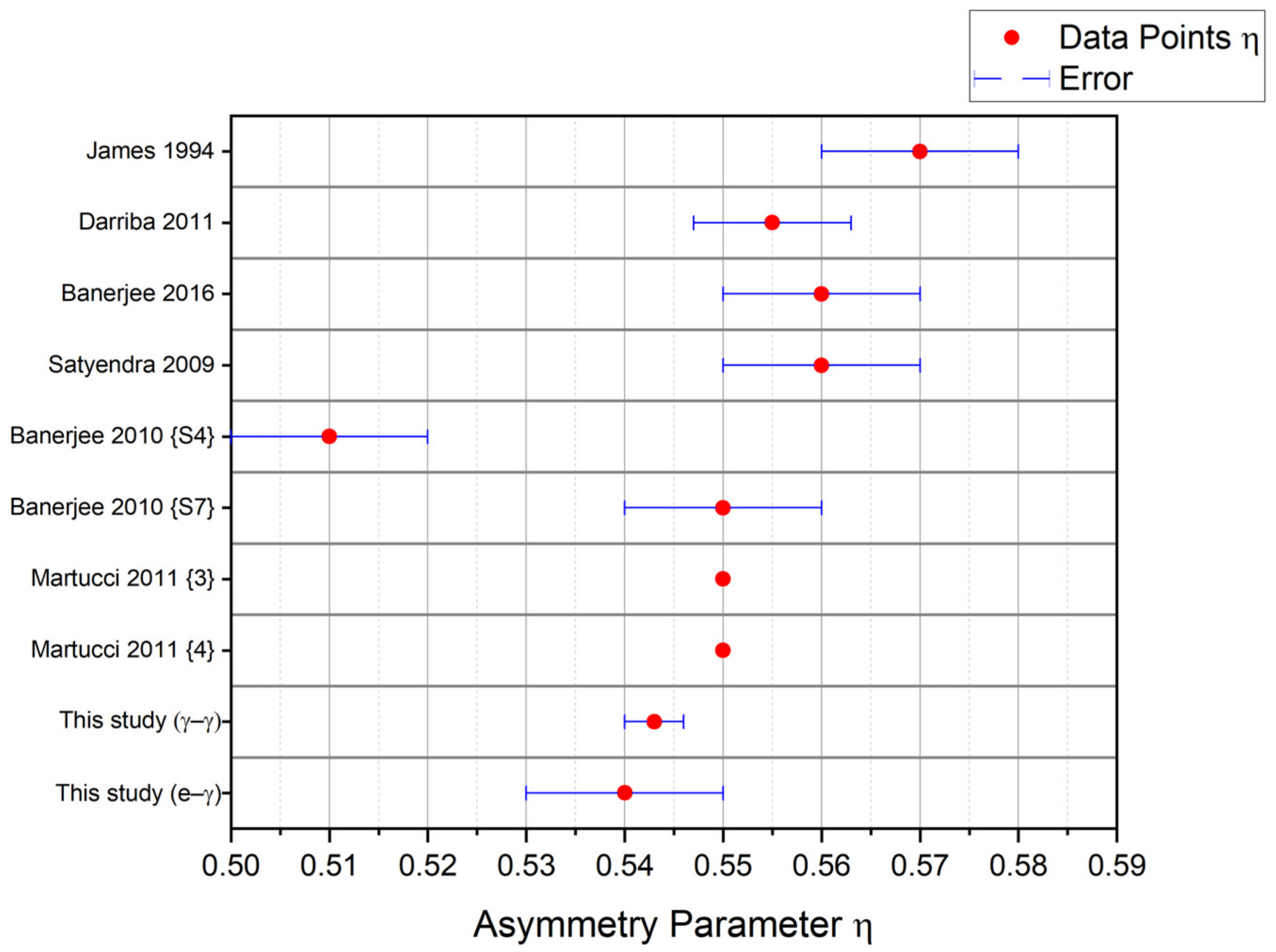
| Paper | (1020 V/m2) | Asymmetry Parameter | Delta Lorentzian (%) | Crystal Type | Sample Preparation | Reference |
|---|---|---|---|---|---|---|
| James 1994 | 141.6 (7) | 0.57 (1) | ≈0.01 | Polycrystal | Thermal Annealing at 1570 K for several hrs | [7] |
| Darriba 2011 | 143.2 (7) | 0.555 (8) | 0.4 (2) | Single Crystal | Thermal Annealing at 1073 K for 6 h | [8] |
| Banerjee 2016 | 141.9 (2) | 0.56 (1) | 0.6 (1) | Polycrystal | Thermal Annealing at 1273 K for 10 h | [11] |
| Satyendra 2009 | 145 (1) | 0.56 (1) | Unknown | Polycrystal | Thermal Annealing at 1273 K for 10 h | [9] |
| Banerjee 2010 {S4} | 149.5 (8) | 0.51 (1) | 5.2 (5) | Polycrystal | Thermal Annealing at 1123 K for 4 h | [10] |
| Banerjee 2010 {S7} | 145.6 (1) | 0.55 (1) | 1.0 (1) | Polycrystal | Thermal Annealing Anatase TiO2 at 1223 K for 8 h (Convert to Rutile TiO2) | [10] |
| Martucci 2011 {3} | 142.06 a | 0.55 a,b | Unknown | Polycrystal | Thermal Annealing Anatase TiO2 at 973 K for 10 h under Nitrogen (Convert to Rutile TiO2) | [15] |
| Martucci 2011 {4} | 139.00 c | 0.55 a,b | Unknown | Polycrystal | Thermal Annealing Anatase TiO2 at 1223 K for 10 h under Nitrogen (Convert to Rutile TiO2) | [15] |
| This study (γ–γ) | 141.6 (2) | 0.543 (3) | N.A. | Single Crystal | Thermal Annealing at 873 K for 5.25 h | N.A. |
| This study (e–γ) | 142.2 (4) | 0.54 (1) | 0.05 ± 0.19 d | Single Crystal | Thermal Annealing at 873 K for 5.25 h | N.A. |
| Sample and Peak Number | Angle (2 × Deg) | Peak Identity (Miller Indices) a | Sample Preparation |
|---|---|---|---|
| Sample from [70], cut along an arbitrary direction. | 62.6 | (002) | Sample is produced in the laboratory setting via the floating zone method. The resulting sample is then cut into 5 × 2 mm2 thin slices alongside an arbitrary direction and the direction of the crystal growth, respectively. |
| Sample from [70], cut perpendicular to the c-axis. | 27.5 | (110) | |
| Reference Sample, Peak 1. | 39.5 | (200) | Sample (10 × 10 × 1.0 mm3) is commercially manufactured by Crystal GmbH [55]. XRD measurement is conducted face-(10 × 1.0 mm2) side up. |
| Reference Sample, Peak 2. | 39.6 | ||
| Sample 1, Peak 1, This study. | 39.7 | (200) | Sample (10 × 10 × 1.0 mm3) is commercially manufactured by Crystal GmbH [55], then 80 keV 181Hf ion-implanted and thermally annealed at 873 K for 5.25 h. XRD measurement is conducted face-(10 × 1.0 mm2) side up. |
| Sample 1, Peak 2, This study. | 39.8 | ||
| Sample 2, Peak 1, This study. | 39.5 | ||
| Sample 2, Peak 2, This study. | 39.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yap, I.C.J.; Schell, J.; Dang, T.T.; Noll, C.; Beck, R.; Köster, U.; Mansano, R.; Hofsäss, H.C. Room-Temperature 181Ta(TiO2): An e-γ TDPAC Study. Crystals 2022, 12, 946. https://doi.org/10.3390/cryst12070946
Yap ICJ, Schell J, Dang TT, Noll C, Beck R, Köster U, Mansano R, Hofsäss HC. Room-Temperature 181Ta(TiO2): An e-γ TDPAC Study. Crystals. 2022; 12(7):946. https://doi.org/10.3390/cryst12070946
Chicago/Turabian StyleYap, Ian Chang Jie, Juliana Schell, Thien Thanh Dang, Cornelia Noll, Reinhard Beck, Ulli Köster, Ronaldo Mansano, and Hans Christian Hofsäss. 2022. "Room-Temperature 181Ta(TiO2): An e-γ TDPAC Study" Crystals 12, no. 7: 946. https://doi.org/10.3390/cryst12070946







