Effect of 5-Amino-1H-Tetrazole on Combustion Pyrolysis Characteristics and Kinetics of a Combustion Tear Gas Mixture
Abstract
:1. Introduction
2. Experiment and Method
2.1. Materials and Main Experimental Equipment
2.2. Test of Combustion Characteristics
2.2.1. Combustion Temperature Test
2.2.2. Burning Rate Test
2.3. Test of Combustion Smoke Characteristics
2.4. Thermal Behavior Analysis
2.5. Pyrolysis Kinetics
3. Results and Discussion
3.1. Analysis of the Combustion Characteristics
3.1.1. Combustion Temperature Analysis
3.1.2. Analysis of Burning Rate
3.2. Smoke Characteristic Analysis
3.3. Pyrolysis Behavior Analysis and Related Kinetic Analysis
3.3.1. Thermal Behavior Analysis of Individual Components
3.3.2. Thermal Behavior Analysis of the Samples
DSC Analysis of the Samples
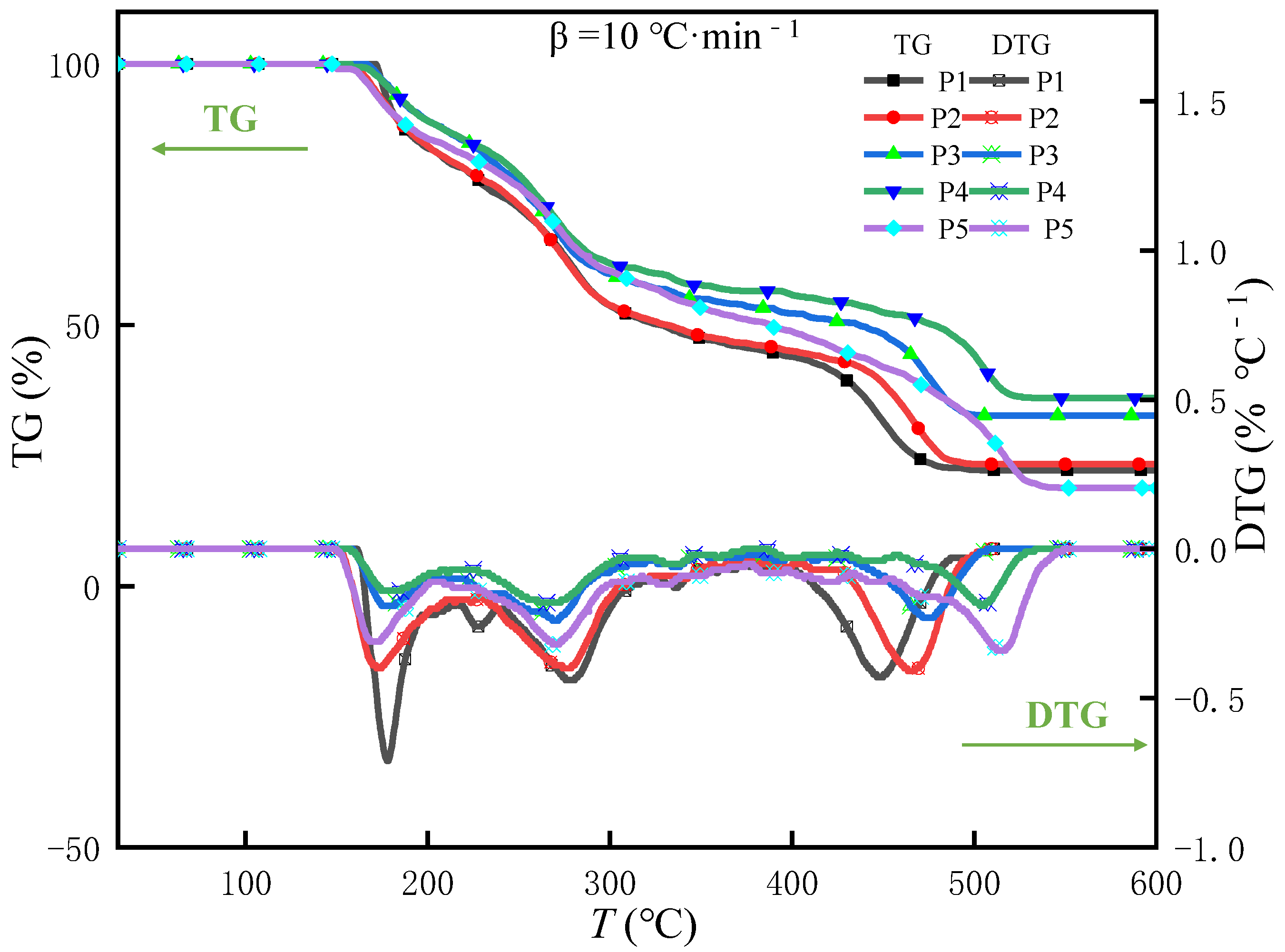
TG-DTG Analysis of the Samples
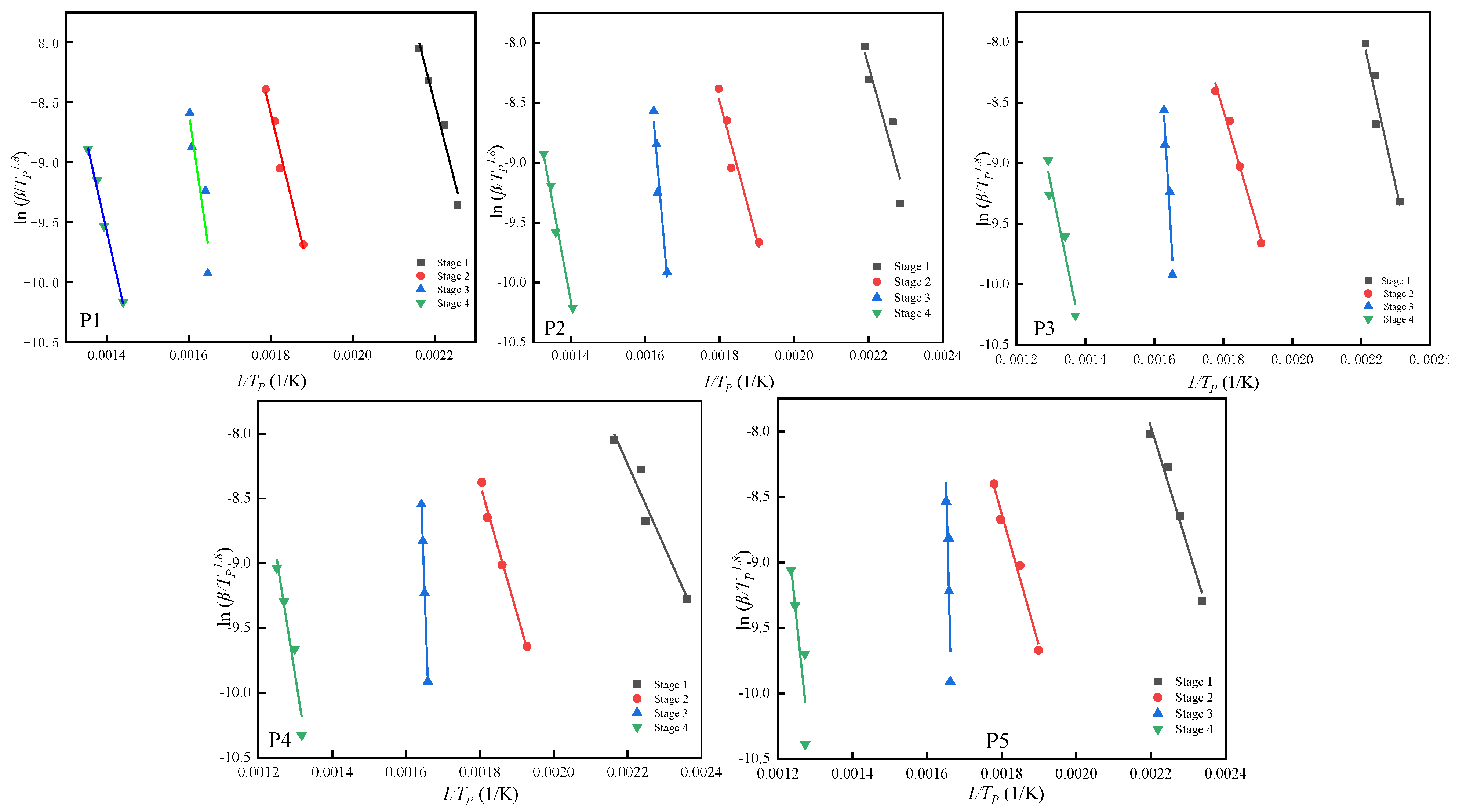
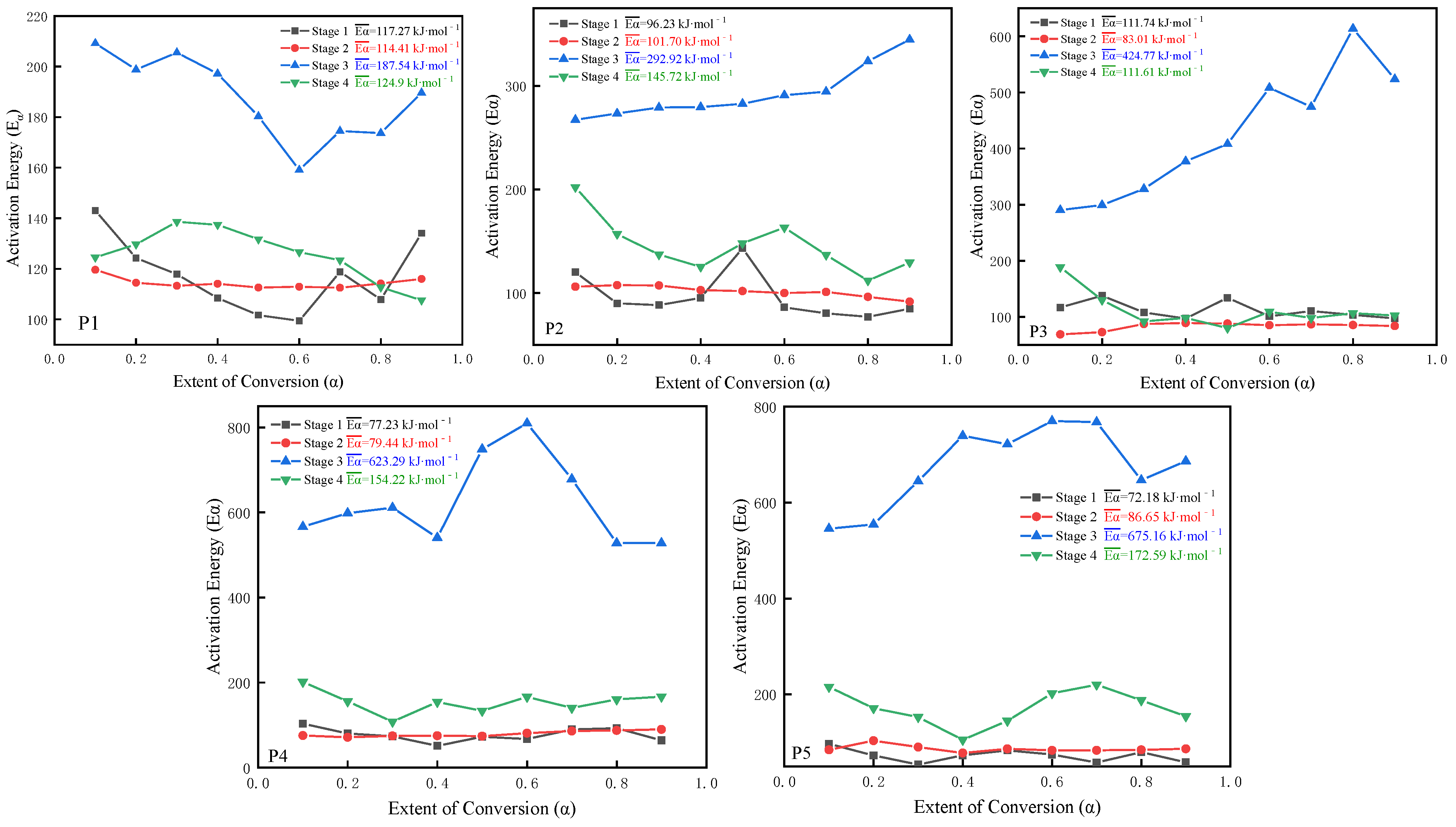
3.3.3. Analysis of the Pyrolysis Kinetics of the Samples
Starink’s Method
Prediction of the Reaction Model of Samples P1–P5
4. Conclusions
- Through a comparison of the maximum combustion temperature and the linear combustion rate of Samples P1–P5 with different amounts of 5AT, it was found that when the amount of 5AT is 10%, the maximum combustion temperature of the sample can be reduced by nearly 70 °C under the condition that the linear combustion rate is basically unchanged, thus improving the combustion environment of the mixture.
- If we compare the Tmax of Samples P1–P5, and the C and AP of smoke, it can be seen that the C and AP of smoke are inversely proportional to the Tmax of the sample. The higher the Tmax of the mixture, the smaller the C and AP values of the corresponding tear gas. As the combustion temperature of the mixed agent is higher, the amount of the pyrolytic tear agent OC in the agent will be greater, and the concentration and particle size of the smoke will be reduced. Combined with the exothermic enthalpy near 340 °C of the DSC curve and the weight loss ratio at the second stage of pyrolysis of Samples P1–P5, this observation is again confirmed. Therefore, adding an appropriate amount of 5AT is of great significance for improving the smoke characteristics of combustion tear gas mixtures.
- The results of calculating the activation energy of Samples P1–P5 at each stage via Starink’s method and the Flynn–Wall–Ozawa method are basically the same, which further verifies that the kinetic parameters obtained by these methods have high reliability. When the OB value in the formula’s design is fixed, with the addition of the 5AT mass fraction, the activation energy of the first and second stages of Samples P2–P5 shows a decreasing trend compared with P1, which confirms that the reaction’s starting temperature of the components after the addition of 5AT, as mentioned in the pyrolysis behavior analysis, is significantly lower, which plays a role in promoting the reaction at this stage.
- According to the Coats–Redfern method, the most likely reaction models of the different formulations at each stage were predicted. It can be concluded that with different amounts of 5AT in the formulation, the reaction models of mixed agents in the first, third, and fourth stages changed significantly, indicating that the addition of 5AT can affect the reaction mechanism at some stages. In addition, for Samples P1–P5, the reaction model at the second stage of pyrolysis is the nucleation model A4, which maintains a high degree of consistency and further verifies the correctness of the physical thermal diffusion weight loss theory of the sample at the second stage of pyrolysis weight loss, which mainly corresponds to OC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.Y.; Mu, Y.L.; Su, S.C.; Hao, H.M.; Li, G.B.; He, J. Study on the properties of a stimulating smoking agent. J. Initiat. Pyrotech. 2013, 1, 36–38. (In Chinese) [Google Scholar]
- Shaw, A.P.; Chen, G.D. Advanced boron carbide-based visual obscurants for military smoke grenades. In Proceedings of the 40th International Pyrotechnics Seminar, Colorado Springs, CO, USA, 13–18 July 2014; pp. 170–191. [Google Scholar]
- Haar, R.J.; Iacopino, V.; Ranadive, N.; Weiser, S.D.; Dandu, M. Health impacts of chemical irritants used for crowd control: A systematic review of the injuries and deaths caused by tear gas and pepper spray. BMC Public Health 2017, 17, 831. [Google Scholar] [CrossRef] [PubMed]
- Hoz, S.S.; Aljuboori, Z.S.; Dolachee, A.A.; Al-Sharshahi, Z.F.; Alrawi, M.A.; Al-Smaysim, A.M. Fatal Penetrating head injuries caused by projectile tear gas canisters. World Neurosurg. 2020, 138, e119–e123. [Google Scholar] [CrossRef] [PubMed]
- Stopyra, J.P.; Winslow, J.E., III; Johnson, J.C., III; Hill, K.D.; Bozeman, W.P. Baby Shampoo to relieve the discomfort of tear gas and pepper spray exposure: A randomized controlled trial. West. J. Emerg. Med. 2018, 19, 294. [Google Scholar] [CrossRef] [Green Version]
- Rothenberg, C.; Achanta, S.; Svendsen, E.R.; Jordt, S. Tear gas: An epidemiological and mechanistic reassessment. Ann. N. Y. Acad. Sci. 2016, 1378, 96–107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corbacɩoğlu, Ş.K.; Güler, S.; Er, E.; Seviner, M.; Aslan, Ş.; Aksel, G. Rare and severe maxillofacial injury due to tear gas capsules: Report of three cases. J. Forensic Sci. 2016, 61, 551–554. [Google Scholar]
- Zhai, H.L.; Cui, X.P. Thermal behavior test and characterization of a capsicum oleoresin (OC) composite material used for burning tear bomb. J. Phys. Conf. Series. IOP Publ. 2021, 1965, 012058. [Google Scholar]
- Talawar, M.B.; Sivabalan, R.; Mukundan, T.; Muthurajan, H.; Sikder, A.K.; Gandhe, B.R.; Rao, A.S. Environmentally compatible next generation green energetic materials (GEMs). J. Hazard. Mater. 2009, 161, 589–607. [Google Scholar] [CrossRef]
- Zhang, D.; Jiang, L.; Lu, S.; Cao, C.-Y.; Zhan, H.-P. Particle size effects on thermal kinetics and pyrolysis mechanisms of energetic 5-amino-1H-tetrazole. Fuel 2018, 217, 553–560. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, S.; Cao, C.Y.; Liu, C.C.; Gong, L.L.; Zhang, H.P. Impacts on combustion behavior of adding nanosized metal oxide to CH3N5-Sr(NO3)2 propellant. Fuel 2017, 191, 371–382. [Google Scholar] [CrossRef]
- Küblböck, T. New Trends in Sustainable Light-and Smoke-Generating Pyrotechnics; Ludwig Maximilian University of Munich: München, Germany, 2020. [Google Scholar]
- Glück, J.; Klapötke, T.M.; Küblböck, T. 5-Amino-1H-tetrazole-based multi-coloured smoke signals applying the concept of fuel mixes. New J. Chem. 2018, 42, 10670–10675. [Google Scholar] [CrossRef]
- Glück, J.; Klapötke, T.M.; Rusan, M.; Shaw, A.P. Improved Efficiency by Adding 5-Aminotetrazole to Anthraquinone-Free New Blue and Green Colored Pyrotechnical Smoke Formulations. Propellants Explos. Pyrotech. 2017, 42, 131–141. [Google Scholar] [CrossRef]
- Zeman, O.; Pelikan, V.; Pachman, J. Diketopyrrolopyrrole—A Greener Alternative for Pyrotechnic Smoke Compositions; ACS Sustainable Chemistry & Engineering: Washington, DC, USA, 2022. [Google Scholar]
- Hemmilä, M.; Hihkiö, M.; Linnainmaa, K. Evaluation of the acute toxicity and genotoxicity of orange, red, violet and yellow pyrotechnic smokes in vitro. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energetic Mater. 2007, 32, 415–422. [Google Scholar] [CrossRef]
- Zarko, V.; Kiskin, A.; Cheremisin, A. Contemporary methods to measure regression rate of energetic materials: A review. Prog. Energy Combust. Sci. 2022, 91, 100980. [Google Scholar] [CrossRef]
- Ambekar, A.; Kim, M.; Lee, W.-H.; Yoh, J.J. Characterization of display pyrotechnic propellants: Burning rate. Appl. Therm. Eng. 2017, 121, 761–767. [Google Scholar] [CrossRef]
- Yi, J.H.; Zhao, F.Q.; Wang, B.Z.; Liu, Q.; Zhou, C.; Hu, R.Z.; Ren, Y.H.; Xu, S.Y.; Xu, K.Z.; Ren, X.N. Thermal behaviors, nonisothermal decomposition reaction kinetics, thermal safety and burning rates of BTATz-CMDB propellant. J. Hazard. Mater. 2010, 181, 432–439. [Google Scholar] [CrossRef]
- Aboulkas, A.; El, B.A. Thermal degradation behaviors of polyethylene and polypropylene. Part I: Pyrolysis kinetics and mechanisms. Energy Convers Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Muravyev, N.V.; Monogarov, K.A.; Asachenko, A.F.; Nechaev, M.S.; Ananyev, I.V.; Fomenkov, I.V.; Kiselev, V.G.; Pivkina, A.N. Pursuing reliable thermal analysis techniques for energetic materials: Decomposition kinetics and thermal stability of dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate (TKX-50). Phys. Chem. Chem. Phys. 2017, 19, 436–449. [Google Scholar] [CrossRef]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Flynn, J.H.; Wall, L.A. General treatment of the thermogravimetry of polymers. J. Res. Natl. Bur. Standards. Sect. A Phys. Chem. 1966, 70, 487. [Google Scholar] [CrossRef] [PubMed]
- Coats, A.W.; Redfern, J.P. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Zhang, D.; Cao, C.-Y.; Lu, S.; Cheng, Y.; Zhang, H.-P. Experimental insight into catalytic mechanism of transition metal oxide nanoparticles on combustion of 5-Amino-1H-Tetrazole energetic propellant by multi kinetics methods and TG-FTIR-MS analysis. Fuel 2019, 245, 78–88. [Google Scholar] [CrossRef]
- Eslami, A.; Hosseini, S.G. Improving safety performance of lactose-fueled binary pyrotechnic systems of smoke dyes. J. Therm. Anal. Calorim. 2011, 104, 671–678. [Google Scholar] [CrossRef]
- Wang, H.; Cao, L.; Chen, Y.K.; Hao, H.M.; Zhang, Z.L. Study on thermal cracking of vanillin nonanoate by pyrolysis gas chromatography-mass spectrometry. J. Anal. Test. 2018, 37, 858–861. (In Chinese) [Google Scholar] [CrossRef]
- Wang, C.Y.; Du, Z.M.; Cong, X.M.; Tian, X.L. Study on thermal decomposition of basic magnesium carbonate. Appl. Chem. Ind. 2008, 37, 657–660. (In Chinese) [Google Scholar] [CrossRef]
- Cao, C.Y.; Zhang, D.; Liu, C.C.; Song, L. Experimental investigation on combustion behaviors and reaction mechanisms for 5-aminotetrazole solid propellant with nanosized metal oxide additives under elevated pressure conditions. Appl. Therm. Eng. 2019, 162, 114207. [Google Scholar] [CrossRef]
- Miyata, Y.; Date, S.; Hasue, K. Combustion mechanism of consolidated mixtures of 5-amino-1H-tetrazole with potassium nitrate or sodium nitrate. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energetic Mater. 2004, 29, 247–252. [Google Scholar] [CrossRef]
- Tabacof, A.; Calado, V.M.A. Thermogravimetric analysis and differential scanning calorimetry for investigating the stability of yellow smoke powders. J. Therm. Anal. Calorim. 2017, 128, 387–398. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Pivkina, A.N.; Koga, N. Critical appraisal of kinetic calculation methods applied to overlapping multistep reactions. Molecules 2019, 24, 2298. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luciano, G.; Svoboda, R. Activation energy determination in case of independent complex kinetic processes. Processes 2019, 7, 738. [Google Scholar] [CrossRef] [Green Version]
- Ambekar, A.; Yoh, J.J. Chemical kinetics of multi-component pyrotechnics and mechanistic deconvolution of variable activation energy. Proc. Combust. Inst. 2019, 37, 3193–3201. [Google Scholar] [CrossRef]
- Ebrahimi-Kahrizsangi, R.; Abbasi, M.H. Evaluation of reliability of Coats-Redfern method for kinetic analysis of non-isothermal TGA. Trans. Nonferrous Met. Soc. China 2008, 18, 217–221. [Google Scholar] [CrossRef]
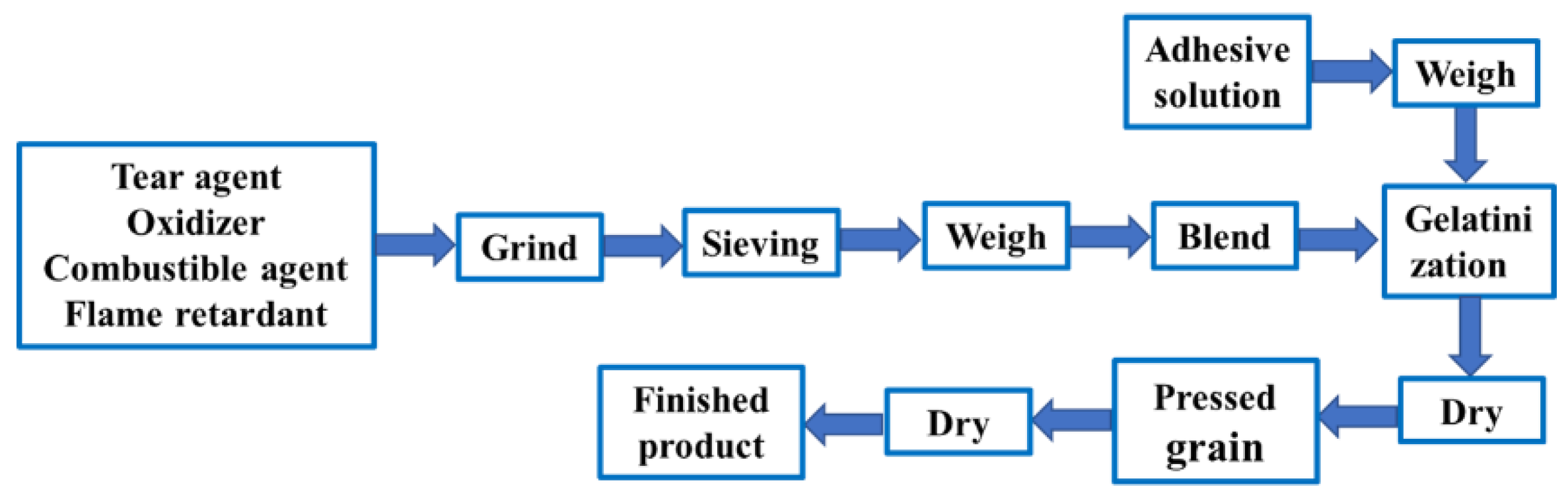




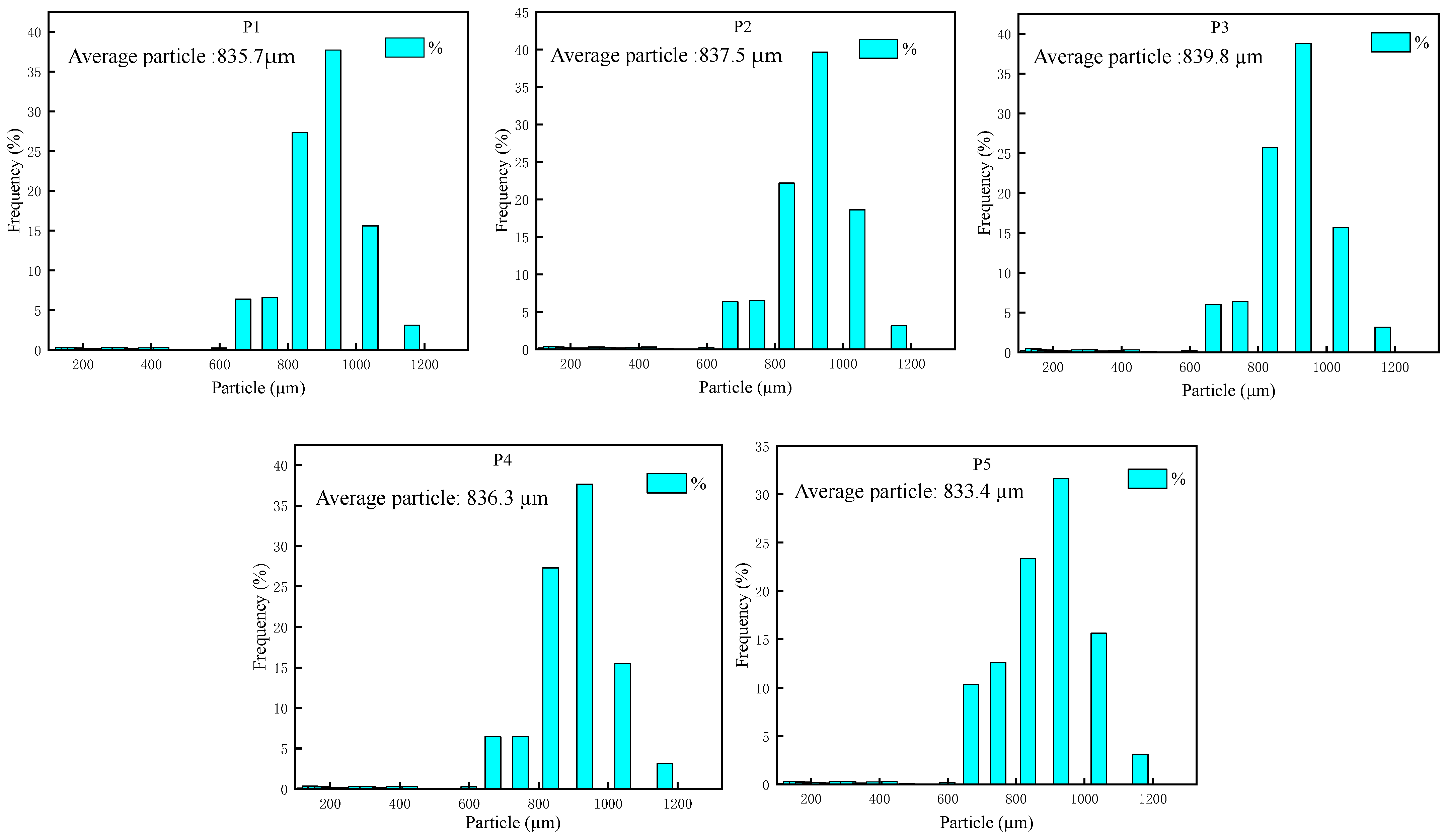

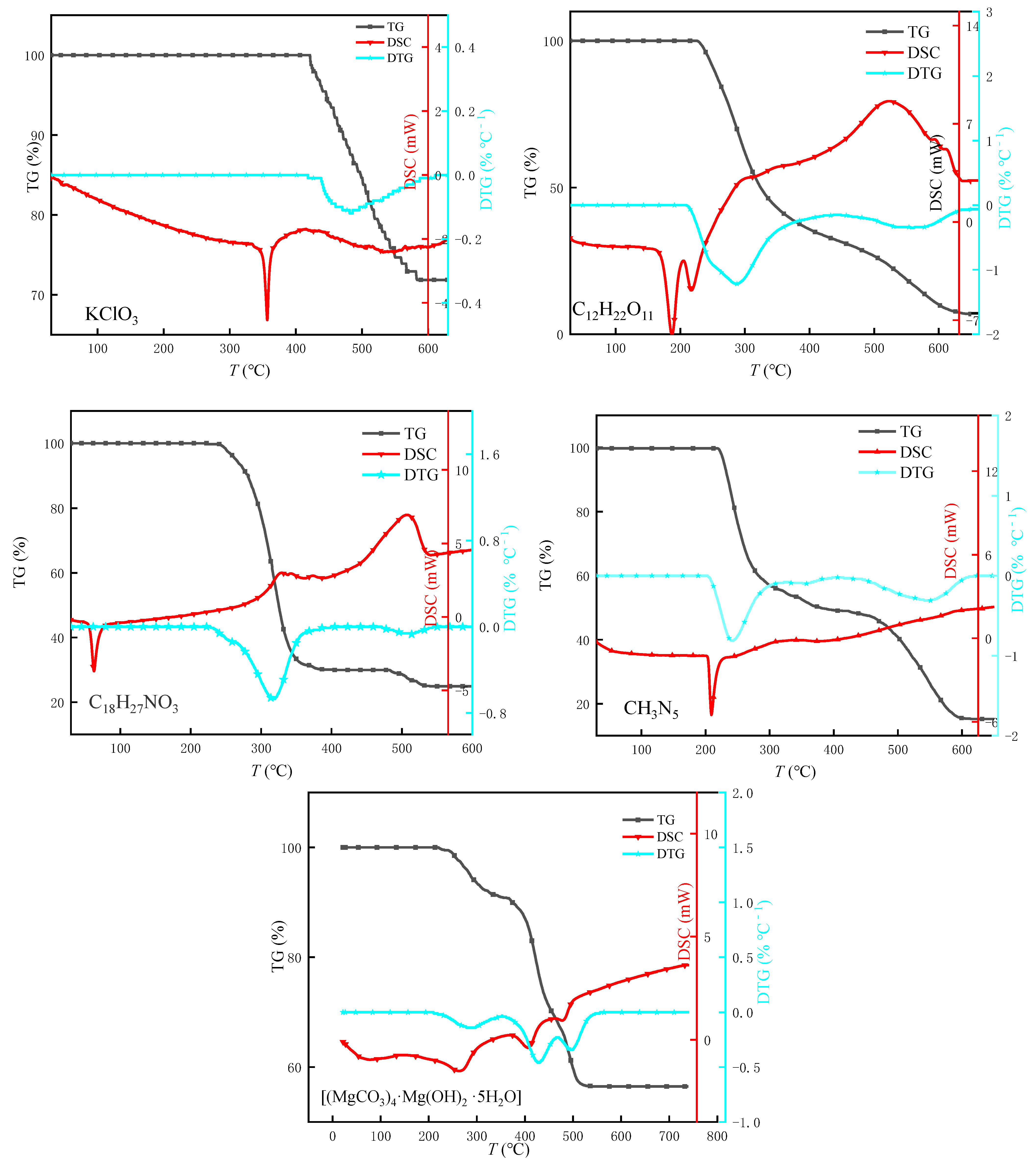
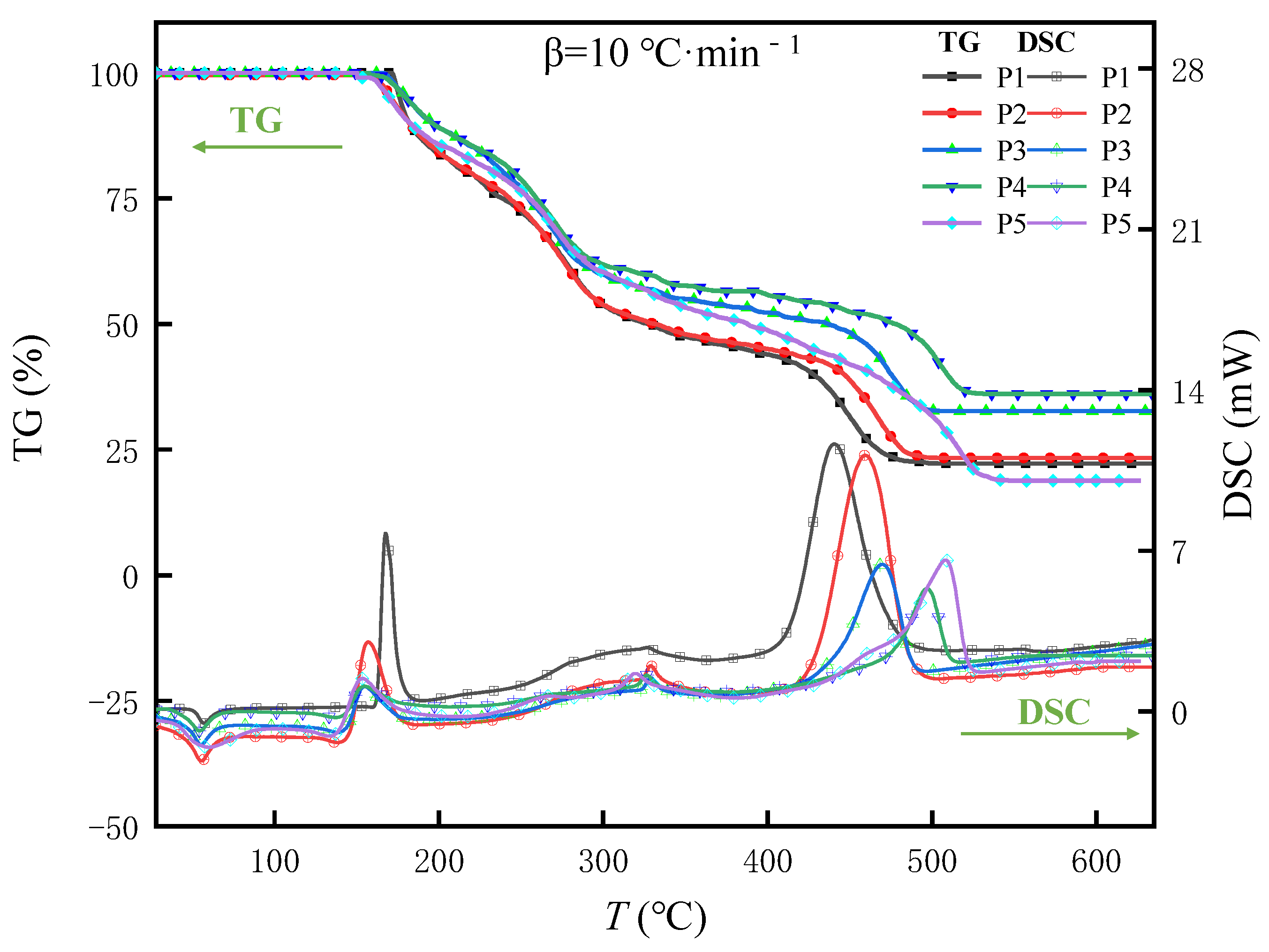


| Component Formula | Oxidant | Combustible Agent | Coolant | Adhesive | Tear Agent | |
|---|---|---|---|---|---|---|
| KClO3 (wt%) | C12H22O11 (wt%) | CH3N5 (wt%) | (MgCO3)4·Mg(OH)2 ·5H2O (wt%) | (C8H6O2)n (wt%) | OC (wt%) | |
| P1 | 32.0 | 27.2 | 0 | 7.1 | 6.3 | 27.4 |
| P2 | 30.4 | 23.8 | 5.0 | 7.1 | 6.3 | 27.4 |
| P3 | 28.9 | 20.3 | 10.0 | 7.1 | 6.3 | 27.4 |
| P4 | 27.3 | 16.9 | 15.0 | 7.1 | 6.3 | 27.4 |
| P5 | 25.8 | 13.4 | 20.0 | 7.1 | 6.3 | 27.4 |
| Reaction Model | g(α) | f(α) | Abbreviation |
|---|---|---|---|
| Power law | α | 1 | P1 |
| Power law | α1/2 | 2α1/2 | P2 |
| Power law | α1/3 | 3α2/3 | P3 |
| Power law | α1/4 | 4α3/4 | P4 |
| Power law | α3/2 | 2/3α1/2 | P2/3 |
| Avrami–Erofeev | [−ln(1−α)]1/2 | 2(1−α) (−ln(1−α))1/2 | A2 |
| Avrami–Erofeev | [−ln(1−α)]1/3 | 3(1−α) (−ln(1−α))2/3 | A3 |
| Avrami–Erofeev | [−ln(1−α)]1/4 | 4(1−α) (−ln(1−α))3/4 | A4 |
| One-dimensional | α2 | 1/2α | D1 |
| Two-dimensional | (1−α)ln(1−α) + α | [−ln(1−α)]−1 | D2 |
| Three-dimensional | [1−(1−α)1/3]2 | 3/2(1−α)2/3[1−(1−α)1/3] | D3 |
| Ginstling-Brounshtein | 1−(2α/3)−(1−α)2/3 | 3/2[(1−α)−1/3-1]−1 | G-B |
| First-order | −ln(1−α) | 1−α | F1 |
| Second-order | (1-α)−1-1 | (1−α)2 | F2 |
| Third-order | [(1−α)−2−1]/2 | (1−α)3 | F3 |
| Contracting area | 1−(1−α)1/2 | 2(1−α)1/2 | C2 |
| Contracting volume | 1−(1−α)1/3 | 3(1−α)2/3 | C3 |
| Sample | Burning Rate Ι (mm·s−1) | Burning Rate ΙΙ (mm·s−1) | Burning Rate ΙΙΙ (mm·s−1) | Average Burning Rate (mm·s−1) | Standard Deviation (σ) |
|---|---|---|---|---|---|
| P1 | 1.05 | 1.08 | 1.08 | 1.07 | 0.0173 |
| P2 | 1.07 | 1.09 | 1.08 | 1.08 | 0.01 |
| P3 | 1.03 | 1.06 | 1.09 | 1.06 | 0.03 |
| P4 | 1.03 | 1.05 | 1.07 | 1.05 | 0.02 |
| P5 | 1.01 | 1.03 | 1.05 | 1.03 | 0.02 |
| Peak Temperature Formula | T1 (°C) | T2 (°C) | T3 (°C) | T4 (°C) | T5 (°C) |
|---|---|---|---|---|---|
| P1 | 60.61 | 171.72 | 330.81 | 443.92 | -- |
| P2 | 59.32 | 160.81 | 332.03 | 462.94 | -- |
| P3 | 58.61 | 158.33 | 332.21 | 473.61 | -- |
| P4 | 58.22 | 157.63 | 330.04 | 506.73 | -- |
| P5 | 62.02 | 162.22 | 276.05 | 327.34 | 516.82 |
| Formula | P1 | P2 | P3 | P4 | P5 |
|---|---|---|---|---|---|
| Exothermic enthalpy (ΔH) | 4.61 J/g | 4.48 J/g | 3.54 J/g | 4.51 J/g | 4.79 J/g |
| (a) Eigenvalues corresponding to the first stage. | ||||||||||||||||||||
| Formula β | P1 | P2 | P3 | P4 | P5 | |||||||||||||||
| To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | |
| 5 | 160.81 | 170.04 | 191.02 | 19.2% | 136.51 | 164.51 | 191.93 | 18.5% | 139.21 | 159.42 | 179.22 | 15.2% | 134.22 | 162.41 | 178.81 | 15% | 138.52 | 154.82 | 190.43 | 16.5% |
| 10 | 152.92 | 176.33 | 194.71 | 15.7% | 148.13 | 168.23 | 198.91 | 15.6% | 144.03 | 172.83 | 194.13 | 10.1% | 142.63 | 171.62 | 190.02 | 10% | 147.03 | 165.81 | 203.42 | 14% |
| 15 | 161.83 | 184.42 | 200.62 | 13.2% | 150.42 | 181.54 | 201.14 | 11.7% | 142.04 | 173.31 | 199.24 | 14% | 147.02 | 174.11 | 205.03 | 14.3% | 140.54 | 172.43 | 214.62 | 18.9% |
| 20 | 158.93 | 189.33 | 209.83 | 17.4% | 151.02 | 183.52 | 208.02 | 16.4% | 144.91 | 178.94 | 214.03 | 17% | 150.04 | 189.02 | 211.03 | 9.7% | 148.04 | 182.22 | 219.13 | 16.1% |
| (b) Eigenvalues corresponding to the second stage. | ||||||||||||||||||||
| Formula β | P1 | P2 | P3 | P4 | P5 | |||||||||||||||
| To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | |
| 5 | 191.02 | 258.82 | 270.02 | 28.4% | 191.92 | 251.62 | 274.81 | 27.8% | 179.22 | 250.52 | 273.12 | 35.7% | 178.81 | 245.63 | 271.21 | 27.5% | 190.42 | 253.62 | 278.02 | 24.2% |
| 10 | 194.71 | 275.63 | 291.41 | 26.7% | 198.93 | 273.04 | 294.22 | 27.5% | 194.13 | 268.13 | 285.63 | 28.9% | 190.02 | 264.42 | 284.42 | 27.1% | 203.43 | 267.72 | 296.42 | 24.8% |
| 15 | 200.62 | 279.22 | 303.32 | 27.5% | 201.12 | 276.33 | 309.73 | 31.9% | 199.22 | 276.54 | 307.42 | 32.6% | 205.04 | 276.31 | 302.73 | 30.6% | 214.61 | 283.53 | 307.23 | 25.4% |
| 20 | 209.81 | 286.33 | 312.04 | 26.4% | 208.03 | 283.14 | 311.02 | 29.9% | 214.03 | 289.72 | 317.44 | 33.6% | 211.05 | 280.82 | 314.01 | 28.71% | 219.12 | 288.81 | 313.82 | 23% |
| (c) Eigenvalues corresponding to the third stage. | ||||||||||||||||||||
| Formula β | P1 | P2 | P3 | P4 | P5 | |||||||||||||||
| To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | |
| 5 | 270.02 | 334.32 | 374.03 | 14.5% | 274.82 | 329.72 | 391.04 | 11.8% | 273.13 | 331.91 | 382.13 | 15.8% | 271.21 | 329.62 | 389.23 | 11.2% | 278.03 | 328.52 | 392.63 | 11.5% |
| 10 | 291.43 | 336.43 | 397.31 | 10.9% | 294.22 | 339.23 | 410.05 | 10.4% | 285.62 | 334.82 | 390.62 | 9.1% | 284.42 | 332.93 | 398.32 | 7% | 296.42 | 329.83 | 410.82 | 13.2% |
| 15 | 303.32 | 349.03 | 423.52 | 10.9% | 309.71 | 340.11 | 414.61 | 9.2% | 307.44 | 340.04 | 407.03 | 8.4% | 302.71 | 334.72 | 413.23 | 7.6% | 307.23 | 330.14 | 413.13 | 10.5% |
| 20 | 312.01 | 350.92 | 426.04 | 11.5% | 311.03 | 343.04 | 419.04 | 11.2% | 317.45 | 341.03 | 414.82 | 8.3% | 314.02 | 336.02 | 440.72 | 6.9% | 313.81 | 332.51 | 422.05 | 10.6% |
| (d) Eigenvalues corresponding to the fourth stage. | ||||||||||||||||||||
| Formula β | P1 | P2 | P3 | P4 | P5 | |||||||||||||||
| To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | To | Tp | Tf | ML | |
| 5 | 374.03 | 421.62 | 465.05 | 23.5% | 391.03 | 438.53 | 482.03 | 20.7% | 382.12 | 456.32 | 486.62 | 26.2% | 389.23 | 486.04 | 499.92 | 26.3% | 392.61 | 512.32 | 532.21 | 28.5% |
| 10 | 397.32 | 444.93 | 499.03 | 21.6% | 410.01 | 462.52 | 501.72 | 20.6% | 390.63 | 472.43 | 502.13 | 19.5% | 398.32 | 496.92 | 512.73 | 19.1% | 410.82 | 513.21 | 540.32 | 28.3% |
| 15 | 423.52 | 453.71 | 512.03 | 17.3% | 414.62 | 469.51 | 513.71 | 21.6% | 407.04 | 499.04 | 531.03 | 21.3% | 413.23 | 514.83 | 544.64 | 22.7% | 413.11 | 529.43 | 573.02 | 28% |
| 20 | 426.04 | 465.74 | 523.02 | 20.1% | 419.03 | 480.24 | 530.04 | 22.2% | 414.82 | 500.82 | 554.02 | 22.1% | 440.73 | 526.91 | 562.03 | 19% | 422.03 | 536.44 | 581.04 | 25.7% |
| Stage | Stage 1 | Stage 2 | Stage 3 | Stage 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Formula | Ea (kJ/mol) | R2 | Ea (kJ/mol) | R2 | Ea (kJ/mol) | R2 | Ea (kJ/mol) | R2 |
| P1 | 110 ± 7 | 0.98223 | 116 ± 7 | 0.98417 | 193 ± 9 | 0.91128 | 124 ± 6 | 0.99518 |
| P2 | 91 ± 8 | 0.93143 | 95 ± 7 | 0.97126 | 299 ± 9 | 0.96533 | 137 ± 7 | 0.99147 |
| P3 | 106 ± 8 | 0.96432 | 80 ± 5 | 0.99133 | 406 ± 8 | 0.97029 | 115 ± 8 | 0.96539 |
| P4 | 78 ± 5 | 0.96847 | 82 ± 7 | 0.99545 | 646 ± 7 | 0.99846 | 148 ± 6 | 0.96738 |
| P5 | 76 ± 6 | 0.98638 | 83 ± 5 | 0.98949 | 659 ± 8 | 0.91439 | 164 ± 8 | 0.90127 |
| Stage | Stage 1 | Stage 2 | Stage 3 | Stage 4 |
|---|---|---|---|---|
| Formula | ||||
| P1 | A3 | A4 | F3 | F1 |
| P2 | F2 | A4 | F3 | F1 |
| P3 | D3 | A4 | F3 | D2 |
| P4 | D3 | A4 | F2 | P2/3 |
| P5 | F3 | A4 | F2 | D2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, H.; Cui, X.; Gan, Y. Effect of 5-Amino-1H-Tetrazole on Combustion Pyrolysis Characteristics and Kinetics of a Combustion Tear Gas Mixture. Crystals 2022, 12, 948. https://doi.org/10.3390/cryst12070948
Zhai H, Cui X, Gan Y. Effect of 5-Amino-1H-Tetrazole on Combustion Pyrolysis Characteristics and Kinetics of a Combustion Tear Gas Mixture. Crystals. 2022; 12(7):948. https://doi.org/10.3390/cryst12070948
Chicago/Turabian StyleZhai, Haolong, Xiaoping Cui, and Yuping Gan. 2022. "Effect of 5-Amino-1H-Tetrazole on Combustion Pyrolysis Characteristics and Kinetics of a Combustion Tear Gas Mixture" Crystals 12, no. 7: 948. https://doi.org/10.3390/cryst12070948
APA StyleZhai, H., Cui, X., & Gan, Y. (2022). Effect of 5-Amino-1H-Tetrazole on Combustion Pyrolysis Characteristics and Kinetics of a Combustion Tear Gas Mixture. Crystals, 12(7), 948. https://doi.org/10.3390/cryst12070948





