Evolution of a Polydisperse Ensemble of Spherical Particles in a Metastable Medium with Allowance for Heat and Mass Exchange with the Environment
Abstract
:1. Introduction
2. The Generalised Model and Methods for Its Solution
2.1. The Model
2.2. The Methods
3. Bulk Crystal Growth
3.1. Kinetic Equation of the First Order with a Sink of Crystals
3.2. Kinetic Equation of the Second Order with a Sink of Crystals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Zettlemoyer, A.C. Nucleation; Dekker: New York, NY, USA, 1969. [Google Scholar]
- Mullin, J.W. Crystallization; Butterworths: London, UK, 1972. [Google Scholar]
- Janse, A.H. Nucleation and Crystal Growth in Batch Crystallizers; Delft University of Technology: Delft, The Netherlands, 1977. [Google Scholar]
- Pot, A. Industrial Sucrose Crystallization; Delft University of Technology: Delft, The Netherlands, 1980. [Google Scholar]
- Kelton, K.F.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials and Biology; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Buyevich, Y.A.; Natalukha, I.A. Unsteady processes of combined polymerization and crystallization in continuous apparatuses. Chem. Eng. Sci. 1994, 49, 3241–3247. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. Mathematical simulation of the crystal nucleation and growth at the intermediate stage of a phase transition. Russ. Metall. (Metally) 2018, 2018, 707–715. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. Effects of external heat/mass sources and withdrawal rates of crystals from a metastable liquid on the evolution of particulate assemblages. Eur. Phys. J. Spec. Top. 2019, 228, 25–34. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Alexandrov, D.V. Dynamics of particulate assemblages in metastable liquids: A test of theory with nucleation and growth kinetics. Phil. Trans. R. Soc. A 2020, 378, 20190245. [Google Scholar] [CrossRef] [Green Version]
- Akselrud, G.A.; Molchanov, A.D. Dissolution of Solids; Khimia: Moscow, Russia, 1977. [Google Scholar]
- Tundal, U.H.; Ryum, N. Dissolution of particles in binary alloys: Part I. Computer simulations. Met. Trans. A 1992, 23, 433–444. [Google Scholar] [CrossRef]
- Wen, H.; Li, T.; Morris, K.R.; Park, K. Dissolution study on aspirin and α-glycine crystals. J. Phys. Chem. B 2004, 108, 11219–11227. [Google Scholar] [CrossRef]
- Oswald, R.; Ulrich, J. Dissolution behavior of lysozyme crystals. Cryst. Growth Des. 2015, 15, 4556–4562. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug dissolution. Int. J. Pharm. 2013, 453, 12–24. [Google Scholar] [CrossRef]
- Dewhirst, M.W.; Secomb, T.W. Transport of drugs from blood vessels to tumour tissue. Nat. Rev. Cancer 2017, 17, 738–750. [Google Scholar] [CrossRef]
- Ivanov, A.A.; Alexandrov, D.V.; Alexandrova, I.V. Dissolution of polydisperse ensembles of crystals in channels with a forced flow. Phil. Trans. R. Soc. A 2020, 378, 20190246. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V.; Okhezin, S.P.; Ivanov, A.A. Dissolution kinetics of particulate assemblages in channels. Eur. Phys. J. Spec. Top. 2020, 229, 3021–3032. [Google Scholar] [CrossRef]
- Yasnikov, G.P. Kinetics of similarity regime of vaporization of a polydisperse system of drops. J. Eng. Phys. 1982, 42, 163–169. [Google Scholar] [CrossRef]
- Masters, K. Spray Drying in Practice; Spray Dry Consult.: Charlottenlund, Denmark, 2002. [Google Scholar]
- Anandharamakrishnan, C.; Padma Ishwarya, S. Spray Drying Technique for Food Ingredient Encapsulation; Wiley Blackwell: Chichester, UK, 2015. [Google Scholar]
- Ivanov, A.A.; Alexandrova, I.V.; Alexandrov, D.V. Evaporation kinetics of a polydisperse ensemble of drops. Phil. Trans. R. Soc. A 2021, 379, 20200309. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V.; Alexandrova, I.V.; Ivanov, A.A. Mathematical modeling of vaporization process for a polydisperse ensemble of liquid drops. Math. Meth. Appl. Sci. 2021, 44, 12101–12107. [Google Scholar] [CrossRef]
- Skripov, V.P. Methastable Liquids; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Buyevich, Y.A.; Natalukha, I.A. Self-oscillating regimes of nucleate, transition and film boiling. Int. J. Heat Mass Trans. 1996, 39, 2363–2373. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Ivanov, A.A.; Alexandrov, D.V. Analytical solution of integro-differential equations describing the process of intense boiling of a superheated liquid. Math. Meth. Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Ivanov, A.A.; Alexandrov, D.V. Approximate analytical solutions of the kinetic and balance equations for intense boiling. Eur. Phys. J. Spec. Top. 2022, 231, 1153–1158. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Barenblatt, G.I.; Librovich, V.B.; Makhviladze, G.M. The Mathematical Theory of Combustion and Explosion; Consultants Bureau: New York, NY, USA, 1985. [Google Scholar]
- Makhviladze, G.M.; Rogatykh, D.I. Nonuniformities in initial temperature and concentration as a cause of explosive chemical reactions in combustible gases. Combust. Flame 1991, 87, 347–356. [Google Scholar] [CrossRef]
- Chan, C.Y.; Kong, P.C. A thermal explosion model. Appl. Math. Comp. 1995, 71, 201–210. [Google Scholar] [CrossRef]
- Ivanov, A.; Alexandrova, I.; Alexandrov, D. Mathematical modeling of the combustion process for a polydispersed fuel. Math. Meth. Appl. Sci. 2021, 44, 12040–12046. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Goldobin, Y.M.; Yasnikov, G.P. Evolution of a particulate system governed by exchange with its environment. Int. J. Heat Mass Trans. 1994, 37, 3003–3014. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Alexandrov, D.V. On the theory of evolution of particulate systems. IOP Conf. Ser. Mater. Sci. Eng. 2017, 192, 012001. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V. Nonlinear dynamics of polydisperse assemblages of particles evolving in metastable media. Eur. Phys. J. Spec. Top. 2020, 229, 383–404. [Google Scholar] [CrossRef]
- Łuczka, J.; Niemec, M.; Rudnicki, R. Kinetics of growth process controlled by convective fluctuations. Phys. Rev. E 2002, 65, 051401. [Google Scholar] [CrossRef]
- Gadomski, A. Kinetic–thermodynamic effects accompanying model protein-like aggregation: The wave-like limit and beyond it. Phys. A 2007, 373, 43–57. [Google Scholar] [CrossRef]
- Alexandrov, D.V. Nucleation and evolution of spherical crystals with allowance for their unsteady-state growth rates. J. Phys. A Math. Theor. 2018, 51, 075102. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V.; Alexandrova, I.V. On the theory of the unsteady-state growth of spherical crystals in metastable liquids. Phil. Trans. R. Soc. A 2019, 377, 20180209. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V.; Nizovtseva, I.G.; Alexandrova, I.V. On the theory of nucleation and nonstationary evolution of a polydisperse ensemble of crystals. Int. J. Heat Mass Trans. 2019, 128, 46–53. [Google Scholar] [CrossRef]
- Niemiec, M.; Olchawa, W.; Schimansky-Geier, L.; Łuczka, J. Kinetics of crystal growth limited by random velocity fields. Int. J. Bifur. Chaos 2008, 18, 2673–2679. [Google Scholar] [CrossRef]
- Zel’dovich, J.B. On the theory of formation of new phases: Cavitation. J. Exp. Theor. Phys. 1942, 12, 525–538. [Google Scholar]
- Lifshitz, E.M.; Pitaevskii, L.P. Physical Kinetic; Pergamon Press: Oxford, UK, 1981. [Google Scholar]
- Alexandrov, D.V. On the theory of transient nucleation at the intermediate stage of phase transitions. Phys. Lett. A 2014, 378, 1501–1504. [Google Scholar] [CrossRef]
- Rubí, J.M.; Gadomski, A. Nonequilibrium thermodynamics versus model grain growth: Derivation and some physical implications. Phys. A 2003, 326, 333–343. [Google Scholar] [CrossRef] [Green Version]
- Gardiner, C.W. Handbook on Stochastic Methods: For Physics, Chemistry and the Natural Sciences; Springer: Berlin, Germany, 1983. [Google Scholar]
- Ivanov, A.A.; Alexandrova, I.V.; Alexandrov, D.V. Phase transformations in metastable liquids combined with polymerization. Phil. Trans. R. Soc. A 2019, 377, 20180215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buyevich, Y.A.; Korolyova, N.A.; Natalukha, I.A. Modelling of unsteady combustion regimes for polydisperse fuels-I. Instability and auto-oscillations. Int. J. Heat Mass Trans. 1993, 36, 2223–2231. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Korolyova, N.A.; Natalukha, I.A. Modelling of unsteady combustion regimes for polydisperse fuels-II. Parametrically controlled combustion. Int. J. Heat Mass Trans. 1993, 36, 2233–2238. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Mansurov, V.V. Kinetics of the intermediate stage of phase transition in batch crystallization. J. Cryst. Growth 1990, 104, 861–867. [Google Scholar] [CrossRef]
- Barlow, D.A. Theory of the intermediate stage of crystal growth with applications to protein crystallization. J. Cryst. Growth 2009, 311, 2480–2483. [Google Scholar] [CrossRef]
- Barlow, D.A. Theory of the intermediate stage of crystal growth with applications to insulin crystallization. J. Cryst. Growth 2017, 470, 8–14. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Malygin, A.P. Transient nucleation kinetics of crystal growth at the intermediate stage of bulk phase transitions. J. Phys. A: Math. Theor. 2013, 46, 455101. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Alexandrova, I.V.; Ivanov, A.A.; Malygin, A.P.; Starodumov, I.O.; Toropova, L.V. On the Theory of the Nonstationary Spherical Crystal Growth in Supercooled Melts and Supersaturated Solutions. Russ. Metall. (Metally) 2019, 2019, 787–794. [Google Scholar] [CrossRef]
- Barlow, D.A.; LaVoie-Ingram, E.; Bayat, J. Population-balance study of protein crystal growth from solution using a hyperbolic rate law. J. Cryst. Growth 2022, 578, 126417. [Google Scholar] [CrossRef]
- Gadomski, A.; Slódmiak, J. A novel model of protein crystal growth: Kinetic limits, length scales and the role of the double layer. Croat. Chem. Acta 2003, 76, 129–136. [Google Scholar]
- Santamaría-Holek, I.; Gadomski, A.; Rubí, J.M. Controlling protein crystal growth rate by means of temperature. J. Phys. Condens. Matter 2011, 23, 235101. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V. Nucleation and crystal growth kinetics during solidification: The role of crystallite withdrawal rate and external heat and mass sources. Chem. Eng. Sci. 2014, 117, 156–160. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V.; Ivanov, A.A. Mathematical modeling of crystallization process from a supercooled binary melt. Math. Meth. Appl. Sci. 2021, 44, 12244–12251. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. How the shift in the phase transition temperature influences the evolution of crystals during the intermediate stage of phase transformations. Eur. Phys. J. Spec. Top. 2020, 229, 2923–2935. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Mansurov, V.V.; Natalukha, I.A. Instability and unsteady processes of the bulk continuous crystallization. Chem. Eng. Sci. 1991, 46, 2573–2588. [Google Scholar] [CrossRef]
- Ivanov, A.A.; Alexandrova, I.V.; Alexandrov, D.V. Towards the theory of phase transformations in metastable liquids. Analytical solutions and stability analysis. Eur. Phys. J. Spec. Top. 2020, 229, 365–373. [Google Scholar] [CrossRef]
- Fedoruk, M.V. Saddle-Point Method; Nauka: Moscow, Russia, 1977. [Google Scholar]
- Vollmer, U.; Raisch, J. H∞-control of a continuous crystallizer. Control Eng. Pract. 2001, 9, 837–845. [Google Scholar] [CrossRef] [Green Version]
- Rachah, A.; Noll, D.; Espitalier, F.; Baillon, F. A mathematical model for continuous crystallization. Math. Methods Appl. Sci. 2016, 39, 1101–1120. [Google Scholar] [CrossRef] [Green Version]
- Melikhov, I.V.; Beloussova, T.Y.; Uludev, N.A.; Blyudev, N.T. Fluctuations in the rate of growth of microcrystals. Kristallografiya 1974, 19, 1263–1268. [Google Scholar]
- Randolph, A.D.; White, E.T. Modeling size dispersion in the prediction of crystal-size distribution. Chem. Eng. Sci. 1977, 32, 1067–1076. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Malygin, A.P. Nucleation kinetics and crystal growth with fluctuating rates at the intermediate stage of phase transitions. Modell. Simul. Mater. Sci. Eng. 2014, 22, 015003. [Google Scholar] [CrossRef]
- Lippmann, S.; Fink, M.; Rettenmayr, M. Experimental determination of the nucleation rate of melt in a solid solution. Acta Mater. 2014, 72, 32–40. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Aseev, D.L.; Nizovtseva, I.G.; Huang, H.-N.; Lee, D. Nonlinear dynamics of directional solidification with a mushy layer. Analytic solutions of the problem. Int. J. Heat Mass Trans. 2007, 50, 3616–3623. [Google Scholar] [CrossRef]
- Nizovtseva, I.G.; Alexandrov, D.V. The effect of density changes on crystallization with a mushy layer. Phil. Trans. R. Soc. A 2020, 378, 20190248. [Google Scholar] [CrossRef] [Green Version]
- Solomatov, V.S.; Stevenson, D.J. Kinetics of crystal growth in a terrestrial magma ocean. J. Geophys. Res. 1993, 98, 5407–5418. [Google Scholar] [CrossRef] [Green Version]
- Alexandrov, D.V.; Malygin, A.P. Analytical description of seawater crystallization in ice fissures and their influence on heat exchange between the ocean and the atmosphere. Dokl. Earth Sci. 2006, 411, 1407–1411. [Google Scholar] [CrossRef]
- Galkin, O.; Vekilov, P.G. Are nucleation kinetics of protein crystals similar to those of liquid droplets? J. Am. Chem. Soc. 2000, 122, 156–163. [Google Scholar] [CrossRef]
- Streets, A.M.; Quake, S.R. Ostwald ripening of clusters during protein crystallization. Phys. Rev. Lett. 2010, 104, 178102. [Google Scholar] [CrossRef]
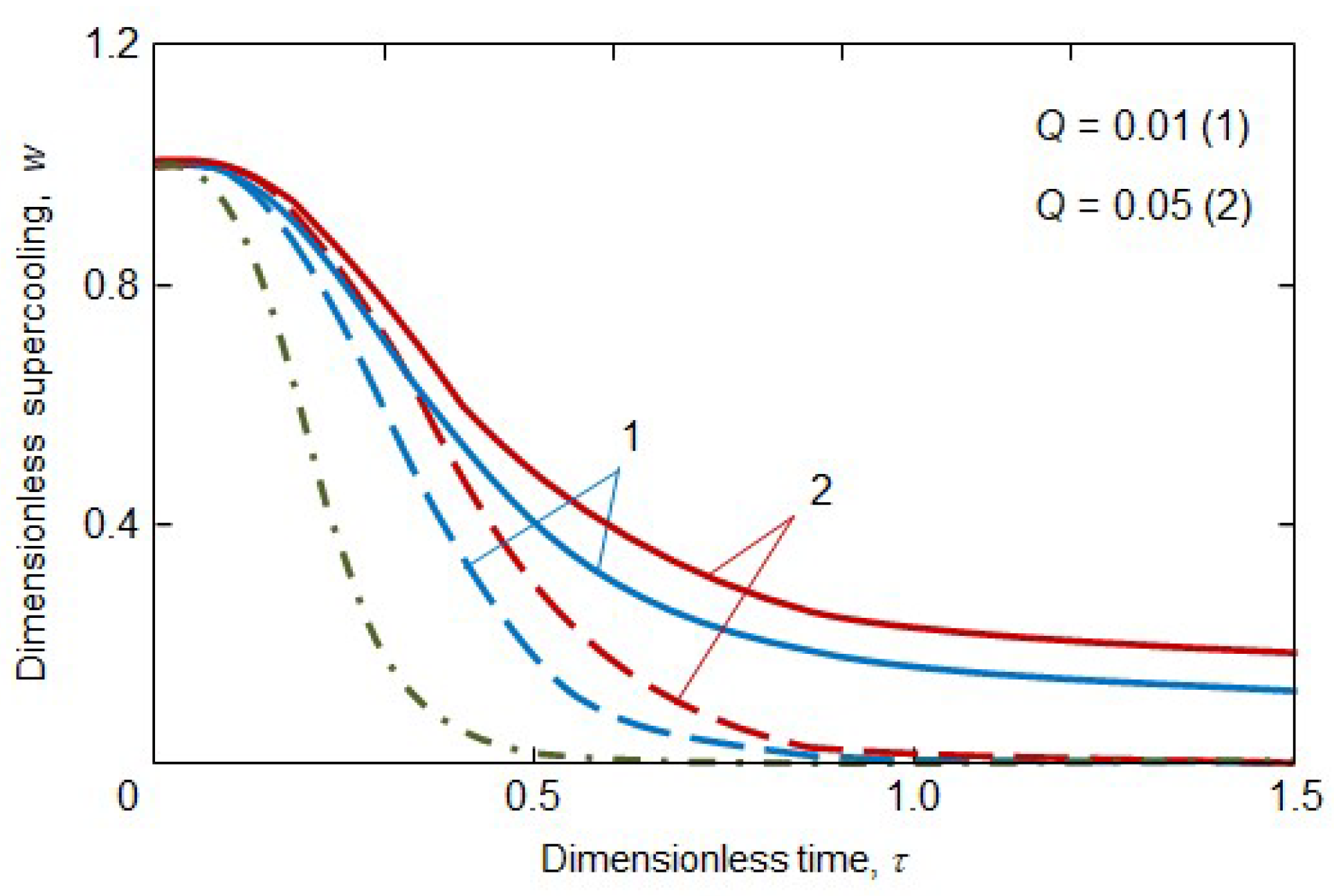
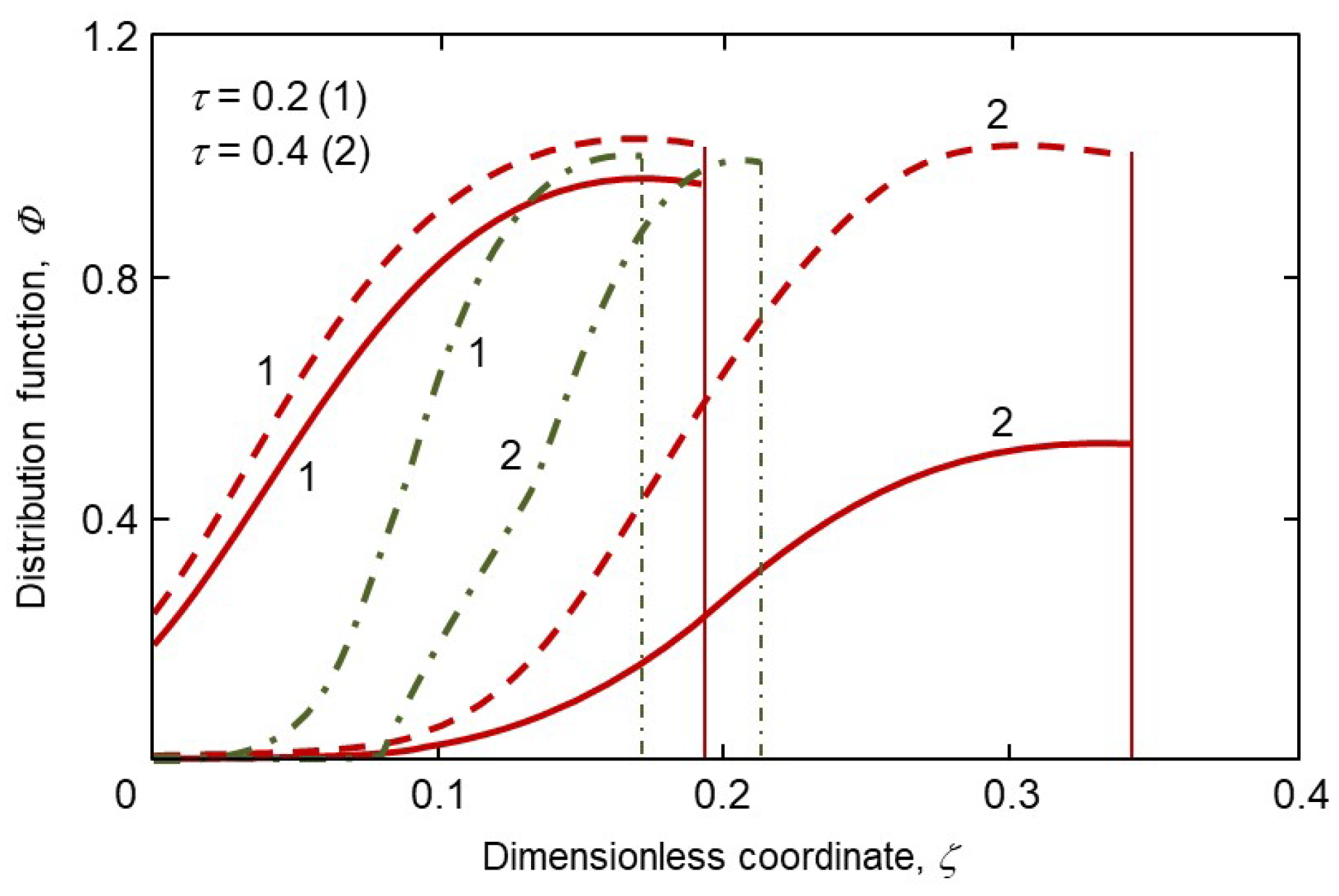
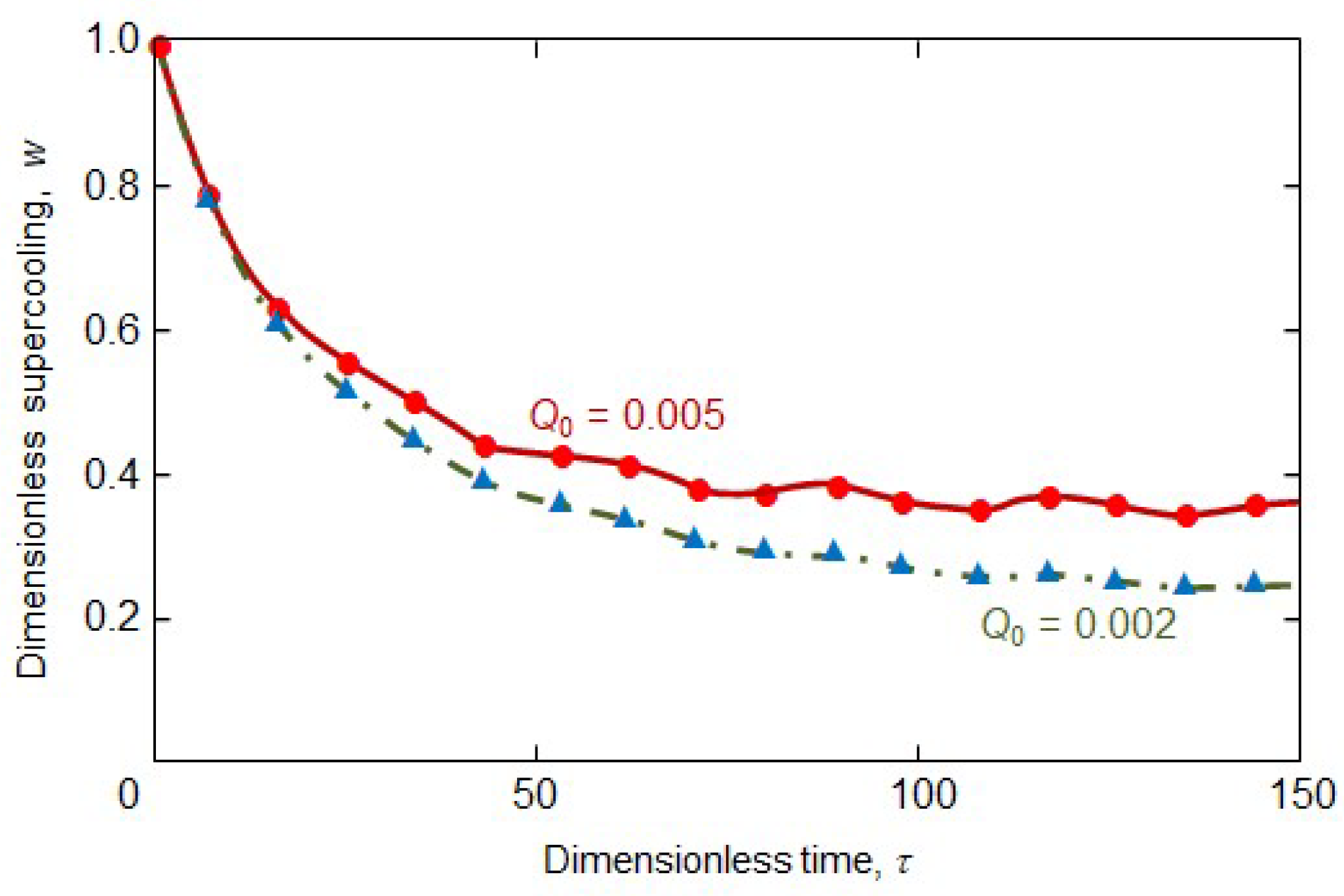

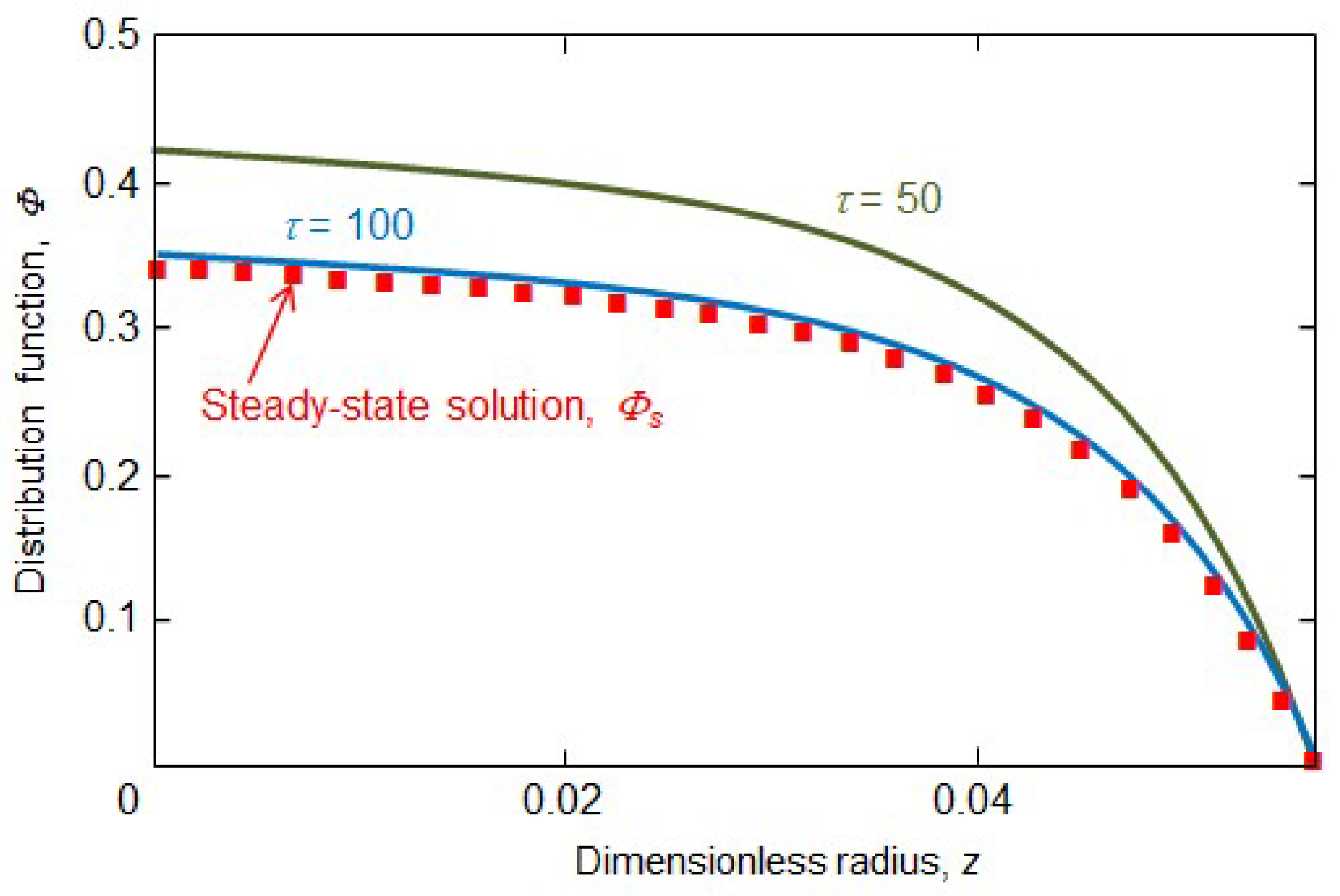
| Supercooled Liquids | Supersaturated Liquids | |||
|---|---|---|---|---|
| WVFZ Mechanism | Meirs Mechanism | WVFZ Mechanism | Meirs Mechanism | |
| I | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandrov, D.V.; Ivanov, A.A.; Nizovtseva, I.G.; Lippmann, S.; Alexandrova, I.V.; Makoveeva, E.V. Evolution of a Polydisperse Ensemble of Spherical Particles in a Metastable Medium with Allowance for Heat and Mass Exchange with the Environment. Crystals 2022, 12, 949. https://doi.org/10.3390/cryst12070949
Alexandrov DV, Ivanov AA, Nizovtseva IG, Lippmann S, Alexandrova IV, Makoveeva EV. Evolution of a Polydisperse Ensemble of Spherical Particles in a Metastable Medium with Allowance for Heat and Mass Exchange with the Environment. Crystals. 2022; 12(7):949. https://doi.org/10.3390/cryst12070949
Chicago/Turabian StyleAlexandrov, Dmitri V., Alexander A. Ivanov, Irina G. Nizovtseva, Stephanie Lippmann, Irina V. Alexandrova, and Eugenya V. Makoveeva. 2022. "Evolution of a Polydisperse Ensemble of Spherical Particles in a Metastable Medium with Allowance for Heat and Mass Exchange with the Environment" Crystals 12, no. 7: 949. https://doi.org/10.3390/cryst12070949
APA StyleAlexandrov, D. V., Ivanov, A. A., Nizovtseva, I. G., Lippmann, S., Alexandrova, I. V., & Makoveeva, E. V. (2022). Evolution of a Polydisperse Ensemble of Spherical Particles in a Metastable Medium with Allowance for Heat and Mass Exchange with the Environment. Crystals, 12(7), 949. https://doi.org/10.3390/cryst12070949







