Transformation of 2D RVE Local Stress and Strain Distributions to 3D Observations in Full Phase Crystal Plasticity Simulations of Dual-Phase Steels
Abstract
:1. Introduction
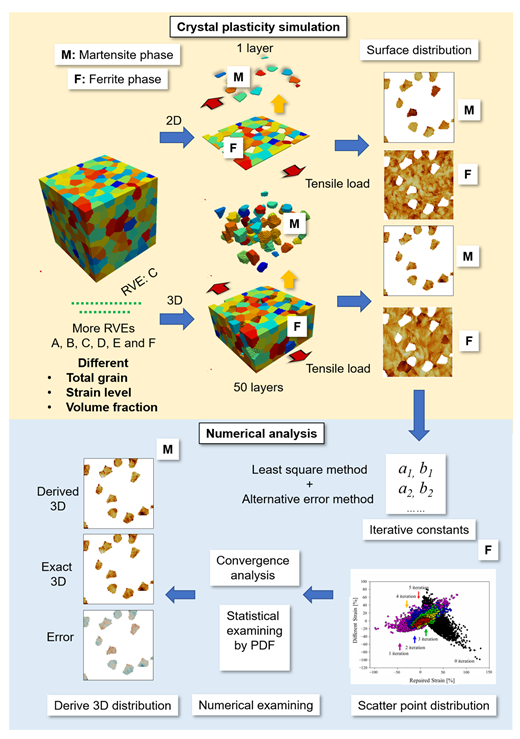
2. Numerical Simulation Model
3. Method
4. Results
4.1. Local Stress/Strain Distribution in 2D and 3D
4.2. Step by Step for Transformation from 2D to 3D
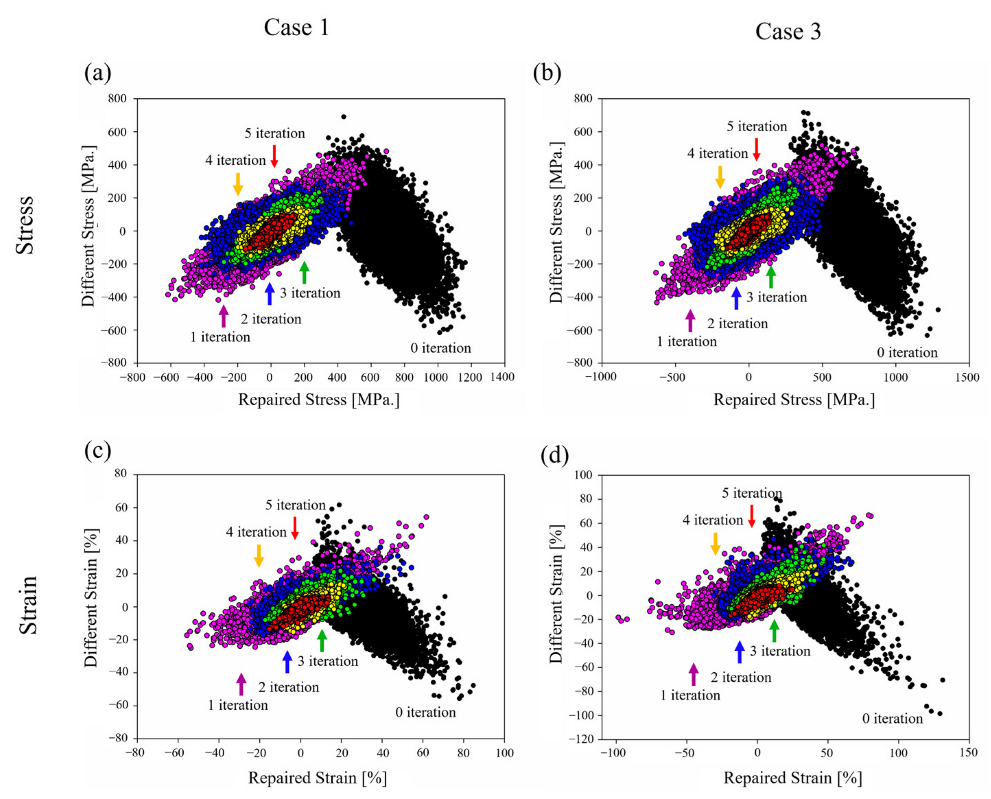
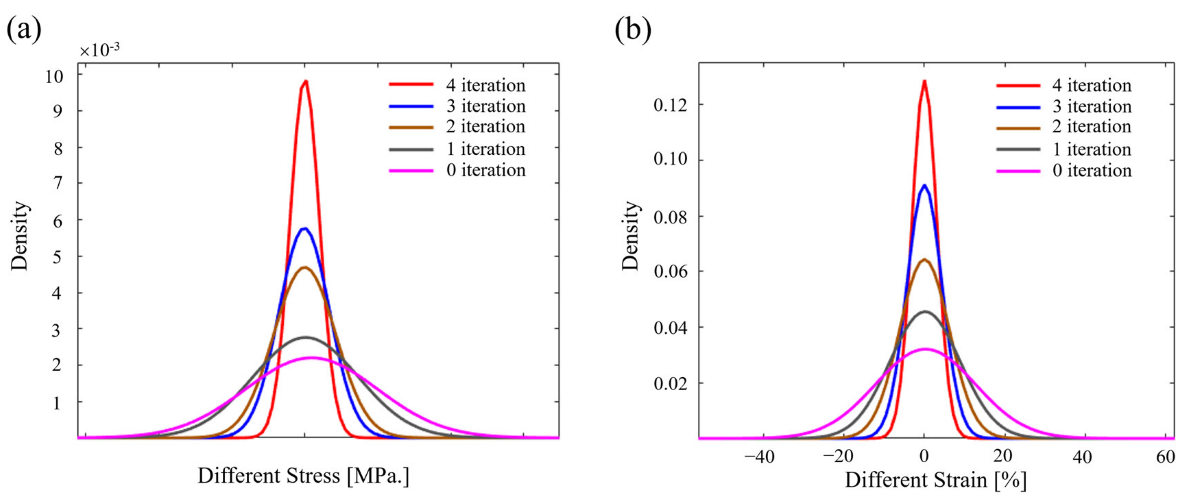
4.3. Convergence and Statistical Analysis
4.4. Derivation of 3D Stress and Strain Distribution from the 2D Result
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Stress | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis Parameter | Total Grain | Strain Level | Volume Fraction | ||||||
| 8400 | 1900 | 770 | 5% | 15% | 25% | 0.1 | 0.15 | 0.2 | |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RVE Iterative Const. | A | B | C | D | D | D | D | E | F |
| −0.86 | −0.78 | −0.88 | −0.7375 | −0.7938 | −0.82 | −0.7938 | −0.725 | −0.766 | |
| 1875 | 1614 | 1746 | 1526 | 2002 | 2222 | 2002 | 2092 | 1956 | |
| 0.31 | 0.23 | 0.36 | 0.14 | 0.24 | 0.34 | 0.24 | 0.21 | 0.17 | |
| 0.67 | 0.76 | 0.63 | 0.84 | 0.74 | 0.64 | 0.74 | 0.77 | 0.81 | |
| 6.02 | 2.87 | −1.003 | 28.96 | 14.86 | 6.64 | 14.86 | 20.6 | −25.19 | |
| 0.67 | 0.76 | 0.63 | 0.84 | 0.74 | 0.64 | 0.74 | 0.79 | 0.81 | |
| 0.32 | 0.23 | 0.36 | 0.15 | 0.25 | 0.35 | 0.25 | 0.23 | 0.18 | |
| 4.67 | 1.05 | −1.00 | 5.69 | 6.49 | 6.37 | 6.49 | 6.55 | −5.52 | |
| 0.31 | 0.23 | 0.36 | 0.14 | 0.25 | 0.35 | 0.25 | 0.23 | 0.17 | |
| 0.68 | 0.76 | 0.63 | 0.86 | 0.75 | 0.65 | 0.75 | 0.77 | 0.82 | |
| 5.68 | 1.35 | −1.00 | 8.39 | 8.43 | 7.14 | 8.43 | 6.24 | −6.69 | |
| 0.68 | 0.76 | 0.63 | 0.86 | 0.75 | 0.65 | 0.75 | 0.77 | 0.82 | |
| Strain | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis Parameter | Total Grain | Strain Level | Volume Fraction | ||||||
| 8400 | 1900 | 770 | 5% | 15% | 25% | 0.1 | 0.15 | 0.2 | |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RVE Iterative Const. | A | B | C | D | D | D | D | E | F |
| −0.31 | 0.09 | 0.5354 | 0.26 | 0.23 | 0.18 | 0.23 | 0.22 | −0.03 | |
| 2.19 | −0.023 | −1.3028 | −0.30 | −0.93 | −1.38 | -0.93 | −0.3 | 0.60 | |
| 0.005 | 0.0007 | 0.015 | 0.003 | 0.002 | 0.002 | 0.002 | 0.006 | 0.001 | |
| 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| 0.17 | −0.12 | −0.4026 | 0.028 | 0.104 | 0.16 | 0.104 | −0.32 | −0.53 | |
| 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| 0.005 | 0.0008 | 0.0164 | 0.003 | 0.003 | 0.002 | 0.003 | 0.006 | 0.001 | |
| 0.0009 | −0.00008 | −0.0058 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.005 | 0.0007 | 0.0156 | 0.003 | 0.003 | 0.002 | 0.003 | 0.006 | 0.001 | |
| 0.99 | 0.99 | 0.9850 | 0.996 | 0.997 | 0.998 | 0.997 | 0.993 | 0.99 | |
| 0.001 | −0.00015 | −0.0091 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.99 | 0.99 | 0.98 | 0.996 | 0.997 | 0.998 | 0.998 | 0.993 | 0.99 | |
References
- Tasan, C.C.; Diehl, M.; Yan, D.; Bechtold, M.; Roters, F.; Schemmann, L.; Zheng, C.; Peranio, N.; Ponge, D.; Koyama, M.; et al. An overview of dual-phase steels: Advances in microstructure-oriented processing and micromechanically guided design. Annu. Rev. Mater. Res. 2015, 45, 391–431. [Google Scholar] [CrossRef]
- Hussein, T.; Umar, M.; Qayyum, F.; Guk, S.; Prahl, U. Micromechanical Effect of Martensite Attributes on Forming Limits of Dual-Phase Steels Investigated by Crystal Plasticity-Based Numerical Simulations. Crystals 2022, 12, 155. [Google Scholar] [CrossRef]
- Biermann, H.; Martin, U.; Aneziris, C.G.; Kolbe, A.; Müller, A.; Schärfl, W.; Herrmann, M. Microstructure and compression strength of novel TRIP-steel/Mg-PSZ composites. Adv. Eng. Mater. 2009, 11, 1000–1006. [Google Scholar] [CrossRef]
- Biermann, H.; Aneziris, C.G. Austenitic TRIP/TWIP Steels and Steel-Zirconia Composites: Design of Tough, Transformation-Strengthened Composites and Structures; Springer Nature: Berlin/Heidelberg, Germany, 2020; Volume 298. [Google Scholar]
- Asghar, W.; Nasir, M.A.; Qayyum, F.; Shah, M.; Azeem, M.; Nauman, S.; Khushnood, S. Investigation of fatigue crack growth rate in CARALL, ARALL and GLARE. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 1086–1100. [Google Scholar] [CrossRef]
- Khan, F.; Qayyum, F.; Asghar, W.; Azeem, M.; Anjum, Z.; Nasir, A.; Shah, M. Effect of various surface preparation techniques on the delamination properties of vacuum infused Carbon fiber reinforced aluminum laminates (CARALL): Experimentation and numerical simulation. J. Mech. Sci. Technol. 2017, 31, 5265–5272. [Google Scholar] [CrossRef]
- Qayyum, F.; Kamran, A.; Ali, A.; Shah, M. 3D numerical simulation of thermal fatigue damage in wedge specimen of AISI H13 tool steel. Eng. Fract. Mech. 2017, 180, 240–253. [Google Scholar] [CrossRef]
- Mukhtar, F.; Qayyum, F.; Shah, M. Studying the effect of thermal fatigue on multiple cracks propagating in an SS316L thin flange on a shaft specimen using a multi-physics numerical simulation model. J. Mech. Eng. 2019, 65, 565–573. [Google Scholar] [CrossRef]
- Hussain, N.; Qayyum, F.; Pasha, R.A.; Shah, M. Development of multi-physics numerical simulation model to investigate thermo-mechanical fatigue crack propagation in an autofrettaged gun barrel. Def. Technol. 2020, 17, 1579–1591. [Google Scholar] [CrossRef]
- Ibrahim, I.; Mohamed, F.; Lavernia, E. Particulate reinforced metal matrix composites—A review. J. Mater. Sci. 1991, 26, 1137–1156. [Google Scholar] [CrossRef]
- Kanouté, P.; Boso, D.P.; Chaboche, J.L.; Schrefler, B. Multiscale methods for composites: A review. Arch. Comput. Methods Eng. 2009, 16, 31–75. [Google Scholar] [CrossRef]
- Hannard, F.; Simar, A.; Maire, E.; Pardoen, T. Quantitative assessment of the impact of second phase particle arrangement on damage and fracture anisotropy. Acta Mater. 2018, 148, 456–466. [Google Scholar] [CrossRef]
- Zhang, J.F.; Zhang, X.X.; Wang, Q.Z.; Xiao, B.L.; Ma, Z.Y. Simulations of deformation and damage processes of SiCp/Al composites during tension. J. Mater. Sci. Technol. 2018, 34, 627–634. [Google Scholar] [CrossRef]
- Lee, S.B.; Lebensohn, R.; Rollett, A.D. Modeling the viscoplastic micromechanical response of two-phase materials using Fast Fourier Transforms. Int. J. Plast. 2011, 27, 707–727. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Kanjarla, A.K.; Eisenlohr, P. An elasto-viscoplastic formulation based on fast Fourier transforms for the prediction of micromechanical fields in polycrystalline materials. Int. J. Plast. 2012, 32–33, 59–69. [Google Scholar] [CrossRef]
- Fujita, N.; Igi, S.; Diehl, M.; Roters, F.; Raabe, D. The through-process texture analysis of plate rolling by coupling finite element and fast Fourier transform crystal plasticity analysis. Model. Simul. Mater. Sci. Eng. 2019, 27, 085005. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Kadkhodapour, J.; Butz, A.; Ziaei-Rad, S.; Schmauder, S. A micro mechanical study on failure initiation of dual phase steels under tension using single crystal plasticity model. Int. J. Plast. 2011, 27, 1103–1125. [Google Scholar] [CrossRef]
- Uthaisangsuk, V.; Prahl, U.; Bleck, W. Stretch-flangeability characterisation of multiphase steel using a microstructure based failure modelling. Comput. Mater. Sci. 2009, 45, 617–623. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Groeber, M.; Ghosh, S.; Uchic, M.D.; Dimiduk, D.M. A framework for automated analysis and simulation of 3D polycrystalline microstructures.: Part 1: Statistical characterization. Acta Mater. 2008, 56, 1257–1273. [Google Scholar] [CrossRef]
- Groeber, M.; Ghosh, S.; Uchic, M.D.; Dimiduk, D.M. A framework for automated analysis and simulation of 3D polycrystalline microstructures. Part 2: Synthetic structure generation. Acta Mater. 2008, 56, 1274–1287. [Google Scholar] [CrossRef]
- Diehl, M.; Groeber, M.; Haase, C.; Molodov, D.A.; Roters, F.; Raabe, D. Identifying structure–property relationships through DREAM. 3D representative volume elements and DAMASK crystal plasticity simulations: An integrated computational materials engineering approach. Jom 2017, 69, 848–855. [Google Scholar] [CrossRef] [Green Version]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.O.; et al. DAMASK–The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Ramazani, A.; Mukherjee, K.; Quade, H.; Prahl, U.; Bleck, W. Correlation between 2D and 3D flow curve modelling of DP steels using a microstructure-based RVE approach. Mater. Sci. Eng. A 2013, 560, 129–139. [Google Scholar] [CrossRef]
- Qayyum, F.; Guk, S.; Prüger, S.; Schmidtchen, M.; Saenko, I.; Kiefer, B.; Kawalla, R.; Prahl, U. Investigating the local deformation and transformation behavior of sintered X3CrMnNi16-7-6 TRIP steel using a calibrated crystal plasticity-based numerical simulation model. Int. J. Mater. Res. 2020, 111, 392–404. [Google Scholar] [CrossRef]
- Qayyum, F.; Guk, S.; Schmidtchen, M.; Kawalla, R.; Prahl, U. Modeling the local deformation and transformation behavior of cast X8CrMnNi16-6-6 TRIP steel and 10% Mg-PSZ composite using a continuum mechanics-based crystal plasticity model. Crystals 2020, 10, 221. [Google Scholar] [CrossRef] [Green Version]
- Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Roters, F. Neighborhood influences on stress and strain partitioning in dual-phase microstructures. Meccanica 2016, 51, 429–441. [Google Scholar] [CrossRef]
- Qayyum, F.; Guk, S.; Prahl, U. Studying the damage evolution and the micro-mechanical response of X8CrMnNi16-6-6 TRIP steel matrix and 10% zirconia particle composite using a calibrated physics and crystal-plasticity-based numerical simulation model. Crystals 2021, 11, 759. [Google Scholar] [CrossRef]
- Qayyum, F.; Guk, S.; Kawalla, R.; Prahl, U. Experimental Investigations and Multiscale Modeling to Study the Effect of Sulfur Content on Formability of 16MnCr5 Alloy Steel. Steel Res. Int. 2018, 90, 1800369. [Google Scholar] [CrossRef]
- Sedighiani, K.; Traka, K.; Roters, F.; Raabe, D.; Sietsma, J.; Diehl, M. Determination and analysis of the constitutive parameters of temperature-dependent dislocation-density-based crystal plasticity models. Mech. Mater. 2022, 164, 104117. [Google Scholar] [CrossRef]
- Sedighiani, K.; Diehl, M.; Traka, K.; Roters, F.; Sietsma, J.; Raabe, D. An efficient and robust approach to determine material parameters of crystal plasticity constitutive laws from macro-scale stress–strain curves. Int. J. Plast. 2020, 134, 102779. [Google Scholar] [CrossRef]
- Weidner, A.; Biermann, H. Review on Strain Localization Phenomena Studied by High-Resolution Digital Image Correlation. Adv. Eng. Mater. 2021, 23, 2001409. [Google Scholar] [CrossRef]
- Weidner, A.; Biermann, H. Combination of Different In Situ Characterization Techniques and Scanning Electron Microscopy Investigations for a Comprehensive Description of the Tensile Deformation Behavior of a CrMnNi TRIP/TWIP Steel. Jom 2015, 67, 1729–1747. [Google Scholar] [CrossRef]
- Weidner, A.; Berek, H.; Segel, C.; Aneziris, C.G.; Biermann, H. In situ tensile deformation of TRIP steel/Mg-PSZ composites. Mater. Sci. Forum 2013, 738–739, 77–81. [Google Scholar] [CrossRef]
- Vinogradov, A.; Lazarev, A.; Linderov, M.; Weidner, A.; Biermann, H. Kinetics of deformation processes in high-alloyed cast transformation-induced plasticity/twinning-induced plasticity steels determined by acoustic emission and scanning electron microscopy: Influence of austenite stability on deformation mechanisms. Acta Mater. 2013, 61, 2434–2449. [Google Scholar] [CrossRef]
- Qayyum, F.; Chaudhry, A.A.; Guk, S.; Schmidtchen, M.; Kawalla, R.; Prahl, U. Effect of 3D Representative Volume Element (RVE) Thickness on Stress and Strain Partitioning in Crystal Plasticity Simulations of Multi-Phase Materials. Crystals 2020, 10, 944. [Google Scholar] [CrossRef]
- Qayyum, F.; Umar, M.; Guk, S.; Schmidtchen, M.; Kawalla, R.; Prahl, U. Effect of the 3rd Dimension within the Representative Volume Element (RVE) on Damage Initiation and Propagation during Full-Phase Numerical Simulations of Single and Multiphase Steels. Materials 2021, 14, 42. [Google Scholar] [CrossRef]
- Umar, M.; Qayyum, F.; Farooq, M.U.; Guk, S.; Kirschner, M.; Korpala, G.; Prahl, U. Exploring the Structure–Property Relationship in Spheroidized C45EC Steel Using Full Phase Crystal Plasticity Numerical Simulations. Steel Res. Int. 2022, 93, 2100452. [Google Scholar] [CrossRef]
- Qayyum, F.; Umar, M.; Elagin, V.; Kirschner, M.; Hoffmann, F.; Guk, S.; Prahl, U. Influence of Non-Metallic Inclusions on Local Deformation and Damage Behavior of Modified 16MnCrS5 Steel. Crystals 2022, 12, 281. [Google Scholar] [CrossRef]
- Umar, M.; Qayyum, F.; Farooq, M.U.; Khan, L.A.; Guk, S.; Prahl, U. Analyzing the cementite particle size and distribution in heterogeneous microstructure of C45EC steel using crystal plasticity based DAMASK code. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021; pp. 15–20. [Google Scholar]
- Jiang, Z.; Guan, Z.; Lian, J. Effects of microstructural variables on the deformation behaviour of dual-phase steel. Mater. Sci. Eng. A 1995, 190, 55–64. [Google Scholar] [CrossRef]
- Eisenlohr, P.; Diehl, M.; Lebensohn, R.A.; Roters, F. A spectral method solution to crystal elasto-viscoplasticity at finite strains. Int. J. Plast. 2013, 46, 37–53. [Google Scholar] [CrossRef]
- Tseng, S.C.; Chao, C.K.; Chen, F.M.; Chiu, W.C. Interfacial stresses of a coated polygonal hole subject to a point heat source. J. Therm. Stresses. 2020, 43, 1487–1512. [Google Scholar] [CrossRef]
- Tseng, S.C.; Chao, C.K.; Chen, F.M. Interfacial stresses of a coated square hole induced by a remote uniform heat flow. International J. Appl. Mech. 2020, 12, 2050063. [Google Scholar] [CrossRef]
- Diehl, M.; Naunheim, Y.; Yan, D.; Morsdorf, L.; An, D.; Tasan, C.C.; Zaefferer, S.; Roters, F.; Raabe, D. Coupled Experimental-Numerical Analysis of Strain Partitioning in Metallic Microstructures: The Importance of Considering the 3D Morphology. In Proceedings of the BSSM 12th International Conference on Advances in Experimental Mechanics, Sheffield, UK, 29–31 August 2017; pp. 1–2. [Google Scholar]
- Diehl, M.; An, D.; Shanthraj, P.; Zaefferer, S.; Roters, F.; Raabe, D. Crystal plasticity study on stress and strain partitioning in a measured 3D dual phase steel microstructure. Phys. Mesomech. 2017, 20, 311–323. [Google Scholar] [CrossRef]
- Chao, C.K.; Tseng, S.C.; Chen, F.M. Mode-III stress intensity factors for two circular inclusions subject to a remote uniform shear load. J. Chin. Inst. Eng. 2018, 41, 590–602. [Google Scholar] [CrossRef]
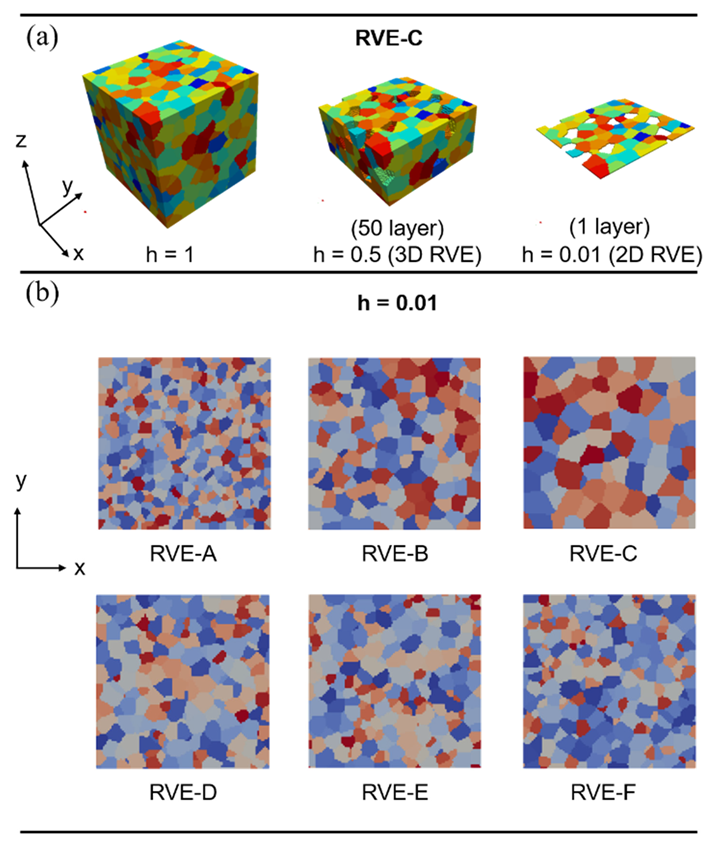



| Case | RVE | Ferrite Grains | Martensite Grains | Total Grain | Strain Level [%] | Volume Fraction | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Avg. | Min. | Max. | Avg. | |||||
| 1 | A | 5.1 | 7.6 | 6.35 | 3.5 | 5.7 | 4.6 | 8400 | 25 | 0.1 |
| 2 | B | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 25 | 0.1 |
| 3 | C | 11.2 | 16.8 | 14.0 | 9.8 | 15.8 | 12.8 | 700 | 25 | 0.1 |
| 4 | D | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 5 | 0.1 |
| 5 | D | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 15 | 0.1 |
| 6 | D | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 25 | 0.1 |
| 7 | D | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 15 | 0.1 |
| 8 | E | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 15 | 0.15 |
| 9 | F | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 | 15 | 0.2 |
| Parameter | Symbol | Ferrite | Martensite | Unit |
|---|---|---|---|---|
| First elastic stiffness constant with normal strain | C11 | 233.3 | 417.4 | GPa |
| Second elastic stiffness constant with normal strain | C12 | 135.5 | 242.4 | GPa |
| First elastic stiffness constant with shear strain | C44 | 128.0 | 211.1 | GPa |
| Initial shear resistance on [111] | S0 [111] | 95 | 406 | MPa |
| Saturation shear resistance on [111] | S∞ [111] | 222 | 873 | MPa |
| Initial shear resistance on [112] | S0 [112] | 96 | 457 | MPa |
| Saturation shear resistance on [112] | S∞ [112] | 412 | 971 | MPa |
| Slip hardening parameter | h0 | 1.0 | 563 | GPa |
| Interaction hardening parameter | hα,β | 1.0 | 1.0 | - |
| Stress exponent | 20 | 20 | - | |
| Curve fitting parameter | 2.0 | 2.0 | - |
| Stress | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis Parameter | Total Grain | Stress/Strain Level, % | Volume Fraction, % | ||||||
| 8400 | 1900 | 770 | 5 | 15 | 25 | 0.1 | 0.15 | 0.2 | |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RVE Iterative Const. | A | B | C | D | D | D | D | E | F |
| −0.76 | −0.81 | −0.75 | −0.63 | −0.74 | −0.78 | −0.74 | −0.66 | −0.66 | |
| 543.73 | 572.10 | 572.15 | 357.41 | 470.71 | 579.71 | 470.71 | 444.5 | 435.8 | |
| 0.35 | 0.37 | 0.34 | 0.31 | 0.38 | 0.41 | 0.38 | 0.33 | 0.31 | |
| 0.64 | 0.62 | 0.65 | 0.68 | 0.61 | 0.59 | 0.61 | 0.64 | 0.66 | |
| −8.62 | −10.73 | −5.70 | −11.48 | −9.46 | −7.43 | −9.46 | −13.85 | −12.25 | |
| 0.64 | 0.64 | 0.68 | 0.69 | 0.62 | 0.60 | 0.62 | 0.69 | 0.72 | |
| 0.35 | 0.36 | 0.32 | 0.31 | 0.37 | 0.40 | 0.37 | 0.30 | 0.27 | |
| −1.41 | −2.97 | −3.13 | −1.38 | -2.44 | −3.03 | −2.44 | −4.95 | −4.28 | |
| 0.35 | 0.36 | 0.32 | 0.31 | 0.37 | 0.40 | 0.37 | 0.30 | 0.27 | |
| 0.65 | 0.64 | 0.68 | 0.69 | 0.62 | 0.60 | 0.62 | 0.70 | 0.72 | |
| −0.18 | −0.54 | −1.03 | −0.253 | −0.36 | −0.42 | −0.36 | −2.2 | −2.4 | |
| 0.65 | 0.64 | 0.68 | 0.69 | 0.62 | 0.59 | 0.62 | 0.70 | 0.72 | |
| Strain | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Analysis Parameter | Total Grain | Strain Level, % | Volume Fraction, % | ||||||
| 8400 | 1900 | 770 | 5 | 15 | 25 | 0.1 | 0.15 | 0.2 | |
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RVE Iterative Const. | A | B | C | D | D | D | D | E | F |
| −0.78 | −0.85 | −0.82 | -0.72 | −0.73 | −0.75 | −0.73 | −0.74 | −0.73 | |
| 22.09 | 25.30 | 25.16 | 4.57 | 13.95 | 23.85 | 13.95 | 14.91 | 14.94 | |
| 0.50 | 0.57 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.51 | 0.48 | |
| 0.50 | 0.44 | 0.50 | 0.5 | 0.50 | 0.49 | 0.50 | 0.48 | 0.51 | |
| 0.01 | 0.51 | −0.31 | −0.05 | −1.87 | −0.38 | −1.87 | 0.21 | 0.16 | |
| 0.50 | 0.44 | 0.51 | 0.50 | 0.50 | 0.49 | 0.50 | 0.49 | 0.53 | |
| 0.50 | 0.56 | 0.49 | 0.49 | 0.49 | 0.50 | 0.49 | 0.50 | 0.47 | |
| −0.06 | −0.11 | −0.30 | −0.02 | −0.08 | −0.16 | −0.08 | −0.21 | −0.21 | |
| 0.50 | 0.56 | 0.48 | 0.49 | 0.49 | 0.50 | 0.49 | 0.50 | 0.47 | |
| 0.50 | 0.43 | 0.51 | 0.50 | 0.50 | 0.49 | 0.50 | 0.49 | 0.53 | |
| −0.005 | −0.01 | −0.04 | −0.02 | −0.007 | −0.01 | −0.007 | −0.04 | −0.04 | |
| 0.50 | 0.43 | 0.51 | 0.50 | 0.50 | 0.49 | 0.50 | 0.49 | 0.52 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tseng, S.; Qayyum, F.; Guk, S.; Chao, C.; Prahl, U. Transformation of 2D RVE Local Stress and Strain Distributions to 3D Observations in Full Phase Crystal Plasticity Simulations of Dual-Phase Steels. Crystals 2022, 12, 955. https://doi.org/10.3390/cryst12070955
Tseng S, Qayyum F, Guk S, Chao C, Prahl U. Transformation of 2D RVE Local Stress and Strain Distributions to 3D Observations in Full Phase Crystal Plasticity Simulations of Dual-Phase Steels. Crystals. 2022; 12(7):955. https://doi.org/10.3390/cryst12070955
Chicago/Turabian StyleTseng, Shaochen, Faisal Qayyum, Sergey Guk, Chingkong Chao, and Ulrich Prahl. 2022. "Transformation of 2D RVE Local Stress and Strain Distributions to 3D Observations in Full Phase Crystal Plasticity Simulations of Dual-Phase Steels" Crystals 12, no. 7: 955. https://doi.org/10.3390/cryst12070955
APA StyleTseng, S., Qayyum, F., Guk, S., Chao, C., & Prahl, U. (2022). Transformation of 2D RVE Local Stress and Strain Distributions to 3D Observations in Full Phase Crystal Plasticity Simulations of Dual-Phase Steels. Crystals, 12(7), 955. https://doi.org/10.3390/cryst12070955









