Phase Diagram Determination and Process Development for Continuous Antisolvent Crystallizations
Abstract
:1. Introduction
2. Materials and Methods
3. Results
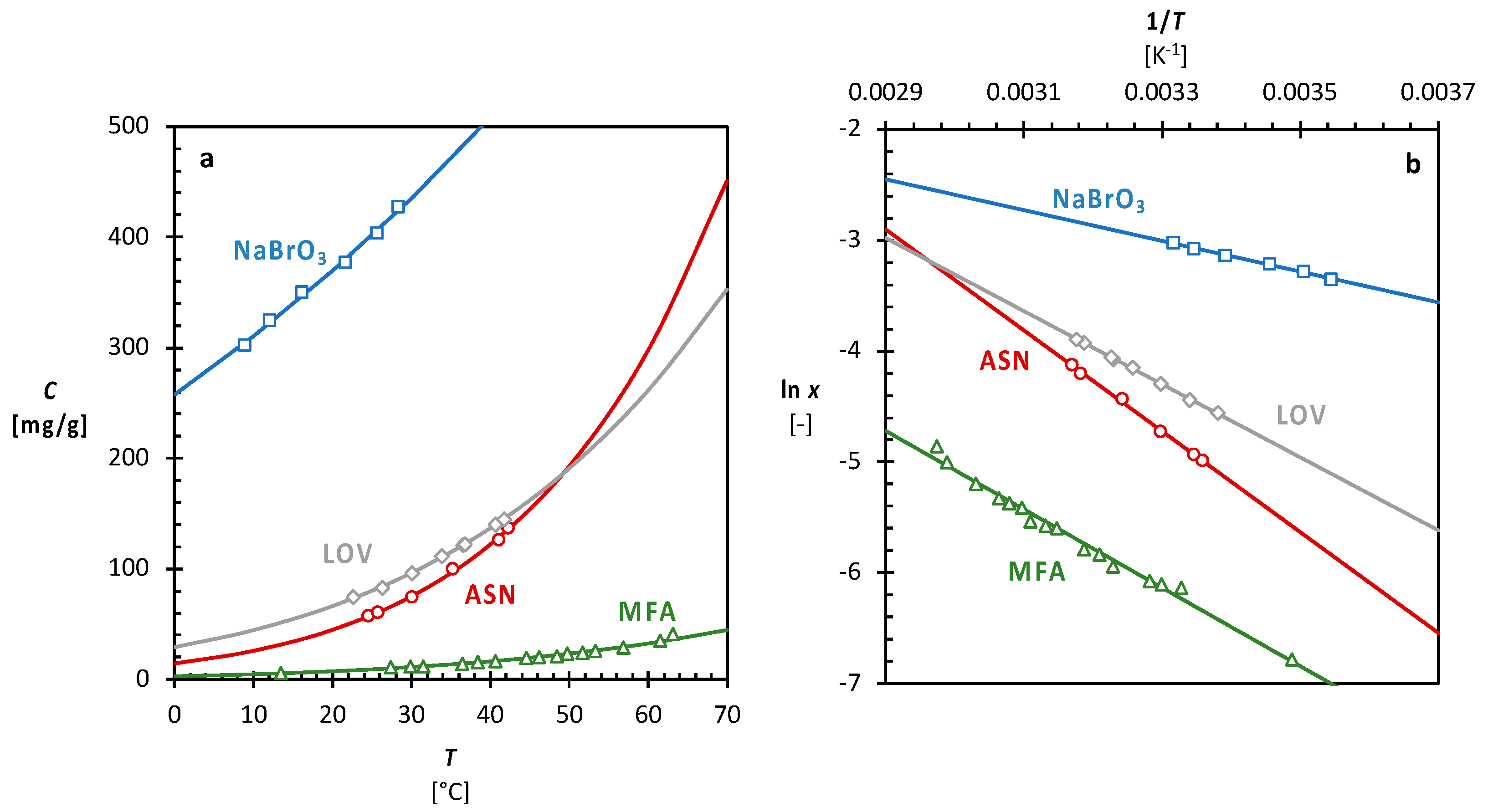
3.1. Single Solvent Solubility
3.2. Solubility in Solvent/Antisolvent Mixtures
3.3. Antisolvent Crystallization Phase Diagrams
3.4. Continuous Antisolvent Crystallization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ter Horst, J.H.; Schmidt, C.; Ulrich, J. Fundamentals of Industrial Crystallization. In Handbook of Crystal Growth; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1317–1346. [Google Scholar]
- Wichianphong, N.; Charoenchaitrakool, M. Statistical optimization for production of mefenamic acid-nicotinamide cocrystals using gas anti-solvent (GAS) process. J. Ind. Eng. Chem. 2018, 62, 375–382. [Google Scholar] [CrossRef]
- Febra, S.A.; Bernet, T.; Mack, C.; McGinty, J.; Onyemelukwe, I.I.; Urwin, S.J.; Sefcik, J.; Ter Horst, J.H.; Adjiman, C.S.; Jackson, G.; et al. Extending the SAFT-γ Mie approach to model benzoic acid, diphenylamine, and mefenamic acid: Solubility prediction and experimental measurement. Fluid Phase Equilibria 2021, 540, 113002. [Google Scholar] [CrossRef]
- Sheikholeslamzadeh, E.; Rohani, S. Solubility prediction of pharmaceutical and chemical compounds in pure and mixed solvents using predictive models. Ind. Eng. Chem. Res. 2012, 51, 464–473. [Google Scholar] [CrossRef]
- Nti-Gyabaah, J.; Chmielowski, R.; Chan, V.; Chiew, Y.C. Solubility of lovastatin in a family of six alcohols: Ethanol, 1-propanol, 1-butanol, 1-pentanol, 1-hexanol, and 1-octanol. Int. J. Pharm. 2008, 359, 111–117. [Google Scholar] [CrossRef] [PubMed]
- Mudalip, S.K.A.; Bakar, M.R.A.; Jamal, P.; Adam, F. Prediction of Mefenamic Acid Solubility and Molecular Interaction Energies in Different Classes of Organic Solvents and Water. Ind. Eng. Chem. Res. 2018, 58, 762–770. [Google Scholar] [CrossRef]
- Reus, M.A.; Van Der Heijden, A.E.D.M.; Ter Horst, J.H. Solubility Determination from Clear Points upon Solvent Addition. Org. Process Res. Dev. 2015, 19, 1004–1011. [Google Scholar] [CrossRef] [Green Version]
- Macedo, E.A. Solubility of amino acids, sugars, and proteins. Pure Appl. Chem. 2005, 77, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Gong, J.B.; Wang, J.K. Solubility of Lovastatin in acetone, methanol, ethanol, ethyl acetate, and butyl acetate between 283 K and 323 K. J. Chem. Eng. Data 2005, 50, 1389–1391. [Google Scholar] [CrossRef]
- Lorimer, J.W. Thermodynamics of solubility in mixed solvent systems. Pure Appl. Chem. 1993, 65, 183–191. [Google Scholar] [CrossRef]
- Sun, H.; Wang, J. Solubility of lovastatin in acetone + water solvent mixtures. J. Chem. Eng. Data 2008, 53, 1335–1337. [Google Scholar] [CrossRef]
- Zijlema, T.G.; Geertman, R.M.; Witkamp, G.-J.; van Rosmalen, G.M.; de Graauw, J. Antisolvent Crystallization as an Alternative to Evaporative Crystallization for the Production of Sodium Chloride. Ind. Eng. Chem. Res. 2000, 39, 1330–1337. [Google Scholar] [CrossRef]
- Oosterhof, H.; Witkamp, G.-J.; van Rosmalen, G.M. Antisolvent crystallization of anhydrous sodium carbonate at atmospherical conditions. AIChE J. 2001, 47, 602–608. [Google Scholar] [CrossRef]
- Johnson, M.D.; Burcham, C.L.; May, S.A.; Calvin, J.R.; McClary Groh, J.; Myers, S.S.; Webster, L.P.; Roberts, J.C.; Reddy, V.R.; Luciani, C.V.; et al. API Continuous Cooling and Antisolvent Crystallization for Kinetic Impurity Rejection in cGMP Manufacturing. Org. Process Res. Dev. 2021, 25, 1284–1351. [Google Scholar] [CrossRef]
- Hussain, M.N.; Jordens, J.; John, J.J.; Braeken, L.; Van Gerven, T. Enhancing pharmaceutical crystallization in a flow crystallizer with ultrasound: Anti-solvent crystallization. Ultrason. Sonochem. 2019, 59, 104743. [Google Scholar] [CrossRef]
- McGinty, J.; Chong, M.W.S.; Manson, A.; Brown, C.J.; Nordon, A.; Sefcik, J. Effect of Process Conditions on Particle Size and Shape in Continuous Antisolvent Crystallisation of Lovastatin. Crystals 2020, 10, 925. [Google Scholar] [CrossRef]
- Raza, S.A.; Schacht, U.; Svoboda, V.; Edwards, D.P.; Florence, A.J.; Pulham, C.R.; Sefcik, J.; Oswald, I.D.H. Rapid Continuous Antisolvent Crystallization of Multicomponent Systems. Cryst. Growth Des. 2018, 18, 210–218. [Google Scholar] [CrossRef] [Green Version]
- Svoboda, V.; MacFhionnghaile, P.; McGinty, J.; Connor, L.E.; Oswald, I.D.H.; Sefcik, J. Continuous Cocrystallization of Benzoic Acid and Isonicotinamide by Mixing-Induced Supersaturation: Exploring Opportunities between Reactive and Antisolvent Crystallization Concepts. Cryst. Growth Des. 2017, 17, 1902–1909. [Google Scholar] [CrossRef] [Green Version]
- Ferguson, S.; Morris, G.; Hao, H.; Barrett, M.; Glennon, B. In-situ monitoring and characterization of plug flow crystallizers. Chem. Eng. Sci. 2012, 77, 105–111. [Google Scholar] [CrossRef]
- Ostergaard, I.; de Diego, H.L.; Qu, H.; Nagy, Z.K. Risk-Based Operation of a Continuous Mixed-Suspension-Mixed-Product-Removal Antisolvent Crystallization Process for Polymorphic Control. Org. Process Res. Dev. 2020, 24, 2840–2852. [Google Scholar] [CrossRef]
- Hoffmann, J.; Flannigan, J.; Cashmore, A.; Briuglia, M.L.; Steendam, R.R.E.; Gerard, C.J.J.; Haw, M.D.; Sefcik, J.; ter Horst, J.H. The unexpected dominance of secondary over primary nucleation. Faraday Discuss. 2022, 235, 109–131. [Google Scholar] [CrossRef]
- Acree, W.E. Comments on “Solubility and Dissolution Thermodynamic Data of Cefpiramide in Pure Solvents and Binary Solvents”. J. Solut. Chem. 2018, 47, 198–200. [Google Scholar] [CrossRef] [Green Version]
- Svärd, M.; Nordström, F.L.; Jasnobulka, T.; Rasmuson, Å.C. Thermodynamics and nucleation kinetics of m-aminobenzoic acid polymorphs. Cryst. Growth Des. 2010, 10, 195–204. [Google Scholar] [CrossRef] [Green Version]
- Pramanik, R.; Bagchi, S. Studies on solvation interaction: Solubility of a betaine dye and a ketocyanine dye in homogeneous and heterogeneous media. Indian J. Chem. Sect. A Inorg. Phys. Theor. Anal. Chem. 2002, 41, 1580–1587. [Google Scholar]
- Ruidiaz, M.A.; Delgado, D.R.; Martínez, F.; Marcus, Y. Solubility and preferential solvation of sulfadiazine in 1,4-dioxane+water solvent mixtures. Fluid Phase Equilibria 2010, 299, 259–265. [Google Scholar] [CrossRef]
- Ter Horst, J.H.; Deij, M.A.; Cains, P.W. Discovering New Co-Crystals. Cryst. Growth Des. 2009, 9, 1531–1537. [Google Scholar] [CrossRef]
- Vellema, J.; Hunfeld, N.G.M.; Van Den Akker, H.E.A.; Ter Horst, J.H. Avoiding crystallization of lorazepam during infusion. Eur. J. Pharm. Sci. 2011, 44, 621–626. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Bernstein, J.L. Remeasurement of optically active NaClO3 and NaBrO3. Acta Crystallogr. Sect. B 1977, 33, 3601–3604. [Google Scholar] [CrossRef] [Green Version]
- Pinho, S.P.; Macedo, E.A. Solubility of NaCl, NaBr, and KCl in water, methanol, ethanol, and their mixed solvents. J. Chem. Eng. Data 2005, 50, 29–32. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Fujiwara, M.; Braatz, R.D. Modelling and control of combined cooling and antisolvent crystallization processes. J. Process Control 2008, 18, 856–864. [Google Scholar] [CrossRef] [Green Version]
- Romero, S.; Escalera, B.; Bustamante, P. Solubility behavior of polymorphs I and II of mefenamic acid in solvent mixtures. Int. J. Pharm. 1999, 178, 193–202. [Google Scholar] [CrossRef]
- SeethaLekshmi, S.; Row, T.N.G. Conformational Polymorphism in a Non-steroidal Anti-inflammatory Drug, Mefenamic Acid. Cryst. Growth Des. 2012, 12, 4283–4289. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001; ISBN 978-0-07-011682-5. [Google Scholar]
- Shayanfar, A.; Fakhree, M.A.A.; Acree, W.E.; Jouyban, A. Solubility of lamotrigine, diazepam, and clonazepam in ethanol + water mixtures at 298.15 K. J. Chem. Eng. Data 2009, 54, 1107–1109. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, W.; Li, X.; Han, D.; Liu, Y.; Du, S.; Zhang, T.; Liu, S.; Gong, J. Solubility of Benzoin in Six Monosolvents and in Some Binary Solvent Mixtures at Various Temperatures. J. Chem. Eng. Data 2017, 62, 3071–3083. [Google Scholar] [CrossRef]
- Pawar, N.; Agrawal, S.; Methekar, R. Continuous Antisolvent Crystallization of α-Lactose Monohydrate: Impact of Process Parameters, Kinetic Estimation, and Dynamic Analysis. Org. Process Res. Dev. 2019, 23, 2394–2404. [Google Scholar] [CrossRef]
- Giulietti, M.; Bernardo, A. Crystallization by Antisolvent Addition and Cooling. Cryst. Sci. Technol. 2012. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Xu, S.; Du, S.; Wang, J.; Gong, J. Progress of Pharmaceutical Continuous Crystallization. Engineering 2017, 3, 354–364. [Google Scholar] [CrossRef]
- Seader, J.D.; Henley, E.J.; Roper, D.K. Separation Process Principles: Chemical and Biochemical Operations, 3rd ed.; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-48183-7. [Google Scholar]






| Compound | NaBrO3 | ASN | MFA | LOV |
|---|---|---|---|---|
| Solvent | Water | Water | Ethanol (EtOH) | Acetone (AcO) |
| Antisolvent | Ethanol (EtOH) | Ethanol (EtOH) | Water | Water |
| N | 22 | 27 | 65 | 39 |
| n | 2 | 1 | 1 | 2 |
| a0 × 10−3 | −1.26 ± 0.2 | −4.84 ± 0.16 | −3.50 ± 0.09 | −2.80 ± 0.36 |
| a1 × 10−3 | −10.8 ± 1.6 | −1.40 ± 0.47 | −2.12 ± 0.64 | −8.30 ± 5.10 |
| a2 × 10−3 | 14.8 ± 2.8 | 12.6 ± 11.2 | ||
| b0 | 1.12 ± 0.55 | 11.5 ± 0.5 | 5.44 ± 0.27 | 5.0 ± 1.2 |
| b1 | 31.4 ± 5.4 | 0.0 ± 1.5 | 0.75 ± 1.97 | 28.8 ± 16.5 |
| b2 | −48.9 ± 9.5 | −60.0 ± 36.2 | ||
| σlnx | 0.8% | 0.7% | 0.8% | 1.7% |
| σx | 3.3% | 3.7% | 5.1% | 8.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mack, C.; Hoffmann, J.; Sefcik, J.; ter Horst, J.H. Phase Diagram Determination and Process Development for Continuous Antisolvent Crystallizations. Crystals 2022, 12, 1102. https://doi.org/10.3390/cryst12081102
Mack C, Hoffmann J, Sefcik J, ter Horst JH. Phase Diagram Determination and Process Development for Continuous Antisolvent Crystallizations. Crystals. 2022; 12(8):1102. https://doi.org/10.3390/cryst12081102
Chicago/Turabian StyleMack, Corin, Johannes Hoffmann, Jan Sefcik, and Joop H. ter Horst. 2022. "Phase Diagram Determination and Process Development for Continuous Antisolvent Crystallizations" Crystals 12, no. 8: 1102. https://doi.org/10.3390/cryst12081102






