Comparison of Brillouin Light Scattering and Density of States in a Supported Layer: Analytical and Experimental Study
Abstract
:1. Introduction
2. Analytical Results
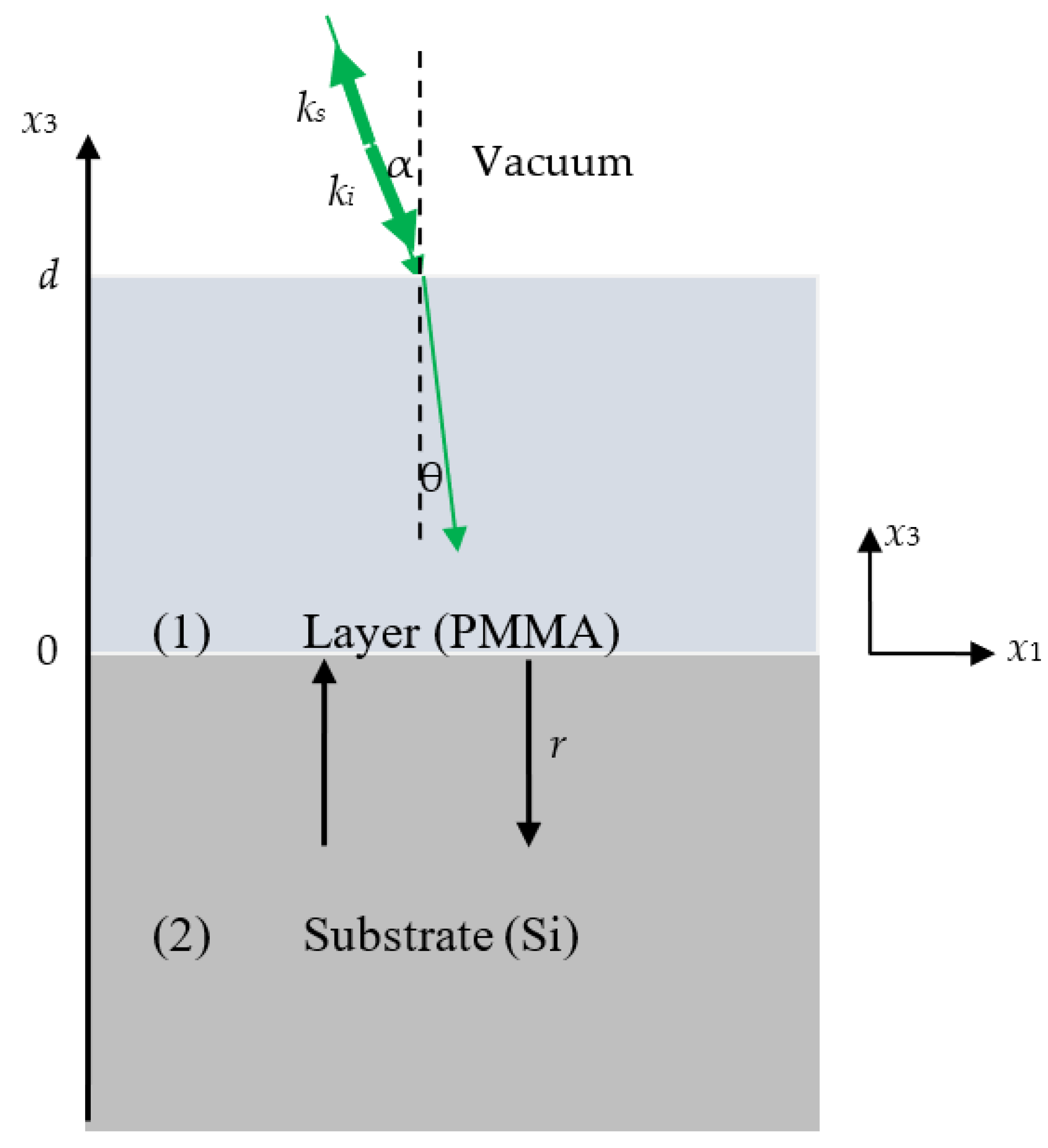
2.1. Scattering Intensity in a Supported Layer
2.2. Density of States and Reflection Delay Time
2.3. Particular Case of a Soft Layer on a Hard Substrate
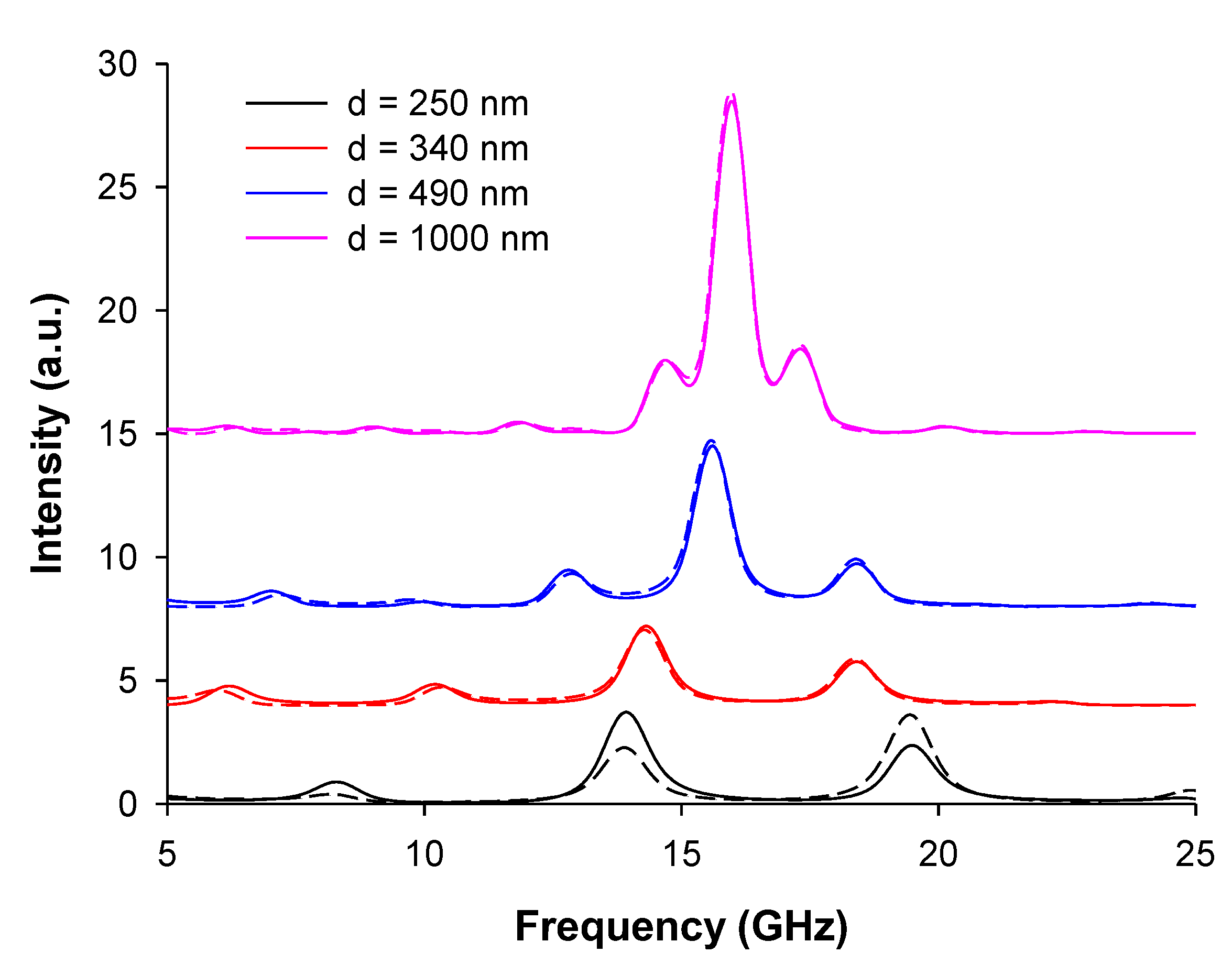
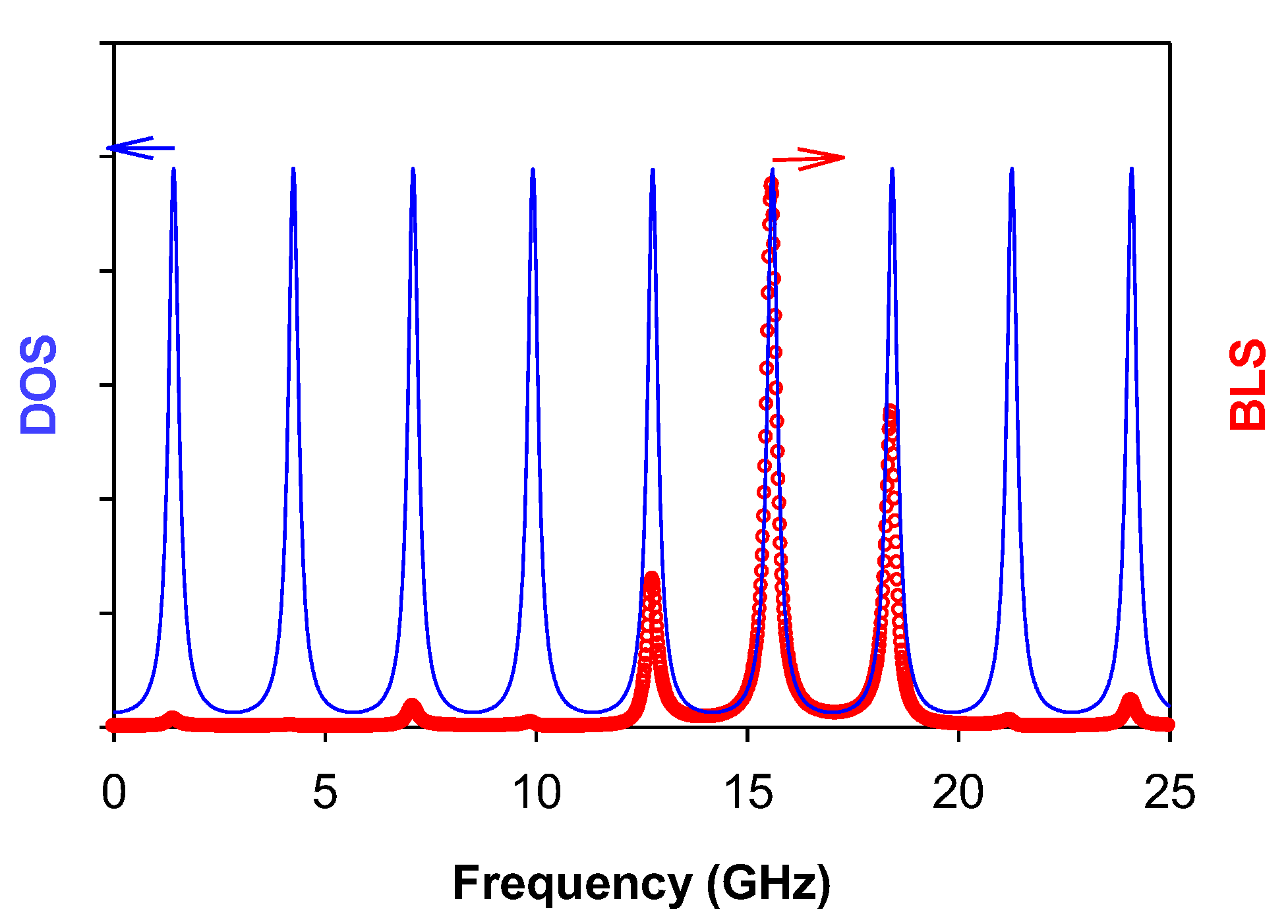
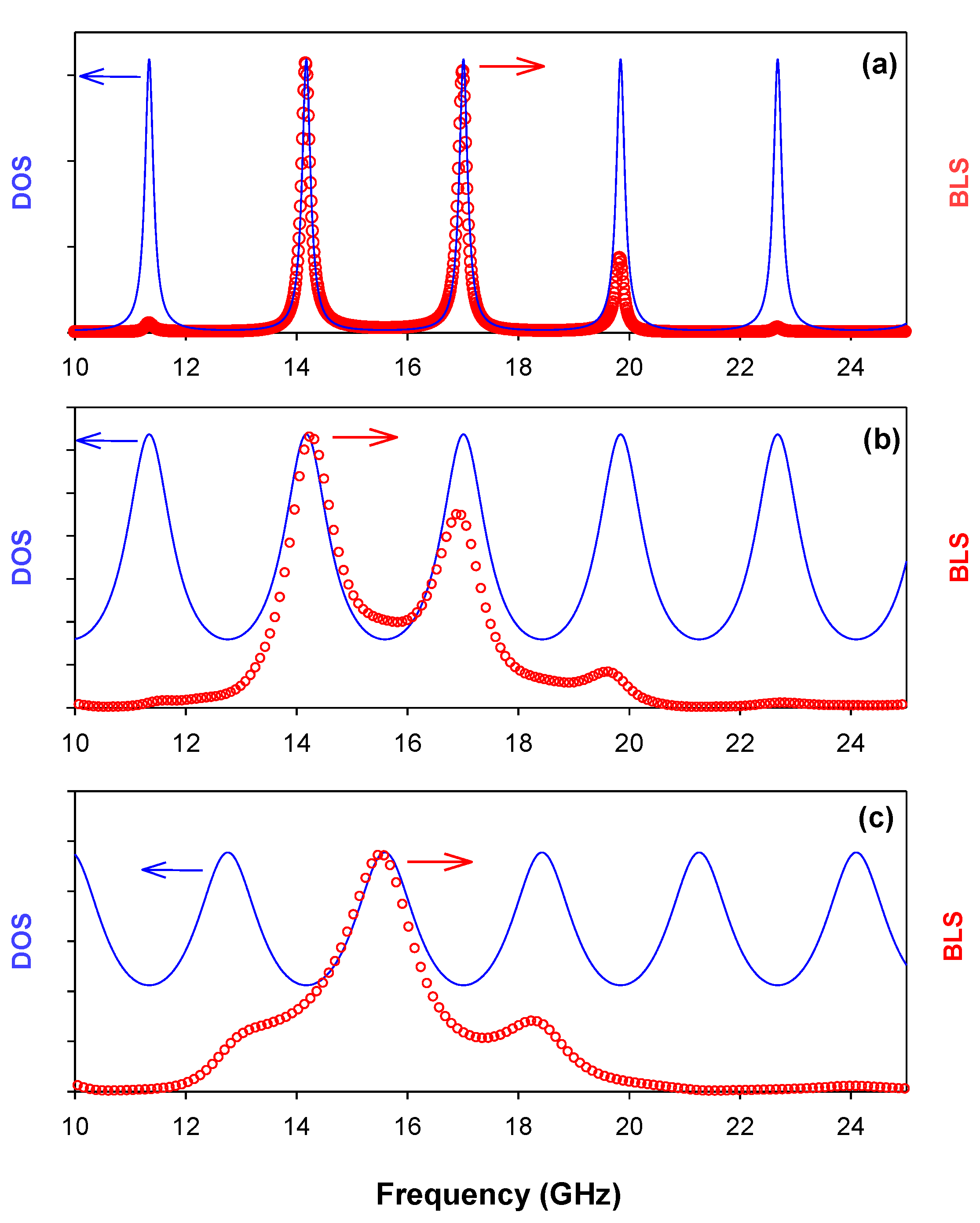
3. Numerical and Experimental Results
3.1. Experimental Setup
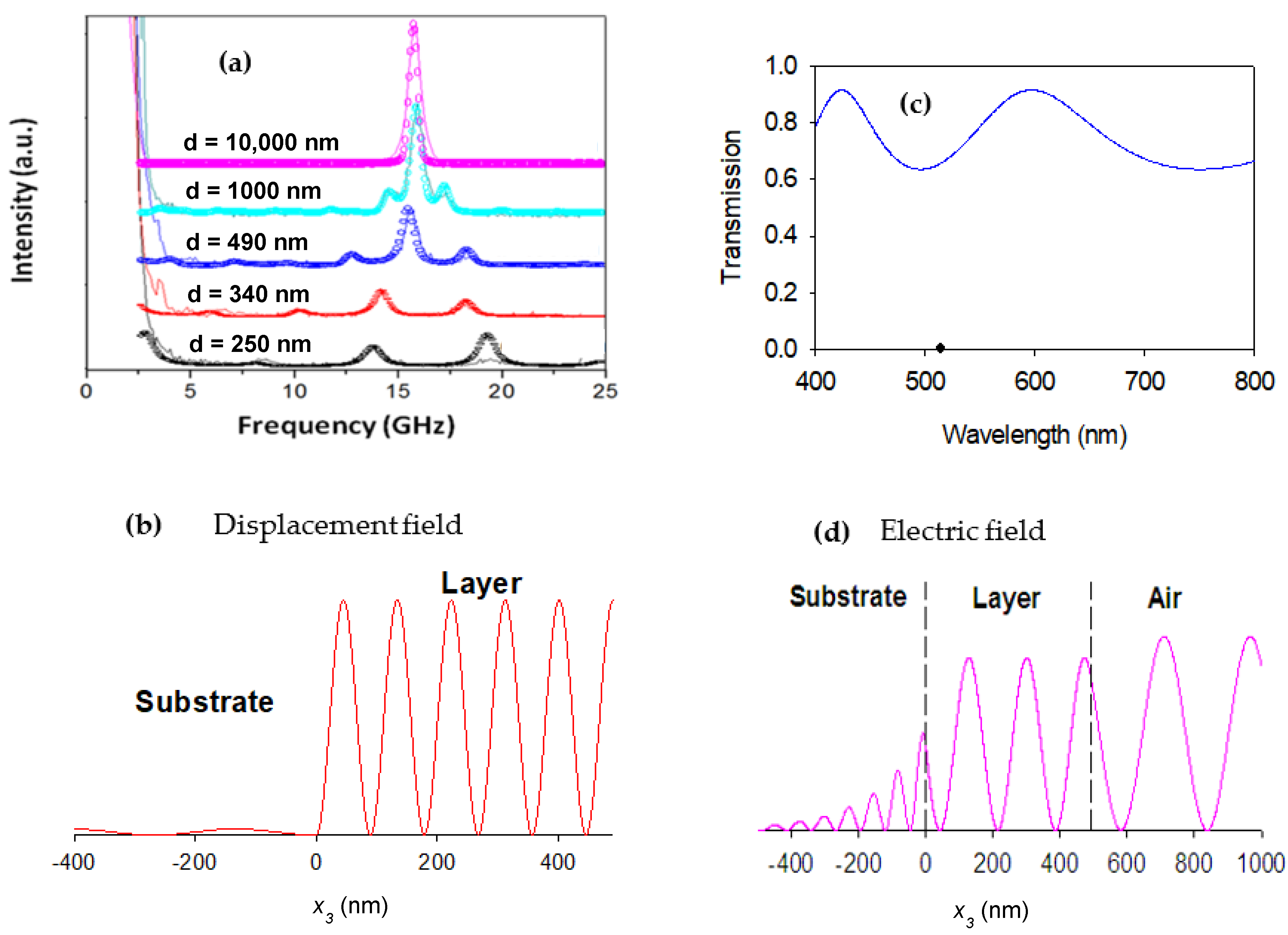
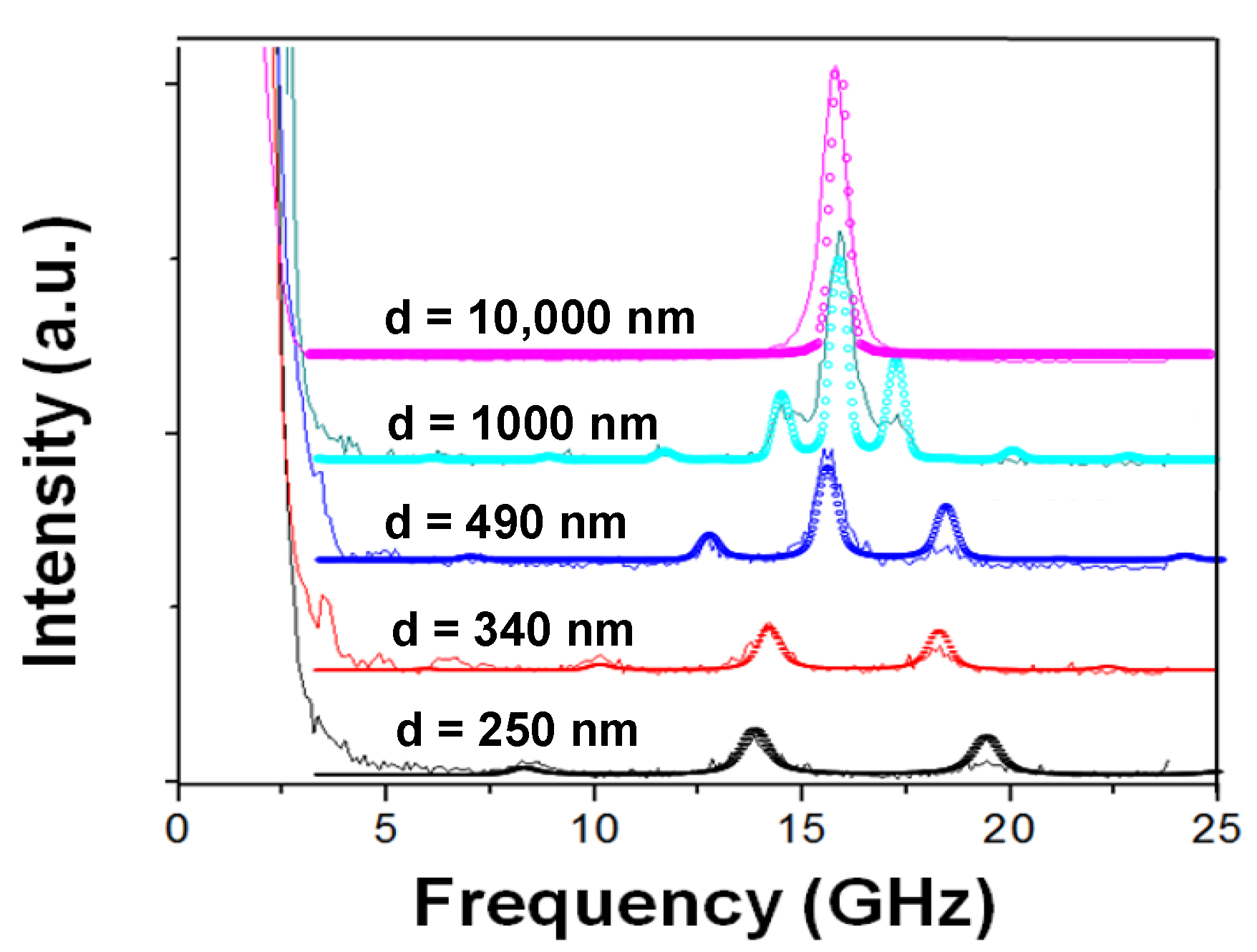
3.2. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Effect of the Moving Interface Mechanism on BLS Spectra
References
- Dobrzynski, L.; El Boudouti, E.H.; Akjouj, A.; Pennec, Y.; Al-Wahsh, H.; Lévêque, G.; Djafari-Rouhani, B. Phononics, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Carlotti, G. Elastic Characterization of Transparent and Opaque Films, Multilayers and Acoustic Resonators by Surface Brillouin Scattering: A Review. Appl. Sci. 2018, 8, 124. [Google Scholar] [CrossRef]
- Bottani, C.E.; Fioretto, D. Brillouin scattering of phonons in complex materials. Adv. Phys. X 2018, 3. [Google Scholar] [CrossRef]
- El Boudouti, E.H.; Djafari-Rouhani, B. Acoustic waves in finite superlattices. Phys. Rev. B 1994, 49, 4586–4592. [Google Scholar] [CrossRef]
- Alami, M.; El Boudouti, E.; Djafari-Rouhani, B.; El Hassouani, Y.; Talbi, A. Surface acoustic waves in one-dimensional piezoelectric-metallic phononic crystal: Effect of a cap layer. Ultrasonics 2018, 90, 80–97. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.A.; Zanoni, R.; Seaton, C.T.; Stegeman, G.I.; Makous, J.; Falco, C.M. Elastic constants of, and Stonely waves in, molybdenum films measured by Brillouin scattering. Appl. Phys. Lett. 1988, 52, 610–612. [Google Scholar] [CrossRef]
- Zhang, X.; Comins, J.D.; Every, A.G.; Stoddart, P.R.; Pang, W.; Derry, T.E. Surface Brillouin scattering study of the surface excitations in amorphous silicon layers produced by ion bombardment. Phys. Rev. B 1998, 58, 13677–13685. [Google Scholar] [CrossRef]
- Zhang, X.; Manghnani, M.H.; Every, A.G. Evidence for a shear horizontal resonance in supported thin films. Phys. Rev. B 2000, 62, R2271–R2274. [Google Scholar] [CrossRef]
- Lai, K.; Finkelstein-Shapiro, D.; Lehmann, S.; Devos, A.; Mante, P.-A. Fano resonance between Stokes and anti-Stokes Brillouin scattering. Phys. Rev. Res. 2021, 3, L032010. [Google Scholar] [CrossRef]
- Wittkowski, T.; Distler, G.; Jung, K.; Hillebrands, B.; Comins, J.D. General methods for the determination of the stiffness tensor and mass density of thin films using Brillouin light scattering: Study of tungsten carbide films. Phys. Rev. B 2004, 69, 205401. [Google Scholar] [CrossRef]
- Izadi, A.; Sinha, M.; Papson, C.; Roccabianca, S.; Anthony, R. Mechanical behavior of SiNC layers on PDMS: Effects of layer thickness, PDMS modulus, and SiNC surface functionality. RSC Adv. 2020, 10, 39087–39091. [Google Scholar] [CrossRef]
- Alonso-Redondo, E.; Belliard, L.; Rolle, K.; Graczykowski, B.; Tremel, W.; Djafari-Rouhani, B.; Fytas, G. Robustness of elastic properties in polymer nanocomposite films examined over the full volume fraction range. Sci. Rep. 2018, 8, 16986. [Google Scholar] [CrossRef] [PubMed]
- Trzaskowska, A.; Mielcarek, S.; Wiesner, M.; Lombardi, F.; Mroz, B. Dispersion of the surface phonons in semiconductor/topological insulator Si/Bi2Te3 heterostructure studied by high resolution Brillouin spectroscopy. Ultrasonics 2021, 117, 106526. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Bandhu, R.S.; Sooryakumar, R.; Jonker, B.T. High-frequency standing longitudinal acoustic resonances in supported thin films. Phys. Rev. B 2003, 67. [Google Scholar] [CrossRef]
- Groenen, J.; Poinsotte, F.; Zwick, A.; Torres, C.M.S.; Prunnila, M.; Ahopelto, J. Inelastic light scattering by longitudinal acoustic phonons in thin silicon layers: From membranes to silicon-on-insulator structures. Phys. Rev. B 2008, 77, 045420. [Google Scholar] [CrossRef]
- Hartschuh, R.; Ding, Y.; Roh, J.H.; Kisliuk, A.; Sokolov, A.P.; Soles, C.L.; Jones, R.L.; Hu, T.J.; Wu, W.L.; Mahorowala, A.P. Brillouin scattering studies of polymeric nanostructures. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 1106–1113. [Google Scholar] [CrossRef]
- Link, A.; Sooryakumar, R.; Bandhu, R.S.; Antonelli, G.A. Brillouin light scattering studies of the mechanical properties of ultrathin low-k dielectric films. J. Appl. Phys. 2006, 100, 013507. [Google Scholar] [CrossRef]
- Nakamura, N.; Ogi, H.; Hirao, M. Stable elasticity of epitaxial Cu thin films on Si. Phys. Rev. B 2008, 77, 245416. [Google Scholar] [CrossRef]
- Zerdali, M.; Hamzaoui, S.; Teherani, F.; Rogers, D. Growth of ZnO thin film on SiO2/Si substrate by pulsed laser deposition and study of their physical properties. Mater. Lett. 2006, 60, 504–508. [Google Scholar] [CrossRef]
- Trzaskowska, A.; Hakonen, P.; Wiesner, M.; Mielcarek, S. Generation of a mode in phononic crystal based on 1D/2D structures. Ultrasonics 2020, 106, 106146. [Google Scholar] [CrossRef]
- Razeeb, K.M.; Dalton, E.; Cross, G.; Robinson, A. Present and future thermal interface materials for electronic devices. Int. Mater. Rev. 2017, 63, 1–21. [Google Scholar] [CrossRef]
- Gomopoulos, N.; Cheng, W.; Efremov, M.; Nealey, P.F.; Fytas, G. Out-of-Plane Longitudinal Elastic Modulus of Supported Polymer Thin Films. Macromolecules 2009, 42, 7164–7167. [Google Scholar] [CrossRef]
- Gomopoulos, N.; Saini, G.; Efremov, M.; Nealey, P.F.; Nelson, K.; Fytas, G. Nondestructive Probing of Mechanical Anisotropy in Polyimide Films on Nanoscale. Macromolecules 2010, 43, 1551–1555. [Google Scholar] [CrossRef]
- Parsons, L.C.; Andrews, G.T. Observation of hypersonic phononic crystal effects in porous silicon superlattices. Appl. Phys. Lett. 2009, 95, 241909. [Google Scholar] [CrossRef]
- Walker, P.M.; Sharp, J.S.; Akimov, A.V.; Kent, A.J. Coherent elastic waves in a one-dimensional polymer hypersonic crystal. Appl. Phys. Lett. 2010, 97, 073106. [Google Scholar] [CrossRef]
- Aliev, G.N.; Goller, B.; Kovalev, D.; Snow, P.A. Hypersonic acoustic mirrors and microcavities in porous silicon. Appl. Phys. Lett. 2010, 96, 124101. [Google Scholar] [CrossRef]
- Hesami, M.; Gueddida, A.; Gomopoulos, N.; Dehsari, H.S.; Asadi, K.; Rudykh, S.; Butt, H.-J.; Djafari-Rouhani, B.; Fytas, G. Elastic wave propagation in smooth and wrinkled stratified polymer films. Nanotechnology 2018, 30, 045709. [Google Scholar] [CrossRef]
- El Boudouti, E.H.; Djafari-Rouhani, B.; Akjouj, A.; Dobrzynski, L. Acoustic waves in solid and fluid layered materials. Surf. Sci. Rep. 2009, 64, 471–594. [Google Scholar] [CrossRef]
- Pennec, Y.; Vasseur, J.O.; Djafari-Rouhani, B.; Dobrzyński, L.; Deymier, P.A. Two-dimensional phononic crystals: Examples and applications. Surf. Sci. Rep. 2010, 65, 229–291. [Google Scholar] [CrossRef]
- Quotane, I.; Amrani, M.; Ghouila-Houri, C.; El Boudouti, E.H.; Krutyansky, L.; Piwakowski, B.; Pernod, P.; Talbi, A.; Djafari-Rouhani, B. A Biosensor Based on Bound States in the Continuum and Fano Resonances in a Solid–Liquid–Solid Triple Layer. Crystals 2022, 12, 707. [Google Scholar] [CrossRef]
- Ezzahri, Y.; Grauby, S.; Rampnoux, J.M.; Michel, H.; Pernot, G.; Claeys, W.; Dilhaire, S.; Rossignol, C.; Zeng, G.; Shakouri, A. Coherent phonons in Si/SiGe superlattices. Phys. Rev. B 2007, 75, 195309. [Google Scholar] [CrossRef]
- Belliard, L.; Huynh, A.; Perrin, B.; Michel, A.; Abadias, G.; Jaouen, C. Elastic properties and phonon generation in Mo/Si superlattices. Phys. Rev. B 2009, 80, 155424. [Google Scholar] [CrossRef]
- Kimura, N.D.L.; Fainstein, A.; Huynh, A.; Perrin, B.; Jusserand, B.; Miard, A.; Lemaitre, A. Coherent Generation of Acoustic Phonons in an Optical Microcavity. Phys. Rev. Lett. 2007, 99, 217405. [Google Scholar] [CrossRef]
- Beardsley, R.P.; Akimov, A.; Henini, M.; Kent, A. Coherent Terahertz Sound Amplification and Spectral Line Narrowing in a Stark Ladder Superlattice. Phys. Rev. Lett. 2010, 104, 085501. [Google Scholar] [CrossRef]
- Lacharmoise, P.; Fainstein, A.; Jusserand, B.; Thierry-Mieg, V. Optical cavity enhancement of light–sound interaction in acoustic phonon cavities. Appl. Phys. Lett. 2004, 84, 3274–3276. [Google Scholar] [CrossRef]
- Maldovan, M.; Thomas, E.L. Simultaneous localization of photons and phonons in two-dimensional periodic structures. Appl. Phys. Lett. 2006, 88, 251907. [Google Scholar] [CrossRef]
- Entezar, S.R.; Namdar, A. Localized modes in defective multilayer structures. Phys. Rev. A 2009, 80, 013814. [Google Scholar] [CrossRef]
- Liang, B.; Guo, X.S.; Tu, J.; Zhang, D.; Cheng, J.C. An acoustic rectifier. Nat. Mater. 2010, 9, 989–992. [Google Scholar] [CrossRef]
- Vollmer, F.; Arnold, S. Whispering-gallery-mode biosensing: Label-free detection down to single molecules. Nat. Methods 2008, 5, 591–596. [Google Scholar] [CrossRef]
- Botsis, J.; Humbert, L.; Colpo, F.; Giaccari, P. Embedded fiber Bragg grating sensor for internal strain measurements in polymeric materials. Opt. Lasers Eng. 2005, 43, 491–510. [Google Scholar] [CrossRef]
- Gomopoulos, N.; Maschke, D.; Koh, C.Y.; Thomas, E.L.; Tremel, W.; Butt, H.-J.; Fytas, G. One-Dimensional Hypersonic Phononic Crystals. Nano Lett. 2010, 10, 980–984. [Google Scholar] [CrossRef]
- Schneider, D.; Liaqat, F.; El Boudouti, E.H.; El Hassouani, Y.; Djafari-Rouhani, B.; Tremel, W.; Butt, H.-J.; Fytas, G. Engineering the Hypersonic Phononic Band Gap of Hybrid Bragg Stacks. Nano Lett. 2012, 12, 3101–3108. [Google Scholar] [CrossRef] [PubMed]
- Schneider, D.; Liaqat, F.; El Boudouti, E.H.; El Abouti, O.; Tremel, W.; Butt, H.-J.; Djafari-Rouhani, B.; Fytas, G. Defect-Controlled Hypersound Propagation in Hybrid Superlattices. Phys. Rev. Lett. 2013, 111, 164301. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Redondo, E.; Gueddida, A.; Huesmann, H.; El Abouti, O.; Tremel, W.; El Boudouti, E.H.; Djafari-Rouhani, B.; Fytas, G. Direction-dependent elastic properties and phononic behavior of PMMA/BaTiO3 nanocomposite thin films. J. Chem. Phys. 2017, 146, 203325. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Redondo, E.; Huesmann, H.; El Boudouti, E.-H.; Tremel, W.; Djafari-Rouhani, B.; Butt, H.-J.; Fytas, G. Phoxonic Hybrid Superlattice. ACS Appl. Mater. Interfaces 2015, 7, 12488–12495. [Google Scholar] [CrossRef]
- Matsuda, O.; Larciprete, M.C.; Voti, R.L.; Wright, O.B. Fundamentals of picosecond laser ultrasonics. Ultrasonics 2014, 56, 3–20. [Google Scholar] [CrossRef]
- Colletta, M.; Gachuhi, W.; Gartenstein, S.A.; James, M.M.; Szwed, E.A.; Daly, B.C.; Cui, W.; Antonelli, G.A. Picosecond ultrasonic study of surface acoustic waves on periodically patterned layered nanostructures. Ultrasonics 2018, 87, 126–132. [Google Scholar] [CrossRef]
- Dehoux, T.; Ghanem, M.A.; Zouani, O.F.; Ducousso, M.; Chigarev, N.; Rossignol, C.; Tsapis, N.; Durrieu, M.-C.; Audoin, B. Probing single-cell mechanics with picosecond ultrasonics. Ultrasonics 2015, 56, 160–171. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics, College ed.; Thomson Learning Inc.: Noida, India, 1976. [Google Scholar]
- Sturhahn, W.; Toellner, T.S.; Alp, E.E.; Zhang, X.; Ando, M.; Yoda, Y.; Kikuta, S.; Seto, M.; Kimball, C.W.; Dabrowski, B. Phonon Density of States Measured by Inelastic Nuclear Resonant Scattering. Phys. Rev. Lett. 1995, 74, 3832–3835. [Google Scholar] [CrossRef]
- Hess, C. Introduction to Scanning Tunneling Spectroscopy of Correlated Materials. In Quantum Materials: Experiments and Theory; Pavarini, E., Koch, E., van den Brink, J., Sawatzky, G., Eds.; Verlag des Forschungszentrum Jülich: Jülich, Germany, 2016. [Google Scholar]
- Neumaier, D.; Turek, M.; Wurstbauer, U.; Vogl, A.; Utz, M.; Wegscheider, W.; Weiss, D. All-Electrical Measurement of the Density of States in (Ga,Mn)As. Phys. Rev. Lett. 2009, 103, 087203. [Google Scholar] [CrossRef]
- Ghislotti, G.; Bottani, C.E. Brillouin scattering from shear horizontal surface phonons in silicon on insulator structures: Theory and experiment. Phys. Rev. B 1994, 50, 12131–12137. [Google Scholar] [CrossRef]
- Chirita, M.; Sooryakumar, R.; Xia, H.; Monteiro, O.R.; Brown, I.G. Observation of guided longitudinal acoustic modes in hard supported layers. Phys. Rev. B 1999, 60, R5153–R5156. [Google Scholar] [CrossRef]
- Zhang, X.; Sooryakumar, R.; Every, A.; Manghnani, M.H. Observation of organ-pipe acoustic excitations in supported thin films. Phys. Rev. B 2001, 64, 081402. [Google Scholar] [CrossRef]
- Sandercock, J.R. Structure in the Brillouin Spectra of Thin Films. Phys. Rev. Lett. 1972, 29, 1735–1738. [Google Scholar] [CrossRef]
- Djafari Rouhani, B.; Khourdifi, E.M. Light Scattering in Semiconductor Structures and Superlattices; Lockwood, D.J., Young, J.F., Eds.; Springer: New York, NY, USA, 1991. [Google Scholar]
- Cuffe, J. Phonon-Photon Interactions in Nanostructures. Ph.D. Thesis, CORK, Faculty of Science, National University of Ireland, Galway, Ireland, 2011. [Google Scholar]
- Szczurowski, M.K.; Martynkien, T.; Statkiewicz-Barabach, G.; Urbanczyk, W.; Khan, L.; Webb, D.J. Measurements of stress-optic coefficient in polymer optical fibers. Opt. Lett. 2010, 35, 2013–2015. [Google Scholar] [CrossRef] [PubMed]
- Donadio, D.; Bernasconi, M.; Tassone, F. Photoelasticity of crystalline and amorphous silica from first principles. Phys. Rev. B 2003, 68. [Google Scholar] [CrossRef]
- Yang, S.; Page, J.H.; Liu, Z.; Cowan, M.L.; Chan, C.T.; Sheng, P. Ultrasound Tunneling through 3D Phononic Crystals. Phys. Rev. Lett. 2002, 88, 104301. [Google Scholar] [CrossRef]
- Khattou, S.; Amrani, M.; Mouadili, A.; El Boudouti, E.H.; Talbi, A.; Akjouj, A.; Djafari-Rouhani, B. Comparison of density of states and scattering parameters in coaxial photonic crystals: Theory and experiment. Phys. Rev. B 2020, 102, 165310. [Google Scholar] [CrossRef]
- Graczykowski, B.; Gueddida, A.; Djafari-Rouhani, B.; Butt, H.-J.; Fytas, G. Brillouin light scattering under one-dimensional confinement: Symmetry and interference self-canceling. Phys. Rev. B 2019, 99, 165431. [Google Scholar] [CrossRef] [Green Version]

| Material | p (Kg/m3) | v (m/s) | p12 | n |
|---|---|---|---|---|
| PMMA | 1150 | 2778 | 0.3 | 1.4932 |
| Si | 2335 | 8431 | 0.01 | 3.5 − 0.26i |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Abouti, O.; Cuffe, J.; El Boudouti, E.H.; Sotomayor Torres, C.M.; Chavez-Angel, E.; Djafari-Rouhani, B.; Alzina, F. Comparison of Brillouin Light Scattering and Density of States in a Supported Layer: Analytical and Experimental Study. Crystals 2022, 12, 1212. https://doi.org/10.3390/cryst12091212
El Abouti O, Cuffe J, El Boudouti EH, Sotomayor Torres CM, Chavez-Angel E, Djafari-Rouhani B, Alzina F. Comparison of Brillouin Light Scattering and Density of States in a Supported Layer: Analytical and Experimental Study. Crystals. 2022; 12(9):1212. https://doi.org/10.3390/cryst12091212
Chicago/Turabian StyleEl Abouti, Ossama, John Cuffe, El Houssaine El Boudouti, Clivia M. Sotomayor Torres, Emigdio Chavez-Angel, Bahram Djafari-Rouhani, and Francesc Alzina. 2022. "Comparison of Brillouin Light Scattering and Density of States in a Supported Layer: Analytical and Experimental Study" Crystals 12, no. 9: 1212. https://doi.org/10.3390/cryst12091212






