X-ray Line Profile Analysis of Austenitic Phase Transition and Morphology of Nickel-Free Fe-18Cr-18Mn Steel Powder Synthesized by Mechanical Alloying
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mechanical Alloying of Powders
2.2. Morphology and Microhardness of Powders
2.3. X-ray Diffraction of Powders
3. Results and Discussion
3.1. Morphology and Microhardness of the MA Powders
3.2. Chemical Composition of Powders
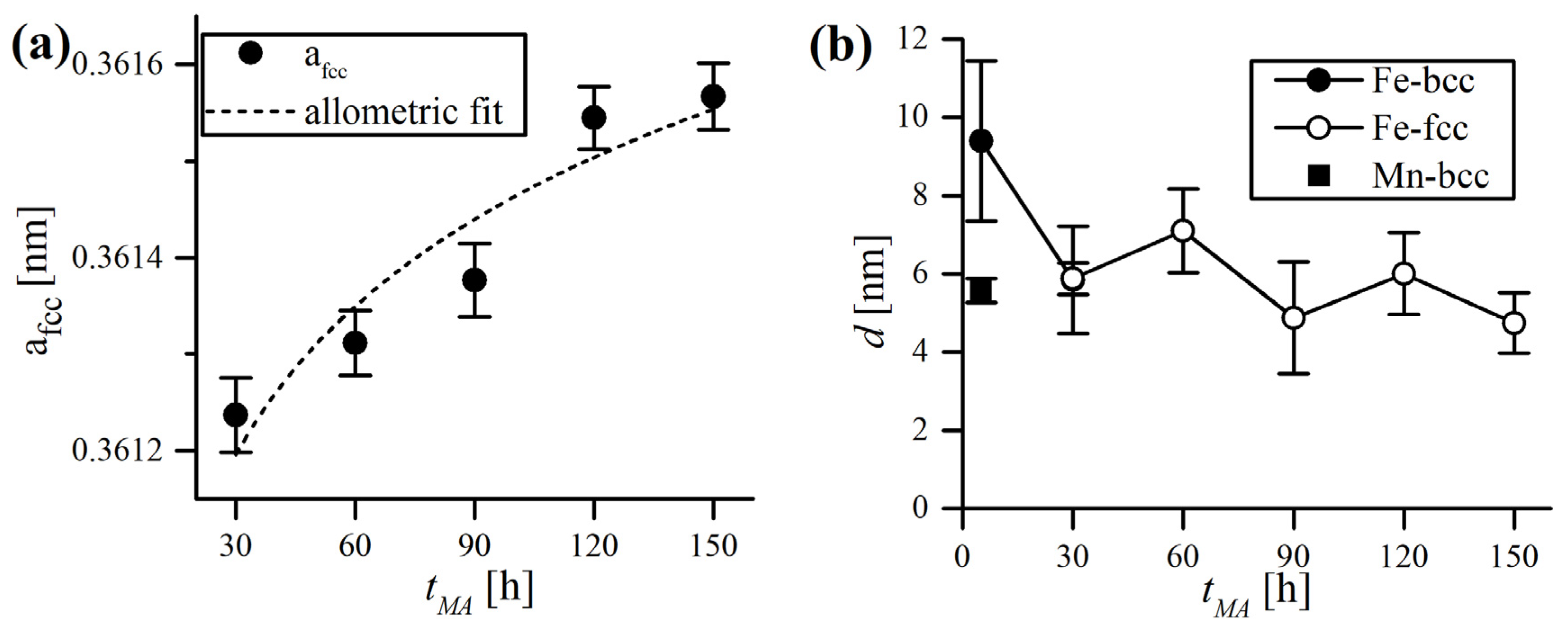
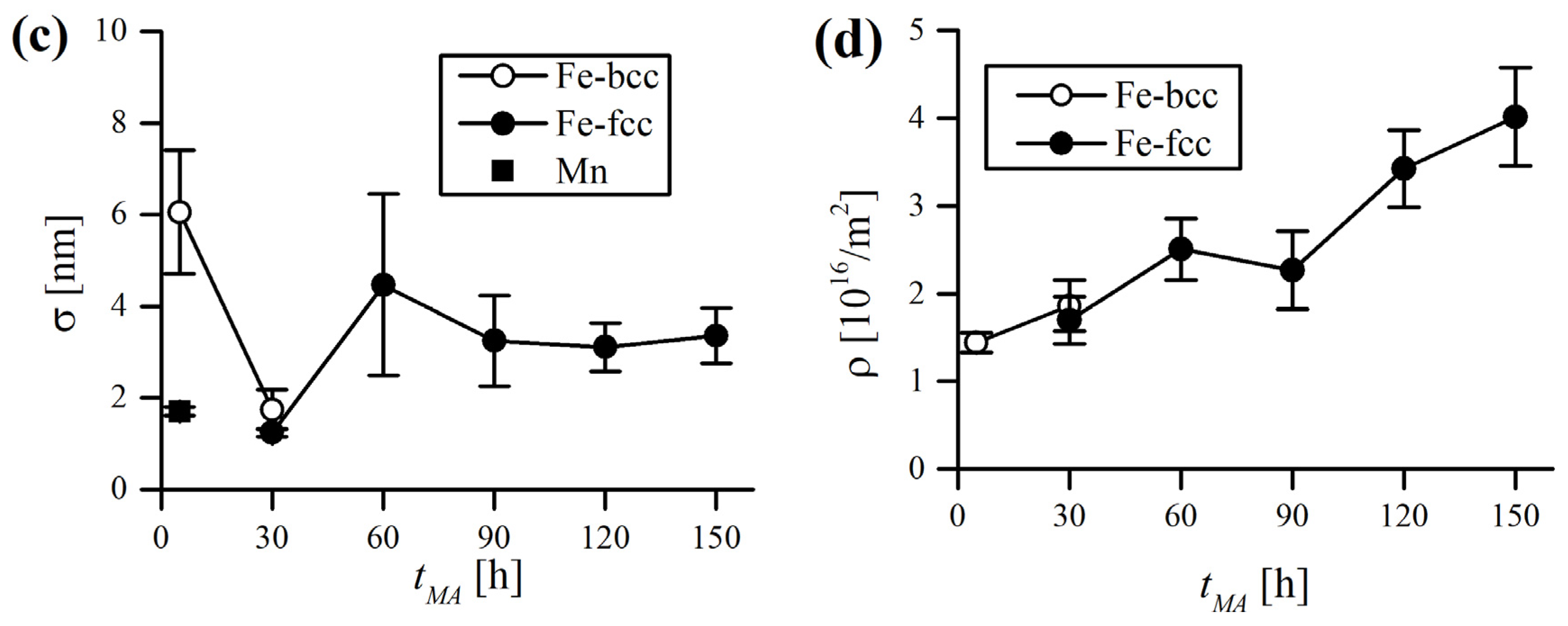
3.3. X-ray Diffraction Analysis of the Powders
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amini, R.; Salahinejad, E.; Askari Bajestani, E.; Hadianfard, M. Microstructural and hardness evolution of mechanically alloyed Fe–Cr–Mn–N. J. Alloys Compd. 2010, 497, 369–372. [Google Scholar]
- Dorofeev, G.A.; Lubnin, A.N.; Ulyanov, A.L.; Kamaeva, L.V.; Lad′yanov, V.I.; Pushkarev, E.S.; Shabashov, V.A. XRD characterization of mechanically alloyed high-nitrogen nanocrystalline Fe–Cr system. Mater. Lett. 2015, 159, 493–497. [Google Scholar] [CrossRef]
- Amornpitoksuk, P.; Suwanboon, S. Correlation of milling time on formation of TiCoSb phase by mechanical alloying. J. Alloys Compd. 2008, 462, 267–270. [Google Scholar] [CrossRef]
- Jain, A.; Agarwal, S.; Jain, I. Correlation between the milling time and hydrogen-storage properties of nanostructured ZrFeNi ternary alloy. J. Alloys Compd. 2009, 480, 325–328. [Google Scholar] [CrossRef]
- Chaisan, W.; Yimnirun, R.; Ananta, S. Effect of vibro-milling time on phase formation and particle size of barium titanate nanopowders. Ceram. Int. 2009, 35, 173–176. [Google Scholar] [CrossRef]
- Sumita, M.; Hanawa, T.; Teoh, S. Development of nitrogen-containing nickel-free austenitic stainless steels for metallic biomaterials—Review. Mater. Sci. Eng. C 2004, 24, 753–760. [Google Scholar] [CrossRef]
- Salahinejad, E.; Amini, R.; Marasi, M.; Sritharan, T.; Hadianfard, M. The effect of nitrogen on the glass-forming ability and micro-hardness of Fe–Cr–Mn–N amorphous alloys prepared by mechanical alloying. Mater. Chem. Phys. 2009, 118, 71–75. [Google Scholar] [CrossRef]
- Rawers, J.C.; Govier, D.; Doan, R. Nitrogen addition to iron powder by mechanical alloying. Mater. Sci. Eng. A 1996, 220, 162–167. [Google Scholar] [CrossRef]
- Amini, R.; Hadianfard, M.; Salahinejad, E.; Marasi, M.; Sritharan, T. Microstructural phase evaluation of high-nitrogen Fe–Cr–Mn alloy powders synthesized by the mechanical alloying process. J. Mater. Sci. 2009, 44, 136–148. [Google Scholar] [CrossRef]
- Haghir, T.; Abbasi, M.; Golozar, M.; Panjepour, M. Investigation of α to γ transformation in the production of a nanostructured high-nitrogen austenitic stainless steel powder via mechanical alloying. Mater. Sci. Eng. A 2009, 507, 144–148. [Google Scholar] [CrossRef]
- Amini, R.; Salahinejad, E.; Hadianfard, M.; Marasi, M.; Sritharan, T. Characterization of Fe–Cr–Mn–N amorphous powders with a wide supercooled liquid region developed by mechanical alloying. Mater. Sci. Eng. A 2010, 527, 1135–1142. [Google Scholar] [CrossRef]
- Tehrani, F.; Abbasi, M.; Golozar, M.; Panjepour, M. The effect of particle size of iron powder on α to γ transformation in the nanostructured high nitrogen Fe–Cr–Mn–Mo stainless steel produced by mechanical alloying. Mater. Sci. Eng. A 2011, 538, 3961–3966. [Google Scholar] [CrossRef]
- Caglioti, G.; Paoletti, A.; Ricci, F.P. Choice of Collimator for a Crystal Spectrometer for Neutron Diffraction. Nucl. Instr. Meth. 1958, 3, 223–228. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M. Fourier modelling of the anisotropic line broadening of X-ray diffraction profiles due to line and plane lattice defects. J. Appl. Crystallogr. 1999, 32, 671–682. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M.; Delhez, R. Line broadening analysis using integral breadth methods: A critical review. J. Appl. Crystallogr. 2004, 37, 381–390. [Google Scholar] [CrossRef]
- Ungár, T.; Révész, Á.; Borbély, A. Dislocations and Grain Size in Electrodeposited Nanocrystalline Ni Determined by the Modified Williamson-Hall and Warren-Averbach Procedures. J. Appl. Crystallogr. 1998, 31, 554–558. [Google Scholar] [CrossRef]
- Ungár, T.; Borbély, A. The effect of dislocation contrast on X-ray line broadening: A new approach to line profile analysis. Appl. Phys. Lett. 1996, 69, 3173–3175. [Google Scholar] [CrossRef]
- Ungár, T.; Dragomir, I.; Révész, Á.; Borbély, A. The contrast factors of dislocations in cubic crystals: The dislocation model of strain anisotropy in practice. J. Appl. Crystallogr. 1999, 32, 992–1002. [Google Scholar] [CrossRef]
- Ungár, T.; Tichy, G. The Effect of Dislocation Contrast on X-Ray Line Profiles in Untextured Polycrystals. Phys. Status Solidi A 1999, 171, 425–434. [Google Scholar] [CrossRef]
- Ustinov, A.I.; Polishchuk, S.S.; Demchenkov, S.A.; Petrushinets, L.V. Effect of microstructure of vacuum-deposited Fe100-xNix (30 < x < 39) foils with FCC structure on their mechanical properties. J. Alloys Compd. 2015, 622, 54–61. [Google Scholar]
- Adams, J.J.; Agosta, D.S.; Leisure, R.G.; Ledbetter, H.M. Elastic constants of monocrystal iron from 3 to 500 K. J. Appl. Phys. 2006, 100, 113530. [Google Scholar] [CrossRef]
- Razumovskiy, I.V.; Hahn, C.; Lukas, M.; Romaner, L. Ab Initio Study of Elastic and Mechanical Properties in FeCrMn Alloys. Materials 2019, 12, 1129. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://metal.elte.hu/anizc/ (accessed on 22 August 2022).
- Rebuffi, L.; Troian, A.; Ciancio, R.; Carlino, E.; Amimi, A.; Leonardi, A.; Scardi, P. On the reliability of powder diffraction Line Profile Analysis of plastically deformed nanocrystalline systems. Sci. Rep. 2016, 6, 20712. [Google Scholar] [CrossRef] [PubMed]
- Langford, J.I.; Louër, D.; Scardi, P. Effect of a crystallite size distribution on X-ray diffraction line profiles and whole-powder-pattern fitting. J. Appl. Crystallogr. 2000, 33, 964–974. [Google Scholar] [CrossRef]
- Wilkens, M. The Determination of Density and Distribution of Dislocations in Deformed Single Crystals from Broadened X-ray Diffraction Profiles. Phys. Stat. Sol. 1970, 2, 359–370. [Google Scholar] [CrossRef]
- Scardi, P.; Leoni, M. In Diffraction Analysis of the Microstructure of Materials; Mittemeijer, E.J., Scardi, P., Eds.; Springer: New York, NY, USA, 2004; pp. 51–91. ISBN 978-3-642-07352-6. [Google Scholar]
- Scardi, P.; Leoni, M. Whole powder pattern modelling. Acta Crystallogr. A 2002, 58, 190–200. [Google Scholar] [CrossRef]
- Leoni, M.; Scardi, P. Nanocrystalline domain size distributions from powder diffraction data. J. Appl. Cryst. 2004, 37, 629–634. [Google Scholar] [CrossRef]
- Ribárik, G.; Jóni, B.; Ungár, T. The Convolutional Multiple Whole Profile (CMWP) Fitting Method, a Global Optimization Procedure for Microstructure Determination. Crystals 2020, 10, 623. [Google Scholar] [CrossRef]
- Leoni, M.; Confente, T.; Scardi, P. PM2K: A flexible program implementing Whole Powder Pattern Modelling. Z. Krist. Suppl. 2006, 23, 249–254. [Google Scholar] [CrossRef]
- Suryanarayana, C. Mechanical alloying and milling. Prog. Mater. Sci. 2001, 46, 1–184. [Google Scholar] [CrossRef]
- Cisneros, M.M.; Valdes, E.; Vazquez, D.; Lopez, H.F.; Mancha, H.; Mendoza, G.; Mendez, M. Development of austenitic nanostructures in High-nitrogen steel powders processed by mechanical alloying. Metall. Mater. Trans. A 2002, 33, 2139–2144. [Google Scholar] [CrossRef]
- Duan, C.; Chen, C.; Zhang, J.; Shen, Y.; Feng, X. Nitriding of Fe-18Cr-8Mn stainless steel powders by mechanical alloying method with dual nitrogen source. Powder Technol. 2016, 294, 330–337. [Google Scholar] [CrossRef]
- Eliades, T.; Pratsinis, H.; Kletsas, D.; Eliades, G.; Makou, M. Characterization and cytotoxicity of ions released from stainless steel and nickel-titanium orthodontic alloys. Am. J. Orthod. Dentofac. Orthop. 2004, 125, 24–29. [Google Scholar] [CrossRef]
- Salahinejad, E.; Amini, R.; Hadianfard, M.J. Structural evolution during mechanical alloying of stainless steels under nitrogen. Powder Technol. 2012, 215, 247–253. [Google Scholar] [CrossRef]
- Ahmed, A.; Ghali, S.; Eissa, M.; El Badry, S. Influence of Partial Replacement of Nickel by Nitrogen on Microstructure and Mechanical Properties of Austenitic Stainless Steel. J. Metall. 2011, 2011, 639283. [Google Scholar] [CrossRef]
- Borbély, A. The modified Williamson-Hall plot and dislocation density evaluation from diffraction peaks. Scr. Mater. 2022, 217, 114768. [Google Scholar] [CrossRef]
- Kumari, S.; Singh, D.K.; Giri, P.K. Strain Anisotropy in Freestanding Germanium Nanoparticles Synthesized by Ball Milling. J. Nanosci. Nanotechnol. 2009, 9, 5231–5236. [Google Scholar] [CrossRef]
- Swygenhoven, H.; Weertman, J.R. Grain boundaries and dislocations. Science 2002, 296, 66–67. [Google Scholar] [CrossRef]
- Seelam, U.M.R.; Suryanarayana, C. Mechanically induced fcc phase formation in nanocrystalline hafnium. J. Appl. Phys. 2009, 105, 063524. [Google Scholar] [CrossRef]
- Loudjani, N.; Benchiheub, M.; Bououdina, M. Structural, Thermal and Magnetic Properties of Nanocrystalline Co80Ni20 Alloy Prepared by Mechanical Alloying. J. Supercond. Nov. Magn. 2016, 29, 2717–2726. [Google Scholar] [CrossRef]
- Mhadhbi, M.; Khitouni, M.; Escoda, L.; Suñol, J.J.; Dammak, M. Characterization of Mechanically Alloyed Nanocrystalline Fe(Al): Crystallite Size and Dislocation Density. J. Nanomater. 2010, 2010, 712407. [Google Scholar] [CrossRef]
- Nazarov, A.A.; Romanov, A.E.; Valiev, R.Z. Disclination ensembles in ultrafine-grained materials produced by severe plastic deformation. Scr. Mater. 1996, 34, 729–734. [Google Scholar] [CrossRef]
- Rawers, J.; Cook, D. Influence of attrition milling on nano-grain boundaries. Nanostruct. Mater. 1999, 11, 331–342. [Google Scholar] [CrossRef]
- Seif, D.; Po, G.; Mrovec, M.; Lazar, M.; Elsässer, C.; Gumbsch, P. Atomistically enabled nonsingular anisotropic elastic representation of near-core dislocation stress fields in α-iron. Phy. Rev. B 2015, 91, 184102. [Google Scholar] [CrossRef]
- Leonardi, A.; Scardi, P. Dislocation effects on the diffraction line profiles from nanocrystalline domains. Metall. Mater. Trans. A 2016, 47, 5722–5732. [Google Scholar] [CrossRef] [Green Version]

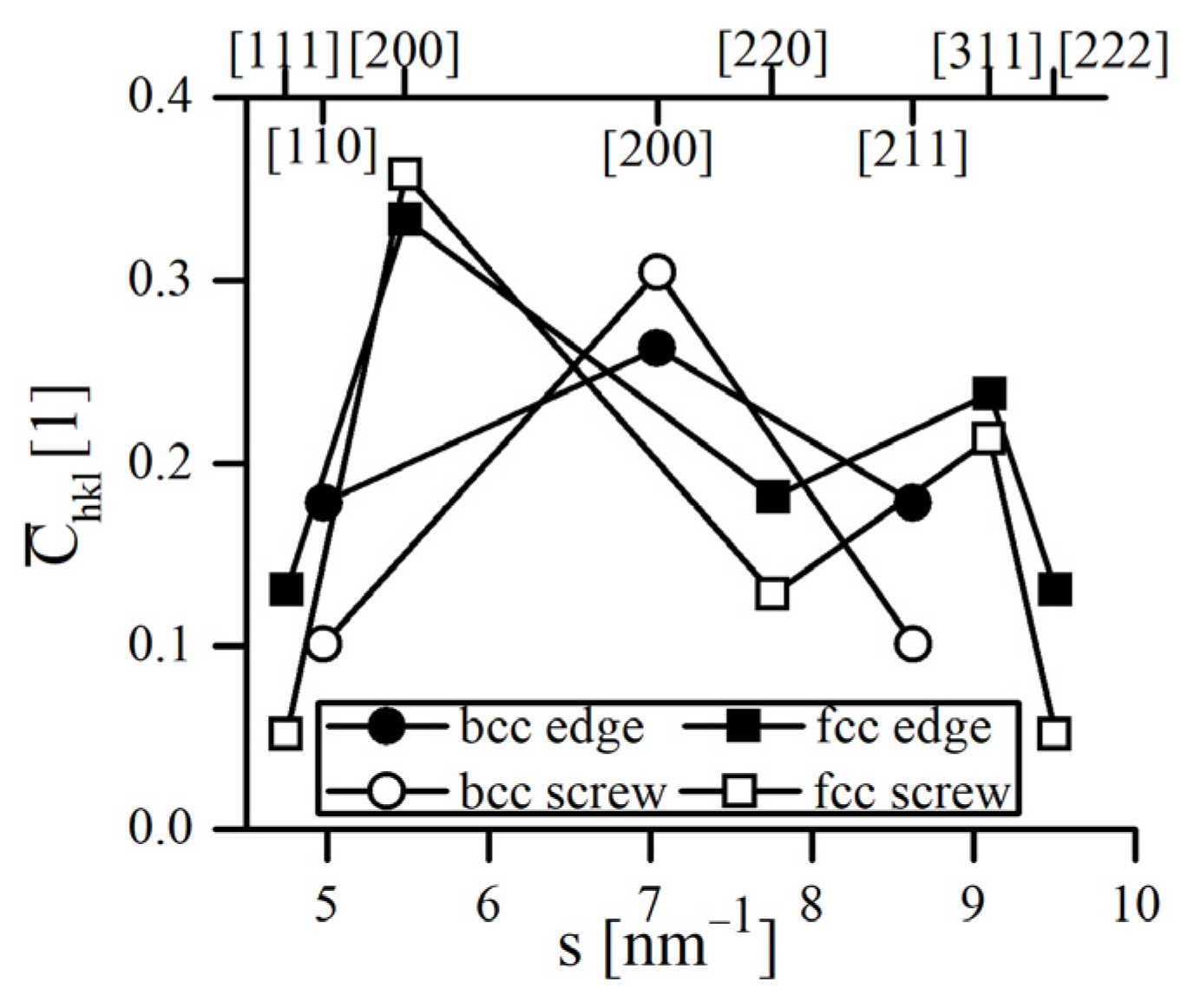



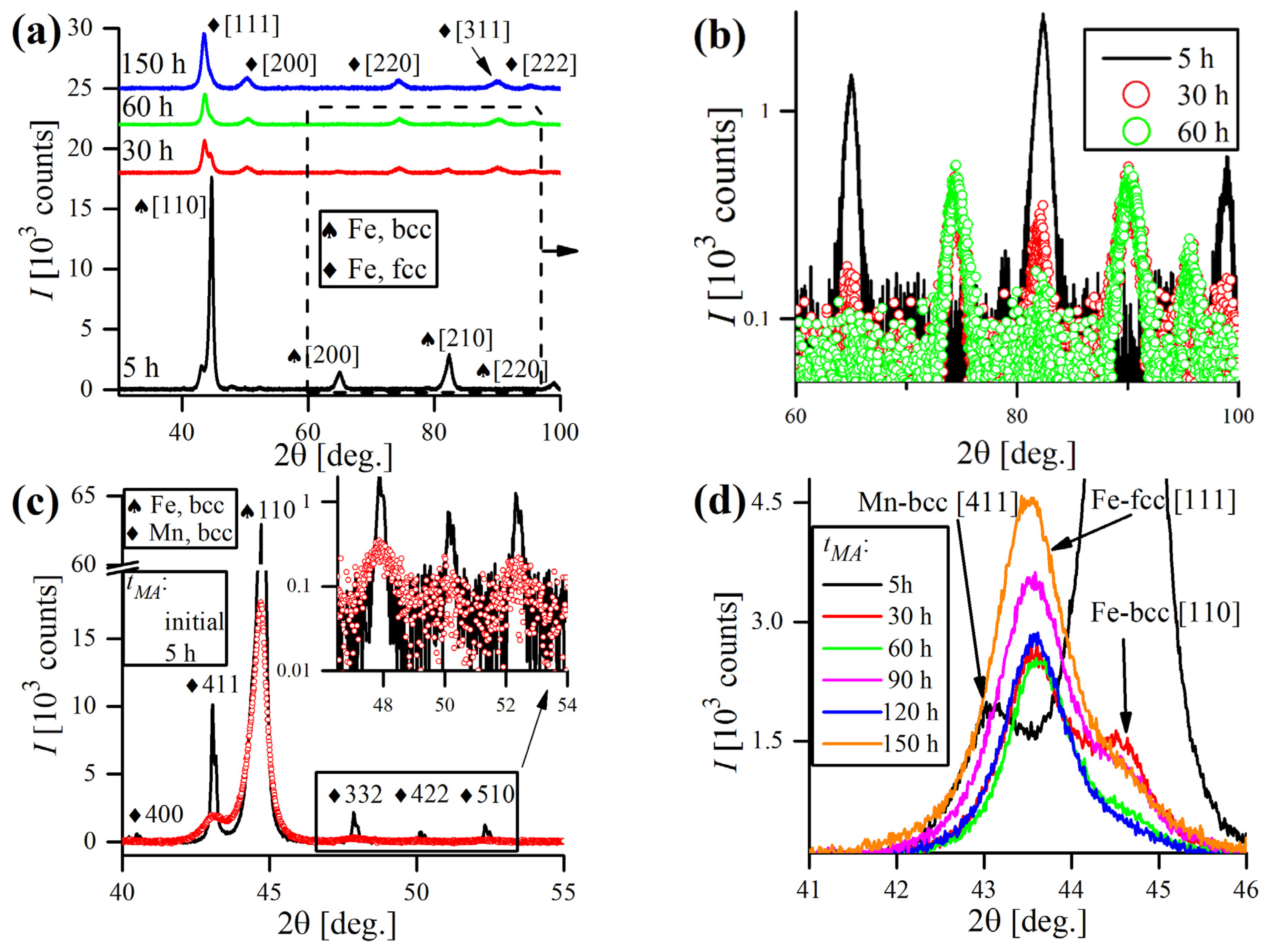
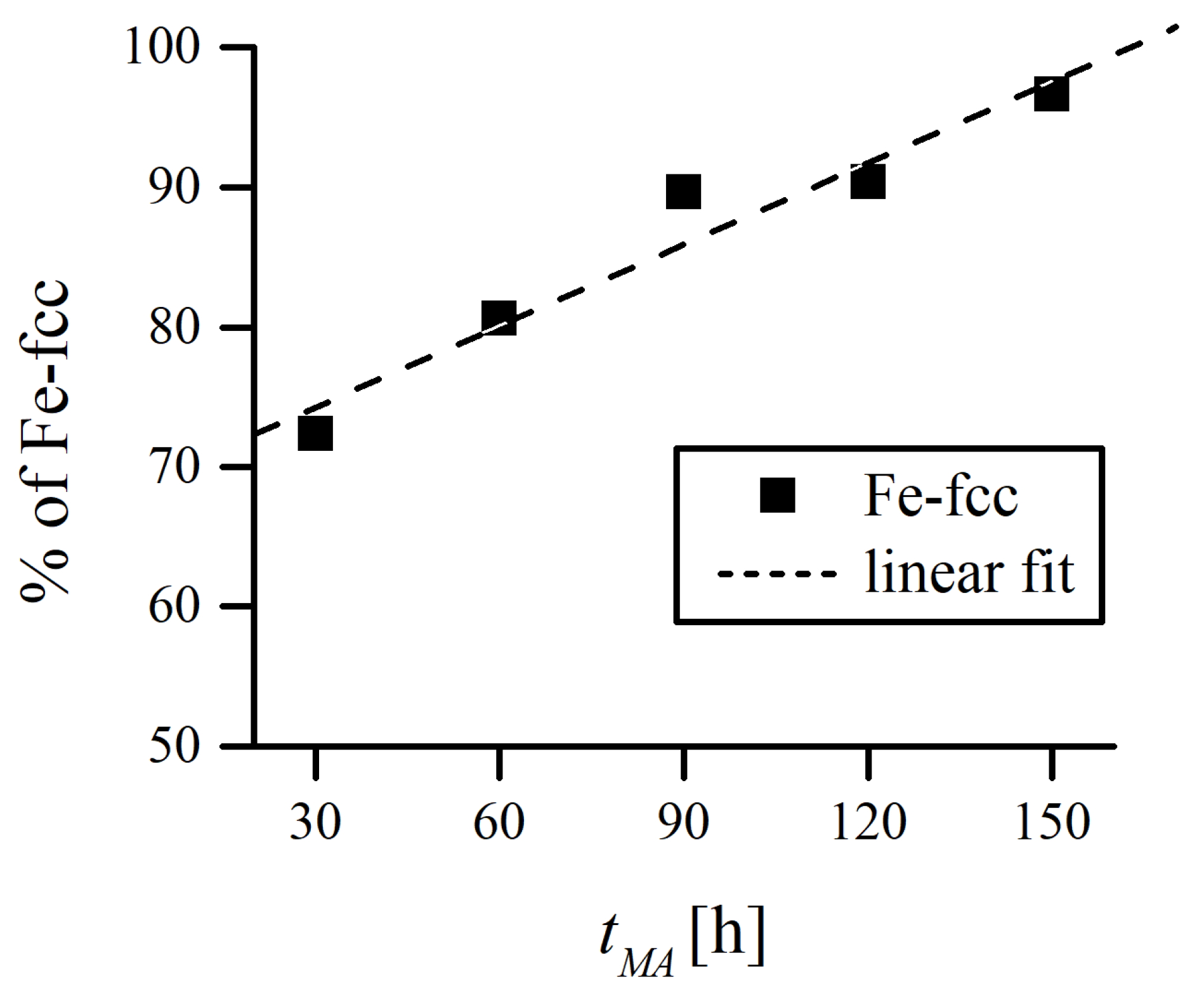

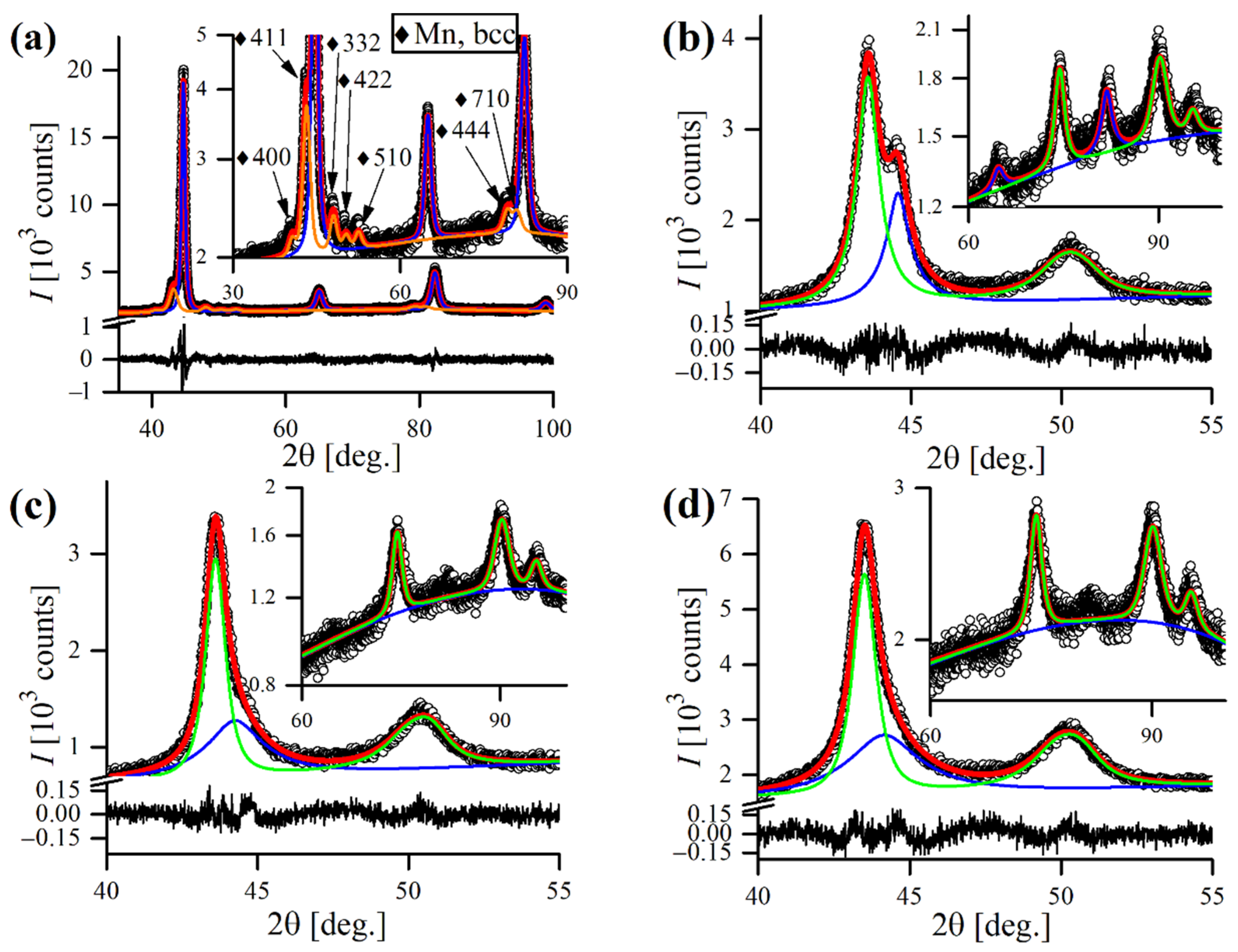



| Parameter | Fe, bcc | Fe-18Cr-18Mn, fcc |
|---|---|---|
| 230 | 219 | |
| 134 | 153 | |
| 116 | 152 | |
| 2.417 | 4.606 | |
| 0.403834 | 0.333565 | |
| 0.361353 | 0.357697 | |
| 0.721 | 1.821 | |
| 2.597 | 2.561 |
| Milling Time (h) | Element Composition (wt. %) | ||||
|---|---|---|---|---|---|
| Fe | Cr | Mn | N | C | |
| 30 | 72.04 ± 3.46 | 12.28 ± 1.25 | 15.67 ± 0.89 | 0.12 ± 0.03 | 0.01 ± 0.01 |
| 60 | 67.08 ± 2.32 | 16.18 ± 0.86 | 16.74 ± 1.58 | 0.28 ± 0.05 | 0.015 ± 0.006 |
| 90 | 64.21 ± 3.86 | 17.86 ± 0.98 | 17.93 ± 2.03 | 0.35 ± 0.01 | 0.016 ± 0.003 |
| 120 | 64.33 ± 1.02 | 17.66 ± 1.53 | 18.01 ± 0.99 | 0.68 ± 0.08 | 0.023 ± 0.007 |
| 150 | 64.22 ± 2.29 | 17.92 ± 1.37 | 17.86 ± 1.24 | 0.93 ± 0.09 | 0.029 ± 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanczuk-Ruszuk, E.; Nowik, K.; Sztorch, B. X-ray Line Profile Analysis of Austenitic Phase Transition and Morphology of Nickel-Free Fe-18Cr-18Mn Steel Powder Synthesized by Mechanical Alloying. Crystals 2022, 12, 1233. https://doi.org/10.3390/cryst12091233
Romanczuk-Ruszuk E, Nowik K, Sztorch B. X-ray Line Profile Analysis of Austenitic Phase Transition and Morphology of Nickel-Free Fe-18Cr-18Mn Steel Powder Synthesized by Mechanical Alloying. Crystals. 2022; 12(9):1233. https://doi.org/10.3390/cryst12091233
Chicago/Turabian StyleRomanczuk-Ruszuk, Eliza, Krzysztof Nowik, and Bogna Sztorch. 2022. "X-ray Line Profile Analysis of Austenitic Phase Transition and Morphology of Nickel-Free Fe-18Cr-18Mn Steel Powder Synthesized by Mechanical Alloying" Crystals 12, no. 9: 1233. https://doi.org/10.3390/cryst12091233
APA StyleRomanczuk-Ruszuk, E., Nowik, K., & Sztorch, B. (2022). X-ray Line Profile Analysis of Austenitic Phase Transition and Morphology of Nickel-Free Fe-18Cr-18Mn Steel Powder Synthesized by Mechanical Alloying. Crystals, 12(9), 1233. https://doi.org/10.3390/cryst12091233







