Structural, Mechanical, Electronic, Optical, and Thermodynamic Properties of New Oxychalcogenide A2O2B2Se3 (A = Sr, Ba; B = Bi, Sb) Compounds: A First-Principles Study
Abstract
:1. Introduction
2. Computational Methodology
3. Results and Discussion
3.1. Crystal Structure
3.2. Mechanical Properties
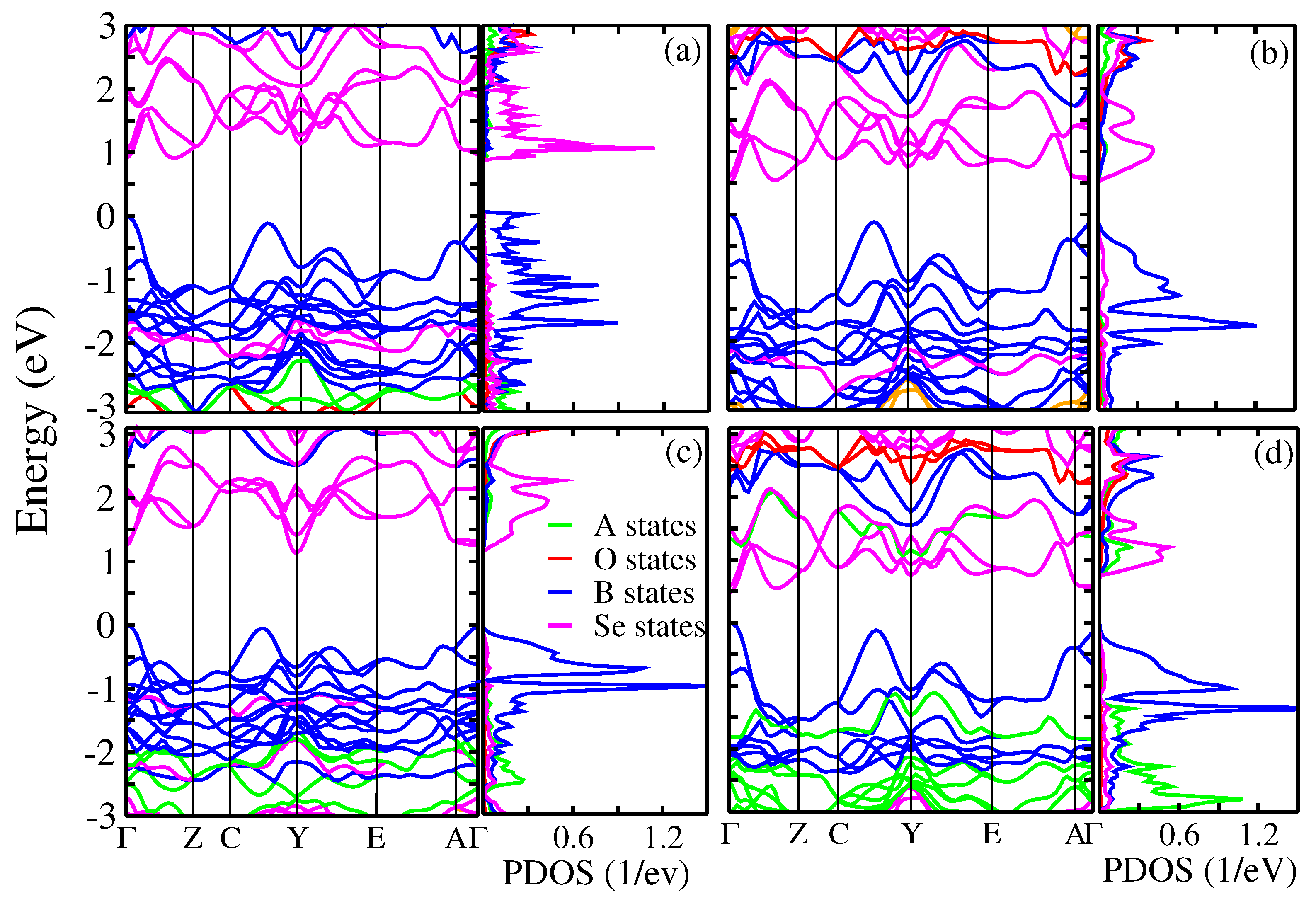
3.3. Electronic Structure
3.4. Optical Properties
3.5. Thermodynamic Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; McClain, R.; Shen, J.; He, J.; Malliakas, C.D.; Spanopoulos, I.; Zhang, C.; Zhao, C.; Wang, Y.; Li, Q.; et al. Christopher Wolverton, and Mercouri G. Kanatzidis. Inorg. Chem. 2022, 61, 8240. [Google Scholar]
- Njema, H.; Debbichi, M.; Boughzala, K.; Said, M.; Bouzouita, K. Structural, electronic and thermodynamic properties of britholites Ca10–xLax (PO4)6–x(SiO4)xF2(0 ≤ x ≥ 6): Experiment and theory. Mater. Res. Bull. 2014, 51, 216. [Google Scholar] [CrossRef]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-Based Layered Superconductor La[O1–xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef] [PubMed]
- Zagorac, D.; Doll, K.; Zagorac, J.; Jordanov, D.; Matović, B. Barium sulfide under pressure: Discovery of metastable polymorphs and investigation of electronic properties on ab initio level. Inorg. Chem. 2017, 56, 10644–10654. [Google Scholar] [CrossRef]
- Wang, R.; Zhao, Y.; Zhang, X.; Huang, F. Structural dimension modulation in a new oxysulfide system of Ae2Sb2O2S3 (Ae = Ca and Ba). Inorg. Chem. Front. 2022, 9, 3552–3558. [Google Scholar] [CrossRef]
- Zhu, W.J.; Hor, P.H.; Jacobson, A.J.; Crisci, G.; Albright, T.A.; Wang, S.-H.; Vogt, T. A2Cu2CoO2S2 (A = Sr, Ba), a novel example of a square-planar CoO2 layer. J. Am. Chem. Soc. 1997, 119, 12398–12399. [Google Scholar] [CrossRef]
- Zhu, W.J.; Hor, P.H. Unusual layered transition-metal oxysulfides: Sr2Cu2MO2S2 (M = Mn, Zn). J. Solid State Chem. 1997, 130, 319–321. [Google Scholar] [CrossRef]
- Zhao, J.; Islam, S.M.; Kontsevoi, O.Y.; Tan, G.; Stoumpos, C.C.; Chen, H.; Li, R.K.; Kanatzidis, M.G. The Two-Dimensional AxCdxBi4–xQ6 (A = K, Rb, Cs; Q = S, Se): Direct Bandgap Semiconductors and Ion-Exchange Materials. J. Am. Chem. Soc. 2017, 139, 6978–6987. [Google Scholar] [CrossRef]
- Pacquette, A.L.; Hagiwara, H.; Ishihara, T.; Gewirth, A.A. Fabrication of an oxysulfide of bismuth Bi2O2S and its photocatalytic activity in a Bi2O2S/In2O3 composite. J. Photochem. Photobiol. A 2014, 277, 27–36. [Google Scholar] [CrossRef]
- Ruleova, P.; Drasar, C.; Lostak, P.; Li, C.-P.; Ballikaya, S.; Uher, C. Thermoelectric properties of Bi2O2Se. Mater. Chem. Phys. 2010, 119, 299–302. [Google Scholar] [CrossRef]
- Yazici, D.; Huang, K.; White, B.D.; Chang, A.H.; Friedman, A.J.; Maple, M.B. Superconductivity of F-substituted Ln OBiS2 (Ln = La, Ce, Pr, Nd, Yb) compounds. Philos. Mag. 2013, 93, 673–680. [Google Scholar] [CrossRef]
- Panella, J.R.; Chamorro, J.; McQueen, T.M. Synthesis and Structure of Three New Oxychalcogenides: A2O2Bi2Se3 (A= Sr, Ba) and Sr2O2Sb2Se3. Chem. Mater. 2016, 28, 890–895. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Mat. 2009, 21, 395502. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Wisesa, P.; McGill, K.A.; Mueller, T. Efficient generation of generalized Monkhorst-Pack grids through the use of informatics. Phys. Rev. B 2016, 93, 155109. [Google Scholar] [CrossRef] [Green Version]
- Yates, J.R.; Pickard, C.J.; Mauri, F. Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B 2007, 76, 024401. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616. [Google Scholar] [CrossRef] [Green Version]
- Baerends, E.J. Perspective on “Self-consistent equations including exchange and correlation effects”. Theor. Chem. Acc. 2000, 103, 265–269. [Google Scholar] [CrossRef]
- Mokhtari, A.; Ribeiro, A. Global Convergence of Online Limited Memory BFGS. J. Mach. Learn. Res. 2015, 16, 3151–3181. [Google Scholar]
- Iuga, M.; Neumann, G.S.; Meinhardt, J. Ab-initio simulation of elastic constants for some ceramic materials. Eur. Phys. J. B 2007, 58, 127–133. [Google Scholar] [CrossRef]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comp. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Debbichi, M.; Alresheedi, F. First-principles calculations of mechanical, electronic and optical properties of a new imidooxonitridophosphate. Chem. Phys. 2020, 538, 110917. [Google Scholar] [CrossRef]
- Voigt, W. Lehrburch der Kristallphys; Teubner Press: Leipzig, Germany, 1928. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. Z. angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Lond. 1952, 65, 349. [Google Scholar]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philosoph. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Saha, S.; Sinha, T.P.; Mookerjee, A. Electronic structure, chemical bonding, and optical properties of paraelectric BaTiO3. Phys. Rev. B 2000, 62, 8828. [Google Scholar] [CrossRef]
- Wooten, F. Optical Properties of Solids; Academic: New York, NY, USA, 1972. [Google Scholar]
- Yu, Y.P.; Cardona, M. Fundamentals of Semiconductors: Physics and Materials Properties, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Ravindran, P.; Delin, A.; James, P.; Johansson, B.; Wills, J.M.; Ahuja, R.; Eriksson, O. Magnetic, optical, and magneto-optical properties of MnX (X = As, Sb, or Bi) from full-potential calculations. Phys. Rev. B 1999, 59, 15680. [Google Scholar] [CrossRef] [Green Version]
- Fox, M. Optical Properties of Solids; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Screiber, E.; Anderson, O.L.; Soga, N. Elastic Constants and Their Measurement; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Duan, Y.H.; Huang, B.; Sun, Y.; Peng, M.J.; Zhou, S.G. Stability, elastic properties and electronic structures of the stable Zr–Al intermetallic compounds: A first-principles investigation. J. Alloys Compd. 2014, 590, 50–60. [Google Scholar] [CrossRef]
- Hu, W.C.; Liu, Y.; Li, D.J.; Zeng, X.Q.; Xu, C.S. First-principles study of structural and electronic properties of C14-type Laves phase Al2Zr and Al2Hf. Comput. Mater. Sci. 2014, 83, 27–34. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M.; Luo, X. Theoretical investigations on phase stability, elastic constants and electronic structures of D022-and L12-Al3Ti under high pressure. J. Alloys Compd. 2013, 556, 214–220. [Google Scholar] [CrossRef]
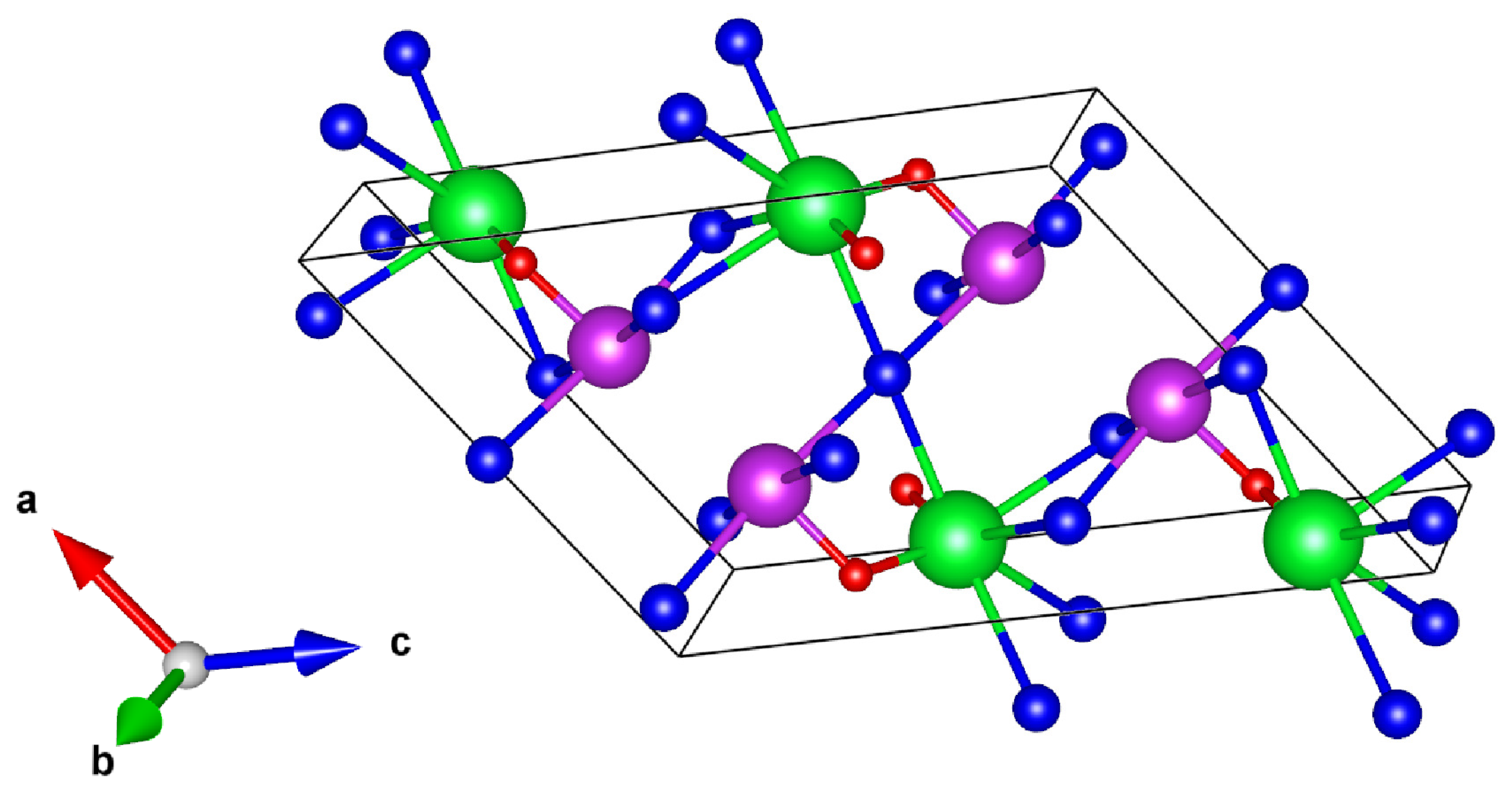

| SrOBiSe | SrOSbSe | BaOBiSe | BaOSbSe | |
|---|---|---|---|---|
| 9.200 | 9.199 | 9.463 | 9.729 | |
| 9.499 | 9.424 | 9.820 | - | |
| 4.005 | 3.957 | 4.095 | 4.122 | |
| 4.084 | 4.057 | 4.190 | - | |
| 13.111 | 12.987 | 13.535 | 13.723 | |
| 13.437 | 13.341 | 13.904 | - | |
| 122.828 | 123.000 | 123.298 | 124.040 | |
| 122.861 | 121.955 | 123.692 | - | |
| E | −2.145 | −2.173 | −2.139 | −2.147 |
| SrOBiSe | SrOSbSe | BaOBiSe | BaOSbSe | |
|---|---|---|---|---|
| 106.86 | 107.04 | 102.65 | 54.30 | |
| 133.74 | 137.47 | 125.26 | 108.80 | |
| 122.92 | 126.51 | 118.39 | 109.62 | |
| 39.56 | 35.86 | 51.37 | 43.83 | |
| 32.48 | 34.53 | 31.00 | 29.42 | |
| 26.02 | 28.87 | 26.00 | 28.07 | |
| 31.42 | 31.87 | 32.16 | 22.79 | |
| 35.93 | 36.20 | 35.23 | 26.23 | |
| 56.48 | 55.99 | 57.86 | 46.94 | |
| 5.37 | 4.85 | 6.93 | 4.14 | |
| 2.10 | 1.05 | 5.57 | 11.66 | |
| 10.66 | 12.69 | 6.35 | 9.04 | |
| 0.48 | 2.40 | 2.10 | 3.14 |
| B | G | E | D | Type | ||
|---|---|---|---|---|---|---|
| SrOBiSe | 66.523 | 34.755 | 88.801 | 0.277 | 1.914 | ductile |
| SrOSbSe | 67.333 | 35.566 | 90.723 | 0.275 | 1.893 | ductile |
| BaOBiSe | 64.817 | 35.201 | 89.417 | 0.270 | 1.841 | ductile |
| BaOSbSe | 46.913 | 30.764 | 75.737 | 0.230 | 1.525 | brittle |
| SrOBiSe | 260.55 | 4000.36 | 2219.89 | 2472.64 |
| SrOSbSe | 293.61 | 4463.99 | 2482.98 | 2765.16 |
| BaOBiSe | 250.38 | 3918.86 | 2189.84 | 2437.81 |
| BaOSbSe | 255.84 | 3833.41 | 2245.95 | 2490.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallah, A.; Debbichi, M.; Dhaou, M.H.; Bellakhdhar, B. Structural, Mechanical, Electronic, Optical, and Thermodynamic Properties of New Oxychalcogenide A2O2B2Se3 (A = Sr, Ba; B = Bi, Sb) Compounds: A First-Principles Study. Crystals 2023, 13, 122. https://doi.org/10.3390/cryst13010122
Mallah A, Debbichi M, Dhaou MH, Bellakhdhar B. Structural, Mechanical, Electronic, Optical, and Thermodynamic Properties of New Oxychalcogenide A2O2B2Se3 (A = Sr, Ba; B = Bi, Sb) Compounds: A First-Principles Study. Crystals. 2023; 13(1):122. https://doi.org/10.3390/cryst13010122
Chicago/Turabian StyleMallah, Abdulrahman, Mourad Debbichi, Mohamed Houcine Dhaou, and Bilel Bellakhdhar. 2023. "Structural, Mechanical, Electronic, Optical, and Thermodynamic Properties of New Oxychalcogenide A2O2B2Se3 (A = Sr, Ba; B = Bi, Sb) Compounds: A First-Principles Study" Crystals 13, no. 1: 122. https://doi.org/10.3390/cryst13010122
APA StyleMallah, A., Debbichi, M., Dhaou, M. H., & Bellakhdhar, B. (2023). Structural, Mechanical, Electronic, Optical, and Thermodynamic Properties of New Oxychalcogenide A2O2B2Se3 (A = Sr, Ba; B = Bi, Sb) Compounds: A First-Principles Study. Crystals, 13(1), 122. https://doi.org/10.3390/cryst13010122






