A Stochastic Thermo-Mechanical Waves with Two-Temperature Theory for Electro-Magneto Semiconductor Medium
Abstract
:1. Introduction
2. Basic Equations
3. Formulation of the Problem
4. Solution of the Problem
5. Applications
6. Stochastic Main Physical Fields
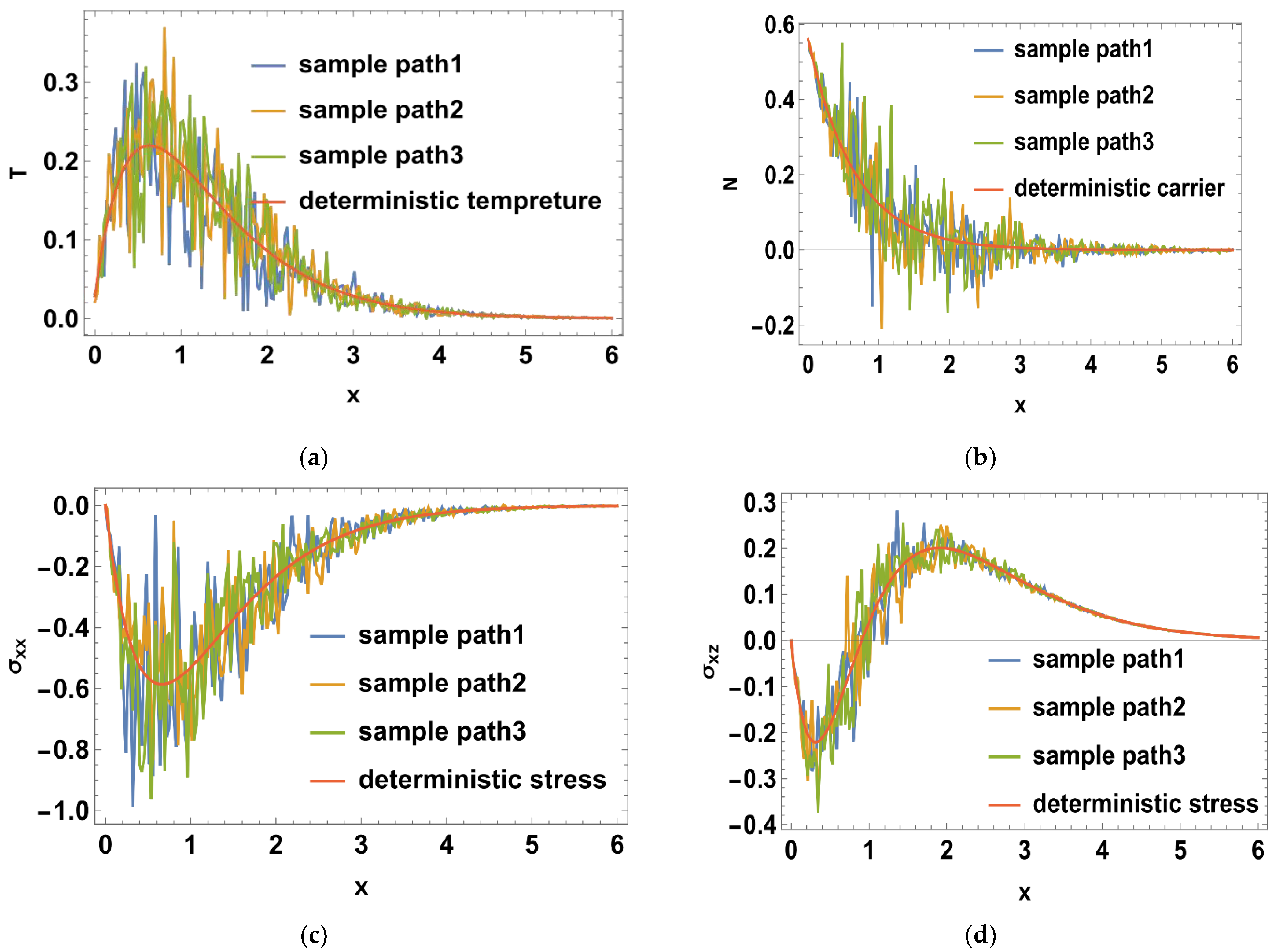
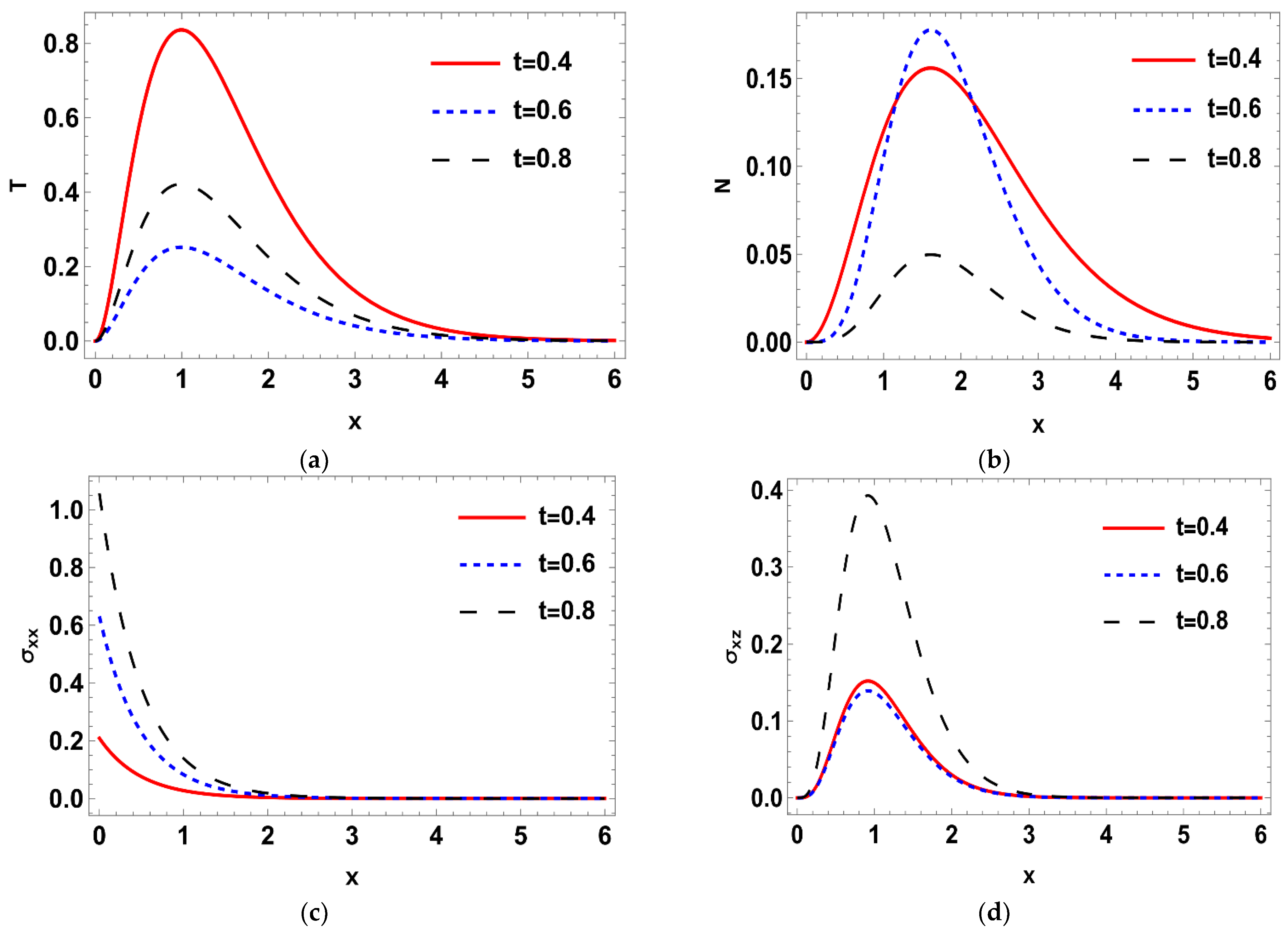
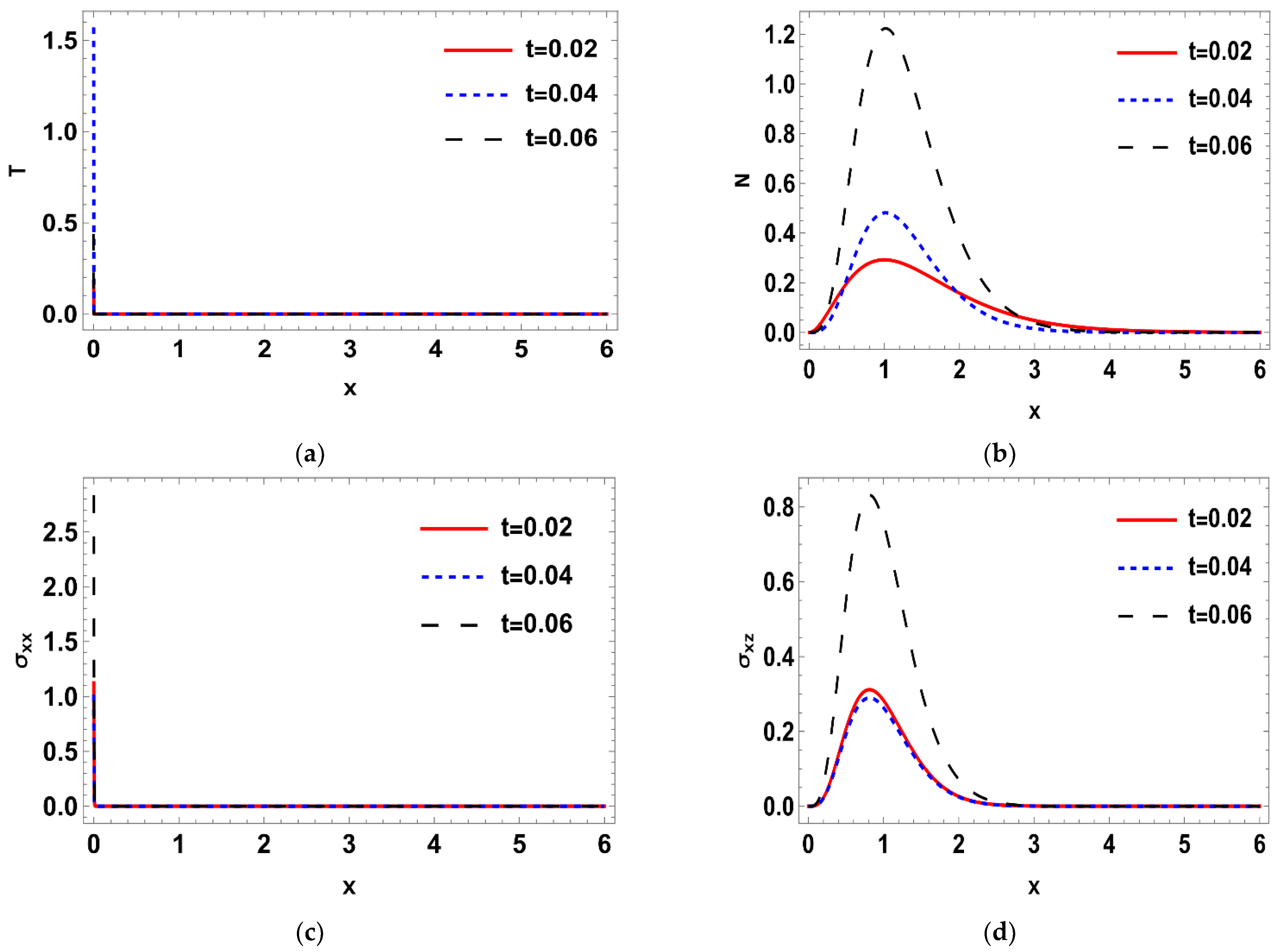
6.1. Stochastic Temperature (Thermal Wave)
6.2. Deterministic Stress Distribution
6.3. Stochastic Stress Distribution
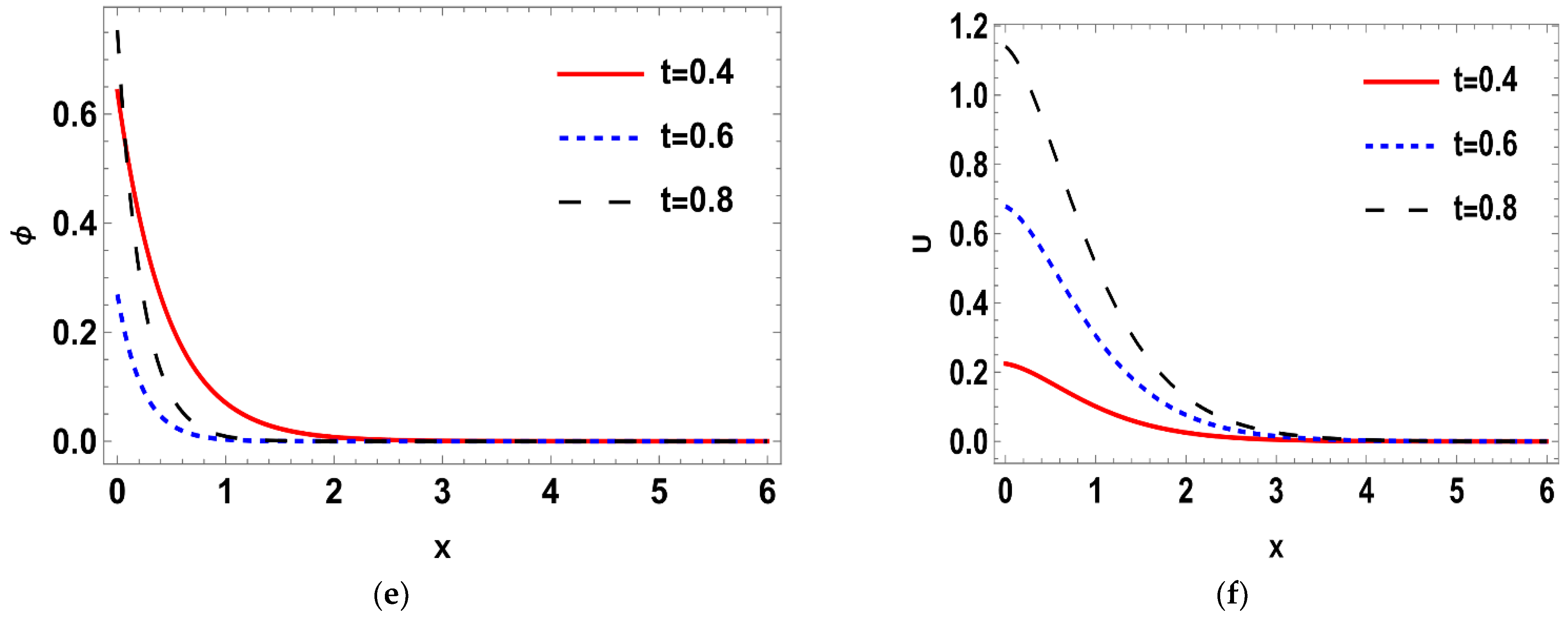
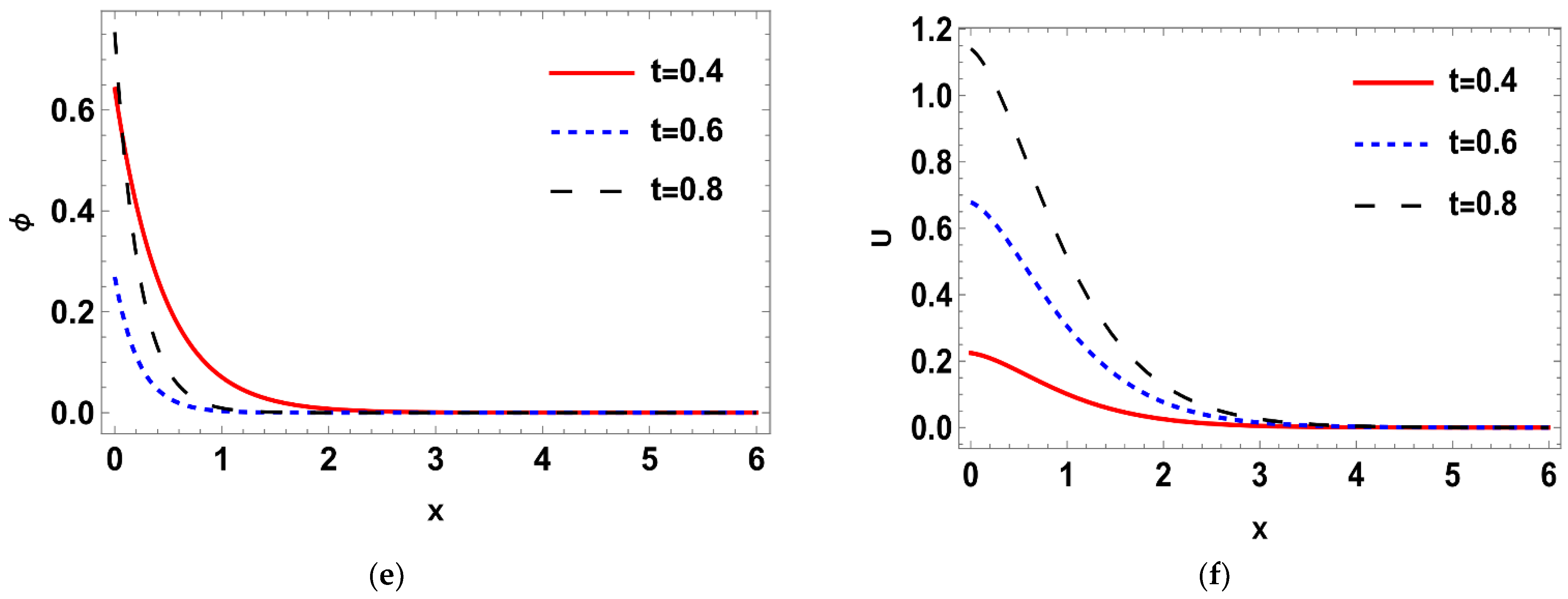
6.4. Deterministic Displacement Distribution
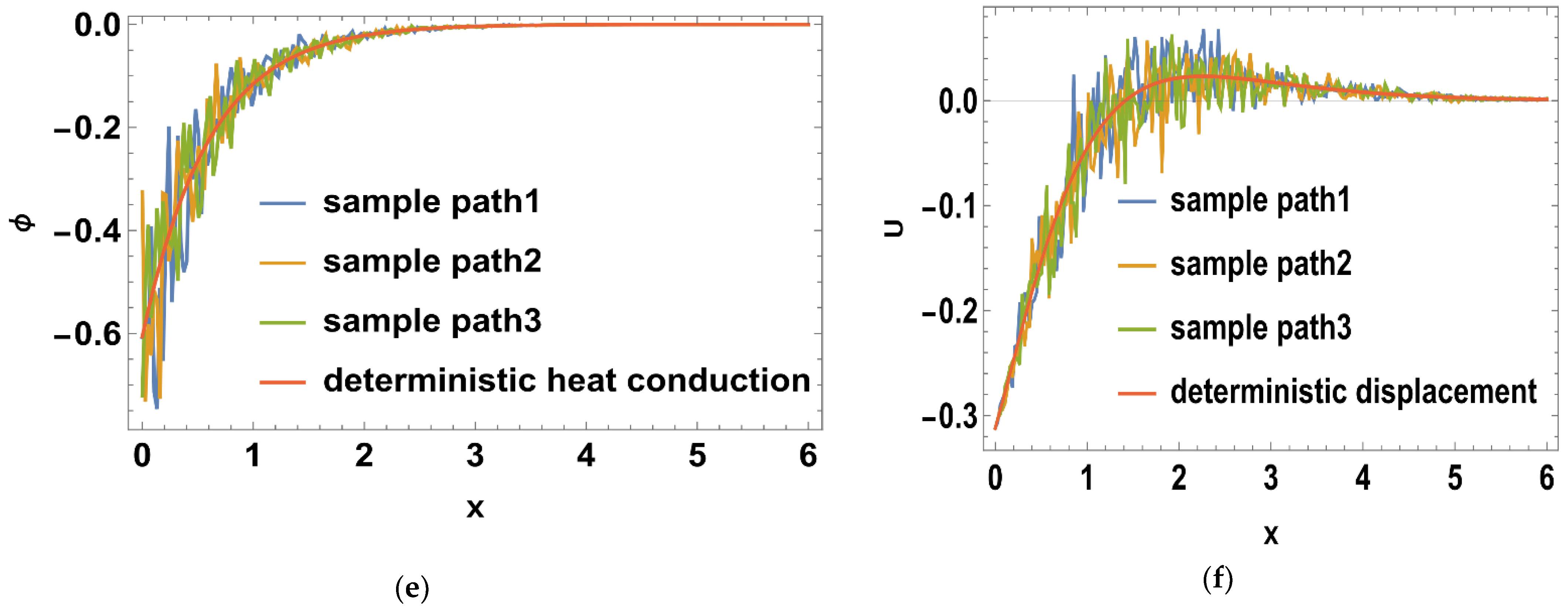
6.5. Stochastic Displacement Distribution
6.6. Deterministic Carrier Density Distribution
6.7. Stochastic Carrier Density Distribution
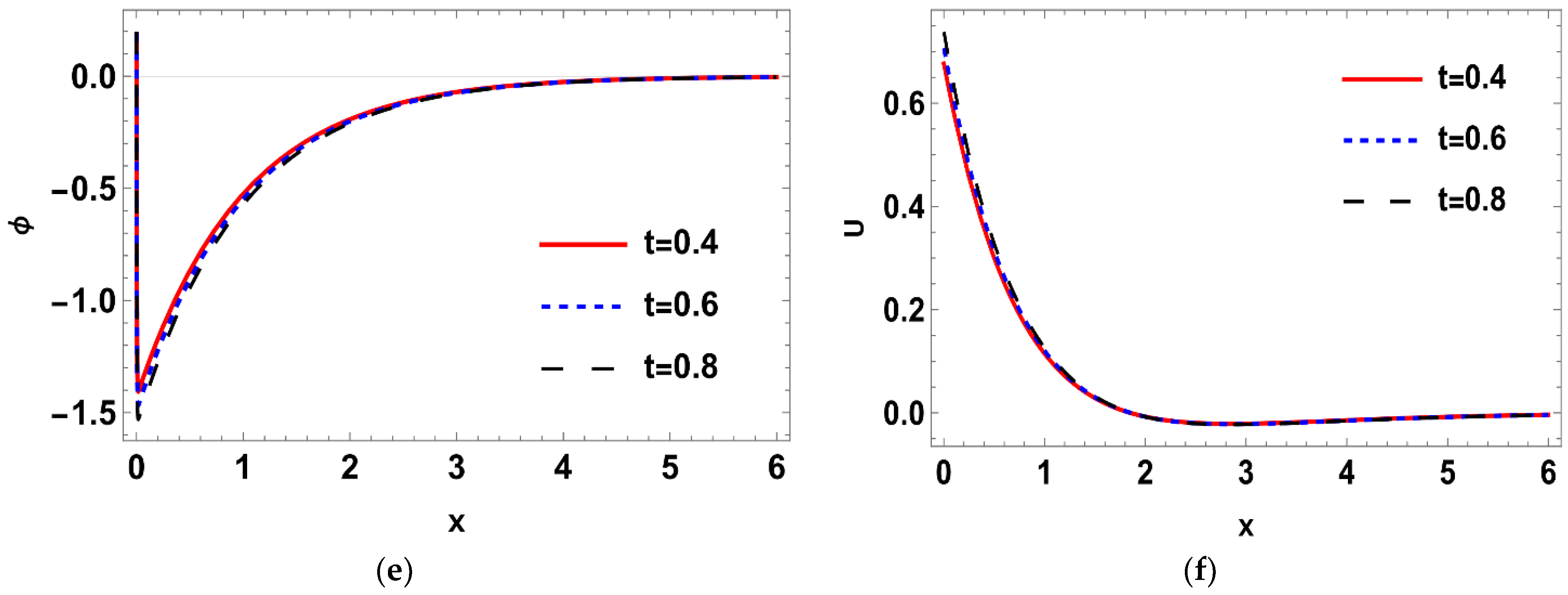
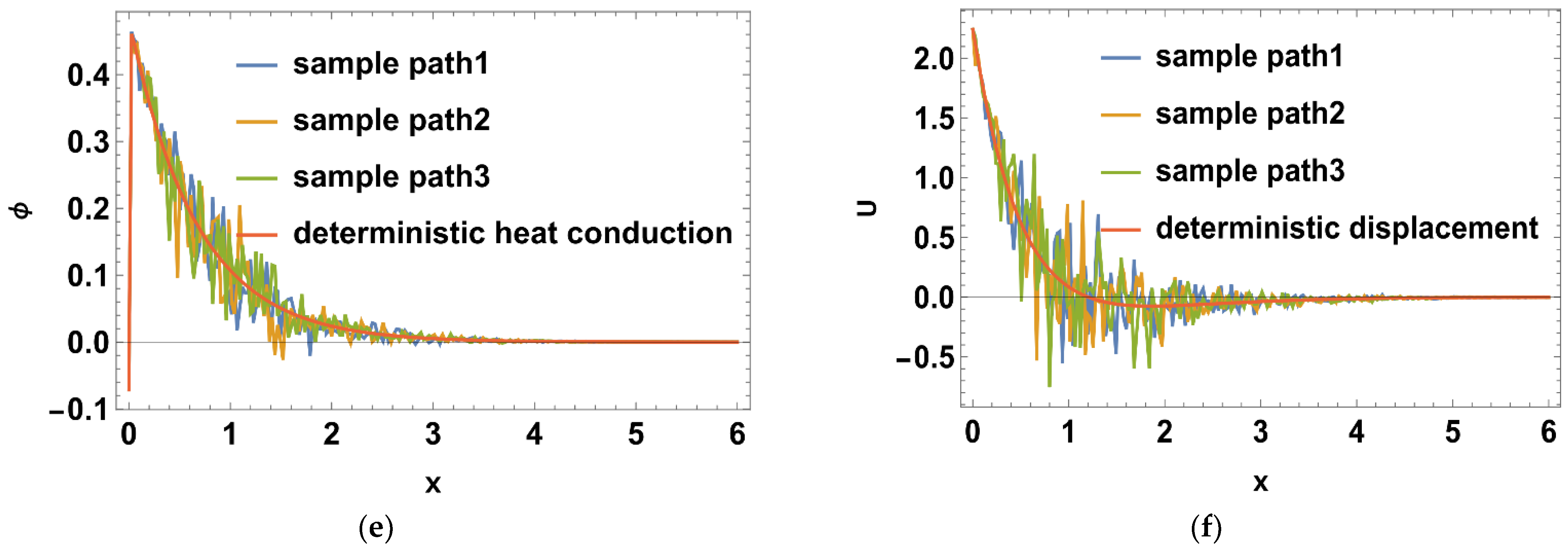
6.8. Deterministic Heat Conduction
6.9. Stochastic Heat Conduction
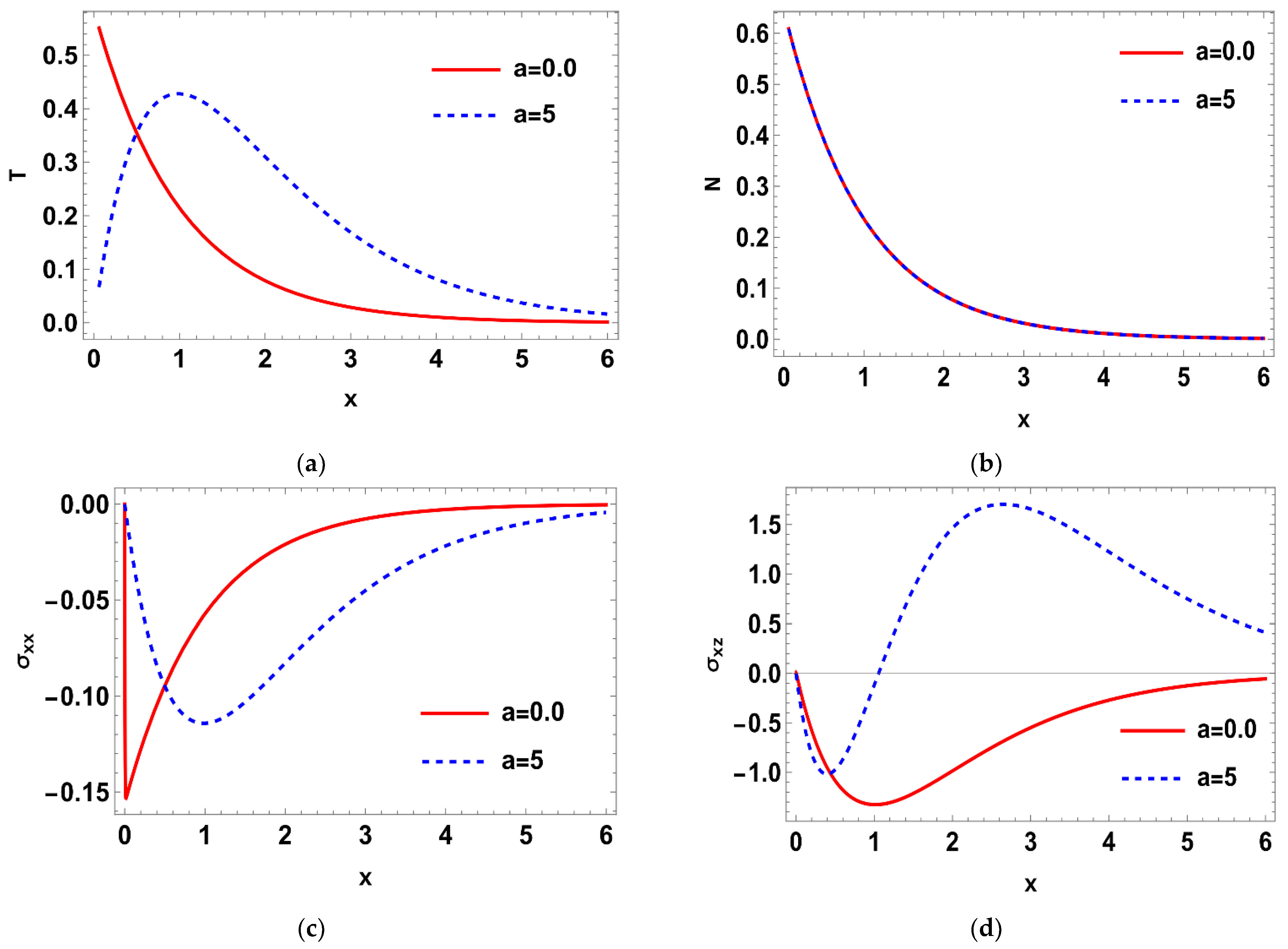
7. Numerical Results and Discussions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Biot, M.A. Thermoclasticity and irreversible thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Thermoelasticity with second sound: A review. Appl. Mech. Rev. 1986, 39, 355–376. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Hyperbolic thermoelasicity: A review of recent literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Sharma, J.N.; Kumar, V.; Chand, D. Reflection of generalized thermoelastic waves from the boundary of a half-space. J. Therm. Stress. 2003, 26, 925–942. [Google Scholar] [CrossRef]
- Fahmy, M.A. Boundary element modeling of 3 T nonlinear transient magneto-thermoviscoelastic wave propagation problems in anisotropic circular cylindrical shells. Compos. Struct. 2021, 277, 114655. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almehmadi, M.M.; Al Subhi, F.M.; Sohail, A. Fractional boundary element solution of three-temperature thermoelectric problems. Sci. Rep. 2022, 12, 6760. [Google Scholar] [CrossRef]
- Fahmy, M.A. 3D Boundary Element Model for Ultrasonic Wave Propagation Fractional Order Boundary Value Problems of Functionally Graded Anisotropic Fiber-Reinforced Plates, Fractal and Fractional. Fractal Fract. 2022, 6, 247. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Alsulami, M.O. Boundary Element and Sensitivity Analysis of Anisotropic Thermoelastic Metal and Alloy Discs with Holes. Materials 2022, 15, 1828. [Google Scholar] [CrossRef]
- Fahmy, M.A. Boundary element modeling of fractional nonlinear generalized photothermal stress wave propagation problems in FG anisotropic smart semiconductors. Eng. Anal. Bound. Elem. 2022, 134, 665–679. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Vlase, S.; Marin, M.; Modrea, A. New analytical method based on dynamic response of planar mechanical elastic systems. Bound. Value Probl. 2020, 2020, 104. [Google Scholar] [CrossRef]
- Zhang, L.; Bhatti, M.M.; Michaelides, E.E.; Marin, M.; Ellahi, R. Hybrid nanofluid flow towards an elastic surface with tantalum and nickel nanoparticles, under the influence of an induced magnetic field. Eur. Phys. J. Spec. Top. 2022, 231, 521–533. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Marin, M. The response of nanobeams with temperature-dependent properties using state-space method via modified couple stress theory. Symmetry 2020, 12, 1276. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Vlase, S.; Bhatti, M.M. On the decay of exponential type for the solutions in a dipolar elastic body. J. Taibah Univ. Sci. 2020, 14, 534–540. [Google Scholar] [CrossRef] [Green Version]
- Gordon, J.P.; Leite, R.C.C.; Moore, R.S.; Porto, S.P.S.; Whinnery, J.R. Long-transient effects in lasers with inserted liquid samples. J. Appl. Phys. 1965, 36, 3–8. [Google Scholar] [CrossRef]
- Kreuzer, L.B. Ultralow gas concentration infrared absorption spectroscopy. J. Appl. Phys. 1971, 42, 2934. [Google Scholar] [CrossRef]
- Tam, A.C. Ultrasensitive Laser Spectroscopy; Kliger, D.S., Ed.; Academic Press: Cambridge, MA, USA, 1983; pp. 1–108. [Google Scholar]
- Tam, A.C. Applications of photoacoustic sensing techniques. Rev. Mod. Phys. 1986, 58, 381. [Google Scholar] [CrossRef]
- Tam, A.C. Photothermal Investigations in Solids and Fluids; Sell, J.A., Ed.; Academic Press: Cambridge, MA, USA, 1989; pp. 1–33. [Google Scholar]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. On the thermodynamics of non-simple elastic materials with two temperatures. ZAMP 1969, 20, 107–112. [Google Scholar] [CrossRef]
- Chen, J.K.; Beraun, J.E.; Tham, C.L. Ultrafast thermoelasticity for short-pulse laser heating. Int. J. Eng. Sci. 2004, 42, 793–807. [Google Scholar] [CrossRef]
- Qiu, T.Q.; Tien, C.L. Heat transfer mechanism during short-pulse laser heating of metals. ASME J. Heat Transf. 1993, 115, 835–841. [Google Scholar] [CrossRef]
- Youssef, H.M. Theory of two-temperature-generalized thermoelasticity. IMA J. Appl. Math. 2006, 71, 383–390. [Google Scholar] [CrossRef]
- Lotfy, K. Two temperature generalized magneto-thermoelastic interactions in an elastic medium under three theories. Appl. Math. Comput. 2014, 227, 871–888. [Google Scholar] [CrossRef] [Green Version]
- Lotfy, K.; Hassan, W. Normal mode method for two-temperature generalized thermoelasticity under thermal shock problem. J. Therm. Stress. 2014, 37, 545–560. [Google Scholar] [CrossRef]
- Hoel, P.G.; Port, S.C.; Stone, C.J. Introduction to Stochastic Processes; Waveland Press: Long Grove, IL, USA, 1986. [Google Scholar]
- Platen, E.; Kloeden, P. Numerical Solution of Stochastic Differential Equations; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Lawler, G.F. Introduction to Stochastic Processes; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Hoel, P.G.; Port, S.C.; Stone, C.J. Introduction to Stochastic Processes; Universal Book Stall: New Delhi, India, 1972. [Google Scholar]
- Sherief, H.H.; El-Maghraby, N.M.; Allam, A.A. Stochastic thermal shock problem in generalized thermoelasticity. Appl. Math. Model. 2013, 37, 762–775. [Google Scholar] [CrossRef]
- Sherief, H.H.; El-Maghraby, N.M.; Allam, A.A. Stochastic thermal shock problem and study of wave propagation in the theory of generalized thermoelastic diffusion. Math. Mech. Solids 2016, 22, 1767–1789. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Applications of Mathematics Series; Springer: Berlin/Heidelberg, Germany, 1992; Volume 23. [Google Scholar]
- Lotfy, K.; Ahmed, A.; El-Bary, A.; Tantawi, R.S. A Novel Stochastic Model of the Photo-Thermoelasticity Theory of the Non-Local Excited Semiconductor Medium. Silicon 2022. [Google Scholar] [CrossRef]
- Bellomo, N.; Flandoli, F. Stochastic partial differential equations in continuum physics—On the foundations of the stochastic interpolation method for ITO’s type equations. Math. Comput. Simul. 1989, 31, 3–17. [Google Scholar] [CrossRef]
- Kant, S.; Mukhopadhyay, S. Investigation of a problem of an elastic half space subjected to stochastic temperature distribution at the boundary. Appl. Math. Model. 2017, 46, 492–518. [Google Scholar] [CrossRef]
- Val’kovskaya, V.I.; Lenyuk, M.P. Stochastic nonstationary temperature fields in a solid circular–cylindrical two-layer plate. J. Math. Sci. 1996, 79, 1483–1487. [Google Scholar] [CrossRef]
- Todorović, D.M. Plasma, thermal, and elastic waves in semiconductors. Rev. Sci. Instrum. 2003, 74, 582–585. [Google Scholar] [CrossRef]
- Vasilev, A.N.; Sandomirskii, V.B. Photoacoustic effects in finite semiconductors. Sov. Phys. Semicond. 1984, 18, 1095. [Google Scholar]
- Christofides, C.; Othonos, A.; Loizidou, E. Influence of temperature and modulation frequency on the thermal activation coupling term in laser photothermal theory. J. Appl. Phys. 2002, 92, 1280. [Google Scholar] [CrossRef]
- Song, Y.Q.; Bai, J.T.; Ren, Z.Y. Study on the reflection of photothermal waves in a semiconducting medium under generalized thermoelastic theory. Acta Mech. 2012, 223, 1545–1557. [Google Scholar] [CrossRef]
- Lotfy, K.; Hassan, W.; Gabr, M.E. Thermomagnetic effect with two temperature theory for photothermal process under hydrostatic initial stress. Results Phys. 2017, 7, 3918–3927. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Abbas, I.A. A study on photothermal waves in an unbounded semiconductor medium with cylindrical cavity. Mech. Time-Depend. Mater. 2016, 21, 61–72. [Google Scholar] [CrossRef]
- Xiao, Y.; Shen, C.; Zhang, W. Screening and prediction of metal-doped α-borophene monolayer for nitric oxide elimination. Mater. Today Chem. 2022, 25, 100958. [Google Scholar] [CrossRef]
- Liu, J.; Han, M.; Wang, R.; Xu, S.; Wang, X. Photothermal phenomenon: Extended ideas for thermophysical properties characterization. J. Appl. Phys. 2022, 131, 065107. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alenazi, A.; Ahmed, A.; El-Bary, A.A.; Tantawi, R.S.; Lotfy, K. A Stochastic Thermo-Mechanical Waves with Two-Temperature Theory for Electro-Magneto Semiconductor Medium. Crystals 2023, 13, 82. https://doi.org/10.3390/cryst13010082
Alenazi A, Ahmed A, El-Bary AA, Tantawi RS, Lotfy K. A Stochastic Thermo-Mechanical Waves with Two-Temperature Theory for Electro-Magneto Semiconductor Medium. Crystals. 2023; 13(1):82. https://doi.org/10.3390/cryst13010082
Chicago/Turabian StyleAlenazi, Abdulaziz, Abdelaala Ahmed, Alaa A. El-Bary, Ramdan S. Tantawi, and Khaled Lotfy. 2023. "A Stochastic Thermo-Mechanical Waves with Two-Temperature Theory for Electro-Magneto Semiconductor Medium" Crystals 13, no. 1: 82. https://doi.org/10.3390/cryst13010082
APA StyleAlenazi, A., Ahmed, A., El-Bary, A. A., Tantawi, R. S., & Lotfy, K. (2023). A Stochastic Thermo-Mechanical Waves with Two-Temperature Theory for Electro-Magneto Semiconductor Medium. Crystals, 13(1), 82. https://doi.org/10.3390/cryst13010082









