Study of Temperature Effects on the Design of Active Region for 808 nm High-Power Semiconductor Laser
Abstract
1. Introduction
2. Theory
- ηslop
- is the slope efficiency;
- Ith
- is the threshold current;
- h
- is the Planck’s constant;
- c
- is the speed of light in vacuum;
- q
- is the amount of elementary charge;
- λ
- is the lasing wavelength;
- ηi
- is the internal quantum efficiency;
- αm
- is the mirror loss, and is the internal optical loss;
- ΔT
- is the temperature rise of the active region relative to the heatsink;
- T0
- and are the characteristic temperatures that depict the temperature sensitivity of threshold current and slope efficiency, respectively;
- L
- is the length of the resonant cavity, and is the width of the device electrode;
- Jtr
- is the transparent current density;
- Γg0
- is the mode gain, which is the product of the optical confinement factor in the quantum well and the material gain .
3. Simulation Model and Epitaxial Parameters
4. Simulation Results and Discussion
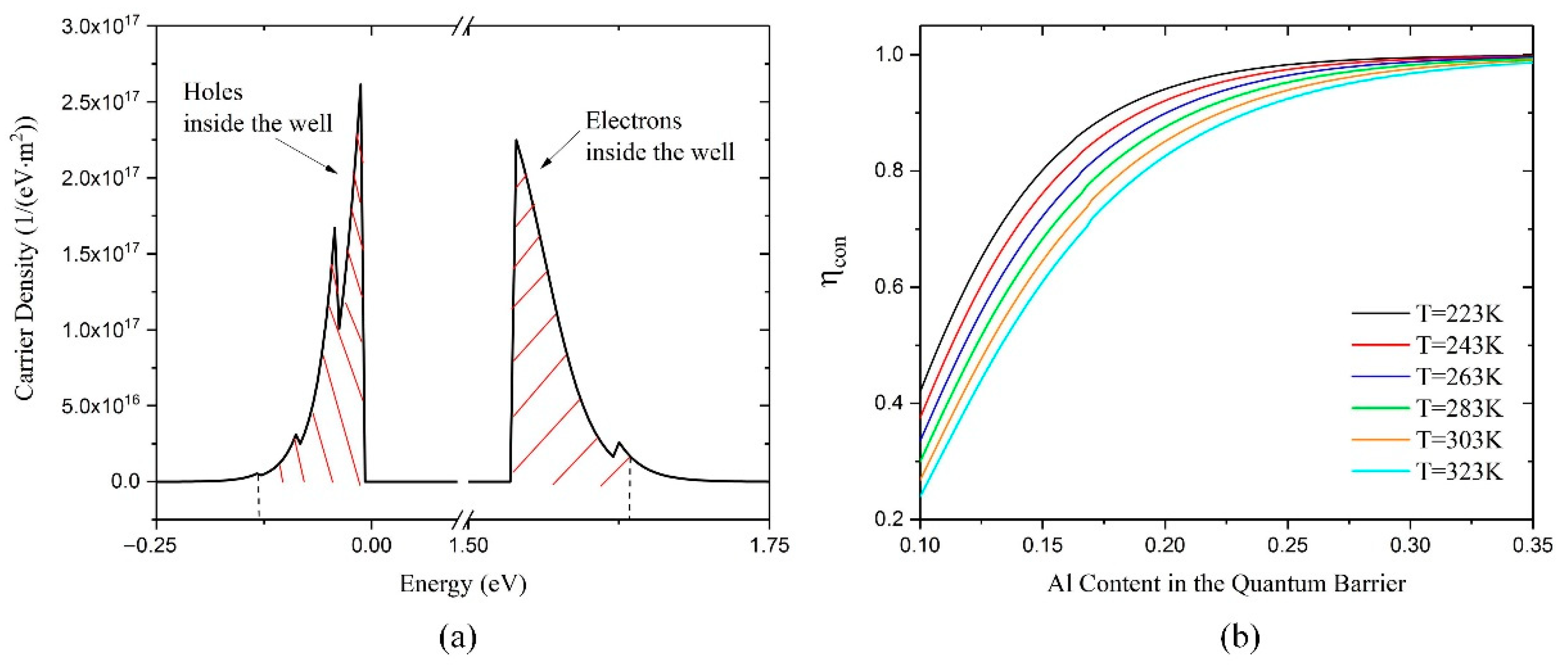
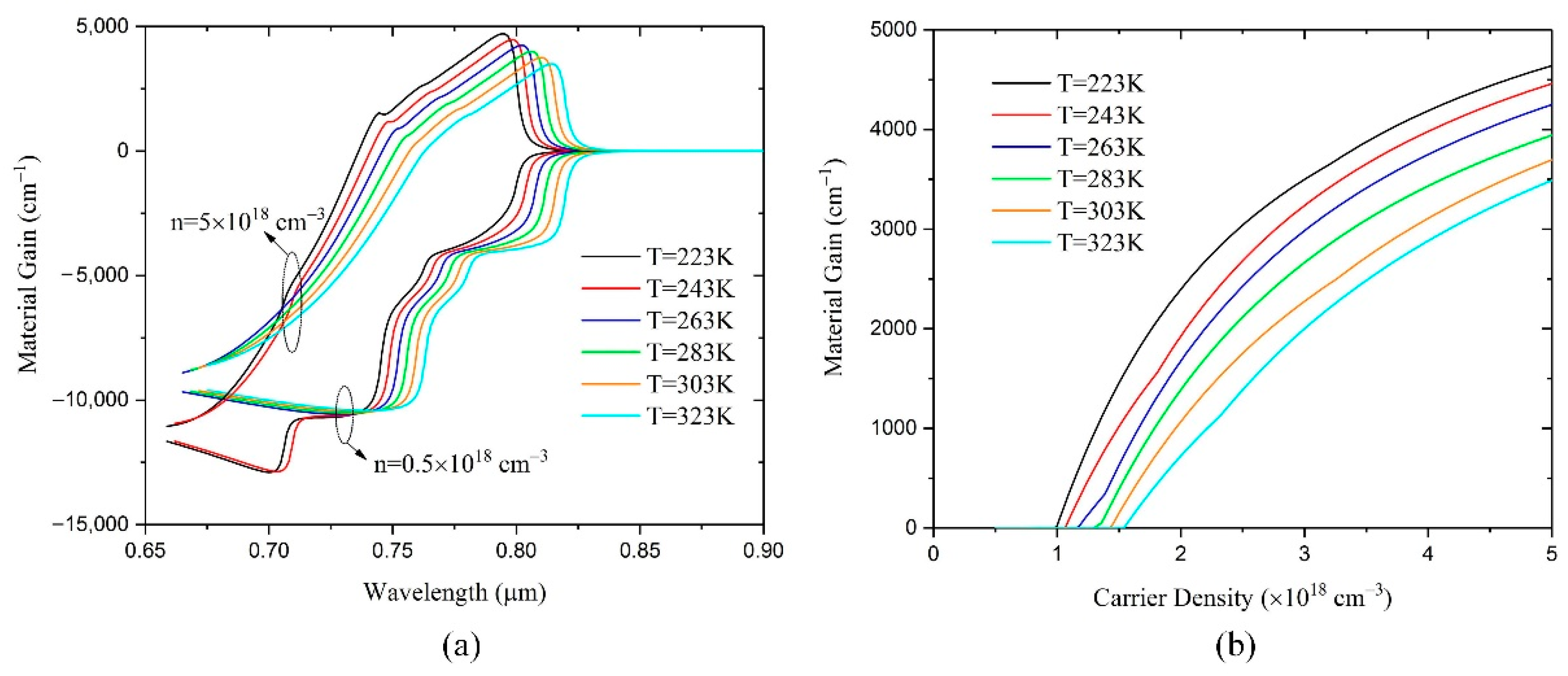
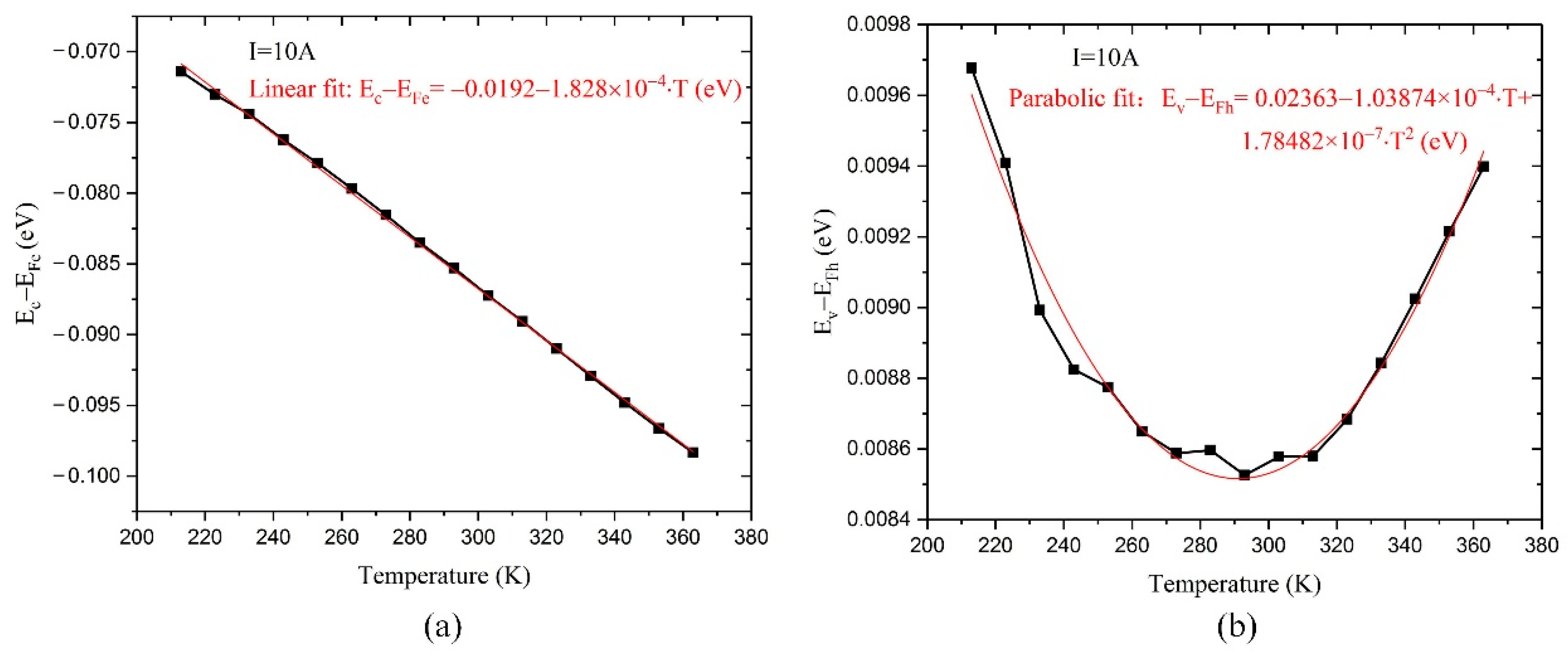
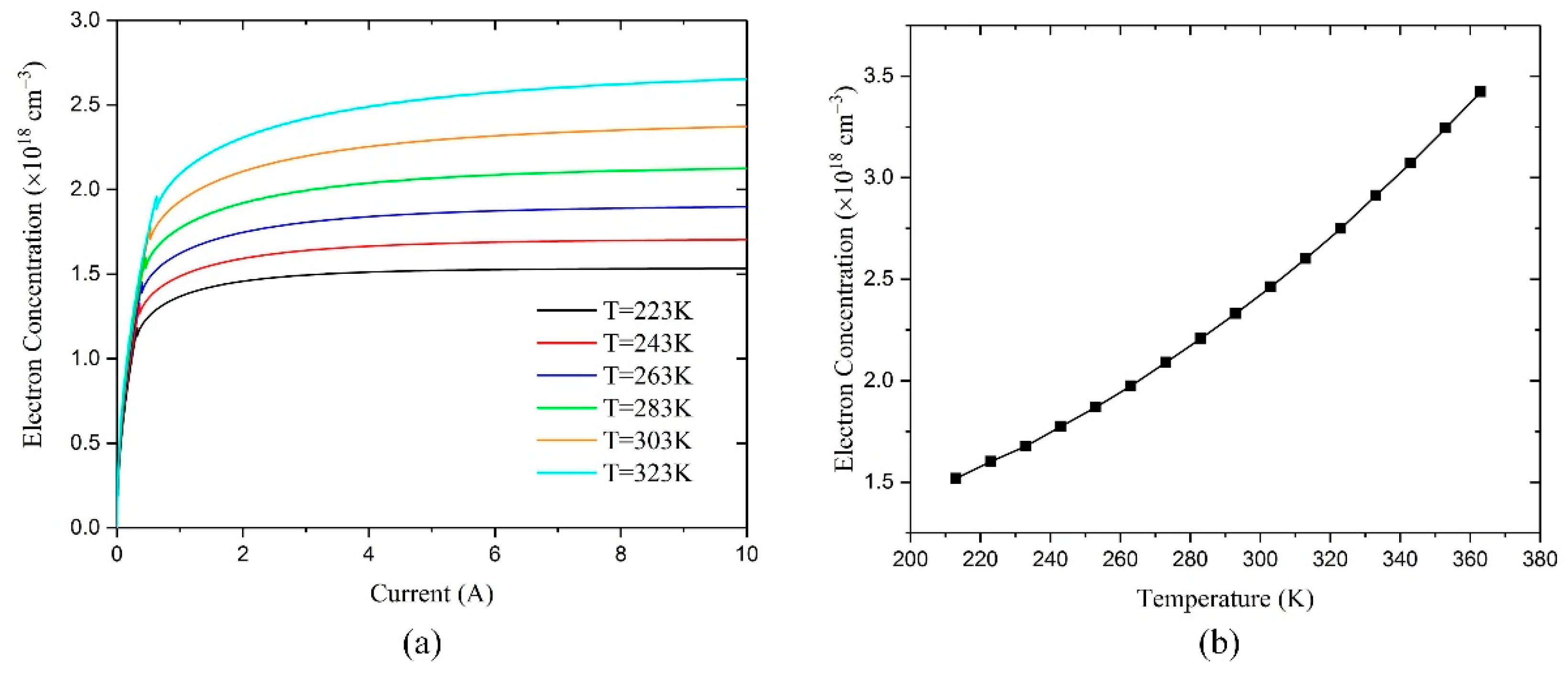
4.1. Temperature Effects in the Quantum Well
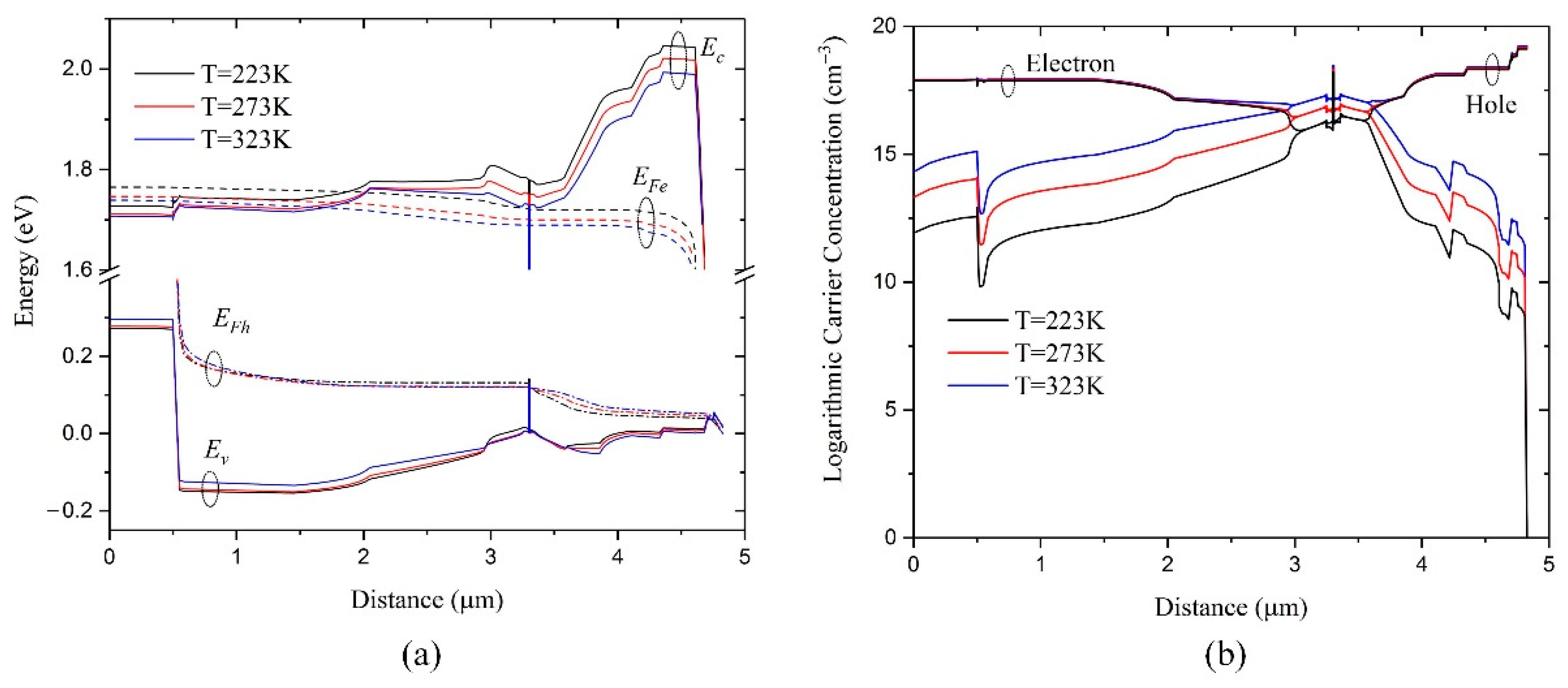
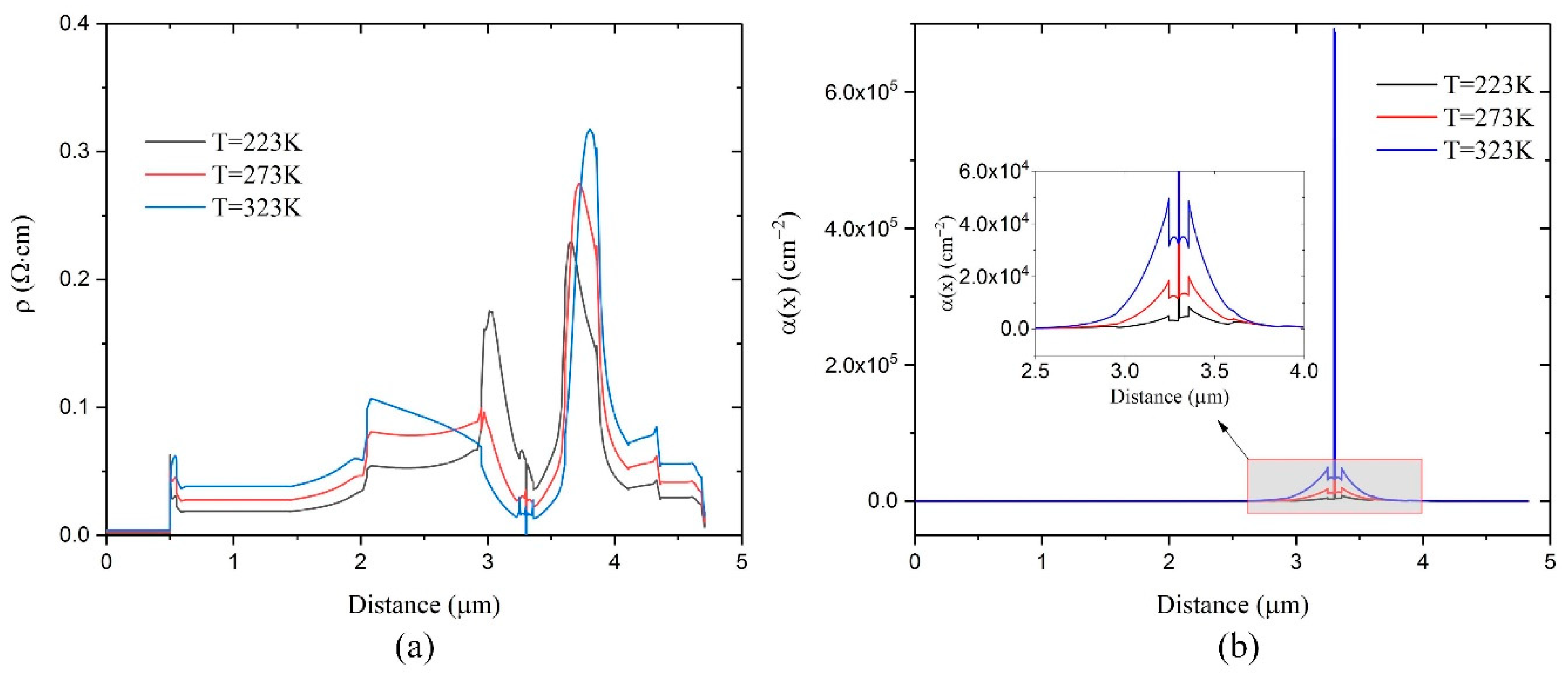
4.2. Temperature Effects in the Whole Epitaxial Direction
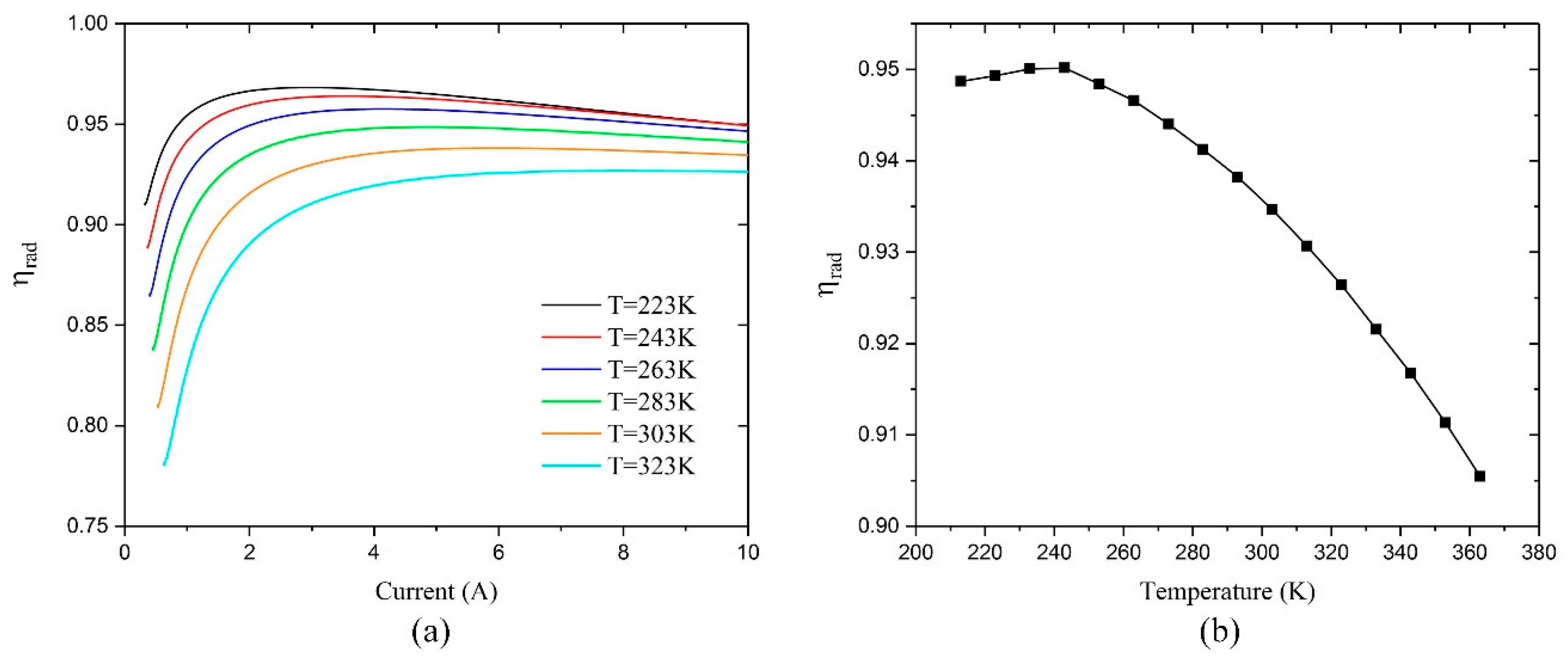
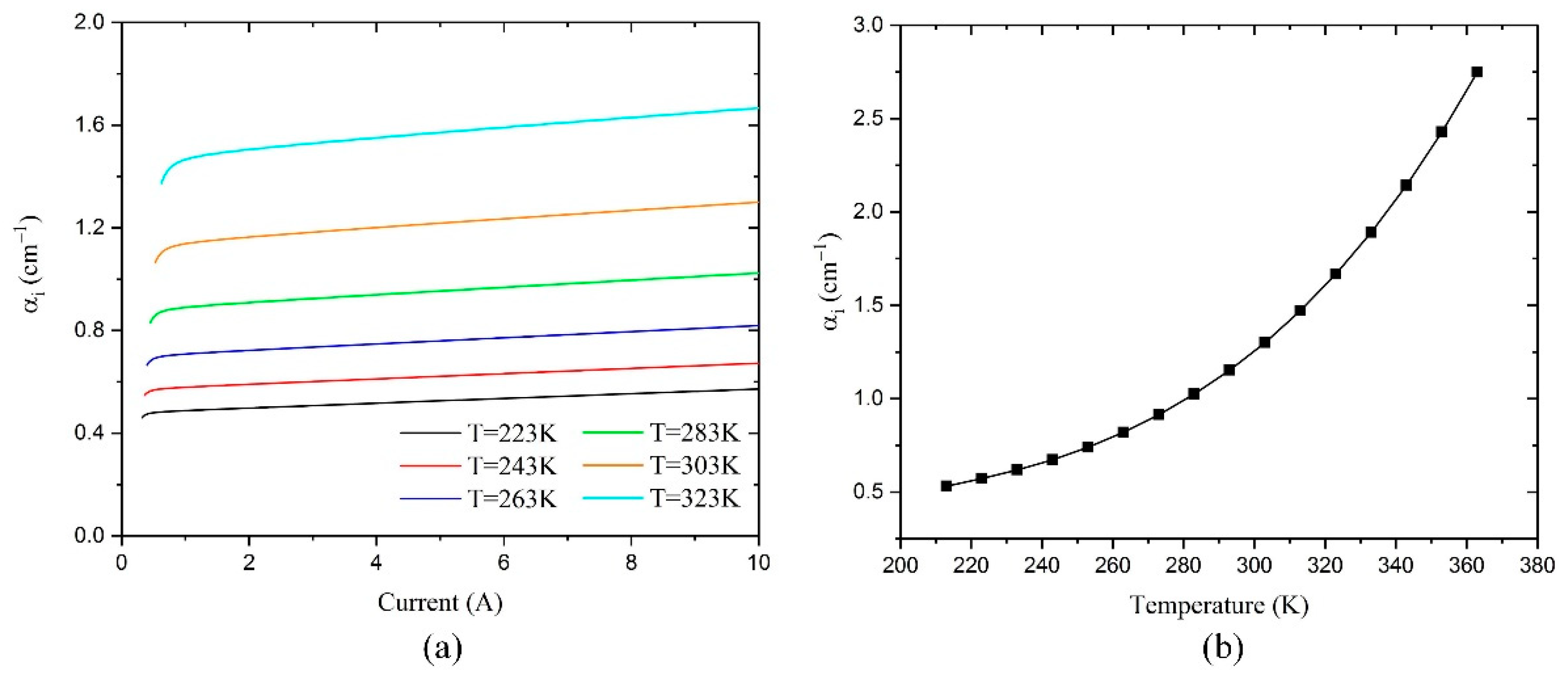
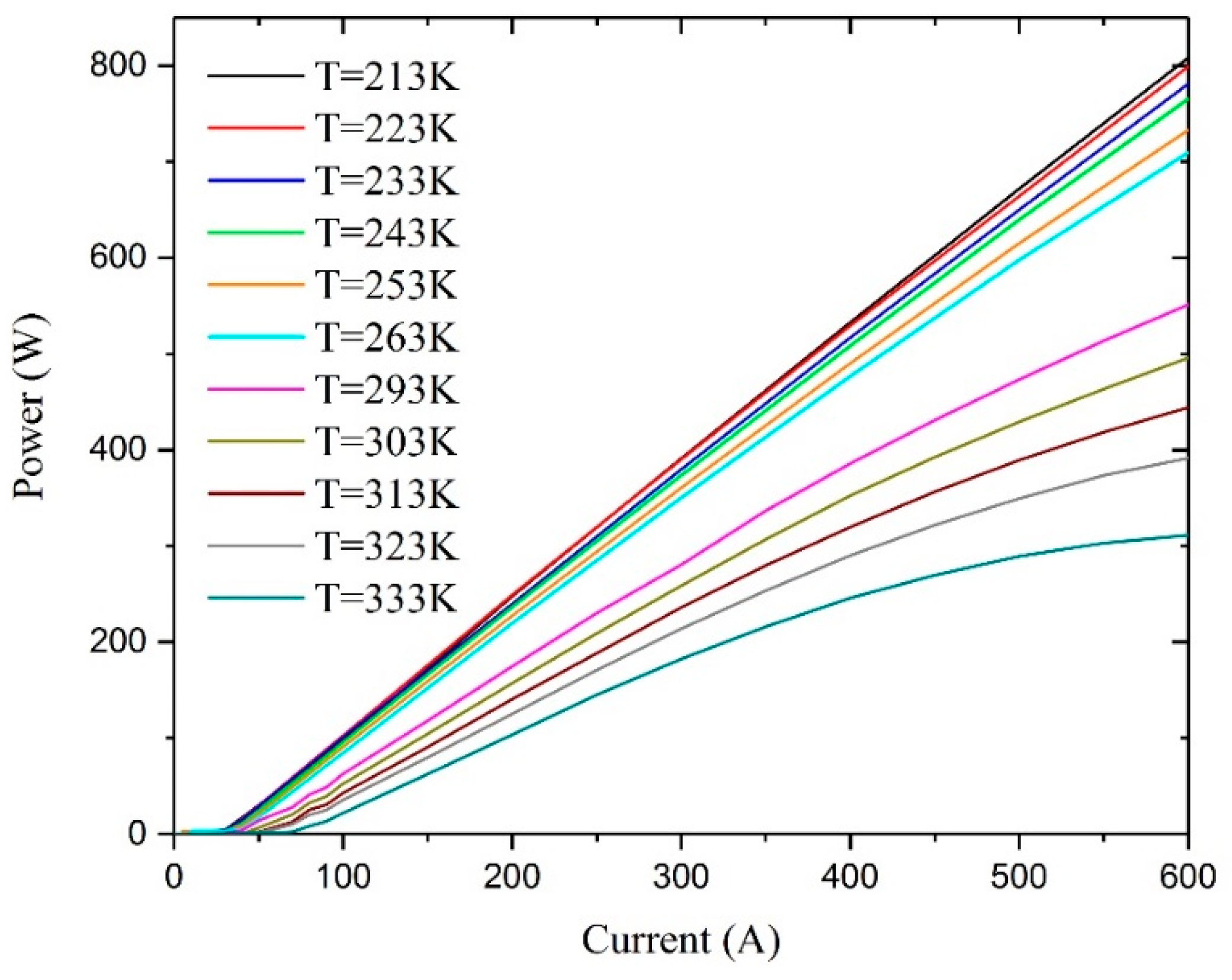
4.3. Temperature Effects on the Slop Efficiency
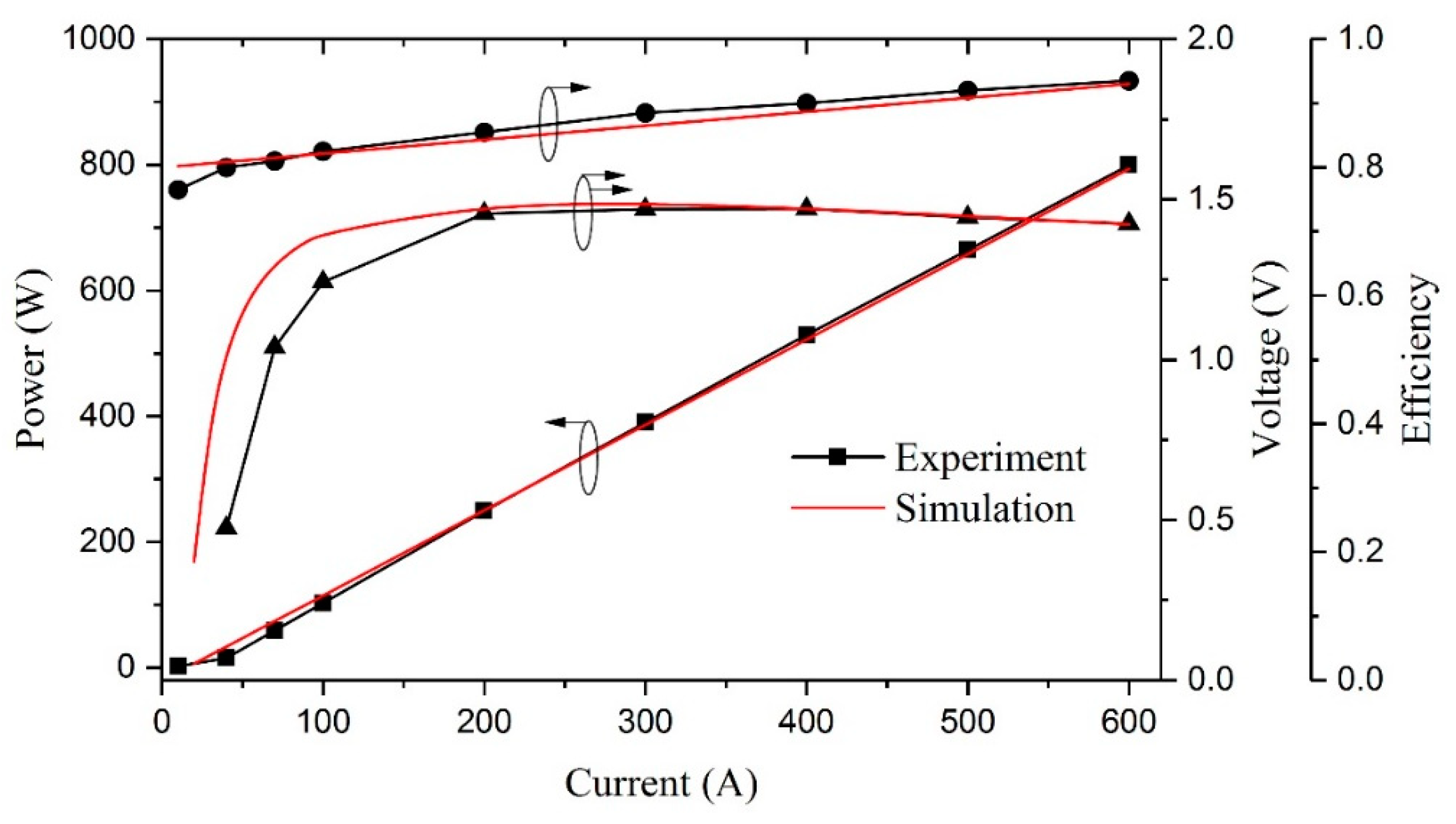
5. Contrast of Simulated and Experimental Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, X.Y.; Wang, J.; Liu, S.P. Present situation of investigations and applications in high power semiconductor lasers. Infrared Laser Eng. 2008, 37, 189–194. [Google Scholar]
- Zhang, Y.; Hao, S.; Zhang, J.; Guo, C.; Wang, W. Study on the Application of Laboratory Environmental Test Methods for Military Materiel-GJB 150A—2009. China Personal Protective Equipment 2017, 03, 28–31. [Google Scholar] [CrossRef]
- Sotoodeh, M.; Khalid, A.H.; Rezazadeh, A.A. Empirical low-field mobility model for III–V compounds applicable in device simulation codes. J. Appl. Phys. 2000, 87, 2890–2900. [Google Scholar] [CrossRef]
- Vurgaftman, I.; Meyer, J.Á.; Ram-Mohan, L.Á. Band parameters for III–V compound semiconductors and their alloys. J. Appl. Phys. 2001, 89, 5815–5875. [Google Scholar] [CrossRef]
- Ho, C.H.; Li, J.H.; Lin, Y.S. Optical characterization of a GaAs/In0.5(AlxGa1-x)0.5P/GaAs heterostructure cavity by piezoreflectance spectroscopy. Opt. Express 2007, 15, 13886–13893. [Google Scholar] [CrossRef] [PubMed]
- Tansu, N.; Mawst, L.J. Current injection efficiency of InGaAsN quantum-well lasers. J. Appl. Phys. 2005, 97, 054502. [Google Scholar] [CrossRef]
- Laikhtman, B.; Gourevitch, A.; Donetsky, D.; Westerfeld, D.; Belenky, G. Current spread and overheating of high power laser bars. J. Appl. Phys. 2004, 95, 3880–3889. [Google Scholar] [CrossRef]
- Arafin, S.; Bachmann, A.; Vizbaras, K.; Hangauer, A.; Gustavsson, J.; Bengtsson, J.; Larsson, A.; Amann, M.C. Comprehensive analysis of electrically-pumped GaSb-based VCSELs. Opt. Express 2011, 19, 17267–17282. [Google Scholar] [CrossRef] [PubMed]
- Ryu, H.Y.; Ha, K.H. Effect of active-layer structures on temperature characteristics of InGaN blue laser diodes. Opt. Express 2008, 16, 10849–10857. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.F.; Wang, Z.F.; Li, T.; Yang, G.W. Efficiency analysis of 808 nm laser diode array under different operating temperatures. Acta Phys. Sin. 2017, 66, 104202. [Google Scholar] [CrossRef]
- Frevert, C.; Crump, P.; Bugge, F.; Knigge, S.; Erbert, G. The impact of low Al-content waveguides on power and efficiency of 9xx nm diode lasers between 200 and 300 K. Semicond. Sci. Technol. 2016, 31, 025003. [Google Scholar] [CrossRef]
- Hasler, K.H.; Frevert, C.; Crump, P.; Erbert, G.; Wenzel, H. Numerical study of high-power semiconductor lasers for operation at sub-zero temperatures. Semicond. Sci. Technol. 2017, 32, 045004. [Google Scholar] [CrossRef]
- Wang, M.P.; Zhang, P.; Nie, Z.Q.; Liu, H.; Sun, Y.B.; Wu, D.H.; Zhao, Y.L. Analysis of Cryogenic Characteristics of High Power Semiconductor Lasers. Acta Phtonica Sin. 2019, 48, 0914002. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Yang, G.; Song, Y. High power, high efficiency continuous-wave 808 nm laser diode arrays. Opt. Laser Technol. 2017, 97, 297–301. [Google Scholar] [CrossRef]
- Chuang, S.L. Fundamentals of Semiconductor Lasers. In Physics of Photonic Devices, 2nd ed.; Jia, D.F., Wang, Z.Y., Sang, M., Yang, T.X., Eds.; Publishing House of Electronics Industry: Beijing, China, 2013; Volume 10, pp. 268–315. [Google Scholar]
- Zou, Y.; Osinski, J.S.; Grodzinski, P.; Dapkus, P.D.; Rideout, W.C.; Sharfin, W.F.; Schlafer, J.; Crawford, F.D. Experimental study of Auger recombination, gain, and temperature sensitivity of 1.5 μm compressively strained semiconductor lasers. IEEE J. Quantum Elect. 1993, 29, 1565–1575. [Google Scholar] [CrossRef]
- Romero, B.; Arias, J.; Esquivias, I.; Cada, M. Simple model for calculating the ratio of the carrier capture and escape times in quantum-well lasers. Appl. Phys. Lett. 2000, 76, 1504–1506. [Google Scholar] [CrossRef]
- Zbroszczyk, M.; Bugajski, M. Design optimization of InGaAlAs/GaAs single and double quantum well lasers emitting at 808 nm. In Proceedings of the Conference on Physics and Simulation of Optoelectronic Devices XII, San Jose, CA, USA, 26 January 2004; pp. 446–453. [Google Scholar]
- Tijero, J.M.G.; Borruel, L.; Vilera, M.; Consoli, A.; Esquivias, I. Simulation and geometrical design of multi-section tapered semiconductor optical amplifiers at 1.57 μm. In Proceedings of the Semiconductor Lasers and Laser Dynamics VI, Brussels, Belgium, 2 May 2014; p. 91342A. [Google Scholar]
- Calciati, M.; Debernardi, P.; Goano, M.; Bertazzi, F. Towards a comprehensive 3D VCSEL model: Electrical simulations with PICS3D. In Proceedings of the Fotonica AEIT Italian Conference on Photonics Technologies, Turin, Italy, 6–8 May 2015. [Google Scholar]
- Xia, C.S.; Li, Z.S.; Crosslight, Y.S. Effect of last barrier on efficiency improvement of blue InGaN/GaN light-emitting diodes. In Proceedings of the 13th International Conference on Numerical Simulation of Optoelectronic Devices, Vancouver, BC, Canada, 19–22 August 2013. [Google Scholar]
- Wu, S.H.; Li, T.; Wang, D.; Yu, X.C.; Wang, Z.F.; Liu, G.J. Optimization of the Epitaxial Structure of Low-Loss 885nm High-Power Laser Diodes. In Proceedings of the Sixteenth National Conference on Laser Technology and Optoelectronics, Shanghai, China, 31 August 2021; p. 53. [Google Scholar]
- Bulashevich, K.A.; Mymrin, V.F.; Karpov, S.Y.; Demidov, D.M.; Ter-Martirosyan, A.L. Effect of free-carrier absorption on performance of 808 nm AlGaAs-based high-power laser diodes. Semicond. Sci. Technol. 2007, 22, 502–510. [Google Scholar] [CrossRef]
- Pikhtin, N.A.; Slipchenko, S.O.; Sokolova, Z.N.; Tarasov, I.S. Internal optical loss in semiconductor lasers. Semiconductors 2004, 38, 360–367. [Google Scholar] [CrossRef]
- Johnson, L.A.; Teh, A. Measuring High Power Laser Diode Junction Temperature and Package Thermal Impedance; Application Note #30; ILX Ligthwave Corporation: Bozeman, MT, USA, 2008. [Google Scholar]

| Physical Effects | Notes |
|---|---|
| Temperature dependence of energy band structure | Adopting k-p theory |
| Carriers capture and escape process in the quantum well | Defined by electron and hole capture times |
| Temperature dependence of electron and hole mobility | Affected by temperature, carrier concentration and applied electric field |
| Main non-radiative recombination | Including Auger recombination and Shockley-Hall-Read (SHR) recombination |
| Temperature dependence of refractive index | Affected by temperature, carrier concentration and wavelength |
| Free carrier absorption | Proportional to carrier concentration and wave intensity |
| Temperature dependence of material gain | Affected by temperature, carrier concentration and spectrum |
| Temperature dependence of carrier concentration | Defined by Fermi-Dirac distribution, applying Poisson and continuity equations |
| Local heat sources | Not included, treated as constant temperature and no thermal gradients |
| Description | Materials | Thickness | Dopant | Doping Concentration (cm−3) |
|---|---|---|---|---|
| P-clap | GaAs | 0.2 | C | 1019→11020 |
| P-cladding | Al0.4Ga0.6As-Al0.5Ga0.5As | 0.5 | C | 21018→4.51018 |
| P-waveguide | AlxGa1-xAs-Al0.4Ga0.6As | 0.8 | C | 1016→21018 |
| Quantum Barrier | AlxGa1-xAs | 0.05 | Undoped | None |
| Quantum Well | In0.14Al0.14Ga0.72As | 0.008 | Undoped | None |
| Quantum Barrier | AlxGa1-xAs | 0.05 | Undoped | None |
| N-waveguide | Al0.35Ga0.65As- AlxGa1-xAs | 1.2 | Si | 1017→51016 |
| N-cladding | Al0.35Ga0.65As | 1.5 | Si | 1018→21017 |
| N-buffer | GaAs | 0.5 | Si | 21018 |
| N-substrate | GaAs | 150 | Si | 21018 |
| T (K) | 223 | 243 | 263 | 283 | 303 | 323 |
|---|---|---|---|---|---|---|
| Al Content | 0.216 | 0.230 | 0.246 | 0.26 | 0.274 | 0.288 |
| T (K) Heatsink | (nm) I = 600 A | Waste Heat Power (W) | T (K) Active Region | Rth (K/W) |
|---|---|---|---|---|
| 213 | 797.58 | 27.74 | 240.1 | 0.97 |
| 223 | 799.77 | 27.40 | 249.2 | 0.95 |
| 233 | 802.37 | 28.86 | 259.9 | 0.93 |
| 243 | 804.90 | 29.69 | 270.3 | 0.92 |
| 253 | 807.26 | 30.80 | 280.1 | 0.87 |
| 263 | 810.09 | 32.26 | 291.8 | 0.89 |
| 293 | 818.11 | 45.27 | 324.9 | 0.70 |
| 303 | 819.16 | 49.12 | 329.2 | 0.53 |
| 313 | 823.06 | 53.27 | 345.3 | 0.60 |
| 323 | 825.30 | 56.99 | 354.5 | 0.55 |
| 333 | 827.99 | 62.95 | 365.6 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Li, T.; Wang, Z.; Chen, L.; Zhang, J.; Zhang, J.; Liu, J.; Zhang, Y.; Deng, L. Study of Temperature Effects on the Design of Active Region for 808 nm High-Power Semiconductor Laser. Crystals 2023, 13, 85. https://doi.org/10.3390/cryst13010085
Wu S, Li T, Wang Z, Chen L, Zhang J, Zhang J, Liu J, Zhang Y, Deng L. Study of Temperature Effects on the Design of Active Region for 808 nm High-Power Semiconductor Laser. Crystals. 2023; 13(1):85. https://doi.org/10.3390/cryst13010085
Chicago/Turabian StyleWu, Shunhua, Te Li, Zhenfu Wang, Lang Chen, Jiachen Zhang, Junyue Zhang, Jiachen Liu, Yeqi Zhang, and Liting Deng. 2023. "Study of Temperature Effects on the Design of Active Region for 808 nm High-Power Semiconductor Laser" Crystals 13, no. 1: 85. https://doi.org/10.3390/cryst13010085
APA StyleWu, S., Li, T., Wang, Z., Chen, L., Zhang, J., Zhang, J., Liu, J., Zhang, Y., & Deng, L. (2023). Study of Temperature Effects on the Design of Active Region for 808 nm High-Power Semiconductor Laser. Crystals, 13(1), 85. https://doi.org/10.3390/cryst13010085







