Ultrahigh-Density Superhard Hexagonal BN and SiC with Quartz Topology from Crystal Chemistry and First Principles
Abstract
:1. Introduction
2. Computational Framework
3. Crystal Chemistry
4. Mechanical Properties from the Elastic Constants
5. Dynamic and Thermal Properties from the Phonons
5.1. Phonon Band Structures
5.2. Thermodynamic Properties
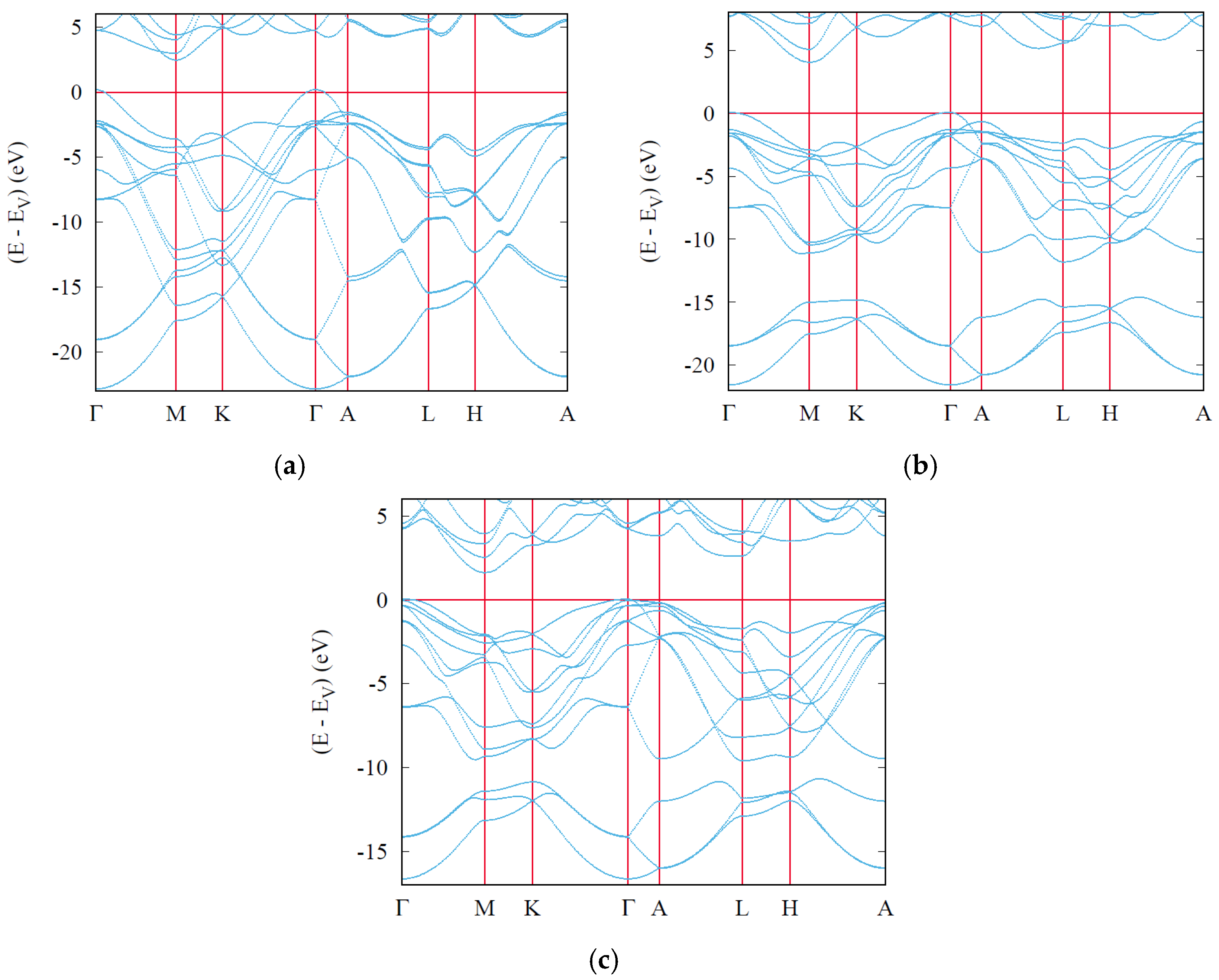
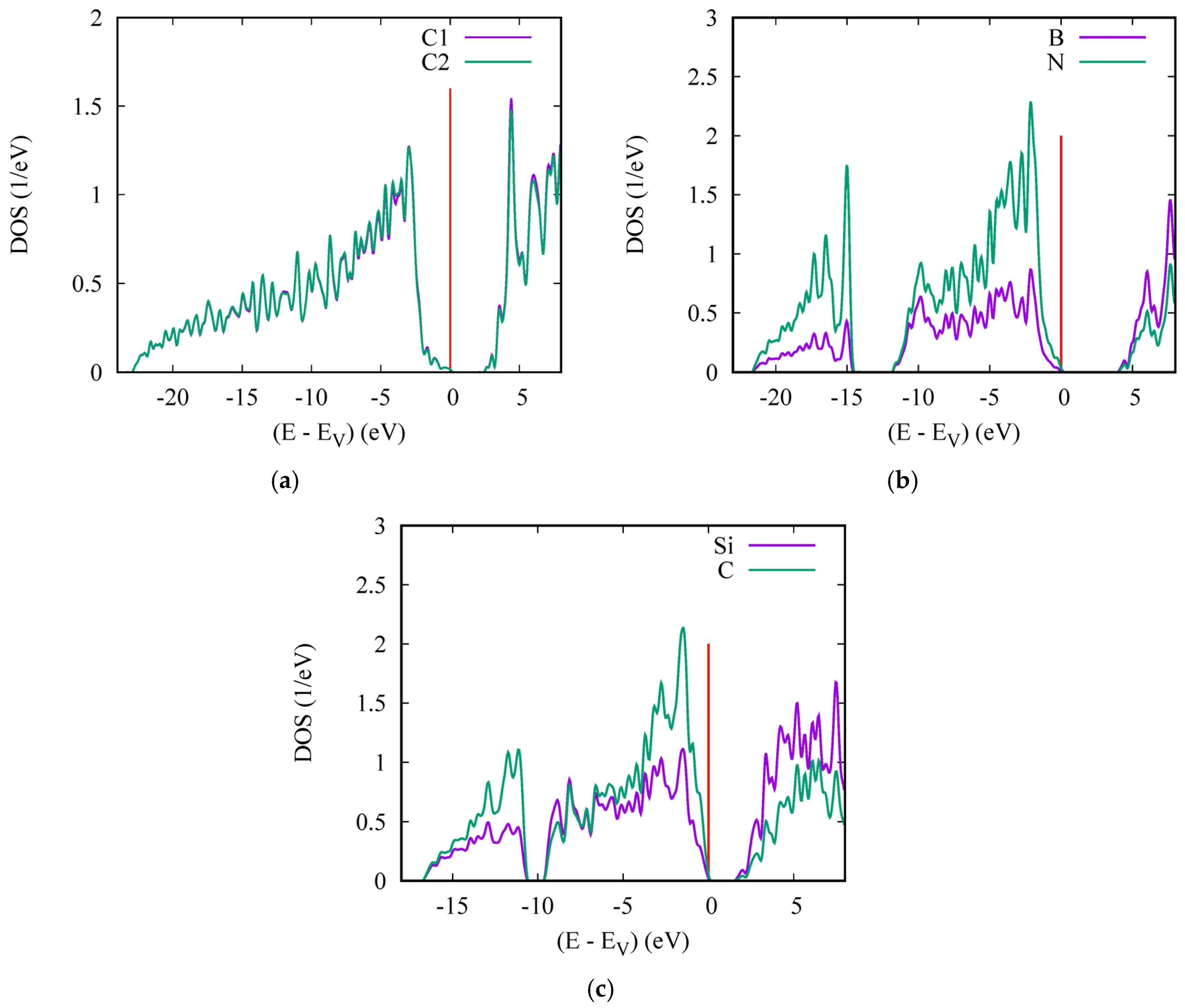
6. Electronic Band Structures and Density of States
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brazhkin, V.V.; Solozhenko, V.L. Myths about new ultrahard phases: Why materials that are significantly superior to diamond in elastic moduli and hardness are impossible. J. Appl. Phys. 2019, 125, 130901. [Google Scholar] [CrossRef]
- Stishov, S.M. Energy, compressibility and covalency in the carbon subgroup. Philos. Mag. Lett. 2000, 80, 125–128. [Google Scholar] [CrossRef]
- Li, Q.; Sun, Y.; Li, Z.; Zhou, Y. Lonsdaleite—A material stronger and stiffer than diamond than diamond. Scr. Mater. 2011, 65, 229–232. [Google Scholar]
- Öhrström, L.; O’Keeffe, M. Network topology approach to new allotropes of the group 14 elements. Z. Kristallogr. 2013, 228, 343–346. [Google Scholar] [CrossRef]
- Shevchenko, A.P.; Shabalin, A.A.; Karpukhin, I.Y.; Blatov, V.A. Topological representations of crystal structures: Generation, analysis and implementation in the TopCryst system. Sci. Technol. Adv. Mat. 2022, 2, 250–265. [Google Scholar] [CrossRef]
- Hoffmann, R.; Kabanov, A.A.; Golov, A.A.; Proserpio, D.M. Homo Citans and carbon allotropes: For an ethics of citation. Angew. Chem. Int. Ed. 2016, 55, 10962–10976. [Google Scholar] [CrossRef]
- Zhu, Q.; Oganov, A.R.; Salvadó, M.A.; Pertierra, P.; Lyakhov, A.O. Denser than diamond: Ab initio search for superdense carbon allotropes. Phys. Rev. B 2011, 83, 193410. [Google Scholar] [CrossRef]
- Luo, B.; Wu, L.; Zhang, Z.; Li, G.; Tian, E. A triatomic carbon and derived pentacarbides with superstrong mechanical properties. iScience 2022, 25, 104712. [Google Scholar] [CrossRef]
- Matar, S.F.; Solozhenko, V.L. First principles search for novel ultrahard high-density carbon allotropes: Hexagonal C6, C9 and C12. J. Superhard Mater. 2023, 45, 239–248. [Google Scholar] [CrossRef]
- McMahon, M.I.; Nelmes, R.J.; Wright, N.G.; Allan, D.R. Crystal structure studies of II-VI semiconductors using angle-dispersive diffraction techniques with an image-plate detector. AIP Conf. Proc. 1994, 309, 633–636. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, J. From ultrasoft pseudopotentials to the projector augmented wave. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. The Generalized Gradient Approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, 2nd ed.; Cambridge University Press: New York, NY, USA, 1986. [Google Scholar]
- Blöchl, P.; Jepsen, O.; Anderson, O. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.; Pack, J. Special k-points for Brillouin Zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Voigt, W. Über die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Annal. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Blaschke, D.N. Averaging of elastic constants for polycrystals. J. Appl. Phys. 2017, 122, 145110. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Eyert, V. Basic notions and applications of the augmented spherical wave method. Int. J. Quantum Chem. 2000, 77, 1007–1031. [Google Scholar] [CrossRef]
- Mukhanov, V.A.; Kurakevych, O.O.; Solozhenko, V.L. The interrelation between hardness and compressibility of substances and their structure and thermodynamic properties. J. Superhard Mater. 2008, 30, 368–378. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef]
- Mazhnik, E.; Oganov, A.R. A model of hardness and fracture toughness of solids. J. Appl. Phys. 2019, 126, 125109. [Google Scholar] [CrossRef]
- Chen, X.-Q.; Niu, H.; Li, D.; Li, Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Matar, S.F. Prediction of novel ultrahard phases in the B–C–N system from first principles: Progress and problems. Materials 2023, 16, 886. [Google Scholar] [CrossRef]
- Bindzus, N.; Straasø, T.; Wahlberg, N.; Becker, J.; Bjerg, L.; Lock, N.; Dippel, A.-C.; Iversen, B.B. Experimental determination of core electron deformation in diamond. Acta Cryst. A 2014, 70, 39–48. [Google Scholar] [CrossRef]
- Ownby, P.D.; Yang, X.; Liu, J. Calculated X-ray diffraction data for diamond polytypes. J. Am. Ceram. Soc. 1992, 75, 1876–1883. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Chernyshev, V.V.; Fetisov, G.V.; Rybakov, V.B.; Petrusha, I.A. Structure analysis of the cubic boron nitride crystals. J. Phys. Chem. Solids 1990, 51, 1011–1012. [Google Scholar] [CrossRef]
- Zhang, J.S.; Bass, J.D.; Taniguchi, T.; Goncharov, A.F.; Chang, Y.-Y.; Jacobsen, S.D. Elasticity of cubic boron nitride under ambient conditions. J. Appl. Phys. 2011, 109, 063521. [Google Scholar] [CrossRef]
- Kurdyumov, A.V.; Solozhenko, V.L.; Zelyavski, W.B. Lattice parameters of boron nitride polymorphous modifications as a function of their crystal-structure perfection. J. Appl. Crystallogr. 1995, 28, 540–545. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Häusermann, D.; Mezouar, M.; Kunz, M. Equation of state of wurtzitic boron nitride to 66 GPa. Appl. Phys. Lett. 1998, 72, 1691–1693. [Google Scholar] [CrossRef]
- Li, Z.; Bradt, R.C. Thermal expansion of the cubic (3C) polytype of SiC. J. Mater. Sci. 1986, 21, 4366–4368. [Google Scholar] [CrossRef]
- Lambrecht, W.R.L.; Segall, B.; Methfessel, M.; van Schilfgaarde, M. Calculated elastic constants and deformation potentials of cubic SiC. Phys. Rev. B 1991, 44, 3685–3694. [Google Scholar] [CrossRef]
- Krishnan, R.S. Raman spectrum of diamond. Nature 1945, 155, 171. [Google Scholar] [CrossRef]
- Dove, M.T. Introduction to Lattice Dynamics; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- DeSorbo, W. Specific heat of diamond at low temperatures. J. Chem. Phys. 1953, 21, 876–880. [Google Scholar] [CrossRef]
- Victor, A.C. Heat capacity of diamond at high temperatures. J. Chem. Phys. 1962, 36, 1903–1911. [Google Scholar] [CrossRef]
- Solozhenko, V.L.; Gavrichev, K.S. Thermodynamic Properties of Boron Nitride; Wide Band Gap Electronic Materials; Springer: Berlin/Heidelberg, Germany, 1995; pp. 377–392. [Google Scholar]
- Glushko, V.P.; Gurvich, L.V.; Bergman, G.A. (Eds.) Thermodynamic Properties of Individual Substances; Nauka: Moscow, Russia, 1978; Volume 2. (In Russian) [Google Scholar]
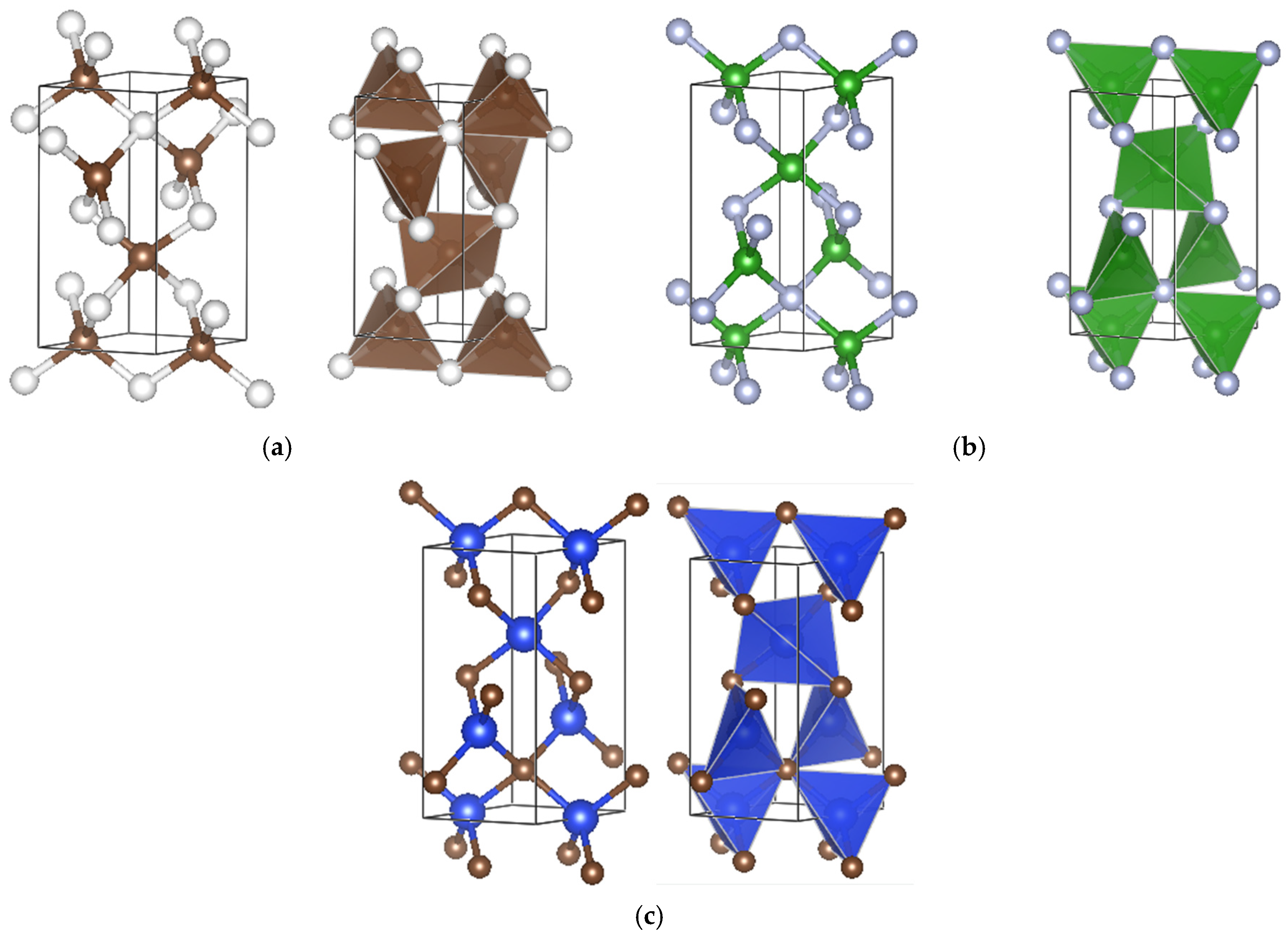


| P6422 (No. 181) | C6 (C13C23) | qtz BN | qtz SiC |
|---|---|---|---|
| a, Å | 2.598 | 2.595 | 3.079 |
| c, Å | 5.586 | 5.799 | 7.054 |
| Vcell, Å3 | 32.65 | 33.83 | 57.90 |
| <Vatom> Å3 | 5.44 | 5.64 | 9.65 |
| Shortest bond, Å | 1.598 | 1.64 | 1.936 |
| Angles (deg.) | 108.73/90.52 | 106.64/92.0 | 105.26/93.01 |
| Atomic positions | C1 (3c) ½, 0, 0 | B (3c) ½, 0, 0 | Si (3c) ½, 0, 0 |
| C2 (3d) ½, 0, ½ | N (3d) ½, 0, ½ | C (3d) ½, 0, ½ | |
| Etotal, eV | −47.87 | −46.65 | −41.79 |
| Ecoh/atom, eV | −1.38 | −1.73 | −1.15 |
| C11 | C12 | C13 | C33 | C44 | C66 | BV | GV | |
|---|---|---|---|---|---|---|---|---|
| qtz C6 [9] | 1184 | 88 | 63 | 1161 | 548 | 539 | 440 | 546 |
| qtz BN | 892 | 164 | 109 | 1013 | 364 | 342 | 396 | 370 |
| qtz SiC | 448 | 87 | 97 | 598 | 180 | 201 | 228 | 197 |
| Space Group | a = b (Å) | c (Å) | ρ (g/cm3) | HV (GPa) | B0 (GPa) | |
|---|---|---|---|---|---|---|
| Diamond | Fd-3m | 3.56661 [31] | 3.517 | 98 | 445 [1] | |
| Lonsdaleite | P63/mmc | 2.5221 [32] | 4.1186 [32] | 3.516 | 97 | 443 |
| qtz C3 #180 [7] | P6222 | 2.605 [7] | 2.801 [7] | 3.635 | 101 | 460 |
| qtz C3 #180 [8] | P6222 | 2.613 [8] | 2.811 [8] | 3.600 | 100 | 456 |
| qtz C6 #181 | P6222 | 2.5970 | 5.5865 | 3.667 | 102 | 464 |
| c-BN #216 | F-43m | 3.6160 [33] | 3.487 | 55 | 381 [34] | |
| w-BN #186 | P63/mc | 2.5505 [35] | 4.210 [35] | 3.475 | 54 | 375 [36] |
| qtz BN #181 | P6422 | 2.5954 | 5.7993 | 3.654 | 58 | 395 |
| SiC (3C) #216 | F-43m | 4.3581 [37] | 3.218 | 34 | 238 | |
| qtz SiC #180 | P6222 | 3.0787 | 7.0537 | 3.450 | 36 | 255 |
| HV | B | GV | E ** | ν ** | KIc ‡ | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| T * | LO † | MO ‡ | CN § | B0 * | BV | |||||
| GPa | MPa·m½ | |||||||||
| Diamond | 98 | 90 | 100 | 93 | 445 [1] | 530 [1] | 1138 | 0.074 | 6.4 | |
| Lonsdaleite | 97 | 90 | 99 | 94 | 443 | 432 | 521 | 1115 | 0.070 | 6.2 |
| qtz C3 #180 [7] | 101 | 90 | – | 88 [7] | 460 | 433 [7] | – | – | – | – |
| qtz C3 #180 [8] | 100 | 88 | 113 [8] | 110 | 456 | 452 [8] | 587 [8] | 1229 | 0.047 | 6.8 |
| qtz C6 #181 | 102 | 90 | 104 | 100 | 464 | 440 | 546 | 1159 | 0.061 | 6.4 |
| c-BN #216 | 55 | 50 | 73 | 67 | 381 [34] | 399 [34] | 887 | 0.112 | 4.8 | |
| w-BN #186 | 54 | 50 | 72 | 65 | 375 [36] | 390 | 397 | 889 | 0.120 | 5.1 |
| qtz BN #181 | 58 | 51 | 63 | 56 | 395 | 396 | 370 | 847 | 0.143 | 6.4 |
| SiC (3C) #216 | 34 | 30 | 32 | 35 | 238 | 225 †† | 199 †† | 461 †† | 0.153 †† | 3.3 |
| qtz SiC #180 | 36 | 31 | 31 | 34 | 255 | 228 | 197 | 460 | 0.165 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matar, S.F.; Solozhenko, V.L. Ultrahigh-Density Superhard Hexagonal BN and SiC with Quartz Topology from Crystal Chemistry and First Principles. Crystals 2023, 13, 1498. https://doi.org/10.3390/cryst13101498
Matar SF, Solozhenko VL. Ultrahigh-Density Superhard Hexagonal BN and SiC with Quartz Topology from Crystal Chemistry and First Principles. Crystals. 2023; 13(10):1498. https://doi.org/10.3390/cryst13101498
Chicago/Turabian StyleMatar, Samir F., and Vladimir L. Solozhenko. 2023. "Ultrahigh-Density Superhard Hexagonal BN and SiC with Quartz Topology from Crystal Chemistry and First Principles" Crystals 13, no. 10: 1498. https://doi.org/10.3390/cryst13101498
APA StyleMatar, S. F., & Solozhenko, V. L. (2023). Ultrahigh-Density Superhard Hexagonal BN and SiC with Quartz Topology from Crystal Chemistry and First Principles. Crystals, 13(10), 1498. https://doi.org/10.3390/cryst13101498






