A Comparison Study of Roseolumiflavin Solvates: Structural and Energetic Perspective on Their Stability
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. X-ray Measurements
2.3. Thermogravimetric Analysis (TGA)
2.4. FTIR Measurements
2.5. Chemicals
2.6. Software
3. Results
3.1. Single Crystal X-ray Diffraction (SCXRD)
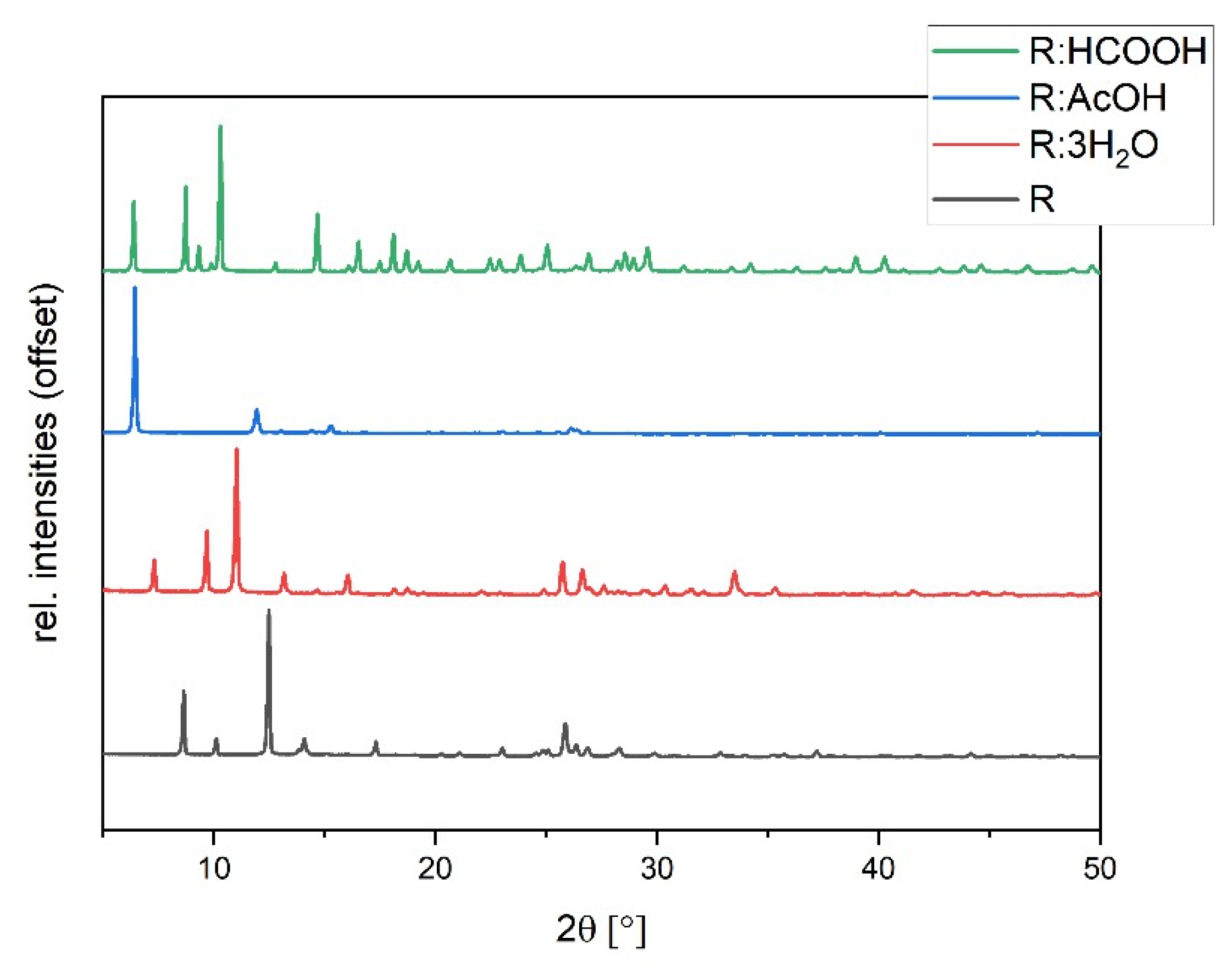
3.2. Powder X-ray Diffraction (PXRD)
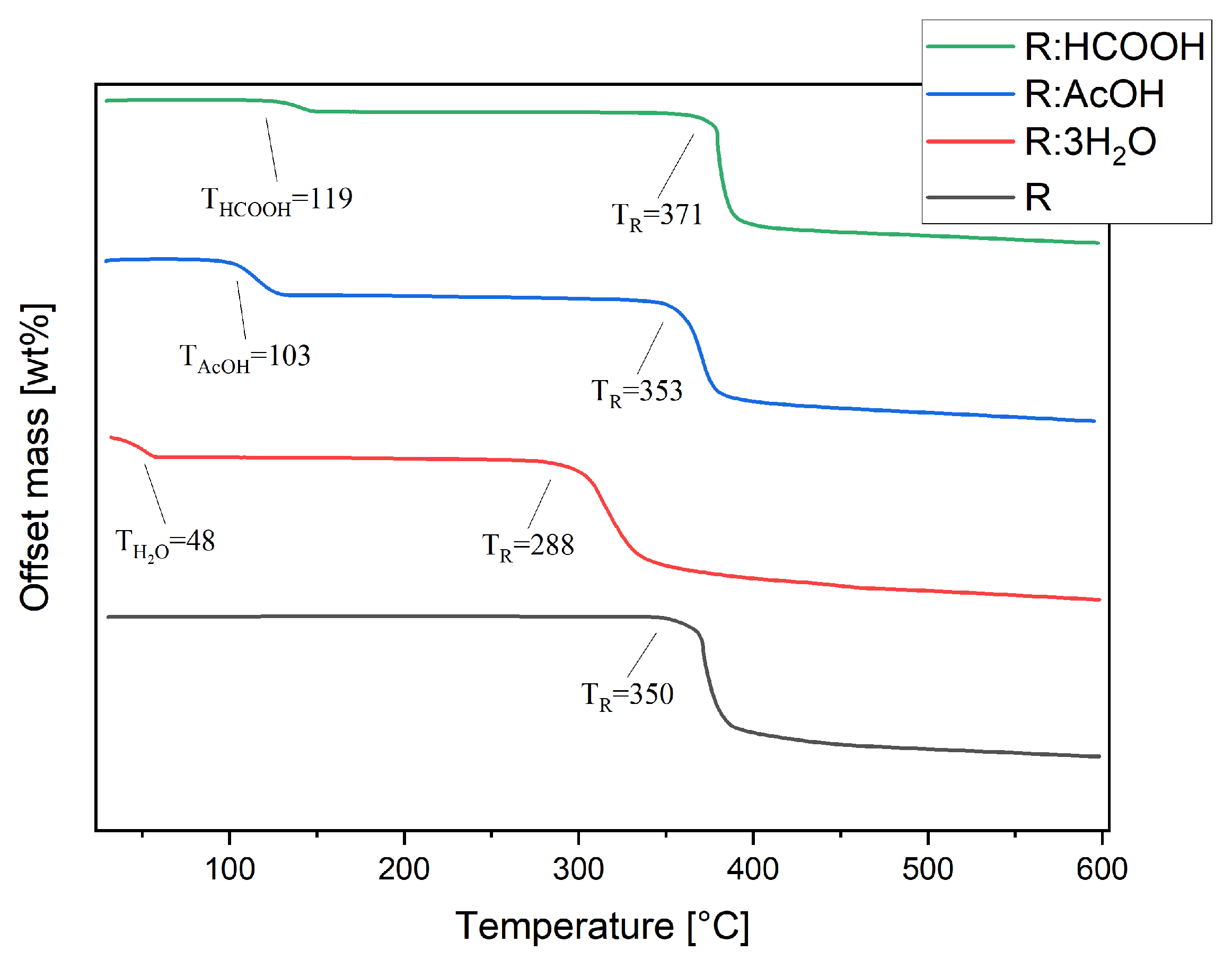
3.3. Thermogravimetric Analysis (TGA)
3.4. Computational Studies
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haj Hassani Sohi, T.; Maass, F.; Czekelius, C.; Suta, M.; Vasylyeva, V. Co-crystallization of organic chromophore roseolumiflavin and effect on its optical characteristics. CrystEngComm 2022, 24, 7315–7325. [Google Scholar] [CrossRef]
- Bera, M.K.; Pal, P.; Malik, S. Solid-state emissive organic chromophores: Design, strategy and building blocks. J. Mater. Chem. C 2020, 8, 788–802. [Google Scholar] [CrossRef]
- Singh, M.; Liu, K.; Qu, S.; Ma, H.; Shi, H.; An, Z.; Huang, W. Recent advances of cocrystals with room temperature phosphorescence. Adv. Opt. Mater. 2021, 9, 2002197. [Google Scholar] [CrossRef]
- Griesser, U.J. The importance of solvates. In Polymorphism in the Pharmaceutical Industry; Hilfiker, R., Ed.; Wiley-VCH: Weinheim, Germany, 2006; pp. 211–233. ISBN 9783527311460. [Google Scholar]
- Boothroyd, S.; Kerridge, A.; Broo, A.; Buttar, D.; Anwar, J. Why do some molecules form hydrates or solvates? Cryst. Growth Des. 2018, 18, 1903–1908. [Google Scholar] [CrossRef]
- Healy, A.M.; Worku, Z.A.; Kumar, D.; Madi, A.M. Pharmaceutical solvates, hydrates and amorphous forms: A special emphasis on cocrystals. Adv. Drug Deliv. Rev. 2017, 117, 25–46. [Google Scholar] [CrossRef]
- Seddon, K.R. Pseudo polymorph: A polemic. Cryst. Growth Des. 2004, 4, 1087. [Google Scholar] [CrossRef]
- Desiraju, G.R. Counterpoint: What’s in a name? Cryst. Growth Des. 2004, 4, 1089–1090. [Google Scholar] [CrossRef]
- Bernstein, J. And another comment on pseudo-polymorphism. Cryst. Growth Des. 2005, 5, 1661–1662. [Google Scholar] [CrossRef]
- Nangia, A. Pseudopolymorph: Retain this widely accepted term. Cryst. Growth Des. 2006, 6, 2–4. [Google Scholar] [CrossRef]
- Grothe, E.; Meekes, H.; Vlieg, E.; Ter Horst, J.H.; de Gelder, R.D. Solvates, salts, and cocrystals: A proposal for a feasible classification system. Cryst. Growth Des. 2016, 16, 3237–3243. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Vittal, J.J.; Ramanan, A. Crystal Engineering: A Textbook; World Scientific: Singapore, 2011; ISBN 978-981-4338-75-2. [Google Scholar]
- Aakeröy, C.B.; Seddon, K.R. The hydrogen bond and crystal engineering. Chem. Soc. Rev. 1993, 22, 397–407. [Google Scholar] [CrossRef]
- Videnova-Adrabińska, V. The hydrogen bond as a design element in crystal engineering. Two- and three-dimensional building blocks of crystal architecture. J. Mol. Struct. 1996, 374, 199–222. [Google Scholar] [CrossRef]
- Komisarek, D.; Pallaske, M.; Vasylyeva, V. Crystal structure and thermal properties of phenibut, phenibut H2O and phenibut HCl: A case for phase stability based on structural considerations. Z. Anorg. Allg. Chemie 2021, 647, 984–991. [Google Scholar] [CrossRef]
- Heinen, T.; Hoelscher, S.; Vasylyeva, V. Structural study of anhydrous and hydrated 5-fluorouracil co-crystals with nicotinamide and isonicotinamide. Z. Kristallogr.—Cryst. Mater. 2022, 237, 109–116. [Google Scholar] [CrossRef]
- Karasulu, B.; Thiel, W. Photoinduced intramolecular charge transfer in an electronically modified flavin derivative: Roseoflavin. J. Phys. Chem. B 2015, 119, 928–943. [Google Scholar] [CrossRef] [PubMed]
- Scarbrough, F.E.; Shieh, H.-S.; Voet, D. The X-ray crystal structure of the molecular complex bis(lumiflavin–2,6-diamino-9-ethylpurine)–ethanol–water. Acta Crystallogr. B Struct. Sci. 1977, 33, 2512–2523. [Google Scholar] [CrossRef]
- Wells, J.L.; Trus, B.L.; Johnston, R.M.; Marsh, R.E.; Fritchie, C.J. Crystal structure of the yellow molecular complex lumiflavin–bis(naphthalene-2,3-diol). Acta Crystallogr. B Struct. Sci. 1974, 30, 1127–1134. [Google Scholar] [CrossRef]
- Kuo, M.C.; Dunn, J.B.R.; Fritchie, C.J. The crystal structure of a flavin molecular complex: 10-propylisoalloxazine–bis(naphthalene-2,3-diol). Acta Crystallogr. B Struct. Sci. 1974, 30, 1766–1771. [Google Scholar] [CrossRef]
- Voet, D.; Rich, A. The crystal and molecular structure of an intermolecular complex between riboflavin and an adenosine derivative. Proc. Natl. Acad. Sci. USA 1971, 68, 1151–1156. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: Extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef] [PubMed]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef] [PubMed]
- CrysAlisPRO, v171.42; Oxford Diffraction/Agilent Technologies UK Ltd.: Yarnton, UK, 2022.
- APEX2, v2012; Bruker AX Inc.: Madison, WI, USA, 2012.
- SAINT, v2018; Bruker Analytical X-ray Systems: Madison, WI, USA, 2018.
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. A Found. Adv. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Komisarek, D.; Haj Hassani Sohi, T.; Vasylyeva, V. Co-crystals of zwitterionic GABA API’s pregabalin and phenibut: Properties and application. CrystEngComm 2022, 24, 8390–8398. [Google Scholar] [CrossRef]
- Emamian, S.; Lu, T.; Kruse, H.; Emamian, H. Exploring nature and predicting strength of hydrogen bonds: A correlation analysis between Atoms-in-Molecules descriptors, binding energies, and energy components of symmetry-adapted perturbation theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D Biol. Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef]
- Etter, M.C.; MacDonald, J.C.; Bernstein, J. Graph-set analysis of hydrogen-bond patterns in organic crystals. Acta Crystallogr. B 1990, 46, 256–262. [Google Scholar] [CrossRef]
- Bader, R.; Nguyen-Dang, T.T. Quantum Theory of Atoms in Molecules–Dalton Revisited; Elsevier: Amsterdam, The Netherlands, 1981; pp. 63–124. ISBN 9780120348145. [Google Scholar]
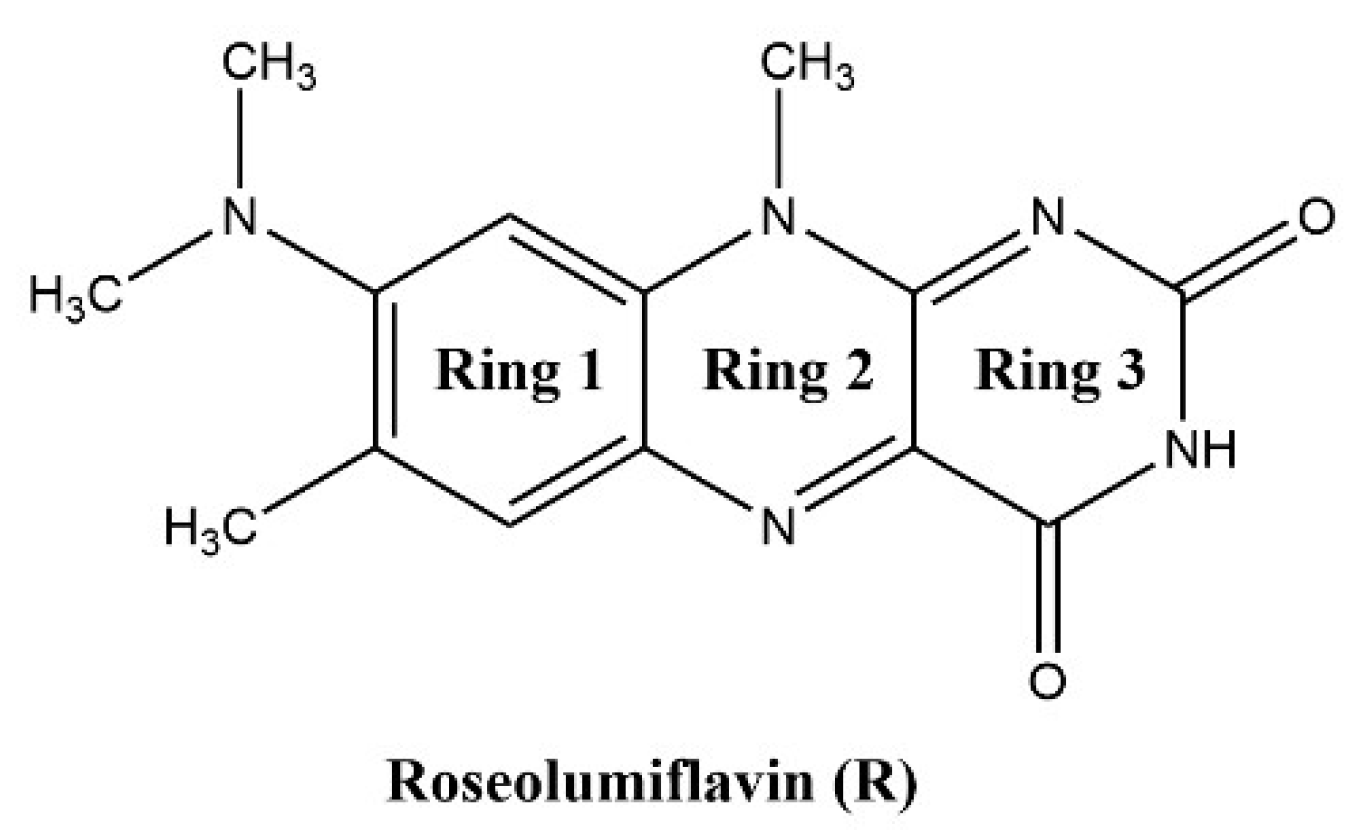
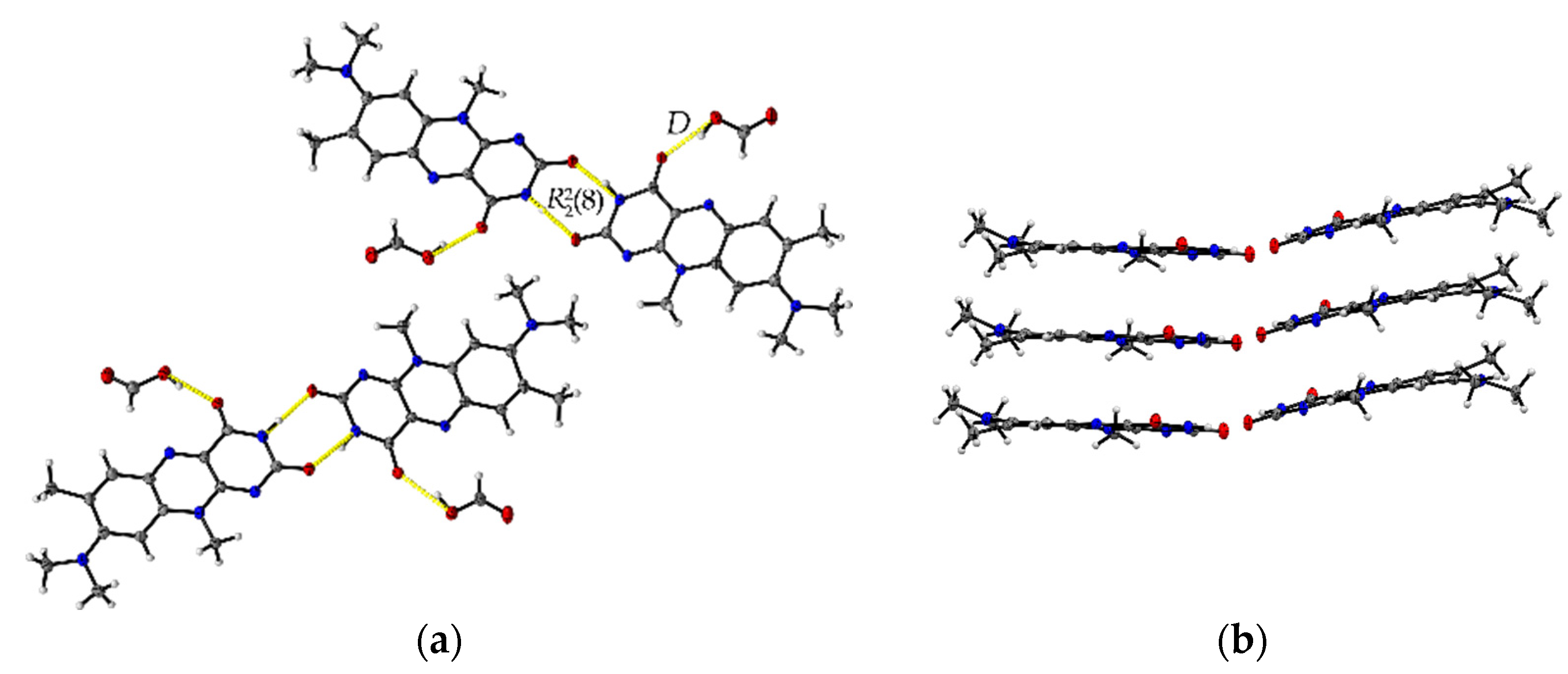
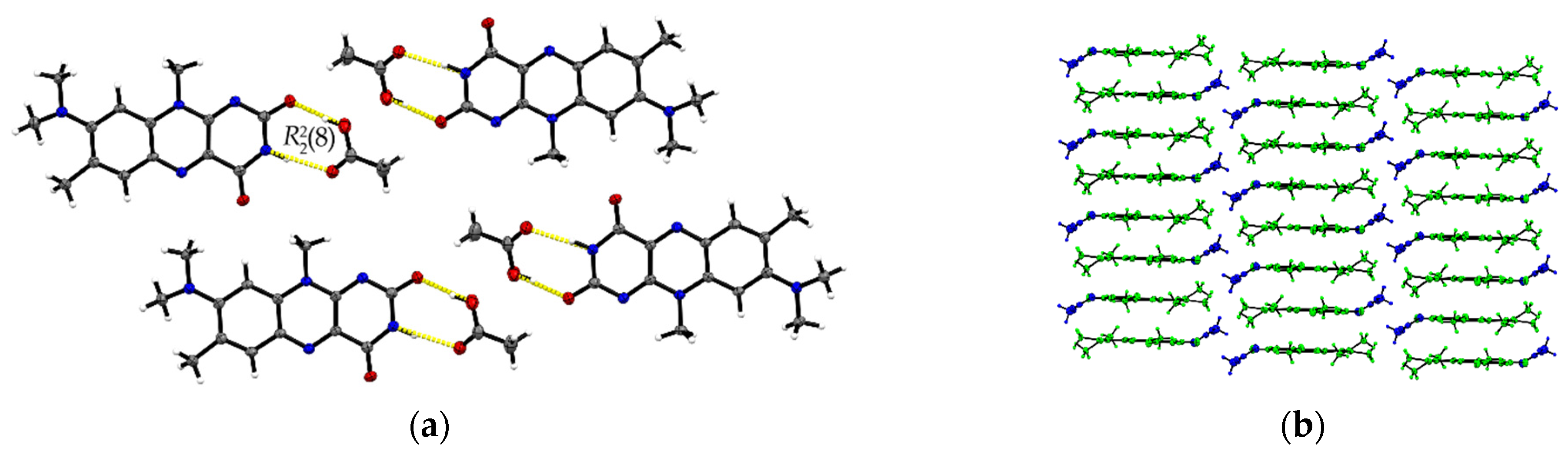
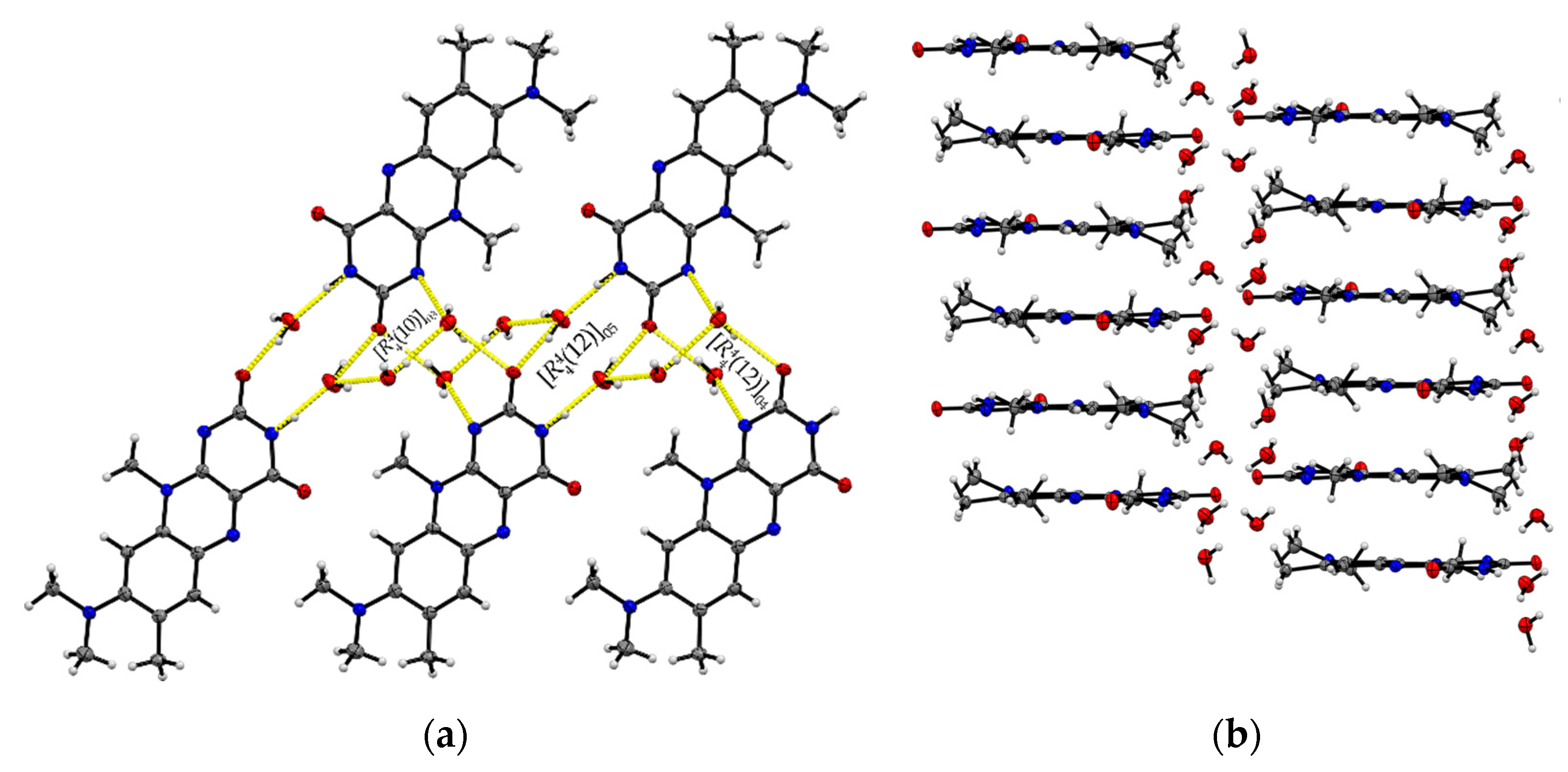

| Name | R:HCOOH | R:AcOH | R:3H2O | R:AcOH:H2O |
|---|---|---|---|---|
| Empirical formula | C14H15N5O2, CO2H2 | C14H15N5O2, C2H4O2 | C14H15N5O2, 3(H2O) | C14H15N5O2, C2H4O2, H2O |
| Molecular weight [g/mol] | 331.33 | 345.36 | 339.36 | 363.38 |
| Temperature [K] | 100(10) | 140(2) | 140(2) | 140(2) |
| Space group | P21 | P | P | P21/c |
| Crystal system | monoclinic | triclinic | triclinic | monoclinic |
| a [Å] | 3.79570(10) | 7.8393(7) | 6.852(6) | 7.1439(9) |
| b [Å] | 20.0858(5) | 8.2797(7) | 9.281(8) | 15.574(2) |
| c [Å] | 18.9737(6) | 14.0559(12) | 12.685(11) | 15.2510(19) |
| α [°] | 90 | 73.647(5) | 79.26(3) | 90 |
| β [°] | 93.755(3) | 77.917(5) | 74.75(3) | 1689.5(4) |
| γ [°] | 90 | 67.478(5) | 87.10(3) | 90 |
| Volume [Å3] | 1443.44(7) | 803.34(13) | 764.6(11) | 1689.5(4) |
| Z/Z’ | 4/2 | 2/1 | 2/1 | 4/1 |
| ρcalc [g/cm3] | 1.525 | 1.428 | 1.474 | 1.429 |
| µ [1/mm] | 0.953 | 0.106 | 0.114 | 0.108 |
| Tmin/Tmax | 0.698/1.000 | 0.959/0.993 | 0.945/0.989 | 0.979/0.996 |
| F(000) | 696 | 364 | 360 | 768 |
| Crystal size [mm3] | 0.01 × 0.02 × 0.18 | 0.07 × 0.08 × 0.40 | 0.10 × 0.10 × 0.50 | 0.04 × 0.10 × 0.20 |
| θ range[°] | 3.1690/76.7990 | 1.520/26.000 | 1.691/24.996 | 1.873/25.990 |
| Completeness [%] | 99.0 | 99.2 | 99.4 | 99.8 |
| Recorded reflections | 4600 | 9851 | 10180 | 12686 |
| Independent reflections | 4165 | 3139 | 2667 | 3310 |
| Goodness-of-fit F2 | 1.057 | 1.047 | 1.026 | 1.037 |
| X-ray source | CuKα (λ = 1.54184 Å) | MoKα (λ = 0.71073 Å) | MoKα (λ = 0.71073 Å) | MoKα (λ = 0.71073 Å) |
| R1/wR2 | 0.0527/0.1474 | 0.0534/0.1584 | 0.0796/0.2499 | 0.0432/0.1205 |
| Structure | Quantum Espresso | Crystal Explorer | AIM | Intermolecular Interaction |
|---|---|---|---|---|
| Elat [kJ/mol] | Etot [kJ/mol] | BEestimated [kJ/mol] | ||
| R | −181.06 | −113.4 | - | cofacial π···π stack |
| −127.1 | - | cofacial π···π stack | ||
| −43.4 | −19.34 | N2-H···O2 | ||
| −19.34 | N2-H···O2 | |||
| −36.5 | −5.56 −5.11 −2.32 −2.09 | C11-H···O1 C13-H···O1 C13-H···N1 C6-H···O1 | ||
| R:HCOOH | −197.58 | −58.5 | −31.15 | O3-H···O1 |
| −27.75 | O7-H···O5 | |||
| −41.6 | −25.88 | O6···H-N2 | ||
| −22.88 | N7-H···O2 | |||
| −36.5 | - | cofacial π···π stack | ||
| −33.2 | −8.95 | C28-H···O6 | ||
| −4.88 | C13-H···O5 | |||
| R:AcOH | −283.55 | −110.0 | - | cofacial π···π stack |
| −70.5 | - | offset π···π stack | ||
| −64.9 | - | offset π···π stack | ||
| −62.0 | −35.95 | O2···H-O3 | ||
| −21.02 | N2-H···O4 | |||
| R:AcOH:H2O | −352.46 | −116.3 | - | cofacial π···π stack |
| −70.5 | - | offset π···π stack | ||
| −34.8 | −23.38 | O4···H-O5 | ||
| −30.8 | −3.57 | O3···H-C1 | ||
| R:3H2O | −395.82 | −110.7 | - | cofacial π···π stack |
| −104.6 | - | cofacial π···π stack | ||
| −32.6 | −0.92 | C6-H···O2 | ||
| −32.4 | −2.69 | C11-H···O2 | ||
| −2.60 | C13-H···O2 | |||
| −18.35 | O1···H-O4 | |||
| −26.5 −25.1 −18.0 | −22.94 −30.11 −10.68 | O1···H-O5 N2-H···O5 N3···H-O4 |
| Structure | π⋯π | π⋯π [Å] |
|---|---|---|
| R | Ring 2–Ring 3 i | 3.576(4) and 3.6280(13) |
| R:AcOH | Ring 2–Ring 2 i Ring 1–Ring 3 i | 3.4567(13) 3.5008(14) |
| R:3H2O | Ring 2–Ring 2 ii Ring 1–Ring 3 ii | 3.697(4) and 3.678(4) 3.678(4) and 3.597(4) |
| R:AcOH:H2O | Ring 2–Ring 2 iii Ring 1–Ring 3 iii | 3.5545(9) 3.5732(10) |
| R:HCOOH | Ring 1–Ring 1 iv Ring 2–Ring 2 iv Ring 3–Ring 3 iv | 3.796(3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haj Hassani Sohi, T.; Maass, F.; Czekelius, C.; Vasylyeva, V. A Comparison Study of Roseolumiflavin Solvates: Structural and Energetic Perspective on Their Stability. Crystals 2023, 13, 1512. https://doi.org/10.3390/cryst13101512
Haj Hassani Sohi T, Maass F, Czekelius C, Vasylyeva V. A Comparison Study of Roseolumiflavin Solvates: Structural and Energetic Perspective on Their Stability. Crystals. 2023; 13(10):1512. https://doi.org/10.3390/cryst13101512
Chicago/Turabian StyleHaj Hassani Sohi, Takin, Felix Maass, Constantin Czekelius, and Vera Vasylyeva. 2023. "A Comparison Study of Roseolumiflavin Solvates: Structural and Energetic Perspective on Their Stability" Crystals 13, no. 10: 1512. https://doi.org/10.3390/cryst13101512
APA StyleHaj Hassani Sohi, T., Maass, F., Czekelius, C., & Vasylyeva, V. (2023). A Comparison Study of Roseolumiflavin Solvates: Structural and Energetic Perspective on Their Stability. Crystals, 13(10), 1512. https://doi.org/10.3390/cryst13101512







