Optimization of Additively Manufactured and Lattice-Structured Hip Implants Using the Linear Regression Algorithm from the Scikit-Learn Library
Abstract
:1. Introduction
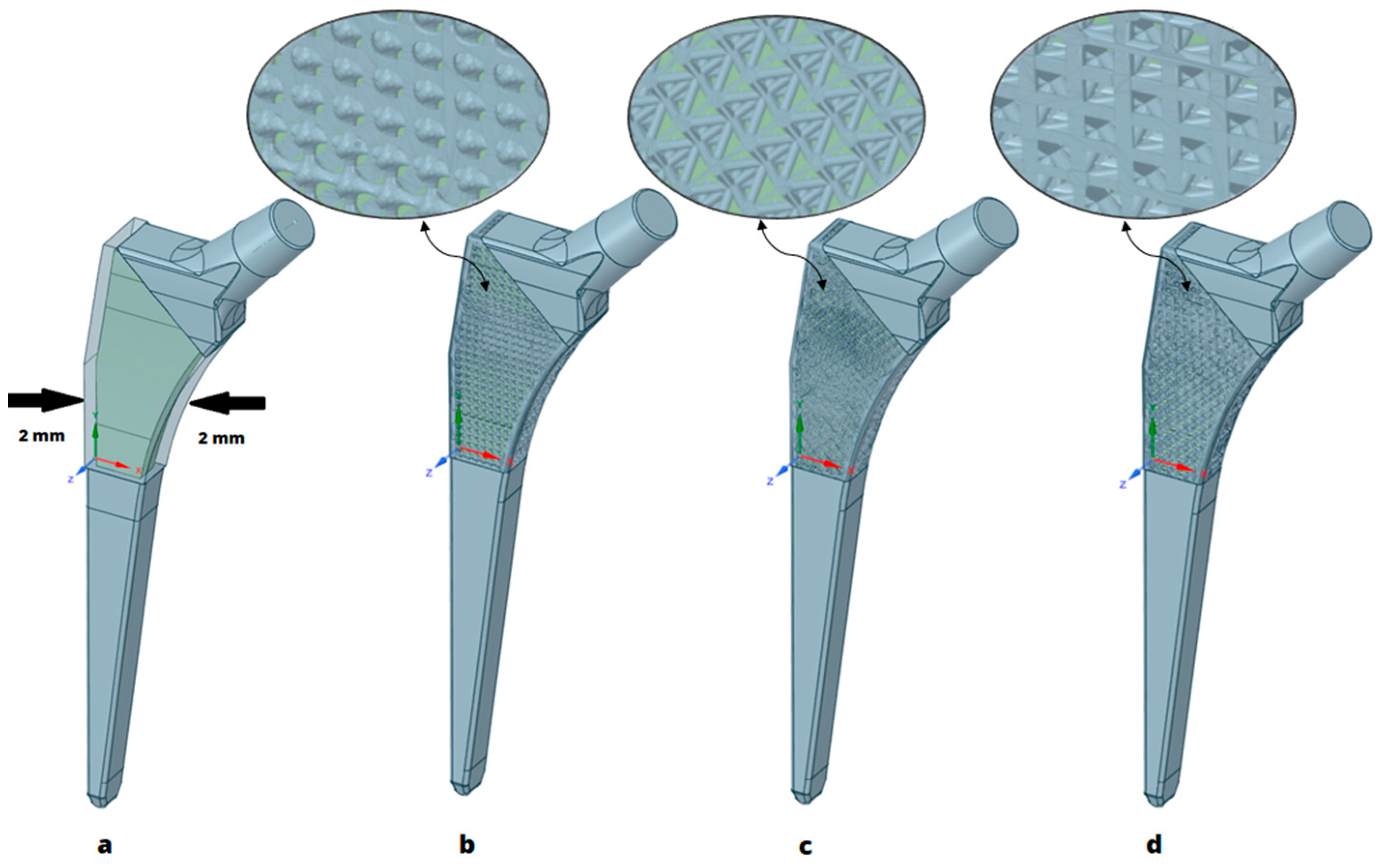
2. Materials and Methods
- where y is the dependent variable, x1, x2, …, xn are the independent variables, β0 is the intercept, and β1, β2, …, βn are the coefficients. The linear regression algorithm aims at estimating the values of the coefficients (β0, β1, β2, …, βn) in a way that minimizes the sum of the squared errors. This procedure, followed by the scikit-learn library, is called the ordinary least squares (OLS) method [44].
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, S.; Zhang, Z.; Gu, G.X. Generative machine learning algorithm for lattice structures with superior mechanical properties. Mater. Horiz. 2022, 9, 952–960. [Google Scholar] [CrossRef] [PubMed]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Abdulhadi, H.S.; Mian, A. Effect of strut length and orientation on elastic mechanical response of modified body-centered cubic lattice structures. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 2219–2233. [Google Scholar] [CrossRef]
- Lancea, C.; Campbell, I.; Chicos, L.-A.; Zaharia, S.-M. Compressive Behaviour of Lattice Structures Manufactured by Polyjet Technologies. Polymers 2020, 12, 2767. [Google Scholar] [CrossRef]
- Arabnejad, S.; Johnston, R.B.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-strength porous biomaterials for bone replacement: A strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef]
- Pobloth, A.M.; Checa, S.; Razi, H.; Petersen, A.; Weaver, J.C.; Schmidt-Bleek, K.; Windolf, M.; Tatais, A.A.; Roth, C.P.; Schaser, K.D.; et al. Mechanobiologically optimized 3D titanium-mesh scaffolds enhance bone regeneration in critical segmental defects in sheep. Sci. Transl. Med. 2018, 10, eaam8828. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, H.; Wang, C.; Zhou, L.; Yuan, S.; Zhang, W. A review of topology optimization for additive manufacturing: Status and challenges. Chinese J. Aeronaut. 2021, 34, 91–110. [Google Scholar] [CrossRef]
- Brackett, D.; Ashcroft, I.; Hague, R. Topology Optimization for Additive Manufacturing. 2011. Available online: https://repositories.lib.utexas.edu/bitstream/handle/2152/88361/2011-27-Brackett.pdf?sequence=2&isAllowed=y (accessed on 1 September 2023).
- Plocher, J.; Panesar, A. Review on design and structural optimisation in additive manufacturing: Towards next-generation lightweight structures. Mater. Des. 2019, 183, 108164. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.L.C.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput. Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- E Murr, L.; M Gaytan, S.; Martinez, E. Fabricating Functional Ti-Alloy Biomedical Implants by Additive Manufacturing Using Electron Beam Melting. J. Biotechnol. Biomater. 2012, 2. [Google Scholar] [CrossRef]
- Kolan, K.; Leu, M.; Hilmas, G.; Comte, T. Effect of Architecture and Porosity on Mechanical Properties of Borate Glass Scaffolds Made by Selective Laser Sintering. Available online: https://www.semanticscholar.org/paper/Effect-of-Architecture-and-Porosity-on-Mechanical-Kolan-Leu/c115808cc26351f8f3f51f8cc5d4deca007b1ec4 (accessed on 17 September 2023).
- Thomas, A.; Kolan, K.C.R.; Leu, M.C.; Hilmas, G.E. Freeform Extrusion Fabrication of Titanium Fiber Reinforced Bioactive Glass Scaffolds. 2015. Available online: https://repositories.lib.utexas.edu/bitstream/handle/2152/89448/2015-134-Thomas.pdf?sequence=2&isAllowed=y (accessed on 17 September 2023).
- Grant, P.S.; Castles, F.; Lei, Q.; Wang, Y.; Janurudin, J.M.; Isakov, D.; Speller, S.; Dancer, C.; Grovenor, C.R.M. Manufacture of electrical and magnetic graded and anisotropic materials for novel manipulations of microwaves. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140353. [Google Scholar] [CrossRef] [PubMed]
- Cortis, G.; Mileti, I.; Nalli, F.; Palermo, E.; Cortese, L. Additive manufacturing structural redesign of hip prostheses for stress-shielding reduction and improved functionality and safety. Mech. Mater. 2022, 165, 104173. [Google Scholar] [CrossRef]
- Alabort, E.; Barba, D.; Reed, R.C. Design of metallic bone by additive manufacturing. Scr. Mater. 2019, 164, 110–114. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Bone tissue regeneration: The role of scaffold geometry. Biomater. Sci. 2015, 3, 231–245. [Google Scholar] [CrossRef]
- Fan, M.; Zeng, T.; Wu, R.; Cui, Y.; Xu, G.; Wang, X.; Cheng, S.; Zhao, J. Microstructure design and mechanical properties of 3D printed graded lattice sandwich structures with tailored porosity. Compos. Struct. 2023, 321, 117323. [Google Scholar] [CrossRef]
- Challapalli, A.; Li, G. Machine learning assisted design of new lattice core for sandwich structures with superior load carrying capacity. Sci. Rep. 2021, 11, 18552. [Google Scholar] [CrossRef]
- Loonen, R.C.; de Vries, S.; Goia, F. 15—Inverse design for advanced building envelope materials, systems and operation. In Rethinking Building Skins; Gasparri, E., Brambilla, A., Lobaccaro, G., Goia, F., Andaloro, A., Sangiorgio, A., Eds.; Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Sawston, UK, 2022; pp. 377–402. [Google Scholar]
- Yu, G.; Xiao, L.; Song, W. Deep learning-based heterogeneous strategy for customizing responses of lattice structures. Int. J. Mech. Sci. 2022, 229, 107531. [Google Scholar] [CrossRef]
- Wang, J.; Panesar, A. Machine learning based lattice generation method derived from topology optimisation. Addit. Manuf. 2022, 60, 103238. [Google Scholar] [CrossRef]
- Ma, S.; Tang, Q.; Liu, Y.; Feng, Q. Prediction of Mechanical Properties of Three-Dimensional Printed Lattice Structures through Machine Learning. J. Comput. Inf. Sci. Eng. 2021, 22, 031008. [Google Scholar] [CrossRef]
- Challapalli, A.; Patel, D.; Li, G. Inverse machine learning framework for optimizing lightweight metamaterials. Mater. Des. 2021, 208, 109937. [Google Scholar] [CrossRef]
- Ghatak, R.; Gorai, A. Metamaterials: Engineered Materials and Its Applications in High Frequency Electronics; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Zheng, X.; Guo, X.; Watanabe, I. A mathematically defined 3D auxetic metamaterial with tunable mechanical and conduction properties. Mater. Des. 2021, 198, 109313. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, T.-T.; Guo, X.; Samitsu, S.; Watanabe, I. Controllable inverse design of auxetic metamaterials using deep learning. Mater. Des. 2021, 211, 110178. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhao, Z.; Lei, H.; Wang, P. A deep learning approach for inverse design of gradient mechanical metamaterials. Int. J. Mech. Sci. 2023, 240, 107920. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, J.; Shanian, A.; Kibsey, M.; Zhao, Y.F. A hybrid deep learning approach for the design of 2D low porosity auxetic metamaterials. Eng. Appl. Artif. Intell. 2023, 123, 106413. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, Y.; Gao, L.; Wang, Z.-P. Deep-learning-based isogeometric inverse design for tetra-chiral auxetics. Compos. Struct. 2022, 280, 114808. [Google Scholar] [CrossRef]
- Hassanin, H.; Alkendi, Y.; Elsayed, M.; Essa, K.; Zweiri, Y. Controlling the Properties of Additively Manufactured Cellular Structures Using Machine Learning Approaches. Adv. Eng. Mater. 2020, 22, 1901338. [Google Scholar] [CrossRef]
- Challapalli, A.; Li, G. 3D printable biomimetic rod with superior buckling resistance designed by machine learning. Sci. Rep. 2020, 10, 20716. [Google Scholar] [CrossRef] [PubMed]
- Cilla, M.; Borgiani, E.; Martínez, J.; Duda, G.N.; Checa, S. Machine learning techniques for the optimization of joint replacements: Application to a short-stem hip implant. PLoS ONE 2017, 12, e0183755. [Google Scholar] [CrossRef]
- Bastek, J.-H.; Kumar, S.; Telgen, B.; Glaesener, R.N.; Kochmann, D.M. Inverting the structure–property map of truss metamaterials by deep learning. Proc. Natl. Acad. Sci. USA 2022, 119, e2111505119. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, N.; Liu, Y.; Chen, W. Prediction of mechanical properties of carbon fiber based on cross-scale FEM and machine learning. Compos. Struct. 2019, 212, 199–206. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, E.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. Available online: http://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html%5Cnhttp://arxiv.org/abs/1201.0490 (accessed on 18 September 2023).
- Alkentar, R.; File, M.; Mankovits, T. Investigation of the Performance of Ti6Al4V Lattice Structures Designed for Biomedical Implants Using the Finite Element Method. Materials 2022, 5, 6335. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Bhaskar, J.; Kumar, A. Design and analysis of hip implant. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Alkentar, R.; Kladovasilakis, N.; Tzetzis, D.; Mankovits, T. Effects of Pore Size Parameters of Titanium Additively Manufactured Lattice Structures on the Osseointegration Process in Orthopedic Applications: A Comprehensive Review. Crystals 2023, 13, 113. [Google Scholar] [CrossRef]
- Laory, I.; Trinh, T.N.; Smith, I.F.C.; Brownjohn, J.M.W. Methodologies for predicting natural frequency variation of a suspension bridge. Eng. Struct. 2014, 80, 211–221. [Google Scholar] [CrossRef]
- Mali, K. Everything you need to Know about Linear Regression! 2023. Available online: https://www.analyticsvidhya.com/blog/2021/10/everything-you-need-to-know-about-linear-regression/#h-simple-linear-regression (accessed on 27 September 2023).
- Biswal, A. Sklearn Linear Regression. 2023. Available online: https://www.simplilearn.com/tutorials/scikit-learn-tutorial/sklearn-linear-regression-with-examples (accessed on 20 September 2023).
- Duan, S.; Xi, L.; Wen, W.; Fang, D. Mechanical performance of topology-optimized 3D lattice materials manufactured via selective laser sintering. Compos. Struct. 2020, 238, 111985. [Google Scholar] [CrossRef]
- Allan, C. Improving the Biomechanical Profile of Additive Hip Implants with Field Optimization. Available online: https://www.ntop.com/resources/blog/improving-the-biomechanical-profile-of-additive-hip-implants-with-field-optimization/ (accessed on 29 September 2023).
- Mao, H.; Rumpler, R.; Göransson, P. An inverse method for characterisation of the static elastic Hooke’s tensors of solid frame of anisotropic open-cell materials. Int. J. Eng. Sci. 2020, 147, 103198. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, Y.; Sun, Y.; Yang, J.; Gong, Y.; Wang, K.; Zhang, Z.; Chen, X.; Bai, L. Design and mechanical testing of porous lattice structure with independent adjustment of pore size and porosity for bone implant. J. Mater. Res. Technol. 2022, 18, 3240–3255. [Google Scholar] [CrossRef]





| Unit-Cell Type | Length (mm) | Thickness (mm) | Porosity (%) |
|---|---|---|---|
| Three-dimensional-lattice infill | 1–1.6 | 0.2–1.5 | 50–83 |
| Double-pyramid lattice and face diagonals | 1.8–2.5 | 0.2–0.6 | 51–86 |
| Octahedral lattice 2 | 2–2.7 | 0.2–0.65 | 51–87 |
| Unit-Cell Type | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Three-dimensional-lattice infill | 27 | 54 | 81 |
| Double-pyramid lattice and face diagonals | 18 | 35 | 54 |
| Octahedral lattice 2 | 18 | 35 | 54 |
| Unit Cell Type | Case 1 Accuracy (%) | Case 2 Accuracy (%) | Case 3 Accuracy (%) |
|---|---|---|---|
| Three-dimensional-lattice infill | 98 | 96 | 96 |
| Double-pyramid lattice and face diagonals | 98 | 98 | 99 |
| Octahedral lattice 2 | 98 | 99 | 99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkentar, R.; Mankovits, T. Optimization of Additively Manufactured and Lattice-Structured Hip Implants Using the Linear Regression Algorithm from the Scikit-Learn Library. Crystals 2023, 13, 1513. https://doi.org/10.3390/cryst13101513
Alkentar R, Mankovits T. Optimization of Additively Manufactured and Lattice-Structured Hip Implants Using the Linear Regression Algorithm from the Scikit-Learn Library. Crystals. 2023; 13(10):1513. https://doi.org/10.3390/cryst13101513
Chicago/Turabian StyleAlkentar, Rashwan, and Tamás Mankovits. 2023. "Optimization of Additively Manufactured and Lattice-Structured Hip Implants Using the Linear Regression Algorithm from the Scikit-Learn Library" Crystals 13, no. 10: 1513. https://doi.org/10.3390/cryst13101513
APA StyleAlkentar, R., & Mankovits, T. (2023). Optimization of Additively Manufactured and Lattice-Structured Hip Implants Using the Linear Regression Algorithm from the Scikit-Learn Library. Crystals, 13(10), 1513. https://doi.org/10.3390/cryst13101513






