Study of the Unstable Rotational Dynamics of a Tor-Fullerene Molecular System
Abstract
:1. Introduction
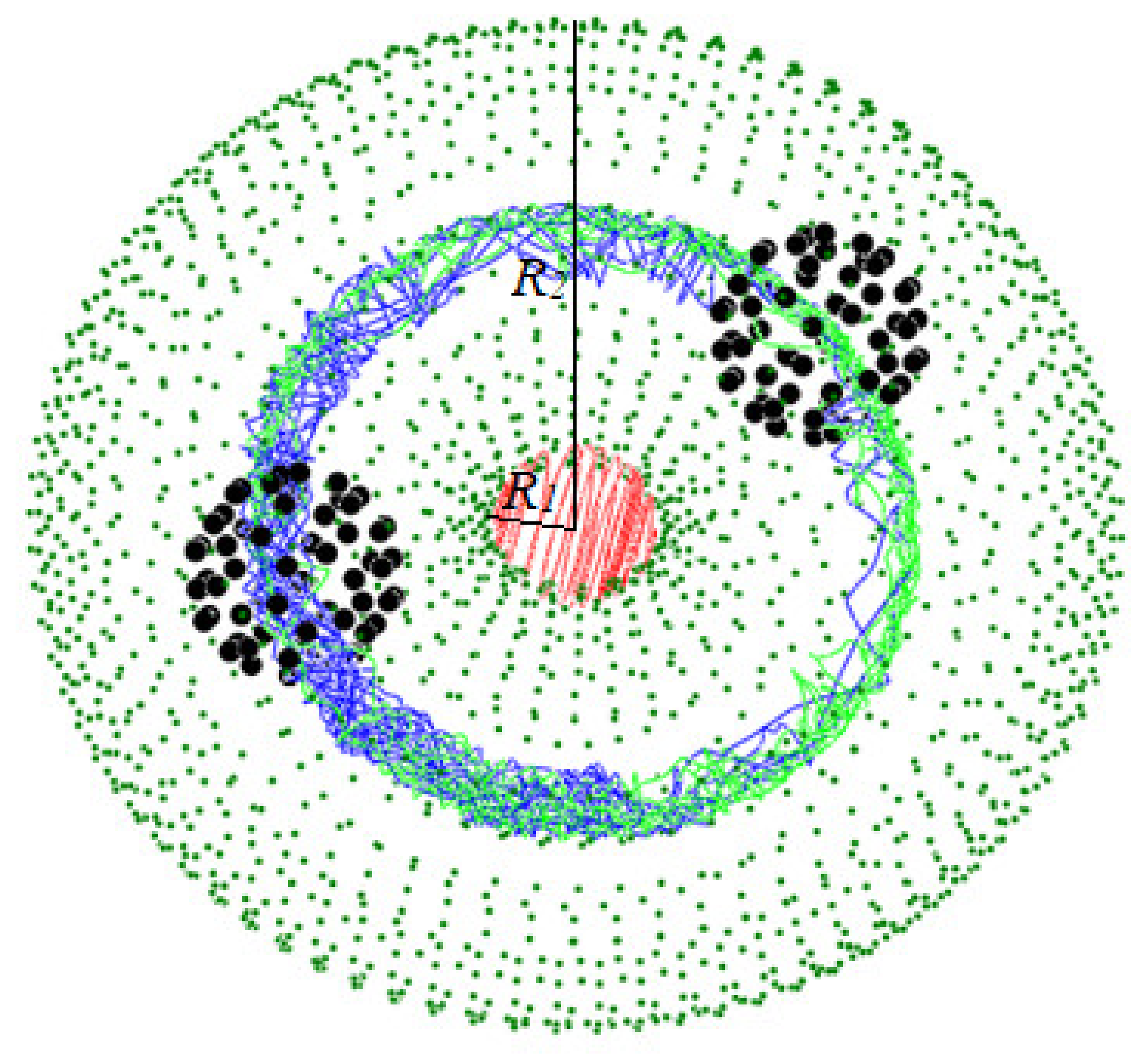
2. Computational and Theoretical Models
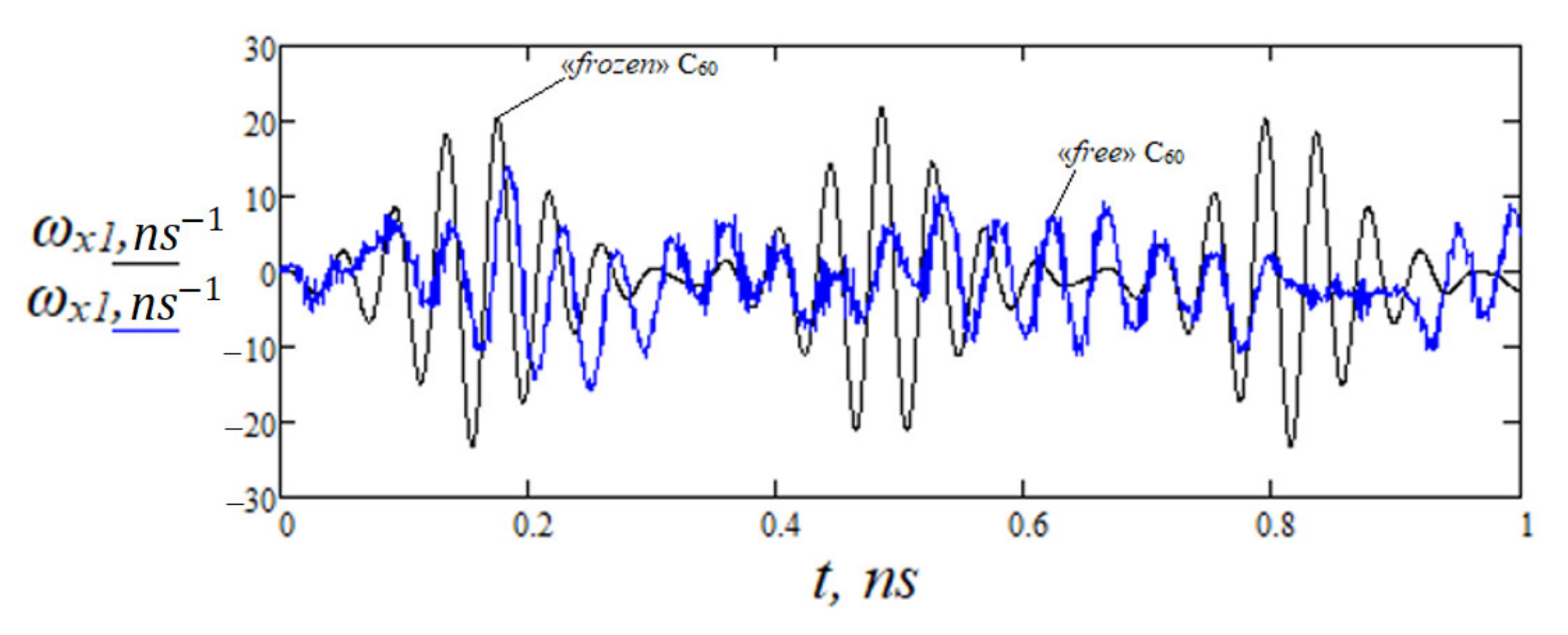
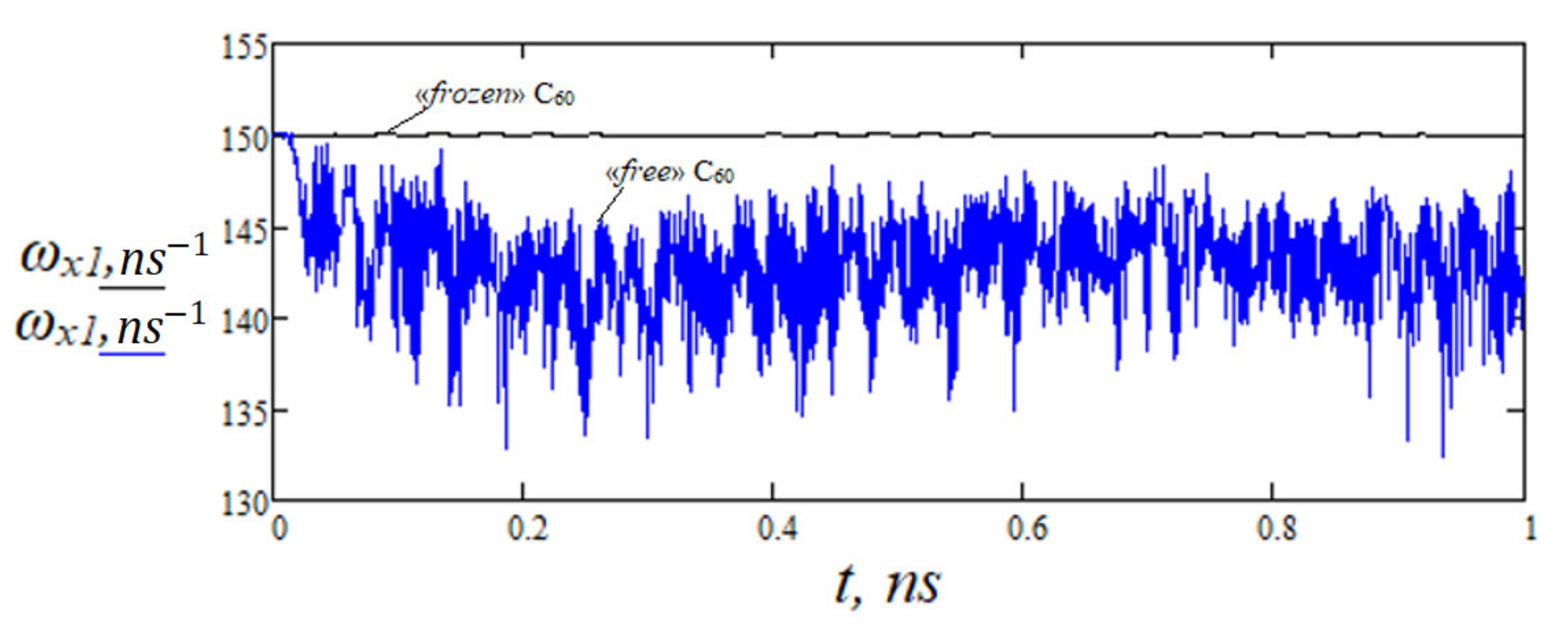
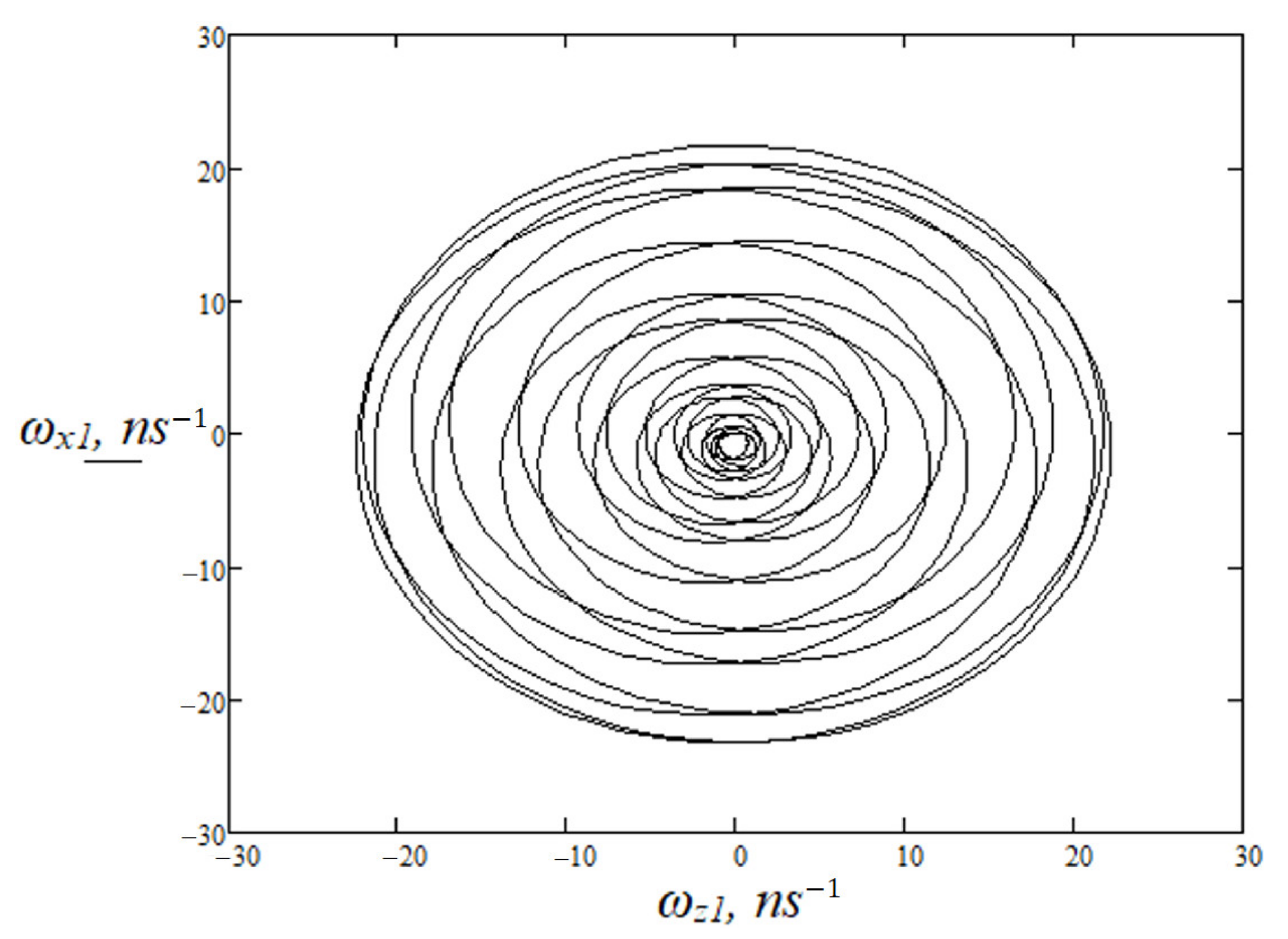
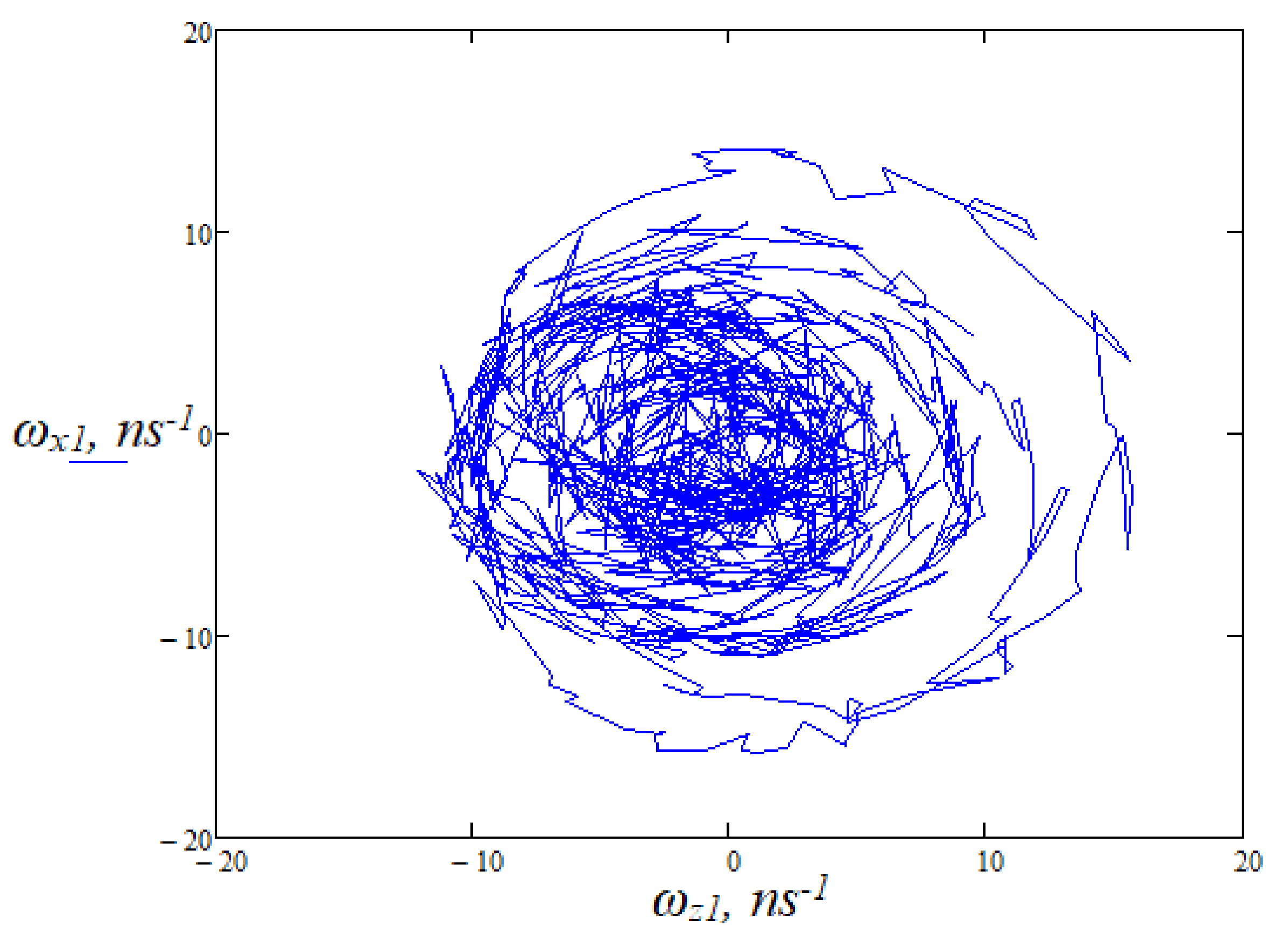
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, C.-D.; Fang, T.-H.; Chan, C.-Y. A molecular dynamics simulation of the mechanical characteristics of a C60-filled carbon nanotube under nanoindentation using various carbon nanotube tips. Carbon 2011, 49, 2053–2061. [Google Scholar] [CrossRef]
- Tu, G.-Y.; Guo, D.-P.; Li, B.-R.; Zhang, H.-L. Transport properties and mechanism of C60 coupled to carbon nanotube electrode. Phys. B Condens. Matter 2011, 406, 2138–2142. [Google Scholar] [CrossRef]
- Kang, J.W.; Hwang, H.J. Comparison of C60 encapsulations into carbon and boron nitride nanotubes. J. Phys. Condens. Matter 2004, 16, 3901. [Google Scholar] [CrossRef]
- Shokri, A.; Nikzad, S. Electrical transport properties of a CNT/C60/CNT hybrid junction with closed end CNT leads using Green’s function method. Eur. Phys. J. B 2013, 86, 22. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, B.E.; Pan, Z.Y.; Wang, Y.X.; Zhu, J. Reduction of the buckling strength of carbon nanotubes resulting from encapsulation of C60 fullerenes. Nanotechnology 2007, 18, 275709. [Google Scholar] [CrossRef]
- Kang, J.W.; Lee, K.W. Molecular dynamics study on the C60 oscillator in a graphene nanoribbon trench. J. Korean Phys. Soc. 2014, 65, 185–189. [Google Scholar] [CrossRef]
- Shokri, A.A.; Nikzad, S. Topology effects of interface and gate voltage on electrical transport through the CNT/C60/CNT junction using the Green’s function method. J. Appl. Phys. 2011, 110, 024303. [Google Scholar] [CrossRef]
- Ulbricht, H.; Moos, G.; Hertel, T. Interaction ofC60with Carbon Nanotubes and Graphite. Phys. Rev. Lett. 2003, 90, 095501. [Google Scholar] [CrossRef] [Green Version]
- Farimani, A.B.; Heiranian, M.; Aluru, N.R. Nano-electro-mechanical pump: Giant pumping of water in carbon nanotubes. Sci. Rep. 2016, 6, 26211. [Google Scholar] [CrossRef]
- Ansari, R.; Sadeghi, F.; Alipour, A. Oscillation of C60 Fullerene in Carbon Nanotube Bundles. J. Vib. Acoust. 2013, 135, 051009. [Google Scholar] [CrossRef]
- Izadi, R.; Nayebi, A.; Ghavanloo, E. Combined molecular dynamics–micromechanics methods to predict Young’s modulus of fullerene-reinforced polymer composites. Eur. Phys. J. Plus 2021, 136, 816. [Google Scholar] [CrossRef]
- Li, S.; Bian, F.; Meng, X.; Zhai, D.; Yang, H.; Qin, G. Ring structure characterization of nanoporous carbon materials prepared by thermal conversion of fullerenes: Insights from ReaxFF molecular dynamics simulations. Carbon 2021, 189, 484–492. [Google Scholar] [CrossRef]
- Abbaspour, M.; Akbarzadeh, H.; Salemi, S.; Tahami, S.F. Formation of methane clathrates into fullerene: A molecular dynamics study. J. Mol. Liq. 2022, 367, 120587. [Google Scholar] [CrossRef]
- Kitjanon, J.; Khuntawee, W.; Phongphanphanee, S.; Sutthibutpong, T.; Chattham, N.; Karttunen, M.; Wong-Ekkabut, J. Nanocomposite of Fullerenes and Natural Rubbers: MARTINI Force Field Molecular Dynamics Simulations. Polymers 2021, 13, 4044. [Google Scholar] [CrossRef] [PubMed]
- Yuan, H.; Kong, W.; Xia, J. Steered molecular dynamics and stability analysis on PAH dimerisation and condensation on fullerene and soot surfaces. Phys. Chem. Chem. Phys. 2021, 23, 19590–19601. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, W.B.; Colherinhas, G. Fullerene C60 spectroscopy in [BMIM][PF6] ionic liquid: Molecular dynamics study using polarization effects. J. Mol. Struct. 2021, 1250, 131887. [Google Scholar] [CrossRef]
- Lun-Fu, A.V.; Bubenchikov, A.M.; Ovchinnikov, V.A. Numerical study of rotational dynamics of carbon nanotori during intermolecular interaction. J. Phys. Conf. Ser. 2022, 2211, 012004. [Google Scholar] [CrossRef]
- Lun-Fu, A.; Bubenchikov, M.; Bubenchikov, A.; Mamontov, D.; Borodin, V. Interaction of molecular tori in columnar structures. J. Phys. Condens. Matter 2022, 34, 125101. [Google Scholar] [CrossRef]
- Bubenchikov, M.; Mamontov, D.; Ovchinnikov, V. Studying the possibility of using fullerenes inside carbon nanotubes as a molecular engine. J. Phys. Conf. Ser. 2022, 2211, 012005. [Google Scholar] [CrossRef]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Mamontov, D.V.; Chelnokova, A.S.; Chumakova, S.P. Movement of fullerenes and their dimers inside carbon nanotubes. Full- Nanotub. Carbon Nanostruct. 2021, 29, 803–809. [Google Scholar] [CrossRef]
- Bubenchikov, A.M.; Bubenchikov, M.A.; Mamontov, D.V.; Kaparulin, D.S.; Lun-Fu, A.V. Dynamic state of columnar structures formed on the basis of carbon nanotori. Full- Nanotub. Carbon Nanostruct. 2021, 29, 825–831. [Google Scholar] [CrossRef]
- Runge, C. Ueber die numerische Auflösung von Differentialgleichungen. Math. Ann. 1895, 46, 167–178. [Google Scholar] [CrossRef] [Green Version]
- Poinsot, L. Theéorie Nouvelle De La Rotation Des Corps; Bachelier: Paris, France, 1834; Volume 1834, pp. 1777–1859. [Google Scholar]
- Levi, M. Classical Mechanics with Calculus of Variations, and Optimal Control: An Intuitive Introduction. Am. Math. Soc. 2014, 69, 1470414449. [Google Scholar] [CrossRef]
- Trivisonno, N.; Garelli, L.; Storti, M. The Tennis Racket Theorem, an Analysis of the Intermediate Axis Theorem. Mecánica Comput. 2021, 38, 1341–1353. [Google Scholar]
- Sarapat, P.; Hill, J.M.; Baowan, D. A Review of Geometry, Construction and Modelling for Carbon Nanotori. Appl. Sci. 2019, 9, 2301. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Wang, B.; Wang, L.; Lu, T.; Fu, Y.; Zhang, H.; Zhang, Z. Fullerene (C60)-based tumor-targeting nanoparticles with “off-on” state for enhanced treatment of cancer. J. Control Release 2016, 235, 245–258. [Google Scholar] [CrossRef] [PubMed]
- Chernozatonskii, L.A.; Artyukh, A.A.; Demin, V. Quasi-one-dimensional fullerene-nanotube composites: Structure, formation energetics, and electronic properties. JETP Lett. 2013, 97, 113–119. [Google Scholar] [CrossRef]
- Singhai, N.J.; Ramteke, S. Functionalized Carbon Nanotubes: Emerging Applications in the Diverse Biomedical Arena. Curr. Nanosci. 2020, 16, 170–186. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borodin, V.; Bubenchikov, M.; Bubenchikov, A.; Mamontov, D.; Azheev, S.; Azheev, A. Study of the Unstable Rotational Dynamics of a Tor-Fullerene Molecular System. Crystals 2023, 13, 181. https://doi.org/10.3390/cryst13020181
Borodin V, Bubenchikov M, Bubenchikov A, Mamontov D, Azheev S, Azheev A. Study of the Unstable Rotational Dynamics of a Tor-Fullerene Molecular System. Crystals. 2023; 13(2):181. https://doi.org/10.3390/cryst13020181
Chicago/Turabian StyleBorodin, Vladislav, Mikhail Bubenchikov, Alexey Bubenchikov, Dmitriy Mamontov, Sergey Azheev, and Alexandr Azheev. 2023. "Study of the Unstable Rotational Dynamics of a Tor-Fullerene Molecular System" Crystals 13, no. 2: 181. https://doi.org/10.3390/cryst13020181
APA StyleBorodin, V., Bubenchikov, M., Bubenchikov, A., Mamontov, D., Azheev, S., & Azheev, A. (2023). Study of the Unstable Rotational Dynamics of a Tor-Fullerene Molecular System. Crystals, 13(2), 181. https://doi.org/10.3390/cryst13020181








