Intrinsic Instability of Perovskite Solar Cells: The Role of a Hole-Blocking Layer
Abstract
1. Introduction
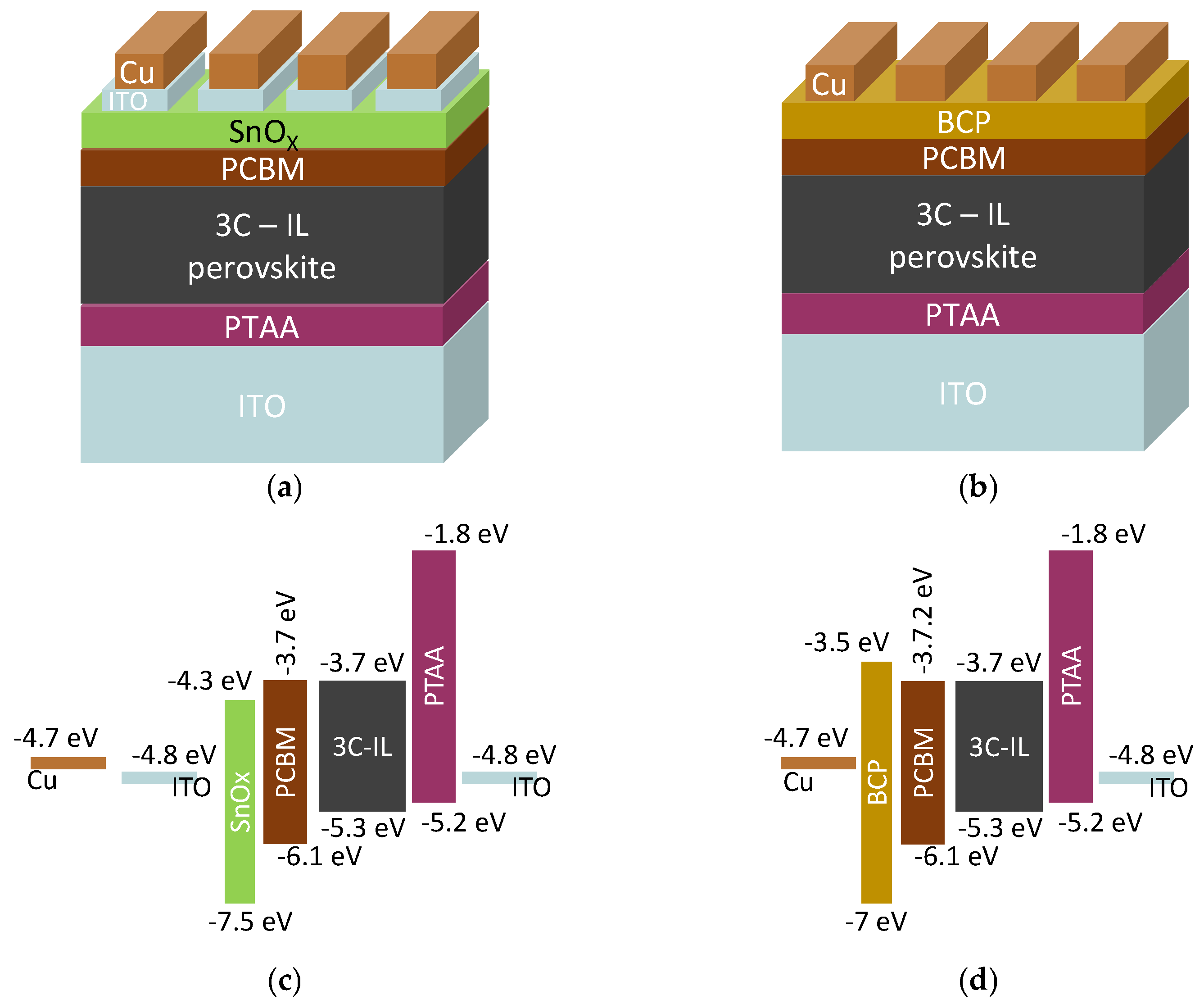
2. Materials and Methods
2.1. Materials
2.2. Devices Fabrication
2.3. Characterization Procedure
3. Results and Discussion
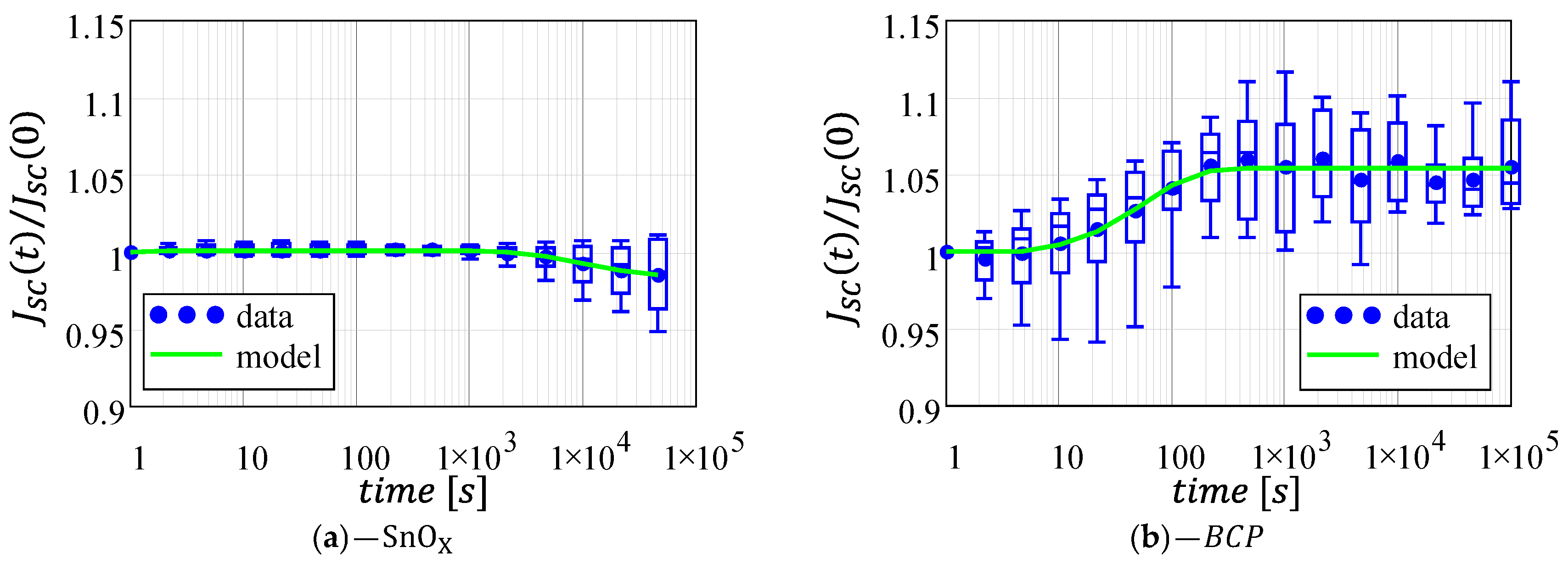
3.1. Short-Circuit Current
3.2. Open-Circuit Voltage
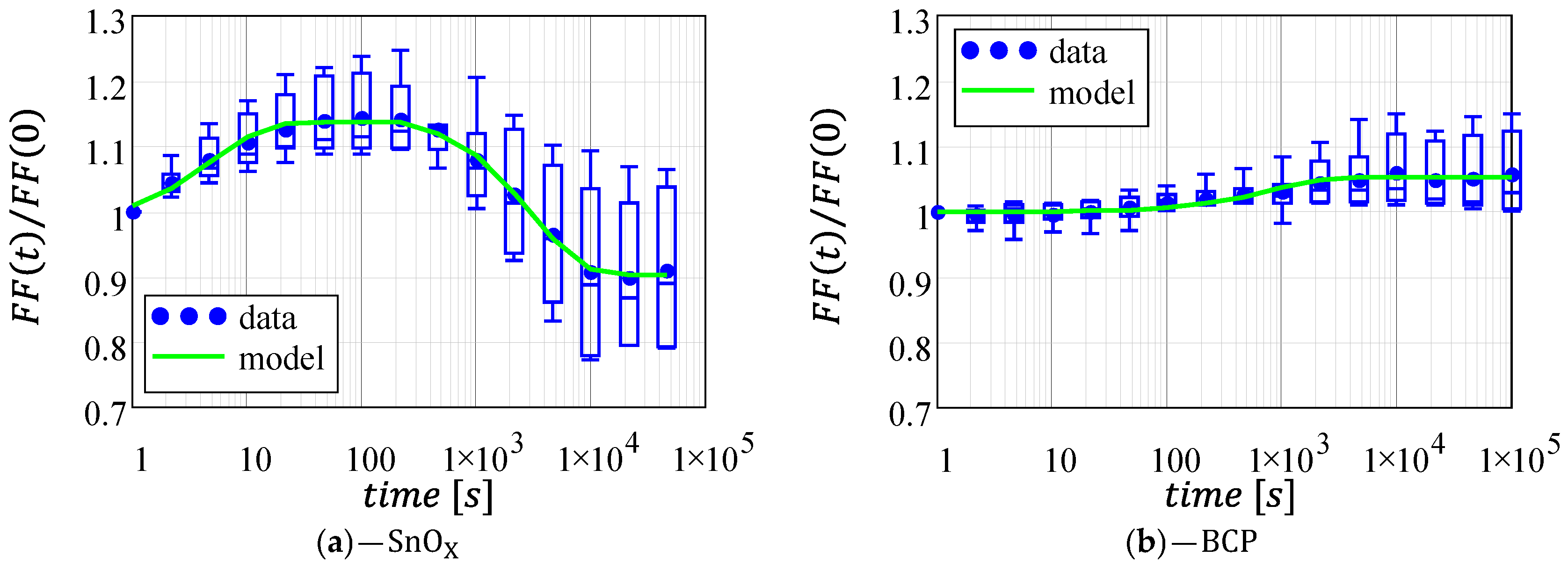
3.3. Fill-Factor
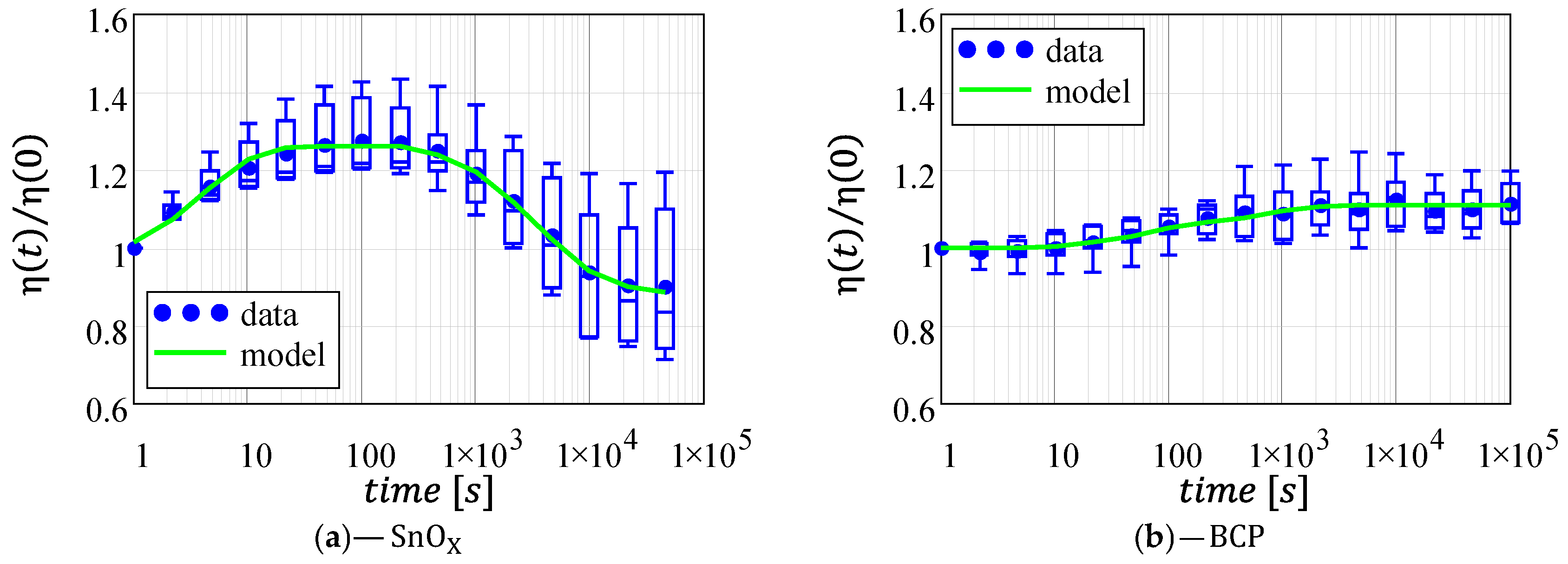
3.4. Power Conversion Efficiency
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Best Research-Cell Efficiency Chart|Photovoltaic Research | NREL. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 12 January 2023).
- Bati, A.S.R.; Zhong, Y.L.; Burn, P.L.; Nazeeruddin, M.K.; Shaw, P.E.; Batmunkh, M. Next-Generation Applications for Integrated Perovskite Solar Cells. Commun. Mater. 2023, 4, 2. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, J.W.; Jung, H.S.; Shin, H.; Park, N.G. High-Efficiency Perovskite Solar Cells. Chem. Rev. 2020, 120, 7867–7918. [Google Scholar] [CrossRef] [PubMed]
- Kang, D.H.; Park, N.G. On the Current–Voltage Hysteresis in Perovskite Solar Cells: Dependence on Perovskite Composition and Methods to Remove Hysteresis. Adv. Mater. 2019, 31, 1805214. [Google Scholar] [CrossRef] [PubMed]
- Harshavardhan Reddy, S.; Di Giacomo, F.; Di Carlo, A.; Reddy, S.H.; Di Giacomo, F.; Di Carlo, A. Low-Temperature-Processed Stable Perovskite Solar Cells and Modules: A Comprehensive Review. Adv. Energy Mater. 2022, 12, 2103534. [Google Scholar] [CrossRef]
- Rizzo, A.; Lamberti, F.; Buonomo, M.; Wrachien, N.; Torto, L.; Lago, N.; Sansoni, S.; Pilot, R.; Prato, M.; Michieli, N.; et al. Understanding Lead Iodide Perovskite Hysteresis and Degradation Causes by Extensive Electrical Characterization. Sol. Energy Mater. Sol. Cells 2019, 189, 43–52. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Z.; Ding, J.; Kong, J.; Li, X. Improving Water-Resistance of Inverted Flexible Perovskite Solar Cells via Tailoring the Top Electron-Selective Layers. Sol. Energy Mater. Sol. Cells 2022, 238, 111609. [Google Scholar] [CrossRef]
- Karim, M.A.; Matsuishi, K.; Chowdhury, T.H.; Chowdhury, W.I.; Abdel-shakour, M.; Islam, A. Bathocuproine Interfacial Layer Leads to Solid Improvement of Reproducibility and Stability of Pb-Free CsBi3I10 Based Perovskite Solar Cells. J. Mater. Sci. Mater. Electron. 2022, 33, 8114–8126. [Google Scholar] [CrossRef]
- Wang, P.; Shao, Z.; Ulfa, M.; Pauporté, T. Insights into the Hole Blocking Layer Effect on the Perovskite Solar Cell Performance and Impedance Response. J. Phys. Chem. C 2017, 121, 9131–9141. [Google Scholar] [CrossRef]
- Gagliardi, S.; Rondino, F.; Paoletti, C.; Falconieri, M. On the Morphology of Nanostructured TiO2 for Energy Applications: The Shape of the Ubiquitous Nanomaterial. Nanomaterials 2022, 12, 2608. [Google Scholar] [CrossRef]
- Zhang, T.; He, Q.; Yu, J.; Chen, A.; Zhang, Z.; Pan, J. Recent Progress in Improving Strategies of Inorganic Electron Transport Layers for Perovskite Solar Cells. Nano Energy 2022, 104, 107918. [Google Scholar] [CrossRef]
- Yates, H.M.; Afzaal, M.; Walter, A.; Hodgkinson, J.L.; Moon, S.J.; Sacchetto, D.; Bräuninger, M.; Niesen, B.; Nicolay, S.; McCarthy, M.; et al. Progression towards High Efficiency Perovskite Solar Cells via Optimisation of the Front Electrode and Blocking Layer. J. Mater. Chem. C 2016, 4, 11269–11277. [Google Scholar] [CrossRef]
- Chen, S.H.; Ho, C.M.; Chang, Y.H.; Lee, K.M.; Wu, M.C. Efficient Perovskite Solar Cells with Low J-V Hysteretic Behavior Based on Mesoporous Sn-Doped TiO2 Electron Extraction Layer. Chem. Eng. J. 2022, 445, 136761. [Google Scholar] [CrossRef]
- Sun, H.; Xie, D.; Song, Z.; Liang, C.; Xu, L.; Qu, X.; Yao, Y.; Li, D.; Zhai, H.; Zheng, K.; et al. Interface Defects Passivation and Conductivity Improvement in Planar Perovskite Solar Cells Using Na2S-Doped Compact TiO2 Electron Transport Layers. ACS Appl. Mater. Interfaces 2020, 12, 22853–22861. [Google Scholar] [CrossRef]
- Cao, Z.; Li, C.; Deng, X.; Wang, S.; Yuan, Y.; Chen, Y.; Wang, Z.; Liu, Y.; Ding, L.; Hao, F. Metal Oxide Alternatives for Efficient Electron Transport in Perovskite Solar Cells: Beyond TiO2 and SnO2. J. Mater. Chem. A 2020, 8, 19768–19787. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, X.; You, J.; Jiang, Q.; Zhang, X.; You, J. SnO2: A Wonderful Electron Transport Layer for Perovskite Solar Cells. Small 2018, 14, 1801154. [Google Scholar] [CrossRef]
- Ferguson, V.; Silva, S.R.P.; Zhang, W. Carbon Materials in Perovskite Solar Cells: Prospects and Future Challenges. Energy Environ. Mater. 2019, 2, 107–118. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, Y.; Wen, J.; Liu, H.; Yang, G.; Qin, P.; Fang, G.; Xiong, L.B.; Guo, Y.X.; Liu, H.R.; et al. Review on the Application of SnO2 in Perovskite Solar Cells. Adv. Funct. Mater. 2018, 28, 1802757. [Google Scholar] [CrossRef]
- Reddy, S.H.; Di Giacomo, F.; Matteocci, F.; Castriotta, L.A.; Di Carlo, A. Holistic Approach toward a Damage-Less Sputtered Indium Tin Oxide Barrier Layer for High-Stability Inverted Perovskite Solar Cells and Modules. ACS Appl. Mater. Interfaces 2022, 14, 51438–51448. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, S.; Wu, S.; Zhang, W.; Zhu, H.; Xiong, Z.; Zhang, Y.; Chen, W. Effect of BCP Buffer Layer on Eliminating Charge Accumulation for High Performance of Inverted Perovskite Solar Cells. RSC Adv. 2017, 7, 35819–35826. [Google Scholar] [CrossRef]
- Di Giacomo, F.; Castriotta, L.A.; Kosasih, F.U.; Di Girolamo, D.; Ducati, C.; Di Carlo, A. Upscaling Inverted Perovskite Solar Cells: Optimization of Laser Scribing for Highly Efficient Mini-Modules. Micromachines 2020, 11, 1127. [Google Scholar] [CrossRef]
- IEC 60904–7:2019; Photovoltaic Devices—Part 7: Computation of the Spectral Mismatch Correction for Measurements of Photovoltaic Devices. BSI Standards Limited: London, UK, 2019; ISBN 978-0-580-97364-2.
- Mun, H.; Yang, H.; Park, J.; Ju, C.; Char, K. High Electron Mobility in Epitaxial SnO2−x in Semiconducting Regime. APL Mater. 2015, 3, 076107. [Google Scholar] [CrossRef]
- Wang, D.; Muhammad, R.; Hussain, F.; Li, Z.; Graziosi, P.; Neophytou, N. Electron and Hole Mobility of SnO2 from Full-Band Electron–Phonon and Ionized Impurity Scattering Computations. Crystals 2022, 12, 1591. [Google Scholar] [CrossRef]
- Devižis, A.; Hertel, D.; Meerholz, K.; Gulbinas, V.; Moser, J.E. Time-Independent, High Electron Mobility in Thin PC61BM Films: Relevance to Organic Photovoltaics. Org. Electron. 2014, 15, 3729–3734. [Google Scholar] [CrossRef]
- Mu, H.; Reddy, I.; Hunt, J.; Severs, P.; Patil, S. Electron Mobility Characterization in OLEDs from Ac Small Signal Optical Modulation. J. Phys. D Appl. Phys. 2010, 43, 195103. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, L.; Wang, H.; Yang, X.; Meng, J.; Liu, H.; Yin, Z.; Wu, J.; Zhang, X.; You, J. Enhanced Electron Extraction Using SnO2 for High-Efficiency Planar-Structure HC(NH2)2PbI3-Based Perovskite Solar Cells. Nat. Energy 2016, 2, 16177. [Google Scholar] [CrossRef]
- Liu, D.; Wang, G.; Luo, K.; He, X.; Ye, Q.; Liao, C.; Mei, J. Understanding the Role of the Electron-Transport Layer in Highly Efficient Planar Perovskite Solar Cells. ChemPhysChem 2017, 18, 617–625. [Google Scholar] [CrossRef]
- McPherson, J.W. Reliability Physics and Engineering: Time-to-Failure Modeling, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-319-93682-6. [Google Scholar]
- Min, H.; Lee, D.Y.; Kim, J.; Kim, G.; Lee, K.S.; Kim, J.; Paik, M.J.; Kim, Y.K.; Kim, K.S.; Kim, M.G.; et al. Perovskite Solar Cells with Atomically Coherent Interlayers on SnO2 Electrodes. Nature 2021, 598, 444–450. [Google Scholar] [CrossRef]


| Architecture | [mA/cm2] | [%] | [V] | [%] |
|---|---|---|---|---|
| 17.6 ± 1.4 | 51.5 ± 7.7 | 0.91 ± 0.05 | 8.4 ± 1.6 | |
| 14.87 ± 0.96 | 63 ± 9 | 1.1 ± 0.02 | 10.5 ± 1.9 |
| Architecture | [%] | [s−1] | [s] | [%] | [s−1] | [s] |
|---|---|---|---|---|---|---|
| SnOX | 0.15 | 0.75 | 0.99 | 1.66 | 8.1·10−5 | 856.8 |
| 5.4 | 0.017 | 4.64 | \ | \ | \ |
| Architecture | [mV] | [s−1] | [s] | [mV] | [s−1] | [s] |
|---|---|---|---|---|---|---|
| 97.7 | 0.3 | 0.81 | 100.2 | 9.6·10−5 | 329.8 | |
| 1.5 | 0.039 | 10 | \ | \ | \ |
| Architecture | [%] | [s−1] | [s] | [%] | [s−1] | [s] |
|---|---|---|---|---|---|---|
| 13.7 | 0.2 | 0.68 | 23.4 | 3.3·10−4 | 237.5 | |
| 5.2 | 1.3·10−3 | 2.15 | \ | \ | \ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lago, N.; Polo, A.; Reddy, S.H.; Di Carlo, A.; Cester, A. Intrinsic Instability of Perovskite Solar Cells: The Role of a Hole-Blocking Layer. Crystals 2023, 13, 185. https://doi.org/10.3390/cryst13020185
Lago N, Polo A, Reddy SH, Di Carlo A, Cester A. Intrinsic Instability of Perovskite Solar Cells: The Role of a Hole-Blocking Layer. Crystals. 2023; 13(2):185. https://doi.org/10.3390/cryst13020185
Chicago/Turabian StyleLago, Nicolò, Andrea Polo, Sathy Harshavardhan Reddy, Aldo Di Carlo, and Andrea Cester. 2023. "Intrinsic Instability of Perovskite Solar Cells: The Role of a Hole-Blocking Layer" Crystals 13, no. 2: 185. https://doi.org/10.3390/cryst13020185
APA StyleLago, N., Polo, A., Reddy, S. H., Di Carlo, A., & Cester, A. (2023). Intrinsic Instability of Perovskite Solar Cells: The Role of a Hole-Blocking Layer. Crystals, 13(2), 185. https://doi.org/10.3390/cryst13020185







