Study on the Depth and Evolution of Keyholes in Plasma-MIG Hybrid Welding
Abstract
:1. Introduction
2. Materials and Methods
2.1. Welding Test System
2.2. Test Material
2.3. Test Design and Inclined Plate Welding Test
3. Keyhole Depth Research Based on Response Surface Method
3.1. Prediction Model Reliability Analysis
3.2. Analysis of Influence of Welding Factors on Keyhole Depth
3.2.1. Effect of Single Factor on Keyhole Depth
3.2.2. The Influence of Multiple Factors Interaction on Keyhole Depth
4. Numerical Simulation of Keyhole Behavior in Plasma-MIG Welding
4.1. Establishment of Analytical Model
4.1.1. Basic Assumption
- (1)
- The molten metal generated in the welding process cannot be compressed and is idealized as a laminar Newtonian body and the plasma arc as Newtonian fluid;
- (2)
- The metal melts under the heating of the arc, and the volume change of the solid phase transformation is negligible, and no metal is lost due to evaporation;
- (3)
- The welding process follows the three conservation laws, that is, the law of conservation of mass, energy, and momentum;
- (4)
- In the molten pool, only liquid surface tension, arc pressure, gravity, electromagnetic force, and buoyancy are considered.
4.1.2. Governing Equation
- (1)
- Mass conservation equationwhere ρ is metal density (kg/m3); Sm is mass added by the sparse phase to the continuous phase (kg).
- (2)
- Energy conservation equationwhere ρ is metal density (kg/m3); λ is thermal conductivity; S is the energy equation source term; cp is the specific heat capacity (J/kg·°C).
- (3)
- Momentum conservation equationwhere ρ is the metal density (kg/m³); v0 is the welding speed (mm/s); u, v, and w are components of welding velocity; μ is the coefficient of metal viscosity; p is the pressure in the fluid.
4.1.3. Heat Source Model
- (1)
- Conical heat source model
- (2)
- Double ellipsoidal heat source model [30]
- (3)
- Droplet heat source model
4.1.4. Model Building and Meshing
4.1.5. Initial Conditions and Boundary Conditions
- (1)
- Initial conditions
- (2)
- Energy boundary conditions
- (3)
- Momentum boundary conditions
4.2. Material Thermal and Physical Parameters and Welding Parameters
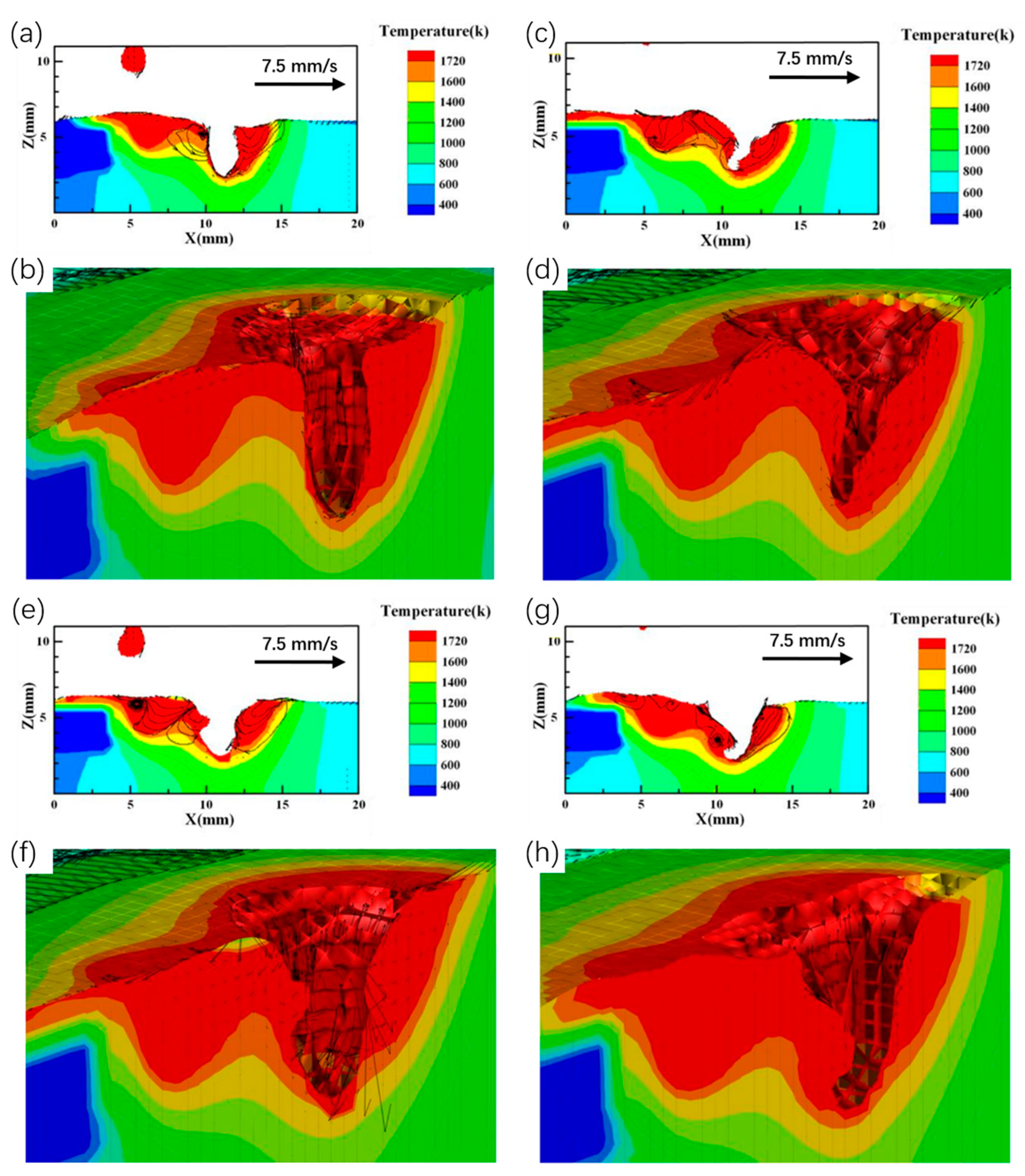
4.3. Keyhole Evolution and Molten Pool Flow Behavior
5. Conclusions
- (1)
- Taking plasma current, MIG current, magnetic field intensity and welding current as input values and keyhole depth as a response value, a prediction model is established. After variance analysis and model reliability analysis, the prediction of this model meets the expected effect. The results show that the influences of the above four factors on keyhole depth are as follows: welding speed > magnetic field intensity > plasma current > MIG current, and the welding speed and magnetic field intensity have significant effects on keyhole depth. Only plasma current and MIG current have significant interaction with each other. No significant interaction was found between the other groups.
- (2)
- The numerical analysis model is established, and the simulation results show that the internal characteristic morphology of the keyhole is like a parabola in the stable welding state. After a certain time of welding, the boundary between the plasma internal weld pool and the MIG internal weld pool disappears, forming a common weld pool. After the MIG arc starts and the droplet transition is completed, there will be an obvious molten pool crest region and depression region between the two arcs. The crest region will oscillate under the action of arc force and plasma flow force. The flow mode and movement mechanism of metal in keyhole are described. New molten metal is produced under the plasma arc. The molten metal in the front end of the keyhole passes through the bottom of the keyhole to the rear end of the keyhole. This will move the keyhole forward.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Shi, Y.; Cui, Y.; Wang, Z.; Hong, X. Prediction of Keyhole TIG Weld Penetration Based on High-Dynamic Range Imaging. J. Manuf. Process. 2021, 63, 179–190. [Google Scholar] [CrossRef]
- Li, Y.; Tian, S.; Wu, C.S.; Tanaka, M. Experimental Sensing of Molten Flow Velocity, Weld Pool and Keyhole Geometries in Ultrasonic-Assisted Plasma Arc Welding. J. Manuf. Process. 2021, 64, 1412–1419. [Google Scholar] [CrossRef]
- Liu, X.F.; Jia, C.B.; Wu, C.S.; Zhang, G.K.; Gao, J.Q. Measurement of the Keyhole Entrance and Topside Weld Pool Geometries in Keyhole Plasma Arc Welding with Dual CCD Cameras. J. Mater. Process. Technol. 2017, 248, 39–48. [Google Scholar] [CrossRef]
- Fabbro, R.; Slimani, S.; Coste, F.; Briand, F. Study of Keyhole Behaviour for Full Penetration Nd-Yag CW Laser Welding. J. Phys. D Appl. Phys. 2005, 38, 1881–1887. [Google Scholar] [CrossRef]
- Jia, C.B.; Wu, C.S.; Zhang, Y.M. Sensing Controlled Pulse Key-Holing Condition in Plasma Arc Welding. Trans. Nonferrous Met. Soc. China English Ed. 2009, 19, 341–346. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Zhang, S.B.; Liu, Y.C. A Plasma Cloud Charge Sensor for Pulse Keyhole Process Control. Meas. Sci. Technol. 2001, 12, 1365–1370. [Google Scholar] [CrossRef] [Green Version]
- Bakkiyaraj, M.; Palanisamy, P.; Balasubramanian, V. Evaluating the Tensile Strength of Friction Welded (AA6061 & AA7075-T6) Dissimilar Joints by Using Response Surface Methodology. Mater. Res. Express 2019, 6, 086527. [Google Scholar] [CrossRef]
- Subramanian, R.; Natarajan, B.; Kaliyaperumal, B.; Chinnasamy, R. Effect of MIG Welding Process Parameters on Microstructure and Tensile Behavior of Hastelloy C276 Using Response Surface Methodology. Mater. Res. Express 2019, 6, 066540. [Google Scholar] [CrossRef]
- Shahi, A.S.; Pandey, S. Modelling of the Effects of Welding Conditions on Dilution of Stainless Steel Claddings Produced by Gas Metal Arc Welding Procedures. J. Mater. Process. Technol. 2008, 196, 339–344. [Google Scholar] [CrossRef]
- Jahanzaib, M.; Hussain, S.; Wasim, A.; Aziz, H.; Mirza, A.; Ullah, S. Modeling of Weld Bead Geometry on HSLA Steel Using Response Surface Methodology. Int. J. Adv. Manuf. Technol. 2017, 89, 2087–2098. [Google Scholar] [CrossRef]
- Song, C.; Dong, S.; He, P.; Yan, S.; Zhao, X. Correlation of Process Parameters and Porosity in Laser Welding of 7A52 Aluminum Alloy Using Response Surface Methodology. Procedia Manuf. 2019, 37, 294–298. [Google Scholar] [CrossRef]
- Rosli, N.A.; Alkahari, M.R.; Ramli, F.R.; Fadzli bin Abdollah, M.; Kudus, S.I.A.; Herawan, S.G. Parametric Optimisation of Micro Plasma Welding for Wire Arc Additive Manufacturing by Response Surface Methodology. Manuf. Technol. 2022, 22, 59–70. [Google Scholar] [CrossRef]
- Apelgren, P.; Amoroso, M.; Säljö, K.; Montelius, M.; Lindahl, A.; Stridh Orrhult, L.; Gatenholm, P.; Kölby, L.; Arulkumar, S.; Parthiban, S.; et al. Ac Ce Pte d M Us Pt. Mater. Today Proc. 2019, 27. 0-31. [Google Scholar]
- Kumar, V.; Mandal, A.; Das, A.K.; Kumar, S. Parametric Study and Characterization of Wire Arc Additive Manufactured Steel Structures. Int. J. Adv. Manuf. Technol. 2021, 115, 1723–1733. [Google Scholar] [CrossRef]
- Li, T.Q.; Wu, C.S. Numerical Simulation of Plasma Arc Welding with Keyhole-Dependent Heat Source and Arc Pressure Distribution. Int. J. Adv. Manuf. Technol. 2015, 78, 593–602. [Google Scholar] [CrossRef]
- Jian, X.; Wu, C.S.; Zhang, G.; Chen, J. A Unified 3D Model for an Interaction Mechanism of the Plasma Arc, Weld Pool and Keyhole in Plasma Arc Welding. J. Phys. D Appl. Phys. 2015, 48, 465504. [Google Scholar] [CrossRef]
- Qiao, J.; Wu, C.; Li, Y. Numerical Analysis of Keyhole and Weld Pool Behaviors in Ultrasonic-Assisted Plasma Arc Welding Process. Materials 2021, 14, 703. [Google Scholar] [CrossRef] [PubMed]
- Kuang, J.H.; Hung, T.P.; Chen, C.K. A Keyhole Volumetric Model for Weld Pool Analysis in Nd:YAG Pulsed Laser Welding. Opt. Laser Technol. 2012, 44, 1521–1528. [Google Scholar] [CrossRef]
- Wu, C.S.; Huo, Y.S. Numerical Analysis of Keyhole Geometry and Temperature Profiles in Plasma Arc Welding. J. Manuf. Process. 2013, 15, 593–599. [Google Scholar] [CrossRef]
- Jian, X.; Wu, C.S. Numerical Analysis of the Coupled Arc-Weld Pool-Keyhole Behaviors in Stationary Plasma Arc Welding. Int. J. Heat Mass Transf. 2015, 84, 839–847. [Google Scholar] [CrossRef]
- Li, T.Q.; Chen, L.; Zhang, Y.; Yang, X.M.; Lei, Y.C. Metal Flow of Weld Pool and Keyhole Evolution in Gas Focusing Plasma Arc Welding. Int. J. Heat Mass Transf. 2020, 150, 119296. [Google Scholar] [CrossRef]
- Hertel, M.; Füssel, U.; Schnick, M. Numerical Simulation of the Plasma-MIG Process-Interactions of the Arcs, Droplet Detachment and Weld Pool Formation. Weld. World 2014, 58, 85–92. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Q.; Pu, J.; Wu, H. Study on the Molten Pool Fluid Behavior of PAW-Cable-Type Seven-Wire GMAW Hybrid Welding. Crystals 2022, 12, 306. [Google Scholar] [CrossRef]
- Gao, Z.; Jiang, P.; Mi, G.; Cao, L.; Liu, W. Investigation on the Weld Bead Profile Transformation with the Keyhole and Molten Pool Dynamic Behavior Simulation in High Power Laser Welding. Int. J. Heat Mass Transf. 2018, 116, 1304–1313. [Google Scholar] [CrossRef]
- Wu, C.S.; Zhang, T.; Feng, Y.H. Numerical Analysis of the Heat and Fluid Flow in a Weld Pool with a Dynamic Keyhole. Int. J. Heat Fluid Flow 2013, 40, 186–197. [Google Scholar] [CrossRef]
- Wu, D.; Tashiro, S.; Hua, X.; Tanaka, M. Analysis of the Energy Propagation in the Keyhole Plasma Arc Welding Using a Novel Fully Coupled Plasma Arc-Keyhole-Weld Pool Model. Int. J. Heat Mass Transf. 2019, 141, 604–614. [Google Scholar] [CrossRef]
- Miao, X.; Zhang, H.; Ge, F.; He, Z.; Gao, J.; Su, Z. Research on Arc Morphology and Keyhole Behavior of Molten Pool in Magnetically Controlled Plasma-GMAW Welding. Int. J. Metals. 2023, 13, 148. [Google Scholar] [CrossRef]
- Xu, G.X.; Wu, C.S.; Qin, G.L.; Wang, X.Y.; Lin, S.Y. Adaptive Volumetric Heat Source Models for Laser Beam and Laser + Pulsed GMAW Hybrid Welding Processes. Int. J. Adv. Manuf. Technol. 2011, 57, 245–255. [Google Scholar] [CrossRef]
- Miao, J.Y. Study on Weldpool Fluid Behavior of Plasma arc Welding + Cable-Wire Pulsed GMAW Hybrid Welding. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2012. (In Chinese). [Google Scholar]
- Goldak, J.; Chakravarti, A.; Bibby, M. A New Finite Element Model for Welding Heat Sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]









| C | Ni | S | Mn | Cr | P | Si | Fe |
|---|---|---|---|---|---|---|---|
| 0.07 | 8–10.5 | 0.03 | 1.00–2.50 | 17.5–19.5 | 0.45 | 0.75 | balance |
| C | Ni | S | Mn | Cr | P | Si | Fe |
|---|---|---|---|---|---|---|---|
| ≤0.080 | 8.00–10.0 | ≤0.030 | 1.40–1.85 | 17.0–19.0 | 0.30–0.65 | ≤0.030 | balance |
| Level | A: IP/A | B: IM /A | C: B/mT | D: v/mm•s−1 |
|---|---|---|---|---|
| 2 | 240 | 320 | 3.3 | 9.5 |
| 1 | 220 | 310 | 2.475 | 8.5 |
| 0 | 200 | 300 | 1.65 | 7.5 |
| −1 | 180 | 290 | 0.825 | 6.5 |
| −2 | 160 | 280 | 0 | 5.5 |
| Serial Number | A (A) | B (A) | C (mT) | D (mm/s) | Keyhole Depth (mm) |
|---|---|---|---|---|---|
| 1 | 180 | 290 | 0.825 | 6.5 | 5.36 |
| 2 | 220 | 290 | 0.825 | 6.5 | 4.83 |
| 3 | 180 | 310 | 0.825 | 6.5 | 4.74 |
| 4 | 220 | 310 | 0.825 | 6.5 | 5.02 |
| 5 | 180 | 290 | 2.475 | 6.5 | 4.69 |
| 6 | 220 | 290 | 2.475 | 6.5 | 4.67 |
| 7 | 180 | 310 | 2.475 | 6.5 | 4.44 |
| 8 | 220 | 310 | 2.475 | 6.5 | 5.25 |
| 9 | 180 | 290 | 0.825 | 8.5 | 4.95 |
| 10 | 220 | 290 | 0.825 | 8.5 | 4.47 |
| 11 | 180 | 310 | 0.825 | 8.5 | 4.16 |
| 12 | 220 | 310 | 0.825 | 8.5 | 4.91 |
| 13 | 180 | 290 | 2.475 | 8.5 | 4.51 |
| 14 | 220 | 290 | 2.475 | 8.5 | 4.42 |
| 15 | 180 | 310 | 2.475 | 8.5 | 4.04 |
| 16 | 220 | 310 | 2.475 | 8.5 | 4.36 |
| 17 | 160 | 300 | 1.65 | 7.5 | 4.28 |
| 18 | 240 | 300 | 1.65 | 7.5 | 5.07 |
| 19 | 200 | 280 | 1.65 | 7.5 | 4.16 |
| 20 | 200 | 320 | 1.65 | 7.5 | 5.05 |
| 21 | 200 | 300 | 0 | 7.5 | 4.98 |
| 22 | 200 | 300 | 3.3 | 7.5 | 4.48 |
| 23 | 200 | 300 | 1.65 | 5.5 | 5.4 |
| 24 | 200 | 300 | 1.65 | 9.5 | 4.49 |
| 25 | 200 | 300 | 1.65 | 7.5 | 4.78 |
| 26 | 200 | 300 | 1.65 | 7.5 | 4.5 |
| 27 | 200 | 300 | 1.65 | 7.5 | 4.38 |
| 28 | 200 | 300 | 1.65 | 7.5 | 4.63 |
| 29 | 200 | 300 | 1.65 | 7.5 | 4.2 |
| 30 | 200 | 300 | 1.65 | 7.5 | 4.35 |
| Source | Quadratic Sum | Degree of Freedom | p-Value | F-Value | Mean Square Error |
|---|---|---|---|---|---|
| Model | 2.91 | 14 | 0.0165 | 3.19 | 0.208 |
| A | 0.286 | 1 | 0.0537 | 4.38 | 0.286 |
| B | 0.0267 | 1 | 0.5322 | 0.4088 | 0.0267 |
| C | 0.3902 | 1 | 0.0273 | 5.98 | 0.3902 |
| D | 1.04 | 1 | 0.0012 | 15.97 | 1.04 |
| AB | 0.6724 | 1 | 0.0058 | 10.31 | 0.6724 |
| AC | 0.0625 | 1 | 0.3432 | 0.9581 | 0.0625 |
| AD | 0.0001 | 1 | 0.9693 | 0.0015 | 0.0001 |
| BC | 0.021 | 1 | 0.5786 | 0.3223 | 0.021 |
| BD | 0.038 | 1 | 0.457 | 0.5829 | 0.038 |
| CD | 0.0042 | 1 | 0.8026 | 0.0648 | 0.0042 |
| A2 | 0.0439 | 1 | 0.4249 | 0.6727 | 0.0439 |
| B2 | 0.0139 | 1 | 0.6512 | 0.2129 | 0.0139 |
| C2 | 0.0792 | 1 | 0.2878 | 1.21 | 0.0792 |
| D2 | 0.317 | 1 | 0.0435 | 4.86 | 0.317 |
| Residual error | 0.9785 | 15 | 0.0652 | ||
| Lack of fit | 0.7606 | 10 | 0.28 | 1.74 | 0.0761 |
| Error | 0.2179 | 5 | 0.0436 | ||
| Total | 3.89 | 29 |
| Designation | Symbol | Numerical Value | Unit |
|---|---|---|---|
| solidus temperature | Ts | 1723 | K |
| liquidus temperature | Tl | 1790 | K |
| latent heat of fusion | Hm | 2.738 × 105 | J/kg |
| density | ρ | 7930 | Kg/m3 |
| coefficient of thermal expansion | β0 | 1.2 × 10−5 | K−1 |
| convective heat transfer coefficient | αc | 80 | W/m2K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, X.; Zhang, H.; Cao, W.; He, Z.; Wang, B.; Ge, F.; Gao, J. Study on the Depth and Evolution of Keyholes in Plasma-MIG Hybrid Welding. Crystals 2023, 13, 412. https://doi.org/10.3390/cryst13030412
Miao X, Zhang H, Cao W, He Z, Wang B, Ge F, Gao J. Study on the Depth and Evolution of Keyholes in Plasma-MIG Hybrid Welding. Crystals. 2023; 13(3):412. https://doi.org/10.3390/cryst13030412
Chicago/Turabian StyleMiao, Xinglin, Hongtao Zhang, Wenhuan Cao, Zhenyu He, Bo Wang, Fuchen Ge, and Jianguo Gao. 2023. "Study on the Depth and Evolution of Keyholes in Plasma-MIG Hybrid Welding" Crystals 13, no. 3: 412. https://doi.org/10.3390/cryst13030412
APA StyleMiao, X., Zhang, H., Cao, W., He, Z., Wang, B., Ge, F., & Gao, J. (2023). Study on the Depth and Evolution of Keyholes in Plasma-MIG Hybrid Welding. Crystals, 13(3), 412. https://doi.org/10.3390/cryst13030412







