Chemical Adsorption of HF, HCl, and H2O onto YF3 and Isostructural HoF3 Surfaces by First Principles
Abstract
1. Introduction
2. Methodology
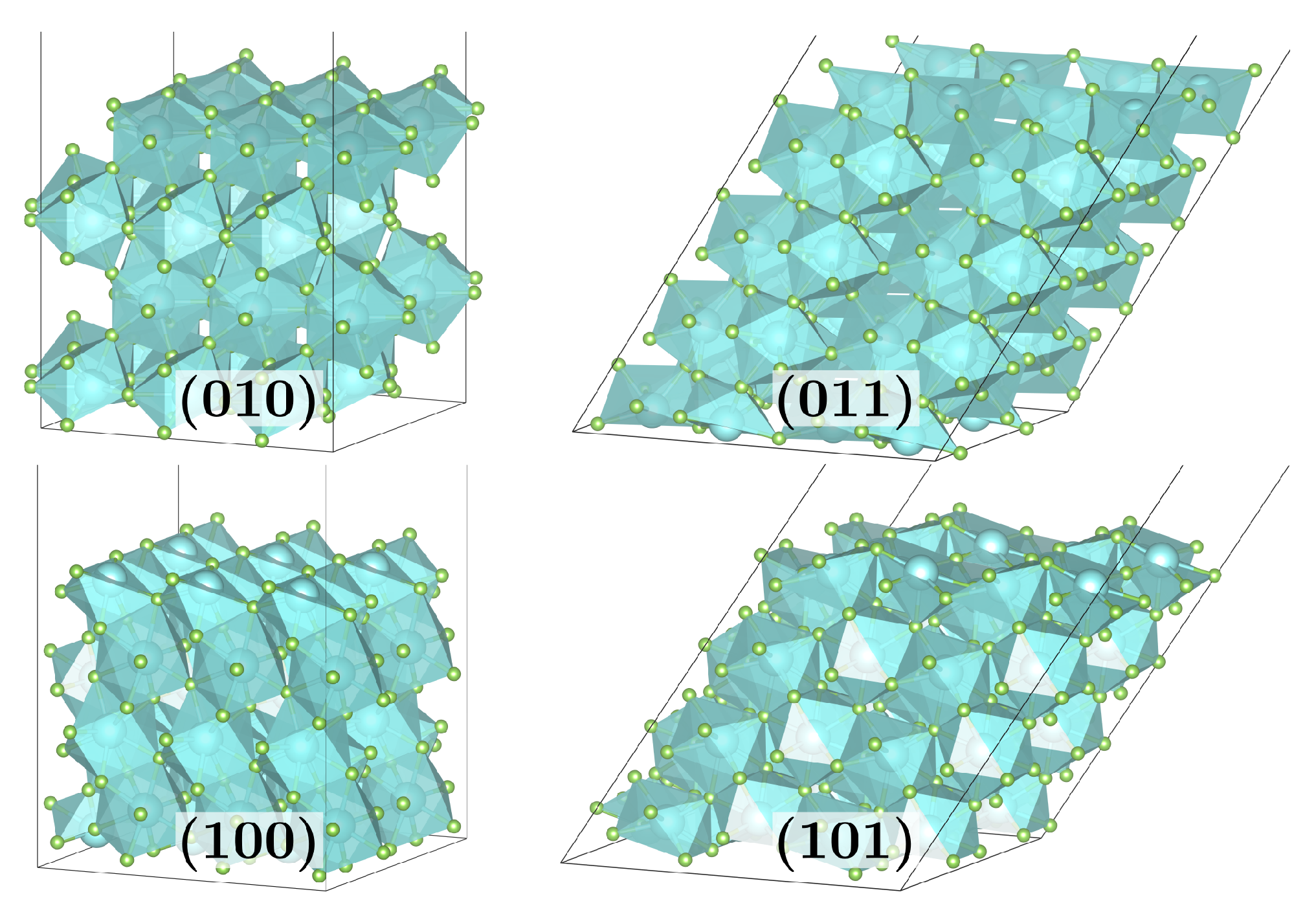
2.1. Crystal Structure and Surfaces
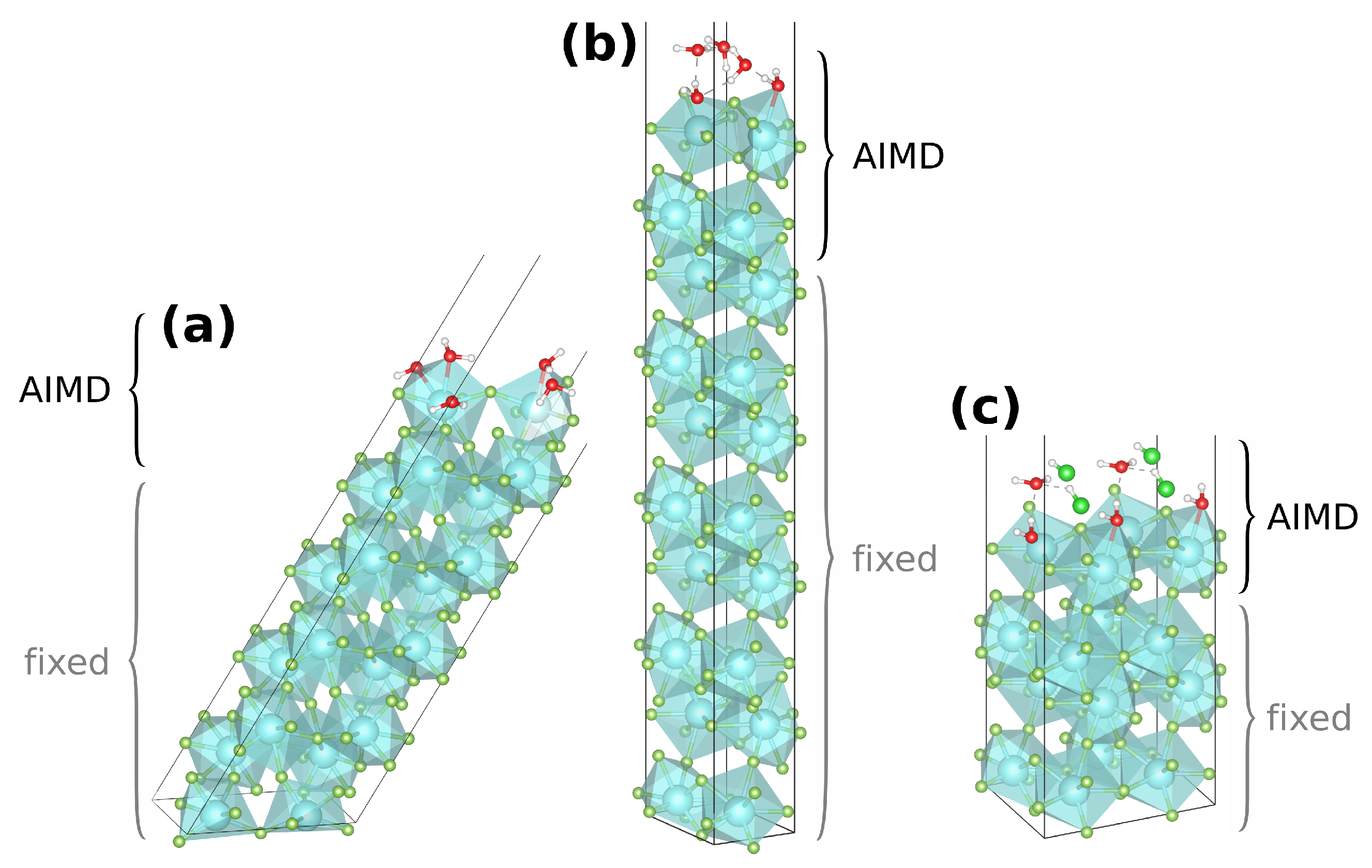
2.2. Scan of Conformational Adsorption Space
2.3. Computational Details
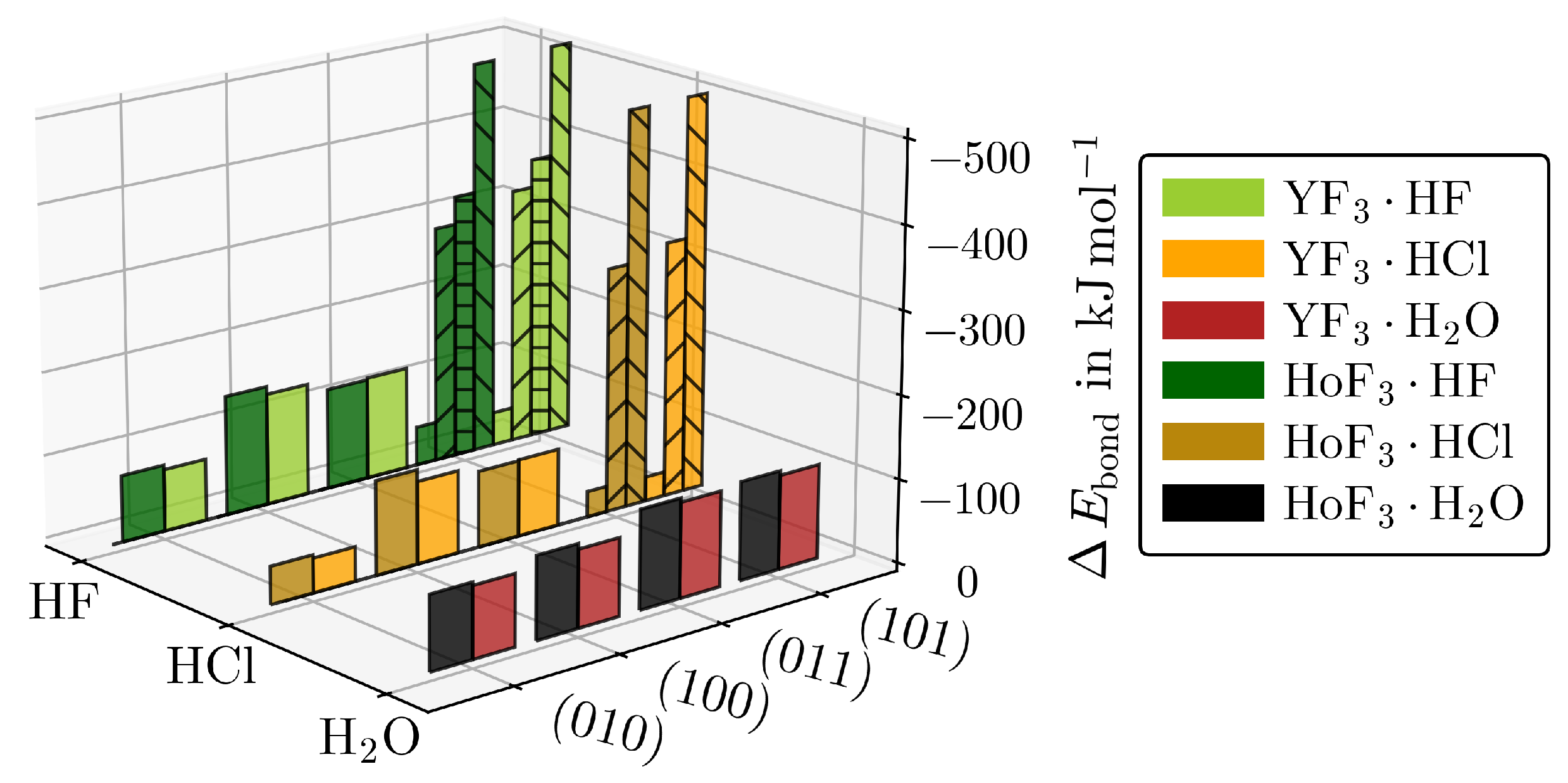
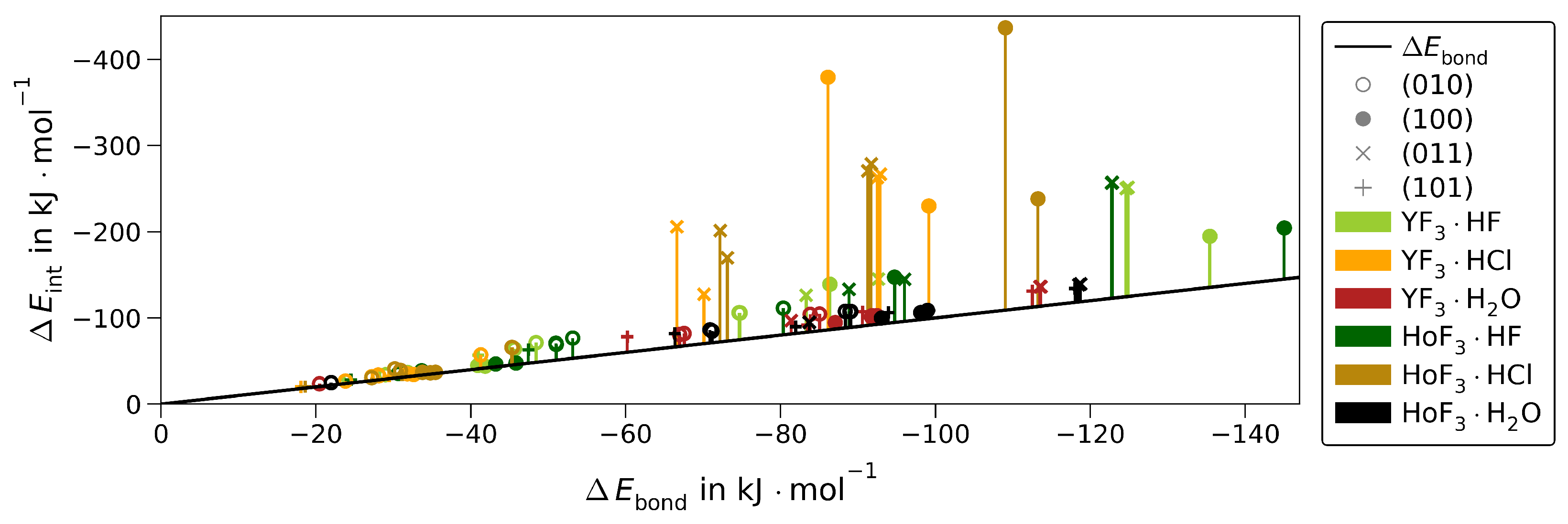
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Atencio, D.; Bastos Neto, A.C.; Pereira, V.P.; Ferron, J.T.M.M.; Hoshino, M.; Moriyama, T.; Watanabe, Y.; Miyawaki, R.; Coutinho, J.M.V.; Andrade, M.B.; et al. Waimirite-(Y), orthorhombic YF3, a new mineral from the Pitinga mine, Presidente Figueiredo, Amazonas, Brazil and from Jabal Tawlah, Saudi Arabia: Description and crystal structure. Mineral. Mag. 2015, 79, 767–780. [Google Scholar] [CrossRef]
- Bau, M. Controls on the fractionation of isovalent trace elements in magmatic and aqueous systems: Evidence from Y/Ho, Zr/Hf, and lanthanide tetrad effect. Contrib. Mineral. Petrol. 1996, 123, 323–333. [Google Scholar] [CrossRef]
- Loges, A.; Migdisov, A.A.; Wagner, T.; Williams-Jones, A.E.; Markl, G. An experimental study of the aqueous solubility and speciation of Y(III) fluoride at temperatures up to 250 °C. Geochim. Cosmochim. Acta 2013, 123, 403–415. [Google Scholar] [CrossRef]
- Guan, Q.; Mei, Y.; Etschmann, B.; Testemale, D.; Louvel, M.; Brugger, J. Yttrium complexation and hydration in chloride-rich hydrothermal fluids: A combined ab initio molecular dynamics and in situ X-ray absorption spectroscopy study. Geochim. Cosmochim. Acta 2020, 281, 168–189. [Google Scholar] [CrossRef]
- Stefanski, J.; Jahn, S. Yttrium speciation in subduction-zone fluids from ab initio molecular dynamics simulations. Solid Earth 2020, 11, 767–789. [Google Scholar] [CrossRef]
- Bau, M.; Dulski, P. Comparative study of yttrium and rare-earth element behaviours in fluorine-rich hydrothermal fluids. Contrib. Mineral. Petrol. 1995, 119, 213–223. [Google Scholar] [CrossRef]
- Schönenberger, J.; Köhler, J.; Markl, G. REE systematics of fluorides, calcite and siderite in peralkaline plutonic rocks from the Gardar Province, South Greenland. Chem. Geol. 2008, 247, 16–35. [Google Scholar] [CrossRef]
- Loges, A.; (Freie Universität Berlin, Berlin, Germany). Private Communication, 2020.
- Zhang, W.; Yan, T. A molecular dynamics investigation of La3+ and Lu3+-ligand speciation in aqueous solution. J. Mol. Liq. 2022, 347, 118367. [Google Scholar] [CrossRef]
- Zalkin, A.; Templeton, D.H. The Crystal Structures of YF3 and Related Compounds. J. Am. Chem. Soc. 1953, 75, 2453–2458. [Google Scholar] [CrossRef]
- Spedding, F.H.; Henderson, D.C. High-temperature heat contents and related thermodynamic functions of seven trifluorides of the rare earths: Y, La, Pr, Nd, Gd, Ho, and Lu. J. Chem. Phys. 1971, 54, 2476–2483. [Google Scholar] [CrossRef]
- Anders, J.; Limberg, N.; Paulus, B. First Principle Surface Analysis of YF3 and Isostructural HoF3. Materials 2022, 15, 6048. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements. J. Phys. Condens. Matter. 1994, 6, 8245–8257. [Google Scholar] [CrossRef]
- NIST Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database Number 101. 2022. Available online: http://cccbdb.nist.gov/ (accessed on 5 December 2022).
- NIST Diatomic Spectral Database, NIST Standard Reference Database 114. Available online: https://www.nist.gov/pml/diatomic-spectral-database (accessed on 5 December 2022).
- Sun, W.; Ceder, G. Efficient creation and convergence of surface slabs. Surf. Sci. 2013, 617, 53–59. [Google Scholar] [CrossRef]
- Tran, R.; Xu, Z.; Radhakrishnan, B.; Winston, D.; Sun, W.; Persson, K.A.; Ong, S.P. Surface energies of elemental crystals. Sci. Data 2016, 3, 160080. [Google Scholar] [CrossRef]
- Larsen, A.H.; Mortensen, J.J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment—a Python library for working with atoms. J. Phys. Condens. Matter. 2017, 29, 273002. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. Constant Temperature Molecular Dynamics Methods. Prog. Theor. Phys. Suppl. 1991, 103, 1–46. [Google Scholar] [CrossRef]
- Pulay, P. Convergence acceleration of iterative sequences. the case of scf iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Wood, D.M.; Zunger, A. A new method for diagonalising large matrices. J. Phys. A Math. Gen. 1985, 18, 1343. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Kerker, G.P. Efficient iteration scheme for self-consistent pseudopotential calculations. Phys. Rev. B 1981, 23, 3082–3084. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Jeffrey, G. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA; Oxford, UK, 1997. [Google Scholar]
- Epstein, G.L.; Reader, J. Spectrum of doubly ionized yttrium (YIII). J. Opt. Soc. Am. 1975, 65, 310–314. [Google Scholar] [CrossRef]
- Johnson, D.A.; Nelson, P.G. Lanthanide Ionization Energies and the Sub-Shell Break. Part 2. The Third and Fourth Ionization Energies. J. Phys. Chem. Ref. Data 2017, 46, 013109. [Google Scholar] [CrossRef]

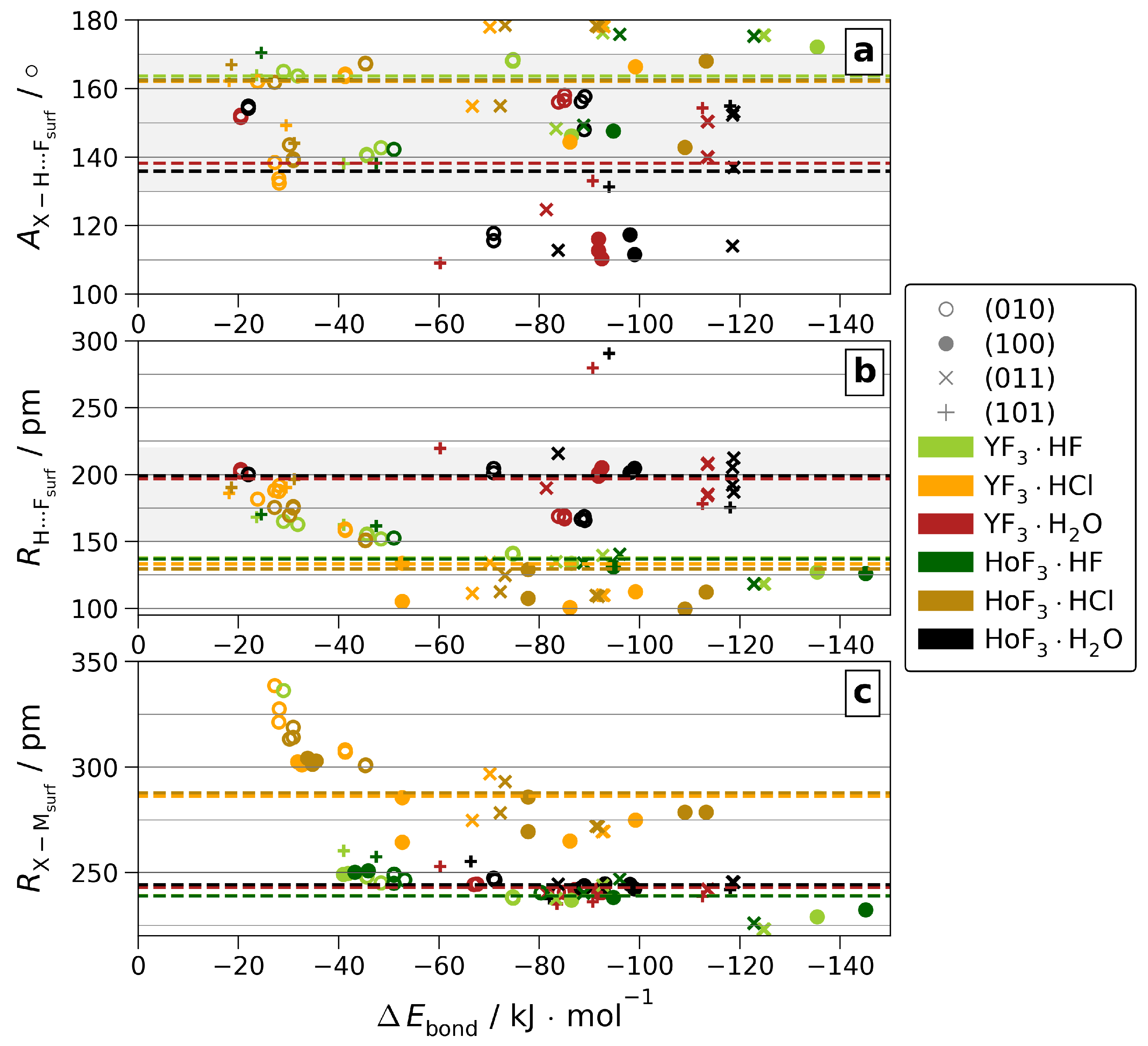
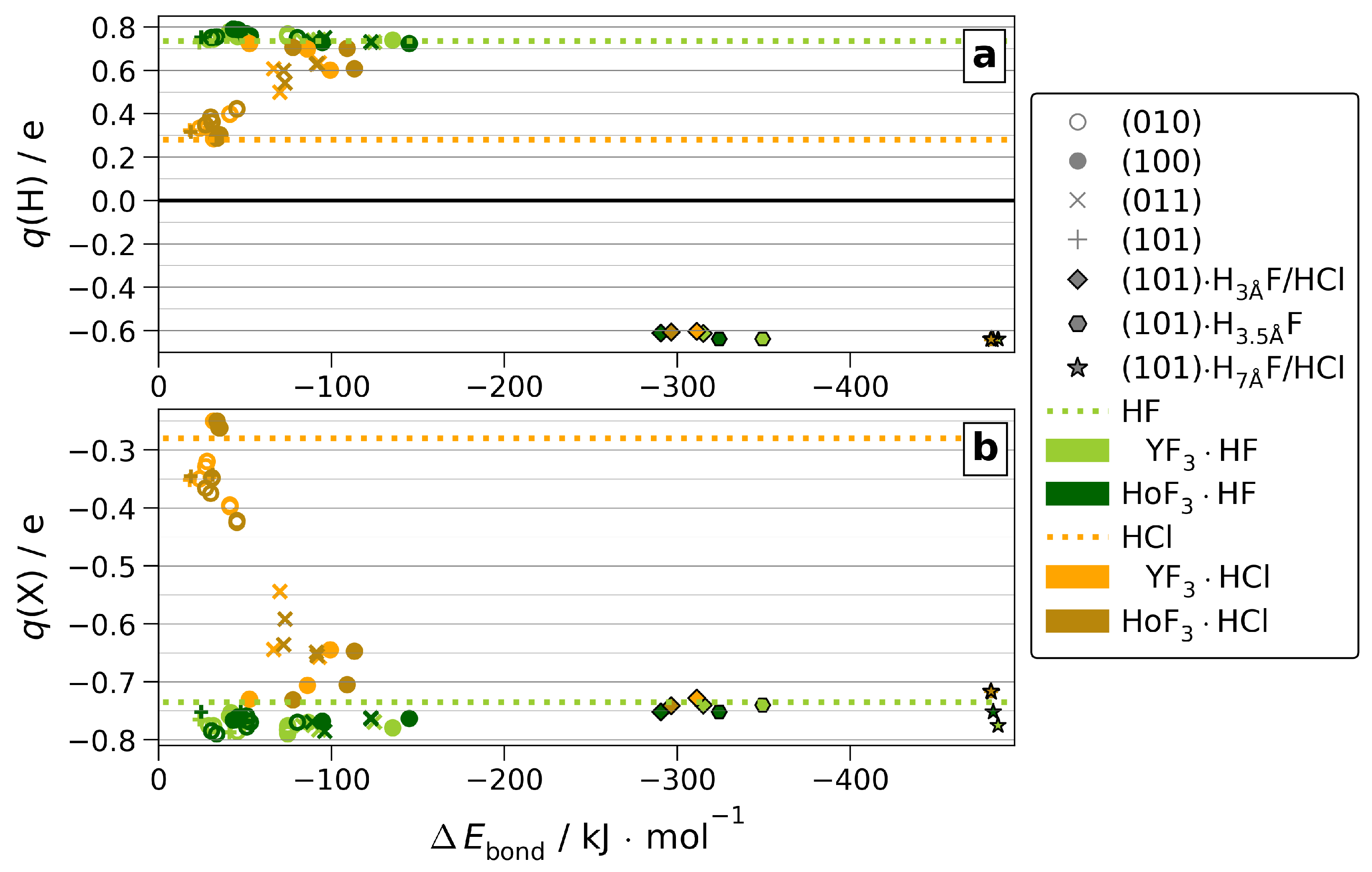
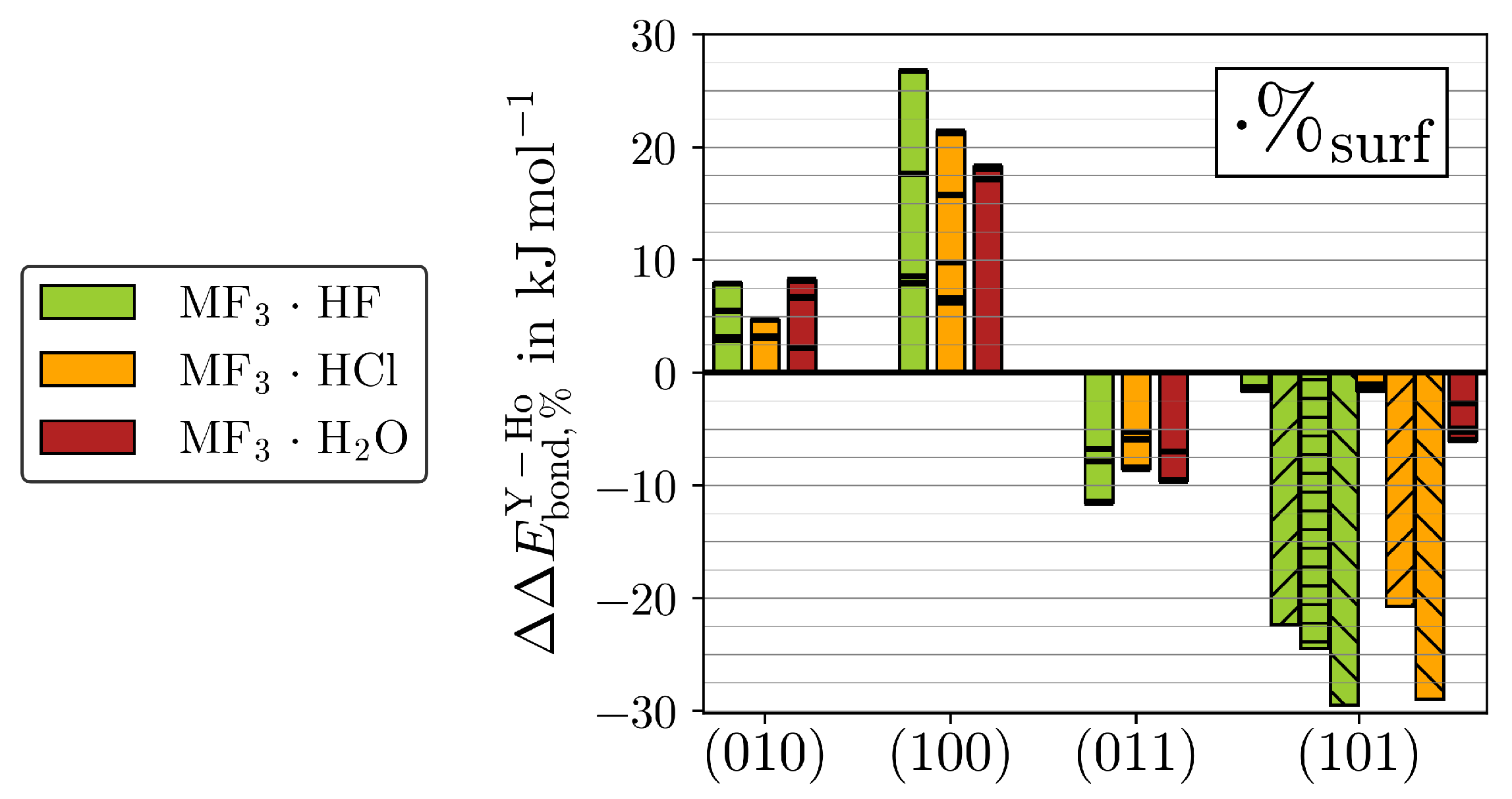
| HF | HCl | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CN | M | |||||||||
| (101)·HF/Cl | 6 | Y | 257 | 285 | ||||||
| Ho | 262 | 292 | ||||||||
| (101)·HF | 6; 7 | Y | 352 | — | ||||||
| Ho | 357 | |||||||||
| (101)·HF/Cl | 6; 6 | Y | 681 | 684 | ||||||
| Ho | 688 | 691 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anders, J.; Wiedenhaupt, H.; Paulus, B. Chemical Adsorption of HF, HCl, and H2O onto YF3 and Isostructural HoF3 Surfaces by First Principles. Crystals 2023, 13, 555. https://doi.org/10.3390/cryst13040555
Anders J, Wiedenhaupt H, Paulus B. Chemical Adsorption of HF, HCl, and H2O onto YF3 and Isostructural HoF3 Surfaces by First Principles. Crystals. 2023; 13(4):555. https://doi.org/10.3390/cryst13040555
Chicago/Turabian StyleAnders, Jennifer, Henrik Wiedenhaupt, and Beate Paulus. 2023. "Chemical Adsorption of HF, HCl, and H2O onto YF3 and Isostructural HoF3 Surfaces by First Principles" Crystals 13, no. 4: 555. https://doi.org/10.3390/cryst13040555
APA StyleAnders, J., Wiedenhaupt, H., & Paulus, B. (2023). Chemical Adsorption of HF, HCl, and H2O onto YF3 and Isostructural HoF3 Surfaces by First Principles. Crystals, 13(4), 555. https://doi.org/10.3390/cryst13040555






