Study on Band Gap Characteristics of Phononic Crystal Double-Layer Beam Structure Attached by Multilayer Cylinder

Abstract

Intended for the vibration and noise control problems faced by many engineering fields, a fresh variety of phononic crystal beam structure was constructed by attaching a one-dimensional periodic multilayer cylinder to a double-layer beam structure. Utilizing the finite element method and the Bloch theorem, the vibration modes of the band structure, the critical point of the band gap and the associated finite structure’s vibration transmission is estimated, and then the band gap characteristics of the structure are comprehensively studied. The results show that reasonable parameter design can achieve vibration and noise control in a certain frequency range. Based on the modal analysis, the mechanism of band gap opening is revealed. By comparing the single-layer beam and double-layer beam with the same parameters, the advantages of the double-layer beam in vibration reduction and noise reduction are shown. The study’s findings offer a fresh concept for ship engineering disciplines including vibration and noise reduction technology.

1. Introduction

With the expansion of the economy in recent years, social progress and the continuous improvement of living standards, more and more people are becoming aware of vibration and noise pollution. In a ship’s environment, vibration and noise problems will have a great impact on the crew’s body, life, rest and work; noise that is too strong will also cause some precision instruments and equipment on board to malfunction, reduce accuracy and shorten service life. As we all know, the main links of acoustic system include the sound source, transmission path and receiver. Therefore, traditional noise control is accustomed to start from one of the three aspects: sound source, pathway or receiver. Relatively speaking, it is often difficult to exert control over the vibration and noise at the sound source when the equipment is already in use, so the most common and effective approach is often control at the propagation path. The most common of these is isolation and absorption of vibration, which is also the more common method used in engineering applications. It is well known that beam-like structures have been widely used in many projects, and are the focus of attention in the area of noise and vibration control. Therefore, the control study of vibration propagation of beam-like structures must play a great role in the realization of noise and vibration reduction in engineering.

The most important feature of phononic crystals, i.e., artificial periodic composite structures, is that they have an elastic wave band gap, and the vibrational noise corresponding to this band gap frequency band will not be able to propagate along the structure. Conceivably, this property can be used to control vibration noise and has attracted widespread scholarly attention. In terms of the band gap formation mechanism, two varieties of phononic crystals exist, Bragg scattering type and local resonance type [1]. While the wavelength corresponding to the frequency in the band gap of the local resonance type is much larger than the lattice constant, it is within the same order of magnitude as the band gap of the Bragg scattering type. Therefore, the damping and noise reduction in the low-frequency band can be realized with the help of local resonance type phonon crystals matching the actual size of the project, which adds the possibility of applying phonon crystals to the low-frequency domain damping and noise reduction [2].

At present, the research on various local resonance type phonon crystals has been widely studied, and the common basic structures are: rods, beams and plates. The bending vibration properties of finite periodic structure beams were studied by Ronghui Ning as well as Shijian Zhu et al. [3] The finite structure vibration transmission rate was specifically bending vibration. By periodically attaching the oscillators to the ferro-mosinco beams, combining experiments and theories, Yu Dianlong and Liu Yaozong et al. [4] studied the corresponding bending vibration characteristics of this structure, and the theoretical and experimental results are basically consistent; this offers a fresh technique for managing beams’ low-frequency bending vibration. Assouar et al. [5] proposed a two- and three-component bilaterally attached type of phonon crystal single-plate structure. Hsu [6] proposed an additional phononic crystal plate structure with a “neck”. Zhou and Wang [7] designed, filled and attached phonon crystal plates based on thin plates and cylindrical oscillators, respectively, and applied the finite element method to investigate the formation mechanism of the local resonance band gap and the band gap of the different structures. The finite element method was applied to reveal the formation mechanism and transmission characteristics of the local resonant band gap of different structures, and the controllable performance of the band gap was discussed. By combining the filled and adhered systems, a new bilateral local resonant phonon crystal plate structure was designed by Li Lockbin, Dou Yihua and Chen Tianning [8], and the dispersion relation, energy transfer spectrum and cell displacement field of this structure were calculated based on the finite element method, and the process of formation of the low-frequency local resonant band gap was further analyzed.

The development of phonon-crystal-related research cannot be separated from the proven band gap calculation methods, which mainly include the plane wave expansion method [9,10,11], the finite element method [12,13,14,15], the transfer matrix method [16,17,18] and the multiple scattering method [19,20]. Among them, the phonon crystal finite element method is based on the traditional finite element method, and the periodic boundary conditions based on Bloch theory are used to effectively obtain the energy band structure, eigenmodes, etc.

The phononic crystal beam is an idealized infinitely long period beam structure. Materials designed on the micron and nanoscale have had a huge and lasting impact in photonics and phononics [21]. However, in practical engineering applications, infinitely long beam structures do not exist, but the band gap band of infinitely periodic structures and the attenuation band of finite periodic structures are more compatible. Therefore, a finite period phononic crystal beam structure model is developed in this paper. Based on the study of the band gap characteristics of existing phonon crystal beam structures with different forms and materials, a one-dimensional cylindrical periodic oscillator is designed first, and then four unit oscillators are taken and arranged vertically periodically to create a new crystal cell, where the upper and lower plates are joined above and below them. The new cell is then arranged horizontally periodically to construct a phonon crystal beam structure, which is equivalent to nested phonon crystals in phonon crystals. Compared with the conventional phonon crystal beam, a wider band gap characteristic will be produced. In this study, the energy band structure is calculated using the finite element approach, to investigate the formation mechanism and the regulation law of the band gap characteristics, and to investigate the generalization of the single/bilayer and the characteristics of the bilayer beam structure by comparing it with the single-layer properties of the relevant structure’s band gap.

2. Models and Methods

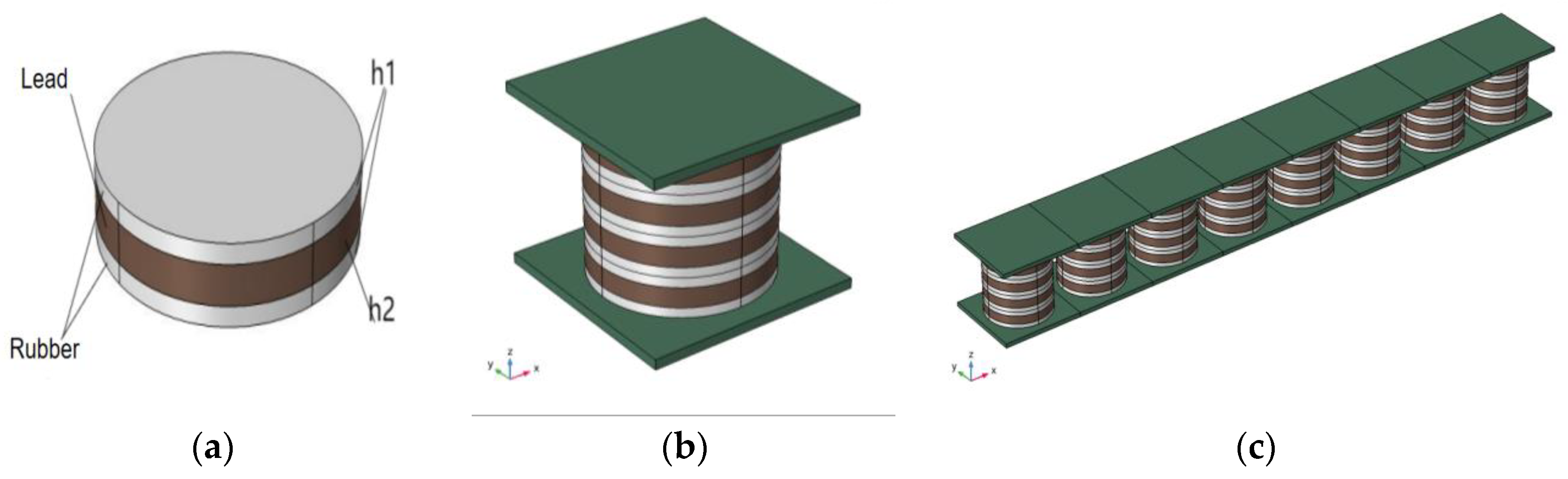
The schematic diagram of the structure of the cylindrical oscillator between the cavities of the double-layer beam is shown in Figure 1a. The figure demonstrates that the oscillator is made by attaching two pieces of rubber and one piece of lead, in which the upper and lower pieces of material are identical in size material, and the radius of the cylindrical lead block in the middle is the same as the upper and lower pieces of rubber, and the height is twice that of a single rubber block. The upper and lower plates of the four-cylinder oscillators are sandwiched together and positioned vertically at regular intervals. The higher and lower plates are made of steel and are joined to the upper and lower plates., thus forming a new cell, whose structure is shown schematically in Figure 1b. The new cell is arranged transversely periodically to form a phonon crystal beam structure, as shown in Figure 1c. The lattice constant, the thickness of the upper and lower plates, the thickness of the rubber layer, the thickness of the lead layer and the total height of the cell oscillator are all specified in the structural model as a, e, h1, h2 and h, respectively. The radius of the cylindrical oscillator of one cell is also specified as r, as shown in Figure 1. The geometric parameters for this structural model are displayed in

Table 1. Material parameters used in calculations.

Materials	Density/(kg/m3)	Modulus of Elasticity/(1010 N/m2)	Poisson’s Ratio
Steel	7780	21.06	0.300
Lead	11,600	4.08	0.369
Rubber	1300	1.175 × 10−5	0.469

and

Table 2. Geometric parameters used in calculations.

a (Unit/mm)	e (Unit/mm)	h1 (Unit/mm)	h2 (Unit/mm)	h (Unit/mm)	r (Unit/mm)
100	5	5	10	20	40

below.

For the purpose of computing and acquiring the cylindrical oscillator’s energy band structure and displacement field, The computer program COMSOL Multiphysics was used to implement the finite element approach. A tetrahedral mesh was chosen to divide the solid model. The boundary conditions are divided into two categories: free boundary and periodic boundary. Among them, the periodic boundary conditions can be obtained by deducing Bloch’s theorem.

$$u(z+a)=u(z)e^{i(ka)}$$

(1)

It is well known that the free vibration equation in the finite element method is relatively easy to obtain, and substituting Equation (1) into it further yields the following:

$$(K-{\omega }^{2}M)u=0$$

(2)

In Equation (2), K and M are not the conventional stiffness and mass matrices, but both contain terms coupled to the Bloch wave vector. It is clear that Equation (2) is a characteristic equation with respect to ω². For each given Bloch wave vector k, we can find answers to its eigenvalues in series and eigenvectors to obtain the final energy band structure map and vibration pattern.

From the findings in the literature [12], it is clear that the number of oscillator cycles also has significant impact on the band gap. Theoretically, the performance of the damping increases with the amount of cycles. However, considering the size limitation and lightweight requirement of the structure in practical problems, a fewer number of cycles are required to satisfy the expected damping effect. In this paper, four cylindrical oscillators are taken and arranged vertically in cycles, and the upper and lower plates are attached beneath them to create a new cell, whose beam structure is schematically shown in Figure 1c. The same calculation is performed for the new cell structure using the phonon crystal finite element method mentioned above. Similarly, it is possible to derive the energy band structure and the displacement field of the beam structure.

3. Numerical Results and Analysis

3.1. Energy Band Structure, Displacement Field and Transmission Curve of Cylindrical Oscillator

The energy band structure of the cylindrical oscillator is given in Figure 2a, where the material parameters and geometric parameters used are shown in Table 1 and Table 2, respectively. The four cylindrical oscillators are vertically stacked periodically, and the excitation and response points are situated at the bottom and top of the upper and lower plates, respectively, to confirm the accuracy of the calculated energy band structure, as shown in Figure 3. The calculated vibration transmission curves in the appropriate directions are shown in Figure 2b.

It can be seen from Figure 2a that the cylindrical oscillator energy band structure opens a wide band gap between 175 and 275 Hz. It can be seen from Figure 2b that the decay frequency domain of the transmission curve is likewise quite wide, essentially matching the energy band structure, and the vibration can be transmitted in a finite framework. This is in line with the finding made in the previous studies that the band gap frequency band of the infinite structure and the decay frequency band of the finite structure coincide with one another. The band gap range of such cylindrical local resonance type oscillators at low and medium frequencies will yield ideal application prospects for achieving a specified range of low-frequency dampening and noise reduction. The displacement fields corresponding to the eigenmodes at the critical places in the energy band structure diagram were extracted to elucidate the mechanism of its band gap creation, as shown in Figure 4.

In the energy band structure of the cylindrical local resonance type cell, for modes B₁ and B₂, rubber serves as the displacement field for longitudinal bending vibration, and the lead block remains stationary as a substrate to achieve dynamic equilibrium of longitudinal vibration. For modes B₃ and B₄, there is a certain amount of torsional vibration in the displacement field. However, the difference is that in mode B₂, the middle lead block remains stationary and the upper and lower rubber layers make some degree of torsional vibration. In mode B₄, the rubber layer of the lead block has a certain degree of torsional vibration. As a result of these modal coupling effects, a vibration band gap in the frequency range of 175~287 Hz is opened.

3.2. Energy Band Structure, Displacement Field and Transmission Curve of Single-Layer Beam under Oscillator Apposition

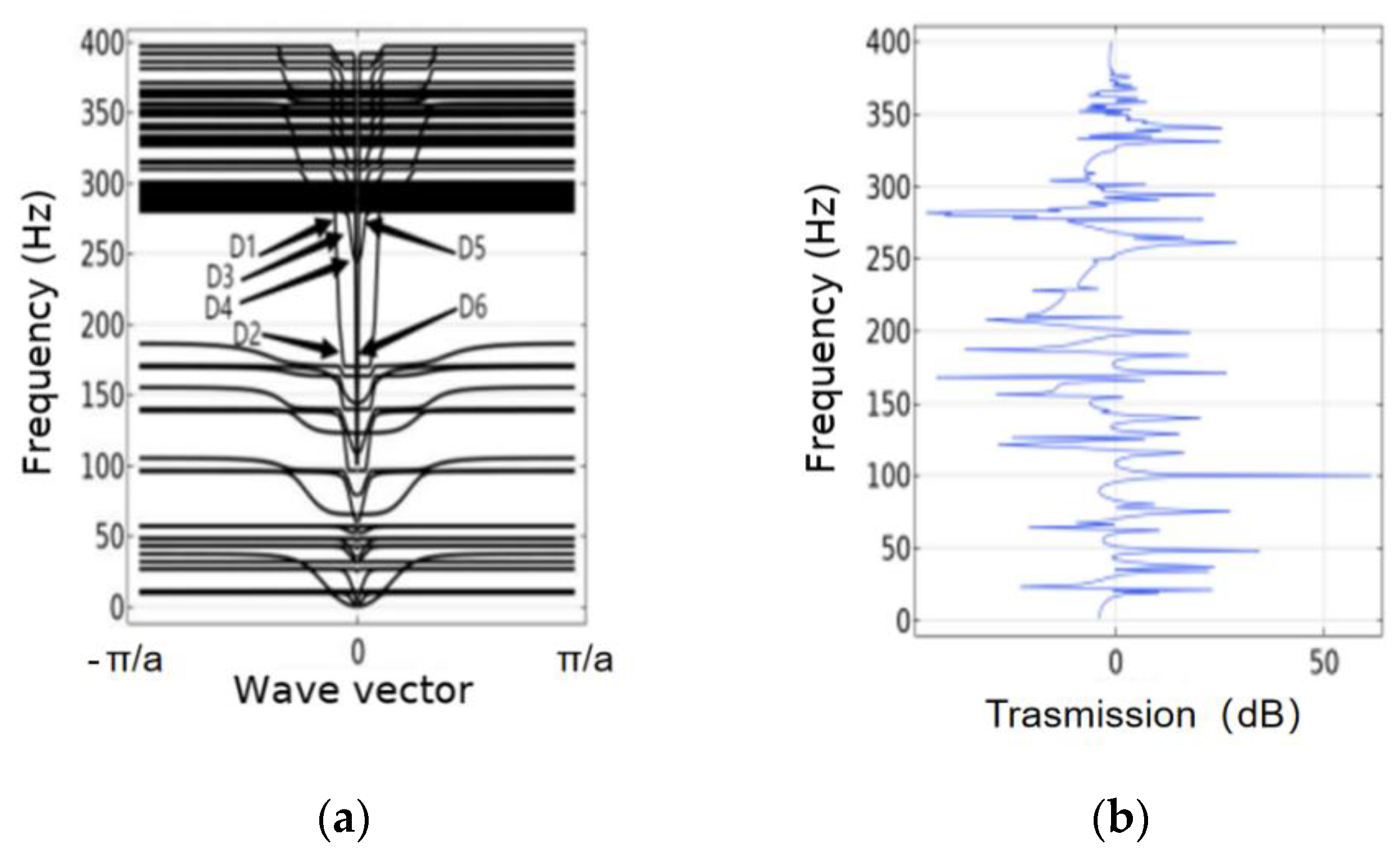
The new cell consists of four cylindrical oscillators and the lower beam, and its energy band structure is shown in Figure 5a, where Table 1 and Table 2 display the material properties utilized in the calculation. In order to confirm the calculated energy band structure’s precision even further, the eight cells were then arranged transversely periodically. The excitation points and corresponding points were placed at the positions shown in Figure 6, and tested to produce the correct vibration transmission curves, as shown in Figure 5b.

It can be seen from the curve of vibration transmission that there is no more significant decay in the frequency domain. To reveal the characteristics of this vibration transmission, the displacement fields corresponding to the eigenmodes labeled in Figure 5a are given, as shown in Figure 7.

In the cell energy band structure of this local resonance type single-layer beam structure, for modes D₁, D₃ and D₅, the displacement field is mainly rotational vibration of the lower plate around the central axis in the horizontal plane. The middle oscillator basically remains stationary, but with a certain degree of vibrational displacement. For D₂ and D₄, the displacement field is mainly vertical vibration along the z-direction, and the middle oscillator basically maintains a certain degree of rest, in which the lowest two oscillators’ vibrational amplitude is marginally greater than that of the upper two oscillators’, indicating that the model plays a certain role in vibration damping. The lower plate of mode D₆ has a certain tilt angle, which is due to the concentration of vibration energy in one side of the plate. The overall model is subjected to vertical vibration along the z-direction, and the middle oscillator and the upper cell basically remain stationary. Among them, modes D₅ and D₆ are the critical positions of the energy band structure diagram’s displacement fields corresponding to the eigenmodes, so the middle oscillator has a smaller amplitude vibration in the beginning stage.

For the local resonant phonon crystal, the local resonance properties of the scatterer have a major role in determining the band gap’s location and size, which is independent of the form of the lattice. By studying and analyzing the above band gap characteristics, it can be seen that the frequency domain of the decay does not appear significantly. This is because the oscillator in the structure does not play its full role when both the excitation and response points are in the lower plate, which also proves that the periodic oscillator has less influence on the vibration of the single-layer beam structure. This also proves that the effect of periodic oscillators on the vibration transmission of the single-layer beam structure is small. It is evident that the generation of band gap in phonon crystals is complex and so are their characteristics. The process of creating the band gap is often the result of a combination of mechanisms, and it is not simply a matter of attaching a periodic oscillator to produce the desired band gap.

3.3. Energy Band Structure, Displacement Field and Transmission Curve of Double−Layer Beam under Oscillator Apposition

If the phononic crystal structure in Figure 5 is added to the upper beam, a phononic crystal double-layer beam structure is formed. The cell energy band structure of this bilayer beam structure is shown in Figure 8a. The parameters used in the calculation are the same as those shown in Figure 6a, and the specific parameters are shown in Table 1 and Table 2. The position of the excitation point is kept constant, and the response point is changed to the position of the upper plate as shown in Figure 9. The resulting transmission curve for vibration is shown in Figure 8b. It can be seen from Figure 8a,b that the band of vibration attenuation essentially matches the band gap range.

From the literature [14], it can be seen that the vibration attenuation of the phononic crystal double-layer beam structure composed of one periodic oscillator is very small, and the attenuation becomes more obvious along with the increase in the number of oscillators. Due to the limitation of the actual size, in this paper, four periodic oscillators are selected as one unit to construct the phononic crystal double-layer beam structure. As can be seen in Figure 8b, the decay band of the vibration transmission curve of the phononic crystal double-layer beam structure is basically the same as the range of the decay band frequencies in Figure 2b, and it has stronger decay characteristics compared to Figure 2b. This is due to the fact that the cylindrical oscillator can open a band gap from 167 to 280 Hz in frequency, and the vertical excitation is transmitted from the lower plate through the oscillator to the upper plate, and when the vibration range is within the band gap range of the oscillator, the vibration transmitted through the oscillator is suppressed, so that the attenuation band in the two figures of Figure 2b and Figure 8b is essentially the same. Thus, the opening of the band gap in this phononic crystal double-layer beam is essentially the cylindrical oscillator playing the role of vibration suppression. This is because the phononic crystal beam structure makes good use of the forbidden band characteristics of the cylindrical oscillator in the low- and middle-frequency domain, thus constituting a double-layer beam structure with low and middle frequencies. In this paper, a one-dimensional cylindrical periodic oscillator is designed first, and then the oscillator period is attached to the double-layer beam. This model is equivalent to nesting phonon crystals in phonon crystals, which improves the damping characteristics to a certain extent.

From Figure 8a, It can be seen that the energy band structure does not appear to have a band gap, but the range of its corresponding vibration transmission curve’s decay frequency domain approximately corresponds to the range of the cylindrical oscillator’s decay frequency domain. As shown in Figure 10, the displacement field of the corresponding attenuation frequency domain is examined in order to learn about its band gap characteristics and identify its phenomenon.

As can be seen from Figure 10, in the attenuation frequency domain, the upper and lower beams remain basically stationary regardless of how the structure vibrates in these modes. This indicates that the vibration will not be transmitted from one beam to the other, further indicating that the double-layer beam structure has effective vibration separation in the relevant frequency domain. Because the decay frequency domain falls in the band gap of the middle oscillator, and because the cylindrical oscillator in the middle of this structure plays a crucial role in vibration isolation, there is no obvious band gap in the energy band structure. However, its related vibration transmission curve has a wide decay frequency domain, explaining why the phenomenon happens. In Figure 10, the displacement fields of modes F₁ and F₄ are mainly cylindrical vibrations along the z-direction, and the resonant band gap of the bending elastic wave is formed by the coupling of the bending elastic wave in the z-direction vibration of the plate. For mode F₂, both its upper and lower beams make a certain degree of transverse displacement vibration, which also proves the idea that different directions and different sizes of wave fields correspond to the same vibration mode from z-axis throughout the beam structure. For modes F₃, F₅ and F₆, the displacement fields are the result of the joint action of the tensile vibration mode and the outward bending vibration mode of the vertical plate of the double-layer steel plate of the cylindrical resonant unit along the z-axis. The vibration energy in F₆ is concentrated in the cylindrical phonon crystal structure, while the upper and lower beams remain basically stationary and stable, because mode F₆ is the displacement field that matches the modulus of eigenmodes at the crucial location in the energy band structure schematic shown above. A local band gap in the frequency domain interval of 167–280 Hz is opened by the coupling action, so that a small amplitude of vibration exists in the middle oscillator from the bottommost part, but the vibration is not transmitted from one side of the plate to the other.

In order to further understand the vibration transmission characteristics of this phononic crystal double-layer beam structure, vibration displacement diagrams in the band gap frequency band were made, as shown in Figure 11a. Here, the model used for the calculation is shown in Figure 9, where the longitudinal displacement excitation is applied at the excitation point and the frequency point is chosen to be f = 220 Hz. From Figure 11a, it can be seen that the vibration cannot propagate through the upper beam when the excitation is applied to the lower beam. This demonstrates that a band gap in the relating finite element structure is opened for vibration attenuation, which prevents the vibration in this frequency range from propagating through the cylindrical phononic crystal beam structure when the source and response domains are on opposite sides of the double-layer structure. However, when the frequency falls in the non-attenuated frequency domain of the finite double-layer beam structure, the vibration pattern is shown in Figure 11b, with the frequency point selected as f = 160 Hz. It is obvious that when the lower beam is exposed to the excitation, the vibration is not well suppressed and can be transmitted to the upper beam, which also reflects the onset of the middle- and low-frequency bands corresponding to the cylindrical phononic crystal beam structure.

3.4. Influencing Factors of Upper and Lower Band Gap Limits and Band Gap Width

(1)

Height of rubber layer

Keeping other parameters unchanged and only changing the height of rubber layer H = 5 mm, 10 mm, 15 mm, 20 mm and 25 mm, the effect of rubber layer height on the band gap of double-layer beam structure was studied. As shown in Figure 12, the upper limit of the band gap gradually decreases, the lower limit of the band gap slightly decreases, but the overall band gap width shows a decreasing trend, as shown by the analysis of the parameters of phononic crystal double-layer beam structure. It is known that with the increase of rubber layer height, the overall band gap width decreases slightly with the increase of the height of the rubber layer. This shows that the thickness of the rubber layer has a small effect on the band gap width. Considering the actual engineering application, a smaller height of rubber layer can be chosen to play the role of vibration and noise reduction.

(2)

Height of lead layer

Keeping other parameters constant, the lead layer heights h = 5 mm, 10 mm, 15 mm, 20 mm and 25 mm were used to study the effect of lead layer height on the band gap of the phononic crystal bilayer beam structure. As shown in Figure 13, with the increase in the lead layer height, the upper limit of the band gap gradually decreases. The lower limit of the band gap basically remains unchanged and floats at the upper limit of 100 Hz, resulting in a slightly decreasing trend of the band gap width. As the height of the lead layer increases, it leads to a gradual decrease in the intrinsic frequency of the local resonator, so the upper limit of the band gap always gradually moves toward a lower frequency. Therefore, decreasing the height of the lead layer within the appropriate range is beneficial to the low-frequency characteristics of the phononic crystal bilayer beam structure.

4. Conclusions

For the issue of engineering vibration noise control, this paper first constructs a cylindrical periodic phononic crystal cell structure, then builds an embedded phononic crystal beam structure. It then utilizes the finite element approach to determine the structure of the energy band, eigenmodes and the corresponding displacement field of this structure and the vibration transmission curve of the corresponding finite period double-layer beam structure. Furthermore, it conducts a comparative analysis of the band gap characteristics exhibited by it, and finally the crystal single-layer beam structure and the phonon crystal double-layer beam structure, the band gap characteristics and the properties of single/double-layer beam vibrations are investigated. The conclusions are summarized as follows.

(1)

By constructing an analysis of the cell structure of a cylindrical periodic phonon crystal, the resulting energy band structure and vibration profile graphs, we can clearly see that a relatively wide band gap opens at low and medium frequencies. By analyzing the eigenmodes of the boundary band at the onset frequency of the band gap and the corresponding displacement fields to the eigenmodes, we can analyze the reason for the opening of the band gap as a result of coupled vibrations. It is found that local resonant phononic crystals have the unique property of suppressing the propagation of vibrations in lower frequencies even with smaller period sizes. In actual engineering structures, not only simple torsional and bending vibrations exist, but also a variety of vibration modes may exist simultaneously, which require consideration of the effect of coupled vibrations on the vibration band gap characteristics of phononic crystal beam structures. For beams, there is more coupling of bending and torsional vibrations, which also provides the possibility to realize low-frequency domain vibration damping and noise reduction applications. This structure has good vibration isolation and noise reduction performance for the double-layer beam structure in the corresponding frequency domain because of the intermediate cylindrical oscillator. This structure is roughly the same as the corresponding cylindrical oscillator attenuation frequency domain.

(2)

The band gap characteristics of single-layer and double-layer structures of phononic crystals are compared and analyzed at the level of the band gap formation mechanism. The single-layer structure is limited to the qualitative study of the band gap formation mechanism with the help of the analysis of the intracellular vibration pattern corresponding to the critical frequency of the band gap on the energy band structure diagram. However, based on the existing studies, the generality of the vibration of single/bilayer beam structures is investigated by comparing them with the corresponding single-layer structures, with respect to the properties of the bilayer structure at the structural level and the band gap level. The phononic crystal double-layer beam structure has a good effect on vibration and noise reduction in a specific frequency range. While, the phononic crystal single-layer beam structure has a general effect, and the difference between the vibration and noise isolation performance of the two is more obvious. Theoretically, the double-layer beam structure of cylindrical phononic crystal constructed in this paper provides a new direction for the application of vibration and noise reduction in a specific frequency range in engineering.