Ellipsometry Characterisation for the Cd1-xZnxTe1-ySey Semiconductor Used in X-ray and Gamma Radiation Detectors
Abstract
:1. Introduction
2. Experimental Details
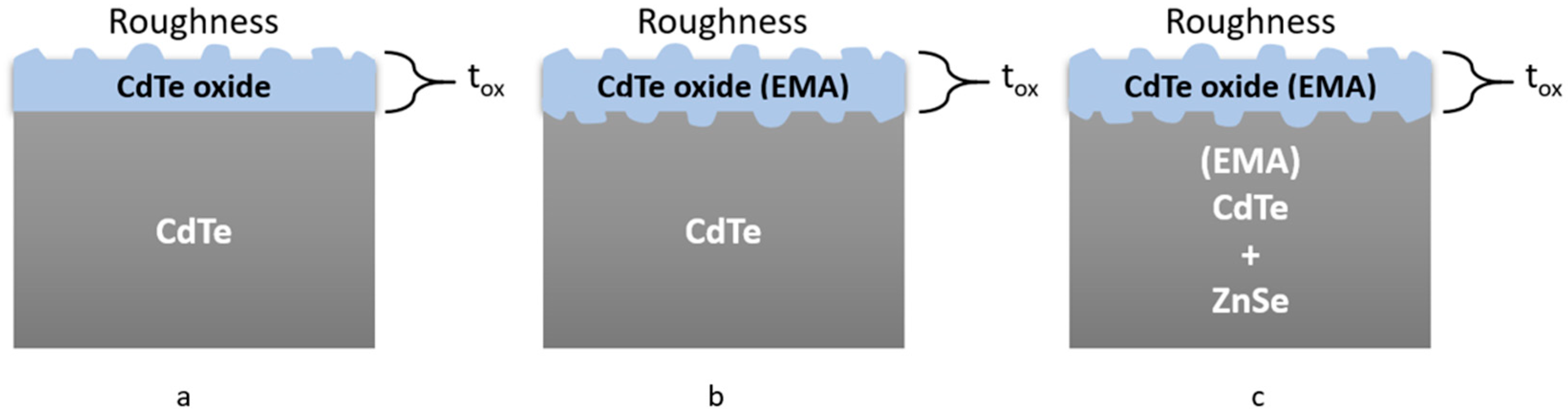
3. Theoretical Background
4. Results and Discussion
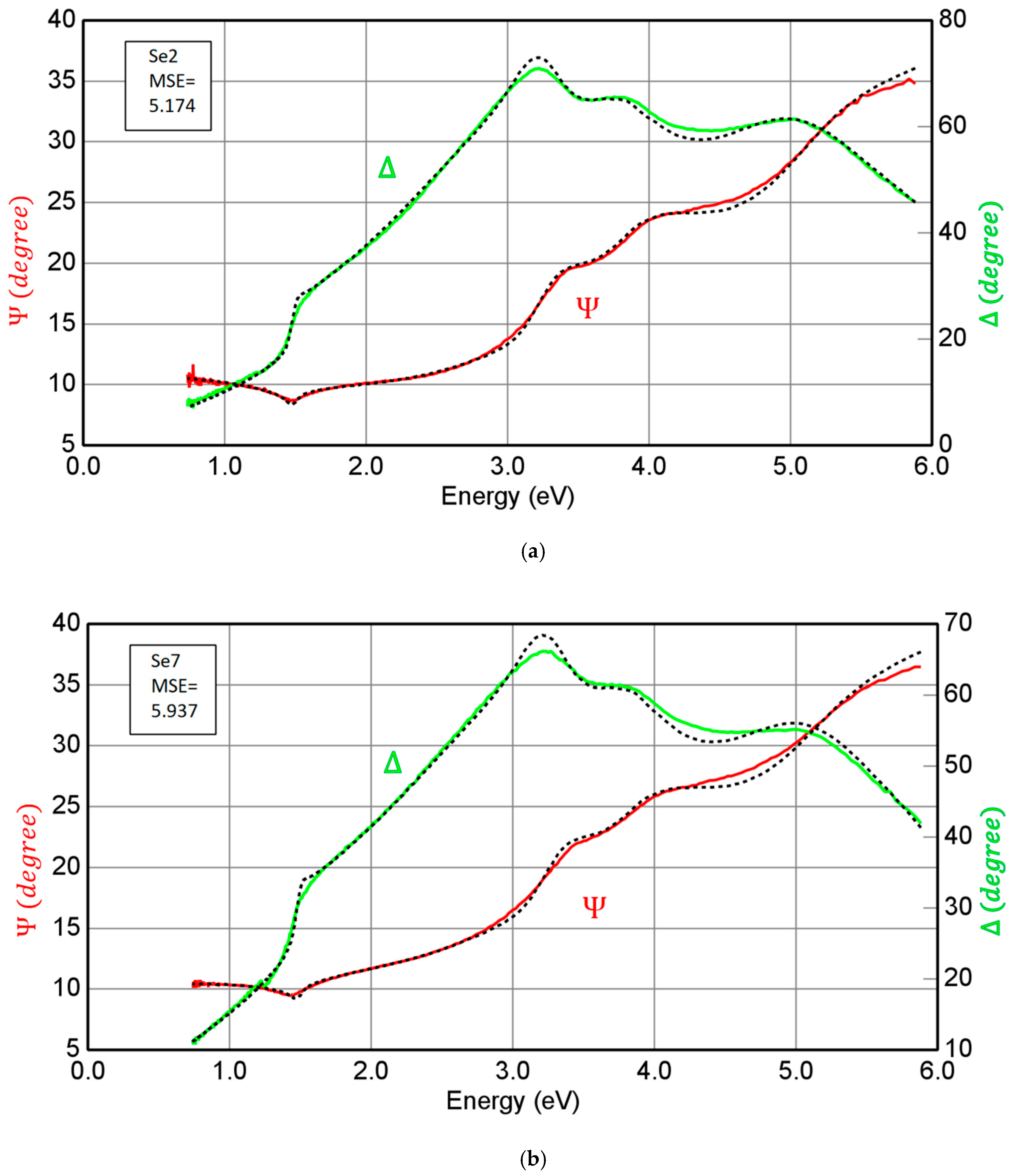
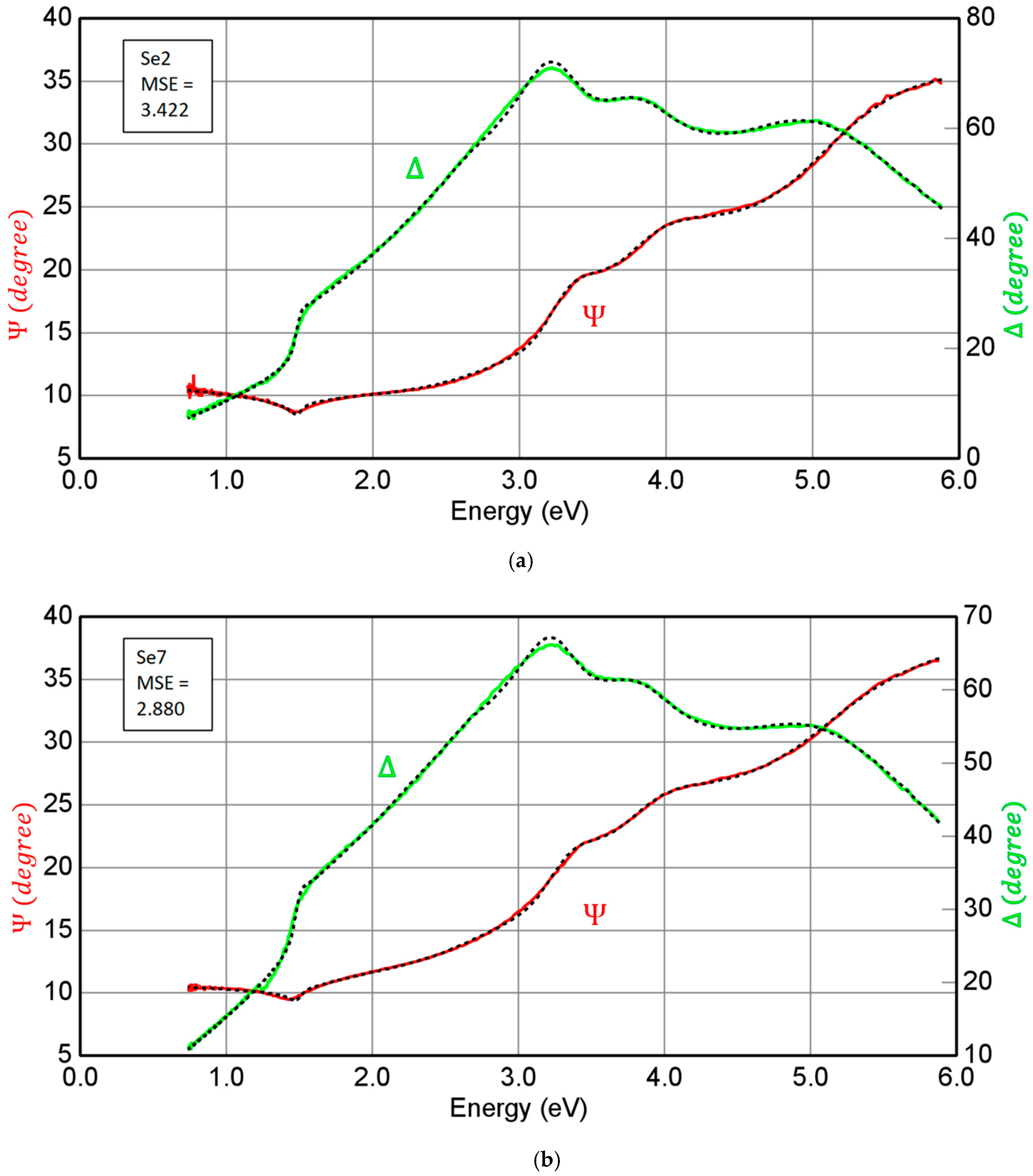
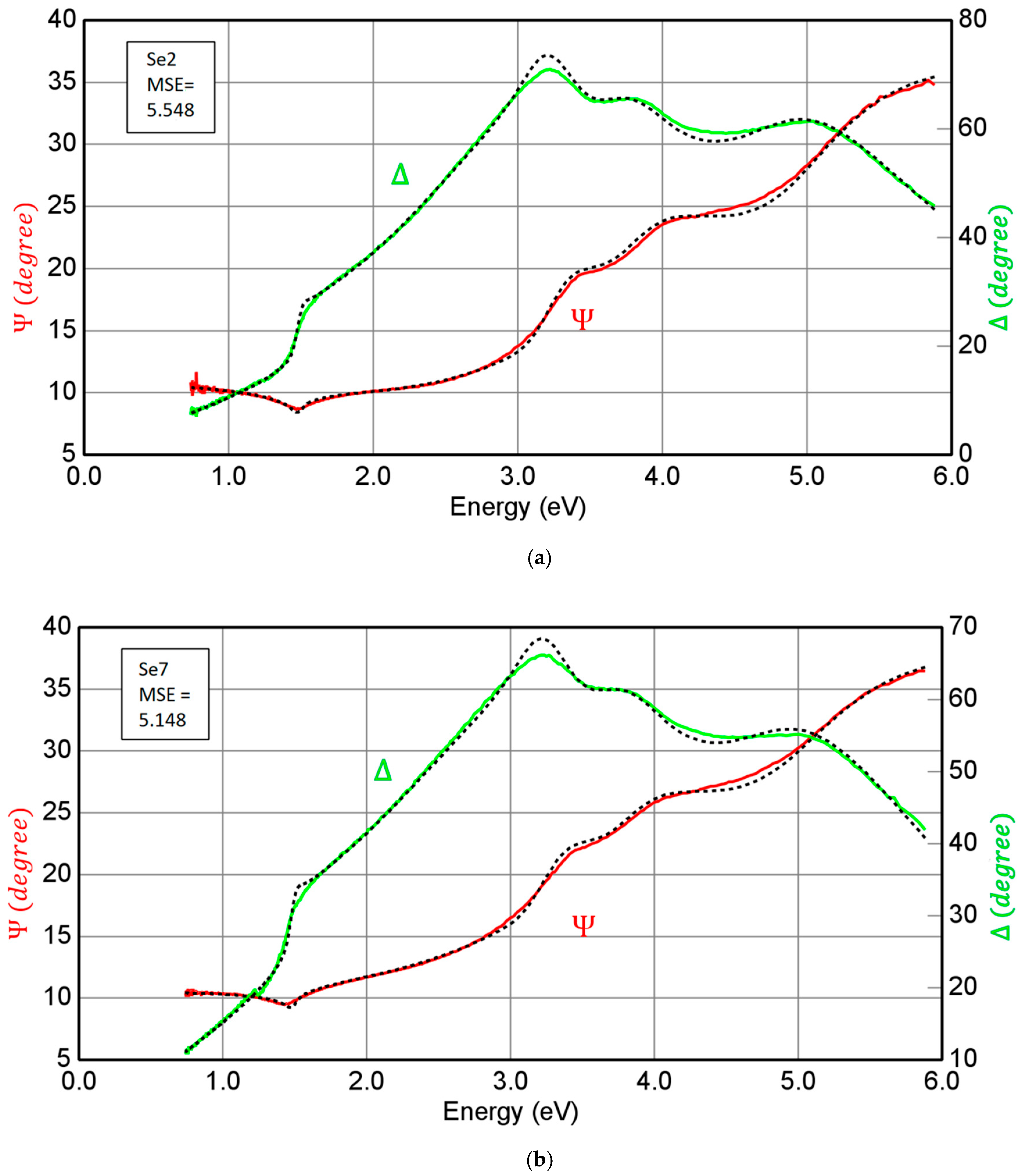
| Se2 | Teox (Å) | Roughness (Å) | MSE |
|---|---|---|---|
| Model 1 | 28 ± 3 A | 93 ± 4 | 5.174 |
| Model 2 | 18 ± 1 A | 76 ± 3 | 5.548 |
| Model 3 | 21 ± 1 A | 84 ± 4 | 3.422 |
| Se7 | Teox (Å) | Roughness (Å) | MSE |
|---|---|---|---|
| Model 1 | 54 ± 6 A | 139 ± 2 | 5.937 |
| Model 2 | 27 ± 1 A | 114 ± 4 | 5.148 |
| Model 3 | 31 ± 3 A | 126 ± 6 | 2.880 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martinez-Herraiz, L.; Ruiz, E.; Brana, A.F.; Plaza, J. Effects of Surface Treatments on the Performance of CdZnTeSe Radiation Detectors. In Proceedings of the 2021 13th Spanish Conference on Electron Devices (CDE), Sevilla, Spain, 9–11 June 2021; pp. 33–36. [Google Scholar] [CrossRef]
- Talwar, D.N.; Becla, P.; Lin, H.-H.; Feng, Z.C. Assessment of intrinsic and doped defects in Bridgman grown Cd1−xZnxTe alloys. Mater. Sci. Eng. B 2021, 269, 115160. [Google Scholar] [CrossRef]
- Kleppinger, J.W.; Chaudhuri, S.K.; Roy, U.N.; James, R.B.; Mandal, K.C. Growth of Cd0.9 Zn0.1Te1−ySey Single Crystals for Room Temperature Gamma-Ray Detection. IEEE Trans. Nucl. Sci. 2021, 2429–2434. [Google Scholar] [CrossRef]
- Roy, U.; Camarda, G.; Cui, Y.; James, R. Advances in CdZnTeSe for Radiation Detector Applications. Radiation 2021, 1, 123–130. [Google Scholar] [CrossRef]
- Roy, U.N.; Camarda, G.S.; Cui, Y.; Yang, G.; James, R.B. Impact of selenium addition to the cadmium-zinc-telluride matrix for producing high energy resolution X-and gamma-ray detectors. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Herraiz, L.; Braña, A.; Plaza, J. Vertical Gradient Freeze Growth of two inches Cd1−x ZnxTe1−y Sey ingots with different Se content. J. Cryst. Growth 2021, 573, 126291. [Google Scholar] [CrossRef]
- Roy, U.N.; Camarda, G.S.; Cui, Y.; Gul, R.; Yang, G.; Zazvorka, J.; Dedic, V.; Franc, J.; James, R.B. Evaluation of CdZnTeSe as a high-quality gamma-ray spectroscopic material with better compositional homogeneity and reduced defects. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef]
- Gul, R.; Roy, U.N.; Camarda, G.S.; Hossain, A.; Yang, G.; Vanier, P.; James, R.B. A comparison of point defects in Cd1−xZnxTe1−ySey crystals grown by Bridgman and traveling heater methods. J. Appl. Phys. 2017, 121, 125705. [Google Scholar] [CrossRef]
- Moravec, P.; Franc, J.; Dědič, V.; Minárik, P.; Elhadidy, H.; Šíma, V.; Grill, R.; Roy, U. Microhardness study of CdZnTeSe crystals for X-ray and gamma ray radiation detectors. In Proceedings of the 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Manchester, UK, 26 October–2 November 2019; pp. 1–4. [Google Scholar]
- Mycielski, A.; Burger, A.; Sowinska, M.; Groza, M.; Szadkowski, A.; Wojnar, P.; Siffert, P. Is the (Cd, Mn) Te crystal a prospective material for X-ray and γ-ray detectors? Phys. Status Solidi (C) 2005, 2, 1578–1585. [Google Scholar] [CrossRef]
- Chaudhuri, S.K.; Sajjad, M.; Mandal, K.C. Pulse-shape analysis in Cd0.9Zn0.1Te0.98Se0.02 room-temperature radiation detectors. Appl. Phys. Lett. 2020, 116, 162107. [Google Scholar] [CrossRef]
- Zázvorka, J.; Franc, J.; Beran, L.; Moravec, P.; Pekárek, J.; Veis, M. Dynamics of native oxide growth on CdTe and CdZnTe X-ray and gamma-ray detectors. Sci. Technol. Adv. Mater. 2016, 17, 792–798. [Google Scholar] [CrossRef]
- Zázvorka, J.; Franc, J.; Statelov, M.; Pekárek, J.; Veis, M.; Moravec, P.; Mašek, K. Optical and electrical study of CdZnTe surfaces passivated by KOH and NH4F solutions. Appl. Surf. Sci. 2016, 389, 1214–1219. [Google Scholar] [CrossRef]
- Agbalagba, E.O.; Drabo, M.L.; Egarievwe, S.U.; Roy, U.N.; Davis, A.H.; Israel, M.B.; Alexander, P.L.; James, R.B. Characterization of CdZnTeSe Nuclear Detector Chemically Etched in Bromine Methanol. Mater. Sci. Appl. 2021, 12, 363–373. [Google Scholar] [CrossRef]
- Yao, H.W.; Erickson, J.C.; Barber, H.B.; James, R.B.; Hermon, H. Optical properties of Cd0.9Zn0.1 Te studied by variable angle spectroscopic ellipsometry between 0.75 and 6.24 eV. J. Electron. Mater. 1999, 28, 760–765. [Google Scholar] [CrossRef]
- Fujiwara, H.; Collins, R.W. (Eds.) Spectroscopic Ellipsometry for Photovoltaics: Volume 1: Fundamental Principles and Solar Cell Characterization; Springer Series in Optical Sciences; Springer International Publishing: Cham, Switzerland, 2018; Volume 212, ISBN 978-3-319-75375-1. [Google Scholar]
- Hilfiker, N.J.; Tiwald, T. Dielectric function modeling. In Spectroscopic Ellipsometry for Photovoltaics. Volume 1: Fundamental Principles and Solar Cell Characterization; Fujiwara, H., Collins Robert, W., Eds.; Springer Nature: Cham, Switzerland, 2018; pp. 115–153, Chapter 5. [Google Scholar]
- Badano, G.; Million, A.; Canava, B.; Tran-Van, P.; Etcheberry, A. Fast Detection of Precipitates and Oxides on CdZnTe Surfaces by Spectroscopic Ellipsometry. J. Electron. Mater. 2007, 36, 1077–1084. [Google Scholar] [CrossRef]
- Batra, V.; Kotru, S.; Varagas, M.; Ramana, C.V. Optical constants and band gap determination of Pb0.95La0.05Zr0.54Ti0.46O3 thin films using spectroscopic ellipsometry and UV–visible spectroscopy. Opt. Mater. 2015, 49, 123–128. [Google Scholar] [CrossRef]
- Chanda, S.; Ghosh, D.; Debnath, B.; Debbarma, M.; Bhattacharjee, R.; Chattopadhyaya, S. Calculations of the structural and optoelectronic properties of cubic Cd x Zn 1− x Se y Te 1− y semiconductor quaternary alloys using the DFT-based FP-LAPW approach. J. Comput. Electron. 2020, 19, 1–25. [Google Scholar] [CrossRef]
- Roy, U.N.; Camarda, G.S.; Cui, Y.; Gul, R.; Hossain, A.; Yang, G.; Zazvorka, J.; Dedic, V.; Franc, J.; James, R.B. Role of selenium addition to CdZnTe matrix for room-temperature radiation detector applications. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef]
- Roy, U.N.; Camarda, G.S.; Cui, Y.; James, R.B. Optimization of selenium in CdZnTeSe quaternary compound for radiation detector applications. Appl. Phys. Lett. 2021, 118, 152101. [Google Scholar] [CrossRef]
- Brill, G.; Chen, Y.; Amirtharaj, P.M.; Sarney, W.; Chandler-Horowitz, D.; Dhar, N.K. Molecular beam epitaxial growth and characterization of Cd-based II–VI wide-bandgap compounds on Si substrates. J. Electron. Mater. 2005, 34, 655–661. [Google Scholar] [CrossRef]
- Hwang, S.; Yu, H.; Bolotnikov, A.E.; James, R.B.; Kim, K. Anomalous Te Inclusion Size and Distribution in CdZnTeSe. IEEE Trans. Nucl. Sci. 2019, 66, 2329–2332. [Google Scholar] [CrossRef]
- Nag, R.; Chaudhuri, S.K.; Kleppinger, J.W.; Karadavut, O.; Mandal, K.C. Characterization of vertical Bridgman grown Cd0.9Zn0.1Te0.97Se0.03 single crystal for room-temperature radiation detection. J. Mater. Sci. Mater. Electron. 2021, 32, 26740–26749. [Google Scholar] [CrossRef]
- Roy, U.N.; Baker, J.N.; Camarda, G.S.; Cui, Y.; Yang, G.; James, R.B. Evaluation of crystalline quality of traveling heater method (THM) grown Cd0.9Zn0.1Te0.98Se0.02 crystals. Appl. Phys. Lett. 2022, 120, 242103. [Google Scholar] [CrossRef]
- Chaudhuri, S.K.; Kleppinger, J.W.; Karadavut, O.; Nag, R.; Mandal, K.C. Quaternary Semiconductor Cd1−xZnxTe1−ySey for High-Resolution, Room-Temperature Gamma-Ray Detection. Crystals 2021, 11, 827. [Google Scholar] [CrossRef]
- Nichelatti, E. Complex refractive index of a slab from reflectance and transmittance: Analytical solution. J. Opt. A Pure Appl. Opt. 2002, 4, 400–403. [Google Scholar] [CrossRef]
- Rakhshani, A.E. Electrodeposited CdTe—Optical properties. J. Appl. Phys. 1997, 81, 7988–7993. [Google Scholar] [CrossRef]
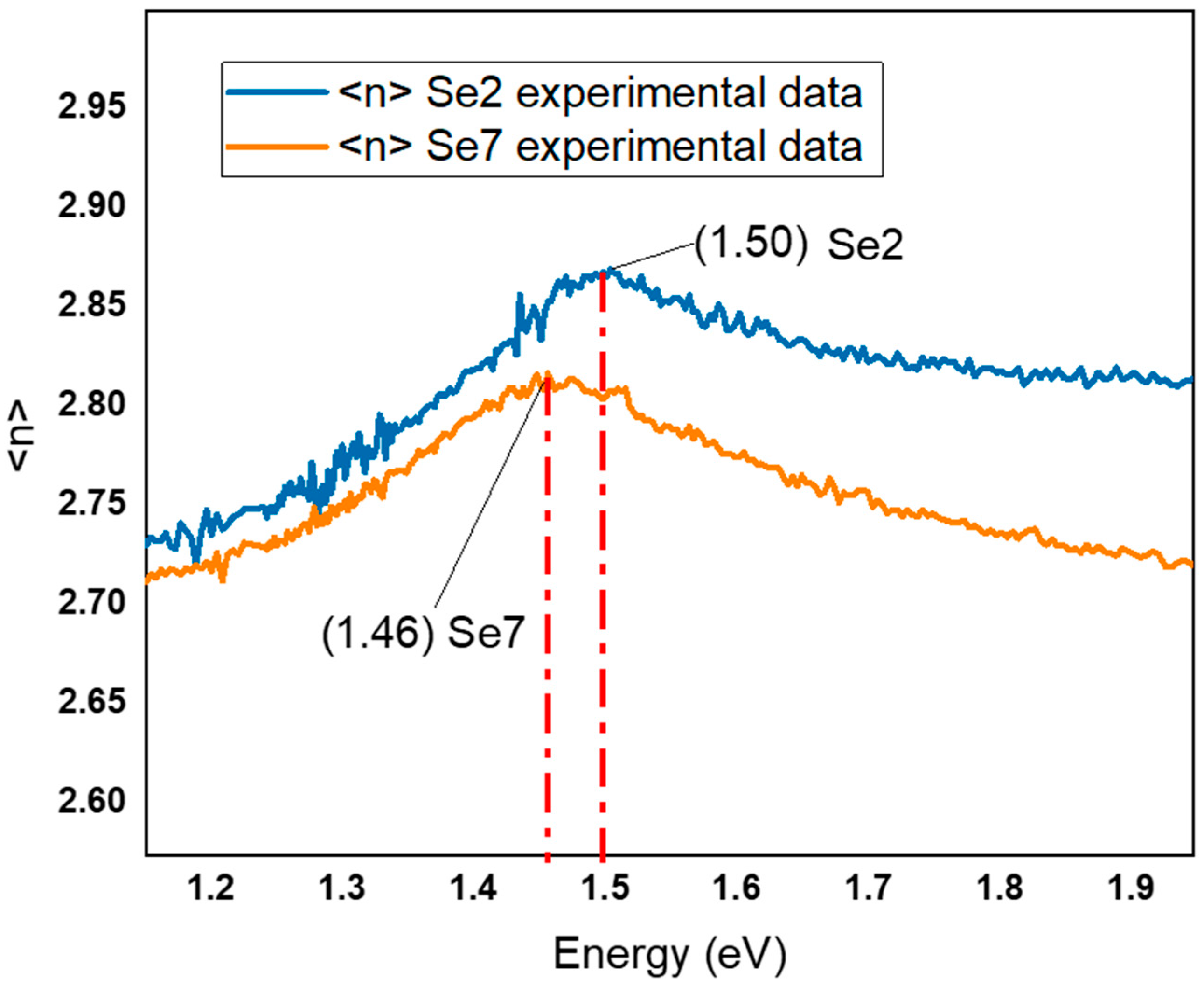
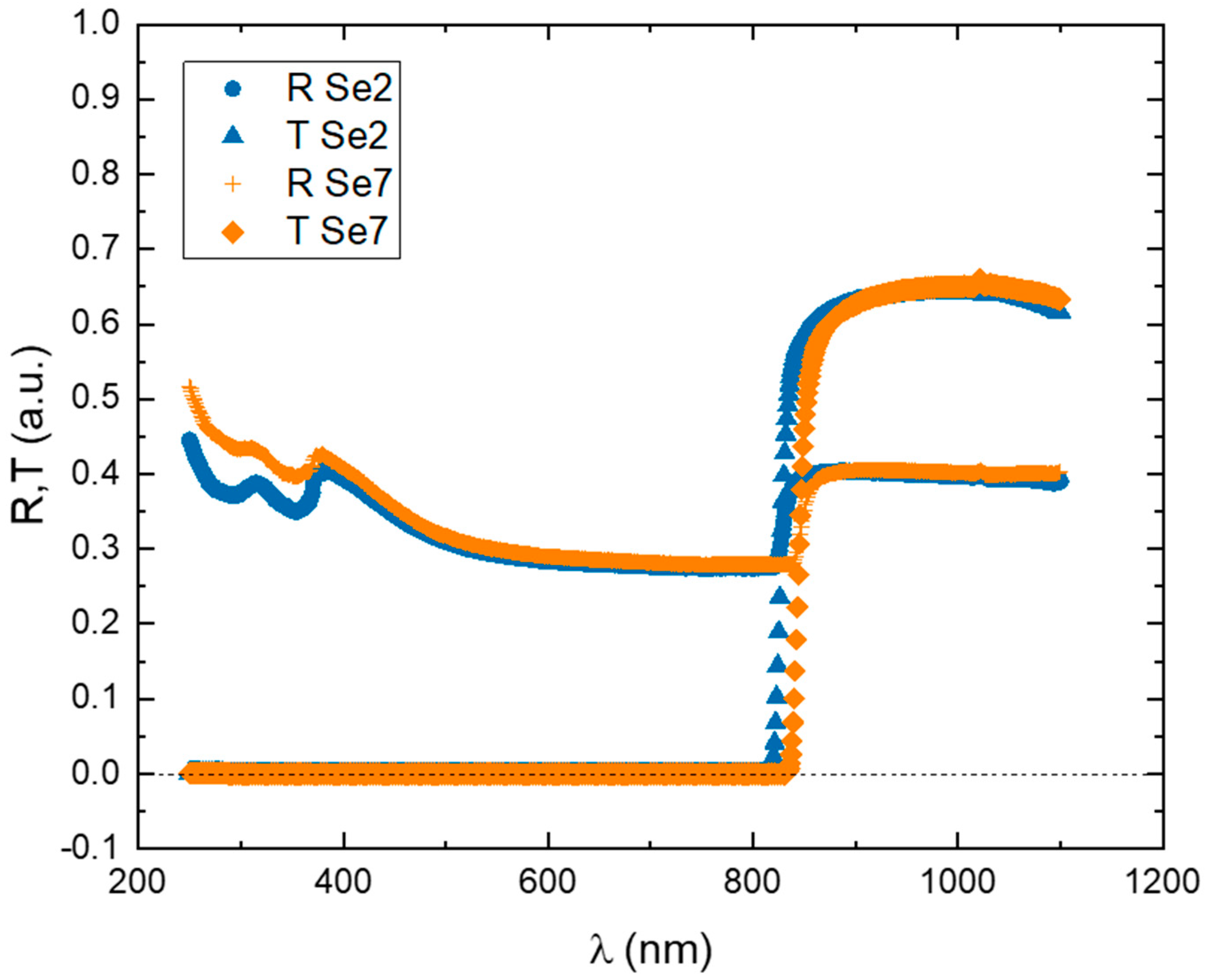
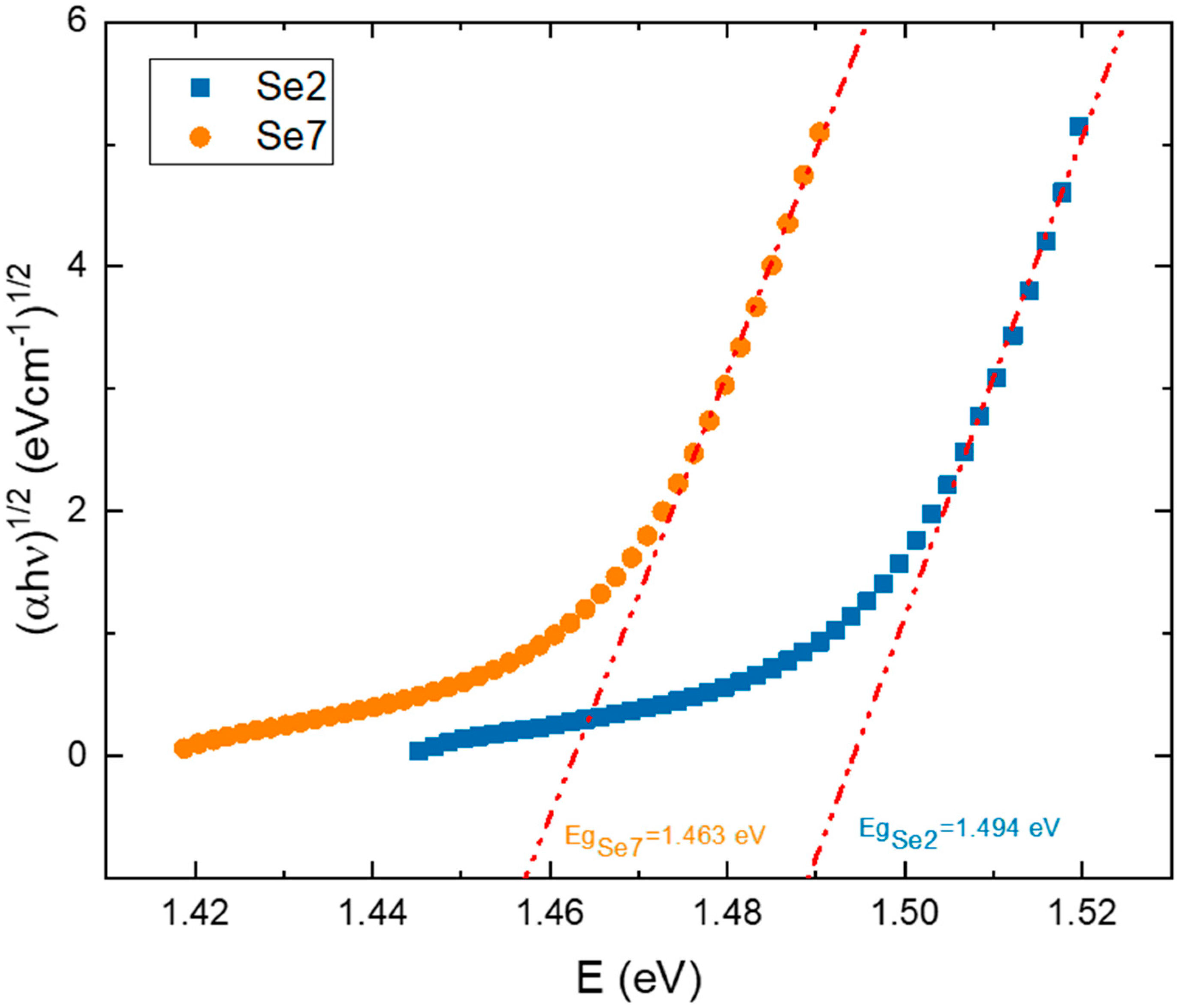
| Sample | A | B | C | Exponent |
|---|---|---|---|---|
| Se2 | 5.7 ± 0.6 | −0.30 ± 0.08 | 0.011 ± 0.003 | 0.6 ± 0.1 |
| Se7 | 4.6 ± 0.4 | −0.17 ± 0.04 | 0.006 ± 0.002 | 0.4 ± 0.1 |
| Sample | CdTe % (a Ratio) | ZnSe % (b Ratio) |
|---|---|---|
| Se2 | 87.1 | 12.9 |
| Se7 | 81.8 | 18.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herraiz, L.M.; Plaza Canga-argüelles, J.L.; Braña de Cal, A.F. Ellipsometry Characterisation for the Cd1-xZnxTe1-ySey Semiconductor Used in X-ray and Gamma Radiation Detectors. Crystals 2023, 13, 693. https://doi.org/10.3390/cryst13040693
Herraiz LM, Plaza Canga-argüelles JL, Braña de Cal AF. Ellipsometry Characterisation for the Cd1-xZnxTe1-ySey Semiconductor Used in X-ray and Gamma Radiation Detectors. Crystals. 2023; 13(4):693. https://doi.org/10.3390/cryst13040693
Chicago/Turabian StyleHerraiz, Lidia Martínez, Jose Luis Plaza Canga-argüelles, and Alejandro Francisco Braña de Cal. 2023. "Ellipsometry Characterisation for the Cd1-xZnxTe1-ySey Semiconductor Used in X-ray and Gamma Radiation Detectors" Crystals 13, no. 4: 693. https://doi.org/10.3390/cryst13040693
APA StyleHerraiz, L. M., Plaza Canga-argüelles, J. L., & Braña de Cal, A. F. (2023). Ellipsometry Characterisation for the Cd1-xZnxTe1-ySey Semiconductor Used in X-ray and Gamma Radiation Detectors. Crystals, 13(4), 693. https://doi.org/10.3390/cryst13040693






