Synthesis and Crystal Structure of Zr3V3GeSn4
Abstract
:1. Introduction
2. Materials and Methods
2.1. Crystal Growth
2.2. Analytical Methods
3. Results
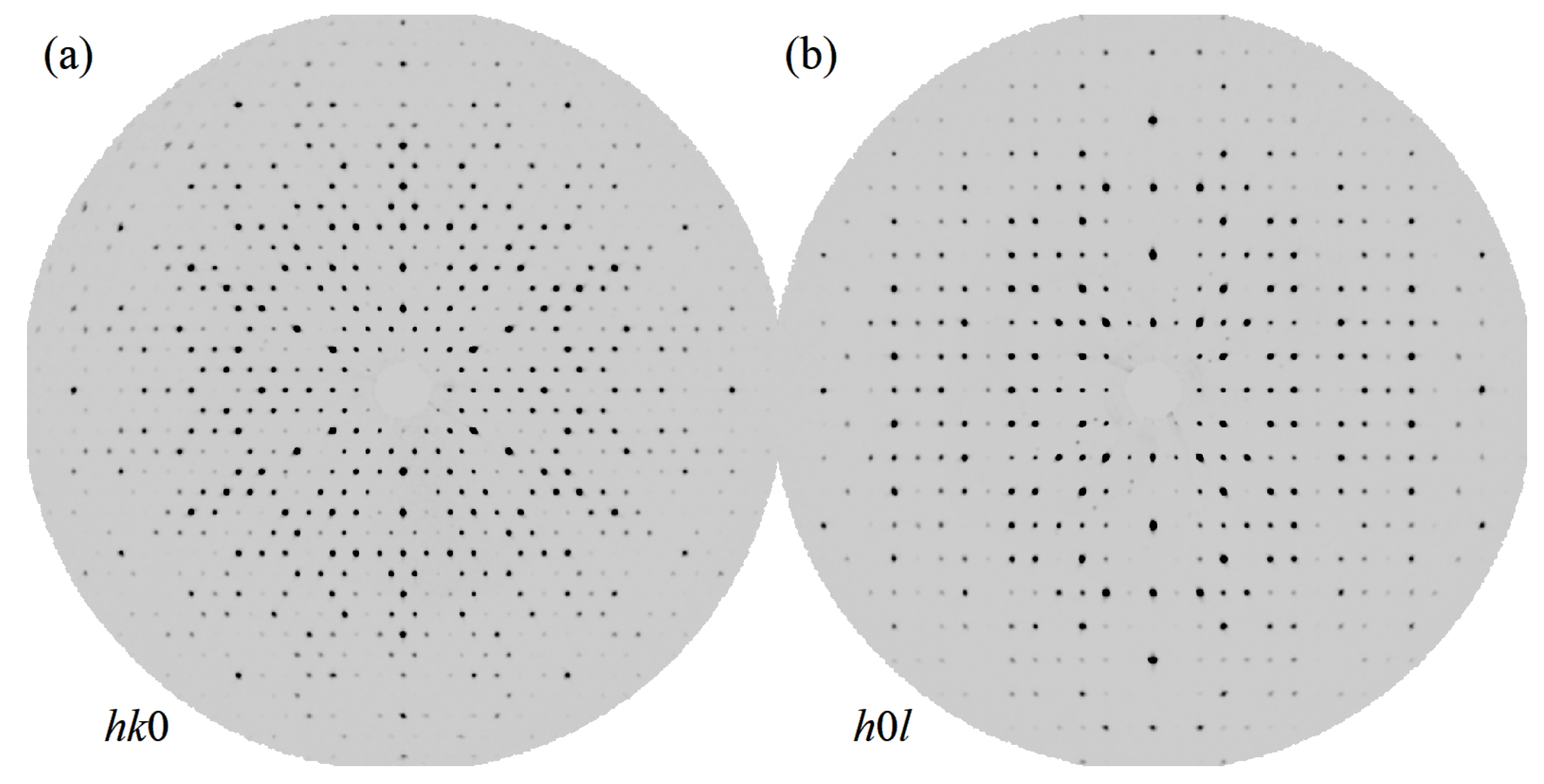
3.1. Structural Commentary
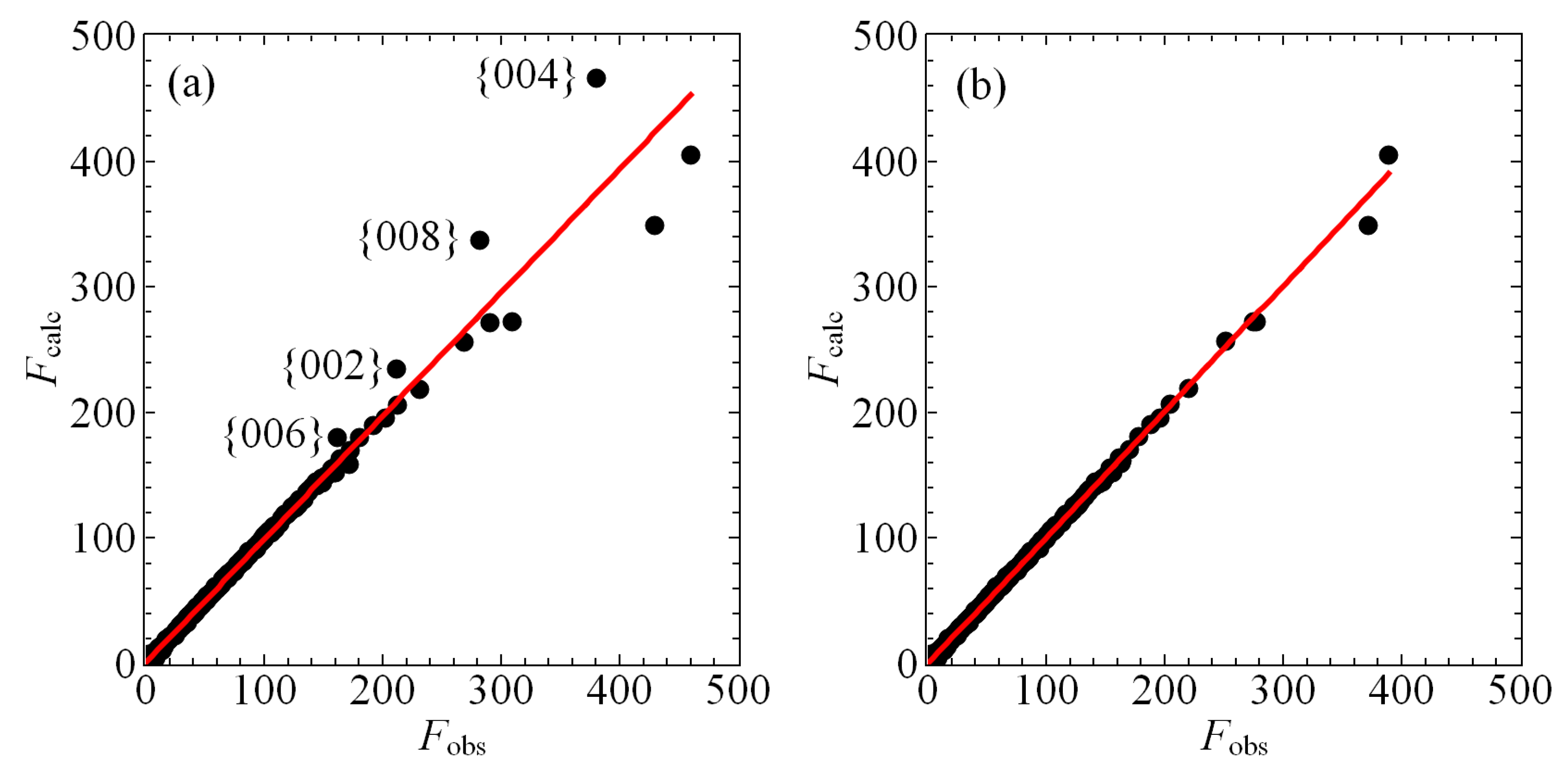
3.2. Details of Structure Solution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADP | Anisotropic displacement parameter |
| BV | Bond valence |
| BVS | Bond valence sum |
| CCD | Charge-coupled device |
| DFT | Density functional theory |
| FM | Ferromagnetic |
| QCP | Quantum critical point |
References
- Wickramaratne, D.; Khmelevskyi, S.; Agterberg, D.F.; Mazin, I.I. Ising Superconductivity and Magnetism in NbSe2. Phys. Rev. X 2020, 10, 041003. [Google Scholar] [CrossRef]
- Simonson, J.W.; Yin, Z.P.; Pezzoli, M.; Guo, J.; Liu, J.; Post, K.; Efimenko, A.; Hollman, N.; Hu, Z.; Lin, H.-J.; et al. From antiferromagnetic insulator to correlated metal in pressurized and doped LaMnPO. Proc. Nat. Acad. Sci. USA 2012, 109, E1815–E1819. [Google Scholar] [CrossRef] [PubMed]
- Jourdan, M.; Minár, J.; Braun, J.; Kronenberg, A.; Chadov, S.; Balke, B.; Gloskovskii, A.; Kolbe, M.; Elmers, H.J.; Schönhense, G.; et al. Direct observation of half-metallicity in the Heusler compound Co2MnSi. Nat. Commun. 2014, 5, 3974. [Google Scholar] [CrossRef]
- Miiller, W.; Wu, L.S.; Kim, M.S.; Orvis, T.; Simonson, J.W.; Gamża, M.; McNally, D.M.; Nelson, C.S.; Ehlers, G.; Podlesnyak, A.; et al. Magnetic structure of Yb2Pt2Pb: Ising moments on the Shastry-Sutherland lattice. Phys. Rev. X 2016, 93, 104419. [Google Scholar] [CrossRef]
- Uhlarz, M.; Pfleiderer, C.; Hayden, S.M. Quantum Phase Transitions in the Itinerant Ferromagnet ZrZn2. Phys. Rev. Lett. 2004, 93, 256404. [Google Scholar] [CrossRef]
- Chen, W.; James, A.D.N.; Dugdale, S.B. Local electron correlation effects on the fermiology of the weak itinerant ferromagnet ZrZn2. Electron. Struct. 2022, 4, 045002. [Google Scholar] [CrossRef]
- Aguayo, A.; Singh, D.J. Itinerant ferromagnetism and quantum criticality in Sc3In. Phys. Rev. B 2002, 66, 020401(R). [Google Scholar] [CrossRef]
- Fei, Z.; Huang, B.; Malinowski, P.; Wang, W.; Song, T.; Sanchez, J.; Yao, W.; Xiao, D.; Zhu, X.; May, A.F.; et al. Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 2018, 17, 778–782. [Google Scholar] [CrossRef]
- de la Barrera, S.C.; Aronson, S.; Zheng, Z.; Watanabe, K.; Taniguchi, T.; Ma, Q.; Jarillo-Herrero, P.; Ashoori, R. Cascade of isospin phase transitions in Bernal-stacked bilayer graphene at zero magnetic field. Nat. Phys. 2022, 18, 771–775. [Google Scholar] [CrossRef]
- Huang, C.-L.; Hallas, A.M.; Grube, K.; Kuntz, S.; Spielß, B.; Bayliff, K.; Besara, T.; Siegrist, T.; Cai, Y.; Beare, J.; et al. Quantum Critical Point in the Itinerant Ferromagnet Ni1−xRhx. Phys. Rev. Lett. 2020, 124, 117203. [Google Scholar] [CrossRef]
- Luo, J.; Yang, J.; Zhou, R.; Mu, Q.G.; Liu, T.; Ren, Z.-A.; Yi, C.J.; Shi, Y.G.; Zheng, G.-Q. Tuning the Distance to a Possible Ferromagnetic Quantum Critical Point in A2Cr3As3. Phys. Rev. Lett. 2020, 123, 047001. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.K.; Shanmukharao, S.S.; Lees, M.R.; Ganesan, V. Disorder-induced critical exponents near a ferromagnetic quantum critical point in Mn1−xCrxSi. Phys. Rev. B 2020, 101, 144436. [Google Scholar] [CrossRef]
- Taufour, V.; Kaluarachchi, U.S.; Khasanov, R.; Nguyen, M.C.; Guguchia, Z.; Biswas, P.K.; Bonfà, P.; De Renzi, R.; Lin, X.; Kim, S.K.; et al. Ferromagnetic Quantum Critical Point Avoided by the Appearance of Another Magnetic Phase in LaCrGe3 under Pressure. Phys. Rev. Lett. 2016, 117, 037207. [Google Scholar] [CrossRef] [PubMed]
- Xiang, L.; Gati, E.; Bud’ko, S.L.; Saunders, S.M.; Canfield, P.C. Avoided ferromagnetic quantum critical point in pressurized La5Co2Ge3. Phys. Rev. B 2021, 103, 054419. [Google Scholar] [CrossRef]
- Gati, E.; Wilde, J.M.; Khasanov, R.; Li, X.; Dissanayake, S.; Gupta, R.; Matsuda, M.; Ye, F.; Haberl, B.; Kaluarachchi, U.; et al. Formation of short-range magnetic order and avoided ferromagnetic quantum criticality in pressurized LaCrGe3. Phys. Rev. B 2021, 103, 075111. [Google Scholar] [CrossRef]
- Iwahara, R.; Sugawara, R.; Rahmanto; Honma, Y.; Matsuoka, K.; Matsuo, A.; Kindo, K.; Tenya, K.; Yokoyama, M. Avoided quantum criticality and cluster-glass formation in itinerant ferromagnet Sr1−x(La0.5K0.5)xRuO3. Phys. Rev. Mater. 2020, 4, 074404. [Google Scholar] [CrossRef]
- Benka, G.; Bauer, A.; Schmakat, P.; Säubert, S.; Seifert, M.; Jorba, P.; Pfleiderer, C. Interplay of itinerant magnetism and spin-glass behavior in FexCr1−x. Phys. Rev. Mater. 2022, 6, 044407. [Google Scholar] [CrossRef]
- Kirkpatrick, T.R.; Belitz, D. Ferromagnetic Quantum Critical Point in Noncentrosymmetric Systems. Phys. Rev. Lett. 2020, 124, 147201. [Google Scholar] [CrossRef]
- Pietrokowsky, P.; Frink, E.P. A constitution diagram for the alloy system titanium tin. Trans. Am. Soc. Met. 1957, 49, 339–358. [Google Scholar]
- Schubert, K.; Frank, K.; Gohle, R.; Maldonado, A.; Meissner, H.G.; Raman, A.; Rossteutscher, W. Einige Strukturdaten metallischer Phasen (8). Naturwissenschaften 1963, 50, 41. [Google Scholar] [CrossRef]
- Gandova, V.; Petrova, I. New thermodynamic investigation of some solid phases of Sn-Ti phase diagram. IOP Conf. Ser. Mater. Sci. Eng. 2020, 878, 012068. [Google Scholar] [CrossRef]
- Oni, A.A.; Hook, D.; Maria, J.P.; LeBeau, J.M. Phase coexistence in Ti6Sn5 intermetallics. Intermetallics 2014, 51, 48–52. [Google Scholar] [CrossRef]
- Drymiotis, F.; Lashley, J.C.; Fisk, Z.; Peterson, E.; Nakatsuji, S. Physical properties of the β-Ti6Sn5 system. Phil. Mag. 2003, 83, 3169–3178. [Google Scholar] [CrossRef]
- Kordan, V.; Zelinska, O.; Pavlyuk, V.; Oschchapovsky, I.; Serkiz, R. Electrochemical lithiation of Ti5M3, Ti3M and Zr3M (M = Sn, Sb) binary intermetallics. Chem. Met. Alloys 2016, 9, 84–91. [Google Scholar] [CrossRef]
- Jeong, T. Electronic structure and magnetic properties of β-Ti6Sn5. J. Magn. Magn. Mater. 2007, 309, 71–74. [Google Scholar] [CrossRef]
- Linsinger, S.; Pöttgen, R. Chains of Condensed RuSm6/2 Octahedra in Sm3RuMg7—A Ternary Ordered Version of the Ti6Sn5 Type. Z. Naturfosch. 2011, 66b, 565–569. [Google Scholar]
- Clausse, T.; Diop, L.V.B.; Martin, N.P.; Sibille, R.; Mazet, T. Zr3Mn3Sn4Ga: A new hexagonal Ti6Sn5-type quaternary intermetallic. Acta Cryst. 2022, B78, 817–822. [Google Scholar] [CrossRef]
- Clark, R.C.; Reid, J.S. The analytical calculation of absorption in multifaceted crystals. Acta Cryst. 1995, A51, 887–897. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Palatinus, L.; Chapuis, G. Superflip—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Cryst. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Becker, P.J.; Coppens, P. Extinction within the limit of validity of the Darwin transfer equations. III. Non-spherical crystals and anisotropy of extinction. Acta Cryst. 1975, A31, 417–425. [Google Scholar] [CrossRef]
- Levi, E.; Aurbach, D.; Gatti, C. Bond Order Conservation Principle and Peculiarities of the Metal-Metal Bonding. Inorg. Chem. 2018, 57, 15550–15557. [Google Scholar] [CrossRef] [PubMed]
- Levi, E.; Aurbach, D.; Gatti, C. A revisit of the bond valence model makes it universal. Phys. Chem. Chem. Phys. 2020, 22, 13839–13849. [Google Scholar] [CrossRef]
- Levi, E.; Aurbach, D.; Gatti, C. Metal–Metal Bond in the Light of Pauling’s Rules. Molecules 2021, 26, 304. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Empirical formula | ZrVGeSn |
| Formula weight | 973.9 |
| Collection temperature (K) | 294(1) |
| Wavelength (Å) | 0.71073 |
| Space group | P 6/m m c (194) |
| a (Å) | 9.2290(2) |
| b (Å) | 9.2290(2) |
| c (Å) | 5.56710(10) |
| Volume (Å) | 410.647(19) |
| Z | 2 |
| Calculated density (g/cm) | 7.8764 |
| Absorption coefficient (mm) | 22.321 |
| F(000) | 842 |
| Crystal size (mm) | 0.053 × 0.042 × 0.463 |
| range of data collection | 4.42–45.48 |
| Index range | |
| Total reflections | 65061 |
| Independent reflections | 695 |
| R | 0.0507 |
| Completeness to | 0.99 |
| Goodness of fit | 2.12 |
| Data/restraints/parameters | 691/0/18 |
| R (on , ) | 0.0156 |
| wR (on , all data) | 0.0280 |
| Site | Wyckoff Pos. | x | y | z | () Å |
|---|---|---|---|---|---|
| Sn1 | 2c | 2/3 | 1/3 | 3/4 | 0.667(7) |
| Sn2 | 6h | 0.786778(14) | 0.213222(14) | 1/4 | 0.624(6) |
| Zr1 | 6h | 0.85347(2) | 0.14653(2) | 3/4 | 0.591(8) |
| Ge1 | 2a | 0 | 0 | 0 | 0.549(10) |
| V1 | 6g | 1/2 | 0 | 1/2 | 0.586(11) |
| Site | U | U | U | U | U | U |
|---|---|---|---|---|---|---|
| Sn1 | 0.571(8) | 0.571(8) | 0.858(13) | 0.286(4) | 0 | 0 |
| Sn2 | 0.573(7) | 0.573(7) | 0.617(8) | 0.204(6) | 0 | 0 |
| Zr1 | 0.632(9) | 0.632(9) | 0.579(11) | 0.369(9) | 0 | 0 |
| Ge1 | 0.521(12) | 0.521(12) | 0.604(18) | 0.261(6) | 0 | 0 |
| V1 | 0.492(13) | 0.530(16) | 0.750(17) | 0.265(8) | 0.045(7) | 0.090(14) |
| Parameter | -TiSn | SmRuMg | ZrMnSnGa | ZrVGeSn |
|---|---|---|---|---|
| a (Å) | 9.248 | 10.341(2) | 9.2073(4) | 9.2290(2) |
| c (Å) | 5.69 | 6.113(1) | 5.6287(2) | 5.56710(10) |
| 1.63 | 1.6916(4) | 1.64577(9) | 1.65778(5) | |
| V (Å) | 421.44 | 566.1 | 413.24(4) | 410.647(15) |
| 2c atom | Sn | MgSm | Sn | Sn |
| 6h atom | Sn | Mg | Sn | Sn |
| 6h atom | Ti | Sm | Zr | Zr |
| 2a atom | Sn | Ru | Ga | Ge |
| 6g atom | Ti | Mg | Mn | V |
| 6h x | 0.795 | 0.77352(13) | 0.78917(3) | 0.786778(14) |
| 6h x | 0.835 | 0.86951(2) | 0.85295(4) | 0.85347(2) |
| Reference | [20] | [26] | [27] | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parks, D.; Niang, K.; Janssen, Y.; Simonson, J.W. Synthesis and Crystal Structure of Zr3V3GeSn4. Crystals 2023, 13, 744. https://doi.org/10.3390/cryst13050744
Parks D, Niang K, Janssen Y, Simonson JW. Synthesis and Crystal Structure of Zr3V3GeSn4. Crystals. 2023; 13(5):744. https://doi.org/10.3390/cryst13050744
Chicago/Turabian StyleParks, Daniel, Karim Niang, Yuri Janssen, and Jack W. Simonson. 2023. "Synthesis and Crystal Structure of Zr3V3GeSn4" Crystals 13, no. 5: 744. https://doi.org/10.3390/cryst13050744
APA StyleParks, D., Niang, K., Janssen, Y., & Simonson, J. W. (2023). Synthesis and Crystal Structure of Zr3V3GeSn4. Crystals, 13(5), 744. https://doi.org/10.3390/cryst13050744







