Next Article in Journal
The Influence of Foundry Scrap Returns on Chemical Composition and Microstructure Development of AlSi9Cu3 Alloy
Previous Article in Journal
Silica–Chitosan Composite Aerogels for Thermal Insulation and Adsorption
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 5
10.3390/cryst13050756
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Ionic Conductivity of Lithium Phosphides

by
Alexey P. Maltsev
,
Ilya V. Chepkasov
*,
Alexander G. Kvashnin
and
Artem R. Oganov
Skolkovo Institute of Science and Technology, Bolshoy Boulevard 30, bld. 1, Moscow 121205, Russia
*
Author to whom correspondence should be addressed.
Crystals 2023, 13(5), 756; https://doi.org/10.3390/cryst13050756
Submission received: 30 March 2023 / Revised: 24 April 2023 / Accepted: 25 April 2023 / Published: 2 May 2023
(This article belongs to the Section Materials for Energy Applications)
Browse Figures
Review Reports Versions Notes

Abstract

:
We comprehensively study the ionic conductivity in lithium phosphides, promising materials for energy storage applications, by using a combination of first-principles computations and machine learning interatomic potentials. Using the quasiharminic approximation, we calculated convex hulls of the Li-P system at various temperatures and the temperature-composition phase diagram was obtained, delineating the stability regions of each phase. The ionic conductivity of stable (Li 3 P, LiP, Li 3 P 7 , Li 3 P 11 , LiP 7 ) and metastable (Li 4 P 3 , Li 5 P 4 , LiP 5 ) compounds was studied as a function of temperature. In some compounds we found have high ionic conductivity at room temperatures (10 − 3 –10 − 2 S cm − 1 ). Structures with the lowest ionic conductivity are LiP, Li 3 P 11 , and LiP 7 , in which diffusion is negligible in the whole temperature range 300–500 K. In Li 3 P, Li 3 P 7 , and Li 4 P 3 , LiP, there is the 3D diffusion of Li atoms, while in Li 5 P 4 the 2D mechanism prevails, and in LiP 5 and LiP 7 the 1D mechanism was observed. This study may provide insights for the development of Li-P materials in lithium ion and lithium metal battery applications.

1. Introduction

Lithium ion batteries (LIB) are widely used [1,2,3,4,5,6,7,8,9]: they are the most effective secondary energy sources for portable and mobile devices [10,11,12,13,14,15,16] and are also used in electric vehicles [17,18,19,20]. However, the maximum specific energy of modern commercial LIBs is about 250 Wh kg − 1 (theoretical capacity of Li in griphite anode is 372 mAh g − 1 ), which does not satisfy new needs [7,14,21,22,23]. To overcome the capacity limitations, the use of other anodes is suggested, such as Li-metal anode [2,3,4,5], or different lithium alloys [24], i.e., silicon anodes have the highest capacity of 3579 mAh g − 1 [25]. The main problems with lithium ion, and especially Li-metal batteries, are dendrite formation and/or large structural changes under lithiation [24,25], leading to poor cyclability, a lower Coulomb efficiency, reduced service life, and short circuits [26]. There are several ways to solve these problems. Safety and durability can be improved by switching from liquid to solid electrolytes, more effectively preventing dendrite formation and short circuits, and thus increasing the safety and cyclability of batteries [21,27,28]. Moreover, the transition to all-solid-state batteries will allow for the use of lithium metal instead of a graphite anode, which will increase the specific capacity of batteries [14,21].
A solid electrolyte, just like a liquid one, must be a good ionic conductor and should not conduct electrons, be thermally stable and, when in contact with the anode, must form stable solid interphases, which must also be good ionic conductors and mechanically and thermally stable [21].
Li-P-S compounds are promising candidates for the role of a solid electrolyte in batteries with a metal lithium anode. For example, batteries with Li 2 S-P 2 S 5 electrolyte were assembled and tested, their interfacial layers with lithium were studied, and the mechanisms of dissolution and precipitation of lithium in Li 2 S-P 2 S 5 were determined using scanning electron microscopy methods [29,30,31]. Liu et al. [32] studied the effect of microstructure modification on the ionic conductivity of Li 3 PS 4 and showed the possibility of its use at room temperature. Li-P-S compounds and the interfacial layers they form in contact with lithium were also studied by first-principles simulations. It was shown [33] that the Li 3 PS 4 -Li 3 PO 4 electrolyte forms interfacial layers Li 3 PS 4 , Li 3 PO 4 , Li 2 O, Li 2 S, of which Li 3 PO 4 is the least stable. In more complex systems, such as Li 7 P 3 S 11 , the ionic conductivity varies from 10 − 5 to 10 − 3 S cm − 1 depending on the morphology [34], and substitution by iodine [35] or other halogens [36] can lead to an increase in ionic conductivity and improve the stability of these solid-state electrolytes.
In some studies, phosphides or even phosporous materials are considered promising anode materials [37,38,39,40,41] because of their high theoretical capacity and low redox potentials, i.e., 2596 mAh g − 1 for Na 3 P [42]. Amine et al. proposed using a composite material based on black phosphorous and showed that ball milling modification helps to achieve a high initial Coulomb efficiency, high reversible capacity and good electrochemical performance [43]. Fang et al. developed a composite phosphorous anode for Na-ion batteries with a high reversible capacity and great electrochemical performance [44]. A hierarchical red phosphorous composite anode for K-ion batteries was designed and showed a high reversible capacity of 566.7 mAh g − 1 after 100 cycles at 0.1 A g − 1 and long cycling stability [45]. Despite the rapid growth of research and recent progress, there are still many unresolved issues that need attention. From this point of view, a complex investigation of the stability and ionic conductivity of all possible compounds in Li-P is essential.
A search for the most stable and the best ionic conductor among Li-P compounds will help to improve existing lithium-based batteries and develop an efficient liquid and solid sodium and potassium ion batteries. This work reports an extensive computational search of all stable Li-P compounds and evaluation of their ionic conductivity by modern computational techniques.

2. Materials and Methods

All density functional theory (DFT) calculations were performed using Vienna Ab initio Simulation Package (VASP) [46,47] using the projector augmented-wave method [48] with a plane-wave basis set [49] and Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional [50]. Energy cutoff was set at 500 eV. Gamma-centered k-points mesh with 2 π × 0.01 Å − 1 spacing was used. Phonon were calculated using the supercell approach and the finite displacement method [51], as implemented in Phonopy package [52]. Ab Initio Molecular Dynamics (AIMD) [53], to collect datasets for the machine learning interatomic potential (MLIP), was run at 1000 K with NPT ensemble and Langevin thermostat [54,55].
Moment tensor potential (MTP) was used as an MLIP. The MTP potentials are non-parametric potentials that use linear regression and invariant polynomials [56]. They are based on tensors of inertia of atomic environments and can approximate any regular function with the necessary symmetries. MTP potentials are up to 150 times faster than GAP potentials with the same magnitude of force RMS error and up to 50 times faster, with an error that is 1.5 times smaller than GAP [56,57]. The MLIP code, which allows for active learning with MTP, has been successfully used in many applications, including a crystal structure search, phase transitions, phase diagram prediction, and thermodynamic and kinetic properties [58,59,60,61,62,63].
MLIP was constructed using MLIP-3 package [64,65] in several stages. At the first stage [56], MTP of the 20th level was pretrained using data collected from AIMD. A total of 24,000 configurations from AIMD calculations were collected, and each 100th configuration was taken for the initial MLIP. At the second stage, 240 unique configurations from the AIMD-dataset were added using select-add function of MLIP-3 package. At the final stage, eight consecutive active learning [58,65] procedures were performed for each structure on the convex hull (or low-lying metastable phases). The extrapolation threshold and threshold-brake grade parameters were set to 2.0 and 35.0, respectively. Molecular dynamics simulations for the active learning were performed in LAMMPS [66,67] code; structures were collected during heating from 0 K to 1000 K with a heating rate 2 × 10 6 K s − 1 and annealing at 1000 K for 10 ns.
The accuracy of the constructed MLIP is shown in Table 1 and Figure 1, Figure 2 and Figure 3. Root mean square (RMS) errors in energies per atom and forces predicted by MLIP are less than 0.019 eV/atom and 0.34 eV/Å, respectively, for the training set. RMS errors in energies and forces for the validation set are 0.012 eV/atom and 0.145 eV/Å.
Ionic conductivity was simulated using LAMMPS at temperatures 300–500 K with the step of 50 K for supercells with 5% vacancies on lithium sites. The size of the supercells was chosen so the number of atoms was approximately equal to 1000 and lattice parameters was close to 3 nm (See Table 2). Each simulation in LAMMPS was performed with NPT ensempble and Nose–Hoover thermostat [68,69] with a 0.5 fs timestep for 0.5 ns.
Diffusion coefficients were calculated using mean square displacements (MSD) of Li + cations:
D = 1 6 lim t → ∞ d d t 1 N ∑ i = 1 N < | r i ( t ) − r i ( 0 ) | 2 >
Activation energy E a was calculated using Arrhenius formula:
D = D 0 e x p ( − E a k B T )
The ionic conductivity of lithium was calculated using Nernst–Einstein formula:
σ = n q 2 D H r k B T
where n is the Li + ion density, q is the formal charge of the lithium (q = 1), k B is Boltzmann constant, T is the temperature and H r is Haven ratio (assumed to be 1).

3. Results and Discussion

Before calculations of ionic conductivity in Li-P systems, we collected information about known stable and metastable Li-P compounds. Computational databases have different information about the stability of various structures. For example, in the OQMD [70,71] database, Li 3 P 11 appears to be stable, while in thr Materials Project [72] database, this structure is not presented at all. Mayo et al. [37] performed first-principles structure prediction and showed that Li 3 P 11 is metastable. However, previously it was shown by Sen and Johari [73] that the methodology used by Mayo et al. [37,74] has led to incorrect results in similar systems. Later, Fei et al. [75] reported that Li 5 P 2 and Li 4 P became stable under high pressures and could be observed at ambient conditions. In order to understand which compounds are stable, we recalculated all known Li-P structures and studied their thermodynamic stability. We also carried out USPEX [76,77,78] calculations in order to predict previously unknown Li-P structures. More than 70 generations of 200 structures each were calculated. We did not find new stable or low-lying metastable phases.
The stability of Li-P compounds was analyzed by the calculation and construction of the convex hull, as shown in Figure 4a. Zero-point energy (ZPE) contribution was taken into account during the calculation of the convex hull. We found seven phases on the convex hull, namely Li − I m 3 ¯ m , Li 3 P − P 6 3 / m m c , [79] LiP − P 2 1 / c , [80] Li 3 P 7 − P 2 1 2 1 2 1 , [81] Li 3 P 11 − C m , LiP 7 − I 4 1 / a c d , [82] P − C m c a (black phosphorous).
Experimentally known LP 5 − P n m a 2 1 [82] is 16 meV/atom above the convex hull according to our DFT calculations. Mayo et al. [37] predicted that Li 4 P 3 − P 2 1 2 1 2 1 was close to the convex hull and was dynamically stable, i.e. had no imaginary phonon frequencies. In our calculation, the Li 4 P 3 − P 2 1 2 1 2 1 phase is 4 meV/atom above the convex hul; see Figure 4a. Li 5 P 4 − C 2 / m was constructed using Na 5 As 4 [83] as a prototype and is also very close to the convex hull (9 meV/atom). Fei et al. [75] predicted two stable compounds, Li 5 P 2 − P 3 m 1 and Li 4 P − R 3 ¯ m , claiming that they become stable at high pressure and can be observed at ambient conditions. According to our calculations, Li 5 P 2 − P 3 m 1 and Li 4 P − R 3 ¯ m are 44 and 60 meV/atom above the convex hull, respectively.
We calculated phonon densities of states (PhDOS) for 20 stable and low-energy metastable structures shown in (Figure 4a). Integration over the phonon DOS allowed us to calculate the zero-point energy and vibrational contribution to the Helmholtz free energy for all studied compounds and construct the convex hulls at finite temperatures. Stability of the predicted compounds at different temperatures is summarized in the composition–temperature phase diagram (Figure 4b). Our calculations show that at temperatures higher than 550 K, Li 3 P 11 − C m becomes metastable; Li 5 P 4 − C 2 / m , on the other hand, becomes stable at T = 700 K and appears on the convex hull.
All Li x P structures can be classified into four categories according to the arrangement of P atoms [37]: (1) 0 ≤x≤ 0.5: tubes, cages, 3-D network—LiP 7 , LiP 6 , LiP 5 , Li 3 P 11 , Li 3 P 7 ; (2) 0.5 ≤x≤ 1.33: infinite or finite chains—LiP 2 , Li 3 P 4 , LiP, Li 5 P 4 , Li 4 P 3 ; (3) 1.33 ≤x≤ 2: P dumbbells—Li 3 P 2 , Li 2 P, Li 5 P 2 ; (4) 1.33 ≤x≤ 2: isolated P ions—Li 3 P, Li 4 P, Li 5 P, Li 6 P. We discuss below how structural topology affects the ionic conductivity.
Figure 5 shows the ionic conductivity of stable systems (Li 3 P, LiP, Li 3 P 7 , Li 3 P 11 , LiP 7 ) and low-lying metastable phases (Li 4 P 3 , Li 5 P 4 , LiP 5 ) with 5% vacancy concentration as a function of temperature. Most structures have high ionic conductivity at room temperature about 10 − 3 –10 − 2 S cm − 1 ; however, for LiP, such values are obtained only at temperatures higher than 400 K, while in LiP 7 diffusion is negligible it the whole temperature range 300–500 K. Curiously, experimental data are controversial: Wegner et al. [84] found the ionic conductivity of Li 3 P to be 10 − 6 –10 − 4 S cm − 1 , but in article [85] 10 − 4 –10 − 2 S cm − 1 at temperatures 300–500 K. We explain such divergence by differences in the microstructure of materials: Wegner et al. [84] studied cold-pressured material, while Nazri [85] studied polycrystalline material, which might have more defects and vacacies. Our results are in good agreement with the earlier work [85]. In a polycrystalline material, diffusion is enhanced at grain boundaries, which explains the difference. In our simulations, we see almost negligible ionic conductivity for most systems without vacancies; however, once vacancies are introduced, ionic conductivity can become very high.
The trajectories of Li + diffusion are shown in Figure 6. Li 3 P, Li 3 P 7 , Li 4 P 3 , LiP are 3D conductors, but in Li 3 P 7 , the diffusion of Li ions prevails along the z-direction: on the Li trajectory, there are screw chains, which are connected though x- and y- directions. In LiP, there are a few Li jumps and small amount of trajectories, indicating a low diffusion rate with high activation energy. Li 5 P 4 is a 2D ionic conductor; trajectory lines are located along the x–y plane and correspond to the diffusion of Li atoms located between P-chain layers. Lithium atoms, which have strong bonds with the four-atom P-chains, do not diffuse, forming a non-conductive layer, and there are only a few, rare Li jumps from non-conductive to conductive layers. One-dimensional diffusion appears in structures with a 3D network of P atoms, so in 3D conductor Li 3 P 7 , 1D conductivity along the y-axis prevails and LiP 5 and LiP 7 are 1D conductors. In LiP 7 , diffusion proceeds through two channels along the z-direction, which are connected to each other and form an extended cross; however, there are only a few trajectory lines, which appear only at elevated temperatures (500–600 K), indicating low diffusion and high activation energy; the ionic conductivity of LiP 7 at 500 K is about 10 − 3 S cm − 1 and negligible at lower temperatures. Li 3 P 11 has dumbbell chains, which are not connected to each other; thus, no spatial diffusion is obtained. Our results indicate that not only does Li 3 P have high ionic conductivity, but almost all other stable and low-energy metastable phases (except Li 3 P 11 and LiP 7 ).

4. Conclusions

We performed an extensive study of lithium–phosphorous compounds as promising candidates for solid-state electrolytes, anodes or components of electrolyte interphase in Li-ion or Li-metal batteries. Our first-principles calculations allowed us to determine the stability regions of all considered structures in the temperature range from 0 to 700 K. We found that Li 3 P − P 6 3 / m m c , LiP − P 2 1 / c , Li 3 P 7 − P 2 1 2 1 2 1 , Li 3 P 11 − C m , LiP 7 − I 4 1 / a c d are stable at room temperature, while at temperatures higher than 550 K Li 3 P 11 becomes metastable, and at temperatures higher than 700 K Li 5 P 4 becomes stable. Our results indicate a variety of metastable compounds, some of which might exist at solid electrolyte interphase during battery operation. The diffusion of Li atoms was studied using molecular dynamics simulations with machine learning interatomic potentials. High lithium diffusion was observed for Li 3 P, LiP 5 , Li 5 P 4 , Li 4 P 3 , and Li 3 P 7 , and their ionic conductivity was in the range 10 − 4 –10 − 2 S cm − 1 at room temperature. We also determined the qualitative dependence of ionic conductivity on the arrangement of phosphorous atoms; namely, the compounds with a 3D network of phosphorus possess 1D conductivity (LiP 5 and LiP 7 ), compounds with phosphorus chains or broken chains display a 2D type of conductivity (i.e., Li 5 P 4 ), while other arrangements lead to 3D conductivity. Lithium phosphides are a promising class of electrolytes for lithium metal batteries.

Author Contributions

Conceptualization, I.V.C. and A.P.M.; methodology, I.V.C. and A.P.M.; writing—original draft preparation, I.V.C., A.P.M., A.G.K. and A.R.O.; visualization, I.V.C. and A.P.M.; supervision, A.R.O. All authors have read and agreed to the published version of the manuscript.

Funding

The study was supported by the Russian Science Foundation. DFT calculations of structural stability were supported by grant No. 19-72-30043, calculations of the ionic conductivity were supported by grant No. 22-73-00219.

Data Availability Statement

Zip-archive, containing folders Diffusion trajectories and MLIP-DFT data. Diffusion trajectories is the folder with diffusion trajectories, calculated at 600 K using LAMMPS. MLIP-DFT data is the folder with interatomic potentials files p.mtp and mlip.ini, training_dft.cfg—final data set for the training of the MLIP, training_mlp.cfg—file with configuration obtained from DFT calculations with recalculated using MLIP enrgies, forces and stresses, validation_dft.cfg and validation_mlp.cfg files, which contain validation data set configurations obtained from DFT calculations and recalculated using MLIP.

Acknowledgments

The research was carried out using resources of the Center for the Information and Computing of Novosibirsk State University and Arkuda supercomputers of Skoltech.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Marom, R.; Amalraj, S.F.; Leifer, N.; Jacob, D.; Aurbach, D. A review of advanced and practical lithium battery materials. J. Mater. Chem. 2011, 21, 9938–9954. [Google Scholar] [CrossRef]
  2. Nazri, G.A.; Pistoia, G. Lithium Batteries: Science and Technology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
  3. Girishkumar, G.; McCloskey, B.; Luntz, A.C.; Swanson, S.; Wilcke, W. Lithium- air battery: Promise and challenges. J. Phys. Chem. Lett. 2010, 1, 2193–2203. [Google Scholar] [CrossRef]
  4. Scrosati, B.; Garche, J. Lithium batteries: Status, prospects and future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
  5. Armand, M.; Tarascon, J.M. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef]
  6. Kim, T.H.; Park, J.S.; Chang, S.K.; Choi, S.; Ryu, J.H.; Song, H.K. The current move of lithium ion batteries towards the next phase. Adv. Energy Mater. 2012, 2, 860–872. [Google Scholar] [CrossRef]
  7. Goodenough, J.B.; Park, K.S. The Li-ion rechargeable battery: A perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef]
  8. Etacheri, V.; Marom, R.; Elazari, R.; Salitra, G.; Aurbach, D. Challenges in the development of advanced Li-ion batteries: A review. Energy Environ. Sci. 2011, 4, 3243–3262. [Google Scholar] [CrossRef]
  9. Goriparti, S.; Miele, E.; De Angelis, F.; Di Fabrizio, E.; Zaccaria, R.P.; Capiglia, C. Review on recent progress of nanostructured anode materials for Li-ion batteries. J. Power Sources 2014, 257, 421–443. [Google Scholar] [CrossRef]
  10. Winter, M.; Brodd, R.J. What are batteries, fuel cells, and supercapacitors? Chem. Rev. 2004, 104, 4245–4270. [Google Scholar] [CrossRef]
  11. Cheng, F.; Liang, J.; Tao, Z.; Chen, J. Functional materials for rechargeable batteries. Adv. Mater. 2011, 23, 1695–1715. [Google Scholar] [CrossRef] [PubMed]
  12. Li, H.; Wang, Z.; Chen, L.; Huang, X. Research on advanced materials for Li-ion batteries. Adv. Mater. 2009, 21, 4593–4607. [Google Scholar] [CrossRef]
  13. Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
  14. Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
  15. Xu, B.; Qian, D.; Wang, Z.; Meng, Y.S. Recent progress in cathode materials research for advanced lithium ion batteries. Mater. Sci. Eng. R Rep. 2012, 73, 51–65. [Google Scholar] [CrossRef]
  16. Li, J.; Barillas, J.K.; Guenther, C.; Danzer, M.A. A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles. J. Power Sources 2013, 230, 244–250. [Google Scholar] [CrossRef]
  17. Chacko, S.; Chung, Y.M. Thermal modelling of Li-ion polymer battery for electric vehicle drive cycles. J. Power Sources 2012, 213, 296–303. [Google Scholar] [CrossRef]
  18. Dunn, J.; Gaines, L.; Kelly, J.; James, C.; Gallagher, K. The significance of Li-ion batteries in electric vehicle life-cycle energy and emissions and recycling’s role in its reduction. Energy Environ. Sci. 2015, 8, 158–168. [Google Scholar] [CrossRef]
  19. Fathabadi, H. Combining a proton exchange membrane fuel cell (PEMFC) stack with a Li-ion battery to supply the power needs of a hybrid electric vehicle. Renew. Energy 2019, 130, 714–724. [Google Scholar] [CrossRef]
  20. Hannan, M.A.; Hoque, M.M.; Hussain, A.; Yusof, Y.; Ker, P.J. State-of-the-art and energy management system of lithium-ion batteries in electric vehicle applications: Issues and recommendations. IEEE Access 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
  21. Lin, D.; Liu, Y.; Cui, Y. Reviving the lithium metal anode for high-energy batteries. Nat. Nanotechnol. 2017, 12, 194–206. [Google Scholar] [CrossRef]
  22. Leisegang, T.; Meutzner, F.; Zschornak, M.; Münchgesang, W.; Schmid, R.; Nestler, T.; Eremin, R.A.; Kabanov, A.A.; Blatov, V.A.; Meyer, D.C. The aluminum-ion battery: A sustainable and seminal concept? Front. Chem. 2019, 7, 268. [Google Scholar] [CrossRef] [PubMed]
  23. Duehnen, S.; Betz, J.; Kolek, M.; Schmuch, R.; Winter, M.; Placke, T. Toward green battery cells: Perspective on materials and technologies. Small Methods 2020, 4, 2000039. [Google Scholar] [CrossRef]
  24. Nitta, N.; Yushin, G. High-capacity anode materials for lithium-ion batteries: Choice of elements and structures for active particles. Part. Part. Syst. Charact. 2014, 31, 317–336. [Google Scholar] [CrossRef]
  25. Obrovac, M.; Christensen, L. Structural changes in silicon anodes during lithium insertion/extraction. Electrochem. Solid-State Lett. 2004, 7, A93. [Google Scholar] [CrossRef]
  26. Xu, W.; Wang, J.; Ding, F.; Chen, X.; Nasybulin, E.; Zhang, Y.; Zhang, J.G. Lithium metal anodes for rechargeable batteries. Energy Environ. Sci. 2014, 7, 513–537. [Google Scholar] [CrossRef]
  27. Famprikis, T.; Canepa, P.; Dawson, J.A.; Islam, M.S.; Masquelier, C. Fundamentals of inorganic solid-state electrolytes for batteries. Nat. Mater. 2019, 18, 1278–1291. [Google Scholar] [CrossRef] [PubMed]
  28. Li, J.; Ma, C.; Chi, M.; Liang, C.; Dudney, N.J. Solid electrolyte: The key for high-voltage lithium batteries. Adv. Energy Mater. 2015, 5, 1401408. [Google Scholar] [CrossRef]
  29. Sakuda, A.; Kitaura, H.; Hayashi, A.; Tadanaga, K.; Tatsumisago, M. All-solid-state lithium secondary batteries with oxide-coated LiCoO2 electrode and Li2S-P2S5 electrolyte. J. Power Sources 2009, 189, 527–530. [Google Scholar] [CrossRef]
  30. Sakuda, A.; Hayashi, A.; Tatsumisago, M. Interfacial observation between LiCoO2 electrode and Li2S-P2S5 solid electrolytes of all-solid-state lithium secondary batteries using transmission electron microscopy. Chem. Mater. 2010, 22, 949–956. [Google Scholar] [CrossRef]
  31. Nagao, M.; Hayashi, A.; Tatsumisago, M.; Kanetsuku, T.; Tsuda, T.; Kuwabata, S. In situ SEM study of a lithium deposition and dissolution mechanism in a bulk-type solid-state cell with a Li2S-P2S5 solid electrolyte. Phys. Chem. Chem. Phys. 2013, 15, 18600–18606. [Google Scholar] [CrossRef]
  32. Liu, Z.; Fu, W.; Payzant, E.A.; Yu, X.; Wu, Z.; Dudney, N.J.; Kiggans, J.; Hong, K.; Rondinone, A.J.; Liang, C. Anomalous high ionic conductivity of nanoporous β-Li3PS4. J. Am. Chem. Soc. 2013, 135, 975–978. [Google Scholar] [CrossRef]
  33. Lepley, N.; Holzwarth, N. Modeling interfaces between solids: Application to Li battery materials. Phys. Rev. B 2015, 92, 214201. [Google Scholar] [CrossRef]
  34. Wenzel, S.; Weber, D.A.; Leichtweiss, T.; Busche, M.R.; Sann, J.; Janek, J. Interphase formation and degradation of charge transfer kinetics between a lithium metal anode and highly crystalline Li7P3S11 solid electrolyte. Solid State Ionics 2016, 286, 24–33. [Google Scholar] [CrossRef]
  35. Rangasamy, E.; Liu, Z.; Gobet, M.; Pilar, K.; Sahu, G.; Zhou, W.; Wu, H.; Greenbaum, S.; Liang, C. An iodide-based Li7P2S8I superionic conductor. J. Am. Chem. Soc. 2015, 137, 1384–1387. [Google Scholar] [CrossRef] [PubMed]
  36. Wenzel, S.; Sedlmaier, S.J.; Dietrich, C.; Zeier, W.G.; Janek, J. Interfacial reactivity and interphase growth of argyrodite solid electrolytes at lithium metal electrodes. Solid State Ionics 2018, 318, 102–112. [Google Scholar] [CrossRef]
  37. Mayo, M.; Griffith, K.J.; Pickard, C.J.; Morris, A.J. Ab initio study of phosphorus anodes for lithium-and sodium-ion batteries. Chem. Mater. 2016, 28, 2011–2021. [Google Scholar] [CrossRef]
  38. Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef]
  39. Kulish, V.V.; Malyi, O.I.; Persson, C.; Wu, P. Phosphorene as an anode material for Na-ion batteries: A first-principles study. Phys. Chem. Chem. Phys. 2015, 17, 13921–13928. [Google Scholar] [CrossRef]
  40. Zhao, S.; Kang, W.; Xue, J. The potential application of phosphorene as an anode material in Li-ion batteries. J. Mater. Chem. A 2014, 2, 19046–19052. [Google Scholar] [CrossRef]
  41. Sun, J.; Lee, H.W.; Pasta, M.; Yuan, H.; Zheng, G.; Sun, Y.; Li, Y.; Cui, Y. A phosphorene–graphene hybrid material as a high-capacity anode for sodium-ion batteries. Nat. Nanotechnol. 2015, 10, 980–985. [Google Scholar] [CrossRef]
  42. Fu, Y.; Wei, Q.; Zhang, G.; Sun, S. Advanced phosphorus-based materials for lithium/sodium-ion batteries: Recent developments and future perspectives. Adv. Energy Mater. 2018, 8, 1703058. [Google Scholar] [CrossRef]
  43. Amine, R.; Daali, A.; Zhou, X.; Liu, X.; Liu, Y.; Ren, Y.; Zhang, X.; Zhu, L.; Al-Hallaj, S.; Chen, Z.; et al. A practical phosphorus-based anode material for high-energy lithium-ion batteries. Nano Energy 2020, 74, 104849. [Google Scholar] [CrossRef]
  44. Fang, K.; Liu, D.; Xiang, X.; Zhu, X.; Tang, H.; Qu, D.; Xie, Z.; Li, J.; Qu, D. Air-stable red phosphorus anode for potassium/sodium-ion batteries enabled through dual-protection design. Nano Energy 2020, 69, 104451. [Google Scholar] [CrossRef]
  45. Feng, W.; Wang, H.; Jiang, Y.; Zhang, H.; Luo, W.; Chen, W.; Shen, C.; Wang, C.; Wu, J.; Mai, L. A Strain-Relaxation Red Phosphorus Freestanding Anode for Non-Aqueous Potassium Ion Batteries. Adv. Energy Mater. 2022, 12, 2103343. [Google Scholar] [CrossRef]
  46. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
  47. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  48. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
  49. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
  50. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
  51. Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-Principles Determination of the Soft Mode in Cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. [Google Scholar] [CrossRef]
  52. Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  53. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef] [PubMed]
  54. Evans, D.J. Computer “experiment” for nonlinear thermodynamics of Couette flow. J. Chem. Phys. 1983, 78, 3297–3302. [Google Scholar] [CrossRef]
  55. Hoover, W.G.; Ladd, A.J.; Moran, B. High-strain-rate plastic flow studied via nonequilibrium molecular dynamics. Phys. Rev. Lett. 1982, 48, 1818. [Google Scholar] [CrossRef]
  56. Shapeev, A.V. Moment tensor potentials: A class of systematically improvable interatomic potentials. Multiscale Model. Simul. 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
  57. Zuo, Y.; Chen, C.; Li, X.; Deng, Z.; Chen, Y.; Behler, J.; Csányi, G.; Shapeev, A.V.; Thompson, A.P.; Wood, M.A.; et al. Performance and cost assessment of machine learning interatomic potentials. J. Phys. Chem. A 2020, 124, 731–745. [Google Scholar] [CrossRef] [PubMed]
  58. Podryabinkin, E.V.; Tikhonov, E.V.; Shapeev, A.V.; Oganov, A.R. Accelerating crystal structure prediction by machine-learning interatomic potentials with active learning. Phys. Rev. B 2019, 99, 064114. [Google Scholar] [CrossRef]
  59. Körmann, F.; Kostiuchenko, T.; Shapeev, A.; Neugebauer, J. B2 ordering in body-centered-cubic AlNbTiV refractory high-entropy alloys. Phys. Rev. Mater. 2021, 5, 053803. [Google Scholar] [CrossRef]
  60. Shapeev, A.V.; Podryabinkin, E.V.; Gubaev, K.; Tasnádi, F.; Abrikosov, I.A. Elinvar effect in β-Ti simulated by on-the-fly trained moment tensor potential. New J. Phys. 2020, 22, 113005. [Google Scholar] [CrossRef]
  61. Novoselov, I.; Yanilkin, A.; Shapeev, A.; Podryabinkin, E. Moment tensor potentials as a promising tool to study diffusion processes. Comput. Mater. Sci. 2019, 164, 46–56. [Google Scholar] [CrossRef]
  62. Novikov, I.S.; Suleimanov, Y.V.; Shapeev, A.V. Automated calculation of thermal rate coefficients using ring polymer molecular dynamics and machine-learning interatomic potentials with active learning. Phys. Chem. Chem. Phys. 2018, 20, 29503–29512. [Google Scholar] [CrossRef] [PubMed]
  63. Rosenbrock, C.W.; Gubaev, K.; Shapeev, A.V.; Pártay, L.B.; Bernstein, N.; Csányi, G.; Hart, G.L. Machine-learned interatomic potentials for alloys and alloy phase diagrams. NPJ Comput. Mater. 2021, 7, 24. [Google Scholar] [CrossRef]
  64. Novikov, I.S.; Gubaev, K.; Podryabinkin, E.V.; Shapeev, A.V. The MLIP package: Moment tensor potentials with MPI and active learning. Mach. Learn. Sci. Technol. 2020, 2, 025002. [Google Scholar] [CrossRef]
  65. Podryabinkin, E.V.; Shapeev, A.V. Active learning of linearly parametrized interatomic potentials. Comput. Mater. Sci. 2017, 140, 171–180. [Google Scholar] [CrossRef]
  66. Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
  67. Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
  68. Hoover, W.G. Constant-pressure equations of motion. Phys. Rev. A 1986, 34, 2499. [Google Scholar] [CrossRef] [PubMed]
  69. Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
  70. Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). Jom 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
  71. Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. NPJ Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
  72. Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
  73. Sen, R.; Johari, P. Comment on “Structure Prediction of Li-Sn and Li-Sb Intermetallics for Lithium-Ion Batteries Anodes”. arXiv 2018, arXiv:1807.10540. [Google Scholar]
  74. Mayo, M.; Morris, A.J. Structure prediction of Li–Sn and Li–Sb intermetallics for lithium-ion batteries anodes. Chem. Mater. 2017, 29, 5787–5795. [Google Scholar] [CrossRef]
  75. Fei, G.; Duan, S.; Zhang, M.; Ren, Z.; Cui, Y.; Chen, X.; Liu, Y.; Yi, W.; Liu, X. Predicted stable Li5P2 and Li4P at ambient pressure: Novel high-performance anodes for lithium-ion batteries. Phys. Chem. Chem. Phys. 2020, 22, 19172–19177. [Google Scholar] [CrossRef] [PubMed]
  76. Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. He J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
  77. Oganov, A.R.; Lyakhov, A.O.; Valle, M. How Evolutionary Crystal Structure Prediction Works and Why. Acc. Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef]
  78. Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 4, 1172–1182. [Google Scholar] [CrossRef]
  79. Dong, Y.; DiSalvo, F.J. Reinvestigation of trilithium phosphide, Li3P. Acta Crystallogr. Sect. E Struct. Rep. Online 2007, 63, i97–i98. [Google Scholar] [CrossRef]
  80. Hönle, W.; von Schnering, H.G. Chemistry and Structural Chemistry of Phosphides and Polyphosphides 23* Zur Struktur von LiP und KSb. Z. Krist. Cryst. Mater. 1981, 155, 307–314. [Google Scholar] [CrossRef]
  81. Manriquez, V.; Hönle, W.; von Schnering, H.G. Zur Chemie und Strukturchemie von Phosphiden und Polyphosphiden. 42. Trilithiumheptaphosphid Li3P7: Darstellung, Struktur und Eigenschaften. Z. Anorg. Allg. Chem. 1986, 539, 95–109. [Google Scholar] [CrossRef]
  82. Wichelhaus, W. Die Lithiumphosphide LiP5 und LiP7. Naturwissenschaften 1972, 59, 78–79. [Google Scholar]
  83. Ozisik, H.; Colakoglu, K.; Deligoz, E.; Ozisik, H. First principles study on the structural, electronic, and elastic properties of Na–As systems. Solid State Commun. 2011, 151, 1349–1354. [Google Scholar] [CrossRef]
  84. Wegner, F.; Kamm, F.; Pielnhofer, F.; Pfitzner, A. Li3As and Li3P revisited: DFT modelling on phase stability and ion conductivity. Z. Anorg. Allg. Chem. 2022, 648, e202100358. [Google Scholar]
  85. Nazri, G. Preparation, structure and ionic conductivity of lithium phosphide. Solid State Ionics 1989, 34, 97–102. [Google Scholar] [CrossRef]
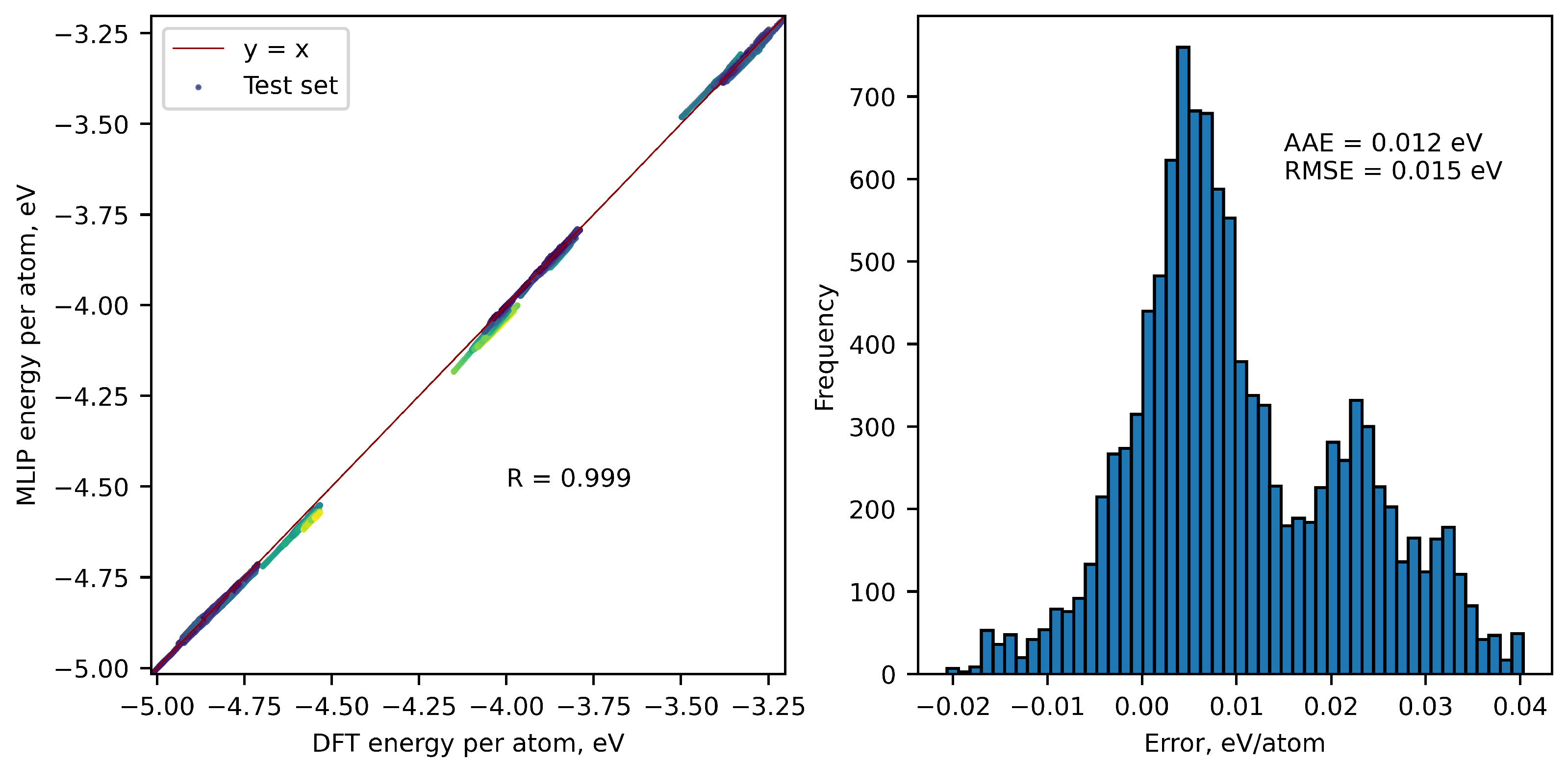
Crystals 13 00756 g001 550
Figure 1. Energy errors on the validation data set and their distribution over the 11,311 configurations. AAE and RMSE denote average absolute error and RMS error, respectively, between DFT and MLIP data of the validation set.
Figure 1. Energy errors on the validation data set and their distribution over the 11,311 configurations. AAE and RMSE denote average absolute error and RMS error, respectively, between DFT and MLIP data of the validation set.
Crystals 13 00756 g001
Crystals 13 00756 g002 550
Figure 2. Force errors on the validation data set and their distribution over the 11,311 configurations (838,824 values of force components). AAE and RMSE denote average absolute error and RMS error, respectively, between DFT and MLIP data of the validation set.
Figure 2. Force errors on the validation data set and their distribution over the 11,311 configurations (838,824 values of force components). AAE and RMSE denote average absolute error and RMS error, respectively, between DFT and MLIP data of the validation set.
Crystals 13 00756 g002
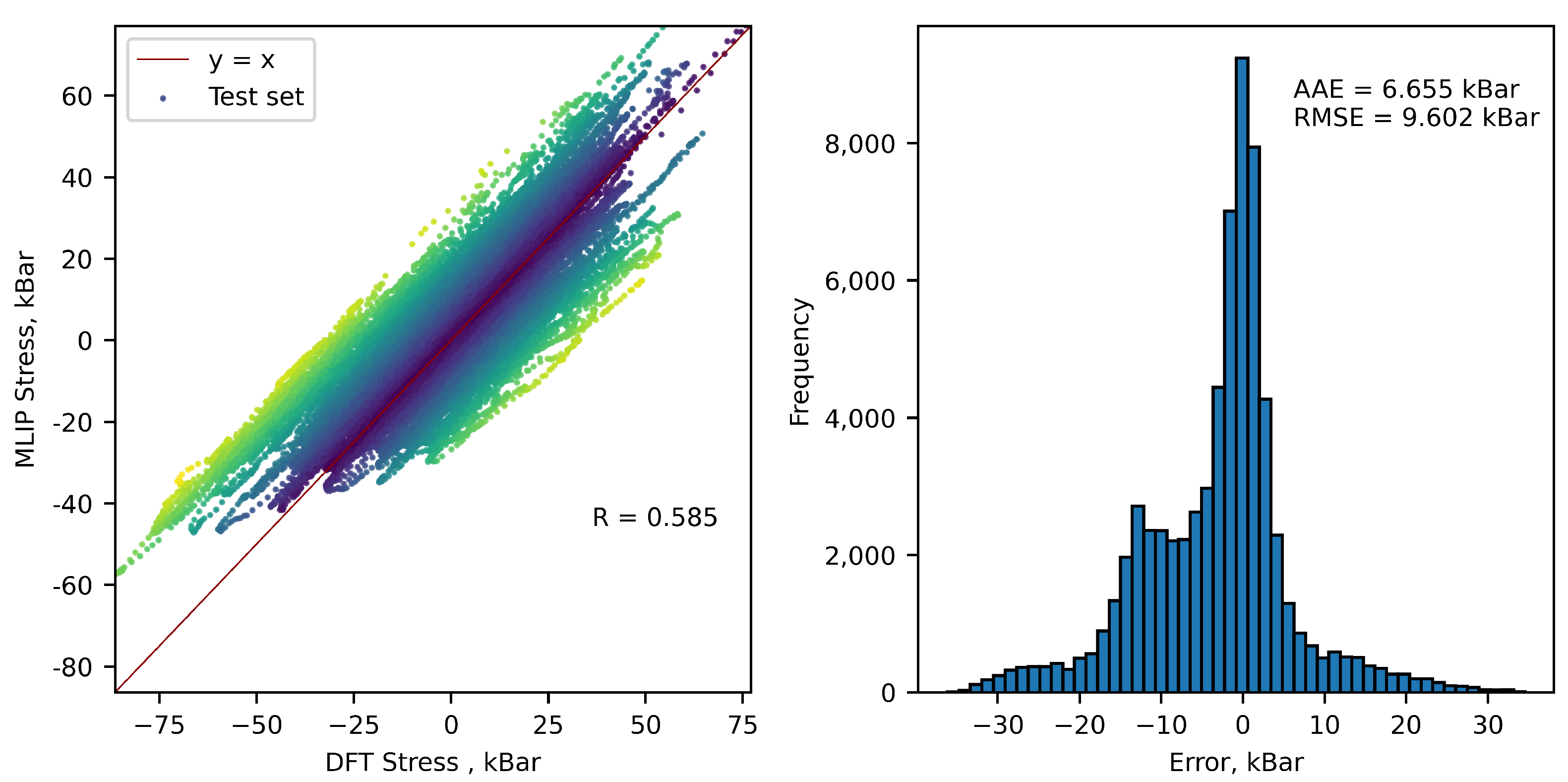
Crystals 13 00756 g003 550
Figure 3. Stress errors on the validation data set and their distribution over the 11,311 configurations (67,866 values of stress components). AAE and RMSE denote average absolute error and RMS error, respectively, between DFT and MLIP data of the validation set.
Figure 3. Stress errors on the validation data set and their distribution over the 11,311 configurations (67,866 values of stress components). AAE and RMSE denote average absolute error and RMS error, respectively, between DFT and MLIP data of the validation set.
Crystals 13 00756 g003
Crystals 13 00756 g004 550
Figure 4. (a) Calculated convex hull of the Li-P system at T = 0 K with ZPE. Blue circles represent stable compounds; red diamonds show metastable structures. (b) Composition–temperature phase diagram; solid line shows temperature region where the structure is stable, while the dashed line shows regions where the structure is metastable. (c) Crystal structures of considered Li-P compounds; big green atoms and small purple atoms are Li and P, respectively.
Figure 4. (a) Calculated convex hull of the Li-P system at T = 0 K with ZPE. Blue circles represent stable compounds; red diamonds show metastable structures. (b) Composition–temperature phase diagram; solid line shows temperature region where the structure is stable, while the dashed line shows regions where the structure is metastable. (c) Crystal structures of considered Li-P compounds; big green atoms and small purple atoms are Li and P, respectively.
Crystals 13 00756 g004
Crystals 13 00756 g005 550
Figure 5. Calculated ionic conductivity of Li-P compounds as a function of temperature. Experimental ionic conductivities were taken from article [85] and refitted by us.
Figure 5. Calculated ionic conductivity of Li-P compounds as a function of temperature. Experimental ionic conductivities were taken from article [85] and refitted by us.
Crystals 13 00756 g005
Crystals 13 00756 g006 550
Figure 6. Calculated trajectories of Li-ion diffusion and their topology (in parentheses). For a better representation, ions are not shown. Trajectories were collected at 600 K for 0.2 ns after 0.1 ns heating.
Figure 6. Calculated trajectories of Li-ion diffusion and their topology (in parentheses). For a better representation, ions are not shown. Trajectories were collected at 600 K for 0.2 ns after 0.1 ns heating.
Crystals 13 00756 g006
Table
Table 1. Errors of the MLIP. MEA, AAD and RMS denote maximal absolute difference, average absolute difference and RMS absolute difference, respectively, between DFT and MLIP data of the training set.
Table 1. Errors of the MLIP. MEA, AAD and RMS denote maximal absolute difference, average absolute difference and RMS absolute difference, respectively, between DFT and MLIP data of the training set.
Number of configurations1047
MAEAADRMS
Errors in energy per atom, eV/atom0.0630.01450.0185
Range of energies per atom in training set, eV/atom−5.09: −3.20
Errors in forces, eV/ Å1.970.270.335
Range of forces in training set, eV/ Å−10.86: +18.18
Errors in stresses, kBar37.765.5768.0
Range of stresses in training set, kBar−84.1: +98.2
Table
Table 2. Details of supercells. N denotes number of atoms in the supercell.
Table 2. Details of supercells. N denotes number of atoms in the supercell.
Super CellLattice ParametersN
a, Åb, Åc, Å α , deg β , deg γ , deg
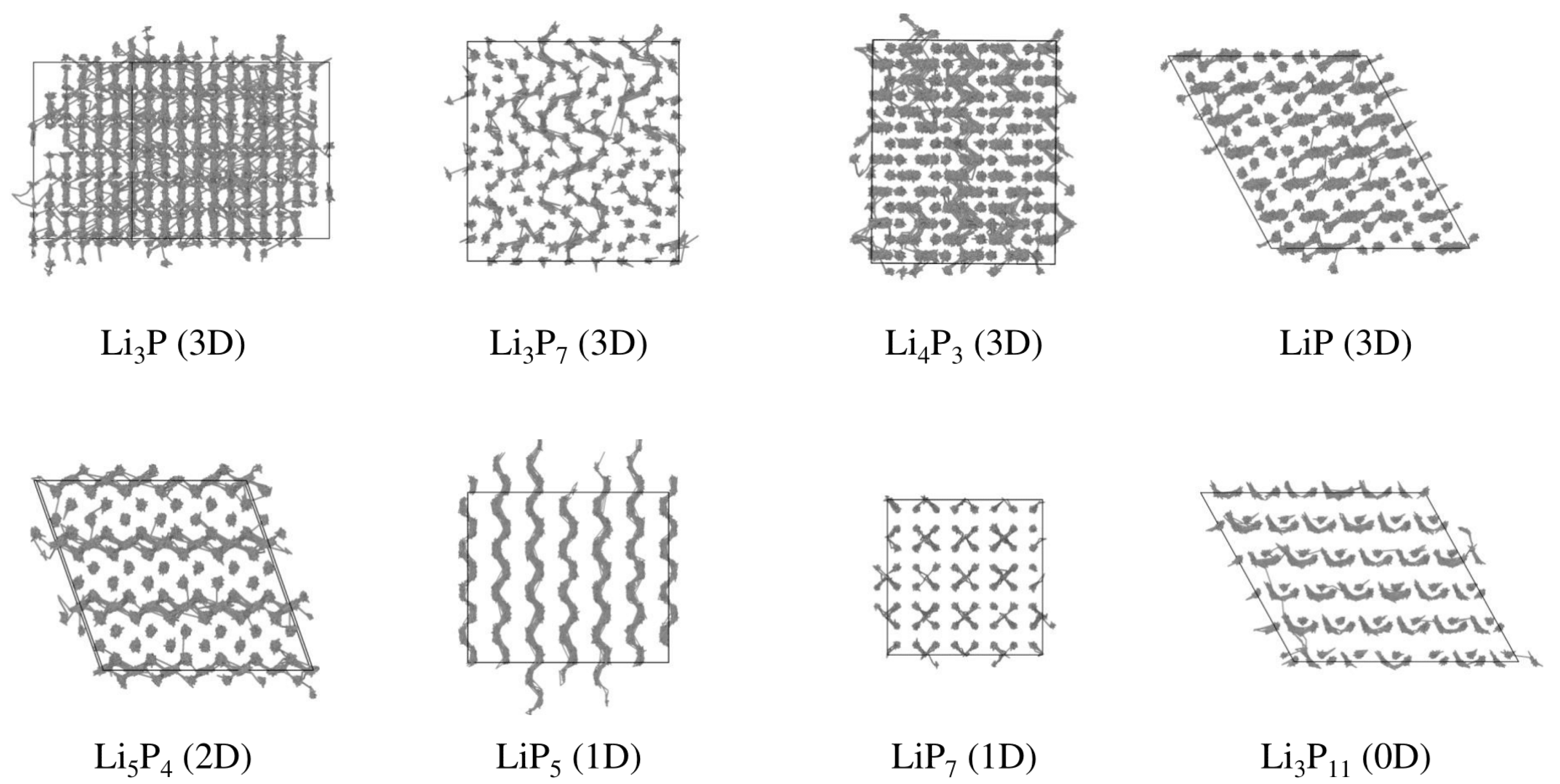
Li 3 P6 × 6 × 325.3625.3622.669090120864
Li 3 P 7 4 × 3 × 330.5229.6331.719090901440
Li 3 P 11 3 × 5 × 539.3330.2133.9490118.95901680
Li 4 P 3 2 × 7 × 322.3327.1730.529090901176
Li 5 P 4 3 × 7 × 326.5927.8425.4590109.37901134
LiP5 × 5 × 327.97524.8230.7790118.16901200
LiP 5 3 × 5 × 431.4533.3926.79090901440
LiP 7 2 × 2 × 227.2927.2929.749090901024
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Maltsev, A.P.; Chepkasov, I.V.; Kvashnin, A.G.; Oganov, A.R. Ionic Conductivity of Lithium Phosphides. Crystals 2023, 13, 756. https://doi.org/10.3390/cryst13050756

AMA Style

Maltsev AP, Chepkasov IV, Kvashnin AG, Oganov AR. Ionic Conductivity of Lithium Phosphides. Crystals. 2023; 13(5):756. https://doi.org/10.3390/cryst13050756

Chicago/Turabian Style

Maltsev, Alexey P., Ilya V. Chepkasov, Alexander G. Kvashnin, and Artem R. Oganov. 2023. "Ionic Conductivity of Lithium Phosphides" Crystals 13, no. 5: 756. https://doi.org/10.3390/cryst13050756

APA Style

Maltsev, A. P., Chepkasov, I. V., Kvashnin, A. G., & Oganov, A. R. (2023). Ionic Conductivity of Lithium Phosphides. Crystals, 13(5), 756. https://doi.org/10.3390/cryst13050756

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop