Abstract
The secondary phase, such as Ni3Al-based L12 γ′, is crucially important for the precipitation strengthening of superalloys. Composition–structure–property relations provide useful insights for guided alloy design. Here we use density functional theory combined with the multiple scattering theory to compute dependencies of the structural energies and equilibrium volumes versus composition for ternary Ni3(Al1−xXx) alloys with X = {Ti, Zr, Hf; V, Nb, Ta; Cr, Mo, W} in L12, D024, and D019 phases with a homogeneous chemical disorder on the (Al1−xXx) sublattice. Our results provide a better understanding of the physics in Ni3Al-based precipitates and facilitate the design of next-generation nickel superalloys with precipitation strengthening.
1. Introduction
Computed dependencies of the relative structural energies on composition can be used to design multi-phase materials and alloys with improved thermomechanical properties (in particular, with better creep and higher strength) [1,2]. Recently, it was shown [3] that local phase transformations inside Ni3Al-based precipitates improve creep at the elevated operation temperatures T in Ni-based superalloys used in jet engines. At high T, local phase transformations are assisted by atomic diffusion. Structural defects (such as stacking faults) interact with diffusing solute atoms and are stabilized by the local chemical composition. Attractive interactions result in energy reduction after the diffusion of particular chemical elements towards defects, which act as sinks. The stabilization of stacking faults inside L12 precipitates reduces creep and improves the mechanical strength of Ni superalloys [4,5]. The stacking of atomic layers in intrinsic and extrinsic stacking faults in the L12 phase locally looks like D019 and D024 structures, respectively. Consequently, the stacking fault energy correlates with the energy difference between the relevant structures. To provide guidance for alloy design, we computed the compositional dependences of these structural energies.
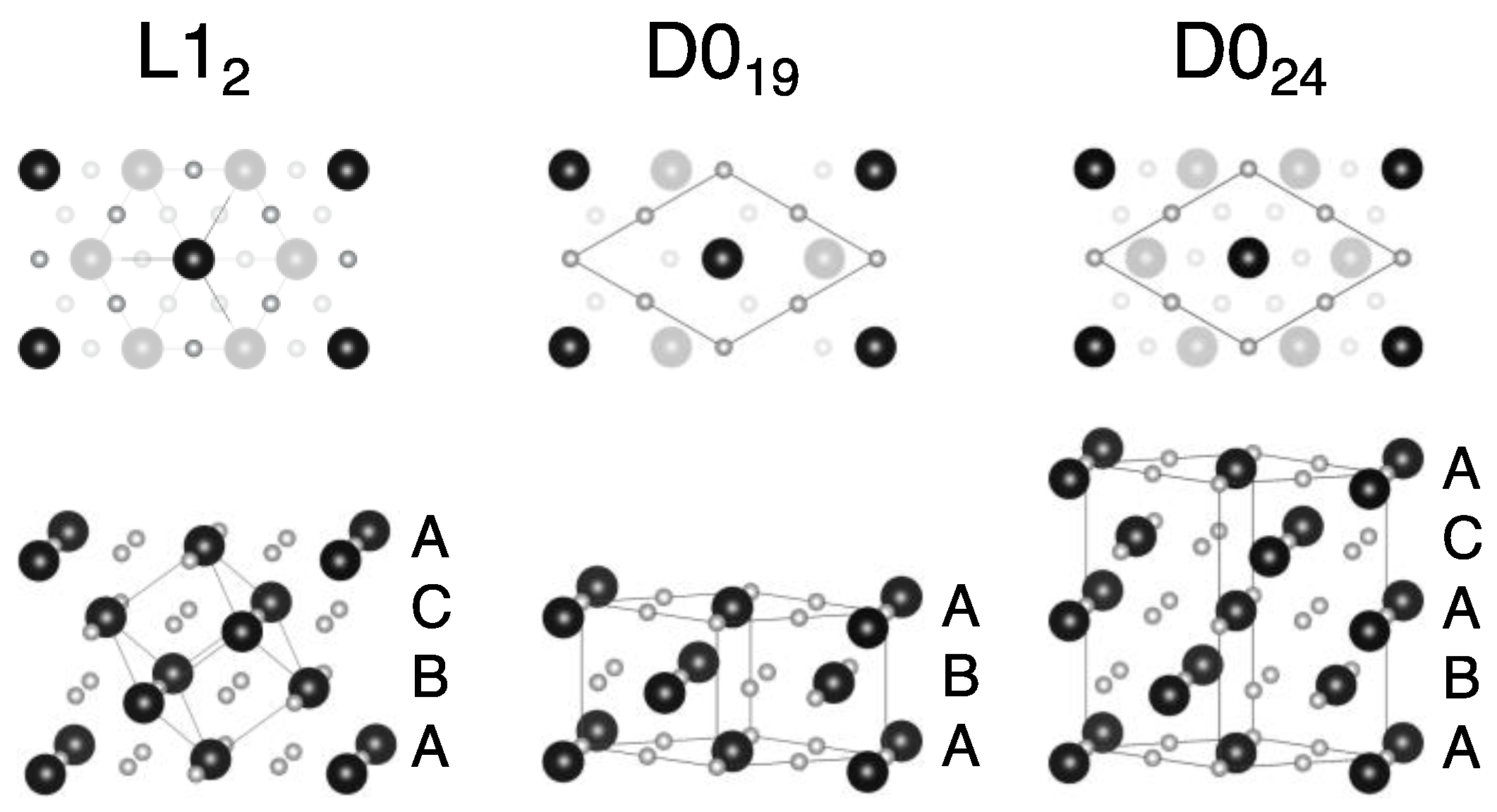
The relevant atomic structures are compared in Figure 1. They differ by the stacking of the atomic layers along the cubic [111] (in L12) and hexagonal (hex) [0001] directions (in D019 and D024 structures). The periodic stacking sequences are [AB] in D019 and [ABAC] in D024; both structures can be viewed locally as stacking faults within the [ABC] stacking in the cubic L12 structure along the [111] direction. In Ni3(Al1−xXx) alloys with chemical disorder on the (Al1−xXx) sublattice, this sublattice is simple cubic in L12, hexagonal close-packed (hcp) in D019, and double hcp (dhcp) in D024.
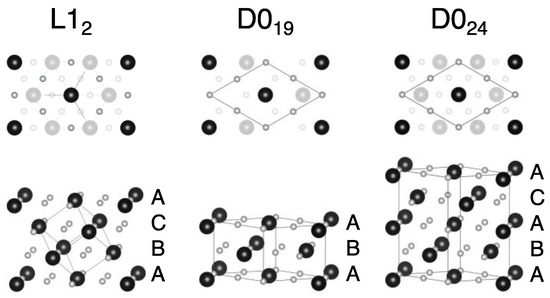
Figure 1.
Atomic structures of L12 (γ’), D019 (χ), and D024 (η) phases, shown for fully relaxed Ni3Ti. The top panel shows cubic (111) and hexagonal (0001) projections, with shaded lower layers. The lower panel compares stacking of atomic layers. Ti is large black; Ni is small grey.
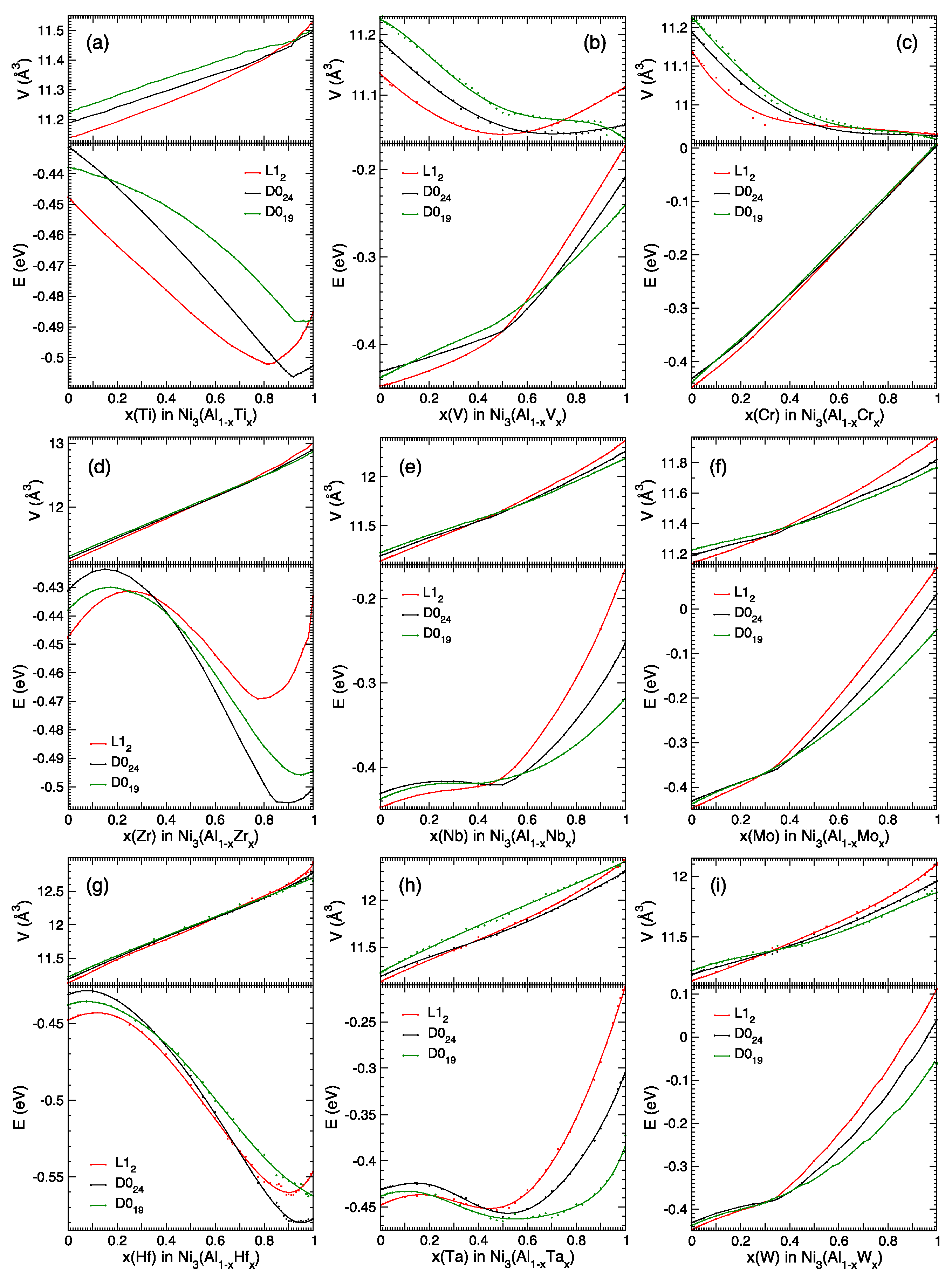
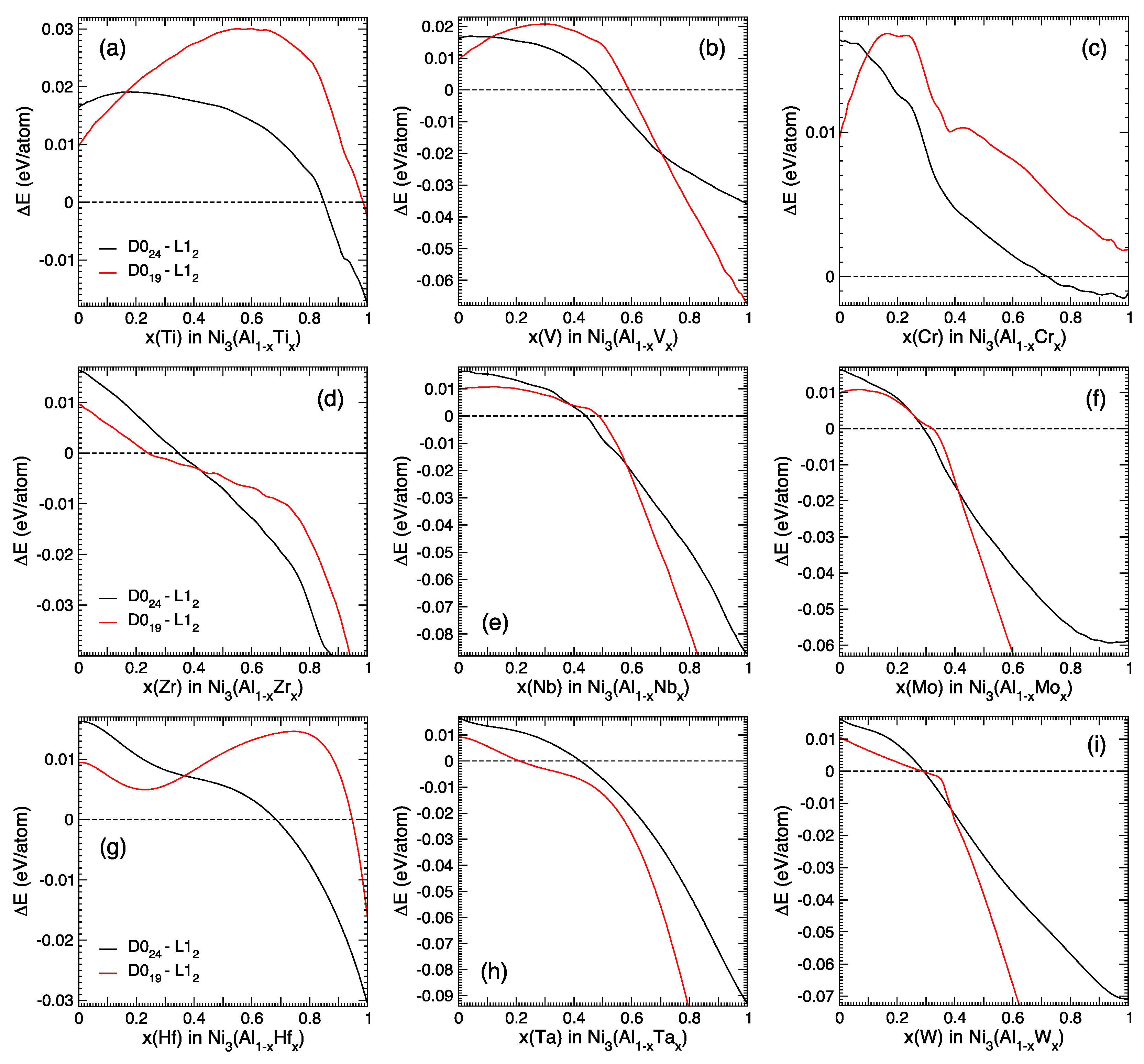
The novelty of our results consists in providing the previously unknown composition-property relations, shown in Figure 2 and Figure 3. To compute the energy-composition dependencies from the first principles, we use well-established theoretical methods [6]. The computed structural formation energies and equilibrium volumes (per atom) versus composition are shown in Figure 2. Relative energies versus composition are in Figure 3. Known composition–property dependencies allow to improve alloys by compositional adjustment.
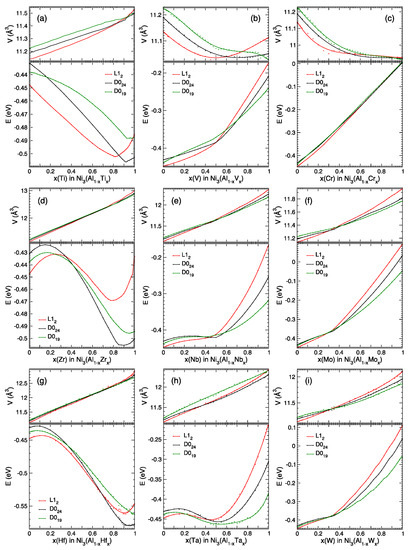
Figure 2.
Equilibrium volume V [Å3/atom] and formation energy E [eV/atom] of the Ni3(Al1−xXx) phases with homogeneous atomic disorder on the Al/X sublattice for group 4, 5, and 6 elements X = {Ti, Zr, Hf; V, Nb, Ta; Cr, Mo, W}. The terminal formation energies of the binary Ni3X alloys are from the full-potential VASP, while the relative mixing energies are from the KKR-CPA calculations. L12 is red, D024 is black, D019 is green.
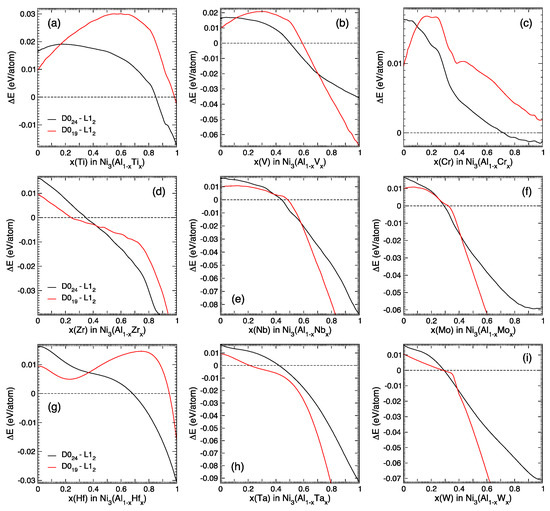
Figure 3.
Relative energies [eV/atom] of the Ni3(Al1−xXx) phases. Data in Figure 2 was approximated by cubic splines and E0(L12) was subtracted. ΔE(D024 − L12) is black and ΔE(D019 − L12) is red.
2. Methods
We use two electronic-structure codes: the all-electron KKR-CPA [7] and the full-potential VASP [8]. The KKR-CPA approach [7] was used to find mixing energies of Ni3(Al1−xXx)1 alloys with a homogeneous chemical disorder on the (Al1−xXx) sublattice. The mixing energies are defined relative to those of the fully ordered terminal Ni3Al and Ni3X compounds in the same phase. The VASP code [8] was used to compute the formation energies of the ordered structures at the terminal Ni3X compositions. In both codes, we use the PBEsol [9] exchange-correlation functional (XC = 116,133). All equilibrium energies and volumes are computed at zero pressure and zero temperature T = 0 K; values are reported per atom, unless specified otherwise.
Within the KKR-CPA code, density functional theory (DFT) is combined with the multiple scattering theory (MST) to compute sets of energies [10] of crystal structures with chemical disorder on sublattices. The homogeneous atomic disorder without a short-range order (SRO) is considered within the coherent potential approximation (CPA) [11] in the Korringa–Kohn–Rostocker (KKR) formalism [12,13].
The terminal binary Ni3X structures are addressed by both KKR and full-potential DFT methods; the latter (implemented in VASP) provides a higher accuracy for structural formation energies, determined relatively to the ground states of elemental solids. To obtain the advantages of both full-potential and MST methods, we used the full-potential formation energies of the terminal Ni3X structures (see Table 1) and combined them with the KKR-CPA mixing energies of disordered Ni3(Al1−xXx) structures. Thus, the formation energy of Ni3(Al1−xXx)1 is , where Emix(x) is the mixing energy at the same composition x, E(0) is the formation energy of Ni3Al, and E(1) is the formation energy of Ni3X in the same phase (L12, D019, or D024) with the same element X.

Table 1.
The computed formation energies [eV/atom] and volumes [Å3/atom] of Ni3X compounds with L12, D019, and D024 structures, fully relaxed.
The KKR-CPA spin-polarized calculations [11,12,13] were performed in primitive unit cells. We used two k-point meshes for the Brillouin Zone (BZ) integration. The primary (secondary) k-mesh was 12 × 12 × 12 (8 × 8 × 8) for the cubic L12, 8 × 8 × 4 (6 × 6 × 4) for the hexagonal (hex) D024 with fixed c/a = (8/3)1/2 (ideal), and 8 × 8 × 10 (6 × 6 × 6) for the hexagonal D019 with fixed c/a = (2/3)1/2 (ideal). We included s, p, d, and f orbitals (lmax = 3) in the basis inside the atomic spheres. For contour integration in the complex plane, we fixed the bottom energy at or below Ebot = −0.9 Ry. We used the muffin-tin approximation with periodic boundary corrections.
At each composition x, the equilibrium volume V0 and the minimal energy E0 were found by fitting the Birch–Murnaghan [14,15] equation of state (EOS), defining the energy versus volume E(V) relation, to 5 DFT points (Neos = 5) with 1.5% step in the lattice constant a. To check the accuracy, we used the fitted linear V0(x) dependence in each Ni3(Al1−xHfx) phase and directly computed DFT energies E[V0(x)], which agreed with the EOS energies E0(x) within the DFT error bars.
The VASP code [8] was compiled with the C2NEB subroutine [16,17]. A dense Γ-centered Monkhorst-Pack mesh [18] with ≥60 k-points per inverse Angstrom (Å) was used for the BZ integration. The plane-wave energy cutoff was increased to ENCUT = 650 eV. We used the Gaussian smearing (ISMEAR = 0) with SIGMA = 0.043 eV, corresponding to kBT at T = 500 K, where kB is the Boltzmann constant. DFT energy was obtained by extrapolation to zero smearing. Stacking fault energies were computed in a supercell with 40 Å between the periodic stacking faults; the energy of an ideal crystal was computed in a primitive unit cell.
3. Results
Using the density functional theory [19,20,21] and the multiple scattering theory [6,22], we computed the equations of state, formation and mixing energies of the ordered Ni3X and disordered Ni3(Al1−xXx) alloys with X = {Ti, Zr, Hf; V, Nb, Ta; Cr, Mo, W} in L12, D019, and D024 phases, shown in Figure 1. Formation energies (computed using VASP, relative to the ground states of elemental solids) of the terminal Ni3X compositions are in Table 1. Mixing energies (relative to the ground states of the terminal Ni3Al and Ni3X compositions) were computed using KKR-CPA. Formation energies versus composition for the partially disordered Ni3(Al1−xXx) structures (with a homogeneous disorder on the Al + X sublattice) are shown in Figure 2. The EOS equilibrium energies E0 and volumes V0 are shown as dots. For X = {Hf, Ta} in Ni3(Al1−xHfx) and Ni3(Al1−xTax), the E(x) lines are the 6th-degree polynomials, fitted to the EOS data points E0. For X = {Cr, W}, the V(x) lines are the 4th-degree polynomials from the least-squares fit to the EOS volumes V0. For the other elements X, lines connect the computed EOS energies E0 and volumes V0, shown as dots.
For completeness, we also provide relative energies ΔE in Figure 3, which is complementary to Figure 2. The differences ΔE are defined relative to E0(L12) at the same composition x. These differences ΔE(D024 − L12) = E(D024) − E(L12) and ΔE(D019 − L12) = E(D019) − E(L12) in Figure 3 provide important additional information, while the shape of each E(x) curve in Figure 2 is related to the stability of each phase. The energy differences ΔE alone are not sufficient for materials design, especially if an unstable phase at some composition x transforms to another phase or segregates into other compositions. For example, E0(x) curves for all 3 phases of Ni3(Al1−xZrx)1 alloys at 0 < x < 0.8 point at a tendency to segregate into Zr-rich and Zr-deficient components; for a concave E(x) dependency with a negative curvature such segregation would result in energy lowering [23].
Our first-principles calculations predict a change of the lowest-energy phase from L12 Ni3Al to D024 for group 4 elements X = {Ti, Zr, Hf} and to D019 for group 5 elements X = {V, Nb, Ta}, with a possible intermediate D024 phase for X = {V, Nb}. However, we did not consider D022 and D0a phases of Ni3(V, Nb) [24] and Ni3Ta [25], reported as more stable than D019 in the phase diagrams [26,27].
The equation of state contains equilibrium energy E0, volume V0, bulk modulus B0, and its dimensionless pressure derivative at constant temperature T. The computed values of B0 and in Table 2 were assessed from the EOS fitted to DFT KKR data. For the computed compositional dependences of B0 and we found that the differences between the linear and higher-degree polynomial approximations were within the error bars. Directly computed values of B0 for Ni3Al and Ni3Ti in Table 2 can be compared with those at the terminal compositions from a linear fit of B0(x) for the Ni3(Al1−xTix) system: B0(L12, x = 0) = 193.13 GPa ≈ 193.1 GPa = B0(L12, Ni3Al); B0(L12, x = 1) = 203.49 GPa ≈ 203.1 GPa = B0(L12, Ni3Ti); B0(D024, x = 0) = 193.16 GPa ≈ 193.8 GPa = B0 (D024, Ni3Al); B0 (D024, x = 1) = 204.92 GPa ≈ 204.7 GPa = B0(D024, Ni3Ti). The computed bulk modulus B0 of L12 Ni3Al is 193 GPa, and the experimental measurements range from 171 GPA [28] and 173.9 GPa [29] to 229.2 GPa [30]. We conclude that our first-principle result reasonably agrees with the available experimental data.

Table 2.
Computed EOS parameters: bulk modulus B0 (GPa) and (dimensionless).
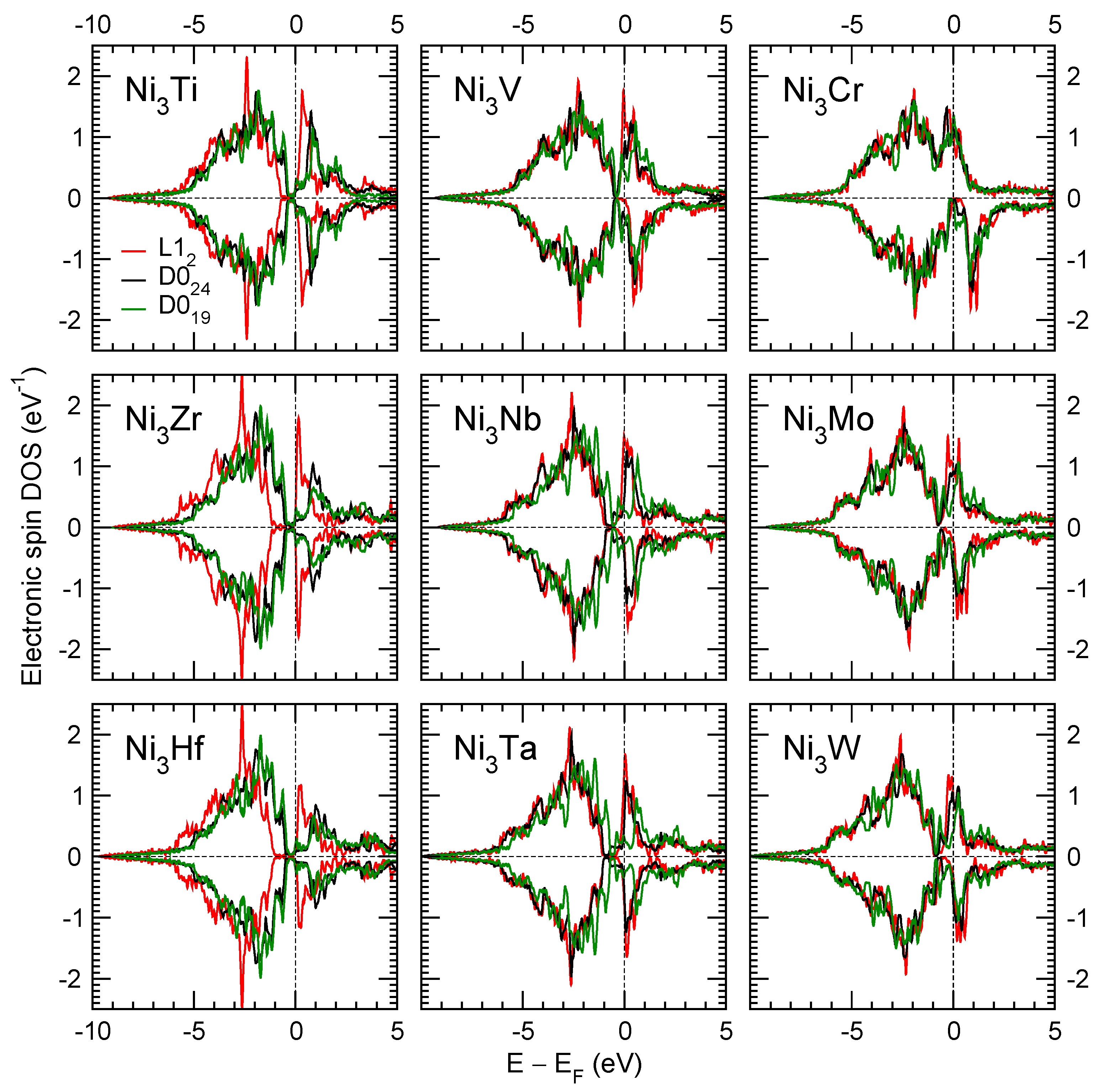
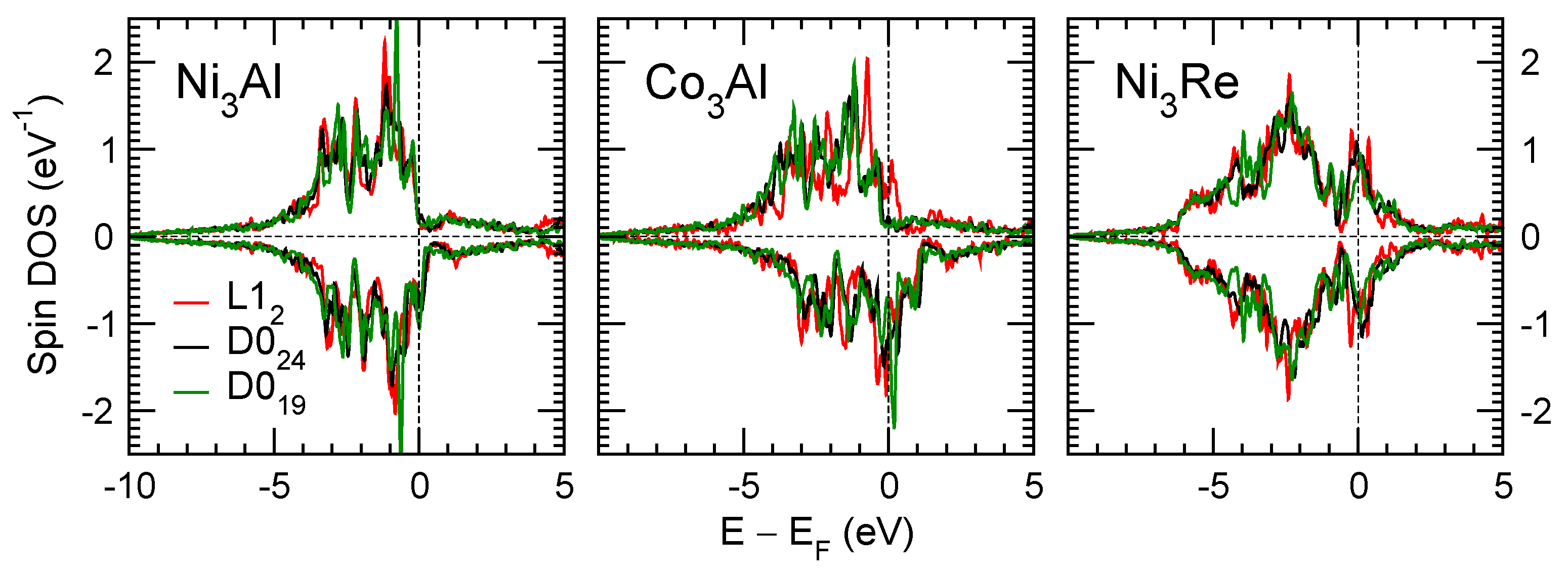
For changing composition x, magnetic and electronic structure changes in the Ni3(Al1−xTix)1 system [31]. Ni3Al is magnetic, while Ni3Ti is non-magnetic, with zero atomic magnetic moments, as shown in Figure 4 in Ref. [31]. The rapid change of the electronic density of states at the Fermi energy EF is responsible for the kink of the E(x) curve in Ni3(Al1−xTix)1, present in each of the 3 phases. EF is in the pseudo-gap in Ni3Ti, but not in Ni3Al, as shown in Figure 4 and Figure 5. Ni3(Al1−xTix)1 crystal structure changes from L12 at smaller x to D024 at x ≥ 0.875. Similar changes in electronic, magnetic, and atomic structure are also expected in other Ni3(Al1−xXx)1 systems.
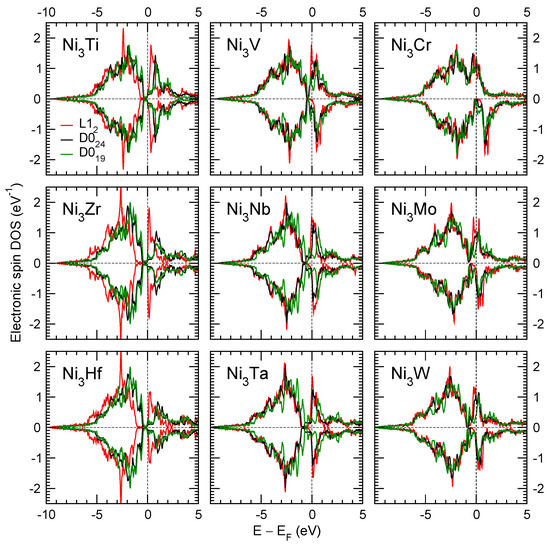
Figure 4.
Spin DOS in L12, D024, and D024 phases of Ni3X compounds.
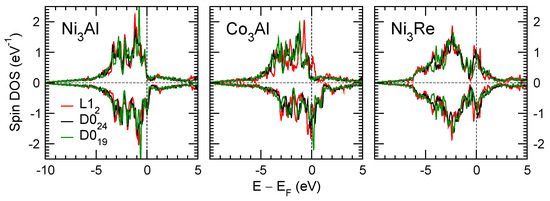
Figure 5.
Spin DOS in L12, D024, and D024 phases of Ni3Al, Co3Al, and Ni3Re compounds.
The computed equation of state can be affected by a magnetic phase transition. This is the case, for example, in D019 Ni3V: due to the disappearance of atomic magnetic moments near V0, the EOS fit of both magnetic states at V > V0 and non-magnetic states at V < V0 results in a larger fitting error and less accurate value of . Two EOS fits of either non-magnetic states at V < V0 (shown in Table 2) or magnetic states at V > V0 provide two different equations of state with similar E0, but different B0 and values.
Our attempts to fit the EOS for the D019 (not the ground state) structure in Ni3Mo and Ni3W resulted in a large fitting error, originating from the peculiarities of the electronic structure. The equilibrium values of E0 and V0 were found reliably by energy minimization. However, the EOS fit of the higher-order terms B0 and was noisy: slightly different calculations provided different results. Ni3Mo crystallized below 910 °C (1183 K) in the orthorhombic D0a oP8 β-Cu3Ti structure with Pmmn space group (no. 59) [32], which was claimed to be stable [33]. The stability of Ni3W oP8 structure [34] is debatable [35] and can be influenced by carbon [36]. Unstable Ni3W L12 and D024 structures have positive formation energies (see Table 1 and Figure 2), while Ni3W D019 structure is not observed experimentally [37]. For comparison, the Cr-Ni system segregates into Cr and Ni solid solutions [38]; there are no stable Ni3Cr compounds, in agreement with our calculations.
Figure 2 allows to roughly estimate temperature-dependent solubility limits of dopants in the Ni3Al L12 phase, using a rapid design estimate of phase-segregation temperature [39]. However, consideration of other phases, such as the orthorhombic Ni3(Nb0.8Ti0.2) δ phase [40], is beyond the scope of the present work.
The Ti-rich Ni3(Al1−xTix)1 alloy was claimed [31] to be a compositional glass—an analogue of a spin glass in the compositional space. Such systems can be described by a truncated cluster expansion [41] with a degeneracy among the interactions [42] and frustration of the ground states [43]. At certain compositions x, we expect similarly frustrated ground states in several Ni3(Al1−xXx)1 systems.
Interestingly, in the Ni3(Al1−xXx)1 systems with X = {Ti, V, Nb}, the full-potential VASP calculations predict repulsion of X = {Ti, V, Nb} from the stacking fault at small concentration x and attraction to the stacking fault at larger x. For Ni3(Al1−xNbx)1, we checked this for both intrinsic and extrinsic stacking faults. The KKR-CPA results in Figure 3 indicate attraction of Nb to the stacking fault at larger x; however, repulsion of Nb at small concentrations x from both intrinsic and extrinsic stacking faults was unexpected [44].
In L12 Ni3Nb (at x = 1), the computed stacking fault energies are negative for both intrinsic and extrinsic stacking faults; this points at the instability of L12 Ni3Nb structure. Indeed, both D024 and D019 structures are lower in energy than L12. At some composition x, a stacking fault energy changes its sign (i.e., becomes zero) in the Ni3(Al1−xNbx)1 system.
In Ni3Al (at x = 0), our computed energy of the intrinsic stacking fault is 0.054 J/m2; this value reasonably agrees with those ranging from 0.037 to 0.092 J/m2 in the literature [44,45,46,47,48,49,50,51]. Depending on the distance L between the periodic stacking faults in a supercell, the intrinsic stacking fault energy varies from 0.065 J/m2 at L ≈ 10 Å to 0.054 J/m2 at L > 40 Å; a monotonic decrease in energy with distance at L > 10 Å points at repulsion between the stacking faults.
The stabilization of stacking faults in L12 precipitates reduces the creep resistance of Ni-based superalloys at high operating temperatures [3,4,5]. Local phase transformation at stacking faults with increased concentration of dopants impedes the propagation of additional dislocations along the stacking fault and thus improves the creep resistance. The D024 and D019 structures locally look like L12 with periodic stacking faults, and the energy differences in Figure 3 correlate with the stacking fault energies. Thus, our results allow the engineering of stacking fault energies and improvement of the creep resistance in Ni superalloys by compositional adjustment. A discussion of a predictor for choosing the right chemical elements with appropriate concentrations that promote the formation and stabilization of η (χ) phases along the superlattice extrinsic (intrinsic) stacking faults can be found in the literature [3,4,5]. A limited amount of relevant DFT data can be found in Figure 6 in Ref. [3]. Here, in Figure 2 and Figure 3, we show that the energy-composition relations are nonlinear. This detailed information can be used as an improved predictor, which takes into account the non-linearity of relative energies versus composition.
4. Discussion
For completeness, we discuss superalloys and their precipitation strengthening. A superalloy is a high-performance metallic alloy that is capable to operate at high temperatures—a fraction of melting point [2,52,53]. Superalloys have common characteristics retained at operating temperature, such as mechanical strength, low creep, surface stability, corrosion and oxidation resistance, radiation tolerance, and metallic electrical and thermal conductivity [54]. Due to their properties, superalloys are used in load-bearing structures at high temperatures and stresses, in highly corrosive or radioactive environments: in engines, generators, heat exchanges, and nuclear reactors. Superalloys find applications in energy, nuclear, chemical processing, automotive, marine, and airspace industries [52,53]. Both superalloys and multiprincipal-element alloys are suitable for 3D printing [55].
Nickel-based superalloys are known for many decades [56]. They are composed by the Ni-rich fcc solid solution (γ phase) and precipitates, most of which have the cubic L12 cP4 crystal structure with Cu3Al prototype (Ni3Al γ′ phase) [57]. The competing phases include the tetragonal D022 (Ni3Nb) γ″ [24], hexagonal D024 (Ni3Ti) η [31], hexagonal D019 (Ni3Sn-type) χ, orthorhombic D0a (Cu3Ti-type) Ni3Ta [25], carbides, etc.
The local phase transformations inside γ’ precipitates followed by diffusion-driven stabilization of the stacking faults were shown to improve mechanical strength and creep in Ni superalloys [4,5]. The solute atoms interact with defects [58], such as dislocations [59], stacking faults [5], twins [60], grain boundaries [61], and surfaces [1]. Altered chemical composition near the surface affects corrosion and oxidation resistance. Stabilization of grain boundaries may improve the strength of a polycrystal towards that of a single crystal.
Previously, the interaction energies between solutes (Co, Cr, Nb, Ta) and stacking faults were computed [4]. We find nonlinearity of the key energies versus composition, see Figure 2 and Figure 3. One reason for that is a change of the electronic structure from that with a relatively high density of states at the Fermi energy in Ni3Al (Figure 5) to a low one (with the Fermi energy in the pseudo-gap, for example, in Ni3Ti, see Figure 4). The computed from the first principles nonlinear (and sometimes non-monotonic) property–composition relations constitute the main novelty of our present research. The property–composition relations and correlations among properties are used in a guided materials design [62].
5. Summary
We have computed the compositional dependencies of the equations of state, structural energies and equilibrium volumes (per atom) for ternary Ni3(Al1−xXx) alloys with X = {Ti, Zr, Hf; V, Nb, Ta; Cr, Mo, W} in L12, D024, and D019 phases with atomic disorder on the (Al1−xXx) sublattice. We considered both formation and relative energies and found their nonlinear dependencies versus composition. Our results provide a better understanding of precipitation in multicomponent Ni superalloys. Our ab initio data is used for designing next-generation alloys with improved properties.
Author Contributions
N.A.Z. conceived the idea, performed calculations, and wrote the manuscript. T.M.S. and J.W.L. participated in discussions and editing. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge funding by NASA’s Aeronautics Research Mission Directorate (ARMD) via Transformational Tools and Technologies (TTT) Project.
Data Availability Statement
Data is available from the authors upon a reasonable request.
Acknowledgments
We thank Anupa R. Bajwa, Mikhail Mendelev, Valery V. Borovikov, and Shreyas J. Honrao for discussion.
Conflicts of Interest
The authors declare no conflict of interest. The opinion of the authors does not represent the opinions of any governmental organizations.
References
- Jena, A.K.; Chaturvedi, M.C. The role of alloying elements in the design of nickel-base superalloys. J. Mater. Sci. 1984, 19, 3121–3139. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Smith, T.M.; Zarkevich, N.A.; Egan, A.J.; Stuckner, J.; Gabb, T.P.; Lawson, J.W.; Mills, M.J. Utilizing local phase transformation strengthening for nickel-base superalloys. Commun. Mater. 2021, 2, 106. [Google Scholar] [CrossRef]
- Smith, T.M.; Esser, B.D.; Antolin, N.; Viswanathan, G.B.; Hanlon, T.; Wessman, A.; Mourer, D.; Windl, W.; McComb, D.W.; Mills, M.J.; et al. Segregation and η phase formation along stacking faults during creep at intermediate temperatures in a Ni-based superalloy. Acta Mater. 2015, 100, 19–31. [Google Scholar] [CrossRef]
- Smith, T.M.; Esser, B.D.; Antolin, N.; Carlsson, A.; Williams, R.E.A.; Wessman, A.; Hanlon, T.; Fraser, H.L.; Windl, W.; McComb, D.W.; et al. Phase transformation strengthening of high-temperature superalloys. Nat. Commun. 2016, 7, 13434. [Google Scholar] [CrossRef]
- Zarkevich, N.A. Theoretical and computational methods for accelerated materials discovery. Mod. Phys. Lett. B 2021, 35, 2130003. [Google Scholar] [CrossRef]
- Johnson, D.D.; Smirnov, A.V.; Khan, S.N. MECCA: Multiple-Scattering Electronic-Structure Calculations for Complex Alloys; KKR-CPA Program; Iowa State University and Ames Laboratory: Ames, Iowa, 2015. [Google Scholar]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Zarkevich, N.A. Structural database for reducing cost in materials design and complexity of multiscale computations. Complexity 2006, 11, 36–42. [Google Scholar] [CrossRef]
- Johnson, D.D.; Nicholson, D.M.; Pinski, F.J.; Gyorffy, B.L.; Stocks, G.M. Density-Functional Theory for Random Alloys: Total Energy within the Coherent-Potential Approximation. Phys. Rev. Lett. 1986, 56, 2088–2091. [Google Scholar] [CrossRef]
- Korringa, J. On the calculation of the energy of a Bloch wave in a metal. Physica 1947, 13, 392–400. [Google Scholar] [CrossRef]
- Kohn, W.; Rostoker, N. Solution of the Schrödinger Equation in Periodic Lattices with an Application to Metallic Lithium. Phys. Rev. 1954, 94, 1111–1120. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Zarkevich, N.A.; Johnson, D.D. Nudged-elastic band method with two climbing images: Finding transition states in complex energy landscapes. J. Chem. Phys. 2015, 142, 024106. [Google Scholar] [CrossRef] [PubMed]
- Zarkevich, N.A. C2-NEB Source Code. Available online: https://lib.dr.iastate.edu/ameslab_software/1/ (accessed on 6 June 2023).
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Martin, R.M.; Reining, L.; Ceperley, D.M. Interacting Electrons: Theory and Computational Approaches; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar]
- Faulkner, J.S.; Stocks, G.M.; Wang, Y. Multiple Scattering Theory. In Electronic Structure of Solids; IOP Publishing: Bristol, UK, 2018. [Google Scholar] [CrossRef]
- Yibole, H.; Pathak, A.K.; Mudryk, Y.; Guillou, F.; Zarkevich, N.; Gupta, S.; Balema, V.; Pecharsky, V.K. Manipulating the stability of crystallographic and magnetic sub-lattices: A first-order magnetoelastic transformation in transition metal based Laves phase. Acta Mater. 2018, 154, 365–374. [Google Scholar] [CrossRef]
- Mignanelli, P.M.; Jones, N.G.; Pickering, E.J.; Messé, O.M.D.M.; Rae, C.M.F.; Hardy, M.C.; Stone, H.J. Gamma-gamma prime-gamma double prime dual-superlattice superalloys. Scr. Mater. 2017, 136, 136–140. [Google Scholar] [CrossRef]
- Kosorukova, T.; Firstov, G.; Noel, H.; Ivanckenko, V. Crystal structure changes in the Ni3Ta intermetallic compound. Chem. Met. Alloy. 2013, 6, 196–199. [Google Scholar] [CrossRef]
- Massalski, T.B. Binary Alloy Phase Diagrams, 2nd ed.; Massalski, T.B., Okamoto, H., Subramanian, P.R., Kacprzak, L., Eds.; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Nash, A.; Nash, P. The Ni−Ta (Nickel−Tantalum) system. Bull. Alloy Phase Diagr. 1984, 5, 259–265. [Google Scholar] [CrossRef]
- Yasuda, H.; Takasugi, T.; Koiwa, M. Elasticity of Ni-based L12-type intermetallic compounds. Acta Metall. Mater. 1992, 40, 381–387. [Google Scholar] [CrossRef]
- Prikhodko, S.V.; Yang, H.; Ardell, A.J.; Carnes, J.D.; Isaak, D.G. Temperature and composition dependence of the elastic constants of Ni3Al. Metall. Mater. Trans. A 1999, 30, 2403–2408. [Google Scholar] [CrossRef]
- Pearson, W.B.; Raynor, G.V. A Handbook of Lattice Spacings and Structures of Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Smith, T.M.; Baum, E.N.; Lawson, J.W. Compositional Glass: A State with Inherent Chemical Disorder, Exemplified by Ti-rich Ni3(Al,Ti)1 D024 Phase. Crystals 2022, 12, 1049. [Google Scholar] [CrossRef]
- Casselton, R.E.W.; Hume-Rothery, W. The equilibrium diagram of the system molybdenum-nickel. J. Less Common Met. 1964, 7, 212–221. [Google Scholar] [CrossRef]
- Wang, Y.; Woodward, C.; Zhou, S.H.; Liu, Z.K.; Chen, L.Q. Structural stability of Ni–Mo compounds from first-principles calculations. Scr. Mater. 2005, 52, 17–20. [Google Scholar] [CrossRef]
- Arapova, L.P. Crystalline structure of the intermetallic phases of WNi3 and MoNi3. Sov. Phys. J. 1973, 16, 1173–1175. [Google Scholar] [CrossRef]
- Isomäki, I.; Hämäläinen, M.; Braga, M.H.; Gasik, M. First principles, thermal stability and thermodynamic assessment of the binary Ni–W system. Int. J. Mater. Res. 2017, 108, 1025–1035. [Google Scholar] [CrossRef]
- Liu, X.; Pilling, J.; Heckel, R.W.; Lee, J.K. Influence of carbon on bond strength betvveen nickel and Ni–W alloys. Mater. Sci. Technol. 1991, 7, 228–238. [Google Scholar] [CrossRef]
- Cury, R.; Joubert, J.M.; Tusseau-Nenez, S.; Leroy, E.; Allavena-Valette, A. On the existence and the crystal structure of Ni4W, NiW and NiW2 compounds. Intermetallics 2009, 17, 174–178. [Google Scholar] [CrossRef]
- Nash, P. The Cr−Ni (Chromium-Nickel) system. Bull. Alloy Phase Diagr. 1986, 7, 466–476. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Tan, T.L.; Johnson, D.D. First-principles prediction of phase-segregating alloy phase diagrams and a rapid design estimate of their transition temperatures. Phys. Rev. B 2007, 75, 104203. [Google Scholar] [CrossRef]
- Lyu, F.; Liu, F.; Hu, X.; Yang, X.; Huang, C.; Shi, D. The δ Phase Precipitation of an Inconel 718 Superalloy Fabricated by Electromagnetic Stirring Assisted Laser Solid Forming. Materials 2019, 12, 2604. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. Reliable First-Principles Alloy Thermodynamics via Truncated Cluster Expansions. Phys. Rev. Lett. 2004, 92, 255702. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Tan, T.L.; Wang, L.L.; Johnson, D.D. Low-energy antiphase boundaries, degenerate superstructures, and phase stability in frustrated fcc Ising model and Ag-Au alloys. Phys. Rev. B 2008, 77, 144208. [Google Scholar] [CrossRef]
- Mydosh, J.A. Spin Glasses: An Experimental Introduction, 1st ed.; CRC Press: London, UK, 1993. [Google Scholar] [CrossRef]
- Rao, Y.; Smith, T.M.; Mills, M.J.; Ghazisaeidi, M. Segregation of alloying elements to planar faults in γ’-Ni3Al. Acta Mater. 2018, 148, 173–184. [Google Scholar] [CrossRef]
- Schoeck, G.; Kohlhammer, S.; Fahnle, M. Planar dissociations and recombination energy of [110] superdislocations in Ni3Al: Generalized Peierls model in combination with ab initioelectron theory. Philos. Mag. Lett. 1999, 79, 849–857. [Google Scholar] [CrossRef]
- Mryasov, O.N.; Gornostyrev, Y.N.; van Schilfgaarde, M.; Freeman, A.J. Superdislocation core structure in L12 Ni3Al, Ni3Ge and Fe3Ge: Peierls–Nabarro analysis starting from ab-initio GSF energetics calculations. Acta Mater. 2002, 50, 4545–4554. [Google Scholar] [CrossRef]
- Wen, Y.-F.; Sun, J.; Huang, J. First—Principles study of stacking fault energies in Ni3Al intermetallic alloys. Trans. Nonferr. Met. Soc. China 2012, 22, 661–664. [Google Scholar] [CrossRef]
- Yu, X.-X.; Wang, C.-Y. The effects of alloying elements on generalized stacking fault energies, strength and ductility of γ′-Ni3Al. Mater. Sci. Eng. A 2012, 539, 38–41. [Google Scholar] [CrossRef]
- Liu, L.-L.; Wu, X.-Z.; Wang, R.; Li, W.-G.; Liu, Q. Stacking fault energy, yield stress anomaly, and twinnability of Ni3Al: A first principles study*. Chin. Phys. B 2015, 24, 077102. [Google Scholar] [CrossRef]
- Hasan, H.; Mlkvik, P.; Haynes, P.D.; Vorontsov, V.A. Generalised stacking fault energy of Ni-Al and Co-Al-W superalloys: Density-functional theory calculations. Materialia 2020, 9, 100555. [Google Scholar] [CrossRef]
- Shang, S.-L.; Shimanek, J.; Qin, S.; Wang, Y.; Beese, A.M.; Liu, Z.-K. Unveiling dislocation characteristics in Ni3Al from stacking fault energy and ideal strength: A first-principles study via pure alias shear deformation. Phys. Rev. B 2020, 101, 024102. [Google Scholar] [CrossRef]
- Sims, C.T.; Hagel, W. (Eds.) Superalloys; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Sims, C.T.; Stoloff, N.S.; Hagel, W.C. (Eds.) Superalloys II: High-Temperature Materials for Aerospace and Industrial Power; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Caballero, F.G. (Ed.) Encyclopedia of Materials: Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Smith, T.M.; Kantzos, C.A.; Zarkevich, N.A.; Harder, B.J.; Heczko, M.; Gradl, P.R.; Thompson, A.C.; Mills, M.J.; Gabb, T.P.; Lawson, J.W. A 3D Printable Alloy Designed for Extreme Environments. Nature 2023, 617, 513–518. [Google Scholar] [CrossRef] [PubMed]
- Reed, R.C.; Rae, C.M.F. 22-Physical Metallurgy of the Nickel-Based Superalloys. In Physical Metallurgy, 4th ed.; Laughlin, D.E., Hono, K., Eds.; Elsevier: Oxford, UK, 2014; pp. 2215–2290. [Google Scholar] [CrossRef]
- Sabol, G.P.; Stickler, R. Microstructure of Nickel-Based Superalloys. Phys. Status Solidi B 1969, 35, 11–52. [Google Scholar] [CrossRef]
- Borovikov, V.V.; Mendelev, M.I.; Smith, T.M.; Lawson, J.W. Dislocation-assisted diffusion-mediated atomic reshuffling in the Kolbe mechanism for micro-twinning in Ni-based superalloys from molecular dynamics simulation. Scr. Mater. 2023, 232, 115475. [Google Scholar] [CrossRef]
- Suzuki, H. Chemical interaction of solute atoms with dislocations. Sci. Rep. Res. Inst. Tohoku Univ. A 1952, 4, 455–463. [Google Scholar] [CrossRef]
- Borovikov, V.V.; Mendelev, M.I.; Smith, T.M.; Lawson, J.W. Molecular dynamics simulation of twin nucleation and growth in Ni-based superalloys. Int. J. Plast. 2023, 166, 103645. [Google Scholar] [CrossRef]
- Alabort, E.; Barba, D.; Sulzer, S.; Lißner, M.; Petrinic, N.; Reed, R.C. Grain boundary properties of a nickel-based superalloy: Characterisation and modelling. Acta Mater. 2018, 151, 377–394. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D.; Pecharsky, V.K. High-throughput search for caloric materials: The CaloriCool approach. J. Phys. D Appl. Phys. 2017, 51, 024002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).