Next Article in Journal
Recent Advances and Challenges in Thin-Film Fabrication Techniques for Low-Temperature Solid Oxide Fuel Cells
Next Article in Special Issue
The Possibility of Layered Non-Van Der Waals Boron Group Oxides: A First-Principles Perspective
Previous Article in Journal
Enhanced Electromagnetic Wave Absorption Properties of FeCo-C Alloy by Exploiting Metamaterial Structure
Previous Article in Special Issue
Ultrafast Mechanism of Material Removal in the Femtosecond Laser Ablation of WS2 and Its Diode Rectification Characteristics
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 7
10.3390/cryst13071007
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Two-Dimensional VSi2X2N2 (X = P, As, Sb, Bi) Janus Monolayers: Spin-Polarized Electronic Structure and Perpendicular Magnetic Anisotropy

by
Zhenxian Zhao
1,
Xiaocha Wang
1,* and
Wenbo Mi
2
1
Tianjin Key Laboratory of Film Electronic & Communicate Devices, School of Integrated Circuit Science and Engineering, Tianjin University of Technology, Tianjin 300384, China
2
Tianjin Key Laboratory of Low Dimensional Materials Physics and Preparation Technology, School of Science, Tianjin University, Tianjin 300354, China
*
Author to whom correspondence should be addressed.
Crystals 2023, 13(7), 1007; https://doi.org/10.3390/cryst13071007
Submission received: 26 May 2023 / Revised: 21 June 2023 / Accepted: 23 June 2023 / Published: 25 June 2023
(This article belongs to the Special Issue Recent Advances in Transition Metal Dichalcogenides (TMDCs) and Their Applications)
Browse Figures
Versions Notes

Abstract

:
The discovery of ferromagnetic two-dimensional (2D) materials provides reference value for the exploration of low-dimensional magnetism and new spintronic devices. The VSi2N4 monolayer is ferromagnetic with half-metallic characteristics, which is a new 2D material in the field of spintronics. Here, the electronic structure and magnetic anisotropy of two-dimensional VSi2X2N2 (X = P, As, Sb, Bi) Janus monolayers are studied systematically via first-principles calculations. The results show that VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 are magnetic, but VSi2Sb2N2 is nonmagnetic. At X = P, As and Bi, VSi2X2N2 Janus monolayers are metallic and ferromagnetic. VSi2P2N2 and VSi2As2N2 show the in-plane magnetic anisotropy, while VSi2Bi2N2 shows the perpendicular magnetic anisotropy (PMA). As the tensile strain increases, the spin-down energy band of the VSi2P2N2 monolayer gradually moves up and the spin-up channel moves down. At ε = +12%, the spin-down band shifts above the Fermi level, showing the half-metallic characteristic with a band gap of 0.775 eV calculated using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function. The magnetic moment of VSi2Sb2N2 is induced at an electric field of −0.4 V/Å and +0.2 V/Å, where PMA appears. These data provide basic theoretical guidance for the development of low-dimensional spintronic devices.

1. Introduction

The unique chemical and physical properties of two-dimensional (2D) materials have garnered significant attention [1,2], with new materials such as silicene, phosphorene and transition metal disulfides emerging following the successful preparation of graphene [3,4,5]. Two-dimensional materials have desirable properties as insulators, semiconductors, metals and superconducting materials [6,7,8]. These materials show great potential for advancement in a variety of fields, including energy harvesting and quantum sensing [9]. Due to their excellent transport capabilities and large power factor, 2D materials hold potential for a wide range of applications [10]. Among them, ferromagnetic semiconductors are easier to integrate into semiconductor devices [11]. The different doping densities can effectively control the magnetic behavior of 2D magnetic materials [12]. It has been confirmed that 122 kinds of stable 2D materials show nonmagnetic to ferromagnetic phase transition after hole-doping [12], which is of great significance for experimental exploration. The bending characteristics of the emerging 2D Xenes can make it a nanotechnology platform with various physical characteristics [13]. The strange quantum effect will appear when symmetry is broken in 2D Xenes, which makes spin manipulation and topological superconductivity possible [14].
In recent years, attention has turned toward a new derivative of 2D materials known as “Janus monolayers” [15,16]. The asymmetric mirror-image structure of Janus materials is the key to extending their electronic properties and discovering novel phenomena [3,17]. The Janus structure can induce an out-of-plane dipole moment on the surface of a material [18,19], which makes it easier to generate out-of-plane piezoelectricity in 2D Janus monolayers [20]. The polar structure of the Janus monolayer can show enhanced Rashba spin–orbit coupling, which has crucial implications for future spintronics [21,22,23]. Numerous Janus materials, including MoSSe, WSS, MoSTe, WSeTe, VSSe, PdSSe and SnSSe, have been reported [24]. First-principles calculations have shown that SnSSe has higher hole and electron mobility than SnS2 and SnSSe monolayers [3,25]. Density functional theory was used to thoroughly study the Janus MXY (M = Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W; X/Y = S, Se, Te) monolayers [26], revealing significant Rashba spin-splitting induced by the intrinsic out-of-plane built-in electric field in the WSeTe Janus monolayer [27]. These findings highlight the unique properties of 2D Janus structures and their potential significance for future research.
The family of 2D MA2Z4 (M = Mo, W, V, Nb, Ta, Ti, Zr, Hf or Cr; A = Si or Ge; Z = N, P or As) is a recent area of focus in 2D materials [28,29,30], with new properties that can be explored by modulating the M, A and Z elements [31]. Spintronic, piezoelectric and topological properties can be obtained by substituting M elements [30,32]. The first successfully manufactured 2D MA2Z4 material was MoSi2N4, which is stable in regard to air, water, acid and heat [33]. Density functional theory calculations have shown that twelve members of its family are thermodynamically stable [34]. Researchers have calculated that the 2D nitride VSi2N4 is half-metallic, with a Curie temperature above room temperature [33,35], which indicates its potential of energy storage applications. While previous studies on VSi2N4 have primarily focused on its electronic structure, magnetic properties and predictions for battery applications, there has been little research on the VSi2X2N2 Janus structure.
In this paper, N atoms in the first and third layers of VSi2N4 are replaced by X (X = P, As, Sb, Bi) atoms. The electronic structure and magnetic properties of the VSi2X2N2 (X = P, As, Sb, Bi) Janus monolayers were predicted using first-principles calculations. The 2D VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 monolayers are ferromagnetic (FM). Among them, VSi2P2N2 and VSi2As2N2 show in-plane magnetic anisotropy (IMA) and VSi2Bi2N2 shows perpendicular magnetic anisotropy (PMA). The influence of in-plane strain and electric fields on the magnetic VSi2X2N2 monolayers are also explored in this work. As the tensile stress increases, the spin-up band of VSi2P2N2 gradually shifts downwards and the spin-down band shifts upwards. At ε = +12%, VSi2P2N2 transforms from metallic to half-metallic. Additionally, VSi2Sb2N2 appears to be magnetic at electric fields of −0.4 V/Å and +0.2 V/Å. Our work reveals that VSi2X2N2 monolayers have rich electronic structures and magnetic properties, which make them promising candidates for spintronic devices.

2. Computational Details

In the Vienna ab initio simulation package, first-principles were used to calculate the lattice optimization and electronic structure using density function theory (DFT) [36,37]. DFT is based on quantum mechanics, which uses the electron density function to express the basic properties of the multi-electron system, and is a typical representation of combining computational simulation with experiment. The generalized gradient approximation (GGA) is obtained by introducing the gradient of electron density when considering the exchange correlation energy functional. The nonlocality of GGA is more favorable to deal with the heterogeneity of density. For the high-electron-density system where exchange correlation energy plays a leading role, GGA greatly optimizes the calculation results of atomic exchange correlation energy. In this paper, the GGA of the Perdew–Burke–Ernzerhof (PBE) exchange–correlation function is adopted [38,39,40]. The projector augmented wave (PAW) method was used to describe the ion–electron interactions [41]. To avoid the periodic interaction between surface atoms [42,43], the layer spacing of VSi2X2N2 monolayers along the z-direction was kept at 20 Å. For geometric optimization and self-consistent calculations, the plane wave cut-off energy value of 500 eV and a 12 × 12 × 1 k-mesh grid were used for sampling in the Monkhorst-Pack [44]. In structural relaxation, the convergence criteria of the energy difference and atomic forces were set to 0.01 eV/Å and 10−5 eV, respectively [38,41]. The molecular dynamics simulations were performed on a 3 × 3 × 1 supercell, setting its front-end thermostat to 300 K and a step size of 1 fs. The magnetic anisotropy energy was calculated by
MAE = E[100] − E[001]
where E[100] and E[001] denote the total energies with the in-plane magnetization direction and the out-of-plane magnetization direction [1,45,46]. The positive and negative values of MAE indicate PMA and IMA.

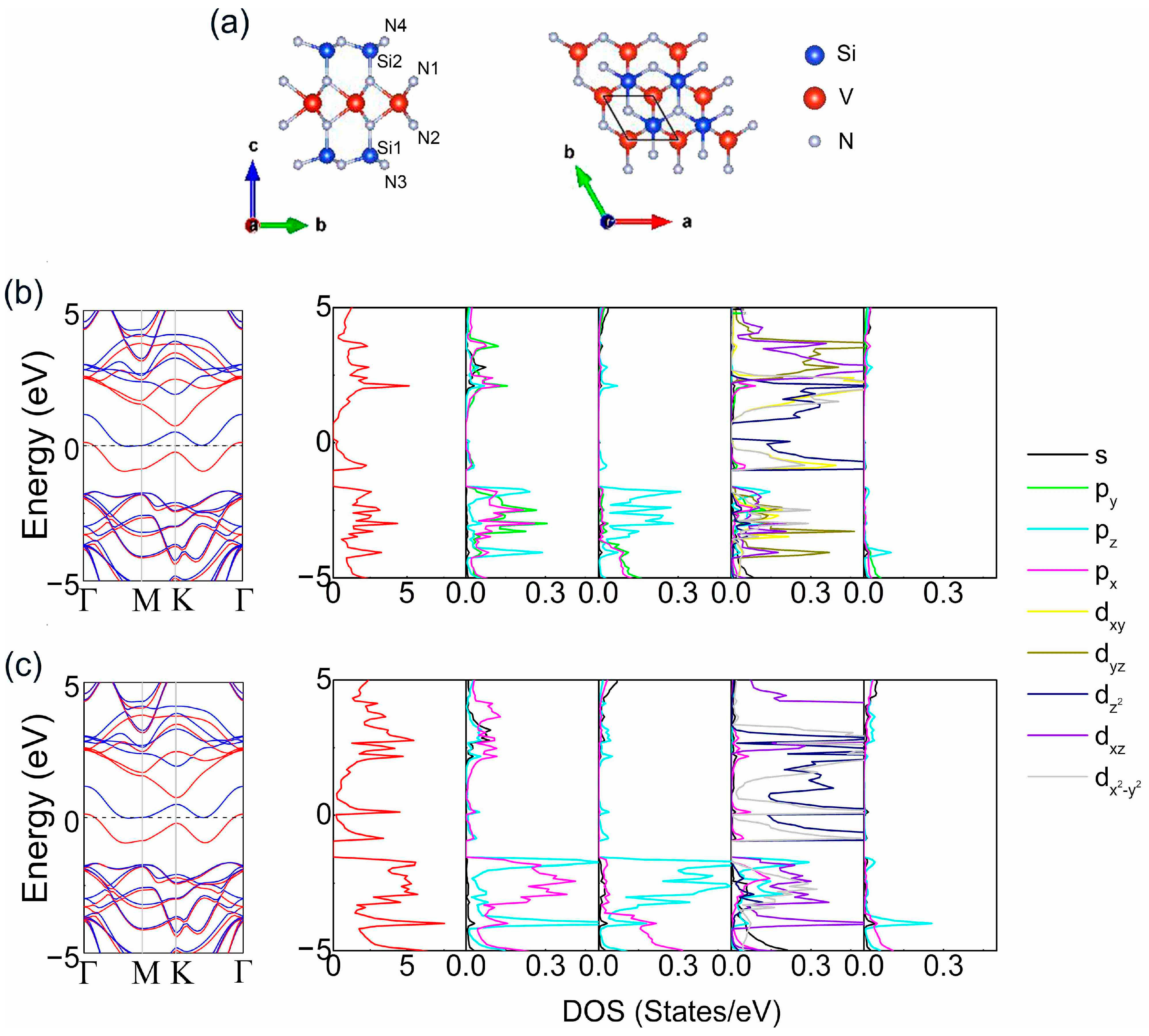
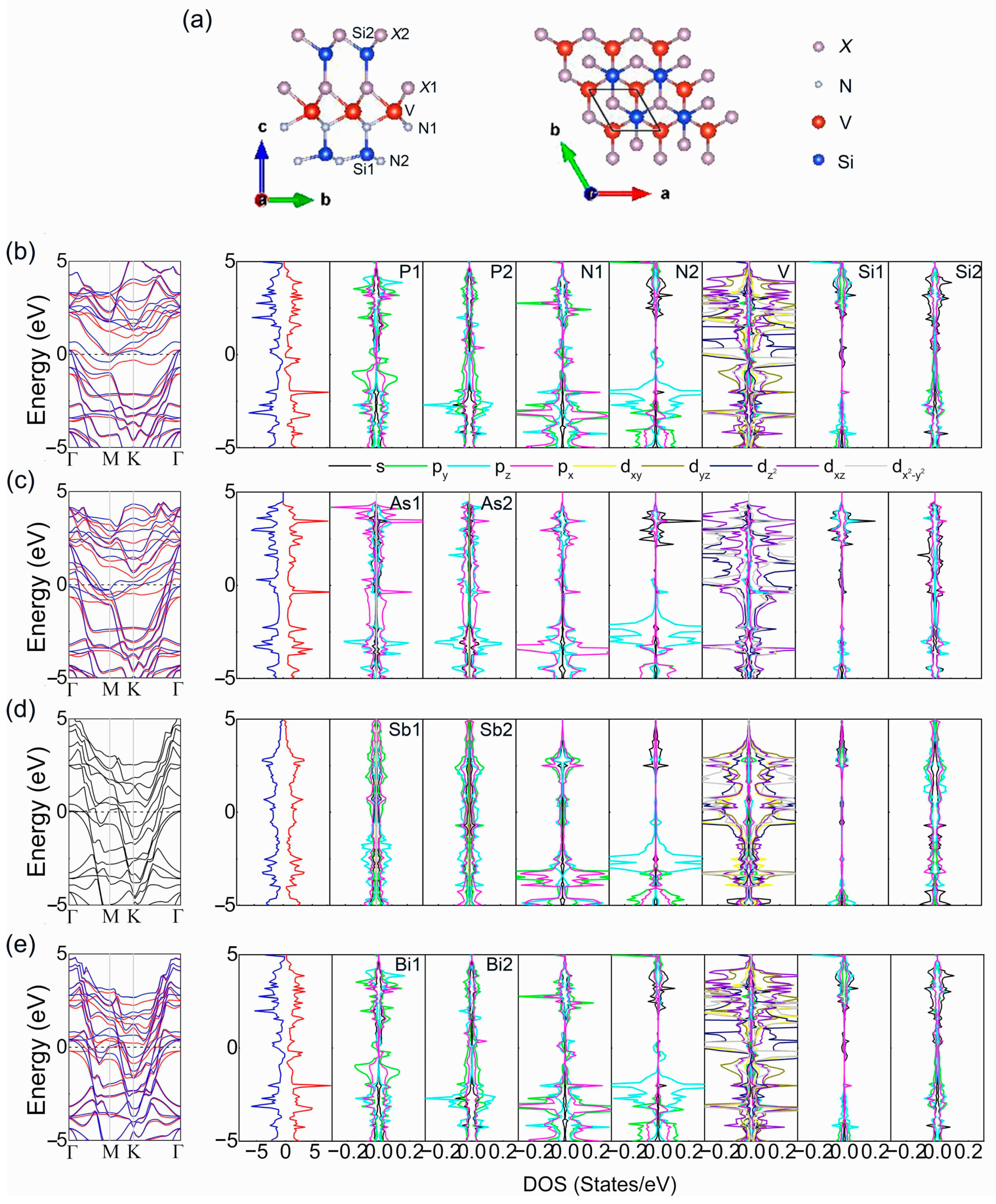
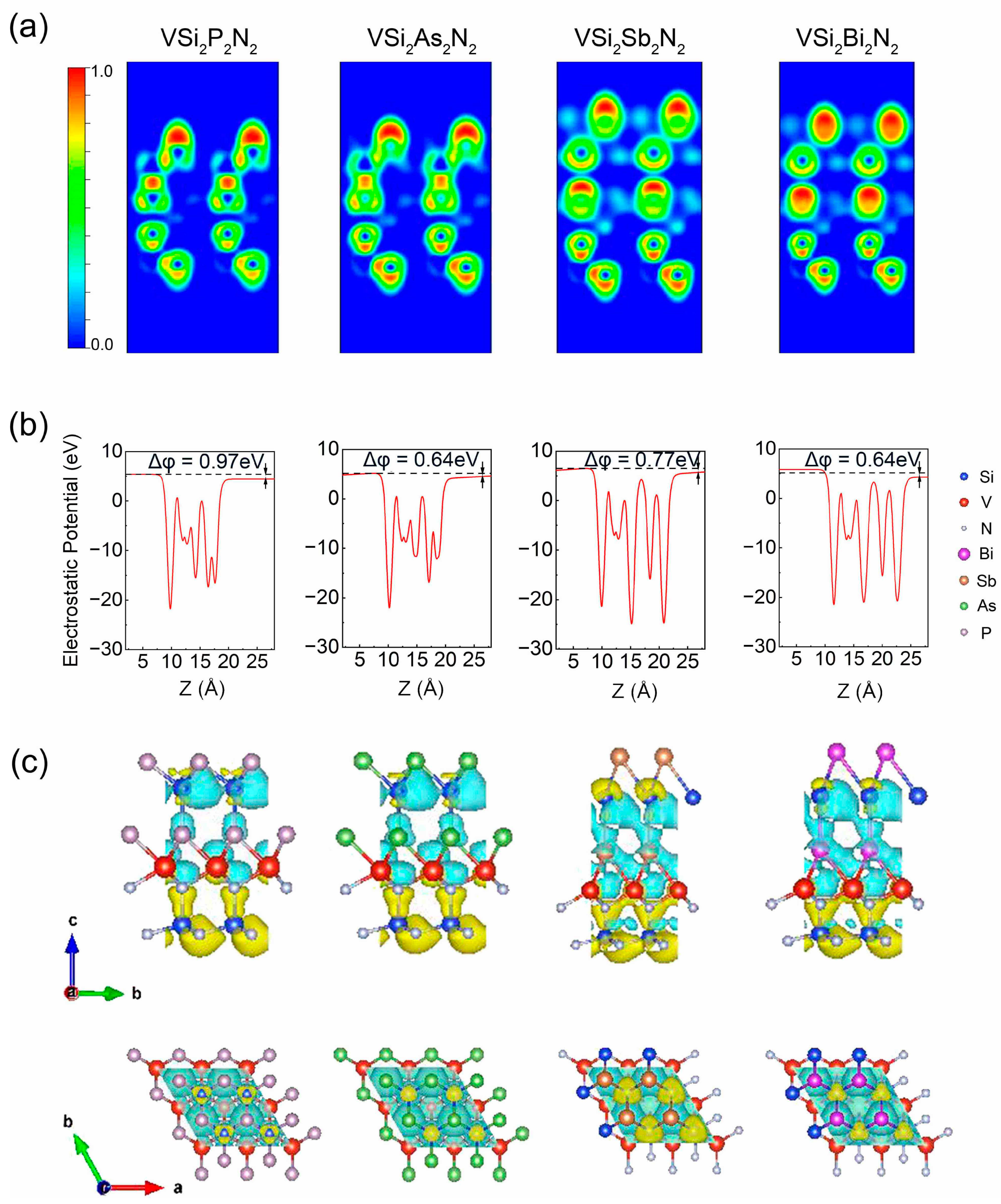
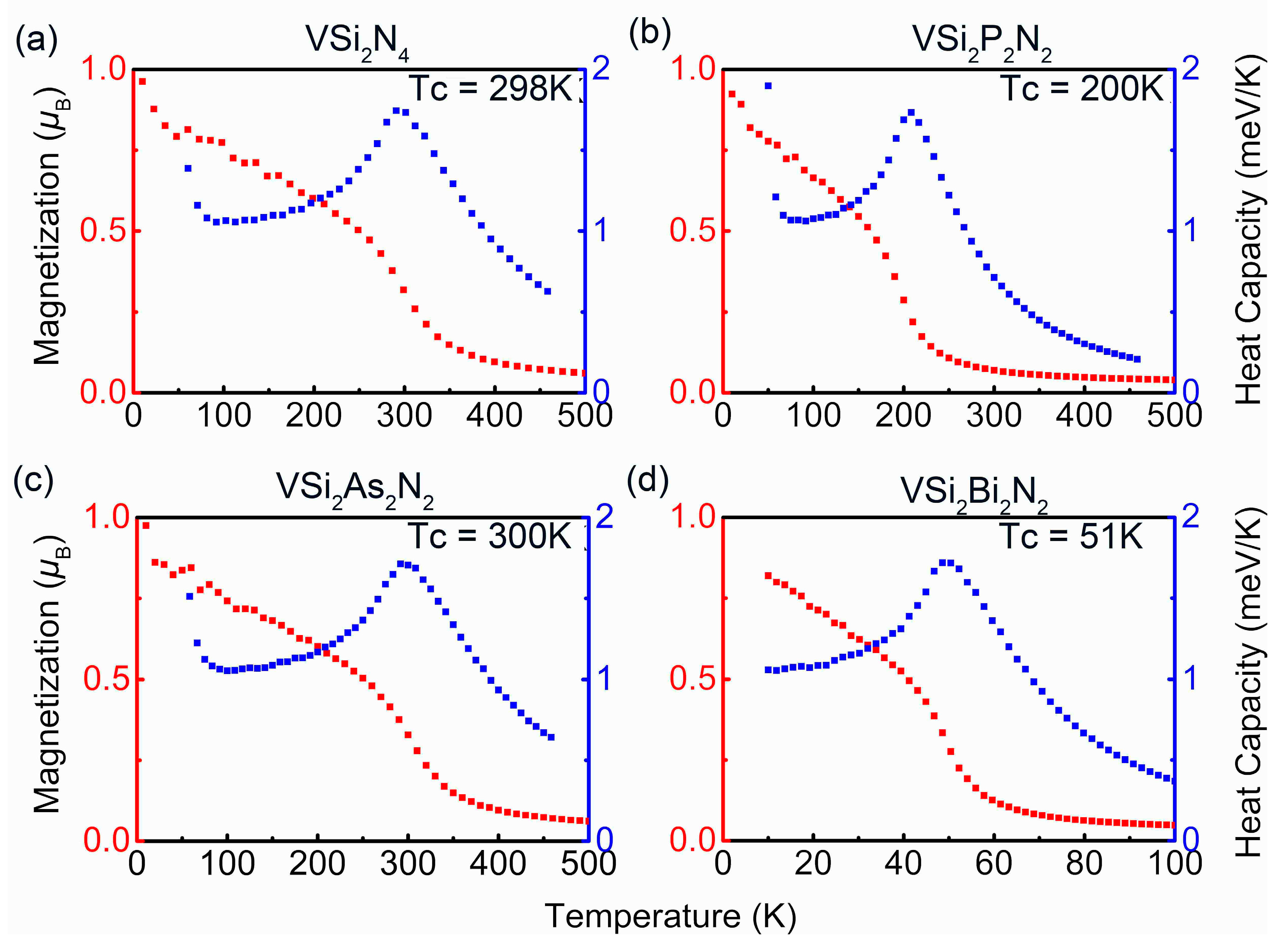
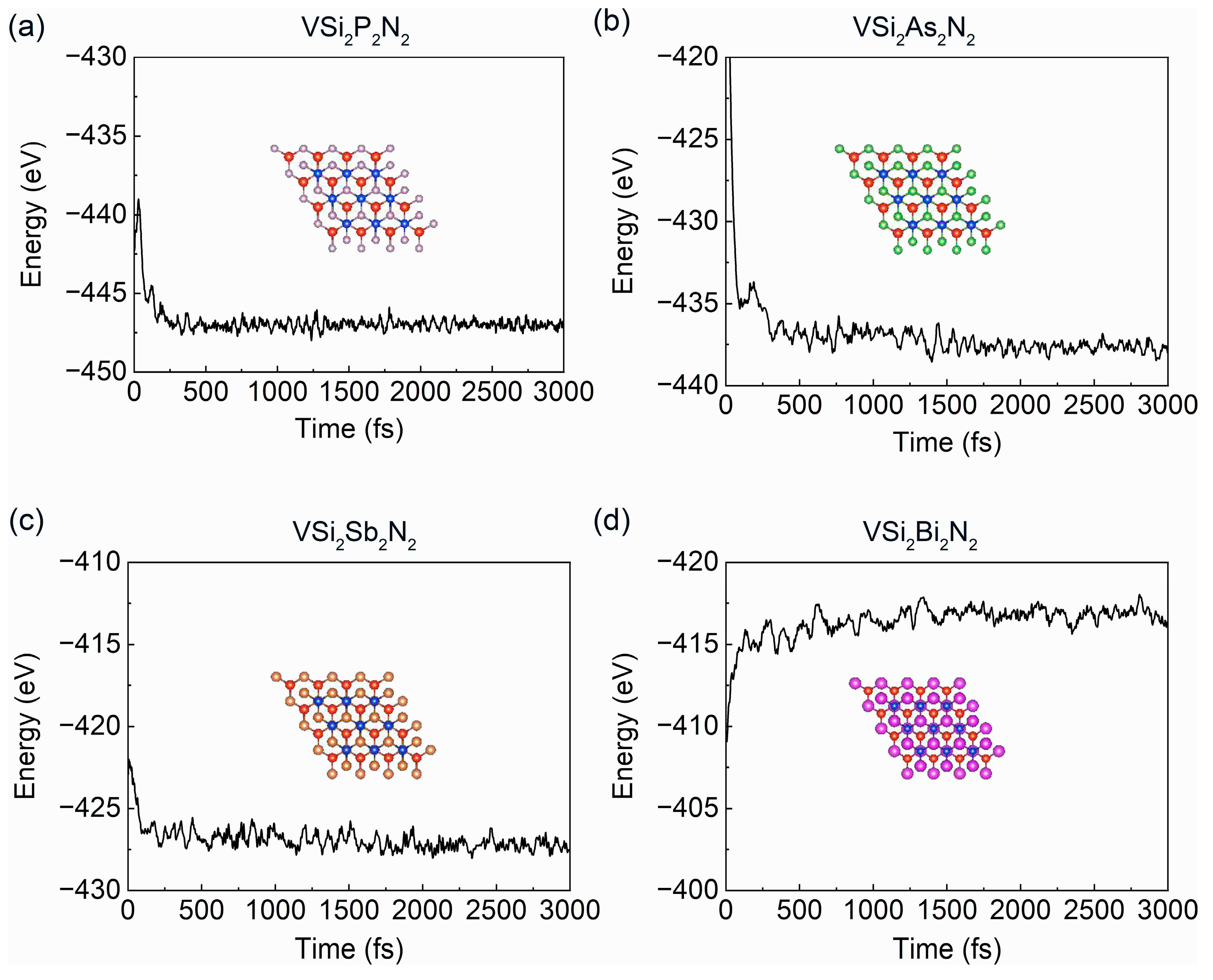
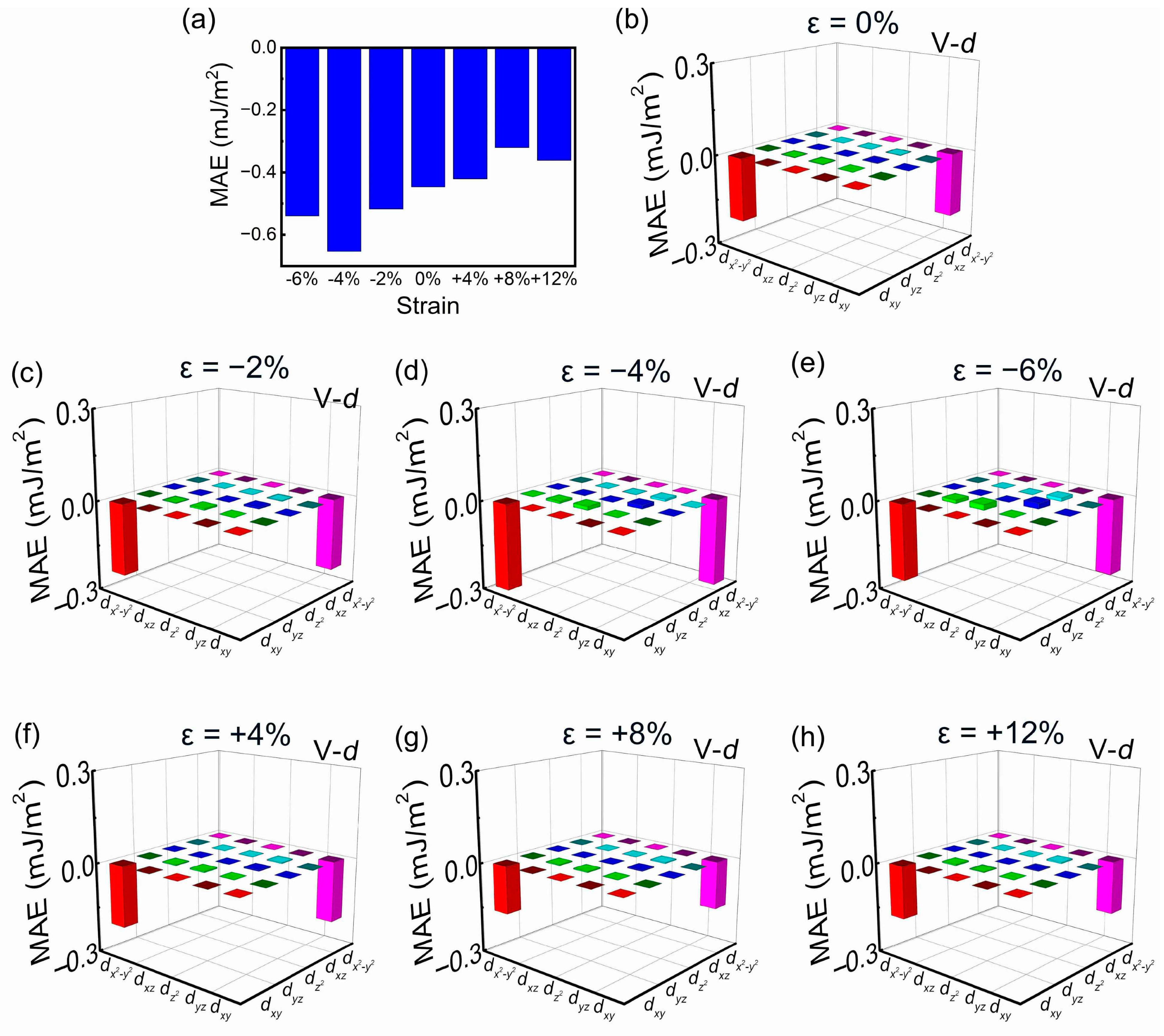
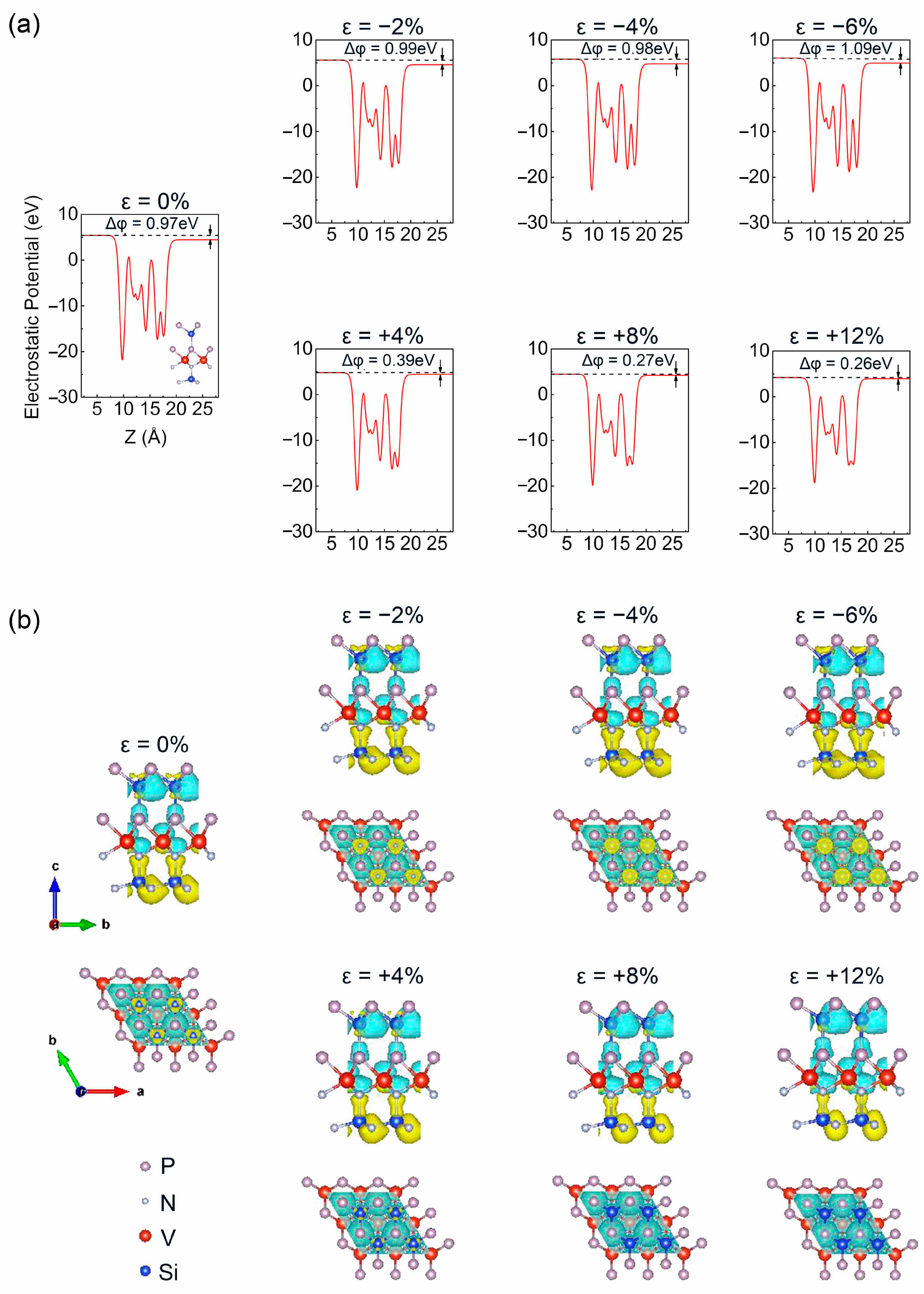
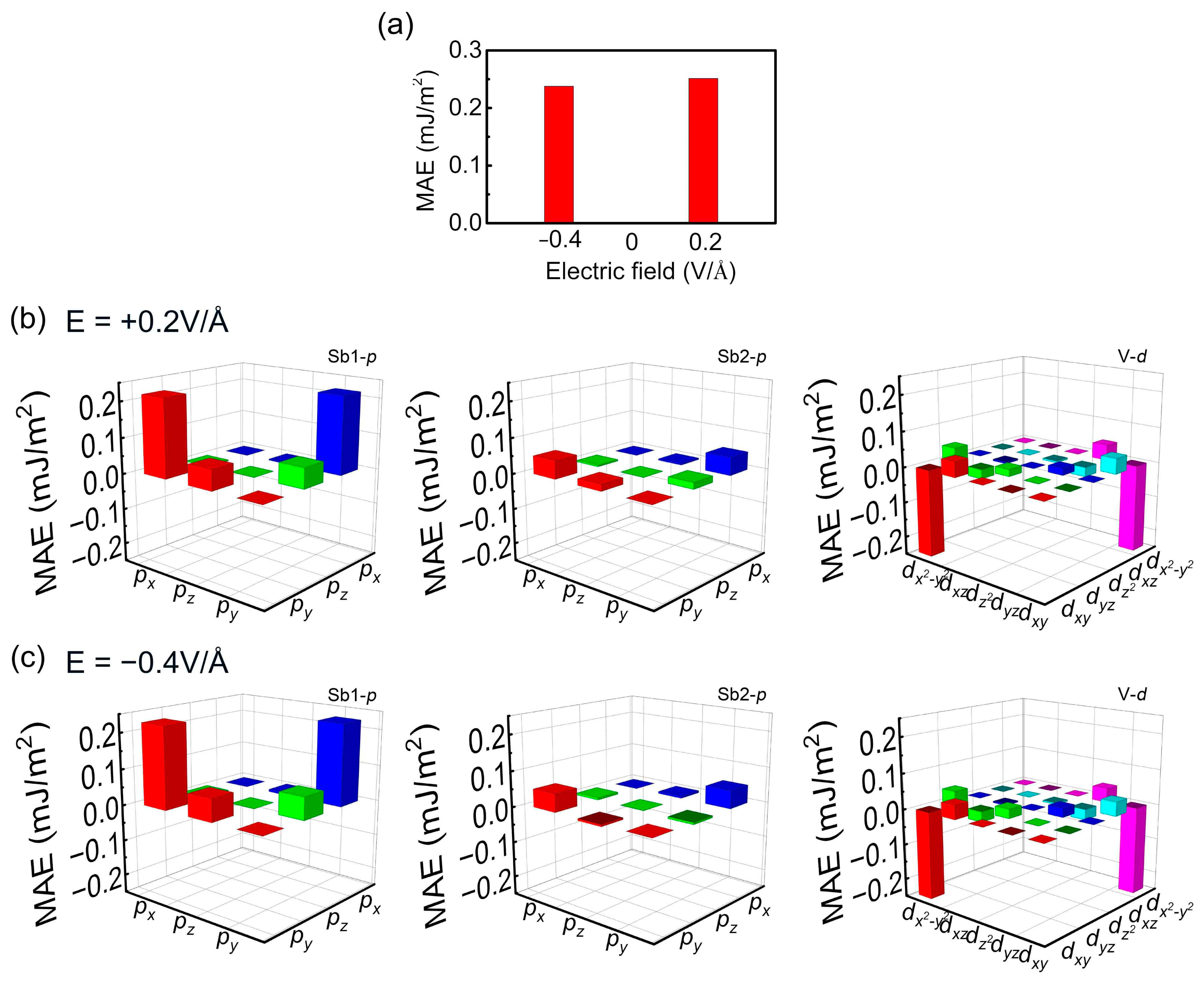
3. Results and Discussion

Figure 1 shows the structure of VSi2N4, which consists of seven layers of atoms. There are two bond lengths in VSi2N4, the V-N bond with a bond length of 2.022 Å, and that of the Si-N bond is 3.355 Å. After structural optimization, the lattice constant of VSi2N4 is a = b = 2.867 Å; this is similar to the previously reported VSi2N4 monolayer with a lattice constant of a = b = 2.842 Å [33]. In Figure 1b,c, the band structure and density of states (DOS) of VSi2N4 without SOC and with SOC are shown. The spin-up band of VSi2N4 is half-metallic while the spin-down band is semiconducting, indicating that VSi2N4 is half-metallic. The DOS of the VSi2N4 monolayer is shown in Figure 1b, where the orbital hybridization near the Fermi level is majorly affected by the d orbitals of the V atoms. By comparing Figure 1b,c, it is found that the SOC effect had no significant effect on the VSi2N4 monolayer.
Based on the structure of VSi2N4, the VSi2X2N2 (X = P, As, Sb, Bi) Janus structures were formed by replacing the N atoms in the upper two layers with elements of the same main group as the N atom. The side and top views of VSi2X2N2 are shown in Figure 2a. The band structures and density of states of VSi2P2N2, VSi2As2N2, VSi2Sb2N2 and VSi2Bi2N2 without SOC effects were calculated, respectively, as shown in Figure 2b,c. The results suggest that VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 are magnetic due to their asymmetric band structures of spin-up and spin-down channels. The magnetism of the monolayer comes from the unsaturated orbit of the transition metal V atom. There is spin splitting in the d orbit of the transition metal atoms, which is the decisive factor to produce magnetism. From the analysis of DOS, VSi2X2N2 is mainly contributed to by the d-orbitals of the V atom and the p-orbitals of the X atom near the Fermi level. Meanwhile, the influence of the SOC effect on VSi2X2N2 (X = P, As, Sb, Bi) was also compared in the calculations (Figure S1). SOC will affect the energy level and make it split. The band structures of VSi2Sb2N2 with SOC and without SOC were compared, and it was found that there was weak splitting in some positions. The magnetic moment of VSi2Sb2N2 was 0.0005μB without SOC, and when with SOC, its magnetic moment was 0.0165μB. Regardless of the influence of SOC, the weak magnetic moment of VSi2Sb2N2 can be ignored. According to the band structure and density of states plots, the SOC effect does not have a significant effect on VSi2X2N2. Therefore, the SOC effect was chosen to be ignored in the subsequent calculations. The lattice constants, magnetic moments and MAE of the optimized Janus VSi2X2N2 structures are listed in Table 1, showing increased lattice constants after replacing the N atomic layer with P, As, Sb and Bi. The VSi2P2N2 and VSi2As2N2 monolayers show IMA, which is consistent with the magnetic anisotropy of VSi2N4, while VSi2Bi2N2 shows PMA, which means that the replacement of the N atom by the Bi atom changed the magnetic anisotropy. The bond length and bond angle of VSi2X2N2 are analyzed in Table S1. Depending on the elements of the VA group, the bond length will increase or decrease accordingly. The bond length between N, P, As, Sb, Bi and V is 2.02 Å, 2.35 Å, 2.47 Å, 2.88 Å and 2.96 Å, respectively. It was discovered that the bond length increases as the atomic radius does. With the increase in the atomic radius of X, the angle between the bond lengths of X-V and V-N also increases. Tables S2–S5 list the optimized atomic coordinates of VSi2X2N2.
The band structures of the spin-up and spin-down channels of VSi2Sb2N2 overlap, which indicates that replacing the N atom with an Sb atom turns it into a nonmagnetic material. VASP provides different pseudopotential files for each element, and the standard pseudopotential of each element is used for calculation in this study. In order to explore whether different pseudopotentials will affect the results, sv and pv pseudopotentials were calculated, respectively. The magnetic moments of VSi2Sb2N2 are 0.0005, 0.0021 and 0.0021 μB when using a standard pseudopotential, sv pseudopotential and pv pseudopotential, and such small magnetic moments can be ignored; it was further verified that VSi2Sb2N2 is not magnetic.
With the purpose of determining the magnetic ground state of the VSi2X2N2 monolayers, a 2 × 2 × 1 supercell was used for calculation. The magnetic moment of the V atom was set to 3 μB. Spin-polarized calculations of the VSi2X2N2 were calculated using the FM, Néel antiferromagnetic, stripy antiferromagnetic and zigzag antiferromagnetic configurations, respectively. The ground state was determined to be FM or AFM based on the energy difference between the interlayer AFM and interlayer FM. When the energy difference is positive, the ground state is FM, and vice versa. The energy difference between the FM and AFM of the VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 magnetic materials are shown in Table 2. By calculating the exchange-related energy ΔE,
ΔE = EAFM − EFM
it was concluded that VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 are FM. The magnitude of the magnetization energy required to magnetize a ferromagnet is different along hard and easy magnetization directions. In order to analyze the MAE of VSi2X2N2 Janus structures, the resolved MAE of the p-orbitals of the P, As and Bi atoms and the d-orbitals of the V atom were calculated. Figure 3a shows the total MAE of VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 magnetic materials, which are −0.45, −0.53 and +3.06 mJ/m2. This means that VSi2P2N2 and VSi2As2N2 show IMA and VSi2Bi2N2 shows PMA. The negative MAE value of VSi2P2N2 mainly comes from the matrix element differences between the dx2−y2 and dxy orbitals and the dxy and dx2−y2 orbitals of the V atom. On the other hand, the positive contributions were provided by the matrix element differences between the pz and py and the py and pz orbitals of the As atom in VSi2As2N2. The matrix element differences between the dx2−y2 and dxy and the dxy and dx2−y2 orbitals of the V atom in VSi2As2N2 provide negative contributions. Since the negative contribution provided by the d-orbitals of the V atom is greater than the positive contribution provided by the p-orbitals of the As atom, the MAE of VSi2As2N2 is negative. As for VSi2Bi2N2, its IMA is attributed to the matrix element differences in the Bi-px and Bi-py orbitals and the V-dx2−y2 and V-dxy orbitals. In particular, the Bi1 atom exerts the largest positive contribution to the p-orbitals.
The types of interaction between the shared and unshared electrons can be distinguished by analyzing the electron density around the interaction point or interface [47]. Therefore, the behavior of the electron localization function in different shared electron interactions within the framework of density function theory was studied in the present work. The space charge distribution of the VSi2X2N2 monolayer is shown in Figure 4a, in which the slice is selected to be perpendicular to the 110 direction. In the VSi2P2N2 and VSi2As2N2 monolayers, the charge density between the P or As atoms in the first and third layers and the Si atoms in the second layer is higher. It shows that the P-Si bond and As-Si bond have a strong interaction. In contrast, the Si atoms in the third layer of the VSi2Sb2N2 and VSi2Bi2N2 monolayers formed separate electron locality. The charge density between X-Si decreases steadily with the increase in the X atomic radius, which suggests that the X-Si bonds eventually weaken. Differential charge density is one of the most critical techniques in the study of the electronic structure, which can be used to analyze the bonding of models after structural optimization. In this study, the electrostatic potential of the VSi2X2N2 monolayers were calculated, respectively (Figure 4b). There are different electronegativities between X and N atoms on either side of VSi2X2N2, which results in an asymmetric dipole distribution. The static potential differences in VSi2P2N2, VSi2As2N2, VSi2Sb2N2 and VSi2Bi2N2 are 0.97 eV, 0.64 eV, 0.77 eV and 1.55 eV, respectively. Figure 4c shows the differential charge density of the VSi2X2N2 monolayers, with the yellow part representing an increase in charge density and the green part representing a decrease in charge density. The charge transfer between the X, Si, V and N atoms was analyzed based on VSi2N4, as shown in Table S6. In Figure 4c, the loss in electrons was concentrated in the middle of the Si2 and the X1 atomic layers, while the accumulation of electrons was concentrated in the middle of the N1 and the Si1 atomic layers. As the radius of the X atom increases, the accumulation of charge in the Si2 layer gradually increases to 1.107 e, 2.2289 e, 2.9747 e and 3.035 e, while the loss in the X1 layer gradually decreases to −0.6343 e, −0.9446 e, −1.2663 e and −1.3339 e, respectively.
The Monte Carlo method is also referred to as a random sampling or statistical testing method. It can be utilized to simulate the Curie temperature (Tc) of magnetic materials using the Ising and Heisenberg models. The Tc of magnetic materials can be simulated using the Ising and Heisenberg models. In this work, the Tc of VSi2N4, VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 was estimated using the Heisenberg model. The Hamiltonian quantities of the Heisenberg model can be described as follows:
H = − J ∑ i < j S i → S j → − D ∑ i S i z 2
where J is the magnetic exchange coupling constant, S is the spin vector and D is the anisotropic energy parameter [48]. According to the heat capacity peak position and magnetic moment change curve analysis, the Tc of VSi2N4, VSi2P2N2, VSi2As2N2 and VSi2Bi2N2 was determined to be 298 K, 200 K, 300 K and 51 K, respectively (Figure 5). Figure 6 illustrates that the total energy of VSi2X2N2 fluctuated within a small range over a 3 ps simulation time, indicating that the VSi2X2N2 has good stability at room temperature and maintains its structural integrity. In addition, the phonon spectrum of VSi2X2N2 was calculated. The phonon spectrum without imaginary frequency reflects that the monolayer structure is dynamically stable (Figure S2).
This study further explored the effect of biaxial strain on electronic structure and the magnetic properties of VSi2P2N2. A range of strains from −6% to +12% was gradually applied to VSi2P2N2, resulting in the change in band structure (Figure S3). As the tensile strain increases, the spin-down channel of the VSi2P2N2 monolayer gradually shifts up, while the spin-up channel shifts down. At ε = +12%, the spin-down band shifts above the Fermi level, showing the half-metallic characteristic with a band gap of 0.775 eV. In Figure S4, the density of states of Vsi2P2N2 at ε = +12% shows that the CBM is located at the M point and the VBM is located at the Γ point. VSi2P2N2 is metal for the −2% to −6% strains. At ε = −4%, the band inversion of VSi2P2N2 was found. The electronic states for each atom of VSi2P2N2 under biaxial strain are shown in Figure S4a–g. The contribution to the total DOS mostly comes from hybridization between the p-orbitals of the P atom, the p-orbitals of the N atom and the d-orbitals of the V atom. As the tensile strains increase, the contribution of the pz and px orbitals of the N and P atoms increases, while that of the py orbitals decreases. The dz2 orbital contribution of the V atom gradually increases, while its dxy and dyz orbitals gradually decrease. The MAE of VSi2P2N2 also changed with the regulation of strain. Figure 7a shows the total MAE of the VSi2P2N2 monolayer under the strain from −6% to +12%, and the MAE shows IMA. At no modulation, the MAE of VSi2P2N2 was −0.53 mJ/m2. The MAE of VSi2P2N2 decreases under tensile strains, but is greater than ε = 0% under compressive strains. In Figure 7b–h, the IMA mainly comes from the matrix element differences between the dx2−y2 and dxy and the dxy and dx2−y2 orbitals of the V atom. The minimum value of IMA is −0.65 mJ/m2 at ε = −4%, while the maximum value of −0.32 mJ/m2 was achieved at ε = +8%. Figure S5 indicates that the matrix element differences between the px and py and the py and px orbitals of the P1 atom provide a minor negative contribution to the IMA. As the compressive strains increase (Figure S5b–d), the matrix element differences between the px and py and the py and px orbitals of the P1 atom of VSi2P2N2 also increase. In contrast, when VSi2P2N2 is at tensile strains (Figure S5e–g), the matrix element differences between the px and py and the py and px orbitals of the P1 atom decrease.
The electrostatic potential difference can be adjusted by the biaxial strain (Figure 8). In the absence of any modulation, the potential difference of VSi2P2N2 is Δφ = 0.97 eV. In Figure 8a, the electrostatic potential difference of VSi2P2N2 increases under the compressive strain. It reaches the maximum value at ε = −6%, where Δφ = +1.09 eV, while at the tensile strains from +2% to +12%, the electrostatic potential gradually decreases. When ε = +12%, the electrostatic potential is the minimum of Δφ = +0.26 eV. Figure 8b shows the distribution of the charge gain and loss of VSi2P2N2 under biaxial strains. It is obvious that the charge is transferred to the N and Si1 atoms while being lost at the P, Si2 and V atoms. The P2 atoms lose an increasing amount of charge as the tensile strain increases, while the P2 atoms in the topmost layer receive more charge with an increase in compressive strain.
Additionally, the effect of the electric field on the VSi2X2N2 monolayers was investigated, in which the VSi2Sb2N2 monolayer showed a considerable response. Figure S6a shows the band structure of VSi2Sb2N2 from a −0.6 V/Å to +0.6 V/Å electric field. It can be seen that the band structure of the spin-down channel shifts upward and the spin-up channel shifts downward at E = −0.4 V/Å and E = +0.2 V/Å, which induces the magnetic appearance of the VSi2Sb2N2 structure. The lattice constants and magnetic moment of VSi2X2 were compared with VSi2X2N2 (Table S7). The spin density distribution shows that the magnetism of VSi2Sb2N2 under the electric field mainly comes from the V atom. The external electric field affects the intensity of orbital hybridization, which leads to a change in the magnetic anisotropy of materials, and then produces the promotion of the magnetic moment. The orbital resolution MAE shows that the exchange between the p orbital of Sb and the d orbital of V has an important contribution to magnetism. The potential difference in VSi2Sb2N2 increases after electric field regulation, which means that the external electric field and the internal electric field cooperate. The bond length and bond angle of VSi2Sb2N2 under different electric fields were compared (Table S8). It was found that the bond length of V-Sb decreases and the bond length of V-N increases with the electric fields of −0.4 V/Å and +0.2 V/Å. At the same time, the bond angle of Sb-V-N was tested. Compared with other electric fields, the Sb-V-N bond angle decreases greatly under the modulation of the −0.4 V/Å and +0.2 V/Å electric fields. The intensity of the electric field affects the change in bond length and bond angle around magnetic atoms, which eventually leads to the change in the electronic structure. The analysis of the density of states reveals that the contribution of the py orbital of the Sb2 atom and the py and pz orbitals of the Si2 atom are enhanced at the −0.4 V/Å electric field. At E = +0.2 V/Å, the dxy orbital action of the V atom is strengthened, while the dx2−y2 orbital action is weakened (Figure S6b). The effect of the electric field on the differential charge density of VSi2Sb2N2 was analyzed in Figure S6c. At the electric fields of −0.4 V/Å and +0.2 V/Å, there is a significant accumulation of charge at the P2 atom, whereas the charge accumulation between the N2 and Si1 atoms decreases, and the charge loss around the P1 atom reduces. Figure 9 describes the total and orbital-resolved MAE of VSi2Sb2N2 at the electric field. The IMA characteristics were shown at the electric fields of −0.4 V/Å and +0.2 V/Å, with an MAE of 0.24 mJ/m2 and 0.25 mJ/m2, respectively. The matrix element differences between the px and py orbitals and the py and px orbitals of the Sb1 atom provide the main PMA contributions. The matrix element differences between the px and py and the py and px orbitals of the Sb2 atom, and the matrix element differences between the dx2−y2 and dyz, the dyz and dx2−y2, the dxz and dxy and the dxy and dxz orbitals of the V atom provide minor positive contributions.

4. Conclusions

The electronic structure and magnetic anisotropy of the VSi2X2N2 (X = P, As, Sb, Bi) Janus structures were predicted using first-principles calculations. At X = P, As and Bi, VSi2X2N2 Janus monolayers are ferromagnetic. The MAE of VSi2P2N2 and VSi2As2N2 shows IMA, which is the same as the VSi2N4 monolayer. However, VSi2Bi2N2 shows PMA. It is noteworthy that as the strain is applied to VSi2P2N2 from −6% to +12%, the band structure of the spin-down channel gradually shifts upwards, while that of the spin-up channel shifts downwards. At ε = +12%, it transforms to a half-metal with a band gap of 0.775 eV calculated using PBE. At this time, the CBM is located at the M point and the VBM is located at the Γ point. At ε = −4%, the band structure flip was found. Additionally, the band structure of the spin-down band moved upwards and the spin-up band moved downwards when the electric fields of −0.4 V/Å and +0.2 V/Å were applied to VSi2Sb2N2, which led to the magnetic characteristic appearing. The theoretical prediction of the 2D VSi2X2N2 Janus structure provides a direction for the experiment. This expands the application of 2D materials in electronic devices and shows a breakthrough in their use in information processing and storage.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/cryst13071007/s1: Figure S1: The band structure and density of states of (a) VSi2P2N2, (b) VSi2As2N2, (c) VSi2Sb2N2, (d) VSi2Bi2N2 with SOC. The Fermi level is set to zero; Figure S2: Phonon spectrum of the (a–d) VSi2X2N2 monolayer; Figure S3: The band structure of VSi2P2N2 under different biaxial strain. Red and blue lines in (a–g) represent the spin-up and spin-down band; Figure S4: The density of states of VSi2P2N2 under different biaxial strain; Figure S5: (a–g) Orbital-resolved MAE of P1-p orbitals in VSi2P2N2 at different in-plane biaxial strains; Figure S6: The band structure (a) and DOS (b) of VSi2Sb2N2 with different external electric field. The red and blue represent the spin-up and spin-down channels, respectively, (c) charge density difference of VSi2Sb2N2 with different external electric field; Table S1: The bond lengths and bond angles of VSi2X2N2 (X = N, P, As, Sb, Bi); Table S2: Atomic coordinates of the optimized structure of VSi2P2N2 monolayer; Table S3: Atomic coordinates of the optimized structure of VSi2As2N2 monolayer; Table S4: Atomic coordinates of the optimized structure of VSi2Sb2N2 monolayer; Table S5: Atomic coordinates of the optimized structure of VSi2Bi2N2 monolayer; Table S6: The charge transfer of each atom of VSi2X2N2 monolayer; Table S7: The lattice constants (a = b), magnetic moment (M) and MAE of VSi2X2 (X = P, As, Sb, Bi); Table S8: The bond lengths (Å) and bond angle (°) of VSi2Sb2N2 under different electric field.

Author Contributions

Conceptualization, Z.Z.; methodology, Z.Z.; software, Z.Z.; validation, Z.Z.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z., X.W. and W.M.; visualization, Z.Z.; supervision, X.W. and W.M.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Luo, M.; Li, Y.D.; Wang, K.J.; Shen, Y.H. Adsorption induced magnetic anisotropy in the two-dimensional magnet CrCl3. Solid State Commun. 2020, 321, 114048. [Google Scholar] [CrossRef]
  2. Zhang, W.; Hao, G.; Zhang, R.; Xu, J.; Ye, X.; Li, H. Effects of vertical strain and electrical field on electronic properties and Schottky contact of graphene/MoSe2 heterojunction. J. Phys. Chem. Solids 2021, 157, 110189. [Google Scholar] [CrossRef]
  3. Marjaoui, A.; Tamerd, M.A.; El Kasmi, A.; Diani, M.; Zanouni, M. First-principles calculations to investigate structural, electronic and optical properties of Janus AsMC3 (M: Sb, Bi) monolayers for optoelectronic applications. Solid State Commun. 2022, 343, 114667. [Google Scholar] [CrossRef]
  4. Li, F.; Yang, D.; Qiao, L.; Eglitis, R.I.; Jia, R.; Yi, Z.; Zhang, H. Novel 2D boron nitride with optimal direct band gap: A theoretical prediction. Appl. Surf. Sci. 2022, 578, 151929. [Google Scholar] [CrossRef]
  5. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [Green Version]
  6. Bafekry, A.; Faraji, M.; Fadlallah, M.M.; Bagheri Khatibani, A.; Abdolahzadeh Ziabari, A.; Ghergherehchi, M.; Nedaei, S.; Shayesteh, S.F.; Gogova, D. Tunable electronic and magnetic properties of MoSi2N4 monolayer via vacancy defects, atomic adsorption and atomic doping. Appl. Surf. Sci. 2021, 559, 149862. [Google Scholar] [CrossRef]
  7. Zhang, C.; Ji, W.; Li, S.; Li, P.; Zhang, C.; Wang, P. 2D ternary nitrides XNY (X =Ti, Zr, Hf; Y = F, Cl, Br) with applications as photoelectric and photocatalytic materials featuring mechanical and optical anisotropy: A DFT study. Solid State Chem. 2021, 303, 122517. [Google Scholar] [CrossRef]
  8. Srivastava, M.; Srivastava, A.; Pandey, S. Suitability of graphene monolayer as sensor for carcinogenic heavy metals in water: A DFT investigation. Appl. Surf. Sci. 2020, 517, 146021. [Google Scholar] [CrossRef]
  9. Sun, Q.; Li, J.; Yang, Z.; Wu, R. Cr2NX2 MXene (X = O, F, OH): A 2D ferromagnetic half-metal. Appl. Phys. Lett. 2021, 119, 062404. [Google Scholar] [CrossRef]
  10. Kanahashi, K.; Pu, J.; Takenobu, T. 2D Materials for large-area flexible thermoelectric devices. Adv. Energy Mater. 2020, 10, 1902842. [Google Scholar] [CrossRef]
  11. Wolf, S.A.; Awschalom, D.D.; Buhrman, R.A.; Daughton, J.M.; von Molnar, S.; Roukes, M.L.; Chtchelkanova, A.Y.; Treger, D.M. Spintronics: A spin-based electronics vision for the future. Science 2001, 294, 1488–1495. [Google Scholar] [CrossRef] [Green Version]
  12. Meng, R.S.; Pereira, L.D.C.; Locquet, J.P.; Afananev, V.; Pourtois, G.; Houssa, M. Hole-doping induced ferromagnetism in 2D materials. NPJ Comput. Mater. 2022, 8, 230. [Google Scholar] [CrossRef]
  13. Molle, A.; Goldberger, J.; Houssa, M.; Xu, Y.; Zhang, S.C.; Akinwande, D. Buckled two-dimensional Xene sheets. Nat. Mater. 2017, 16, 163–169. [Google Scholar] [CrossRef]
  14. Wang, J.; Xu, Y.; Zhang, S.C. Two-dimensional time-reversal-invariant topological superconductivity in a doped quantum spin-Hall insulator. Phys. Rev. B 2014, 90, 054503. [Google Scholar] [CrossRef] [Green Version]
  15. Qi, S.; Jiang, J.; Wang, X.; Mi, W. Valley polarization, magnetic anisotropy and Dzyaloshinskii-Moriya interaction of two-dimensional graphene/Janus 2H-VSeX (X = S, Te) heterostructures. Carbon 2021, 174, 540–555. [Google Scholar] [CrossRef]
  16. Chauhan, P.; Singh, J.; Kumar, A. Mechanical, optical and thermoelectric properties of Janus BiTeCl monolayer. J. Phys. Chem. Solids 2022, 167, 110758. [Google Scholar] [CrossRef]
  17. Ji, Y.; Yang, M.; Lin, H.; Hou, T.; Wang, L.; Li, Y.; Lee, S.T. Janus structures of transition metal dichalcogenides as the heterojunction photocatalysts for water splitting. J. Phys. Chem. C 2018, 122, 3123–3129. [Google Scholar] [CrossRef]
  18. Bao, J.; Qiu, J.; Liu, X. Large in-plane piezoelectricity of Janus Bi2X2Y (X = S, Se, Te; Y = S, Se, Te; X≠Y) monolayers with polyatomic thickness. Mater. Lett. 2021, 296, 129878. [Google Scholar] [CrossRef]
  19. Zhang, J.; Jia, S.; Kholmanov, I.; Dong, L.; Er, D.; Chen, W.; Guo, H.; Jin, Z.; Shenoy, V.B.; Shi, L.; et al. Janus monolayer transition-metal dichalcogenides. ACS Nano 2017, 11, 8192–8198. [Google Scholar] [CrossRef] [Green Version]
  20. Wang, L.; Lin, Z.; Du, Y.; Qiu, J.; Chen, X.; Yu, J. The piezoelectricity of 2D Janus ZnBrI: Multiscale prediction. Chem. Phys. Lett. 2022, 794, 139506. [Google Scholar] [CrossRef]
  21. Ma, X.; Tian, Y.; Zhao, P.; Wu, X.; Jing, T.; Zhang, J. Janus MoCrSSe monolayer: A strong two-dimensional polar antiferromagnet. Appl. Surf. Sci. 2022, 581, 152420. [Google Scholar] [CrossRef]
  22. Manchon, A.; Koo, H.C.; Nitta, J.; Frolov, S.M.; Duine, R.A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 2015, 14, 871–882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Zhou, W.; Chen, J.; Zhang, B.; Duan, H.; Ouyang, F. Manipulation of the Rashba spin-orbit coupling of a distorted 1T-Phase Janus WSSe monolayer: Dominant role of charge transfer and orbital components. Phys. Rev. B 2021, 103, 195114. [Google Scholar] [CrossRef]
  24. Sengupta, A. First principles design of 2 dimensional Nickel dichalcogenide Janus materials NiXY (X,Y = S, Se, Te). Comp. Mater. Sci. 2022, 206, 111278. [Google Scholar] [CrossRef]
  25. Guo, S.; Guo, X.; Han, R.; Deng, Y. Predicted Janus SnSSe monolayer: A comprehensive first-principles study. Phys. Chem. Chem. Phys. 2019, 21, 24620–24628. [Google Scholar] [CrossRef] [Green Version]
  26. Shi, W.; Wang, Z. Mechanical and electronic properties of Janus monolayer transition metal dichalcogenides. J. Phys. Condens. Matter 2018, 30, 215301. [Google Scholar] [CrossRef]
  27. Cheng, Y.; Zhu, Z.; Tahir, M.; Schwingenschlögl, U. Spin-orbit–induced spin splittings in polar transition metal dichalcogenide monolayers. Europhys. Lett. 2013, 102, 57001. [Google Scholar] [CrossRef]
  28. Novoselov, K.S. Discovery of 2D Van Der Waals layered MoSi2N4 family. Natl. Sci. Rev. 2020, 7, 1842–1844. [Google Scholar] [CrossRef]
  29. Cui, Z.; Luo, Y.; Yu, J.; Xu, Y. Tuning the electronic properties of MoSi2N4 by molecular doping: A first principles investigation. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 134, 114873. [Google Scholar] [CrossRef]
  30. Hong, Y.; Liu, Z.; Wang, L.; Zhou, T.; MA, W.; Xu, C.; Feng, S.; Chen, L.; Chen, M.; Sun, D.; et al. Chemical vapor deposition of layered two-dimensional MoSi2N4 materials. Science 2020, 369, 670–674. [Google Scholar] [CrossRef]
  31. Yang, J.S.; Zhao, L.; Li, S.Q.; Liu, H.; Wang, L.; Chen, M.; Gao, J.; Zhao, J. Accurate electronic properties and non-linear optical response of two-dimensional MA2Z4. Nanoscale 2021, 13, 5479–5488. [Google Scholar] [CrossRef]
  32. Yang, C.; Song, Z.; Sun, X.; Lu, J. Valley pseudospin in monolayer MoSi2N4 and MoSi2As4. Phys. Rev. B 2021, 103, 035308. [Google Scholar] [CrossRef]
  33. Wang, Z.; Zhang, G.; Wang, Y.; Huang, C.; Liu, Y.; Ouyang, C.; Hu, J. Heavy 2D VSi2N4: High capacity and full battery open-circuit voltage as Li/Na-ion batteries anode. Appl. Surf. Sci. 2022, 593, 153354. [Google Scholar] [CrossRef]
  34. Mortazavi, B.; Javvaji, B.; Shojaei, F.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi2N4 family confirmed by first-principles. Nano Energy 2021, 82, 105716. [Google Scholar] [CrossRef]
  35. Akanda, M.R.K.; Lake, R.K. Magnetic properties of NbSi2N4, VSi2N4, and VSi2P4 monolayers. Appl. Phys. Lett. 2021, 119, 052402. [Google Scholar] [CrossRef]
  36. Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115. [Google Scholar] [CrossRef] [PubMed]
  37. Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal- amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
  38. Perdew, J.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
  39. Grimme, S.; Semiempirical, J. GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
  40. Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef]
  41. Blöchl, P. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  42. Fu, L.Q.; Wang, X.C.; Mi, W.B. Spin-dependent electronic structure and magnetic properties of 2D Janus Mn2CFCl/CuBiP2Se6 van der Waals multiferroic heterostructures. Adv. Theor. Simul. 2021, 4, 2100302. [Google Scholar] [CrossRef]
  43. Hu, J.; Ouyang, C.; Yang, S.A.; Yang, H.Y. Germagraphene as a promising anode material for lithium-ion batteries predicted from first-principles calculations. Nanoscale Horiz. 2019, 4, 457–463. [Google Scholar] [CrossRef] [Green Version]
  44. Chadi, D.J. Special points for Brillouin-zone integrations. Phys. Rev. B 1977, 16, 1746–1747. [Google Scholar] [CrossRef]
  45. Daalderop, G.H.O.; Kelly, P.J.; Schuurmsans, M.F.H. First-principles calculation of the magnetocrystalline anisotropy energy of iron, cobalt, and nickel. Phys. Rev. B 1990, 41, 11919. [Google Scholar] [CrossRef]
  46. Gao, Y.Q.; Zhou, B.Z.; Wang, X.C. Biaxial strain, electric field and interlayer distance-tailored electronic structure and magnetic properties of two-dimensional g-C3N4/Li-adsorbed Cr2Ge2Te6 van der Waals heterostructures. Phys. Chem. Chem. Phys. 2021, 23, 6171–6181. [Google Scholar] [CrossRef]
  47. Koumpouras, K.; Larsson, J.A. Distinguishing between chemical bonding and physical binding using electron localization function (ELF). J. Phys. Condens. Matter 2020, 32, 315502. [Google Scholar] [CrossRef]
  48. Li, S.; Zhou, M.; Wang, X.; Zheng, F.; Shao, X.; Zhang, P. Two-dimensional uranium halide monolayers UX3 (X = Cl, Br) with high Curie temperatures. Phys. Lett. A 2021, 394, 127078. [Google Scholar] [CrossRef]
Crystals 13 01007 g001 550
Figure 1. (a) Side and top views of VSi2N4. Band structure and DOS of VSi2N4 (b) without SOC and (c) with SOC. The Fermi level was set to zero.
Figure 1. (a) Side and top views of VSi2N4. Band structure and DOS of VSi2N4 (b) without SOC and (c) with SOC. The Fermi level was set to zero.
Crystals 13 01007 g001
Crystals 13 01007 g002 550
Figure 2. (a) Side and top views of VSi2X2N2 (X = P, As, Sb, Bi) monolayers. The band structure and DOS of (b) VSi2P2N2, (c) VSi2As2N2, (d) VSi2Sb2N2 and (e) VSi2Bi2N2 without SOC. The Fermi level was set to zero.
Figure 2. (a) Side and top views of VSi2X2N2 (X = P, As, Sb, Bi) monolayers. The band structure and DOS of (b) VSi2P2N2, (c) VSi2As2N2, (d) VSi2Sb2N2 and (e) VSi2Bi2N2 without SOC. The Fermi level was set to zero.
Crystals 13 01007 g002
Crystals 13 01007 g003 550
Figure 3. (a) Total MAE of VSi2P2N2, VSi2As2N2 and VSi2Bi2N2. Orbital-resolved MAE of (b) P1-p, (c) P2-p and (d) V-d orbitals in VSi2P2N2, (e) As1-p and (f) As2-p, and (g) V-d orbitals in VSi2As2N2, (h) Bi1-p, (i) Bi2-p and (j) V-d orbitals in VSi2Bi2N2.
Figure 3. (a) Total MAE of VSi2P2N2, VSi2As2N2 and VSi2Bi2N2. Orbital-resolved MAE of (b) P1-p, (c) P2-p and (d) V-d orbitals in VSi2P2N2, (e) As1-p and (f) As2-p, and (g) V-d orbitals in VSi2As2N2, (h) Bi1-p, (i) Bi2-p and (j) V-d orbitals in VSi2Bi2N2.
Crystals 13 01007 g003
Crystals 13 01007 g004 550
Figure 4. (a) Side and top views of the 2D ELF of VSi2X2N2. (b) The planar average of electrostatic potential for VSi2X2N2. (c) The charge density difference in VSi2P2N2, VSi2As2N2, VSi2Sb2N2 and VSi2Bi2N2. The isosurface value was set as 0.03 e/Å3.
Figure 4. (a) Side and top views of the 2D ELF of VSi2X2N2. (b) The planar average of electrostatic potential for VSi2X2N2. (c) The charge density difference in VSi2P2N2, VSi2As2N2, VSi2Sb2N2 and VSi2Bi2N2. The isosurface value was set as 0.03 e/Å3.
Crystals 13 01007 g004
Crystals 13 01007 g005 550
Figure 5. Magnetization (red) and heat capacity (blue) of (a) VSi2N4, (b) VSi2P2N2, (c) VSi2As2N2 and (d) VSi2Bi2N2 as a function of temperature.
Figure 5. Magnetization (red) and heat capacity (blue) of (a) VSi2N4, (b) VSi2P2N2, (c) VSi2As2N2 and (d) VSi2Bi2N2 as a function of temperature.
Crystals 13 01007 g005
Crystals 13 01007 g006 550
Figure 6. Simulation of potential energy fluctuations in (a–d) VSi2X2N2 (X = N, P, As, Sb, Bi) after 3 ps.
Figure 6. Simulation of potential energy fluctuations in (a–d) VSi2X2N2 (X = N, P, As, Sb, Bi) after 3 ps.
Crystals 13 01007 g006
Crystals 13 01007 g007 550
Figure 7. (a) The dependence of MAE in VSi2P2N2 at different strains. Orbital-resolved MAE of V-d orbitals in VSi2P2N2 at (b–h) 0%, −2%, −4%, −6%, +4%, +8% and +12% strains.
Figure 7. (a) The dependence of MAE in VSi2P2N2 at different strains. Orbital-resolved MAE of V-d orbitals in VSi2P2N2 at (b–h) 0%, −2%, −4%, −6%, +4%, +8% and +12% strains.
Crystals 13 01007 g007
Crystals 13 01007 g008 550
Figure 8. (a) The planar average of electrostatic potential of VSi2P2N2 from −6% to +12% strains. (b) Charge density difference in VSi2P2N2 at different strains, where yellow and blue regions represent the charge gain and loss.
Figure 8. (a) The planar average of electrostatic potential of VSi2P2N2 from −6% to +12% strains. (b) Charge density difference in VSi2P2N2 at different strains, where yellow and blue regions represent the charge gain and loss.
Crystals 13 01007 g008
Crystals 13 01007 g009 550
Figure 9. Magnetic anisotropy under different external electric fields of VSi2Sb2N2. (a) Total magnetic anisotropy. Magnetic anisotropy of Sb1, Sb2 and V atoms (b) with E = +0.2 V/Å and (c) E = −0.4 V/Å, respectively.
Figure 9. Magnetic anisotropy under different external electric fields of VSi2Sb2N2. (a) Total magnetic anisotropy. Magnetic anisotropy of Sb1, Sb2 and V atoms (b) with E = +0.2 V/Å and (c) E = −0.4 V/Å, respectively.
Crystals 13 01007 g009
Table
Table 1. The lattice constants (a = b), magnetic moment (M) and MAE of VSi2X2N2.
Table 1. The lattice constants (a = b), magnetic moment (M) and MAE of VSi2X2N2.
a = b (Å)M (μB)MAE
VSi2N42.870.91IMA
VSi2P2N23.090.68IMA
VSi2As2N23.080.97IMA
VSi2Sb2N23.01//
VSi2Bi2N23.080.59PMA
Table
Table 2. The energy difference between diverse magnetic configurations and the FM of VSi2X2N2 (X = P, As, Sb, Bi).
Table 2. The energy difference between diverse magnetic configurations and the FM of VSi2X2N2 (X = P, As, Sb, Bi).
ΔEFM (eV)ΔENéel-AFM (eV)ΔEstripy-AFM (eV)ΔEzigzag-AFM (eV)Magnetic Ground State
VSi2P2N200.1240.1240.124FM
VSi2As2N200.1910.1910.191FM
VSi2Sb2N2/////
VSi2Bi2N200.0310.0250.030FM
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhao, Z.; Wang, X.; Mi, W. Two-Dimensional VSi2X2N2 (X = P, As, Sb, Bi) Janus Monolayers: Spin-Polarized Electronic Structure and Perpendicular Magnetic Anisotropy. Crystals 2023, 13, 1007. https://doi.org/10.3390/cryst13071007

AMA Style

Zhao Z, Wang X, Mi W. Two-Dimensional VSi2X2N2 (X = P, As, Sb, Bi) Janus Monolayers: Spin-Polarized Electronic Structure and Perpendicular Magnetic Anisotropy. Crystals. 2023; 13(7):1007. https://doi.org/10.3390/cryst13071007

Chicago/Turabian Style

Zhao, Zhenxian, Xiaocha Wang, and Wenbo Mi. 2023. "Two-Dimensional VSi2X2N2 (X = P, As, Sb, Bi) Janus Monolayers: Spin-Polarized Electronic Structure and Perpendicular Magnetic Anisotropy" Crystals 13, no. 7: 1007. https://doi.org/10.3390/cryst13071007

APA Style

Zhao, Z., Wang, X., & Mi, W. (2023). Two-Dimensional VSi2X2N2 (X = P, As, Sb, Bi) Janus Monolayers: Spin-Polarized Electronic Structure and Perpendicular Magnetic Anisotropy. Crystals, 13(7), 1007. https://doi.org/10.3390/cryst13071007

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop