Density Functional Theory Study of Electronic Structure and Optical Properties of Ln³⁺-Doped γ-Bi₂MoO₆ (Ln=Gd, Ho, Yb)

Abstract

Based on density functional theory (DFT), theoretical models of three kinds of lanthanide rare earth metal ion-doped γ-Bi₂MoO₆ were constructed (Ln-BMO (Ln=Gd, Ho, Yb)). The geometric structure, electronic structure, and optical properties of the model were calculated, and the influence of doped Ln³⁺ ions on the structures and properties of the system was analyzed. The results revealed that the substitution of smaller ionic radius Ln³⁺ ions for Bi³⁺ ions caused a contraction of the lattice parameters. At the same time, the contribution of the [Ln]4d near valence band and conduction band reduced the bandwidth of γ-Bi₂MoO₆, forming the Ln-O ionic bond with different strengths to obtain higher charge conductivity and charge-separation ability. Secondly, Ln³⁺ ions have a strongly ionic charge, which leads to the appearance of optical absorption bands in the infrared region and part of the visible region. This reduces the reflection in the visible region, improves the utilization rate, delays the loss of electron energy, and promotes phase matching in the visible region. And the Gd³⁺-doped system has better photocatalytic activity than the other Ln³⁺-doped system. This research provides theoretical insights into doped lanthanide rare earth ions and also provides strategies for the modification of γ-Bi₂MoO₆ nanomaterials.

1. Introduction

Semiconductor crystal materials possess the characteristics of periodicity and symmetry in the atomic structure, enabling interaction and transformation of various forms of energy within the crystal, including power, heat, light, electricity, etc. [1,2,3,4]. It is the exceptional versatility and remarkable stability of semiconductor crystals that make indispensable core materials in advanced fields such as laser technology, atomic energy technology, and optoelectronic technology.

Extensive studies have been conducted by numerous scholars on various semiconductor crystal materials, including TiO₂ [5,6,7], ZnO [8,9], SnO₂ [10,11], MnO₂ [12,13], SiX (X=C, N) [14,15,16], CdS [17], BiOX (X=Br, I, Cl) [18,19], and Bi₂XO₆ (X=Mo, W, V) [20]; these studies have focused on optics, mechanics, electricity, and heat with applications in fields such as photoelectric catalysis. Among them, the bismuth molybdate material has a special layered “sandwich” structure, which is a prevalent crystal structure in the Aurivillius family. The special perovskite-layered structure can be expressed by the general formula (Bi₂O₂)(Mo_nO_3n+1), where n represents the number of perovskite layers, and when the value of n is different, it shows different structures. When n = 1, the crystal structure is γ-phase (γ-Bi₂MoO₆), and the γ-phase is an orthorhombic structure; when n = 2 and 3, the crystal structure is β-phase (β-Bi₂Mo₂O₉) and α-phase (α-Bi₂Mo₃O₁₂), where the β-phase and α-phase exhibit a monoclinic structure. Currently, bismuth molybdate crystals with these three structures have shown potential applications in various areas, including the degradation of pollution [21,22], batteries and capacitors [23,24,25], hydrogen evolution [26,27], oxidation [28,29], gas-sensitive response [30,31], etc.

In the field of photocatalytic degradation, scholars have investigated the crystal structure of the bismuth molybdate material and found that among the three crystal structures, γ-Bi₂MoO₆ with an orthogonal structure has a suitable band gap width (2.5–2.8 eV). This structure has a strong response to visible light, making it a photocatalytic material which is driven by visible light. However, due to the large electron effective reciprocity mass, electron–hole-pair recombination, and small specific surface area, the photocatalytic activity of bismuth molybdate crystals is limited [32,33]. Therefore, it is necessary to modify the intrinsic material by doping, recombination, modification, and loading to improve its properties. Doping is one of the effective methods to modify intrinsic materials.

Meng et al. [34]. successfully synthesized the Fe³⁺-doped photocatalytic material Fe-BMO, which exhibited excellent photocatalytic activity for photocatalytic nitrogen fixation. According to the results of experiments and DFT, the introduction of the iron medium reduces the work function of the intrinsic material and promotes the migration of surface electrons, while accelerating the redox between Fe³⁺/Fe²⁺ to facilitate charge collection. Yu et al. [35] fluorinated Bi₂MoO₆ materials that were prepared by the combination of solvothermal and calcination methods, which showed excellent degradation efficiency for dyes, antibiotics, phenols, and other pollutants. The study demonstrated that doped F^- ions promoted the ability of the intrinsic material surface and oxygen vacancies to capture electrons, and increased the output of active functional groups. Secondly, the introduction of F^- ions made the valence band of the intrinsic material have a stronger positive potential and improved the oxidation ability of holes. Li et al. [36] successfully prepared Lu³⁺-doped Bi₂MoO₆ nanorods. According to the combination of experiment and DFT, it was found that by doping different amounts of Lu³⁺ ions, the intrinsic material gradually transformed from nano-sheet to a rod-like morphology. At the same time, the lattice surface selectively exposed the (0 0 1) surface, and Lu³⁺ ions also promoted the generation of oxygen vacancy in the intrinsic lattice to promote charge separation and light response.

The electronic and optical properties of compounds can be improved by doping rare earth metal ions, transition metal ions, and non-metal ions. Alemi et al. [37] prepared three different lanthanide rare earth ions Ln³⁺ (Ln=Gd, Ho, Yb)-doped γ-Bi₂MoO₆ by thermal polymerization, and found that different rare earth metal ions doped to form flakes with different shape structures; all three types of doping promoted the photocatalytic activity of the intrinsic material. It was mainly attributed to the enlarged specific surface area and reduced bandgap, resulting in a larger reaction contact area and better electron separation efficiency. At the same time, in the photocatalytic experiment, through the comparison of different concentrations of dopant ions, it was found that the photocatalytic performance of the product Gd_0.5Bi_1.5MoO₆ was improved the most, which was attributed to the half-filled electronic configuration of Gd³⁺ ions.

From the experimental point of view, this paper comprehensively analyzes the influence and improvement of three kinds of the doping of lanthanide rare earth metal ions on the photocatalytic performance of γ-Bi₂MoO₆, but does not involve the corresponding theoretical part. Considering the significance of lanthanide rare earth metal ions for improving the photocatalytic activity of γ-Bi₂MoO₆, this paper constructs theoretical models for three lanthanide rare earth metal ion-doped γ-Bi₂MoO₆ (Ln-BMO (Ln=Gd, Ho, Yb)), and calculates and analyzes the geometric structure, electronic structure, and optical properties of Ln-BMO by density functional theory (DFT). Compared with the experimental data, this study not only provides theoretical support for the experiment, but also provides the basis and guidance for rare earth metal ion-doped γ-Bi₂MoO₆.

2. Materials and Methods

2.1. Theoretical Model

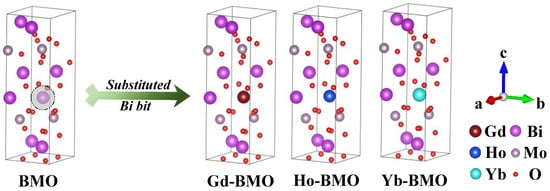
As described in the introduction, γ-Bi₂MoO₆ can be represented by the general formula (Bi₂O₂)(Mo_nO_3n+1), where n = 1, in which the structure is formed by the interlacing of MoO₆ octahedron and Bi-O layer (Bi₂O₂). As for the initial file of γ-Bi₂MoO₆ crystal, the cif file (mp-23064) is downloaded from the materials project resource library [38,39,40]. This crystal structure belongs to the orthorhombic structure, and the space group number is 29, corresponding to Pca21. The lattice parameters of the original file are a = 5.527 Å, b = 5.528 Å, c = 16.298 Å, α = β = γ = 90°, Vo = 497.973 ų. The crystal structure contains two non-equivalent Bi³⁺ and one Mo⁶⁺ which bond with six non-equivalent O²⁻, respectively, forming the Bi₂O₂ tetrahedron and MoO₆ octahedra [38]. The 2 × 1 × 1 supercell is used to construct the model. The doping model of three rare earth metal ions is constructed by replacing Bi atoms near the center of the supercell system, which is named Ln-BMO (Ln=Gd, Ho, Yb), and the undoped system is named BMO. The structural models are shown in Figure 1.

2.2. Computational Details

Vienna Ab-initio Simulation Package (VASP) is a first-principle program based on the combination of plane wave basis sets and ultrasoft pseudopotential. It is widely used in material simulation calculations due to its high precision and convenient use [41]. The DFT calculation method of this work was carried out using the VASP software combined with the projected augmented wave (PAW) method, and the related functional description is calculated using the generalized gradient approximation (GGA-PBE) [42].

To achieve structural convergence of BMO and Ln-BMO, a 6 × 6 × 2 K-point network is used to optimize the structure. At the same time, the truncation energy (ENCUT) is set to 520 eV, the energy standard for optimal convergence (EDIFF) is set at 1 × 10⁻⁵ eV, and the interatomic energy convergence standard (EDIFFG) is set at 1 × 10⁻² eV/Å. For the highly symmetric integration path of energy band calculation, G (0 0 0) —Z (0 0 0.5) —Y (0 0.5 0) —X (0.5 0 0) —V (0.5 0.5 0) —U (0.5 0 0.5) —T (0 0.5 0.5) —R (0.5 0.5 0.5) —G (0 0 0) are put under fractional coordinates for calculation purposes [43,44,45]. Related subsequent data processing is assisted by the VASPKIT integration package. For optical properties, the K point network of 18 × 18 × 6 at higher points is used to obtain more accurate data points to calculate optical properties. The relevant calculation of optical parameters in the calculation process covers the energy range of infrared (IR), visible (VR), and ultraviolet (UV).

3. Results and Discussion

3.1. SCF Structure Converges

Firstly, the crystal structures of BMO and Ln-BMO were optimized and converged. In previous work, the lattice parameters of pure BMO and Ln-BMO with different proportions were calculated using X-ray diffraction spectral data. The results were compared to relevant information after DFT structure convergence, as shown in

Table 1. This experimental result and DFT structure convergence result of lattice parameters of BMO and Ln-BMO.

Photocatalysts	Lattice Parameters [37] (EXP)/(Å)			Lattice Parameters (DFT)/(Å)			Average Relative Error/(%)
	a	b	c	a	b	c
BMO	5.465	5.510	16.179	5.654	5.676	16.371	2.552
0.25 Gd-BMO	5.460	5.500	16.177	5.652	5.661	16.350	2.504
0.50 Gd-BMO	5.459	5.487	16.152	5.639	5.656	16.224	2.273
0.25 Ho-BMO	5.438	5.513	16.194	5.651	5.693	16.399	2.806
0.50 Ho-BMO	5.429	5.498	16.180	5.649	5.679	16.366	2.829
0.25 Yb-BMO	5.465	5.488	16.191	5.646	5.667	16.376	2.577
0.50 Yb-BMO	5.421	5.498	16.180	5.629	5.644	16.392	2.598

. In this table, EXP represents experimental data and DFT represents structure convergence data. From Table 1, it is found that the lattice parameters of the intrinsic materials tend to shrink with the doping of lanthanide rare earth metal ions, and also shrink with the increase in doping ion concentration. Through the doping of three lanthanide rare earth ions, lanthanide rare earth metal ions with smaller radius replace Bi³⁺ ions in the intrinsic material, resulting in the reduction of lattice parameters, which is consistent with the experimental analysis. At the same time, the average relative errors between theoretical calculation and experimental data are also given in the table, and the error is controlled within 3%. The possible causes of the error involve experimental measurement error and convergence error. It shows that the model and convergence accuracy of theoretical calculation are reliable.

3.2. Electronic Structure Information

To better illustrate how the doping of lanthanide rare earth metal ions affects the electronic structure of intrinsic materials, static calculations were carried out through the converged structural model, and the band structure, electron state density, and differential charge density of BMO and Ln-BMO were obtained. The detailed calculation results and analysis are as follows.

3.2.1. Band Structure

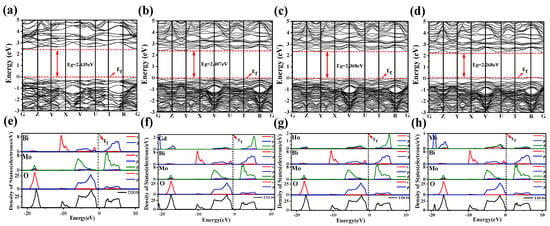
The band structures are obtained through theoretical calculation and simulation, and are shown in Figure 2a–d. Firstly, it should be noted that the maximum conduction band (CBM) and minimum valence band (VBM) of the band structure of BMO and Ln-BMO are in the same position in K-space, indicating that the materials before and after doping belong to the direct band gap semiconductor. It has better responsive activity than other semiconductor materials [46]. Compared to BMO, the electronic states of Ln-BMO in the VB and CB are denser, indicating that more electron states are generated in the valence and conduction bands. The introduction of the Ln³⁺ ions is the main reason for the appearance of these new electronic states. Secondly, the band gap value (Eg) of the band structure can reflect the carrier migration efficiency. In the figure, the undoped BMO band gap is Eg = 2.435 eV, while the calculated band gaps of Gd-BMO, Ho-BMO, and Yb-BMO doped with lanthanide rare earth metal ions are 2.407 eV, 2.368 eV, and 2.268 eV, respectively.

Table 2. Experimental result and DFT structure convergence result of band gap of BMO and Ln-BMO.

Photocatalysts	Band Gap [37] (EXP)/(eV)	Band Gap (DFT)/(eV)	Relative Error/(%)
BMO	2.53	2.435	3.755
0.50 Gd-BMO	2.49	2.407	3.334
0.50 Ho-BMO	2.43	2.368	2.551
0.50 Yb-BMO	2.36	2.268	3.893

lists the comparison of the band gap between experimental and theoretical calculations. The experimental and theoretical trends are unified, and the errors are controlled within 4%. In addition, the carrier mobility is inversely proportional to the effective mass of the electron [47]. The equation ($y=A+Bx+C{x}^2$) is used for the quadratic fitting of the valence band top, and then the relevant electron effective mass can be obtained by fitting coefficient C. The relevant results are shown in Table S1. The effective mass of electron of the intrinsic material is effectively reduced by Ln³⁺ doping. Among them, 0.5 Gd-BMO has the lowest electron effective mass (m = 0.624 m_e), indicating that its carrier migration efficiency is the best. These results show that the bandwidth decreases by the doping of lanthanide rare earth ions, which promotes the visible light response and promotes the carrier mobility of the intrinsic material.

3.2.2. Density of Electronic States

To determine the contribution of Ln atoms and other atomic orbitals to the electronic structure of BMO and Ln-BMO, the total density of state (TDOS) and the partial density of state (PDOS) are calculated, and the calculated results are shown in Figure 2e–h. For BMO, the Fermi energy from −20.0 eV to −15.0 eV is mainly contributed by O atoms; Mo atoms also contribute in the interval, and mainly come from [O] 1s and [Mo] 4d orbitals, while only [Bi] 6s orbital contributes near 10.0 eV. Secondly, from the energy of −6.0 eV to 0.0 eV in PDOS, Bi, Mo, and O can be found to participate in contribution, which can be composed of [O] 2p—[Mo] 4d and [O] 2p—[Bi] 6s orbital interactions [48]. The similar pattern accounts for the orbital contribution from 0.0 eV to 8.0 eV, which explains the formation of a conductive state between the [Bi] 6p, [Mo] 4d, and [O] 2p orbits.

As for the doped materials with three lanthanide rare earth metal ions, compared with BMO, it is found that the introduction of Ln³⁺ ions does not significantly effect the orbital contribution of Bi, Mo, and O atoms, indicating that a small amount of Ln³⁺ doping (0.25 Ln-BMO and 0.5 Ln-BMO) cannot change the crystal structure of γ-Bi₂MoO₆, which is consistent with the experimental analysis. Furthermore, the orbital contributions of [Gd] 4d, [Ho] 4d, and [Yb] 4d are found at −5.0 eV to 0.0 eV and 0.0 eV to 8.0 eV, and their contributions near CBM and VBM lead to the change in BMO band gap. It can be inferred that the Ln³⁺ doping generates new interactions, which makes it easier for the intrinsic structure to excite electrons into the conduction band, and obtain higher charge conductivity and effective charge separation ability, thus proving that the doping of Ln³⁺ ion can effectively improve the photocatalytic ability [49].

3.2.3. Differential Charge Density

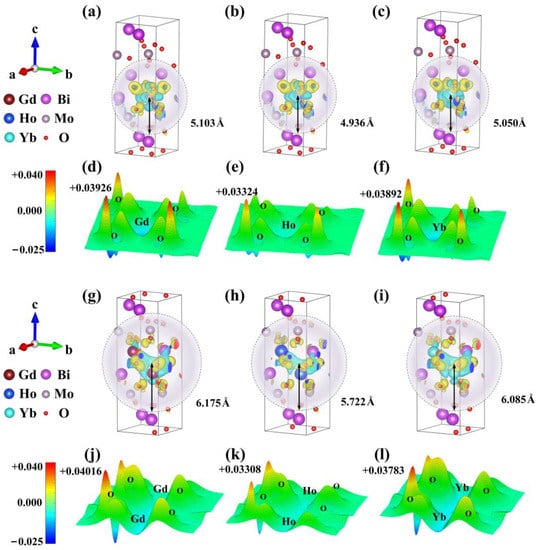
The differential charge density of Ln³⁺ ions in Ln-BMO is calculated by DFT, which reveals the influence of lanthanide rare earth metal ions doping on the electron transport performance of γ-Bi₂MoO₆ (Figure 3a–c,g–i). The yellow part represents electron depletion and the blue part represents electron accumulation. Three lanthanide rare earth ions show similar differential charge densities, indicating that the doping of the three ions has similar properties. The differential charge density shows that electrons accumulate near the three types of Ln atoms, while the depletion of electrons occurs in O near Ln atoms, and the nearby Bi atoms and Mo atoms are also disturbed. In particular, the interaction between the Ln atoms forms an Ln-Ln ionic bond in 0.5 Ln-BMO, which further facilitates electron transfer. In addition, the influence range of different Ln atoms on the electron density of the intrinsic material is estimated. This shows that the influence of Gd³⁺ doping on the electron density of the system reaches 5.103 Å and 6.175 Å, which are higher than the values for Ho³⁺ and Yb³⁺. The result shows that the photogenerated electrons of BMO are transferred to doped-ion sites, which inhibits the recombination of electron–hole pairs, and the influence range of 0.5 Gd-BMO on the electron density is stronger, which is consistent with the experimental analysis [50].

At the same time, the 3D differential charge cross-section is drawn based on differential charge density. The (0 0 1) (8.100 Å away from the origin), (0 1 0) (4.900 Å away from the origin), and (1 0 0) (4.320 Å away from the origin) cross-section of convergence structure is selected. As shown in Figure 3d–f,j–l and Figure S1, the blue part represents electron depletion and the red part represents electron accumulation. The darker the color, the higher the peak value, which represents more electron transfer. The figure reveals that the doping of Ln³⁺ ions forms ionic bonds with different strengths of Ln-O, and the strength of the ionic bond is an important factor affecting the change in charge compensation [51]. According to the peak value, the peak intensity of 0.25 Gd-BMO reaches + 0.03926 e/bohr³ (0 0 1), + 0.03819 e/bohr³ (0 1 0), and + 0.03824 e/bohr³ (1 0 0), which is higher than the other two doped systems and shows isotropy under different cross sections. Similarly, the ionic bond strength of 0.5 Gd-BMO is also higher than the two other doping systems, showing strong electron transfer ability. The results show that Ln-O ionic bonds with different strengths are formed and charge compensation is generated in BMO system, showing the improvement of photo response and decolorization ability, and the Gd³⁺ doping effect is more obvious.

3.3. Optical Structure Information

As a photocatalytic material that relies on visible light response, it is necessary to study its optical properties. The dielectric constant, as a bridge between the process of inter-band transition and the electronic structure of a solid, reflects the band structure and other spectral information of a solid [52]. Thus, we analyze the influence of the doping of lanthanide rare earth metal ions on the optical properties of BMO and Ln-BMO materials. For the calculation of optical properties, we calculate the complex dielectric function, complex refractive index, reflectivity, absorption coefficient, and electron energy loss function of the material using Equations (1)–(9). Among them, the Kramers–Kronig transformation dispersion relation of the imaginary part is used to solve the solution of the real part of the complex permittivity [53]. The detailed formula is explained in the Supplementary Materials.

$$\epsilon \left(\omega \right)={\epsilon }_1\left(\omega \right)+i{\epsilon }_2\left(\omega \right)$$

(1)

$$N\left(\omega \right)=\sqrt{\epsilon \left(\omega \right)}=n\left(\omega \right)+i\kappa \left(\omega \right)$$

(2)

$${\epsilon }_1\left(\omega \right)=1+\frac{2}{\pi }{\rm P}{{\displaystyle \int }}_0^{\infty }\frac{{\epsilon }_2{\left(\omega \prime \right)}^{}{\omega }^{\prime }}{{{\omega }^{\prime }}^2-{\omega }^2}d{\omega }^{\prime }$$

(3)

$${\epsilon }_2\omega =\frac{e^2}{{\omega }^2\pi m^2}{\displaystyle \sum }_{v,c}{{\displaystyle \int }}_{BZ}d\stackrel{\rightharpoonup }{k}{\left|\langle {\Psi }_{ck}\left|\hat{e}·\stackrel{\rightharpoonup }{p}\right|{\Psi }_{vk}\rangle \right|}^2\delta \left(E_c\left(k\right)-E_v\left(k\right)-\hslash \omega \right)$$

(4)

$$n\left(\omega \right)={\left(\frac{\sqrt{{\epsilon }_1{}^2\left(\omega \right)+{\epsilon }_2{}^2\left(\omega \right)}+{\epsilon }_1\left(\omega \right)}{2}\right)}^{\frac{1}{2}}$$

(5)

$$\kappa \left(\omega \right)={\left(\frac{\sqrt{{\epsilon }_1{}^2\left(\omega \right)+{\epsilon }_2{}^2\left(\omega \right)}-{\epsilon }_1\left(\omega \right)}{2}\right)}^{\frac{1}{2}}$$

(6)

$$R\left(\omega \right)=\frac{{\kappa }^2\left(\omega \right)+{\left[1-n\left(\omega \right)\right]}^2}{{\kappa }^2\left(\omega \right)+{\left[1+n\left(\omega \right)\right]}^2}$$

(7)

$$\alpha \left(\omega \right)=\frac{2\omega \kappa \left(\omega \right)}{c}=\frac{4\pi \kappa \left(\omega \right)}{{\lambda }_0}$$

(8)

$$L\left(\omega \right)=Im\left(\frac{-1}{\epsilon \left(\omega \right)}\right)=\frac{{\epsilon }_2{}^2\left(\omega \right)}{{\epsilon }_1{}^2\left(\omega \right)+{\epsilon }_2{}^2\left(\omega \right)}$$

(9)

3.3.1. Complex Dielectric Constant $\epsilon \left(\omega \right)$

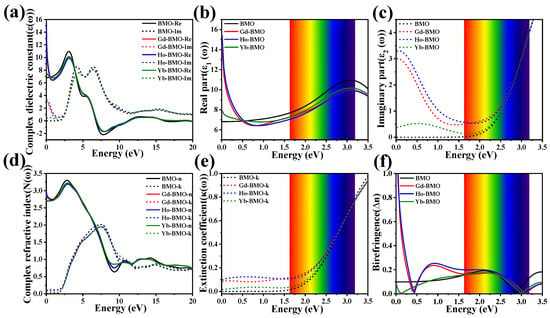
The complex dielectric constant is mainly manifested in the binding and dissipative ability of charge, which can indirectly reflect the light utilization ability of semiconductor photocatalytic materials. According to Equations (3) and (4), the complex dielectric constant is shown in Figure 4a–c and Figure S2a–c. Firstly, we find the real part and imaginary parts of the complex dielectric constant of BMO and Ln-BMO show similar curves in the whole photon energy range. In the real part curve, BMO shows obvious peaks at 3.082 eV, 5.674 eV, and 7.713 eV, while the real part of the dielectric constant of Ln-BMO migrates to high energy. For the imaginary part curve, BMO has an obvious peak at 4.167 eV and 6.442 eV. Interestingly, the doping of Ln³⁺ ions induces the peak value at the lower energy to shift positively, while the opposite trend is observed for peak values at higher energies. These phenomena may be attributed to the interaction between [Ln] 4d and the intrinsic material.

For the photon energy range of the visible region (1.64–3.19 eV), the real part of the complex dielectric constant can approximately describe the energy stored in a material upon exposure to photon radiation. In the infrared region, the real part of Ln-BMO shows high peaks, which are not present in the intrinsic materials. And for 0.5 Ln-BMO, the peak value of the infrared region has a different degree of change. These peaks correspond to electron transitions between the band gaps, which are attributed to the long-lived electronic energy levels of [Ln] 4d and the interaction between [O] 2p and [Ln] 4d [54,55].

When the photon energy is 0, the actual value is expressed as the static dielectric constant, in which Gd³⁺ and Ho³⁺ ion doping significantly improve it, and the higher the static dielectric constant is, the better the refraction coefficient is. In the visible region, the real part of the permittivity of Ln-BMO decreases slightly compared with BMO.

The imaginary part reflects the energy dissipated from the material to the outside upon exposure to photon radiation. Compared with the intrinsic material, Ln-BMO is enhanced in the infrared and visible regions, indicating that the carriers of the doped materials with Ln³⁺ ions are more active and the optical activity is enhanced [56]. The direct band gap of the corresponding system can be determined by the imaginary part of the dielectric constant. According to the calculation, the direct optical band gap of the BMO, Gd-BMO, Ho-BMO, and Yb-BMO systems is 2.454 eV, 2.436 eV, 2.417 eV, and 2.402 eV, respectively. The optical band gap is generally larger than the electronic band gap [57]. At the same time, it is found that the imaginary part of the dielectric constant of 0.5 Gd-BMO increases more strongly in the visible region, indicating that the appropriate amount of Gd³⁺ ions doped can improve the photo-response intensity of the material and obtain better photocatalytic activity.

3.3.2. Complex Refractive Index $n\left(\omega \right)$ and Birefringence $∆n$

The complex refractive index and birefringence index of materials are important optical constants for analyzing the absorption spectrum. The parameters calculated according to Equations (5) and (6) are shown in Figure 4d,e and Figure S2d–f. The real part determines the propagation speed of light in the material, while the extinction coefficient of the imaginary part represents the attenuation of light propagation in the material, and also indirectly represents the absorption capacity of the material. The extinction coefficient is the main analysis part of the complex refractive index. Among them, the attenuation of Ln-BMO is enhanced in the infrared and visible regions, which further indicates that the doping of Ln³⁺ ions leads to the enhancement of the light absorption capacity in the intrinsic material. In particular, 0.5 Gd-BMO has the largest enhancement amplitude in the visible region, indicating that Gd³⁺ ion doping promotes the absorption of visible light and light response.

As for the real part of the complex refractive index, it can be analyzed by solving the birefringence. The birefringence can be obtained by the difference of the real part of the complex refractive index of the three spindles of the crystal. For BMO crystals, the birefringence can be obtained from $∆n=n_{\parallel z}-n_{\perp z}$; the results are shown in Figure 4f. Near the visible region, the birefringence of BMO is relatively stable around 0.1, but it approaches 0 near 2.854 eV, which may affect the phase matching in this region [58]. For Ln-BMO, this point is shifted to 3.086 eV, and the Gd-BMO is shifted more obviously. This shift phenomenon promotes the phase matching of the intrinsic material in the visible region.

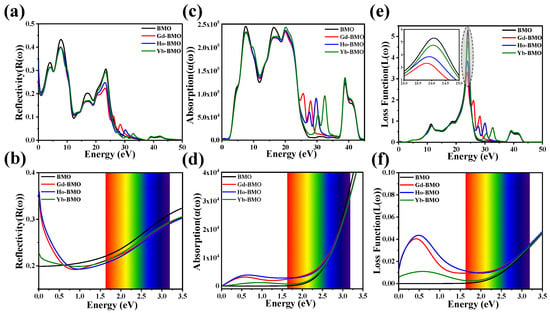
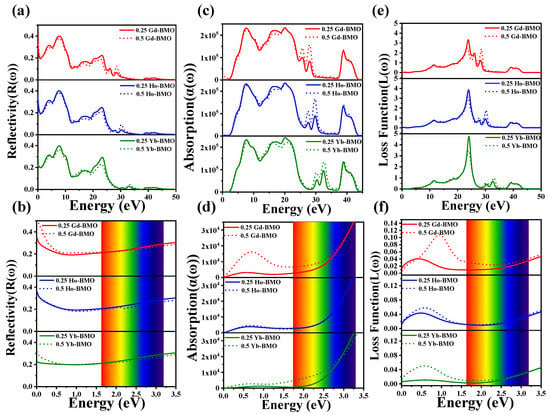
3.3.3. Reflectivity $R\left(\omega \right)$ and Absorption Coefficient $\alpha \left(\omega \right)$

The reflectivity and absorption coefficients of materials are crucial parameters in the calculation of optical properties. The percentage of the radiant energy reflected by the material in the total radiant energy is called reflectivity, and the amount of radiant energy absorbed by the material is called the absorption coefficient. The reflectivity and absorption coefficient of intrinsic material and doped material are calculated according to Equations (7) and (8). Figure 5a and Figure 6a shows the calculated reflectance. The intrinsic material and the doped material exhibit similar reflectivity curves, indicating that the doping of a small amount of Ln³⁺ ions (0.25 Ln-BMO and 0.5 Ln-BMO) does not change the optical structure of the intrinsic material, which is consistent with the previous analysis. The reflectivity of all calculated materials reaches its maximum at 7.850 eV, reaching approximately 40%. And, characteristic peaks different from those of the intrinsic materials appear at 28.471 eV, 30.219 eV, and 32.943 eV, which correspond to the doping of Gd³⁺, Ho³⁺, and Yb³⁺, respectively. With the increase in doping concentration, the corresponding characteristic peak is more obvious. Secondly, element doping reduces the reflectivity of intrinsic materials in non-characteristic bands, which confirms the enhancement of optical absorption. Figure 5c and Figure 6c shows the calculated absorption coefficient. The valence and conduction bands of BMO and Ln-BMO are continuous, and the corresponding absorption curves are also continuous [59]. The increase in photon energy promotes light absorption in the material, indicating the direct transition process of electrons. At the same time, the Ln-BMO observes characteristic peaks similar to the corresponding energy value of the reflectivity, which promotes the intrinsic material to have stronger light absorption in the higher photon energy band.

For the photon energy range of visible light, its reflectivity and absorption coefficient are shown in Figure 5b,d, and Figure 6b,d. Firstly, the reflectivity of Ln-BMO is lower than BMO in the visible light region, but higher than BMO in the energy range less than 0.6 eV. And with the increase in doping concentration, its reflectivity in the visible region is lower, indicating that the doping of lanthanide rare earth metal ions can reduce the reflection in the visible light region and increase the utilization rate of the material for visible light. As for the calculated absorption coefficient, it can be observed that the doping of Ln³⁺ ions presents a new absorption peak that cannot appear in the intrinsic material in the infrared region and visible region (less than 2.0 eV), which is attributed to the introduction of the Ln³⁺ ions. And Ln³⁺ ions have a smaller ionic radius and a stronger ionic charge that leads to the extra electronic state in the band gap, resulting in the appearance of the low-energy absorption band [54]. Especially in the visible region, 0.25 Gd-BMO and 0.5 Gd-BMO exhibit a strong absorption coefficient and low reflectance, which further indicates that Gd-BMO has a strong light response and transmittance, and explains the reason that Gd-BMO has strong light catalytic ability, which is consistent with the previous analysis.

3.3.4. Energy Loss Function $L\left(\omega \right)$

The electron energy loss function is mainly manifested in the primary process of energy loss caused by inelastic scattering, which cannot involve the characteristic excitation of the ground state process. According to Equation (9), the energy loss function of intrinsic material and doped material is calculated with the energy of the incident photon. Figure 5e,f and Figure 6e,f display the loss functions of the calculation systems. In the figure, the main peaks are in 24.090 eV, 24.042 eV, 23.885 eV, and 23.794 eV, corresponding to BMO, Yb-BMO, Ho-BMO, and Gd-BMO, respectively, which are represented as plasma peaks. These peaks illustrate the collective excitation of electron charge density in the crystal structure [60]. And Ln³⁺ doping causes the plasma peak value to shift to the lower energy level, which may be attributed to the new spin–orbit effect of Ln³⁺ and leads to the change in crystal field effect. Secondly, similar to the reflectance and absorption coefficient, the characteristic peaks of corresponding elements are also observed. No significant electron energy loss is observed in the infrared and visible energy ranges. Although the electron energy loss function increases with the doping of Ln³⁺, such an enhancement has no obvious effect on the optical response, and the energy loss is the result of ionization and electric dipole oscillation by external fields [61].

4. Conclusions

Based on the theoretical calculation of DFT and GGA-PBE method, the geometric structure, electronic structure, and optical properties of lanthanide rare earth metal ion-doped γ-Bi₂MoO₆ are calculated and analyzed. For the γ-Bi₂MoO₆-doped structure, a small amount of Ln³⁺ doping (0.25 Ln-BMO and 0.5 Ln-BMO) with a smaller radius will replace Bi³⁺ ions, leading to lattice parameter contraction. And different strengths of Ln-O ionic bonds and charge influence range are generated in the structure, which promotes the photogenerated electrons of γ-Bi₂MoO₆ to the dopant ion site and promotes charge compensation. Secondly, the contribution of [Ln] 4d in the vicinity of CBM and VBM reduces the bandwidth of γ-Bi₂MoO₆, which enhances the light absorption capacity of the intrinsic material. And because of the near infrared characteristics of Ln³⁺, the utilization rate and phase matching of visible light region are improved, and the loss of electron energy is reduced. Among the three Ln³⁺, 0.5 Gd-BMO has strong ionic bond strength and charge influence range, and has better absorption, reflectivity and loss function in the visible region, showing better photocatalytic activity than the other two elements. This research provides theoretical insights into lanthanide rare earth ion doping and also provides strategies for the modification of γ-Bi₂MoO₆ nanomaterials.