Next Article in Journal
Research Progress in the Industrial Crystallization of Citrate—A Review
Previous Article in Journal
Microstructural Control by Cooling Rate in β-type and Sintered Ti-3.6Fe-5Zr-0.2B (Mass%) Alloy Fabricated by Spark Plasma Sintering and Heat Treatment
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 8
10.3390/cryst13081185
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

First Principle Study on Structural, Thermoelectric, and Magnetic Properties of Cubic CdCrO3 Perovskites: A Comprehensive Analysis

by
S. Satapathy
1,2,*,
Mohammed Batouche
3,
Taieb Seddik
3,
Mostafa M. Salah
4,* and
K. K. Maurya
1,2,*
1
CSIR-National Physical Laboratory, Dr. K.S. Krishnan Marg, New Delhi 110012, India
2
Academy of Scientific and Innovative Research (AcSIR), Ghaziabad 201002, India
3
Laboratoire de Physique Quantique et de Modélisation Mathématique (LPQ3M), Département de Technologie, Université de Mascara, Mascara 29000, Algeria
4
Electrical Engineering Department, Future University in Egypt, Cairo 11835, Egypt
*
Authors to whom correspondence should be addressed.
Crystals 2023, 13(8), 1185; https://doi.org/10.3390/cryst13081185
Submission received: 28 June 2023 / Revised: 20 July 2023 / Accepted: 26 July 2023 / Published: 30 July 2023
(This article belongs to the Special Issue Perovskite: Design, Property, and Application)
Browse Figures
Versions Notes

Abstract

:
The primary objective of contemporary manufacturing is to produce items that are low-cost, environmentally friendly, and energy efficient. This study aimed to investigate compounds that fulfil these criteria, with a focus on CdCrO3. The full potential linearized augmented plane wave program (FP LAPW), as in Wien2K, was employed to examine the structural, electronic, thermodynamic, and transport characteristics of the material. Structural optimization was carried out using generalized gradient approximation (GGA), with lattice constants that were deemed satisfactory based on previous theoretical and experimental results. Calculations of the magnetic characteristics of CdCrO3 show that the Cr atoms are principally responsible for magnetism. The quasi-harmonic Debye model allows for the identification of thermodynamic properties including trends, the relative Debye temperature, thermal expansion parameter, relative volume, and heat capacity at various pressures and temperatures. At constant volume, a heat capacity of 52 J/mol K was determined. The thermoelectric properties were examined using the Boltzmann transport offered by the BoltzTrap program. At room temperature, CdCrO3 had a figure of merit (ZT) value that was almost equal to one, indicating that it may be used to make thermoelectric devices with the highest possible efficiency.

1. Introduction

Inorganic materials known as perovskite oxides have gained considerable attention recently due to their extraordinary properties and electrical, structural, optical, thermoelectric, and elastic behavior [1,2,3]. These materials possess different crystalline phases and physicochemical properties, including ferromagnetism, anti-ferromagnetism, ferroelectricity, ferro-elasticity, anti-ferroelectricity, and others. Ferromagnetic perovskite materials, in particular, have become more prominent in spintronics, a field that explores how to use electron spin to store, process, and transmit information [4,5]. The flexible crystal structure of perovskite oxides, which enables the development of several materials with distinctive electrical and other properties, is one of its most alluring features. To maintain the stability of the ABO3 compound’s structure, the standard cubic ABO3 crystal structure is commonly utilized, where A and B represent two different cations, O represents an anion, and the radius of B is substantially lower than that of the A-cation. An oxygen atom normally occupies the unit cell’s center in an ideal cubic ABO3 structure, which also places a B atom in the center and another atom frequently at one of the cell’s corners [6,7,8]. RE-TM-O3 perovskites have recently become the subject of rare earth studies. Replacing some of the cations (B) or the TM with magnetic elements has been observed to result in the emergence of unexpected magneto-electric and multiferroic characteristics in materials [9,10,11]. The interplay between electric and magnetic orders in these materials has sparked immense interest due to their potential for use in next-generation electronic devices, data storage, and spintronics [12,13]. These materials exhibit both ferroelectric and ferromagnetic orders that are coupled through strain or spin interactions, resulting in the emergence of novel properties. Furthermore, several researchers have investigated the magnetic and electrical properties of various perovskites using ab-initio methods. For instance, the suitability of the PrCrO3 compound for spintronics applications was confirmed based on its electronic and magnetic properties, as concluded by M. Yaseen et al. in 2020 [14]. Rashid et al. investigated the electrical and magnetic properties of the cubic CeCrO3 compound in the FM phase using density functional theory, specifically the mBJ approximation [15]. Their investigation revealed that the material had half-metallic, ferromagnetic, and total magnetic moments of 4.0 B. The characteristics of CaCrO3, BaCrO3, and SrCrO3, in particular the length of the Cr-O bond, have been the subject of recent study. Materials made of RCrO3 are incredibly adaptable and have outstanding physical studies. These characteristics include, among others, the magnetocaloric effect (MCE), exchange bias, and magnetization reversal. The peculiar magnetic characteristics of RCrO3 are a result of its intricate magnetic structure. Despite the scientific community’s interest in ferromagnetism in transition metal oxides and their prospective applications, [16] there is currently no literature on the physical properties of RCrO3 (R = Ca, Sr, Ba, Cd, etc.) for electrical or spintronic devices. Designing devices with the best implementation requires an understanding of the physical properties of materials. Stable phases of novel materials can be created using non-equilibrium progression conditions in molecular beam epitaxy (MBE) or any other physical vapor deposition techniques. This study aims to explore the structural, thermoelectric, and magnetic properties of the CdCrO3 cubic perovskite using density functional theory (DFT) [17] to evaluate its potential industrial applications. The FP-LAPW-GGA (PBE) method was used to analyze its features. Furthermore, the lack of available data on the material indicates that this study is the first of its kind to explore these properties, which may lead to future research in the field.

2. Computational Method

We performed a study on CdCrO3 to assess its structural, magnetic, elastic, and electronic properties using the DFT framework and the FP-LAPW [18] tool from WIEN2k [19]. In our simulations, we took the spin-orbit effect into account using semi-relativistic techniques. The magnetoelectronic properties were determined through DFT calculations, taking exchange and correlations into account. To achieve convergence in the basis set, we used a plane wave cut-off value of RMT × Kmax = 7 [20,21]. To improve the wave functions inside the muffin-tin spheres, we expanded the radial eigenfunctions by spherical harmonics up to lmax = 10. Additionally, we raised the potential Fourier charge density of the interstitial region to Gmax = 14. We applied the tetrahedron technique in the irreducible Brillouin zone with a k-grid of 10 × 10 × 10 and a charge convergence of 10−5 as the convergence condition. We also investigated the thermoelectric transport features by employing the quasi-harmonic Debye model [22] and the BoltzTraP method [23] in order to calculate the thermodynamic parameters such as the heat capacity, thermal expansion, and Debye temperature at high pressures and temperatures. We found that a denser k-point grid is necessary for accurate predictions of transport parameters.

3. Results and Discussion

3.1. Structural Properties

For a description of geometric structure as mentioned earlier, we enhanced the topologies of the perovskite compounds under investigation while taking into account their cubic structure. Their fully relaxed structure is shown in Figure 1. The component atoms Cd and Cr are located at (0,0,0) and (1/2,1/2,1/2), respectively, whereas the halide ion O is located at (1/2,1/2, u) (u = 0.249). The examined compounds were discovered to have a Pm-3m space group in a cubic structure [24]. The optimal lattice parameters were determined using PBE-GGA functional and the Birch Murnaghan equation of state [25] against volume (a.u) in the three phases of non-magnetic (NM), ferromagnetic (FM), and antiferromagnetic phase (AFM), as shown in Figure 2. The computed results of the structural optimization are shown in Table 1. The computed outcomes were found to be in accordance with earlier reports, suggesting the reliability of our computation. Moreover, it has been remarked that the FM phase has minimum energy, suggesting a ferromagnetic ground state for this perovskite. Furthermore, we estimated the tolerance factor (τ) [26,27] to support the cubic structural parameters. The tolerance factor in the range 0.96–1.04 suggests the cubic crystal structure. The computed τ for the CdCrO3 was found to be 0.97, suggesting a cubic structure. Additionally, it was possible to determine the thermodynamic stability by taking into account the formation energy (Ef), which was calculated as [28,29,30]:
E f   =   1 N   ( E C d C r O 3   +   E C d   +   E C r   +   3 E O )
The computed formation energy was found to be negative, reflecting the thermodynamic stability of the investigated CdCrO3. The above outcomes reflect the structural stability of the investigated CdCrO3.

3.2. Electronic Properties

The study of electronic properties is an essential aspect of materials science and is crucial for developing new materials with specific properties for various applications. The electronic band structure of a material is a graphical representation of the allowed energy levels for electrons in a solid [32]. This is determined by the behavior of electrons in the valence and conduction bands and the size of the gap between these bands. The energy gap is a fundamental aspect of the electronic band structure, and its size determines whether a material is an insulator, semiconductor, or metal. The behavior of electrons in the valence and conduction bands and the size of the gap between these bands are critical factors that determine the electronic properties of a material, including its electrical conductivity, optical properties, and magnetic behavior. In this study, the electronic properties of the CdCrO3 compound were investigated via the most stable structure in balance states and optimized lattice parameters. Figure 3a,b illustrates the electronic band structures for both spin-up and spin-down polarization with GGA. The results indicate that CdCrO3 is a metallic compound using the GGA-PBE approach, which means that it has high electrical conductivity and behaves as a conductor of electricity. Furthermore, when the Coulomb repulsion terms (GGA+U) [33,34] are introduced, the metallic character is kept in the majority band structure, as shown in Figure 4a,b; however, for the minority band structure, this results in a semiconductor character, suggesting the half metallic nature of the CdCrO3 compound. This is an important finding as it distinguishes CdCrO3 from other perovskite compounds that are insulators or semiconductors. The absence of an energy gap in CdCrO3 suggests that the compound has potential applications in electronic devices that require high electrical conductivity, such as interconnects in microprocessors and other electronic components.
The total and partial (projected) densities of states (TDOSs and PDOSs, respectively) determined for CdCrO3 are shown in Figure 5. The Fermi level, EF, is represented by the vertically broken line. We determined the PDOSs of Cd, Cr, and O in CdCrO3 to better understand how each atom contributes to the total TDOSs. The fact that the total DOSs at the Fermi level have non-zero values utilizing the GGA method is evidence that CdCrO3 should exhibit metallic conductivity for both spin channels [35,36]. The large contribution of the Cr ‘d’ states at the Fermi level is what causes this trend. In contrast, the Hubbard parameter has an impact on the Cr ‘d’ states, separating them in the majority spin and moving them towards higher energies, which results in the creation of a band gap in the minority spin. The GGA+U approximation revealed that the CdCrO3 perovskite is composed of half-metallic components. Additionally, the TDOSs curves of CdCrO3 show that the valence and conduction bands of this material primarily consist of Cr’d’ orbitals with O ‘p’. Electrical stability is significantly influenced by the DOSs at EF. The Fermi level’s position and EF strength affect the phase stability of intermetallic complexes. Those with lower EF values are more stable when compared to those with higher EF values.

3.3. Magnetic Properties

Magnetism is a fundamental property of materials that has significant applications in various fields, including electronics, energy, and medicine. To study the magnetic properties of materials, one of the crucial considerations is the magnetic moment. The magnetic moment reveals the components and frequency of the material’s magnetic field. In this context, the magnetic moments of spins in the CdCrO3 compound were investigated. CdCrO3 is a complex compound that contains multiple elements, including cadmium (Cd), chromium (Cr), and oxygen (O). The total and partial magnetic moments with polarized spin in the interstitial sites and the muffin-tin spheres were estimated using the GGA and GGA+U models to investigate the magnetic properties of the compound. Table 2 displays the conclusions of these calculations. They are metallic because the total magnetic moments per cell unit were near to an integer Bohr magneton of 2 μB. It was interestingly found that the Cd and O atom magnetic moments were extremely modest and had no impact on the overall moment [37]. Nevertheless, they played a crucial role in the development of magnetism. The environment of these atoms also had an impact on the magnitude of the major band gap in the compound CdCrO3. This means that when examining the magnetic properties of materials, it is important to take these atoms’ magnetic moments into account because they are not insignificant. As can be seen in Table 2, the interstitial region was also discovered to have a significant magnetic moment. The result of a sizable charge transfer from Cd and Cr to O is this effect, which can be used to explain the magnetic moment in the interstitial area. This is explained by the fact that the electro-negativity of the O anion, which is 3.5 on Pauling’s scale, is higher than that of the Cd and Cr, whose electro-negativity values are both 1.69 higher than the O anion. The magnetic moment in the interstitial area is caused by a significant charge transfer from Cd and Cr to O as a result of the difference in electro-negativity values. Furthermore, the significant magnetic moment in the interstitial region can have important implications on the compound’s properties [38]. For instance, the magnetic moment can affect the electronic and optical properties of the compound, which are essential for various applications. Furthermore, the stability and symmetry of the compound’s structure can be affected by the magnetic moment in the interstitial area.

3.4. Thermodynamic Properties

We calculated the thermodynamic characteristics of the CdCrO3 under investigation using Gibbs2 [22,39]. The compound under study had its thermal characteristics estimated for a temperature range of 0–800 K. The quasi-harmonic model was used to take pressure variations between 0 and 15 GPa into account. For the investigated CdCrO3 compound, the bulk modulus is greatest at 210 GPa at 0 K, as observed in Figure 6a. According to this, B increases when pressure is applied at a specific temperature and decreases when the pressure is constant [40]. Additionally, the bulk modulus gradually decreases above 200 K and remains constant between 0 and 200 K. The entropy of CdCrO3 varies with temperature, as shown in Figure 6b. It has been noted that the curves are exponential in nature. It was discovered to be almost 120.66 J·mol−1K−1 for the examined CdCrO3 at zero pressure and 300 K. The vibrational properties of the compounds are influenced by the heat capacity. However, at low temperatures, it is directly proportional to T3, while at intermediate temperatures, it depends on atomic vibration [41]. At high temperatures, the heat capacity at constant volume approaches the Dulong–Petit limit. The plot for Cv is shown in Figure 6c and contains two phases: the first phase, where T is below 300 K, shows a sharp increase in Cv with temperature, and the second phase, where T is over 300 K, shows a progressive increase in Cv with temperature. The Cv augments when it approaches the Dulong–Petit limit at greater temperatures during its final phase. CdCrO3 computed heat capacities of 52 J/molK at constant volume, as shown in Figure 6c. The CP of CdCrO3 is depicted in Figure 6d for different pressures. As shown in Figure 6d, the CP curves are initially sharply enhanced. Yet, the growth rate of the curves eventually slows down. At relatively low temperatures, only acoustic vibrations can cause vibrational excitations. It follows that variations in temperature and pressure have an equal impact on heat capacity. Through study of the thermal expansion coefficient α (T), the compounds’ structural stability can be determined. The fluctuation of α (T) with temperature and pressure is depicted in Figure 6e. Due to the use of a harmonic of the Debye model approximation [42], a strong rise is seen for both compounds up to 200 K. Nonetheless, the thermal expansion coefficient steadily decreases as the temperature rises, indicating that the CdCrO3 crystal has good volume invariance. For CdCrO3, we determined the Debye temperature (θD), which is depicted in Figure 6f. We can see that at 0 K and 40 GPa pressure, the θD of CdCrO3 is 575. With constant pressure and temperature, as depicted in Figure 6f, it linearly decreases. It was noted that the pressure effect increased the Debye D temperature. Extensive analysis of the thermodynamic properties will provide insight into the experimental efforts.

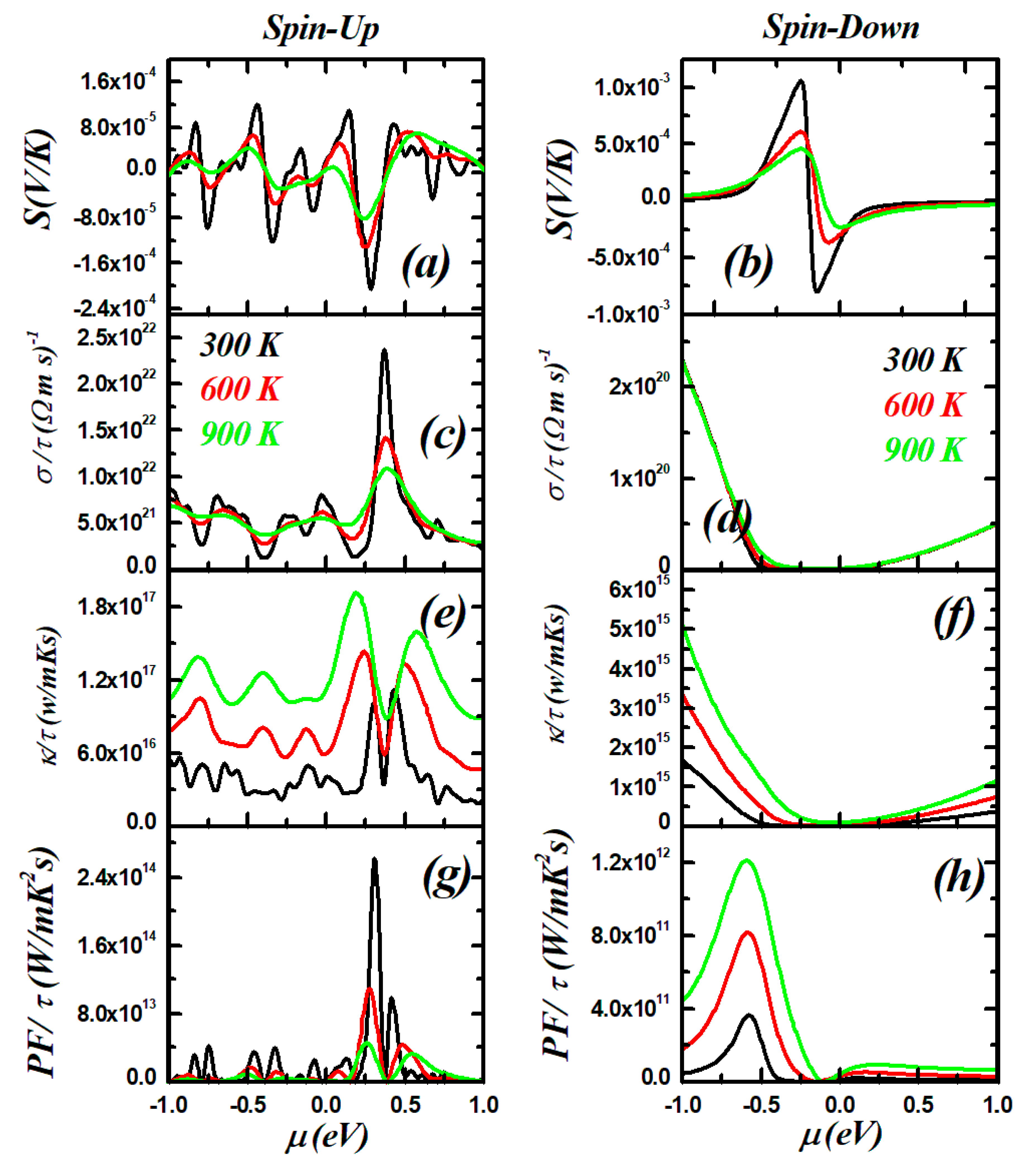
3.5. Thermoelectric Properties

The ability of thermoelectric materials to convert thermal energy into useful energy and vice versa has made them a subject of interest worldwide. In this section, we mainly focus on the analysis of several transport coefficients of CdCrO3 in both up- and down-spin states, such as electrical conductivity (σ/τ), Seebeck coefficient (S), and the merit factor (ZT). To calculate the thermoelectric parameters, we utilized the BoltzTraP code [23] and an approximation of charge carrier constant relaxation durations.
Figure 7 displays the chemical potential dependence of the Seebeck coefficient (S), electrical conductivity (σ/τ), electronic thermal conductivity (κ/τ), and power factor (PF/τ) at different temperatures of 300 K, 600 K, and 900 K for CdCrO3. It was observed that the S values were negative at the Fermi level (µf = 0), suggesting that the majority charge carriers are electrons for both spin channels (Figure 7a,b) and thus confirming the n-type conductivity of this CdCrO3 perovskites [43,44]. Moreover, it was also observed that the Seebeck coefficient value decreased with the increasing temperature. Furthermore, Figure 7c,d depicts the variation in electrical conductivity (σ/τ) of CdCrO3 with chemical potential. There is a difference in the electrical conductivity calculated for the spin-up state and that obtained for the spin-down state of CdCrO3. For the spin-up state, we found that σ/τ behaves as a metal, while for the spin-down state, it looks like a semiconductor. The same trend was observed in the case of the electronic thermal conductivity (κe/τ) (see Figure 7e,f) as κe is related to the electrical conductivity (σ) through the Wiedemann–Franz [45,46] relation κe = LσT, where L is the Lorenz number. Figure 7g,h represents the variation in the power factor (PF) with the chemical potential for CdCrO3. It was noted that CdCrO3 has a maximum value of PF for n-type in the majority spin whereas it has a maximum for p-type in the minority spin.
It is well know that the figure of merit [47] is given by:
Z T = S 2 σ κ T
where κ = κe + κl is the total thermal conductivity [48]. Therefore, one has to estimate the lattice thermal conductivity (κl) using the following formula:
κ l = A · M ¯ θ D 3 δ γ 2 T n 2 / 3
where M ¯ represents the average atomic mass of all constituent atoms, A is a constant calculated as A = 2.43 · 10 − 8 1 − 0.514 γ + 0.228 γ 2 , n is the number of atoms in the primitive cell, δ is the average atomic volume, T is the absolute temperature, γ is the Grüneisen parameter, and θD is the Debye temperature [49]. The estimated κl for the CdCrO3 compound is depicted in Figure 8a. From this figure, it can be well observed that the κl decreases with the temperature increase. Now, considering the total S, σ, and κ and using a constant relaxation time τ ≈ 10−14 s, the total ZT of the CdCrO3 material is evaluated, as shown in Figure 8b. At 300 K, the maximum ZT is marked to be 0.4 and 0.8 for p-type and n-type doping, respectively, suggesting the optimum thermoelectric response of the studied compound at room temperature. These ZT maximum values correspond to the carrier concentrations of about 4.22 × 1019 cm−3 and 2.31 × 1022 cm−3 for p-type and n-type doping, respectively. Moreover, by increasing the temperature, these ZTmax values gradually decrease.

4. Conclusions

In this study, the structural, elastic, vibrational, and thermodynamic characteristics of CdCrO3 perovskite were examined using the FP-LAPW and quasi-harmonic Debye models. Using the generalised gradient approximation of Perdew–Burke and Ernzerh of exchange correlation (GGA-PBE), we were able to optimise the lattice parameters. The computed structural characteristics, such as the equilibrium lattice constant, bulk modulus, and pressure derivative, are consistent with previous studies. According to the overall density of states and the electronic energy band structure, both materials are half-metallic and have Cd-4d Cr ‘d’ electronic orbitals as their dominant conductivity. Through the quasi-harmonic Debye model, we also identified thermodynamic properties, such as the relative Debye temperature, thermal expansion parameter, relative volume, heat capacity at different temperatures and pressures, and trends. In the study, 52 J/molK of heat capacity was discovered at constant volume. At high temperatures, the CdCrO3 compound shows good volume invariance, according to the coefficient of thermal expansion. This study is a part of a larger theoretical undertaking that also includes our investigation into the characteristics of this compound and could inspire further studies in this area.

Author Contributions

Conceptualization, S.S., T.S., M.M.S. and K.K.M.; methodology, S.S., M.B., M.M.S. and K.K.M.; software, S.S., M.B., T.S., M.M.S. and K.K.M.; validation, K.K.M.; formal analysis, M.B. and T.S.; investigation, K.K.M.; writing—original draft preparation, S.S.; writing—review and editing, S.S., M.B. and K.K.M.; visualization, K.K.M. All persons who meet authorship criteria are listed as authors, and all authors certify that they have participated sufficiently in the work to take public responsibility for the content, including participation in the concept, design, analysis, writing, or revision of the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data are included within this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Attfield, J.P.; Lightfoot, P.; Morris, R.E. Perovskites. Dalton Trans. 2015, 44, 10541–10542. [Google Scholar] [CrossRef] [PubMed]
  2. Bednorz, J.G.; Müller, K.A. Perovskite-Type Oxides—The New Approach to High-T c Superconductivity. Rev. Mod. Phys. 1988, 60, 585. [Google Scholar] [CrossRef] [Green Version]
  3. Miyasaka, T.; Kulkarni, A.; Kim, G.M.; Öz, S.; Jena, A.K. Perovskite Solar Cells: Can We Go Organic-free, Lead-free, and Dopant-free? Adv. Energy Mater. 2020, 10, 1902500. [Google Scholar] [CrossRef]
  4. Behera, D.; Manzoor, M.; Sharma, R.; Salah, M.M.; Stich, I.; Mukherjee, S.K. A Comprehensive First-Principles Investigation of SnTiO3 Perovskite for Optoelectronic and Thermoelectric Applications. Crystals 2023, 13, 408. [Google Scholar] [CrossRef]
  5. Singh, P.K.; Singh, R.; Singh, V.; Bhattacharya, B.; Khan, Z.H. New Class of Lead Free Perovskite Material for Low-Cost Solar Cell Application. Mater. Res. Bull. 2018, 97, 572–577. [Google Scholar]
  6. Aboub, Z.; Seddik, T.; Daoudi, B.; Boukraa, A.; Behera, D.; Batouche, M.; Mukherjee, S.K. Impact of La, Ni-Doping on Structural and Electronic Properties of SrTiO3 for Photocatalytic Water Splitting. Inorg. Chem. Commun. 2023, 153, 110871. [Google Scholar] [CrossRef]
  7. Sakhya, A.P.; Rai, D.P.; Dutta, A.; Thapa, R.K.; Sinha, T.P. Electronic, Optical and Thermoelectric Properties of PrMO3(M=Al, Ga, In) from First-Principles Calculations. RSC Adv. 2016, 6, 59988–59997. [Google Scholar] [CrossRef]
  8. Vali, R. Lattice Dynamics of Cubic SrZrO3. J. Phys. Chem. Solids 2008, 69, 876–879. [Google Scholar] [CrossRef]
  9. Abbad, A.; Benstaali, W.; Bentounes, H.A.; Bentata, S.; Benmalem, Y. Search for Half-Metallic Ferromagnetism in Orthorhombic Ce(Fe/Cr)O3 Perovskites. Solid State Commun. 2016, 228, 36–42. [Google Scholar] [CrossRef]
  10. Mekam, D.; Kacimi, S.; Djermouni, M.; Azzouz, M.; Zaoui, A. Ab Initio Calculations on RE–TM–O3 Perovskites: A Comparative Study of Cation Effect. Results Phys. 2012, 2, 156–163. [Google Scholar] [CrossRef] [Green Version]
  11. Lim, J.B.; Zhang, S.; Shrout, T.R. Modified Pb(Yb, Nb)O3–PbZrO3–PbTiO3 Ternary System for High Temperature Applications. Ceram. Int. 2012, 38, 277–282. [Google Scholar] [CrossRef]
  12. He, Z.; Peng, J.; Lei, C.; Xie, S.; Zou, D.; Liu, Y. Prediction of Superior Thermoelectric Performance in Unexplored Doped-BiCuSeO via Machine Learning. Mater. Des. 2023, 229, 111868. [Google Scholar] [CrossRef]
  13. Wang, Z.; He, Z.; Lei, C.; Zou, D.; Liu, Y. Phase Transition Enhanced Thermoelectric Performance for Perovskites: The Case of AgTaO3. Curr. Appl. Phys. 2023, 48, 84–89. [Google Scholar] [CrossRef]
  14. Yaseen, M.; Ambreen, H.; Iqbal, J.; Shahzad, A.; Zahid, R.; Kattan, N.A.; Ramay, S.M.; Mahmood, A. Electronic, Optical and Magnetic Properties of PrXO3(X=V, Cr): First-Principle Calculations. Philos. Mag. 2020, 100, 3125–3140. [Google Scholar] [CrossRef]
  15. Rashid, M.; Iqbal, M.A.; Noor, N.A. DFT-MBJ Study of Electronic and Magnetic Properties of Cubic CeCrO3 Compound: An Ab-Initio Investigation. Sci. Inq. Rev. 2017, 1, 27–36. [Google Scholar] [CrossRef]
  16. Gupta, P. Study of Negative Magnetization, Exchange Bias and Magnetization Switching in Rare Earth Chromites. Ph.D. Thesis, CSIR-National Chemical Laboratory, Pune, India, 2015. [Google Scholar]
  17. Hohenberg, P.; Kohn, W. Density Functional Theory (DFT). Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
  18. Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S.B. Full-Potential, Linearized Augmented Plane Wave Programs for Crystalline Systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
  19. Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. Wien2k. In An Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties; TECH Technological University: Mexico City, Mexico, 2001; Volume 60. [Google Scholar]
  20. Saxena, A.; Dixit, A.; Behera, D.; Abraham, J.A.; Sharma, R.; Mukherjee, S.K. Insight on Structural, Electronic and Thermoelectric Properties of Perovskite AgBaCl3 by an Ab-Initio for Solar Cell and Renewable Energy. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
  21. Manzoor, M.; Behera, D.; Sharma, R.; Iqbal, M.W.; Mukherjee, S.K.; Khenata, R.; Alarfaji, S.S.; Alzahrani, H.A. Investigation of the Structural, Mechanical, Optoelectronic and, Thermoelectric Characteristics of Cubic GeTiO3: An Ab Initio Study. Mater. Today Commun. 2023, 34, 105053. [Google Scholar] [CrossRef]
  22. Blanco, M.A.; Francisco, E.; Luana, V. GIBBS: Isothermal-Isobaric Thermodynamics of Solids from Energy Curves Using a Quasi-Harmonic Debye Model. Comput. Phys. Commun. 2004, 158, 57–72. [Google Scholar] [CrossRef]
  23. Madsen, G.K.H.; Singh, D.J. BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
  24. Jain, E.; Behera, D.; Agrawal, Y.; Yugbodh, K.; Abraham, J.A.; Sharma, R.; Mukherjee, S.K. First Principles Investigation on Half Metallic Ferromagnetism Properties of Cubic VLaO3 Compound. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
  25. Katsura, T.; Tange, Y. A Simple Derivation of the Birch–Murnaghan Equations of State (EOSs) and Comparison with EOSs Derived from Other Definitions of Finite Strain. Minerals 2019, 9, 745. [Google Scholar] [CrossRef] [Green Version]
  26. Fedorovskiy, A.E.; Drigo, N.A.; Nazeeruddin, M.K. The Role of Goldschmidt’s Tolerance Factor in the Formation of A2BX6 Double Halide Perovskites and Its Optimal Range. Small Methods 2020, 4, 1900426. [Google Scholar] [CrossRef]
  27. Behera, D.; Mukherjee, S.K. Theoretical Investigation of the Lead-Free K2InBiX6(X = Cl, Br) Double Perovskite Compounds Using First Principle Calculation. JETP Lett. 2022, 116, 537–546. [Google Scholar] [CrossRef]
  28. Hossain, K.M.; Hasan, M.Z.; Ali, M.L. Understanding the Influences of Mg Doping on the Physical Properties of SrMoO3 Perovskite. Results Phys. 2020, 19, 103337. [Google Scholar] [CrossRef]
  29. Marronnier, A.; Lee, H.; Geffroy, B.; Even, J.; Bonnassieux, Y.; Roma, G. Structural Instabilities Related to Highly Anharmonic Phonons in Halide Perovskites. J. Phys. Chem. Lett. 2017, 8, 2659–2665. [Google Scholar] [CrossRef] [Green Version]
  30. Pan, Y.; Lin, Y.; Liu, G.; Zhang, J. Influence of Transition Metal on the Mechanical and Thermodynamic Properties of IrAl Thermal Barrier Coating. Vacuum 2020, 174, 109203. [Google Scholar] [CrossRef]
  31. Terkhi, S.; Bentata, R.; Bendahma, F.; Lantri, T.; Bentata, S.; Aziz, Z.; Abbar, B. Half-Metallic Ferromagnetic Behavior of Cubic Lanthanide Based on Perovskite-Type Oxide NdCrO3: First-Principles Calculations. Indian J. Phys. 2021, 95, 833–839. [Google Scholar] [CrossRef]
  32. Dixit, A.; Behera, D.; Tripathi, S.K.; Srivastava, A.; Sharma, R.; Khenata, R.; Albalawi, H.; Mahmoud, Z.; Mukherjee, S.K. Vibrational, Mechanical, Electronic and Thermodynamic Properties of Rhenium-Based Perovskites XReO3(X=Li, Be) by an Ab-Initio Computation. Mater. Sci. Eng. B 2023, 294, 116545. [Google Scholar] [CrossRef]
  33. Cococcioni, M.; De Gironcoli, S. Linear Response Approach to the Calculation of the Effective Interaction Parameters in the Method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef] [Green Version]
  34. Yaakob, M.K.; Hussin, N.H.; Taib, M.F.M.; Kudin, T.I.T.; Hassan, O.H.; Ali, A.M.M.; Yahya, M.Z.A. First Principles LDA+ U Calculations for ZnO Materials. First Princ. LDA+U Calc. ZnO Mater. 2014, 155, 15–22. [Google Scholar] [CrossRef]
  35. Behera, D.; Dixit, A.; Nahak, B.; Srivastava, A.; Sharma, R.; Khenata, R.; Bin-Omran, S.; Abdelmohsen, S.A.M.; Abdelbacki, A.M.M.; Mukherjee, S.K. Theoretical Insight on the Electronic Band Structure, Mechanical, Vibrational and Thermodynamic Characteristic of Antiperovskites RE3InN (RE=Y and La). Mater. Today Commun. 2023, 35, 105618. [Google Scholar] [CrossRef]
  36. Behera, D.; Dixit, A.; Kumari, K.; Srivastava, A.; Sharma, R.; Mukherjee, S.K.; Khenata, R.; Boumaza, A.; Bin-Omran, S. Structural, Elastic, Mechanical, and Thermodynamic Characteristic of NaReO3 and KReO3 Perovskite Oxides from First Principles Study. Eur. Phys. J. Plus 2022, 137, 1345. [Google Scholar] [CrossRef]
  37. Behera, D.; Abraham, J.A.; Sharma, R.; Mukerjee, S.K.; Jain, E. First Principles Study of New D0 Half-Metallic Ferromagnetism in CsBaC Ternary Half-Heusler Alloy. J. Supercond. Nov. Magn. 2022, 35, 3431–3437. [Google Scholar] [CrossRef]
  38. Behera, D.; Azzouz-Rached, A.; Bouhenna, A.; Salah, M.M.; Shaker, A.; Mukherjee, S.K. First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications. Crystals 2023, 13, 618. [Google Scholar] [CrossRef]
  39. Otero-de-la-Roza, A.; Luaña, V. Gibbs2: A New Version of the Quasi-Harmonic Model Code. I. Robust Treatment of the Static Data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
  40. Verma, A.S.; Kumar, A. Bulk Modulus of Cubic Perovskites. J. Alloys Compd. 2012, 541, 210–214. [Google Scholar] [CrossRef]
  41. Fitzgerel, R.K.; Verhoek, F.H. The Law of Dulong and Petit. J. Chem. Educ. 1960, 37, 545. [Google Scholar] [CrossRef]
  42. Inaba, H.; Yamamoto, T. Debye Temperature of Materials. Netsu Sokutei 1983, 10, 132–145. [Google Scholar]
  43. Sun, J.; Singh, D.J. Thermoelectric Properties of N-Type SrTiO3. APL Mater. 2016, 4, 104803. [Google Scholar] [CrossRef] [Green Version]
  44. Wang, H.; Su, W.; Liu, J.; Wang, C. Recent Development of N-Type Perovskite Thermoelectrics. J. Mater. 2016, 2, 225–236. [Google Scholar] [CrossRef] [Green Version]
  45. Jonson, M.; Mahan, G.D. Mott’s Formula for the Thermopower and the Wiedemann-Franz Law. Phys. Rev. B 1980, 21, 4223. [Google Scholar] [CrossRef]
  46. Behera, D.; Mohammed, B.; Taieb, S.; Mokhtar, B.; Al-Qaisi, S.; Mukherjee, S.K. First-Principle Investigations on Optoelectronics and Thermoelectric Properties of Lead-Free Rb2InSbX6(X=Cl, Br) Double Perovskites: For Renewable Energy Applications. Eur. Phys. J. Plus 2023, 138, 520. [Google Scholar] [CrossRef]
  47. Seddik, T.; Batouche, M. Bulk to Low Dimensional 2D Thermoelectric Materials: Latest Theoretical Research and Future View. In Progress in Nanoscale and Low-Dimensional Materials and Devices: Properties, Synthesis, Characterization, Modelling and Applications; Springer: Berlin/Heidelberg, Germany, 2022; pp. 571–588. [Google Scholar]
  48. Moutassem, M.; Seddik, T.; Mohammed, D.E.S.; Batouche, M.; Khachai, H.; Khenata, R.; Ahmed, R.; Srivastava, V.; Bouhemadou, A.; Kushwaha, A.K. Metal to Semiconductor Transition and Figure of Merit Enhancement of Li2CuAs Compound by Na Substitution. Bull. Mater. Sci. 2022, 45, 110. [Google Scholar] [CrossRef]
  49. Julian, C.L. Theory of Heat Conduction in Rare-Gas Crystals. Phys. Rev. 1965, 137, A128. [Google Scholar] [CrossRef]
Crystals 13 01185 g001 550
Figure 1. Computed crystal structure of cubic CdCrO3.
Figure 1. Computed crystal structure of cubic CdCrO3.
Crystals 13 01185 g001
Crystals 13 01185 g002 550
Figure 2. Total energy with the volume optimization curve of CdCrO3 in its NM, FM, and AFM phases.
Figure 2. Total energy with the volume optimization curve of CdCrO3 in its NM, FM, and AFM phases.
Crystals 13 01185 g002
Crystals 13 01185 g003 550
Figure 3. Spin-polarized band structures of perovskite oxide CdCrO3 using GGA–PBE: (a) spin up and (b) spin down.
Figure 3. Spin-polarized band structures of perovskite oxide CdCrO3 using GGA–PBE: (a) spin up and (b) spin down.
Crystals 13 01185 g003
Crystals 13 01185 g004 550
Figure 4. Spin-polarized band structures of perovskite oxide CdCrO3 using GGA–PBE+U: (a) spin up and (b) spin down.
Figure 4. Spin-polarized band structures of perovskite oxide CdCrO3 using GGA–PBE+U: (a) spin up and (b) spin down.
Crystals 13 01185 g004
Crystals 13 01185 g005 550
Figure 5. (a) Total and partial density of states of perovskite oxide CdCrO3 at the equilibrium lattice constant using GGA–PBE and GGA + U, (b) Cd, (c) Cr, and (d) O.
Figure 5. (a) Total and partial density of states of perovskite oxide CdCrO3 at the equilibrium lattice constant using GGA–PBE and GGA + U, (b) Cd, (c) Cr, and (d) O.
Crystals 13 01185 g005
Crystals 13 01185 g006 550
Figure 6. (a) Volume (V), (b) entropy (S), (c) heat capacity at constant volume (CV), (d) heat capacity at constant pressure (Cp), (e) thermal expansion coefficient (α), and (f) Debye temperature (θD) versus the different temperatures for CdCrO3.
Figure 6. (a) Volume (V), (b) entropy (S), (c) heat capacity at constant volume (CV), (d) heat capacity at constant pressure (Cp), (e) thermal expansion coefficient (α), and (f) Debye temperature (θD) versus the different temperatures for CdCrO3.
Crystals 13 01185 g006
Crystals 13 01185 g007 550
Figure 7. The Seebeck coefficient (S) (a) Spin-Up, (b) Spin-Down, electrical conductivity (σ/τ), (c) Spin-Up, (d) Spin-Down, electronic thermal conductivity (κe/τ) (e) Spin-Up, (f) Spin-Down, power factor (S2σ) versus the chemical potential (µ) at different temperatures for CdCrO3 (g) Spin-Up, and (h) Spin-Down.
Figure 7. The Seebeck coefficient (S) (a) Spin-Up, (b) Spin-Down, electrical conductivity (σ/τ), (c) Spin-Up, (d) Spin-Down, electronic thermal conductivity (κe/τ) (e) Spin-Up, (f) Spin-Down, power factor (S2σ) versus the chemical potential (µ) at different temperatures for CdCrO3 (g) Spin-Up, and (h) Spin-Down.
Crystals 13 01185 g007
Crystals 13 01185 g008 550
Figure 8. Computed lattice thermal conductivity (κL) and figure of merit (ZTTotal) for CdCrO3.
Figure 8. Computed lattice thermal conductivity (κL) and figure of merit (ZTTotal) for CdCrO3.
Crystals 13 01185 g008
Table
Table 1. Calculated values of equilibrium lattice parameters a (Å), bulk modulus B (GPa), pressure derivative of bulk modulus (B′), minimum energy (E), and Formation energy (Ef) of the cubic perovskite CdCrO3.
Table 1. Calculated values of equilibrium lattice parameters a (Å), bulk modulus B (GPa), pressure derivative of bulk modulus (B′), minimum energy (E), and Formation energy (Ef) of the cubic perovskite CdCrO3.
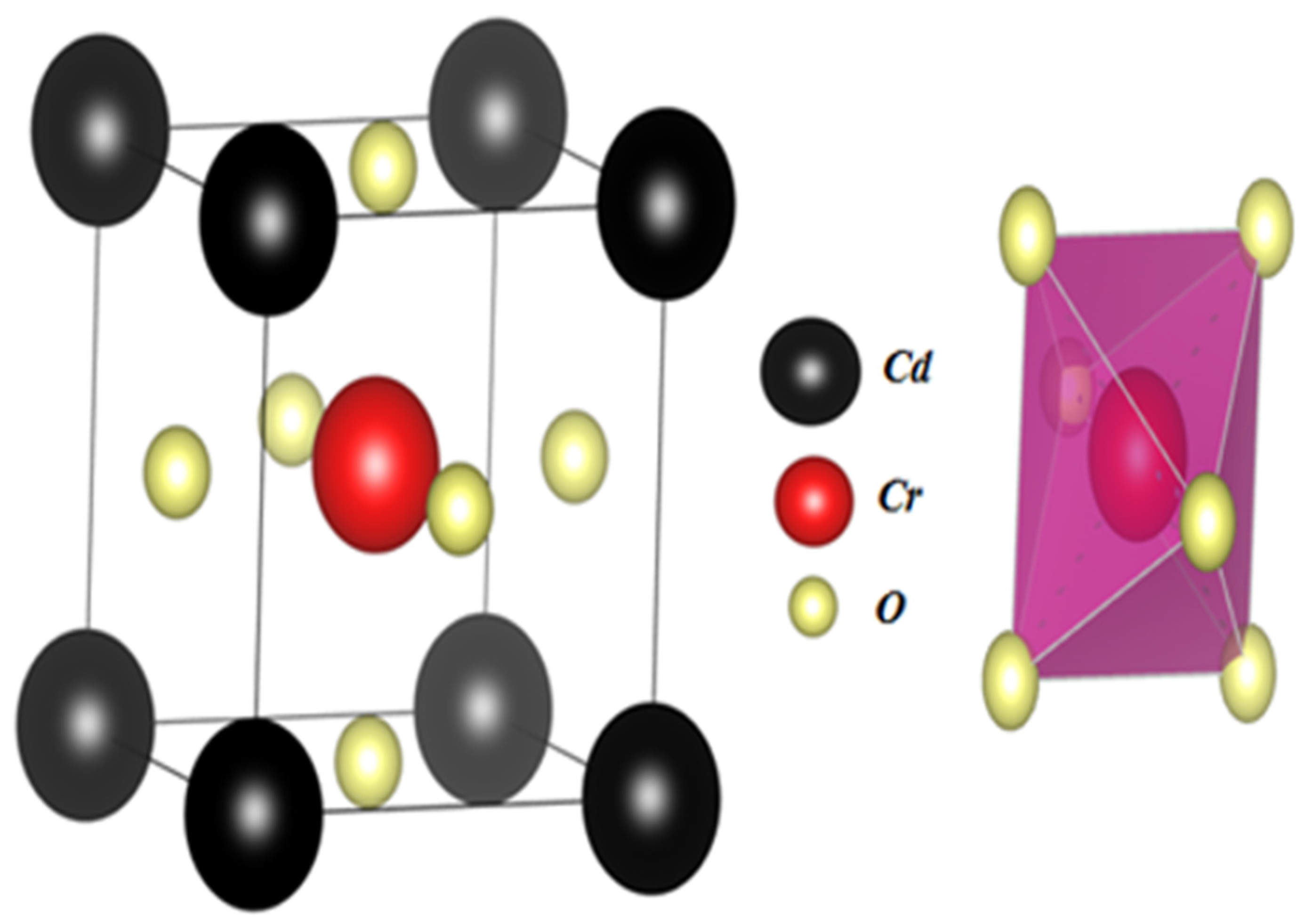
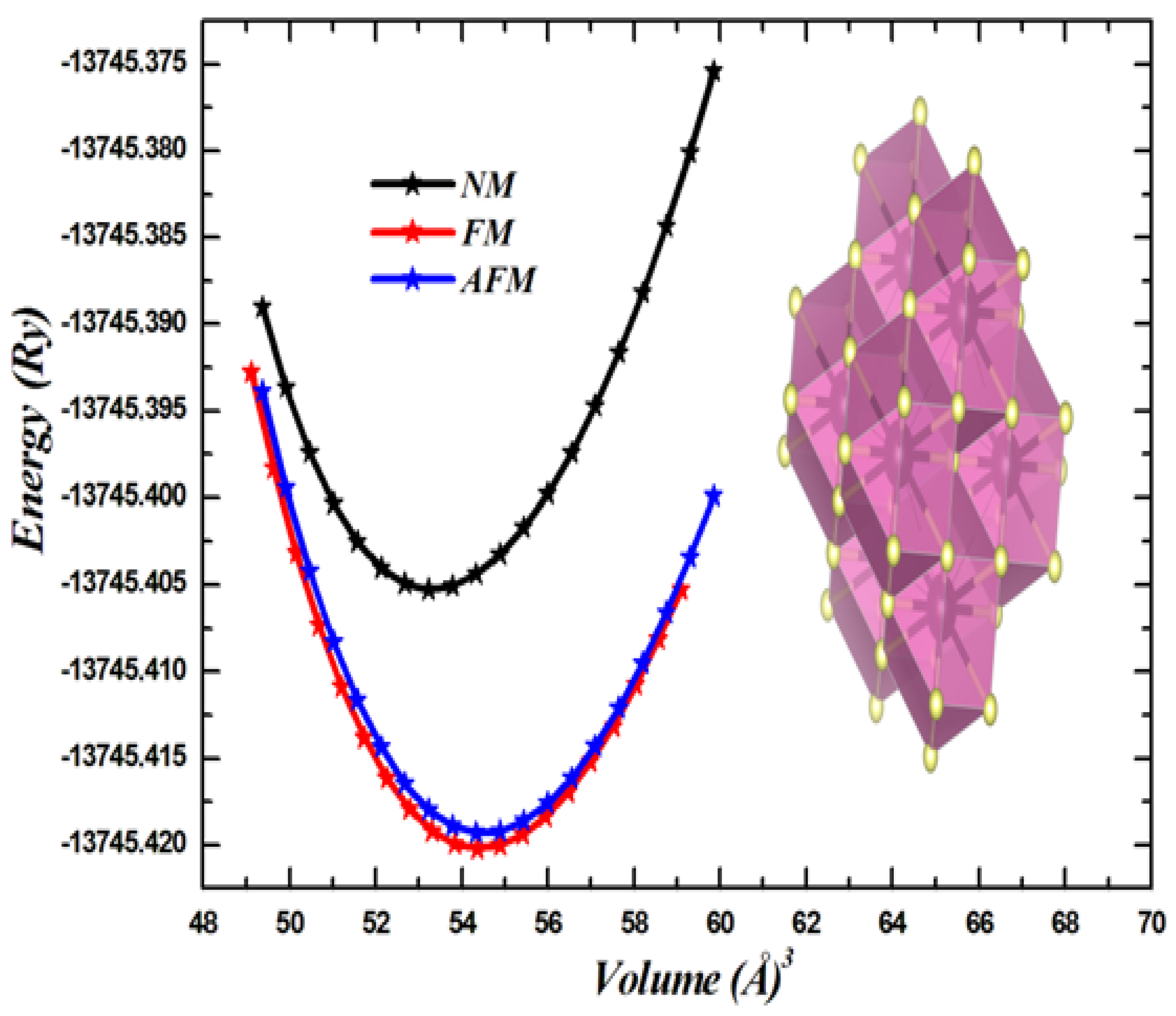
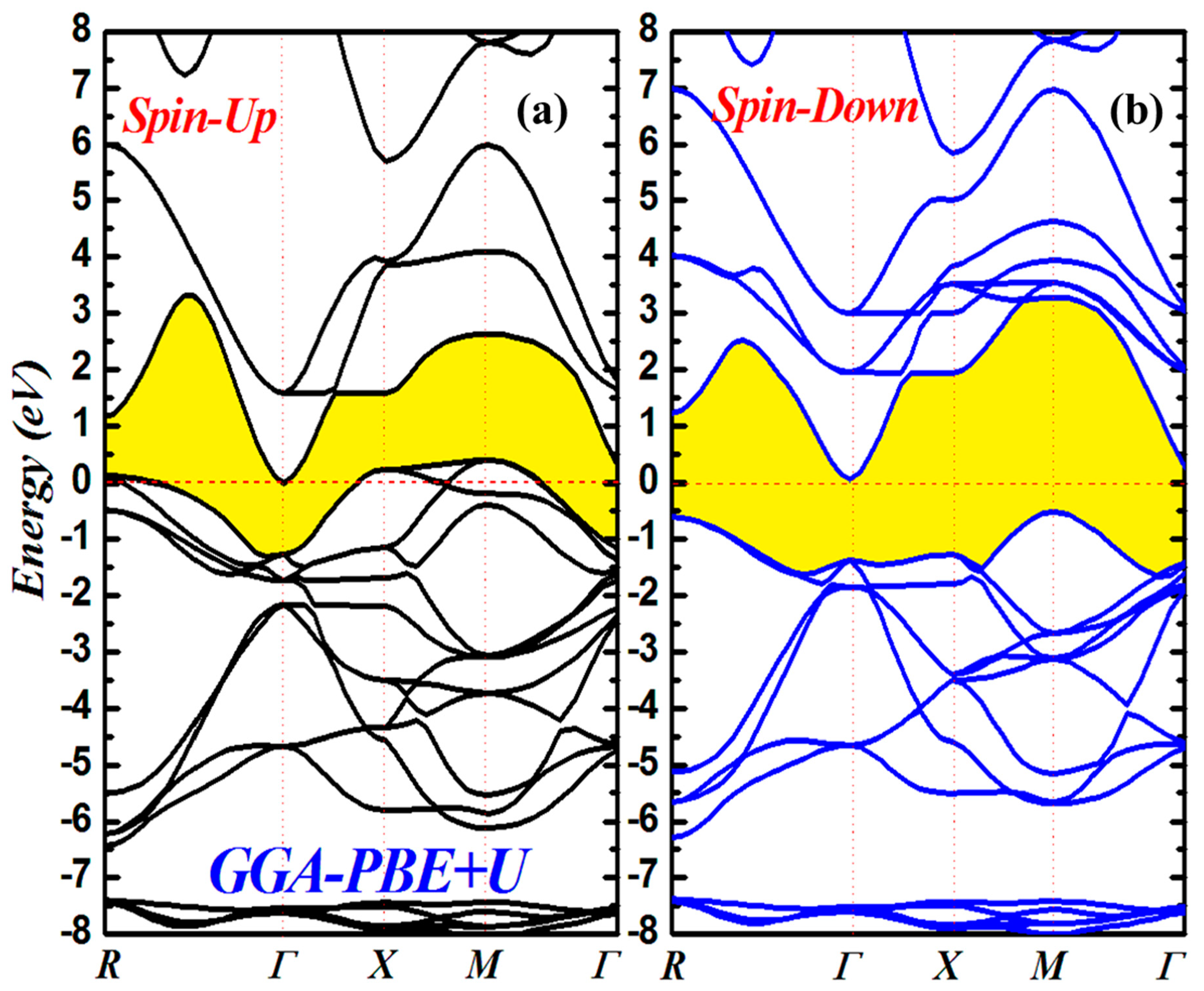
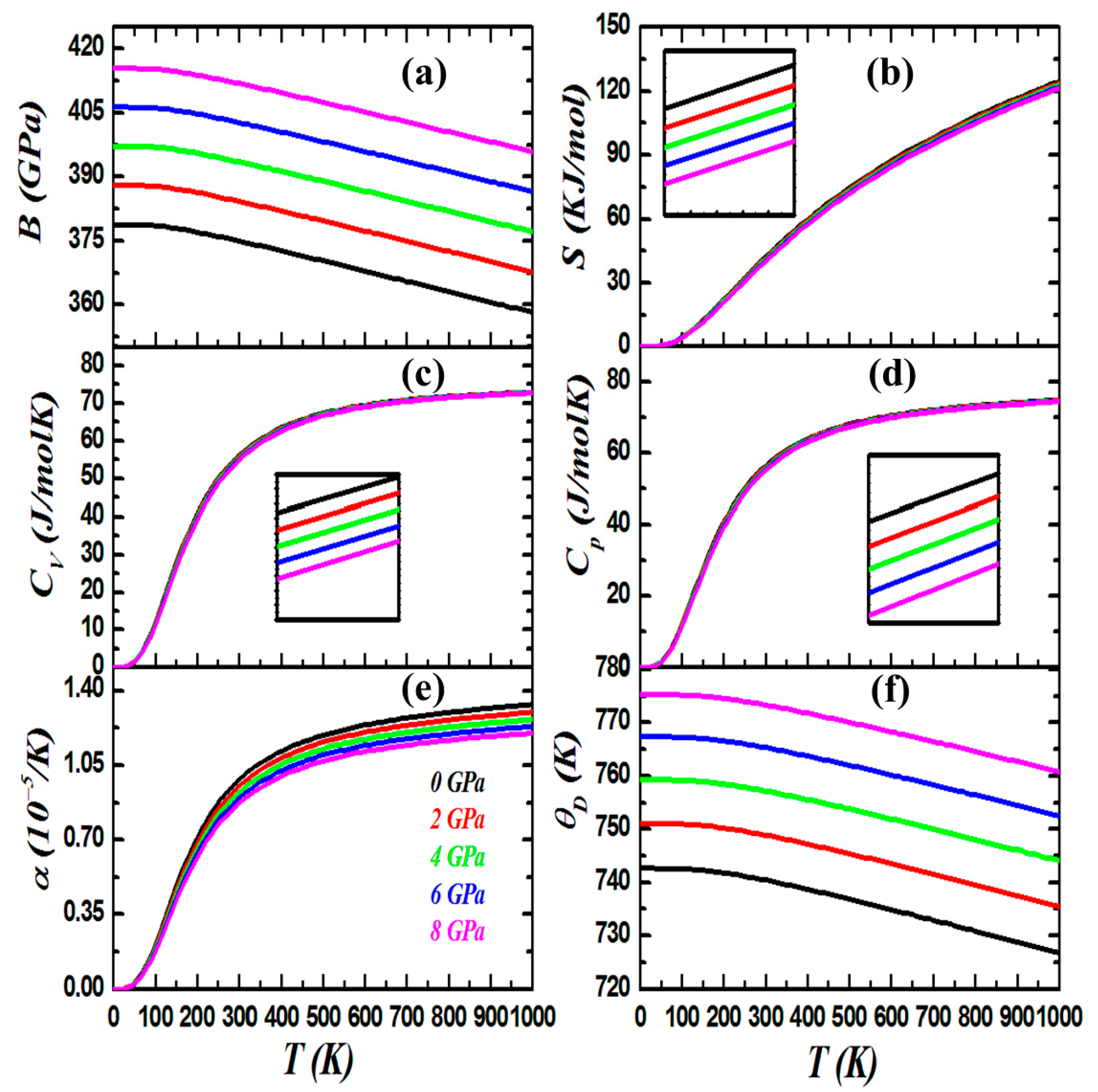
CompoundStatesaBB’E (Ry) ∆ E = E ( F M ) − E ( A F M ) Ef (eV)
NM3.76200.884.65−13,745.405290
CdCrO3FM3.78190.884.89−13,745.420172852 mRy−4.11
(This study)AFM3.79192.014.58−13,745.419320
NM3.74226.45
NdCrO3 [31]FM3.80208.93
(other Study)AFM3.95189.90
Experimental3.890
Table
Table 2. Computed magnetic properties of CdCrO3.
Table 2. Computed magnetic properties of CdCrO3.
MTotMcdMCrMoMintEg (eV)TC (K)
GGA1.990.0451.67−0.0040.292 89.46
Up 0
Down 0
GGA+U1.990.0361.91−0.0770.276
Up 0
Down 0.759
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Satapathy, S.; Batouche, M.; Seddik, T.; Salah, M.M.; Maurya, K.K. First Principle Study on Structural, Thermoelectric, and Magnetic Properties of Cubic CdCrO3 Perovskites: A Comprehensive Analysis. Crystals 2023, 13, 1185. https://doi.org/10.3390/cryst13081185

AMA Style

Satapathy S, Batouche M, Seddik T, Salah MM, Maurya KK. First Principle Study on Structural, Thermoelectric, and Magnetic Properties of Cubic CdCrO3 Perovskites: A Comprehensive Analysis. Crystals. 2023; 13(8):1185. https://doi.org/10.3390/cryst13081185

Chicago/Turabian Style

Satapathy, S., Mohammed Batouche, Taieb Seddik, Mostafa M. Salah, and K. K. Maurya. 2023. "First Principle Study on Structural, Thermoelectric, and Magnetic Properties of Cubic CdCrO3 Perovskites: A Comprehensive Analysis" Crystals 13, no. 8: 1185. https://doi.org/10.3390/cryst13081185

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop