Investigation of the High-Pressure Behaviors of Amblygonite by Single-Crystal X-ray Diffraction, Raman Spectroscopy, and DFT Calculations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Computer Simulations
3. Results
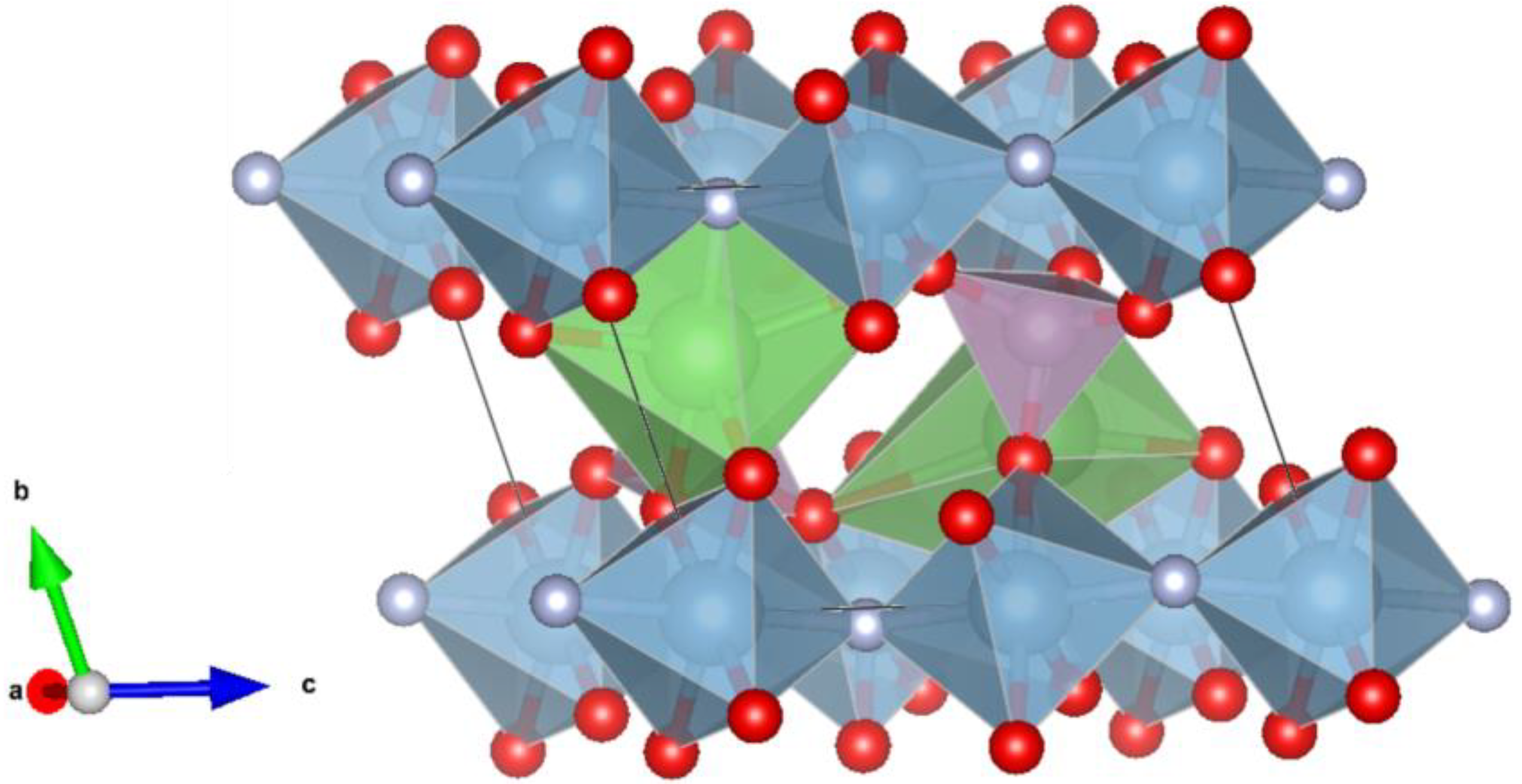
3.1. Sample Characterization
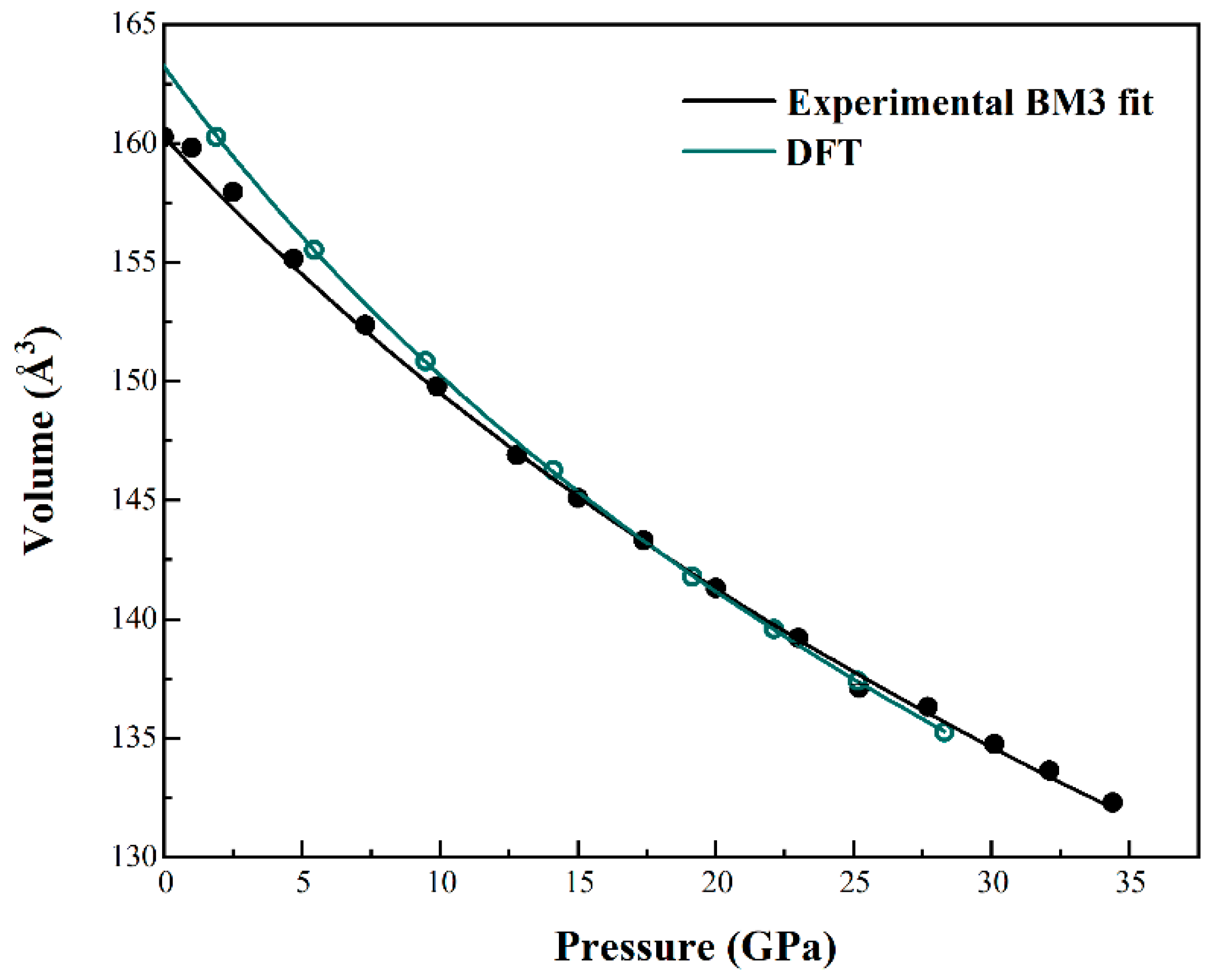
3.2. Room-T compressibility
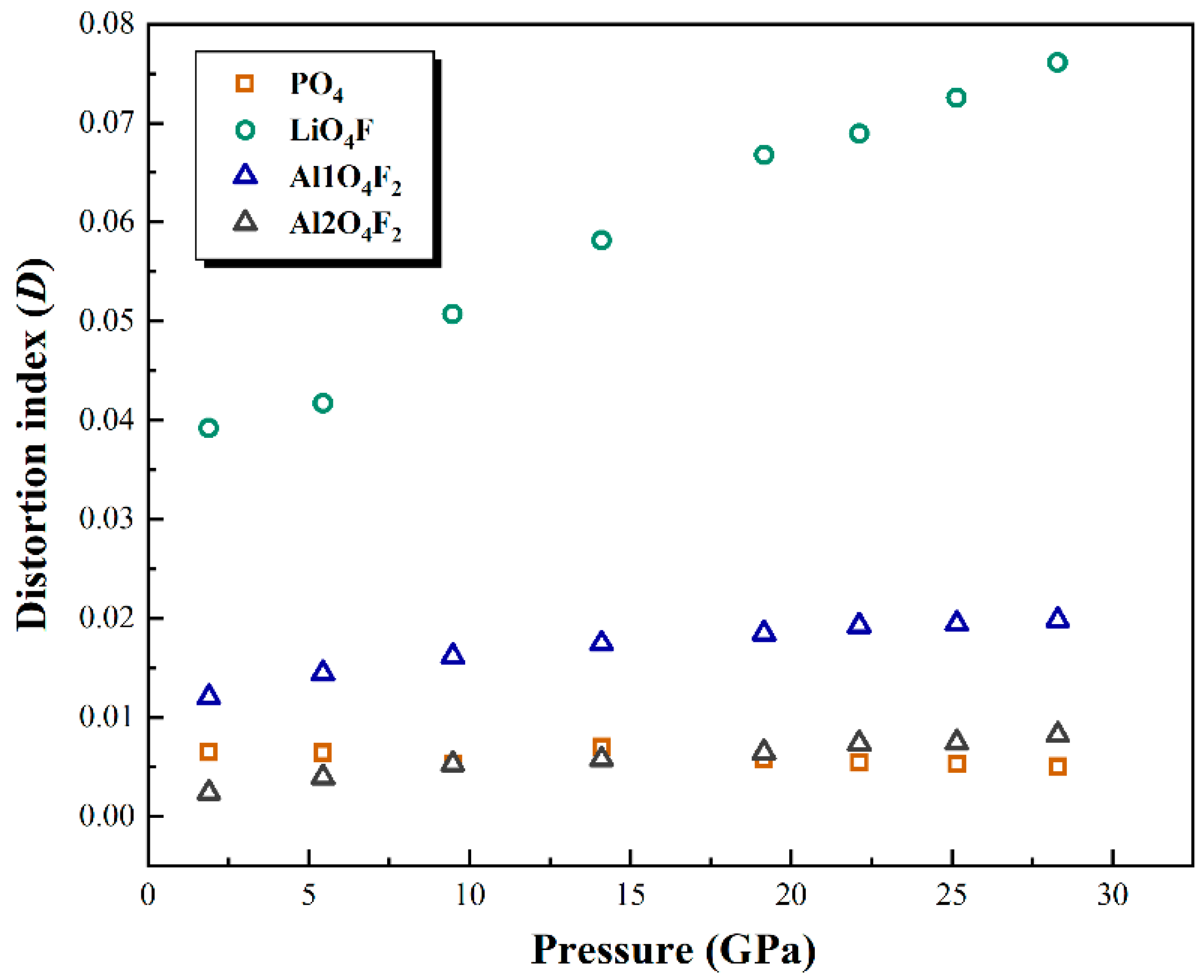
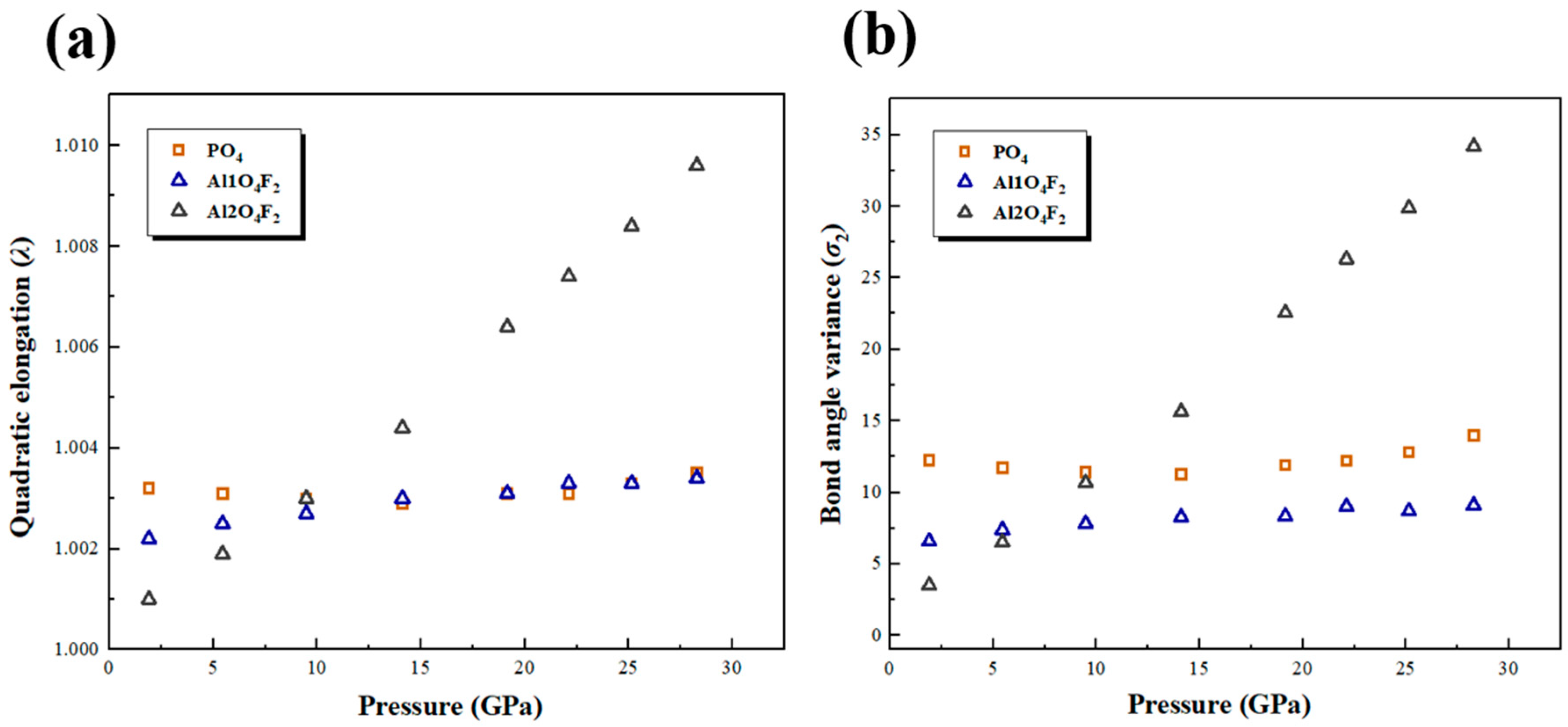
3.3. Polyhedral Compression and Distortion
3.4. Vibrational Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dias, L.N.; Pinheiro, M.V.B.; Moreira, R.L.; Krambrock, K.; Guedes, K.J.; Filho, L.M.; Karfunkel, J.; Scholz, R. Spectroscopic characterization of transition metal impurities in natural montebrasite/amblygonite. Am. Mineral. 2011, 96, 42–52. [Google Scholar] [CrossRef]
- London, D.; Morgan Vi, G.B.; Wolf, M.B. Amblygonite-montebrasite solid solutions as monitors of fluorine in evolved granitic and pegmatitic melts. Am. Mineral. 2001, 86, 225–233. [Google Scholar] [CrossRef]
- Shirose, Y.; Uehara, S. Microtexture investigation of amblygonite–montebrasite series with lacroixite: Characteristics and formation process in pegmatites. Am. Mineral. J. Earth Planet. Mater. 2018, 103, 75–84. [Google Scholar] [CrossRef]
- Trunilina, V.A.; Orlov, Y.S.; Zaitsev, A.I.; Roev, S.P. High-phosphorous lithium–fluorine granites of Eastern Yakutia (Verkhoyansk–Kolyma orogenic region). Russ. J. Pac. Geol. 2019, 13, 82–98. [Google Scholar] [CrossRef]
- Garate-Olave, I.; Roda-Robles, E.; Gil-Crespo, P.P.; Pesquera, A. Phosphate mineral associations from the Tres Arroyos aplite-pegmatites (Badajoz, Spain): Petrography, mineral chemistry, and petrogenetic implications. Can. Mineral. 2020, 58, 747–765. [Google Scholar] [CrossRef]
- Roda-Robles, E.; Pesquera, A.; Gil-Crespo, P.P.; Vieira, R.; Lima, A.; Garate-Olave, I.; Martins, T.; Torres-Ruiz, J. Geology and mineralogy of Li mineralization in the Central Iberian Zone (Spain and Portugal). Mineral. Mag. 2016, 80, 103–126. [Google Scholar] [CrossRef]
- Roda-Robles, E.; Villaseca, C.; Pesquera, A.; Gil-Crespo, P.P.; Vieira, R.; Lima, A.; Garate-Olave, I. Petrogenetic relationships between Variscan granitoids and Li-(FP)-rich aplite-pegmatites in the Central Iberian Zone: Geological and geochemical constraints and implications for other regions from the European Variscides. Ore Geol. Rev. 2018, 95, 408–430. [Google Scholar] [CrossRef]
- Veksler, I.V.; Thomas, R. An experimental study of B-, P-and F-rich synthetic granite pegmatite at 0.1 and 0.2 GPa. Contrib. Mineral. Petrol. 2002, 143, 673–683. [Google Scholar] [CrossRef]
- Greiner, D.J.; Bloss, F.D. Amblygonite-montebrasite optics; response to (OH (super-)) orientation and rapid estimations of F from 2V. Am. Mineral. 1987, 72, 617–624. [Google Scholar]
- Groat, L.A.; Chakoumakos, B.C.; Brouwer, D.H.; Hoffman, C.M.; Fyfe, C.A.; Morell, H.; Schultz, A.J. The amblygonite (LiAlPO4F)-montebrasite (LiAlPO4OH) solid solution: A combined powder and single-crystal neutron diffraction and solid-state 6Li MAS, CP MAS, and REDOR NMR study. Am. Mineral. 2003, 88, 195–210. [Google Scholar] [CrossRef]
- Groat, L.A.; Raudsepp, M.; Hawthorne, F.C.; Ercit, T.S.; Sherriff, B.L.; Hartman, J.S. The amblygonite-montebrasite series; characterization by single-crystal structure refinement, infared spectroscopy, and multinuclear MAS-NMR spectroscopy. Am. Mineral. 1990, 75, 992–1008. [Google Scholar]
- Williams, Q. A vibrational spectroscopic study of hydrogen in high pressure mineral assemblages. High-Press. Res. Appl. Earth Planet. Sci. 1992, 67, 289–296. [Google Scholar]
- Rivers, M.; Prakapenka, V.B.; Kubo, A.; Pullins, C.; Holl, C.M.; Jacobsen, S.D. The COMPRES/GSECARS gas-loading system for diamond anvil cells at the Advanced Photon Source. High Press. Res. 2008, 28, 273–292. [Google Scholar] [CrossRef]
- Dewaele, A.; Torrent, M.; Loubeyre, P.; Mezouar, M. Compression curves of transition metals in the Mbar range: Experiments and projector augmented-wave calculations. Phys. Rev. B 2008, 78, 104102. [Google Scholar] [CrossRef]
- Qin, F.; Wu, X.; Zhang, D.; Qin, S.; Jacobsen, S.D. Thermal Equation of State of Natural Ti-Bearing Clinohumite. J. Geophys. Res. Solid Earth 2017, 122, 8943–8951. [Google Scholar] [CrossRef]
- Zhang, D.; Dera, P.K.; Eng, P.J.; Stubbs, J.E.; Zhang, J.S.; Prakapenka, V.B.; Rivers, M.L. High pressure single crystal diffraction at PX^ 2 JoVE. J. Vis. Exp. 2017, 119, e54660. [Google Scholar]
- Bruker. APEX3 Crystallography Software Suite, v2018.7-2; Bruker AXS Inc.: Madison, WI, USA, 2016. [Google Scholar]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Gonzalez-Platas, J.; Alvaro, M.; Nestola, F.; Angel, R.J. EosFit7-GUI: A new GUI tool for equation of state calculations, analyses, and teaching. J. Appl. Crystallogr. 2016, 49, 1377–1382. [Google Scholar] [CrossRef]
- Mao, H.K.; Xu, J.; Bell, P.M. Calibration of the ruby pressure gauge to 800 kbar under quasi-hydrostatic conditions. J. Geophys. Res. 1986, 91, 4673–4676. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Baur, W.H. Die Kristallstruktur des Edelamblygonits LiAlPO4(OH, F). Acta Crystallogr. 1959, 12, 988–994. [Google Scholar] [CrossRef]
- Angel, R.J.; Gonzalez-Platas, J.; Alvaro, M. EosFit7c and a Fortran module (library) for equation of state calculations. Z. Kryst. 2014, 229, 405–419. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef]
- Errandonea, D.; Achary, S.N.; Diaz-Anichtchenko, D.; Bandiello, E.; Marqueño, T.; Shukla, R.; Tyagi, A.K.; Popescu, C.; Alabarse, F.G. Equations of State and Crystal Structures of KCaPO4, KSrPO4, and K2Ce(PO4)2 under High Pressure: Discovery of a New Polymorph of KCaPO4. Cryst. Growth. Des. 2023, 23, 2782–2794. [Google Scholar] [CrossRef]
- Baur, W.H. The geometry of polyhedral distortions. Predictive relationships for the phosphate group. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1974, 30, 1195–1215. [Google Scholar] [CrossRef]
- Robinson, K.; Gibbs, G.V.; Ribbe, P.H. Quadratic elongation: A quantitative measure of distortion in coordination polyhedra. Science 1971, 172, 567–570. [Google Scholar] [CrossRef]
- Errandonea, D.; Gomis, O.; Rodríguez-Hernández, P.; Muñoz, A.; Ruiz-Fuertes, J.; Gupta, M.; Achary, S.N.; Hirsch, A.; Manjon, F.J.; Peters, L.; et al. High-pressure structural and vibrational properties of monazite-type BiPO4, LaPO4, CePO4, and PrPO4. J. Phys-Condens. Mat. 2018, 30, 065401. [Google Scholar] [CrossRef] [PubMed]
- Rondeau, B.; Fritsch, E.; Lefevre, P.; Guiraud, M.; Fransolet, A.M.; Lulzac, Y. A Raman investigation of the amblygonite–montebrasite series. Can. Mineral. 2006, 44, 1109–1117. [Google Scholar] [CrossRef]
- Cooper, M.A.; Hawthorne, F.C.; Abdu, Y.A.; Ball, N.A.; Ramik, R.A.; Tait, K.T. Wopmayite, ideally Ca6Na3Mn(PO4)3(PO3OH)4, a new phosphate mineral from the Tanco Mine, Bernic Lake, Manitoba: Description and crystal structure. Can. Mineral. 2013, 51, 93–106. [Google Scholar] [CrossRef]
- Ding, X.; Li, J.; Chou, I.M.; Chen, Z.; Li, S. Raman spectroscopic identification of cookeite in the crystal-rich inclusions in spodumene from the Jiajika lithium pegmatite deposit, China, and its geological implications. Eur. J. Mineral. 2020, 32, 67–75. [Google Scholar] [CrossRef]
- Pommier, C.J.S.; Denton, M.B.; Downs, R.T. Raman spectroscopic study of spodumene (LiAlSi2O6) through the pressure-induced phase change from C2/c to P21/c. J. Raman Spectrosc. 2003, 34, 769–775. [Google Scholar] [CrossRef]
- Hofmann, A.W. Chemical differentiation of the Earth: The relationship between mantle, continental crust, and oceanic crust. Earth Planet. Sci. Lett. 1988, 90, 297–314. [Google Scholar] [CrossRef]
- Tang, Y.J.; Zhang, H.F.; Deloule, E.; Su, B.X.; Ying, J.F.; Santosh, M.; Xiao, Y. Abnormal lithium isotope composition from the ancient lithospheric mantle beneath the North China Craton. Sci. Rep. 2014, 4, 4274. [Google Scholar] [CrossRef] [PubMed]
- Ottolini, L.; Le Fèvre, B.; Vannucci, R. Direct assessment of mantle boron and lithium contents and distribution by SIMS analyses of peridotite minerals. Earth Planet. Sci. Lett. 2004, 228, 19–36. [Google Scholar] [CrossRef]
- Gonzalez-Platas, J.; Rodriguez-Hernandez, P.; Muñoz, A.; Rodríguez-Mendoza, U.R.; Nénert, G.; Errandonea, D. A high-pressure investigation of the synthetic analogue of chalcomenite, CuSeO3∙2H2O. Crystals 2019, 9, 643. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, F.; Hou, B.; Hu, K.; Niu, J.; Zhang, D. Investigation of the High-Pressure Behaviors of Amblygonite by Single-Crystal X-ray Diffraction, Raman Spectroscopy, and DFT Calculations. Crystals 2023, 13, 1269. https://doi.org/10.3390/cryst13081269
Qin F, Hou B, Hu K, Niu J, Zhang D. Investigation of the High-Pressure Behaviors of Amblygonite by Single-Crystal X-ray Diffraction, Raman Spectroscopy, and DFT Calculations. Crystals. 2023; 13(8):1269. https://doi.org/10.3390/cryst13081269
Chicago/Turabian StyleQin, Fei, Bingxu Hou, Kailan Hu, Jingjing Niu, and Dongzhou Zhang. 2023. "Investigation of the High-Pressure Behaviors of Amblygonite by Single-Crystal X-ray Diffraction, Raman Spectroscopy, and DFT Calculations" Crystals 13, no. 8: 1269. https://doi.org/10.3390/cryst13081269
APA StyleQin, F., Hou, B., Hu, K., Niu, J., & Zhang, D. (2023). Investigation of the High-Pressure Behaviors of Amblygonite by Single-Crystal X-ray Diffraction, Raman Spectroscopy, and DFT Calculations. Crystals, 13(8), 1269. https://doi.org/10.3390/cryst13081269




