Effect of a Long-Range Dislocation Pileup on the Atomic-Scale Hydrogen Diffusion near a Grain Boundary in Plastically Deformed bcc Iron
Abstract
:1. Introduction
2. Computer Model Setup
3. Simulation Results
3.1. The Dislocation Pileup-Induced Internal Stress near a H-Charged GB
3.2. H Atom Diffusion near the Slip–GB Intersection
3.3. H Diffusion Heterogeneity and Its Dependence on Local Stresses
4. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ossai, C. Advances in asset management techniques: An overview of corrosion mechanisms and mitigation strategies for oil and gas pipelines. Int. Sch. Res. Netw. 2012, 2012, 570143. [Google Scholar] [CrossRef]
- Beachem, C. A new model for hydrogen-assisted cracking (hydrogen embrittlement). Met. Trans. 1972, 3, 437–451. [Google Scholar] [CrossRef]
- Birnbaum, H.; Sofronis, P. Hydrogen-enhanced localized plasticity—A mechanism for hydrogen related fracture. Mater. Sci. Eng. A 1994, 176, 191–202. [Google Scholar] [CrossRef]
- Ferreira, P.; Robertson, I.; Birnbaum, H. Hydrogen effects on the interaction between dislocations. Acta Mater. 1998, 46, 1749–1757. [Google Scholar] [CrossRef]
- Kacher, J.; Robertson, I. Quasi-four-dimensional analysis of dislocation interactions with grain boundaries in 304 stainless steel. Acta Mater. 2012, 60, 6657–6672. [Google Scholar] [CrossRef]
- Kacher, J.; Robertson, I. In situ and tomographic analysis of dislocation/grain boundary interactions in alpha-titanium. Philos. Mag. 2014, 94, 814–829. [Google Scholar] [CrossRef]
- Guo, Y.; Collins, D.; Tarleton, E.; Hofmann, F.; Tischler, J.; Liu, W.; Xu, R.; Wilkinson, A.; Britton, T. Measurement of stress fields near a grain boundary exploring blocked arrays of dislocations in 3D. Acta Mater. 2015, 96, 229–236. [Google Scholar] [CrossRef]
- Andani, M.; Lakshmanan, A.; Sundararaghavan, V.; Allison, J.; Misra, A. Estimation of micro-Hall-Petch coefficients for prismatic slip system in Mg-4Al as a function of grain boundary parameters. Acta Mater. 2022, 226, 117613. [Google Scholar] [CrossRef]
- Lynch, S. Interpreting hydrogen-induced fracture surfaces in terms of deformation processes: A new approach. Scr. Mater. 2011, 65, 851–854. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Eisenlohr, P.; Bieler, T.; Crimp, M.; Mason, D. Twin nucleation by slip transfer across grain boundaries in commercial purity titanium. Metall. Mater. Trans. A 2010, 41, 421. [Google Scholar] [CrossRef]
- Kacher, J.; Eftink, B.; Cui, B.; Robertson, I. Dislocations interactions with grain boundaries. Curr. Opin. Solid State Mater. Sci. 2014, 18, 227–243. [Google Scholar] [CrossRef]
- Robertson, I.M.; Sofronis, P.; Nagao, A.; Martin, M.; Wang, S.; Gross, D.; Nygren, K. Hydrogen embrittlement understood. Metall. Mater. Trans. A 2015, 46, 2323–2341. [Google Scholar] [CrossRef]
- Kimizuka, H.; Ogata, S. Slow diffusion of hydrogen at a screw dislocation core in α-iron. Phys. Rev. B 2011, 84, 024116. [Google Scholar] [CrossRef]
- Sanchez, J.; Fullea, J.; Andrade, M.; De Andres, P. Ab initio molecular dynamics simulation of hydrogen diffusion in α-iron. Phys. Rev. B 2010, 81, 132102. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Zhu, J.H.; Wu, H.H. Molecular dynamics studies of the grain-size dependent hydrogen diffusion coefficient of nanograined Fe. Int. J. Hydrogen Energy 2021, 46, 5842–5851. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W. Atomic mechanism and prediction of hydrogen embrittlement in iron. Nat. Mater. 2013, 12, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Ouyang, B.; Curtin, W.; Song, J. Atomistic investigation of the influence of hydrogen on dislocation nucleation during nanoindentation in Ni and Pd. Acta Mater. 2016, 116, 364–369. [Google Scholar] [CrossRef]
- Yavas, D.; Phan, T.; Xiong, L.; Hebert, K.; Bastawros, A. Mechanical degradation due to vacancies produced by grain boundary corrosion of steel. Acta Mater. 2020, 200, 471–480. [Google Scholar] [CrossRef]
- Huang, S.; Chen, D.; Song, J.; McDowell, D.; Zhu, T. Hydrogen embrittlement of grain boundaries in nickel: An atomistic study. npj Comput. Mater. 2017, 3, 28. [Google Scholar] [CrossRef]
- Song, J.; Curtin, W. Mechanisms of hydrogen-enhanced localized plasticity: An atomistic study using alpha-Fe as a model system. Acta Mater. 2014, 68, 61–69. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Y.; Huang, M.; Zhao, L.; Liang, S.; Li, Z. Study on hydrogen-affected interaction between dislocation and grain boundary by MD simulation. Comput. Mater. Sci. 2021, 196, 110562. [Google Scholar] [CrossRef]
- Jin, Z.; Gumbsch, P.; Albe, K.; Ma, E.; Lu, K.; Gleiter, H.; Hahn, H. Interactions between non-screw lattice dislocations and coherent twin boundaries in face-centered cubic metals. Acta Mater. 2008, 56, 1126–1135. [Google Scholar] [CrossRef]
- Chassagne, M.; Legros, M.; Rodney, D. Atomic-scale simulation of screw dislocation-coherent twin boundary interaction in Al, Au, Cu, and Ni. Acta Mater. 2011, 59, 1456–1463. [Google Scholar] [CrossRef]
- Wang, J. Atomistic simulations of dislocation pileup: Grain boundaries interactions. J. Mater. 2015, 67, 1515–1525. [Google Scholar] [CrossRef]
- Szajewski, B.; Curtin, W. Analysis of spurious image forces in atomistic simulations of dislocations. Model. Simul. Mater. Sci. Eng. 2015, 23, 025008. [Google Scholar] [CrossRef]
- Sofronis, P.; McMeeking, R. Numerical analysis of hydrogen transport near a blunting crack tip. J. Mech. Phys. Solid 1989, 37, 317–350. [Google Scholar] [CrossRef]
- Liang, Y.; Sofronis, P. Micromechanics and numerical modeling of the hydrogen-particle-matrix interaction in nickel-base alloys. Model. Simul. Mater. Sci. Eng. 2003, 11, 523–551. [Google Scholar] [CrossRef]
- Novak, P.; Yuan, R.; Somerday, B.; Sofronis, P.; Ritchie, R. A statistical, physical-based, micro-mechanical model of hydrogen-induced intergranular fracture in steel. J. Mech. Phys. Solids 2010, 58, 206–226. [Google Scholar] [CrossRef]
- Oriani, R. The diffusion and trapping of hydrogen in steels. Acta Metall. 1970, 18, 147–157. [Google Scholar] [CrossRef]
- Sofronis, P.; Liang, Y.; Aravas, N. Hydrogen induced shear localization of the plastic flow in metals and alloys. Eur. J. Mech. A/Solids 2001, 20, 857–872. [Google Scholar] [CrossRef]
- Barrera, O.; Tarleton, E.; Tang, H.; Cocks, A. Modelling the coupling between hydrogen diffusion and the mechanical behaviour of metals. Comput. Mater. Sci. 2016, 122, 219–228. [Google Scholar] [CrossRef]
- Zirkle, T.; Costello, L.; McDowell, D. Crystal plasticity modeling of hydrogen and hydrogen-related defects in initial yield and plastic flow of single-crystal stainless steel 316 L. Metall. Mater. Trans. A 2021, 52, 3961–3977. [Google Scholar] [CrossRef]
- Asano, S.; Otsuka, R. The lattice hardening due to dissolved hydrogen in iron and steel. Scr. Mater. 1976, 10, 1015–1020. [Google Scholar] [CrossRef]
- Abraham, D.; Altstetter, C. The effect of hydrogen on the yield and flow stress of an austenitic stainless steel. Met. Trans. A 1995, 26, 2849–2858. [Google Scholar] [CrossRef]
- Matsui, H.; Kimura, H.; Moriya, S. The effect of hydrogen on the mechanical properties of high purity iron I. Softening and hardening of high purity iron by hydrogen charging during tensile deformation. Mat. Sci. Eng. 1979, 40, 207–216. [Google Scholar] [CrossRef]
- Matsui, H.; Kimura, H.; Kimura, A. The effect of hydrogen on the mechanical properties of high purity iron III. The dependence of softening on specimen size and charging current density. Mat. Sci. Eng. 1979, 40, 227–234. [Google Scholar] [CrossRef]
- Moriya, S.; Matsui, H.; Kimura, H. The effect of hydrogen on the mechanical properties of high purity iron II. Effect of quenched-in hydrogen below room temperature. Mat. Sci. Eng. 1979, 40, 217–226. [Google Scholar] [CrossRef]
- Eastman, J.; Heubaum, N.; Matsumoto, T.; Birnbaum, H. The effect of hydrogen on the solid solution strengthening and softening of nickel. Acta Metall. 1982, 30, 1579–1586. [Google Scholar] [CrossRef]
- Meyers, S.; Baskes, M.; Birnbaum, H.; Corbett, J.; DeLeo, G.; Estreicher, S.; Haller, E.; Jena, P.; Johnson, N.; Kirchheim, R.; et al. Hydrogen interactions with defects in crystalline solids. Rev. Mod. Phys. 1992, 64, 559–617. [Google Scholar] [CrossRef]
- Ilin, D.; Saintier, N.; Olive, J.; Abgrall, R.; Aubert, I. Simulation of hydrogen diffusion affected by stress-strain heterogeneity in polycrystalline stainless steel. Int. J. Hydrogen Energy 2014, 39, 2418–2422. [Google Scholar] [CrossRef]
- Charles, Y.; Nguyen, H.; Gasperini, M. Comparison of hydrogen transport through pre-deformed synthetic polycrystals and homogeneous samples by finite element analysis. Int. J. Hydrogen Energy 2017, 42, 20336–20350. [Google Scholar] [CrossRef]
- Abdolvand, H. Progressive modelling and experimentation of hydrogen diffusion and precipitation in anisotropic polycrystals. Int. J. Plast. 2019, 116, 39–61. [Google Scholar] [CrossRef]
- Arnaudov, N.; Kolyshkin, A.; Weihe, S. Micromechanical modeling of fatigue crack initiation in hydrogen atmosphere. Mech. Mater. 2020, 149, 103557. [Google Scholar] [CrossRef]
- Hassan, U.; Govind, K.; Hartmaier, A. Micromechanical modelling of coupled crystal plasticity and hydrogen diffusion. Philos. Mag. 2019, 99, 92–115. [Google Scholar] [CrossRef]
- Hussein, A.; Krom, A.; Dey, P.; Sunnardianto, G.; Moultos, O.; Walters, C. The effect of hydrogen content and yield strength on the distribution of hydrogen in steel: A diffusion coupled micromechanical FEM study. Acta Mater. 2021, 209, 116799. [Google Scholar] [CrossRef]
- Tondro, A.; Taherijam, M.; Abdolvand, H. Diffusion and redistribution of hydrogen atoms in the vicinity of localized deformation zones. Mech. Mater. 2023, 177, 104544. [Google Scholar] [CrossRef]
- Oh, C.; Kim, Y.; Yoon, K. Coupled analysis of hydrogen transport using ABAQUS. J. Solid Mech. Mater. Eng. 2010, 4, 908–917. [Google Scholar] [CrossRef]
- Barrera, O.; Bombac, D.; Chen, Y.; Daff, T.; Galindo-Nava, E.; Gong, P.; Haley, D.; Horton, R.; Katzarov, I.; Kermode, J.; et al. Understanding and mitigating hydrogen embrittlement of steels: A review of experimental, modelling and design progress from atomistic to continuum. J. Mater. Sci. 2016, 53, 6251–6290. [Google Scholar]
- Diaz, A.; Alegre, J.; Cuesta, I. Coupled hydrogen diffusion simulation using a heat transfer analogy. Int. J. Mech. Sci. 2016, 115–116, 360–369. [Google Scholar] [CrossRef]
- Rimoli, J.; Ortiz, M. A three-dimensional multiscale model of intergranular hydrogen-assisted cracking. Philos. Mag. 2010, 90, 2939–2963. [Google Scholar] [CrossRef]
- Wu, Q.; Zikry, M. Prediction of diffusion assisted hydrogen embrittlement failure in high strength martensitic steels. J. Mech. Phys. Solids 2015, 85, 143–159. [Google Scholar] [CrossRef]
- Pu, C.; Gao, Y.; Wang, Y.; Sham, T. Diffusion-coupled cohesive interface simulations of stress corrosion intergranular cracking in polycrystalline materials. Acta Mater. 2017, 136, 21–31. [Google Scholar] [CrossRef]
- Benabou, L. Coupled stress-diffusion modelling of grain boundary seggregation and dynamic embrittlement in a copper alloy. Model. Simul. Mater. Sci. Eng. 2019, 27, 045007. [Google Scholar] [CrossRef]
- Valverde-Gonzalez, A.; Martinez-Paneda, E.; Quintanas-Corominas, A.; Reinoso, J.; Paggi, M. Computational modelling of hydrogen assisted fracture in polycrystalline materials. Int. J. Hydrogen Energy 2022, 47, 32235–32251. [Google Scholar] [CrossRef]
- Chakraborty, A.; Lebensohn, R.; Capolungo, L. Coupled chemo-mechanical modeling of point-defect diffusion in a crystal plasticity fast Fourier transform framework. J. Mech. Phys. Solids 2023, 173, 105190. [Google Scholar] [CrossRef]
- Kumar, A.; Mahajan, D. Hydrogen distribution in metallic polycrystals with deformation. J. Mech. Phys. Solids 2020, 135, 103776. [Google Scholar] [CrossRef]
- Xiong, L.; Deng, Q.; Tucker, G.; McDowell, D.; Chen, Y. A concurrent scheme for passing dislocations from atomistic to continuum domains. Acta Mater. 2012, 60, 899–913. [Google Scholar] [CrossRef]
- Xu, S.; Payne, T.; Chen, H.; Liu, Y.; Xiong, L.; Chen, Y.; McDowell, D. PyCAC: The concurrent atomistic-continuum simulation environment. J. Mater. Res. 2018, 33, 857–871. [Google Scholar] [CrossRef]
- Xu, S.; Xiong, L.; Chen, Y.; McDowell, D. Validation of the concurrent atomistic-continuum method on screw dislocation/stacking fault interactions. Crystals 2017, 7, 120. [Google Scholar] [CrossRef]
- Xiong, L.; Chen, Y. Multiscale modeling and simulation of single-crystal MgO through an atomistic field theory. Int. J. Solids Struct. 2009, 46, 1448–1455. [Google Scholar] [CrossRef]
- Ji, R.; Phan, T.; Chen, Y.; McDowell, D.; Xiong, L. A finite-temperature coarse-grained atomistic approach for understanding the kink-controlled dynamics of micrometer-long dislocations in high-Peierls-barrier materials. MRS Commun. 2022, 12, 1077–1085. [Google Scholar] [CrossRef]
- Xiong, L.; Chen, Y.; Lee, J. Modeling and simulation of boron-doped nanocrystalline silicon carbide thin film by a field theory. J. Nanosci. Nanotechnol. 2009, 9, 1034. [Google Scholar] [CrossRef]
- Su, Y.; Phan, T.; Xiong, L.; Kacher, J. Multiscale computational and experimental analysis of the slip-GB reactions: In-situ high-resolution electron backscattered diffraction and concurrent atomistic-continuum simulations. Scr. Mater. 2023, 232, 115500. [Google Scholar] [CrossRef]
- Peng, Y.; Ji, R.; Phan, T.; Gao, W.; Levitas, V.; Xiong, L. An atomistic-to-microscale computational analysis of the dislocation pileup-induced local stresses near an interface in plastically deformed two-phase materials. Acta Mater. 2022, 226, 117663. [Google Scholar] [CrossRef]
- Xu, Y.; Joseph, S.; Karamched, P.; Fox, K.; Rugg, D.; Dunne, F.P.; Dye, D. Predicting dwell fatigue life in titanium alloys using modeling and experiments. Nat. Commun. 2020, 11, 5868. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Che, R.; Xiong, L.; Chen, Y.; McDowell, D.L. A quasistatic implementation of the concurrent atomistic-continuum method for fcc crystals. Int. J. Plast. 2015, 72, 91–126. [Google Scholar] [CrossRef]
- Eshelby, J.; Frank, F.; Nabarro, F. XLI. The equilibrium of linear arrays of dislocations. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1951, 42, 351–364. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 252, 561–569. [Google Scholar]
- Vasoya, M.; Kondori, B.; Benzerga, A.A.; Needleman, A. Energy dissipation rate and kinetic relations for Eshelby transformations. J. Mech. Phys. Solids 2020, 136, 103699. [Google Scholar] [CrossRef]
- Meng, F.; Du, J.P.; Shinzato, S.; Mori, H.; Yu, P.; Matsubara, K.; Ishikawa, N.; Ogata, S. General-purpose neural network interatomic potential for the alpha-iron and hydrogen binary system: Toward atomic-scale understanding of hydrogen embrittlement. Phys. Rev. Mater. 2021, 5, 113606. [Google Scholar] [CrossRef]
- Peng, Y. An Atomistic-to-Mesocale Prediction of the Complex Reaction between the Plastic Flow and the Interfaces in Heterogeneous Materials. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2023. [Google Scholar]

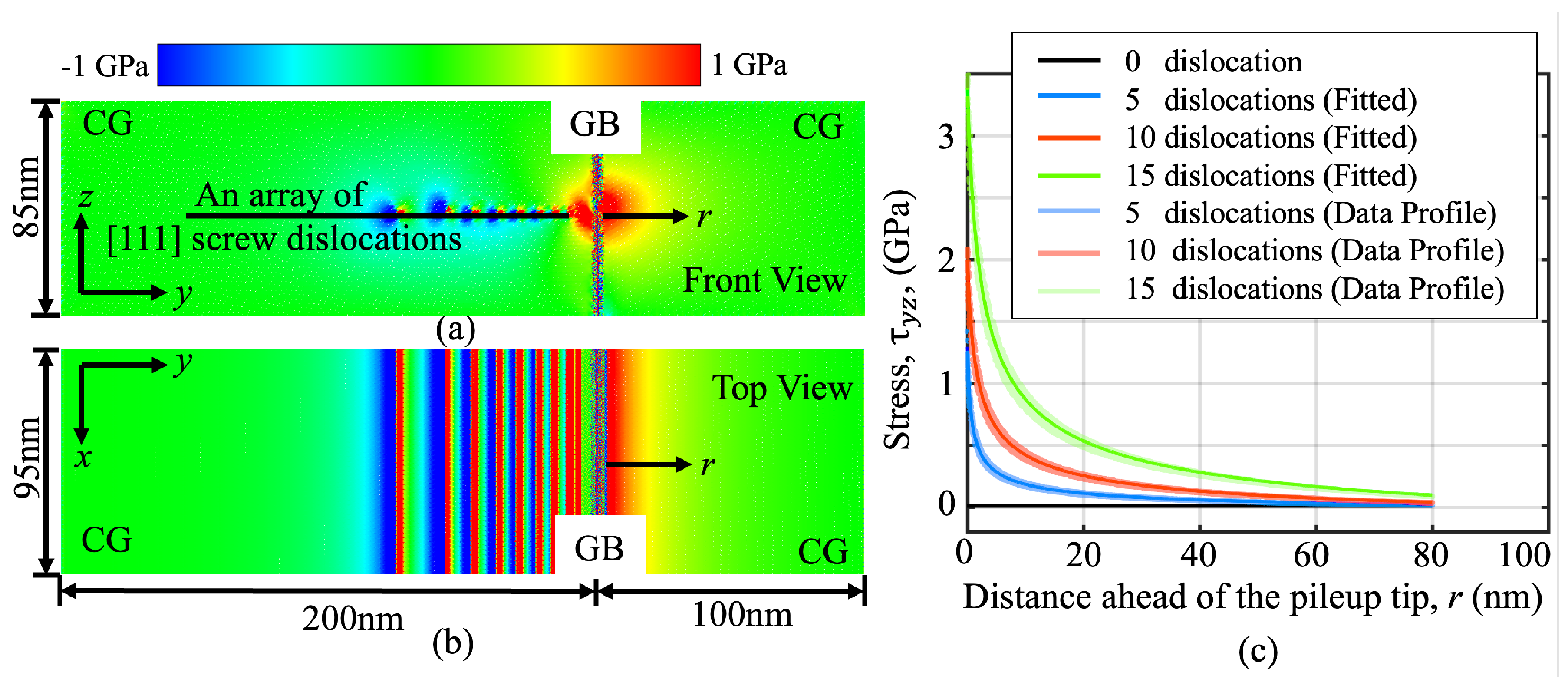

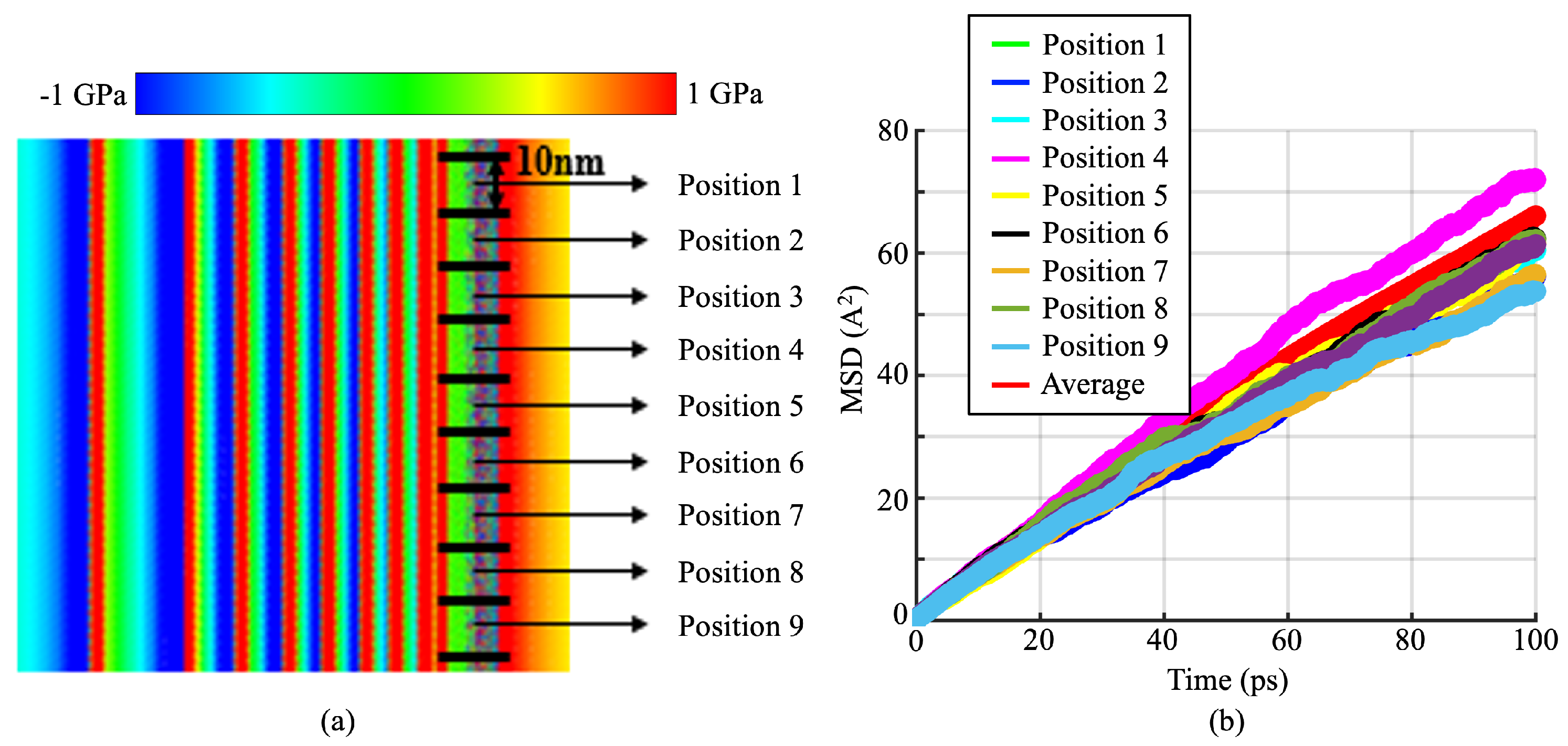
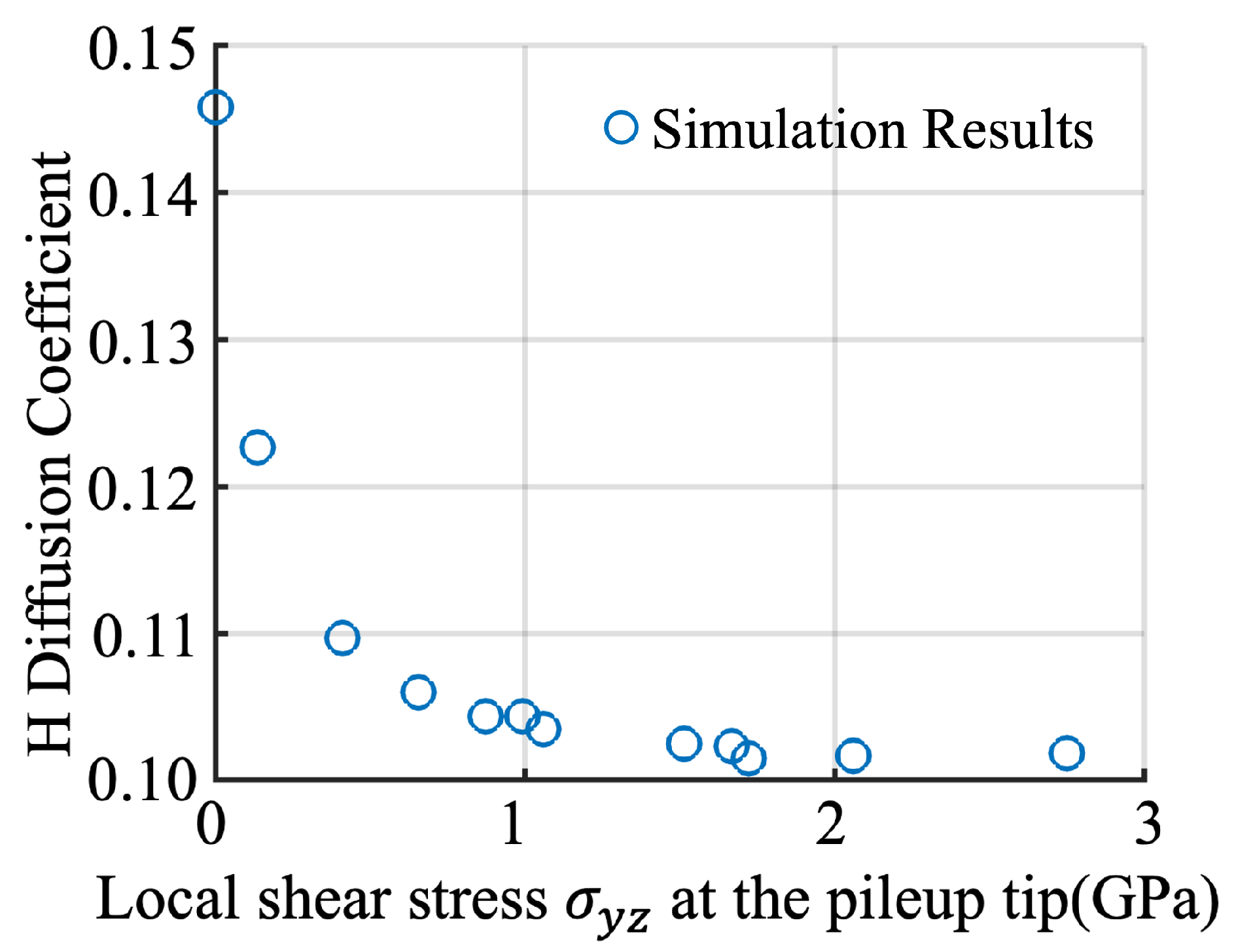
| Number of Dislocations | 0 | 5 | 10 | 15 |
| Stress Intensity Factor(GPa/m) | 0 | 0.82 | 1.98 | 4.12 |
| H Diffusion Coefficient | 0.146 | 0.110 | 0.104 | 0.102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Ji, R.; Phan, T.; Chen, X.; Zhang, N.; Xu, S.; Bastawros, A.; Xiong, L. Effect of a Long-Range Dislocation Pileup on the Atomic-Scale Hydrogen Diffusion near a Grain Boundary in Plastically Deformed bcc Iron. Crystals 2023, 13, 1270. https://doi.org/10.3390/cryst13081270
Peng Y, Ji R, Phan T, Chen X, Zhang N, Xu S, Bastawros A, Xiong L. Effect of a Long-Range Dislocation Pileup on the Atomic-Scale Hydrogen Diffusion near a Grain Boundary in Plastically Deformed bcc Iron. Crystals. 2023; 13(8):1270. https://doi.org/10.3390/cryst13081270
Chicago/Turabian StylePeng, Yipeng, Rigelesaiyin Ji, Thanh Phan, Xiang Chen, Ning Zhang, Shuozhi Xu, Ashraf Bastawros, and Liming Xiong. 2023. "Effect of a Long-Range Dislocation Pileup on the Atomic-Scale Hydrogen Diffusion near a Grain Boundary in Plastically Deformed bcc Iron" Crystals 13, no. 8: 1270. https://doi.org/10.3390/cryst13081270
APA StylePeng, Y., Ji, R., Phan, T., Chen, X., Zhang, N., Xu, S., Bastawros, A., & Xiong, L. (2023). Effect of a Long-Range Dislocation Pileup on the Atomic-Scale Hydrogen Diffusion near a Grain Boundary in Plastically Deformed bcc Iron. Crystals, 13(8), 1270. https://doi.org/10.3390/cryst13081270






